International Journal of Nonferrous Metallurgy
Vol.2 No.3(2013), Article ID:33922,5 pages DOI:10.4236/ijnm.2013.23017
Kinetics Analyzing of Direction Reduction on Manganese Ore Pellets Containing Carbon
Key Laboratory for Ferrous Metallurgy and Resources Utilization of Ministry of Education, Wuhan University of Science and Technology, Wuhan, China
Email: *tale-2002@163.com
Copyright © 2013 Bo Zhang, Zheng-Liang Xue. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 27, 2013; revised March 28, 2013; accepted April 8, 2013
Keywords: Kinetics Model; Manganese Ore Pellets Containing Carbon; Self-Reduction
ABSTRACT
Using high temperature carbon tube furnace, reduction of manganese ore pellets containing carbon was investigated. The reaction was divided into two stages at five minutes after reaction, and the kinetics model of reduction process was established. The experimental results showed that, the reaction rate in the earlier stage was controlled by the chemical reactions between FeO, MnO and carbon reductant, and the activation energy was 28.85 KJ/mol. In the later stage, as the carbon reductant replaced by CO, the reaction rate was controlled by CO-diffusing in solid products, and the corresponding activation energy was 86.56 KJ/mol. Reaction rate of the later stage was less than the earlier one.
1. Introduction
The technology of hot metal pretreatment and less slag steelmaking are mature increasingly since 1990s. The basic theory and industrial application of direct alloying by manganese ore under the condition of less slag steelmaking were researched systematically and deeply, by the main steel enterprises and research institutes in Japan [1-4]. In China, however, due to the condition restriction of hot metal pretreatment and the less slag steelmaking, the yield of manganese fluctuates in 5% - 25% generally, so that the economic benefits is not obvious. Therefore, the new technology of direct alloying by manganese ore in converter needs to be explored. In this paper, based on the new process of direct alloying using manganese oxide composite pellets in converter which were proposed by Xue Zheng Liang et al. [5], the kinetics model was established according to the kinetics analyzing in reduction process, which provided a theoretical basis for direct alloying by manganese ore.
2. Experimental Research Method
The manganese ore grain were crushed to 10 mm size collected from the mine, and then heated to 1000˚C and kept for 30 min for high temperature treatment under the protection of N2, in which water of crystallization and carbonate fully decomposed. The chemical composition of manganese ore after high temperature treatment is shown in Table 1.
The samples were pressed to φ10 × 10 mm cylindrical with the well mixed and wetted manganese ore, which were crushed to −0.074 mm after high temperature treatment and reductant by using sodium silicate. The samples were stoved for reservation. The C/O molar ratio is expressed by the molar proportion of C in carbon black and O in manganese oxide and ferric oxide, calculate the amount of carbon black according to the C/O molar ratio is 1.0.
Reduction experiments were carried out in 25 kW high temperature carbon tube furnace with rapid heating function, and the internal diameter of carbon tube furnace is 70 mm. Corundum crucible was built-in furnace in Ar protection and increased temperature within furnace. When the predetermined temperature reached, cylindrical samples were put in (sample weight is approximately 100 g). The reaction temperature is set as 1823 K 1873 K and 1923 K, and reaction time is set as 3 min, 4 min, 5 min, 10 min and 15 min. Corundum crucible and specimen

Table 1. Raw Material Components, %.
were hanged out from the high temperature zone quickly, and cooled under an Ar atmosphere. The reduction degree was calculated according to the weight change of the pellets and the detection result of chemical composition.
3. Reduction Kinetics Analysis
3.1. Reduction Degree Calculation
The oxygen loss ratio of the reduction is calculated through the following formula according to the chemical test results before and after the reaction:
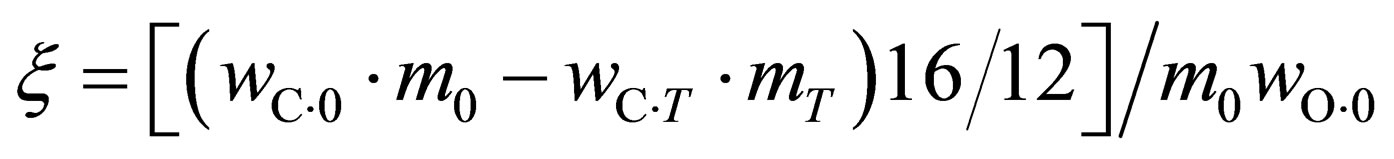 (1)
(1)
where, m0 and mT are the weight before and after the reaction, respectively,  ,
, 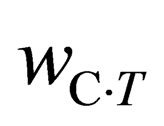 are carbon content in the sample before and after the reaction, respectively, and
are carbon content in the sample before and after the reaction, respectively, and  is oxygen content of the sample before the reaction.
is oxygen content of the sample before the reaction.
3.2. Reduction Reaction
The oxide reduction rate  is calculated according to the above Equation (1), thus the relationship between reduction rate and reduction time under different temperature can be achieved as shown in Figure 1.
is calculated according to the above Equation (1), thus the relationship between reduction rate and reduction time under different temperature can be achieved as shown in Figure 1.
Figure 1 shows that the reduction rate of the carbonmanganese pellets had little changed with the reduction temperature increases. The change of reduction rate in the slope can be divided into two phases, the initial reduction rate is relatively fast, while after 5 minutes reduction rate decreases and eventually gentle. Therefore, it is possible to divide reduction process into two stages at 5 minutes, earlier stage and later stage. At the earlier stage, the reaction can be considered as a typical direct reduction process between reductant carbon and FeO, MnO due to the lack of CO; at the later stage, as the solid
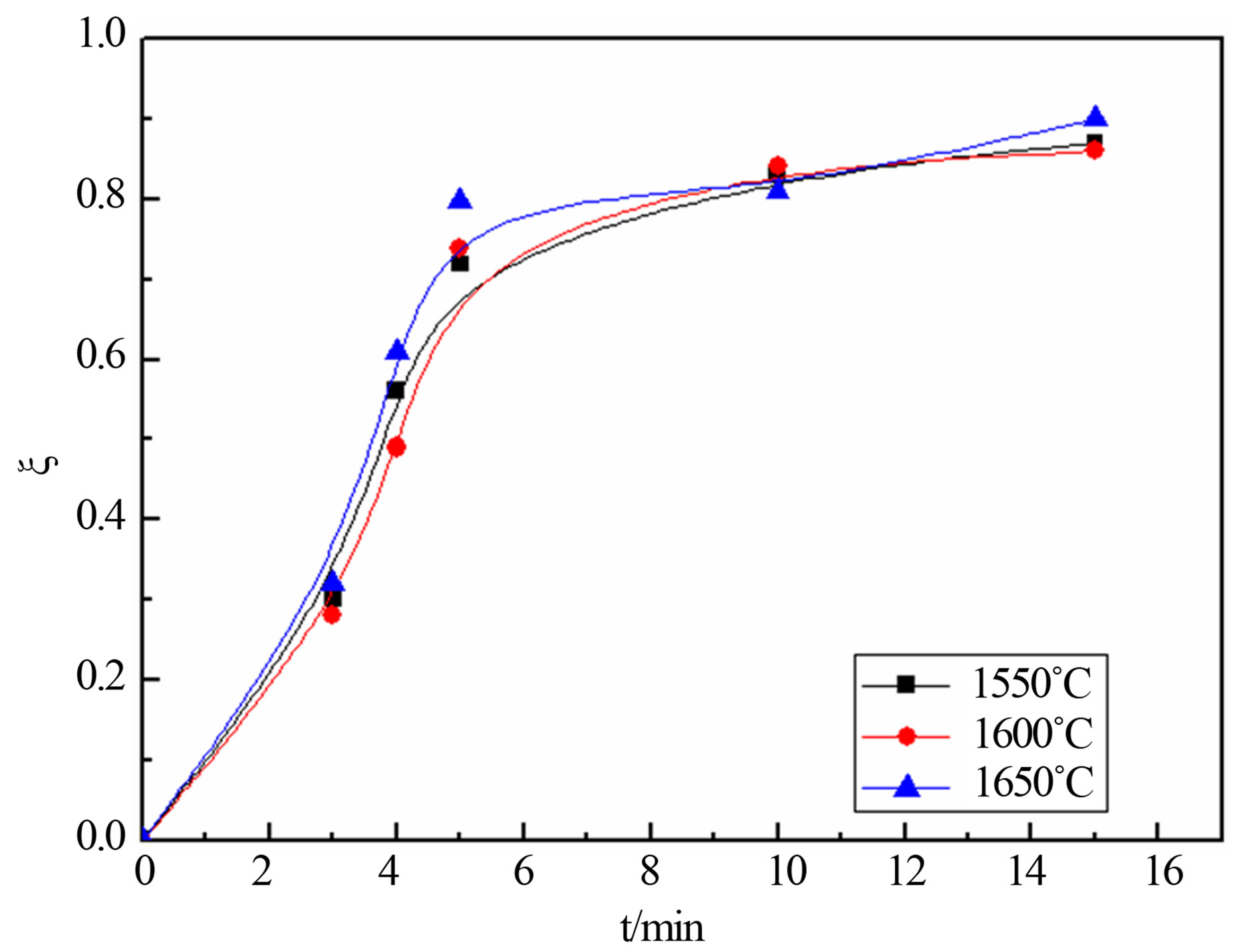
Figure 1. degree reduction-time curve at different temperatures.
products increases, reductant carbon cannot be contacted with the oxide, so CO substituted carbon to take part in reduction reaction with FeO and MnO.
4. Kinetics of Reduction Reaction
4.1. Kinetic Model of the Earlier Stage
In the earlier stage, the reduction rate depends on the contact area between the solid carbon and the metal oxide [6], which can be expressed as follows:
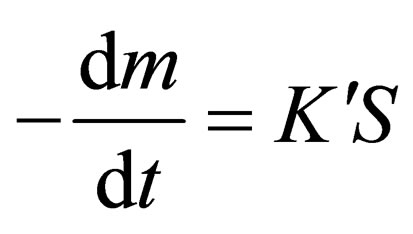 (3)
(3)
where, 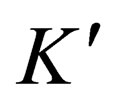 is a constant; t is reaction time;m is ore quality,
is a constant; t is reaction time;m is ore quality,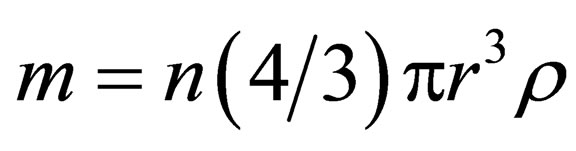 ; S is the surface area of slag,
; S is the surface area of slag,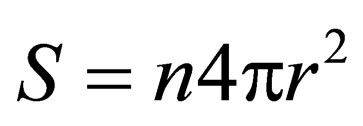 .
.
Substitution of m and s into Equation (3) can be obtained Equation (4) as follows:
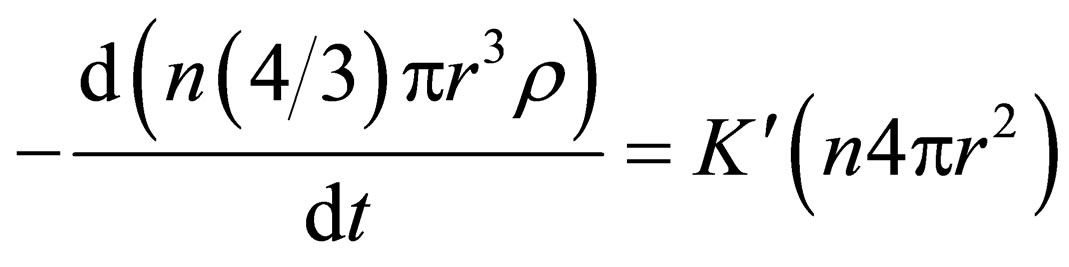 (4)
(4)
Hence:
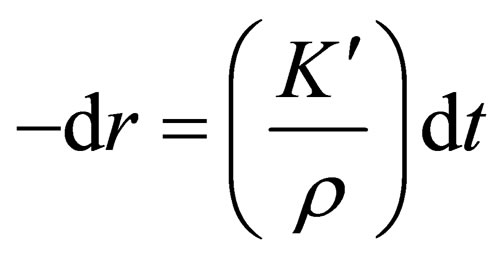 (5)
(5)
By taking the integral for t of the Equation (5):
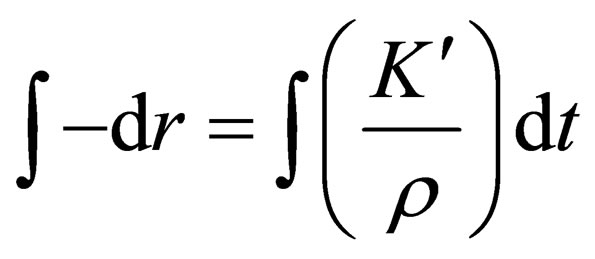 ,so a new equation can be obtained as follows:
,so a new equation can be obtained as follows:
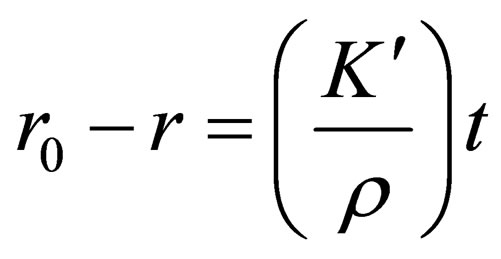 (6)
(6)
And the reduction rate can be expressed as:
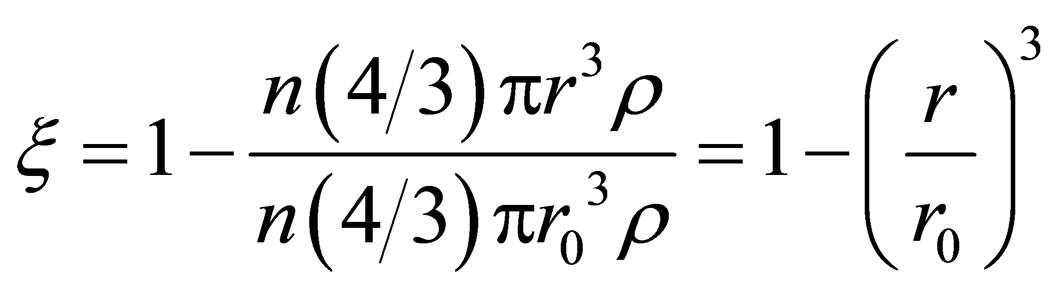 (7)
(7)
So:
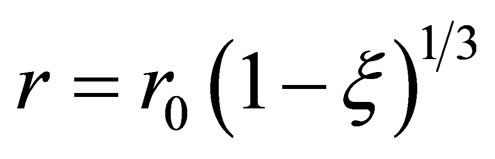 (8)
(8)
Equation (9) can be obtained by substituting Equation (8) into Equation (6).
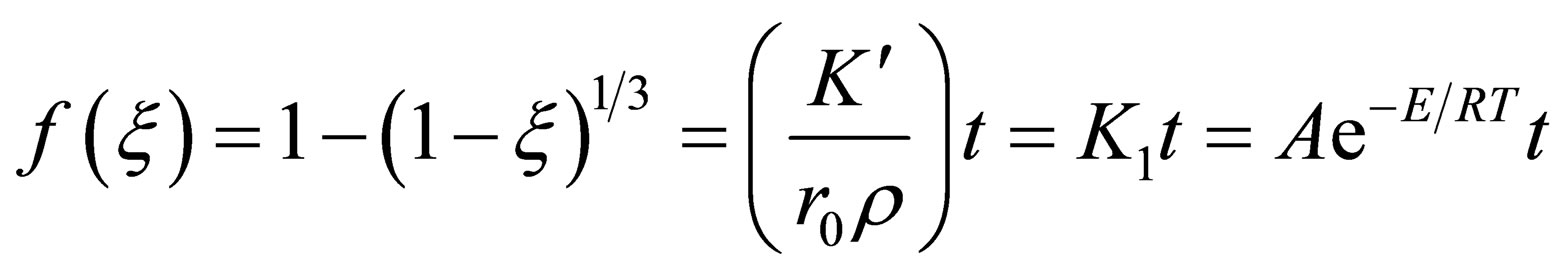 (9)
(9)
where, 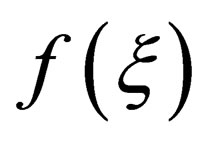 is only related with
is only related with ;
;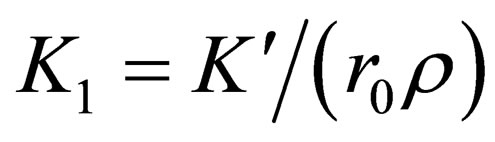 , is rate constant; A is the frequency factor; E is the apparent activation energy; T is the absolute temperature. Both sides of the equation can be obtained for t differential:
, is rate constant; A is the frequency factor; E is the apparent activation energy; T is the absolute temperature. Both sides of the equation can be obtained for t differential:
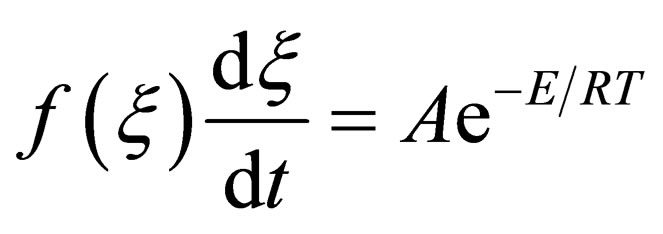 (10)
(10)
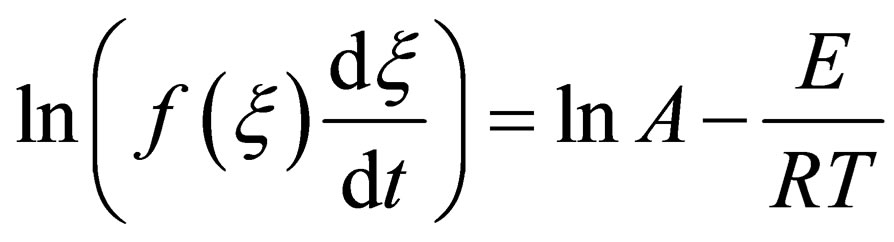 (11)
(11)
According to the test data, calculate the value of k in the respective temperature, and taking the average, the relation between lnk and T–1 is plotted in Figure 2. It is clearly that lnk and T–1 has a very good linear correlation, and we can calculate the frequency factor A = 0.0038 and the apparent activation energy E = 28.85 KJ/mol can be achieved. Therefore, in the restored earlier stage, the pellet reduction kinetics equation can be expressed as:
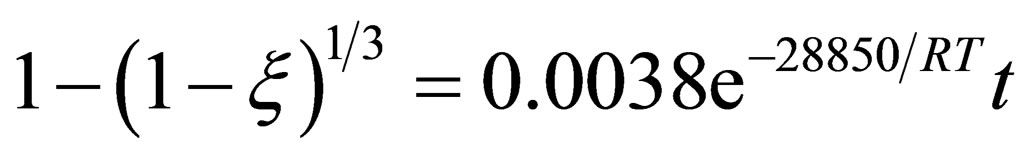 (12)
(12)
4.2. Kinetic Model of the Later Stage
In the later stage of reaction, the reaction rate mainly depends on CO diffusion through the metal and the solid product layer, so the diffusion step is restrictive step. The mainly practical equations on diffusion control are Jander Equation (13) and Ginstling-Brounshtein Equation [7,8] (14).
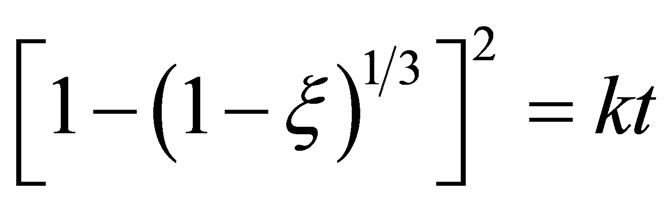 (13)
(13)
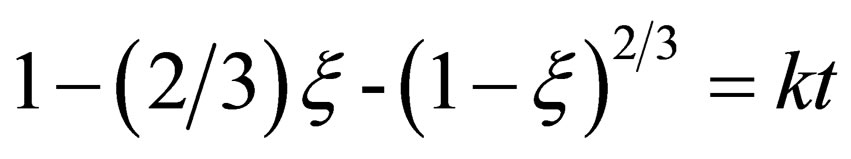 (14)
(14)
where:  is the reduction rate of the pellets; k is the reaction rate constant; t is the reaction time. The relation between lnk and T–1 is plotted in Figure 3, it can be seen from the figure that the lnk does not have a good linear correlation with T–1. Therefore, it is not suitable to calculate the kinetic parameters in the later stage of reduction by this method, and has some limitations to calculate the reaction kinetic through the above methods.
is the reduction rate of the pellets; k is the reaction rate constant; t is the reaction time. The relation between lnk and T–1 is plotted in Figure 3, it can be seen from the figure that the lnk does not have a good linear correlation with T–1. Therefore, it is not suitable to calculate the kinetic parameters in the later stage of reduction by this method, and has some limitations to calculate the reaction kinetic through the above methods.
In recent years, Zhou Guozhi [9] deduced a new dynamic model for gas-solid phase reaction system (as shown in Equation (15)), which assumed the diffusion process as the reaction restrictive step, the new model introduced a new concept of characteristic time to analysis reaction rate, and expressed analytically the
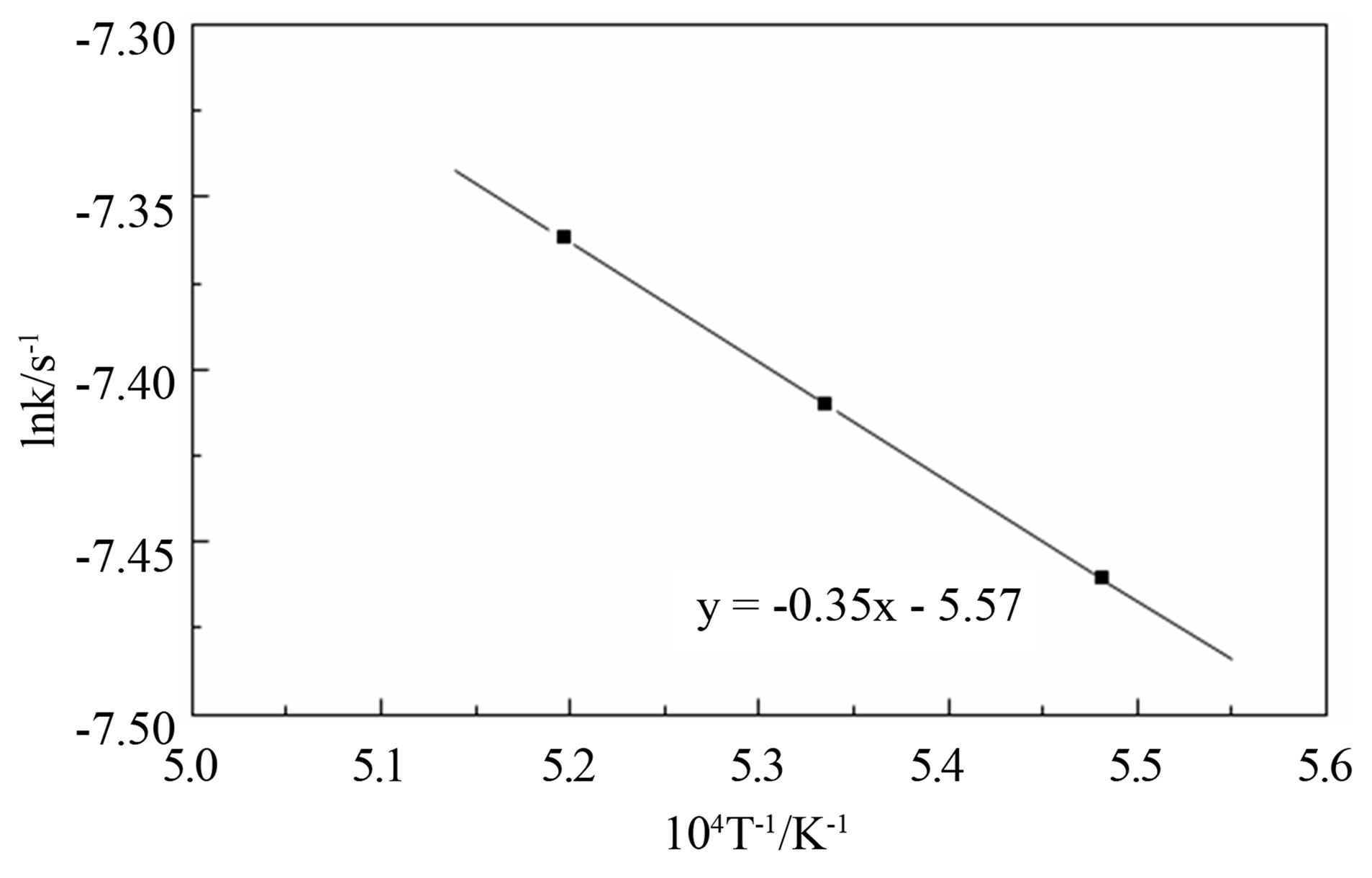
Figure 2. Restore the initial kinetic parameters illustrations.
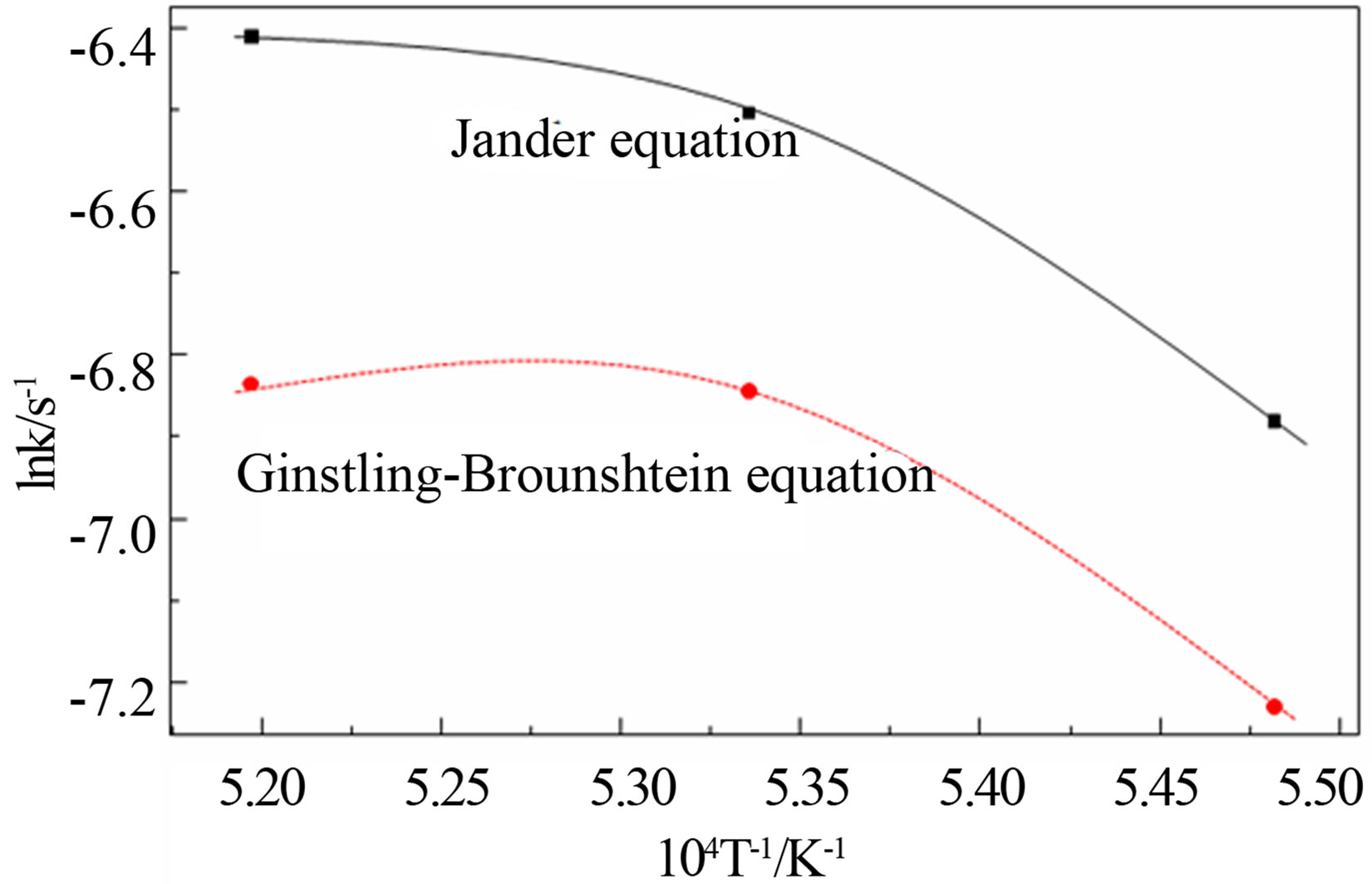
Figure 3. Kinetic parameters in the late period of reduction.
impact of factors on gas-solid phase reaction kinetics (temperature, pressure, and particle radius, etc.) through a simple explicit function. According to the research of Cheng GongWei [10] and Liu SongLi [6], it shown that the model had a characteristic of simple, accurate and practical, and had very good guidance on dynamics analysis that based on carbon pellet reduction process.
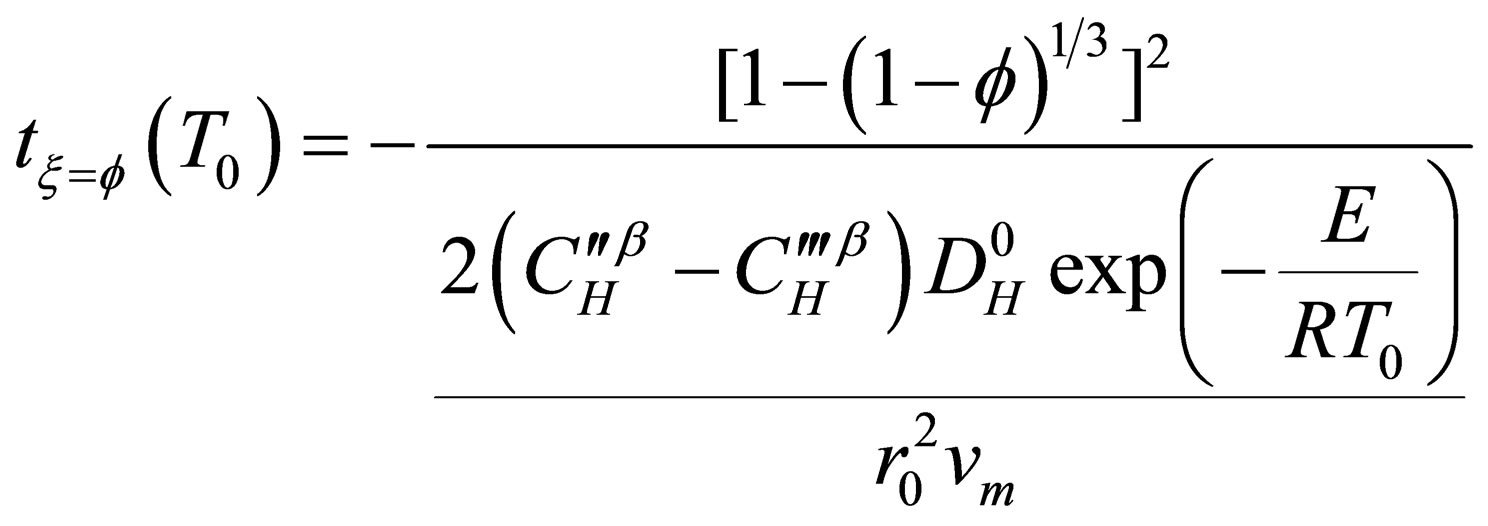 (15)
(15)
where: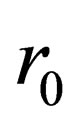 is the radius of particles;
is the radius of particles; 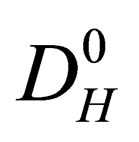 is the diffusion constant of the diffusion materials;
is the diffusion constant of the diffusion materials;  is the diffusion concentration of total diffusion materials of the resultant phase in vapor balance;
is the diffusion concentration of total diffusion materials of the resultant phase in vapor balance; 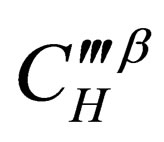 is the diffusion concentration of diffusion materials of the resultant phase close to the unreacted materials interface;
is the diffusion concentration of diffusion materials of the resultant phase close to the unreacted materials interface; 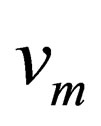 is correlation coefficient that depends on the material reaction;
is correlation coefficient that depends on the material reaction; 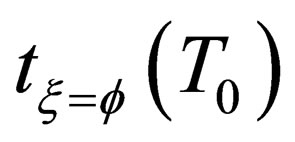 is the characteristic time of the reaction, and the physical meaning is the time that the reaction fraction reach to
is the characteristic time of the reaction, and the physical meaning is the time that the reaction fraction reach to 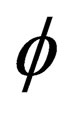 while T = T0 ,it will decrease with the increasing of temperature and pressure and the decrease of particle diameter, it can be used to show the speed of the reaction.
while T = T0 ,it will decrease with the increasing of temperature and pressure and the decrease of particle diameter, it can be used to show the speed of the reaction.
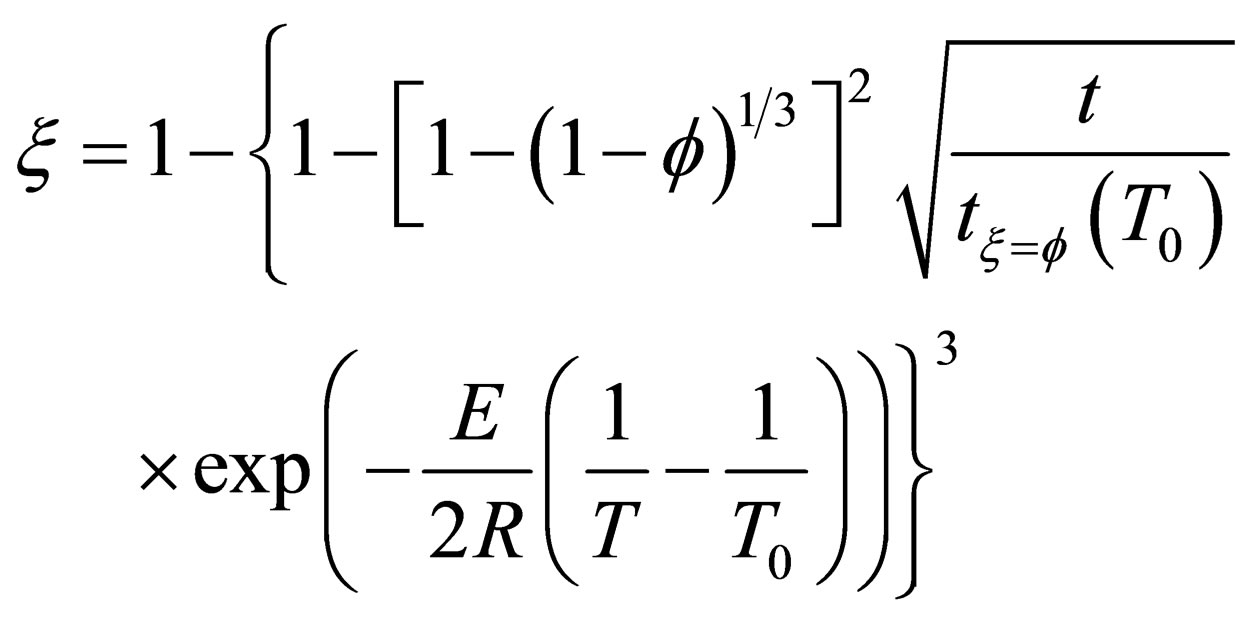 (16)
(16)
Where, E is the activation energy; R is the gas constant; T is the absolute temperature; rate; t is reaction time. The reaction time is constant, the equation of activation energy can be calculated from measuring T1 and T2,  and
and .
.
 (17)
(17)
According to the test results, the activation energy E can be calculated under different temperature in the following three groups in Table 2.
When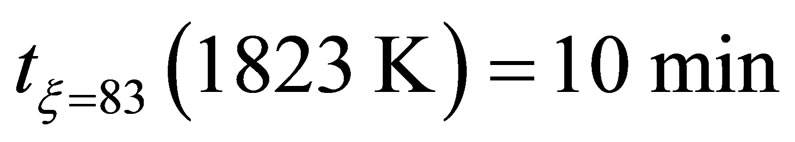 , it can be found that the reduction kinetics equation of pellets in the later stage of reaction can be expressed as fellow:
, it can be found that the reduction kinetics equation of pellets in the later stage of reaction can be expressed as fellow:
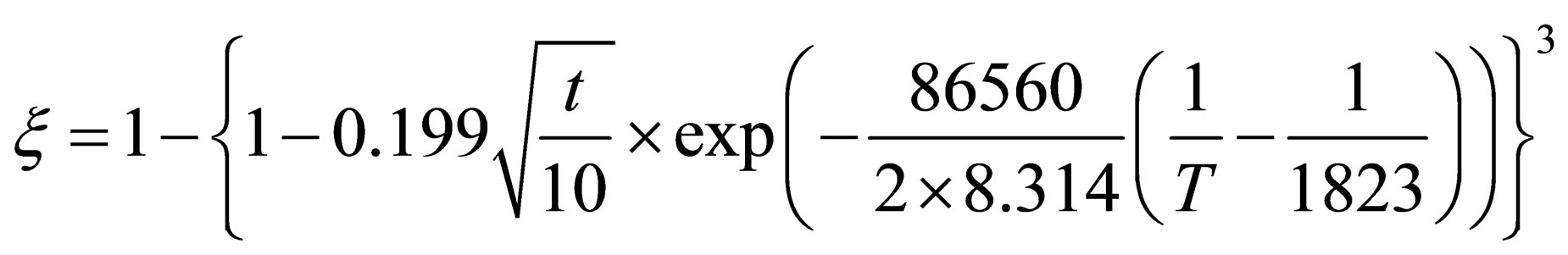 (18
(18
5. Kinetics Model Result and Discussion
United Equation (12) and Equation (18), predicting the reduction degree changes of carbon-bearing pellet respectively in temperature T = 1823 K, T = 1873 and T = 1923 K. The forecast result and the actual experimental data are shown in the follows.
Figure 4 shows that calculated value and actual value agrees well under the 1823 K, 1873 K and 1923 K. In the earlier stage of reaction, calculated value was higher than the actual value slightly. This may be related with the experimental conditions and operation. The samples were putted into the furnace when the temperature rise to a predetermined, so there are need some preheating time before, and carbon and metal oxide also need certain incubation period to begin to reaction. But model calculation is in a kind of ideal state. So calculated value is more than test value at the beginning. The later reaction activation energy is far less than the reaction activation energy of earlier, so reaction rate of the later stage is less than the earlier one.
6. Conclusion
According to the reduction results of carbon manganese ore pellets, reduction process can be divided into two stages. The reaction of direct contact of carbon reductant and FeO, MnO are the main reaction during the earlier stage of reduction process. Reaction rate is controlled by chemical reaction and its kinetics equation is: 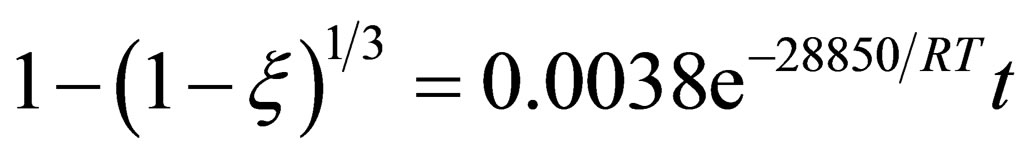 . CO replace carbon as the reducing agent at the later of reaction. Reaction rate at the later stage of the reaction is controlled by CO-diffusion reaction in solid products and its kinetics equation is:
. CO replace carbon as the reducing agent at the later of reaction. Reaction rate at the later stage of the reaction is controlled by CO-diffusion reaction in solid products and its kinetics equation is:

Table 2. activation energy in different temperature ranges.
 (a)
(a)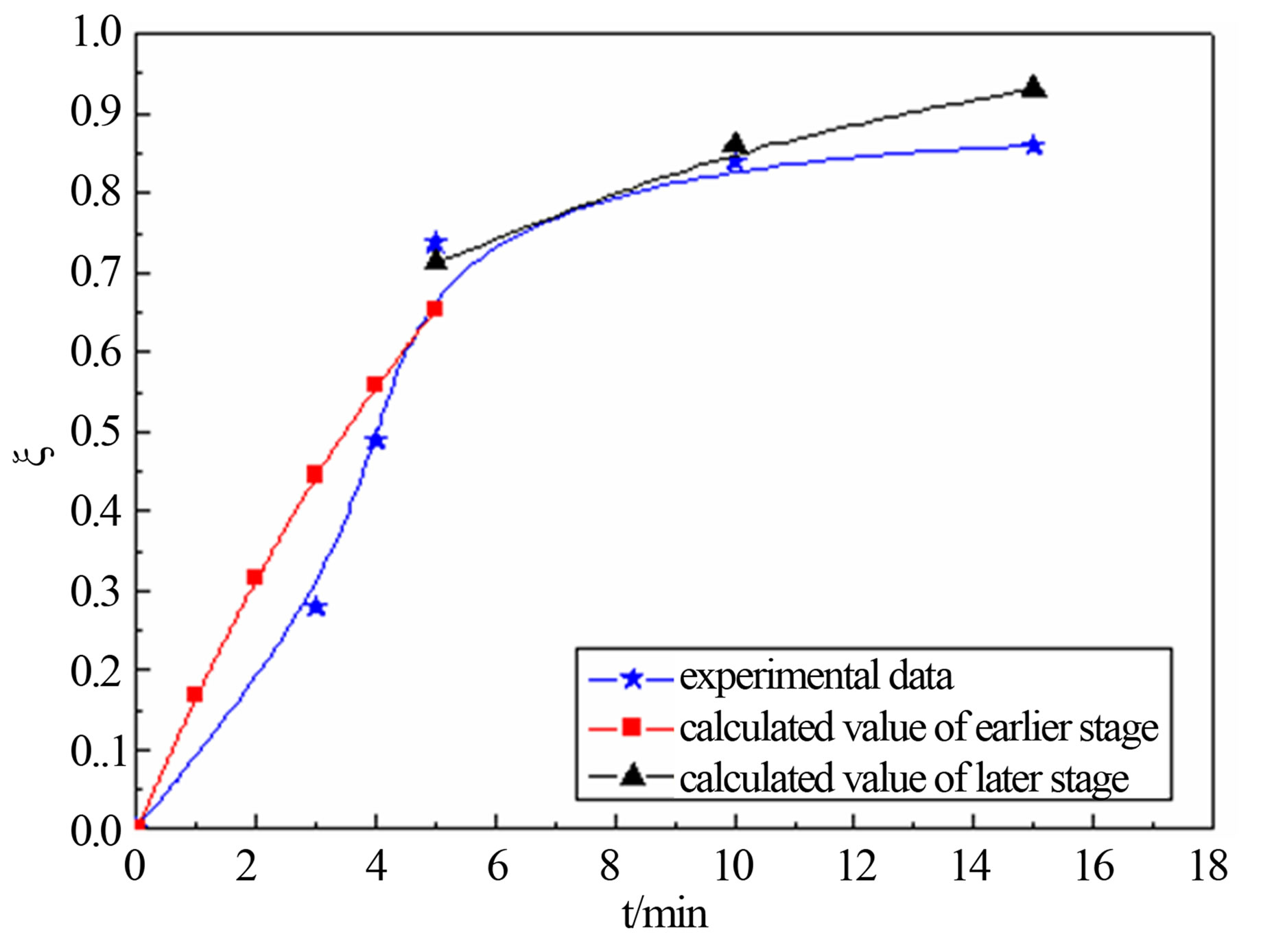 (b)
(b)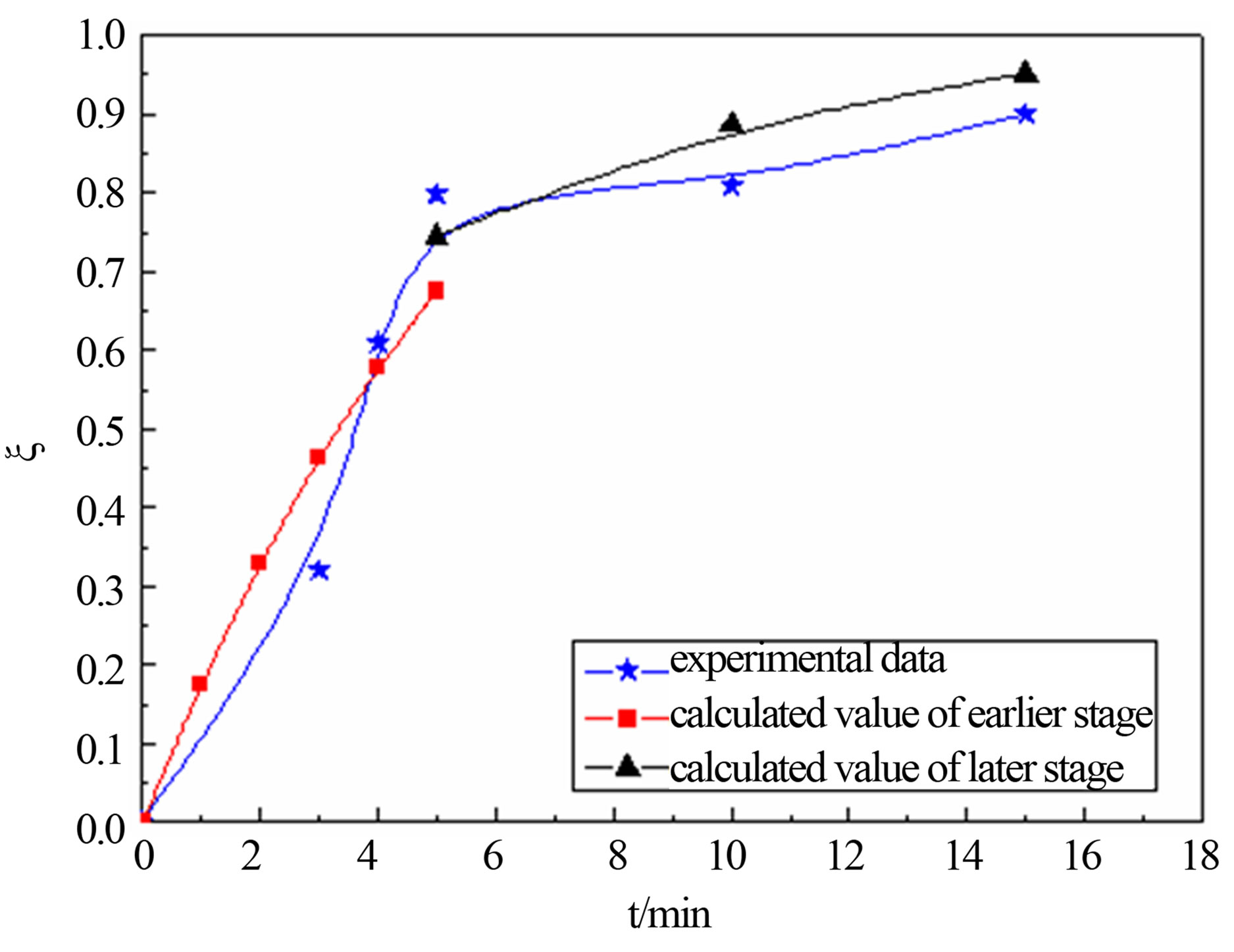 (c)
(c)
Figure 4. calculated values comparison of actual value for degree reduction-time curve at different temperatures; (a) 1823 K; (b) 1873 K; (c) 1923 K.
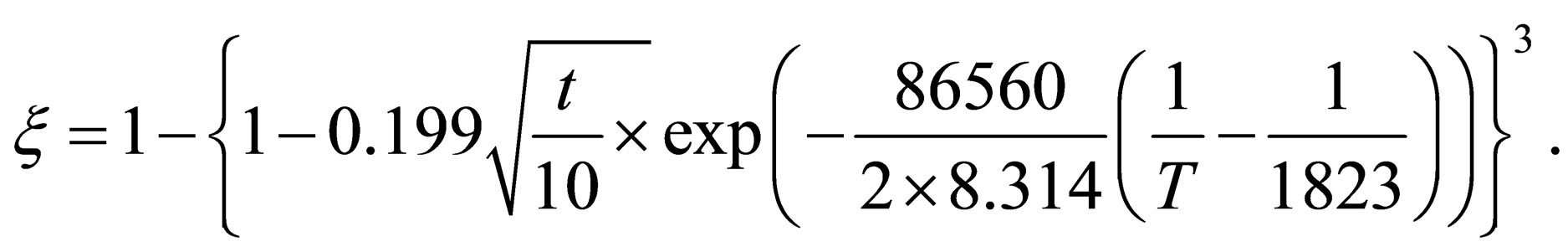
REFERENCES
- L. Z. Shan, et al., “Industrialization of a New Steelmaking Process Utilizing Hot Metal Pretreatment and Smelting Reduction,” Iron & Steel, Vol. 2, 1988, pp. 64-71.
- A. M. H. Jin, “Improvement of Mn Yield in Less Slag Blowing at BOF by Use of Sintered Ore,” Iron & Steel, Vol. 8, 1993, pp. 45-51.
- R. S. Li, Y. M. Feng and G. Z. Wei, “Application of Poor Manganese Ore in the Converter Steelmaking Process,” Steelmaking, Vol. 20, No. 1, 2004, pp. 13-15.
- Z. L. Meng and X. U. Yang, “Discussion on Manganese Alloyed in Top-Blown Converter,” Laiwu Steel Technology, Vol. 4, No. 8, 2002, pp. 33-35.
- Z. L. Xue, Y. Yu, W. Wang, et al., “Steelmaking Process with Manganese Oxide Composite Mass of Direct Alloying by the Combined Blowing Converter,” Invention Patent: ZL201010245102.1.
- S. L. Liu and C. G. Bai, “Kinetics of Vanadium-Titanium Iron Concentrate Pellets Containing Carbon Direct Reduction,” Journal of iron and Steel Research, Vol. 4, No. 23, 2011, pp. 5-8.
- W. Jander, “Reactions in the Solid State at High Temperatures,” Zeitschrift für Anorganische und Allgemeine Chemie, Vol. 163, No. 1-2, 1927, pp. 1-30. doi:10.1002/zaac.19271630102
- A. M. Ginstling and V. I. Brounshtein, “Concerning the Diffusion Kinetics of Reactions in Spherical Particles,” J. Appl. ChcilL USSR, Vol. 23, 1950, pp. 1327-1338.
- K. C. Chou, Q. Li, Q. Lin, et al., “Kinetics of Absorption and Desorption of Hydrogen in Alloys Powder,” International Journal of Hydrogen Energy, Vol. 30, 2005, pp. 301-309. doi:10.1016/j.ijhydene.2004.04.006
- H. W. Cheng and X. G. Lu, “Reduction Kinetics Mechanism of Carbon Containing Pellets,” Chinese Journal of Rare Earths, Vol. 8, No. 26, 2008, pp. 103-108.
NOTES
*Corresponding author.

