Computational Water, Energy, and Environmental Engineering
Vol.3 No.3(2014), Article
ID:48232,9
pages
DOI:10.4236/cweee.2014.33013
Coupling Analysis of Disaster Bearing Capacity of Urban Lifeline System Based on Brittleness Entropy
Wei Huang1,2*, Xinnan Zhang1,2, Chenmin Li3, Fengzhou Wang3, Zhenli Ma3
1College of Hydrology and Water Resources, Hohai University, Nanjing, China
2National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, Hohai University, Nanjing, China
3College of Computer and Information Engineering, Hohai University, Nanjing, China
Email: *wei.huang923@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 15 May 2014; revised 26 June 2014; accepted 25 July 2014
ABSTRACT
Urban or regional disaster bearing capacity mainly depends on the disaster bearing capacity of lifeline systems. In the analysis of disaster bearing capacity evaluation of lifeline system, we should not only investigate the complexity, balance and reliability of network characteristics, but also consider the relation between each subsystem. A new brittleness entropy of city disaster vulnerability associated coupling analysis method is proposed based on the brittleness of complex system theory. Correlation characteristics are reflected and evaluated in the brittle link entropy and the whole lifeline system, and then the vulnerability of city lifeline system can be quantified in flood scenarios. As a result of the coupling analysis and calculation, power system has the greatest effect among other subsystems. Because the key factors and influence of water supply system are uncertainties, the water supply system work or supply should be restored first after the disaster. The results show that the method can provide the basis for the optimization of system management, and control the repair work after disaster and coordination between subsystems.
Keywords:Disaster Bearing Capacity, Lifeline System, System Coupling, Brittleness Entropy

1. Introduction
Modern city is a complex system which includes the collection of social, economic, natural, cultural and other factors. It is not only the gathering place of human social life and economic development, but also a high incidence of natural disasters and the risk of accidents [1] . Due to the special function and spatial structure, the degree of modernization and competitiveness of a city is not only to consider the social status of the city’s economic environment and development, but also to consider the city’s disaster bearing capacity under the natural disasters condition. An important feature of the modern city is highly dependent on a variety of lifeline systems. Urban lifeline system is an important part of the modern city, which is the necessary system to maintain the urban functions. The stability of lifeline system has a very important significance for maintaining the normal operation of the modern city. Therefore, lifeline system for natural disasters capacity can well reflect the city’s capacity to natural disasters.
The features of the city will produce an urban disaster’s chain reaction, and will affect a wider area, resulting in the loss of many within the system and multi-level effects. Nowadays, the disaster bearing capacity of urban lifeline system focuses on the extreme disaster of small probability, such as earthquakes. Wang has studied the seismic response of seismic waves under urban network. Ohtake [2] assessed the earthquakes damage of the water supply network in artificial disturbance. Shinozuka [3] has studied lifeline earthquake engineering based on GIS technology in Memphis. O’Rourke [4] proposed the assessment framework of complex seismic response lifeline systems based on interdependence between lifeline systems. But, there are less studies of the urban lifeline system’s impact assessment beyond the urban flood scenario. Just through the value of network connectivity reliability to illustrate the performance of disaster bearing of lifeline system [5] , description and analysis of the relationship between mutual connection and influence of each subsystem in lifeline system was of insufficiency. According to the theory of complex system brittleness, this paper proposed an analyzed method about the lifeline system’s coupling degree under the condition of disaster based on the brittleness entropy.
2. Brittleness Theory of Complex Systems
The complex system is that a large number of interwoven coupled components exist in the system, the internal structure is complex, and the overall behavior shows uncertainty and nonlinear, not through the local characteristics of the system, the system of concrete or abstract description of the whole system characteristics [6] -[8] . When the complex system scale is increasing, coupling internal subsystems become more closely, self-organizing capacity will drop the system itself. Once the system is in the internal and external factors, the breakdown of one or several subsystems will cause a sudden collapse of the whole system; this phenomenon is called the brittleness of complex system. The brittleness of complex system theory is the main mechanism of the collapse of complex system. Through the analysis of complex system brittleness process, it can be find out the complex system collapsed by subsystem. The system is easy to collapse because the destruction of the system structure is brittle. During the process of system collapse, the degree of disorder is increased. Entropy as a measure of the degree of disorder system, it can be used as the performance index of brittleness.
2.1. Basic Theory of Entropy
The concept of entropy is first put forward in the thermodynamic field to refer to a state of thermodynamic system. It is used to describe the degree system disorders [9] . Since the beginning of 1960’s, the concepts of Boltzmann entropy, Shannon entropy, and Keermogeluofu entropy had been proposed. Shannon suggested “entropy” to represent the uncertainty of information systems in 1948, and derived a numerical value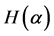 , which can reasonably estimate the uncertainty degree of random test. The specific expression of
, which can reasonably estimate the uncertainty degree of random test. The specific expression of 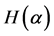 is given as follows:
is given as follows:
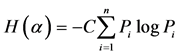 (1)
(1)
where  is the entropy of
is the entropy of![]() ,
, 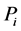 represents the probability of the result of various incompatible trials.
represents the probability of the result of various incompatible trials. 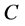 is the coefficient which value depends on the unit of measure.
is the coefficient which value depends on the unit of measure.
The entropy theory can be used to carry on the research on the uncertainty of complex system because the complex system has uncertainty characteristics [10] -[12] . When the complex system is running, the exchange energy or substances will take place among the subsystems and between the system and environment. If the exchange system makes the system itself in more disordered state, it may lead to the breakdown of the key subsystem, and even lead to the collapse of the whole system finally. Therefore the fundamental method to avoid the collapse of the system is adding to the negative entropy flow to suppress internal complex system entropy through the exchange of energy, information or material with the outside world.
2.2. Brittleness Risk Entropy
On the brittleness of complex system in the process of analysis, subsystem collapse is due to the influence of subsystem from the surrounding of the association, which caused the brittle events, and eventually led to the brittle [13] . But the complexity of system internal system level relations and the correlation structure is extremely complex, and the state variables of each system are very complex and uncertain. How to observe information into brittleness factors from each sub system will help us to grasp the brittleness factors of each subsystem information.
We can use ![]() to express the relationship between the brittleness of system changes over time:
to express the relationship between the brittleness of system changes over time:

 (2)
(2)
Assume that the system at the ![]() time, when
time, when![]() , which means the brittle link of subsystem is closer, when
, which means the brittle link of subsystem is closer, when![]() , which means the brittle link of subsystem is decreasing, when
, which means the brittle link of subsystem is decreasing, when![]() , which means the brittle link of subsystem remains constant state relatively.
, which means the brittle link of subsystem remains constant state relatively.
Brittle relationship structure and brittle potential function of traditional analysis calculation, or the system test, in various brittle conditions to obtain the data, and use various statistical methods to calculate, are unrealistic, or costly. Connection degree in set pair analysis is a very important concept. Using the concept of connection degree, in a complex system brittleness unit, can be used to analyze the brittleness contact degree among the subsystems.
According to the set pair theory, the brittle link between systems can use state between brittle with once, opposite degree, volatility to describe [14] [15] . The degree of brittleness in the transmission and diffusion between the subsystems are associated with brittle link function between subsystems. Takeing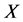 ,
,![]() as two brittle subsystems, when the subsystem
as two brittle subsystems, when the subsystem 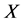 collapses by interference, it means in the state vectors of subsystem
collapses by interference, it means in the state vectors of subsystem ![]() relating to the brittleness, there is at least one
relating to the brittleness, there is at least one 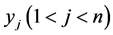 under the influence of brittle link and catastrophic changes, namely, the subsystem
under the influence of brittle link and catastrophic changes, namely, the subsystem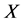 ,
, ![]() is called the same brittleness, when the functions of subsystems relating to their state vectors reached the scope out-of-work, which probability value is
is called the same brittleness, when the functions of subsystems relating to their state vectors reached the scope out-of-work, which probability value is![]() .
. ![]() and
and 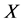 subsystem is a brittle one, its occurrence probability value was
subsystem is a brittle one, its occurrence probability value was![]() . Said the other without any effect on the state of the subsystem
. Said the other without any effect on the state of the subsystem 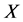 is brittle opposition, its occurrence probability value was
is brittle opposition, its occurrence probability value was![]() , and said the state and trend of the same, subsystem and trend opposite and subsystem
, and said the state and trend of the same, subsystem and trend opposite and subsystem 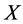 is brittle fluctuation, the probability value is
is brittle fluctuation, the probability value is![]() . The three brittle link probability and 1:
. The three brittle link probability and 1:
![]() (3)
(3)
Combining entropy, brittleness can be defined as brittle syntropy entropy, brittle opposite entropy and brittle fluctuation entropy, and the expressions for the three kinds of entropy:
Brittle syntropy entropy:
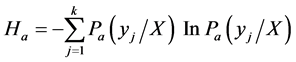 (4)
(4)
Brittle opposite entropy:
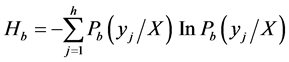 (5)
(5)
Brittle fluctuation entropy:
 (6)
(6)
The subsystem ![]() influenced by
influenced by , should be integrated with a brittle, brittle opposite and brittle fluctuation. When
, should be integrated with a brittle, brittle opposite and brittle fluctuation. When  collapses, the subsystem
collapses, the subsystem ![]() collapses as well, meantime, the brittleness link entropy can be defined.
collapses as well, meantime, the brittleness link entropy can be defined.
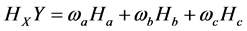 (7)
(7)
![]() ,
, 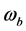 ,
, 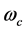 as the weight coefficient of brittle, brittle opposite and same brittle fluctuation. When there is a combination of a certain probability distribution makes
as the weight coefficient of brittle, brittle opposite and same brittle fluctuation. When there is a combination of a certain probability distribution makes 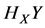 the maximum, the subsystem
the maximum, the subsystem 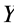 is largest affected by the collapse of
is largest affected by the collapse of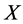 . Similarly, the rest brittle link entropy of subsystems can be defined.
. Similarly, the rest brittle link entropy of subsystems can be defined.
The weight coefficient in Formula (5) can be determined according to relevant methods of the catastrophe theory. Catastrophe theory was put forward by Rene. Thom in 1972 is an emerging mathematical discipline specially studying the continuous changes and internal system of “shock” phenomenon, mainly by means of topology, the singularity and describing various phenomena from the traits of a form of suddenly jumping to radically different another form, which is used to explain the nature and social phenomenon occurring in the phenomenon of “mutation”. Sudden one of the characteristics of complex system’s brittleness is the event, so it can be used for calculation of mutation theory. A core content of catastrophe evaluation is the normalized formula that will evaluate the variables in the system of numerical conversion into the same dimension compare under, layer by layer to the recursive algorithm, and function to get the top target value [16] . For the potential function , all its critical points are set into a balance surface
, all its critical points are set into a balance surface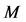 , when
, when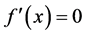 , the equilibrium surface equation can be obtained; When
, the equilibrium surface equation can be obtained; When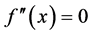 , the singularity set
, the singularity set ![]() of
of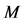 can be obtained. Combining
can be obtained. Combining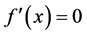 with
with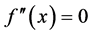 , the divergence equation
, the divergence equation 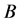 reflecting the state variables with the relationship among control variables in the form of decomposition can be obtained. We can derive corresponding normalization formula according to the potential function and divergence equation of mutation model.
reflecting the state variables with the relationship among control variables in the form of decomposition can be obtained. We can derive corresponding normalization formula according to the potential function and divergence equation of mutation model.
![]() (8)
(8)
Make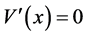 , the equilibrium equation of curved surface
, the equilibrium equation of curved surface :
:
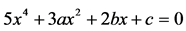 (9)
(9)
Make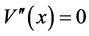 , get its singular set
, get its singular set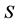 :
:
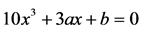 (10)
(10)
Simultaneous equations (9) and (10) elimination![]() , capable of swallowtail catastrophe model normalization equation was obtained:
, capable of swallowtail catastrophe model normalization equation was obtained:

Swallowtail catastrophe progression method considering three control variables, respectively corresponding to the three aspects of the same, volatility and opposition to phylogenetic influence mutation, ![]() ,
, 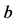 ,
, ![]() is present
is present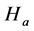 ,
, 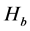 ,
, 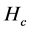 respectively, The weight coefficient
respectively, The weight coefficient![]() ,
, 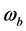 ,
, 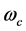 is equal to
is equal to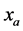 ,
, 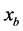 ,
,  respectively, then:
respectively, then:
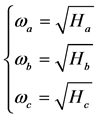 (11)
(11)
In the formula, 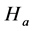 ,
, 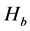 ,
, 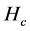 are the absolute value, respectively
are the absolute value, respectively
3. Coupling Analysis of Urban Lifeline Systems
3.1. Interactions in Urban Lifeline Systems
Urban lifeline system usually includes power system, communication system, transportation system, water supply system, drainage system, gas supply system etc. Each subsystem is composed of many interrelated and interaction function nodes, eventually forming a huge urban lifeline system network. Due to that the flood system has a direct influence to the power system, transportation system, communication system, drainage system, gas supply system etc., the first level of the coupling risk conduction layer can be established, that is 1) flood → power system, 2) flood → transportation system, 3) flood → communication system, 4) flood → water supply system, 5) flood → drainage system, 6) flood → gas supply system.
The power system failure will cause the following “conduction path”: 1) Power failure may lead to crisis of urban water supply and drainage system, then can trigger social security issues such as urban environmental pollution and food hygiene, 2) In order to ensure the electricity needs of people who live in the city and important department production, the power supply may be reduced or partly interrupted when the power system was destroyed. The result of communication power was interrupted, 3) Power-down may also lead to urban traffic paralysis, triggering a city station airport congestion and passenger backlog and other social security issues, 4) power-down may lead to urban gas supply disruption, equipment stops running, and increase the security risk of the fire and explosion. Then the second level of the coupling risk conduction layer can be established, that is: 1) flood → power system → water supply system, 2) flood → power system → drainage system, 3) flood → power system → transportation system, 4) flood → power system → communication system, 5) flood → power system → gas supply system.
Similarly, when the transportation system is damaged, it can cause indirectly influence of the electric power system, communication system, water supply, drainage system and gas supply system etc. When the communication system is damaged, it can cause indirectly influence of drainage system and gas supply system. When the water supply system is damaged, it can cause indirectly influence of the power system, drainage system and gas supply system. When the drainage system is damaged, it can cause indirectly influence of the water supply system and gas supply system. When the gas supply system is damaged, it can cause indirectly influence of the power system. An interwoven and interaction coupling risk transmission network of urban lifeline system can be established in the flood scenario. The diagram is as shown Figure 1.
According to the interaction and impact ways of urban lifeline system disasters, the effect type of urban lifeline system can be divided into structural effect, substitution effect and function effect. Combined the structure of Figure 1, the structural effect of urban lifeline system to the city in the connection can be analyzed:
(1) For power system, there are exist the conduct path, which is floods → power systems → transportation systems, floods → power systems → communication systems, floods → power systems → water supply systems, floods → power systems → drainage systems, and floods → power systems → gas supply systems. The tectonic relationship matrix between power system and other subsystem can be expressed.
(2) For transportation system, the conduct path is floods → transportation systems → power systems, floods → transportation systems → communication systems, floods → transportation systems → drainage systems, and floods → transportation systems → gas supply systems. The tectonic relationship matrix between transportation system and other subsystem can be expressed.
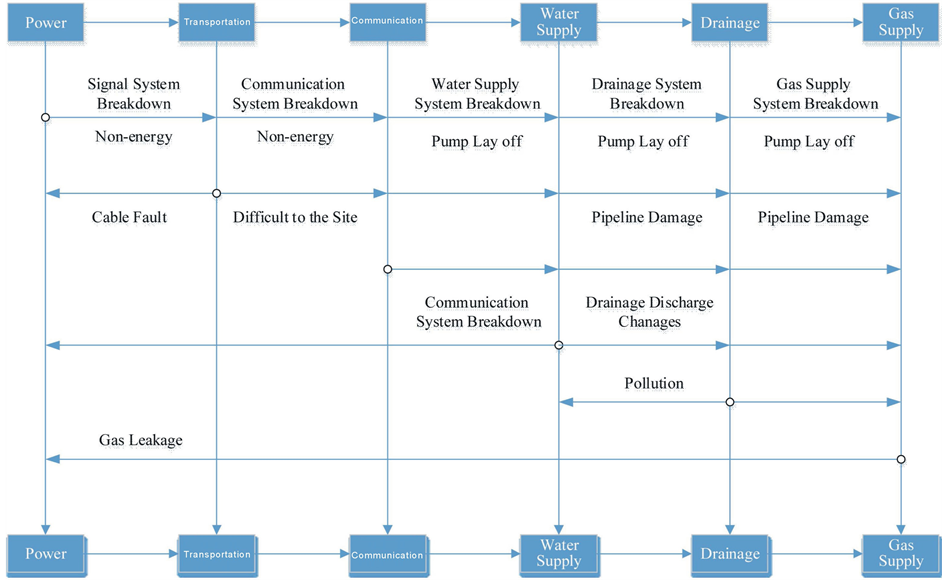
Figure 1. The schematic diagram of coupling risk of city lifeline system.
(3) For communication system, the conduct path is floods → communication systems → water supply systems, floods → communication systems → drainage systems, and floods → communication systems → gas supply systems. The tectonic relationship matrix between communication system and other subsystem can be expressed: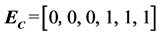 .
.
(4) For water supply system, the conduct path is floods → water supply systems → power systems, floods → water supply systems → drainage systems, and floods → water supply systems → gas supply systems. The tectonic relationship matrix between water supply system and other subsystem can be expressed: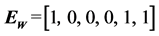 .
.
(5) For drainage system, the conduct path is floods → drainage system → water supply systems, and floods → drainage system → gas supply systems. The tectonic relationship matrix between drainage system and other subsystem can be expressed: .
.
(6) For gas supply system, the conduct path is floods → gas supply system → power systems. The tectonic relationship matrix between gas supply system and other subsystem can be expressed: .
.
The function associated coupling matrix of urban lifeline system in flood scenarios can be expressed as follows:
 (12)
(12)
Analyzing the replace influence of the urban lifeline system: for a power system: floods→power systems→ transportation systems→power systems, which means in the flood situations there is interactional relationship between power system and traffic system. Thus, there is mutual condition in power system as opposed to transport system, which is denoted as 1.
But for floods → power systems → communication systems, there does not exist the influence between power system and communication system. So, the power system with respect to the transportation systems does not have constraints, which can be written as 0.
For water supply system, there exist the conduct paths, which are floods → power systems → water supply systems 1. Then, the power system with respect to the water supply systems has constraints, which can be written as 1.
For drainage system, the conduct path is floods → power systems → drainage system. Then, the power system with respect to the drainage system has no constraints, which can be written as 0.
For gas system, the conduct path is floods → power systems → gas system → power systems. Then, the power system with respect to the gas system has no constraints, which can be written as 0.
The functional contact matrix of power system and other subsystems can be obtained,
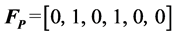
Similarly, the urban lifeline system coupled matrix in the flood scenario can be obtained after the other subsystems’ functional link matrix can be calculated. The results are as follows:
 (13)
(13)
The function associated coupling matrix of urban lifeline system in flood scenarios 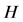 can be expressed as follows:
can be expressed as follows:
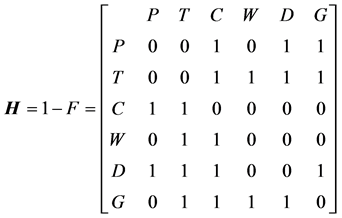 (14)
(14)
3.2. Disaster Bearing Capacity Assessment of Urban Lifeline Systems
According to the main category links between urban lifeline systems and brittleness entropy classification, we can define the tectonic influence of lifeline systems as brittle same entropy, the effect be defined as brittle opposition entropy, and the restore influence of function is defined as brittle entropy fluctuations. The process of computing lifeline system coupling is as follows:
First, the urban lifeline system’s integrated matrix can be constructed based on three coupled matrix:
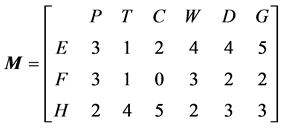 (15)
(15)
then calculated the integrated matrix of each column, and were drawn by the association of five subsystems affect other subsystems:
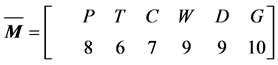 (16)
(16)
then calculated the probability of each subsystem,![]() ,
,![]() ,
,![]() . The probability of power system is shown as follows:
. The probability of power system is shown as follows:

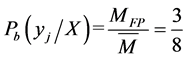
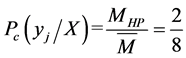
Then we can get the corresponding entropy, 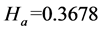 ,
, 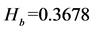 ,
,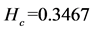 . Similarly, the risk of other subsystems can be obtained entropy values, which is shown in the following table 1.
. Similarly, the risk of other subsystems can be obtained entropy values, which is shown in the following table 1.
The comprehensive risk entropy of the city lifeline system is:![]()
 (17)
(17)
where![]() ,
,  ,
, 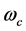 are the weight coefficients by using catastrophe progression method, respectively. The brittle relationship between systems from large to small is as follows: power system, water supply/drainage system, gas supply system, transportation system and communication system, that means power system disasters is contacting with other subsystem in the brittle relationship. Therefore, the top priority in flood risk after the relief effort is to restore the power systems smooth in the city lifeline system. Thereby reducing system failures due to power bring disasters to other lifeline systems by chain-effects.
are the weight coefficients by using catastrophe progression method, respectively. The brittle relationship between systems from large to small is as follows: power system, water supply/drainage system, gas supply system, transportation system and communication system, that means power system disasters is contacting with other subsystem in the brittle relationship. Therefore, the top priority in flood risk after the relief effort is to restore the power systems smooth in the city lifeline system. Thereby reducing system failures due to power bring disasters to other lifeline systems by chain-effects.
4. Conclusion
The problem of lifeline system’s coupling relationship is more difficult to quantify. In this paper, we used the brittleness risk entropy to quantify the interconnectedness of lifeline system, and used the value of 0 - 1 to quantify and indicate the coupling relationship between urban lifeline systems. This method solves the common problem of the existing flood risk systems research that emphasizes the overall risk, rather than the risk of the relevant parts of the internal system. This will contribute to finding “vulnerable areas” easily in the future risk management decision-making process, and taking timely measures to remedy or avoid disaster. It solves the problems which not only subjectively determines its value previously, but also provides basis for the scientific and rational view of the lifeline system’s disaster bearing capacity of quantization, optimization system of organization and management and control of post disaster restoration work. It is a question worth considering for human life which depends on lifeline system.
Acknowledgements
This work is supported by State Natural Sciences Foundation Monumental Projects (No. 41030636), and National Natural Science Foundation of China (No. 51179047).
References
- Zhang J.Q., Norb, O. and Hiokanzu, T. (2006) Integrated Natural Disaster Risk Management: Comprehensive and Integrated Model and Chinese Strategy Choice. Journal of Natural Disasters, 15, 29-37.
- Kimiyasu, O. and Tatsuo, O. (2004) Damage Estimation of the Water Supply Pipelines Buried in Artificially Altered Ground. Proceedings of 13th World Conference on Earthquake Engineering, Vancouer, 1-6 August 2004, 1011-1020.
- Shinozuka, M., Chang, S.E., Eguchi, R.T., Abrams, D.P., Hwang, H.H.M. and Rose, A. (1997) Advances in Earthquake Loss Estimation and Application to Memphis, Tennessee. Earthquake Spectra, 13, 739-758. http://dx.doi.org/10.1193/1.1585978
- O’rourke, T.D., Wang, Y. and Shi P.X. (2004) Advances in Lifeline Earthquake Engineering. Proceedings of 13th World Conference of Earthquake Engineering, Vancouer, 1-6 August 2004, 432-458.
- Lindsay, J. (2003) The Determinants of disaster vulnerability Achieving Sustainable Mitigation through Population Health. Natural Hazards, 28, 291-304.
- Wang, S., Wang Y., Feng J.W. and Du, C. (2012) Complex System Important Node Collapse Control Based on Constraint Entropy. China Safety Science Journal, 5, 10-16.
- Chen, J. and Sun L.F. (2009) Evaluation of Node Importance in Complex Networks. Journal of Southwest Jiao Tong University, 44, 426-429.
- Xu, L.Z., Li, X.F. and Yang, S.X. (2011) Intelligent Information Processing and System Optimization. Intelligent Automation and Soft Computing, 17, 829-833. http://dx.doi.org/10.1080/10798587.2011.10643191
- Li, S.F., Yu, P. and Sun, S.H. (2010) Entropy Weight Based Fuzzy Matter Element Model for Evaluating and Zoning of Regional Flood Disaster Vulnerability. Journal of Natural Disasters, 19, 124-131.
- Wen, R.Z., Tao, X.X. and Xie, L.L. (2000) Earthquake Damage Analysis of Coupling Lifeline Systems. Journal of Natural Disasters, 9, 105-110.
- Guo, Y.J., Guo, Y.P. and Lv, J.Y. (2005) Brittleness of General Systems. Control Theory and Applications, 24, 1-4.
- Huang, W., Zhang, X.N., Zhang, W.T. and Wei. X.D. (2011) An Improved Contract Net Protocol with Multi-Agent for Reservoir Flood Control Dispatch. Journal of Water Resource and Protection, 3, 735-746.http://dx.doi.org/10.4236/jwarp.2011.310084
- Menoni, S. (2011) Chains of Damages and Failures in a Metropolitan Environment: Some Observations on the Kobe Earthquake in 1995. Journal of Hazardous Materials, 86, 101-119.
- Menonia, S., Pergalanib, F., Bonib, M.P. and Petrini, V. (2009) Lifelines Earthquake Vulnerability Assessment: A Systemic Approach. Soil Dynamics and Earthquake Engineering, 22, 1199-1208.
- Tan, A.P., Ou, J.P. and Zhang, K.X. (2005) Seismic Performance Assessment of Lifeline Systems. Journal of HARBIN Institute of Technology, 37, 151-155.
- Tan, Y.J. and Wu, J. (2004) Network Structure Entropy and Its Application to Scale-free Networks. Systems Engineering-Theory & Practice, 6, 1-3.
NOTES
![]()
*Corresponding author.


