Journal of Financial Risk Management
Vol.04 No.03(2015), Article ID:60075,18 pages
10.4236/jfrm.2015.43014
Predicting Conditional Autoregressive Value-at-Risk for Stock Markets during Tranquil and Turbulent Periods
Anastassios A. Drakos1, Georgios P. Kouretas2*, Leonidas Zarangas3
1Department of Business Administration, Athens University of Economics and Business, Athens, Greece
2IPAG Business School, France and Department of Business Administration, Athens University of Economics and Business, Athens, Greece
3Department of Finance & Auditing, Technological Educational Institute of Epirus, Preveza, Greece
Email: *kouretas@aueb.gr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 August 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
This paper analyzes the predictive performance of the Conditional Autoregressive Value at Risk (CAViaR) developed by Engle & Manganelli (2004) for major equity markets during tranquil and turbulent periods. The CAViaR model shifts the focus of attention from the distribution of returns directly to the behaviour of the quantile. We compare the predictive performance of four alternative CAViaR specifications, namely Adaptive, Symmetric Absolute Value, Asymmetric Slope and Indirect GARCH(1,1) models due to Engle & Manganelli (2004) along with the improved asymmetric CAViaR (I-CAViaR) model due to Huang et al. (2009) . We employ daily returns for six stock markets indices, namely S & P500, FTSE100, NIKKEI225, DAX30, CAC40 and Athens Exchange General index for the period January 2, 1995 to August 23, 2013. We compare the predictive performance of the alternative specifications for three subperiods: before, during and after the recent 2007-2009 financial crisis. The comparison is done with the use of a battery of tests which includes unconditional and conditional coverage tests, the Dynamic Quantile high-order independence test and the White (2000) empirical coverage probability and predictive quantile loss tests. The main findings of the present analysis is that the CAViaR quantile regression models and the I-CAViaR model have shown significant success in predicting the VaR measure for various periods although this performance varies over the three periods before, during and after the 2007-2009 financial crisis.
Keywords:
Non-Linear Regression Quantile, CAViaR, VaR, Quantile Loss, Reality Check, Backtesting

1. Introduction
The global financial crisis of 2007-2009 has called once again into question financial risk management practices, and one key issue is whether risk measures can actually be forecasted accurately enough to accomplish this task. Thus the current financial crisis has indeed highlighted once again the importance of risk management where institutions such as banks and major hedge fund companies are found to inevitably fail from time to time as we have witnessed the last twenty years. Quantitative risk measure forecasting has become, at least since the market crash in 1987 and then as a consequence of the financial crisis of 1997-1998, as well as the bankruptcy of several financial institutions such as the BCCI and Barings international banks that led to increased price volatility and financial uncertainty the benchmark for measuring market risk. Such financial uncertainty has increased the likelihood of financial institutions suffering substantial losses as a result of their exposure to unpredictable market changes. These events have made investors become more cautious in their investment decisions, while it has also led to an increased need for more careful study of price volatility in stock markets. Moreover, the recent crisis has shown the necessity of having adequate risk-management protocols in order to achieve greater resilience, and hence, the need to improve the existing procedures for quantifying the market risk. The present paper is motivated mainly by this concern.
In bank regulation, the effectiveness of capital requirements in preventing funding shortfall rests upon the estimation accuracy of market risk measures. Market risk is one of the four types of risk that financial institutions can expose them to. It is considered the most significant one since it represents potential economic loss caused by the reduction in the market value of a portfolio. The existence of market risk and recent financial disasters has raised the need for the development of practical risk management tools for financial institutions. This need had been reinforced by the Basel Committee of Banking Supervision (1996) which called for the use of internal market risk management to capital requirement by financial institutions such as banks and investment firms.1 The Basel II Accord is designed to monitor and encourage sensible risk-taking using appropriate models to calculate VaR and daily capital changes. For a financial institution, measuring the market risk it faces is an essential task. Specifically, a possible method of measurement is the evaluation of losses likely to be incurred when the price of the portfolio’s assets declines.
Value-at-Risk has become the standard tool used by financial analysts to measure market risk. VaR is defined as a certain amount lost on a portfolio of financial assets with a given probability over a fixed number of days. The confidence level represents “extreme market conditions” with a probability that is usually taken to be 99% or 95%. This implies that only 1% (5%) of the cases will lose more than the reported VaR of a specific portfolio. VaR is widely used because of its simplicity. Essentially, the VaR provides a single number that represents market risk and therefore it is easily understood.2
Although the VaR is conceptually a simple measure of market risk, there exists a controversy with respect to the suitability of the alternative existing techniques employed to estimate the VaR. Indeed, the measurement of VaR is a very interesting statistical problem. Artzner et al. (1997, 1999) have derived a set of axioms that specify a coherent risk measure. Thus, a risk measure must possess the following characteristics. First, it should not exceed the maximum possible loss which can occur. Second, the proposed risk measure should be greater than the mean loss, implying capital adequacy to cover losses. Third, in the event that there is a proportional change in the loss, then we require the risk measure to change proportionally as well. Finally, it must satisfy the property of superadditivity, implying that the risk measure calculated for two separate losses should be equal to the risk measure calculated on the sum of the two portfolios. As Boyle et al. (2005), Alexander et al. (2006) and Longin (2001) among others emphasized, the VaR methodology had certain limitations since it did not satisfy the properties of subadditivity and excess of the mean loss. Given these reservations regarding the use of the VaR as a measure for market risk, several researchers have developed alternative risk measures.3
Calculating the VaR requires accurate knowledge of the distribution of extreme events. This is a difficult task since the distribution of portfolio returns is not constant over time and, given that VaR is nothing more than a specific quantile of future portfolio values subject to current information, we must find an appropriate model for time varying conditional quantiles. This crucial issue is coupled with the need for providing accurate estimates of the chosen distribution of portfolio returns.
During the last two decades a large number of alternative models have been developed to estimate VaR. These alternative methodologies have mainly focused on modeling the entire distribution of returns and are based on the strict assumptions of normality or i.i.d. returns. However, as Engle & Manganelli (2004) argue, if we do not correctly estimate the underlying market risk then this can lead to an allocation of capital below first-best and that can affect the profitability and/or the financial stability of the corresponding bank or investment firm. Engle & Manganelli (2004) have proposed an alternative approach that models not the entire distribution but rather focuses on the regression quantile which does not require the above mentioned strict assumptions. This methodology, which is called Conditional Autoregressive Value at Risk (CAViaR), uses an autoregressive process in order to model the evolution of the regression quantile over time. The estimation of the unknown parameters is done with the use of the framework suggested by Koenker & Bassett (1978) . Furthermore, Engle & Manganelli (2004) prove that these estimators are asymptotically efficient and consistent. Finally, they develop the Dynamic Quantile test which is used to examine the quality of the CAViaR results.4
The main objective of this paper is to investigate the predictive performance of various types of the CAViaR specifications for stock market returns during tranquil and turbulent periods. The choice of this particular semiparametric method is motivated by the fact that CAViaR does not require any assumption on the distribution of a time series and computes the VaR directly by quantile regression, implying that the model allows the time series to switch from one stochastic process to another. We estimate and perform an evaluation of the predictive performance of two of the four alternative CAViaR specifications, namely, Symmetric Absolute Value and Asymmetric Slope. Furthermore, given the recent financial crisis we are further interested in evaluating the predictive performance of the alternative specifications for three out-of-sample evaluation periods (before-crisis, crisis and after-crisis). Within this framework we consider the issue of model stability. It is well documented that the model parameters are estimated from real data, which are often subject to structural changes due to regime shifts or events such as financial crises.
Recently, Huang et al. (2009) developed an improved CAViaR specification to account for some shortcomings of the original specification. Specifically, they argue that the asymmetric specification of Engle & Manganelli (2004) which is used to investigate the different effects of positive and negative returns on the VaR prediction requires the estimation of four parameters in the optimization procedure. This complicated model may lead to more estimation errors leading to an unstable or unrobust model. Therefore, this extension of the constant-parameter CAViaR allows us to examine whether the parameters of an individual risky asset are driven by the market index return. This extended model allows the tails of a financial series to follow different stochastic process and it allows VaR to be influenced by the volatility level of the driving index.
The main objective of this paper is to investigate the predictive performance of various types of the conditional autoregressive value-at-risk (CAViaR) specification during tranquil and turbulence periods. To this end we employ daily returns for six stock markets indices, namely S & P500, FTSE100, NIKKEI225, DAX30, CAC40 and Athens Exchange General Index for the period January 2, 1995 to August 23, 2013. We compare the predictive performance of the alternative specifications for three subperiods: before, during and after the recent 2007-2009 financial crisis.
The main findings of the present analysis is that the CAViaR quantile regression models and the I-CAViaR model have shown significant success in predicting the VaR measure for various periods although this performance varies over the three periods before, during and after the 2007-2009 financial crisis.
The remainder of the paper is organized as follows. Section 2 presents some of the most widely used VaR models. In section 3 we discuss the CAViaR methodology and its proposed alternative specifications. In Section 4 we report our empirical results, and finally section 5 provides our concluding remarks.
2. Value-at-Risk-Models and Methods
During the 1990s several alternative modeling methodologies for the estimation of the VaR were advanced. The purpose of these models was to provide risk managers with a comprehensive and intuitively easily understood measure of the VaR. The motivation for the development of the VaR models relies on the stylized characteristics of financial data which were first documented by Mandelbrot (1963) and Fama (1965) . To recapitulate, these characteristics imply that the returns of financial assets have leptokurtic distributions, that their distributions are negatively skewed and finally that they exhibit volatility clustering. As Manganelli & Engle (2004) and Engle & Manganelli (2004) point out, these alternative methodologies adopted a common general structure: (a) Mark- to-market the portfolio on a daily basis; (b) Estimation of the distribution of returns; and (c) Computation of the portfolio’s VaR. The main difference among the alternative methodologies is linked to the estimation of the appropriate distribution of the portfolio returns. We can briefly discuss the advantages and disadvantages of the alternative VaR models using the following broad classification.5
The first class of models is fully parametric and includes applications such as J.P. Morgan’s Riskmetrics (1996) and GARCH models. These methodologies combine an econometric model with the assumption of conditional normality for the returns series. Specifically, these models rely on the specification of the variance equation of the portfolio returns and the assumption that the standardized errors are i.i.d. Additionally, when the GARCH methodology is applied we are also required to specify the distribution of the errors, which is usually taken to be the normal one, while it is assumed that the negative returns follow the same process as the rests of portfolio returns ( Bams et al., 2005 ; Burns, 2005 ; Angelidis et al., 2004 ; Alexander et al., 2006 ; Pojarlev & Polasek, 2000 ; Polasek & Pojarlev, 2005 ; Kuester et al., 2006 ; Haas et al., 2006 ; Guidolin & Timmerman, 2006 ; Chen et al., 2013 ) are among the numerous applications employing alternative GARCH specifications. McAleer et al. (2008) develop a new Portfolio Spillover GARCH model and they examine its forecasting performance relative to that of the VARMA-GARCH with spillover effects and the CCC model with no spillovers. They find that spillovers effects are statistically significant.
The application of the parametric methodologies has been criticized since they tend to give coefficients which underestimate the VaR, mainly due to their failure to take into account the characteristic that the distribution of the portfolio returns has heavy tails. This underestimation of the VaR, as well as possible misspecifications with respect to the variance equation along with the distribution of errors, can be corrected by allowing alternative distributions of the errors such as the Gaussian, Student’s-t and Generalized Error Distribution. However, it is further shown that the GARCH-type models provide satisfactory estimates of the quantile only when a bad event has already occurred.
The second approach for the estimation of the distribution of profits and losses is the non-parametric historical simulation. This methodology makes no assumption about the distribution of the portfolio returns and is based on the concept of rolling windows. The idea is to select a window which is usually taken to be anywhere between 6 months to 2 years and assume that any portfolio return has the same likelihood to occur. Moreover, a return which falls outside the chosen window has probability equal to zero to occur. This methodology has several deficiencies. It is inappropriate to provide extreme quantiles since we cannot extrapolate beyond past observations. The proposed solution to this problem is the increase of the sample of observations, but this will lead to estimates of the VaR which are biased downwards (or upwards) since we have a mixture of periods with low volatility with periods of high volatility.
Within this group of VaR models falls the hybrid approach developed by Boudoukh et al. (1998) , which combines the historical simulation and Riskmetrics. This methodology applies weights to the portfolio returns that decline exponentially. Although this approach improves on the previously discussed methodologies, it also has problems since the selection of the parameters as well the calculation of the VaR does not depend on sound statistical theory but is rather ad hoc.
The final group for the estimation of the VaR is the semiparametric models. The first approach in this category is the Extreme Value Theory proposed by Danielsson et al. (1998) and Danielsson & de Vries (2000) . The advantage of this approach is that it is based on sound statistical theory which offers a parametric form for the tail of a distribution. This approach focuses on the asymptotic form of the tail, rather than modeling the complete distribution of portfolio returns and therefore we are able to obtain more efficient forecasts of the risk associated with a particular market position. Although this methodology is very appealing it does have two shortcomings. First, as Danielsson & de Vries (2000) argue, this approach performs well at very low quantiles but fails to provide accurate estimations of the VaR at levels which are not considered very extreme. Second, this methodology is also based on the assumption of i.i.d. standardized errors which is, as we have already discussed, an important limitation. Despite its limitations this approach has found substantial applications recently ( Longin, 2000 ; McNeil & Saladin, 2000 ; McNeil & Frey, 2000 ; Naftci, 2000 ; Bekiros & Georgoutsos, 2005a,b ; Brooks et al., 2005 ; Schaumburg, 2012 ).
Engle & Manganelli (2004) proposed an alternative semiparametric method to estimate VaR, namely Conditional Autoregressive Value at Risk (CAViaR). This approach is based on the simple intuition that it is better to model the quantile directly as it evolves through time instead of attempting to model and estimate the entire distribution of portfolio returns. Modelling the quantile instead of the entire distribution has the main advantage that we are not required to adopt the set of extreme assumptions which are invoked by alternative methodologies, among them normality or that returns are i.i.d. In addition, CAViaR takes into consideration volatility clustering of portfolio returns that leads to the understanding that the corresponding distributions are autocorrelated. As a consequence the VaR must also follow a similar pattern since it is directly linked with the standard deviation of the distribution. Therefore, Engle & Manganelli (2004) developed CAViaR in order to take into account of the particular characteristic of the VaR. Furthermore, Manganelli & Engle (2004) demonstrate that the CAViaR model outperforms most of the indirect-VAR methodologies. This outcome is reached through Monte Carlo simulations. They simulated 1000 samples of 2000 observations for seven different processes.
There are several papers that have extended and applied the CAViaR approach in a number of different ways. In an early study, Kouretas & Zarangas (2005) employ the CAViaR model to measure the market risk of five major equity markets, six blue chip stocks from the Athens Exchange, and six major company stocks listed on the New York Stock Exchange (NYSE). They compare four alternative CAViaR specifications with mixed results. Giacomini & Komunnjer (2005) find that CAViaR is most accurate at the 1% quantile level, but the GARCH model with Gaussian distributed errors is better than CAViaR at the 5% quantile level. Bao et al. (2006) compare the performance of CAViaR and other VaR measures for five East and Southeast Asian markets before, during and after the financial crisis of 1997-1998. They conclude that CAViaR models are quite satisfactory in a stable period but their performance in less satisfactory during turbulent periods. Kuester et al. (2006) compare CAViaR and alternative approaches for univariate VaR forecasts using daily return data on the NASDAQ Composite Index and alternative evaluation criteria. They conclude that CAViaR specifications performs well overall using unconditional and conditional tests for the predictive performance of VaR, although its forecasting performance is less accurate during periods of crisis and very high volatility.
Gourieroux & Jasiak (2008) argue that a drawback of the dynamic quantile models is the lack of an internal mechanism that would ensure that the conditional quantiles evaluated at different probability levels do not cross. They develop the Dynamic Additive Quantile model, which ensures the monotonicity of conditional quantile functions and using data for the Toronto Stock Exchange market index and it is shown the DAQ model provides better asymptotically efficient estimations. Huang et al. (2009) develop an extension of the CAViaR model (a) with a proposition of a new asymmetric CAViaR specification and (b) a mixed data regression model for multi- period VaR prediction. Using market data on WTI daily spot oil prices the improved CAViaR specifications performed well in a battery of evaluation criteria. Huang et al. (2010) introduce a time-varying CAViaR model and using data to construct size weighted portfolios from the NYSE, AMEX and NASDAQ they show that the time-varying model provides better VaR forecasts than the constant parameter CAViaR when there are spillover effects from one market segment to other markets or market segments. Yu et al. (2010) extend the CAViaR specifications using two approaches, namely the threshold and mixture type indirect-GARCH CAViaR models. Gerlach et al. (2011) also propose a nonlinear CAViaR model. Chen et al. (2012) adopt the Threshold CAViaR and the indirect CAViaR model and using data from major stock market indices they provide clear evidence that the CAViaR class of models outperform in forecasting VaR performance other competing parametric, semiparametric and nonparametric models. Jeon & Taylor (2013) proposed a model of CAViaR with implied volatility and they find that the implied volatility has more explanatory power that the standard VaR models. Finally, Rubia et al. (2013) analyze tail-predictability in the returns of several representative portfolios on the US stock exchange. They show that the CAViaR models are very suitable in accurate VaR forecasts when different variables which are related to market-wide measures of trading activity and liquidity.
3. CAViaR
3.1. General Framework
Engle & Manganelli (2004) and Manganelli & Engle (2001) consider a vector of portfolio returns that is ob-
servable, defined as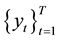 . Let
. Let
 be the probability tied to VaR,
be the probability tied to VaR,
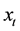 be a vector of observable variables at time t, and
be a vector of observable variables at time t, and
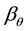 be a vector of unknown parameters. They also define
be a vector of unknown parameters. They also define
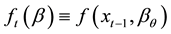 as the
as the
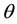 -quantile
-quantile
of the distribution of the portfolio returns at time t which has been formed at time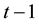 .6 Therefore, a general formulation of CAViaR can be written as follows:
.6 Therefore, a general formulation of CAViaR can be written as follows:
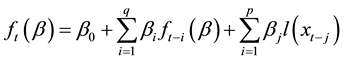 (1)
(1)
where
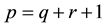 is the dimension of
is the dimension of
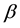 and l is a function of a finite number of lagged values of observables. Moreover, in order for the quantile to have a smooth transition they use the autoregressive terms
and l is a function of a finite number of lagged values of observables. Moreover, in order for the quantile to have a smooth transition they use the autoregressive terms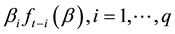 . Finally, they use the term
. Finally, they use the term
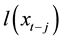 to provide a relationship between the
to provide a relationship between the
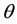 -quantile
-quantile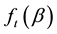 and the observable variables which are included in the information set. As
Engle & Manganelli (2004)
point out, we can consider the lagged portfolio returns as the best choice for
and the observable variables which are included in the information set. As
Engle & Manganelli (2004)
point out, we can consider the lagged portfolio returns as the best choice for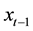 . This implies that as
. This implies that as
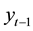 becomes negative, then one should expect the VaR to increase, while the VaR tends to decline in good days. Therefore, we expect that changes in
becomes negative, then one should expect the VaR to increase, while the VaR tends to decline in good days. Therefore, we expect that changes in

The purpose is to develop alternative specifications for the function l and then estimate the different models. Engle & Manganelli (2004) propose four alternative CAViaR specifications which we will estimate in our case.
3.2. Adaptive Specification
The first specification is called Adaptive and takes the following formulation:

where G is some positive finite number and we that as


3.3. Symmetric Absolute Value Specification
A second specification is called Symmetric Absolute Value (SAV) and its mathematical formulation is given by:

This model responds symmetrically to past portfolio returns and it is mean reverting since the coefficient of the lagged VaR is not constrained to equal one. Furthermore, we could properly specify this quantile specification using a GARCH model with the standard deviation (and not the variance), which is considered to follow a symmetric distribution with i.i.d. errors.7
3.4. Asymmetric Slope Specification
The Asymmetric Slope (AS) is the third commonly used specification to estimate the l function. It is written as follows:

The Asymmetric Slope model allows for an asymmetric response to positive and negative past portfolio returns.8 Again this model is mean reverting. As with the SAV model we can correctly specify this specification by fitting a GARCH process with the standard deviation, following this time an asymmetric distribution with i.i.d. errors.
3.5. Indirect GARCH(1,1)
The final specification is called Indirect GARCH (1,1) which is also mean reverting and as with the SAV specification, it responds symmetrically to past returns. This specification can be correctly modeled under the assumption that the underlying data process follows a true GARCH(1,1) with an i.i.d. error distribution.9 The algebraic expression of this specification is as follows:

Thenext step to the analysis is the estimation of the parameters of the alternative CAViaR models. They are estimated using linear and non-linear quantile techniques. These techniques were first introduced by Koenker & Basett (1978) who provide a thorough analysis of how to apply the concept of sample quantile to a linear regression model. We consider the following model proposed by Engle & Manganelli (2004) :

where








defines the

Within this framework, Engle & Manganelli (2004) show that the only assumption required is the appropriate specification of the quantile process and, more specifically, we do not have to specify the entire distribution of the error terms. Furthermore, even if we erroneously specify the regression quantile process, Engle & Manganelli (2004) argue that we can still obtain a minimization of Equation (5) that satisfies the Kullback-Leibler Information Criterion (which measures the deviation between the true specification and the actual model).
3.6. Improved CAViaR
As we already discussed Huang et al. (2009) argue that in practice CAViaR may face some implementation challenges. Thus, in case we investigate the different effects of positive and negative returns on the prediction from a VaR model then we may use the asymmetric CAViaR specification. This requires estimating four parameters in the optimization framework which may lead to more estimation errors and this could result to an unstable or unrobust model. Based on the exponentially weighted moving average volatility prediction idea in Riskmetrics (1996) , Hull & White (1998) , and Huang et al. (2009) they propose an improved asymmetric CAViaR model:

where

prediction to respond asymmetrically to positive and negative returns. Thus, if we consider that
Engle & Manganelli (2004)
consider the case where

3.7. Evaluation Performance Tests
Engle & Manganelli (2004) also propose a new test for the evaluation of the alternative specifications which has better power properties than other existing tests. This test allows for the inclusion of a variety of alternative specifications. They define:

where the function










An important issue when we compare alternative models in terms of predictive performance using the same data, is the need to take into account the dependence among the models. White (2000) developed a test of superior unconditional predictive ability among multiple models accounting for specification search. Furthermore, we note that when we apply backtesting procedure we may be interested not only to the behaviour of hit sequence (i.e. whether an exceedance occurs) but also in the magnitude of the exceedance. In general, a backtest could be based on a function of the observed return series and the corresponding VaR predictions. This would imply the construction of a general loss function which could be evaluated using past data on returns and the reported VaR series. Following Bao et al. (2006) and Huang et al. (2009) define the loss function as

The null hypothesis is that the empirical value of




4. Empirical Results
We apply the alternative CAViaR model specifications on daily data for the period March 3, 1995 to August 28, 2013 for the following general stock indices: S & P500, FTSE100, NIKKEI225, DAX30, CAC40 and the Athens Exchange General Index. The data was taken from Datastream. Given our earlier discussion that financial returns exhibit certain properties which imply that it is unreasonable to assume that stock return series follow a certain stochastic process. This evidence motivates this study to consider the CAViaR model by accommodating different processes into the prediction horizon. Table 1 reports summary statistics for each stock market daily returns. The significant negative skewness and kurtosis show that the return process deviates from the normal distribution. The daily returns are computed as 100 times the difference of the log of the prices. Finally in order to implement our analysis we construct historical series of portfolio for each case and we choose a specification of the functional form of the quantile.
Our analysis begins with estimation of the Symmetric, Asymmetric and the Indirect GARCH (1,1) CAViaR specifications due to Engle & Manganelli (2004) and the Improved Asymmetric CAViaR due to Huang et al. (2009) described in Section 3. For the estimation of the models we used the first 4364 observations and the last 500 to conduct the out-of-sample testing performance.
We estimate 1% and 5% one day Value-at-Risk.13 As
Engle & Manganelli (2004)
proved, all the models are both continuous and continuously differentiable in
Our results are summarized in Tables 1-6. Each table reports the value of the estimated parameters, the respective standard errors and the one-sided p-values. Furthermore, each table shows the value of the regression objective function given by equation (3) above. Finally, we report the percentage of times the VaR is exceeded and the in-and out-of-sample p-value of the Dynamic Quantile test. The computation of the VaR series with the CAViaR models has been done with the initialization of






The results obtained for the pre-crisis period are reported in Table 1 and Table 2. The first important observation we make in both tables is that the coefficient

Table 1. Estimates and Relevant Statistics for the four Conditional Autoregressive Value at Risk Models-Pre Crisis period (03/01/1995-14/9/2007).
Note: Significant coefficients at 5% level of significance are given in bold; shaded boxes denote rejection from the DQ test at 1% significance level.
Table 2. Estimates and Relevant Statistics for the four Conditional Autoregressive Value at Risk Models-Pre Crisis period (03/01/1995-14/9/2007).
Note: Significant coefficients at 5% level of significance are given in bold; shaded boxes denote rejection from the DQ test at 1% significance level.
Table 3. Estimates and Relevant Statistics for the four Conditional Autoregressive Value at Risk Models-Crisis period (17/09/2007-31/08/2009).
Note: Significant coefficients at 5% level of significance are given in bold; shaded boxes denote rejection from the DQ test at 1% significance level.
Table 4. Estimates and Relevant Statistics for the four Conditional Autoregressive Value at Risk Models-Crisis period (17/09/2007- 31/08/2009).
Note: Significant coefficients at 5% level of significance are given in bold; shaded boxes denote rejection from the DQ test at 1% significance level.
Table 5. Estimates and Relevant Statistics for the four Conditional Autoregressive Value at Risk Models-Post Crisis period (01/09/2009-23/08/2013).
Note: Significant coefficients at 5% level of significance are given in bold; shaded boxes denote rejection from the DQ test at 1% significance level.
Table 6. Estimates and Relevant Statistics for the four Conditional Autoregressive Value at Risk Models-Post Crisis period (01/09/2009-23/08/2013).
Note: Significant coefficients at 5% level of significance are given in bold; shaded boxes denote rejection from the DQ test at 1% significance level.
cation provides the best estimates at the 1% benchmark. Furthermore, the Symmetric Absolute Value, the Asymmetric Slope and the Indirect GARCH provide in-sample hits near the value of 1, but the out-of sample hits are some distance from this value. This is less problematic for the case of the I-CAViaR specification.
We then turn to the results for the 5% VaR. We first discuss the results for the CAC40, the DAX30 and the ASE stock indices. The in-sample hits range from 4.9% to 5.1% for the Symmetric Absolute Value, the Asymmetric Slope and the Indirect GARCH models, while the I-CAViaR specification is on target in most cases as well. The out-of sample forecasts are very accurate for the case of DAX40 when we apply any of these three models, and also for the case of CAC40 when we apply the Indirect GARCH specification. When we turn to the case of the FTSE100, S & P500 and NIKKEI225 indices note that we obtain estimates which are extremely close to the value of 5%, which is taken as evidence that they describe the evolution of the tail for all cases under consideration. Looking into the out-of-sample forecasts, the performance is similar to the one obtained in the first set of market indices. Finally, a similar pattern emerges for all three specifications as well the I-CAViaR model when we examine the five stock indices.
A final comment we make is that in most cases the estimation of the Asymmetric Slope model gives coefficient estimates for the negative lagged returns which are always statistically significant while the estimates associated with the positive returns are not significantly different from zero. Therefore, we may argue there are possible strong asymmetric influences on VaR measures of lagged returns. This finding is further reinforced by the estimates of the I-CAViaR model.
The overall results from the present analysis show that the DQ test statistics select different CAViaR specifications for different confidence internals which may lead to the argument that the process guiding the tail behaviour changes over time.
With respect to the empirical loss function results we observe that the values of the

5. Summary and Concluding Remarks
The recent financial crisis of 2007-2009 has brought in surface the need for more accurate measurement of the downside risk of financial institutions. A significant contribution to this increased volatility has been the substantial rise of capital flows from mature markets towards the emerging markets of Southeast Asia and the economies of transition. The 1997-1998 financial crisis as well as the bankruptcy of several financial institutions during the 1990s had shown quite convincingly how important the development is for the stability of the global financial system and adoption of the appropriate mechanisms for measuring market risk. However, the recent financial turbulence and the reversal of capital flows in an effort of the hedge funds to liquidate their investment in emerging markets have once again led to increase volatility in the global financial markets.
The Riskemetrics methodology by Morgan Stanley (1996) provided the first econometric methodology for the measurement of market risk based on the concept of VaR which was introduced in Banking Supervision’s (1996) “Amendment to the Capital Accord to Incorporate Market Risks”. This led to a fast growing literature on the development of alternative methodologies to measure VaR. The present paper utilized the CAViaR modeling procedure, which had been proposed by Engle & Manganelli (2004) . This is a semiparametric method which shifts the analysis of developing a good measure of the VaR from the distribution of the portfolio returns directly to the behavior of the quantile. This methodology is considered to have several advantages over competing VaR methodologies like the GARCH models and the Extreme Value Theory.
We applied this methodology to estimate the VaR using daily observations for the period January 3, 1995 to August 28, 2013. We studied the behaviour of alternative CAViaR specifications for six stock market indices, namely the S & P 500, FTSE 100, DAX30, CAC40, NIKKE225 and the Athens Exchange General Index.
Our overall results led to the conclusion that this methodology provided very accurate measurement of the VaR for all stock price indices. This evidence is based on a battery in-sample and out-of-sample forecasting performance. Furthermore, our findings show that the CAViaR quantile regression models and the I-CAViaR model have shown significant success in predicting the VaR measure for various periods although this performance varies over the three periods before, during and after the 2007-2009 financial crisis. These findings may be of interest to portfolio managers, private and institutional investors as well as hedge funds that are active in mature and emerging stock markets.
Acknowledgements
We thank participants at the 6th International Conference on Mathematical and Statistical Methods for Actuarial Sciences and Finance, 22-24 April 2014 and at seminars at Athens University of Economics and Business, European University Institute, Hebrew University of Jerusalem, University of Crete, University of Piraeus and Central Bank of Cyprus for their very helpful comments. Kouretas acknowledges financial support from a Marie CurieTransfer of Knowledge Fellowship of the European Community’s Sixth Framework Programme under contract number MTKD-CT-014288, as well as from the Research Committee of the University of Crete under researchgrants #2016, #2030 and #2257. We thank Carol Alexander, Richard Baillie, Manthos Delis, Dimitris Georgoutsos, Dashan Huang, Michael McAleer, Simone Manganelli, Stavros Stavroyiannis, Chris Tsoumas, Elias Tzavalis and Mark Wohar for many helpful comments and discussions. We also thank Dashan Huang and Baimin Yu for providing us with the MATLAB codes for estimating the improved asymmetric CAViaR model. Finally, we thank the editor and an anonymous referee for their constructive comments which improved the manuscript substantially. The usual caveat applies.
Cite this paper
AnastassiosA. Drakos,Georgios P.Kouretas,LeonidasZarangas, (2015) Predicting Conditional Autoregressive Value-at-Risk for Stock Markets during Tranquil and Turbulent Periods. Journal of Financial Risk Management,04,168-186. doi: 10.4236/jfrm.2015.43014
References
- 1. Alexander, S. (2005). The Present and Future of Financial Risk Management. Journal of Financial Econometrics, 3, 3-25.
http://dx.doi.org/10.1093/jjfinec/nbi003 - 2. Alexander, S., Coleman, T. F., & Li, Y. (2006). Minimizing CVaR and VaR for a Portfolio of Derivatives. Journal of Banking and Finance, 30, 583-605.
http://dx.doi.org/10.1016/j.jbankfin.2005.04.012 - 3. Aloui, C., & ben Hamida, H. (2014). Modelling and Forecasting Value at Risk and Expected Shortfall for GCC Stock Markets: Do Long Memory, Structural Breaks, Asymmetry, and Fat-Tails Matter? North American Journal of Economics and Finance, 29, 349-380.
http://dx.doi.org/10.1016/j.najef.2014.06.006 - 4. Angelidis, T., Benos, A., & Degiannakis, S. (2004). The Use of GARCH Models in VaR Estimation. Statistical Methodology, 1, 105-128.
http://dx.doi.org/10.1016/j.stamet.2004.08.004 - 5. Artzner, P., Delbaen, F., Eber, J.-M., & Heath, D. (1997). Thinking Coherently. Risk, 10, 68-71.
- 6. Artzner, P., Delbaen, F., Eber, J.-M., & Heath, D. (1999). Coherent Measures of Risk. Mathematical Finance, 9, 203-228.
http://dx.doi.org/10.1111/1467-9965.00068 - 7. Bams, D., Lehnert, T., & Wolff, C. C. P. (2005). An Evaluation Framework for Alternative VaR-Models. Journal of International Money and Finance, 24, 922-958.
http://dx.doi.org/10.1016/j.jimonfin.2005.05.004 - 8. Bank for International Settlements (1988). International Convergence of Capital Measurement and Capital Standards. BCBS Publication Series, No.4.
- 9. Banking Supervision’s (1996). Amendment to the Capital Accord to Incorporate Market Risks.
- 10. Bank for International Settlements (1999a). Capital Requirements and Bank Behavior: The Impact of the Basel Accord. BCBS Working Paper Series, No. 1.
- 11. Bank for International Settlements (1999b). A New Capital Adequacy Framework. BCBS Publications Series, No. 50.
- 12. Bank for International Settlements (1999c). Supervisory Lesson to Be Drawn from the Asian Crisis. BCBS Working Paper Series, No. 2.
- 13. Bank for International Settlements (2001). The New Basel Capital Accord. Basel: BIS.
- 14. Basel Committee on Banking Supervision (1996). Amendment to the Capital Accord to Incorporate Market Risks.
- 15. Bao, Y., Lee, T., & Saltoglu, B. (2006). Evaluating the Predictive Performance of Value-at-Risk Models in Emerging Markets: A Reality Check. Journal of Forecasting, 25, 101-128.
http://dx.doi.org/10.1002/for.977 - 16. Bekiros, S., & Georgoutsos, D. A. (2005a). Estimation of Value-at-Risk by Extreme Value and Conventional Methods: A Comparative Evaluation of Their Predictive Performance. Journal of International Financial Markets, Institutions and Money, 15, 209-228.
http://dx.doi.org/10.1016/j.intfin.2004.05.002 - 17. Bekiros, S., & Georgoutsos, D. A. (2005b). Extreme Returns and the Contagion Effect between the Foreign Exchange and the Stock Market: Evidence from Cyprus. Multinational Finance Journal, Forthcoming.
- 18. Boudoukh, J., Richardson, M., & Whitelaw, R. F. (1998). The Best of Both Worlds. Risk, 11, 64-67.
- 19. Boyle, P., Hardy, M., & Vorst, T. (2005). Life after VaR. Journal of Derivatives, 13, 48-55.
http://dx.doi.org/10.3905/jod.2005.580517 - 20. Brooks, C., Clare, A. D., Dalle-Mulle, J. W., & Persand, G. (2005). A Comparison of Extreme Value Theory Approaches for Determining Value at Risk. Journal of Empirical Finance, 12, 339-352.
http://dx.doi.org/10.1016/j.jempfin.2004.01.004 - 21. Burns, P. (2005). The Quality of Value at Risk via Univariate GARCH. Working Paper, Burns Statistics.
- 22. Chen, C. W. S., Gerlach, R., Hwang, B. B. K., & McAller, M. (2012). Forecasting Value-at-Risk Using Nonlinear Regression Quantiles and the Intra-Day Range. International Journal of Forecasting, 28, 557-574.
http://dx.doi.org/10.1016/j.ijforecast.2011.12.004 - 23. Chernozhukov, V. (1999). Specification and Other Tests Processes for Quantile Regression. Stanford University, Mimeograph.
- 24. Christoffersen, P. F. (1998). Evaluating Interval Forecasts. International Economic Review, 39, 841-864.
http://dx.doi.org/10.2307/2527341 - 25. Danielsson, J., Hartmann, P., & de Vries, C. (1998). The Cost of Conservatism. Risk, 11, 101-103.
- 26. Danielsson, J., & de Vries, C. (2000). Value-at-Risk and Extreme Returns. Annales d’Economie et de Statistique, 60, 239-270.
- 27. Drzik, J. (2005). New Directions in Risk Management. Journal of Financial Econometrics, 3, 26-36.
http://dx.doi.org/10.1093/jjfinec/nbi007 - 28. Duffie, D., & Pan, J. (1997). An Overview of Value at Risk. Journal of Derivatives, 4, 7-49.
http://dx.doi.org/10.3905/jod.1997.407971 - 29. Engle, R. F., & Manganelli, S. (2004). CAViaR: Conditional Autoregressive Value at Risk by Regression Quantile. Journal of Business and Economic Statistics, 22, 367-381.
http://dx.doi.org/10.1198/073500104000000370 - 30. Fama, E. F. (1965). The Behaviour of Stock Market Prices. Journal of Business, 38, 34-105.
http://dx.doi.org/10.1086/294743 - 31. Giacomini, R., & Komunjer, I. (2005). Evaluation and Combination of Conditional Quantile Forecasts. Journal of Economic and Business Statistics, 23, 416-431.
http://dx.doi.org/10.1198/073500105000000018 - 32. Gourieroux, C., & Jasiak, J. (2008). Dynamic Quantile Models. Journal of Econometrics, 147, 198-205.
http://dx.doi.org/10.1016/j.jeconom.2008.09.028 - 33. Granger, C. W. J., White, H., & Kamstra, M. (1989). Interval Forecasting: An Analysis Based upon ARCH-Quantiles Estimators. Journal of Econometrics, 40, 87-96.
http://dx.doi.org/10.1016/0304-4076(89)90031-6 - 34. Gerlach, R., Chen, C. W. S., & Chan, N. Y. C. (2011). Bayesian Time-Varying Quantile Forecasting for Value-at-Risk in Financial Markets. Journal of Business and Economic Statistics, 23, 416-431.
http://dx.doi.org/10.1198/jbes.2010.08203 - 35. Guidolin, M., & Timmermann, A. (2006). Term Structure of Risk under Alternative Econometric Specifications. Journal of Econometrics, 131, 285-308.
http://dx.doi.org/10.1016/j.jeconom.2005.01.033 - 36. Haas, M., Mittnik, S., & Paolella, M. (2006). Value-at-Risk Prediction: A Comparison of Alternative Strategies. Journal of Financial Econometrics, 4, 53-89.
- 37. Huang, D., Yu, B., Lu, Z., Fabozzi, F. J., Focardi, S., & Fukushima, M. (2010). Index-Exciting CAViaR: A New Empirical Time-Varying Risk Model. Studies in Nonlinear Dynamics and Econometrics, 14, 1-24.
http://dx.doi.org/10.2202/1558-3708.1805 - 38. Huang, D., Yu, B., Fabozzi, F. J., & Fukushima, M. (2009). CAViaR-Based Forecast for Oil Price Risk. Energy Economics, 31, 511-518.
http://dx.doi.org/10.1016/j.eneco.2008.12.006 - 39. Hull, J., & White, A. (1998). Value-at-Risk When Daily Changes in Market Variables Are Not Normally Distributed. Journal of Derivatives, 5, 9-19.
http://dx.doi.org/10.3905/jod.1998.407998 - 40. Jeon, J., & Taylor, J. W. (2013). Using CAViaR Models with Implied Volatility for Value-at-Risk Estimation. Journal of Forecasting, 32, 62-74.
http://dx.doi.org/10.1002/for.1251 - 41. Jimenez-Martin, J. A. (2009). The Ten Commandments for Managing Value-at-Risk and the Basel II Accord. Journal of Economic Surveys, 23, 850-855.
http://dx.doi.org/10.1111/j.1467-6419.2009.00590.x - 42. Jorion, P. (2000). Value at Risk (2nd ed.). New York: McGraw Hill.
- 43. Koenker, R., & Bassett, G. (1978). Regression Quantiles. Econometrica, 46, 33-50.
http://dx.doi.org/10.2307/1913643 - 44. Koenker, R., & Bassett, G. (1982). Robust Tests for Heteroskedasticity Based on Regression Quantiles. Econometrica, 50, 43-61.
http://dx.doi.org/10.2307/1912528 - 45. Koenker, R., & Zhao, Q. (1996). Conditional Quantile Estimation and Inference for ARCH Models. Econometric Theory, 12, 265-283.
http://dx.doi.org/10.1017/S0266466600007167 - 46. Kouretas, G. P., & Zarangas, L. (2005). Conditional Autoregressive Value-at-Risk by Regression Quantiles: Estimating Market Risk for Major Stock Market. Working Paper, Crete: Department of Economics, University of Crete.
- 47. Kuester, R. F., Mittnik, S., & Paolella, M. (2006). Value-at-Risk Prediction: A Comparison of Alternative Strategies. Journal of Financial Econometrics, 4, 53-89.
http://dx.doi.org/10.1093/jjfinec/nbj002 - 48. Longin, F. M. (2000). From VaR to Stress Testing: The Extreme Value Approach. Journal of Banking and Finance, 24, 1097-1130.
http://dx.doi.org/10.1016/S0378-4266(99)00077-1 - 49. Longin, F. M. (2001). Beyond the VaR. Journal of Derivatives, 8, 36-48.
- 50. Mandelbrot, B. (1963). The Variation of Certain Speculative Prices. Journal of Business, 36, 394-419.
- 51. Manganelli, S., & Engle, R. F. (2004). A Comparison of Value-at-Risk Models in Finance. In G. Szego (Ed.), Risk Measures for the 21st Century (pp. 123-143). Chichester: John Wiley.
- 52. McAleer, M., & Da Veiga, B. (2008). Forecasting Value-at-Risk with a Parsimonious Portfolio Spillover GARCH (PS- GARCH) Model. Journal of Forecasting, 27, 1-19.
http://dx.doi.org/10.1002/for.1049 - 53. McAleer, M., Jimenez-Martin, J. A., & Perez-Amaral, T. (2013). Has the Basel Accord Improved Risk Management during the Global Financial Crisis? North American Journal of Economics and Finance, 26, 250-265.
http://dx.doi.org/10.1016/j.najef.2013.02.004 - 54. McNeil, A. J., & Frey, R. (2000). Estimation of Tail-Related Risk Measures for Heteroskedastic Financial Time Series: An Extreme Value Approach. Journal of Empirical Finance, 7, 271-300.
http://dx.doi.org/10.1016/S0927-5398(00)00012-8 - 55. McNeil, A. J., & Saladin, T. (2000). Developing Scenarios for Future Extreme Losses Using the POT Model. In P. Embrehts (Ed.), Extremes and Integrated Risk Management. London: RISK Publications.
- 56. Naftci, S. (2000). Value at Risk Calculations, Extreme Events, and Tail Estimation. Journal of Derivatives, 7, 23-37.
http://dx.doi.org/10.3905/jod.2000.319126 - 57. Pojarlev, M., & Polasek, W. (2000). Value at Risk Estimation for Stock Indices Using the Basle Committee Proposal Form 1995, Mimeograph.
- 58. Polasek, W., & Pojarlev, M. (2005). VaR Evaluations Based on Volatility Forecasts of GARCH Models, Mimeograph.
- 59. Portnoy, S. (1991). Asymptotic Behavior of Regression Quantiles in Non-Stationary Dependent Cases. Journal of Multivariate Analysis, 38, 100-113.
http://dx.doi.org/10.1016/0047-259X(91)90034-Y - 60. RiskMetrics (1996). Technical Document. Morgan Guarantee Trust Company of New York.
- 61. Romero, P. A., Muela, S. B., & Martin, C. L. (2013). A Comprehensive Review of Value at Risk Methodologies. Fundacion De Las Cajas De Ahorros, Documento de Trabajo No 711/2013.
- 62. Rubia, A., & Sanchis-Marco, L. (2013). On Downside Risk Predictability through Liquidity and Trading Activity: A Dynamic Quantile Approach. International Journal of Forecasting, 29, 202-219.
http://dx.doi.org/10.1016/j.ijforecast.2012.09.001 - 63. Schaumburg, J. (2012). Predicting Extreme Value at Risk: Nonparametric Quantile Regression with Refinements from Extreme Value Theory. Computational Statistics and Data Analysis, 56, 4081-4096.
http://dx.doi.org/10.1016/j.csda.2012.03.016 - 64. Schwert, G. W. (1988). Why Does Stock Market Volatility Change over Time? Journal of Finance, 44, 1115-1153.
http://dx.doi.org/10.1111/j.1540-6261.1989.tb02647.x - 65. Sener, E., Baronyan, S., & Ali Menguturk, L. (2012). Ranking the Predictive Performances of Value-at-Risk Estimation Methods. International Journal of Forecasting, 28, 849-873.
http://dx.doi.org/10.1016/j.ijforecast.2011.10.002 - 66. Taylor, S. J. (1986). Modelling Financial Time Series. New York: Wiley and Sons Ltd.
- 67. White, H. (1994). Estimation, Inference and Specification Analysis. Cambridge: Cambridge University Press.
http://dx.doi.org/10.1017/CCOL0521252806 - 68. White, H. (2000). A Reality Check for Data Snooping. Econometrica, 68, 1097-1126.
http://dx.doi.org/10.1111/1468-0262.00152 - 69. Yu, P. L. H., Li, W. K., & Jin, S. (2010). On Some Models for Value-at-Risk. Econometric Reviews, 29, 622-641.
http://dx.doi.org/10.1080/07474938.2010.481972
NOTES
*Corresponding author.
1For a detailed analysis see the Basel Committee on Banking Supervision’s (1996) , “Amendment to the Capital Accord to Incorporate Market Risks”. Duffie & Pan (1997) , Alexander (2005) and Drzik (2005) provide a comprehensive overview of value at risk measures.
2See also Bank for International Settlements (1988, 1999a,b,c, 2001) . Jimenez-Martin (2009) and McAleer et al. (2013) provide a more recent evaluation of managing value-at-risk under the provisions of the Basle II accord.
3CVaR is an alternative risk measure that satisfies the coherency criteria by Artzner et al. (1997, 1999) . Its advantage over VaR measures is that it focuses on both the frequency and the size of extreme events.
4 Chernozhukov (1999) has derived independently the same dynamic quantile test.
5 Jorion (2000) and Kuester et al. (2006) provide a complete analysis of the VaR methodology and alternative estimation methodologies. Romero et al. (2013) gives an updated survey of alternative VaR methodologies.
6For simplicity we have eliminated the subscript θ from the vector of unknown parameters.
7See also Taylor (1986) , Schwert (1988) and Engle (2002).
8
9It is worth noting that the CAViaR specifications are more general than the fitted GARCH models. They can allow for a wide range of assumptions with respect to the error distribution and they can also handle distributions with non-i.i.d. errors.
10Following the seminal paper by Koenker & Bassett (1978) , a number of alternative regression quantile models have been developed over the last twenty years that take into account alternative assumptions about the errors. Among others, Koenker & Bassett (1982) allow for the case of heteroskedastic errors, whereas Portnoy (1991) considers the case of non-stationary dependent errors. Furthermore, we have extensions that cover the cases of time series models, simultaneous equations and censored regression models and recently we also have extensions that deal with the case of autoregressive quantiles ( Koenker & Zhao, 1996 ). See Engle & Manganelli (2004) for the relevant literature. All these models differ from the Engle & Manganelli (2004) CAViaR models since they are linear in the parameters.
11The complete derivation of the two tests is given in Engle & Manganelli (2004: pp. 370-371) . Granger et al. (1989) and Christoffersen (1998) are among other studies which have developed test statistics for the validity of the forecast model, but as Engle & Manganell (2004) point out, they have low power against misspecification introduced by the presence of serial correlation in the conditional probabilities leading to a quantile measurement error.
12 Aloui et al. (2014) provide further analysis of forecasting measures whereas Sener et al. (2012) analyze the ranking of predictive performance of value-at-risk estimations methods.
13To estimate the Adaptive model we set G = 10, in all cases where G entered the definition of the Adaptive model in section 3.
14All assumptions which these models need to satisfy are given in Appendix A of Engle & Manganelli (2004) ; and they refer to asymptotic results but are difficult to verify in finite samples.
15As Engle & Manganelli (2004) point out, the lagged hit variables contain the indicator function. Given that the indicator function is Lipschitz continuous it satisfies condition, DQ3 of theorem 4 ( Engle & Manganelli, 2004 ).
16The calculation of the two statistics is described in Engle and Manganelli, theorems 3 and 4. Furthermore, for the optimization procedures we adopt the strategy explained in Engle & Manganelli (2004) . The computations were made in Matlab 6.1 using the functions fminsearch and fminunc as the optimization algorithms while the loops to compute the recursive quantile functions were coded in C and have been developed by Manganelli.











