American Journal of Climate Change
Vol.05 No.04(2016), Article ID:72031,24 pages
10.4236/ajcc.2016.54036
Global Climate Model Selection for Analysis of Uncertainty in Climate Change Impact Assessments of Hydro-Climatic Extremes
Patrick A. Breach1*, Slobodan P. Simonovic1, Zhiyong Yang2
1Department of Civil and Environmental Engineering, Western University, London, Canada
2Department of Water Resources, China Institute of Water Resources and Hydropower Research, Beijing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 6, 2016; Accepted: November 13, 2016; Published: November 16, 2016
ABSTRACT
Regional climate change impact assessments are becoming increasingly important for developing adaptation strategies in an uncertain future with respect to hydro- climatic extremes. There are a number of Global Climate Models (GCMs) and emission scenarios providing predictions of future changes in climate. As a result, there is a level of uncertainty associated with the decision of which climate models to use for the assessment of climate change impacts. The IPCC has recommended using as many global climate model scenarios as possible; however, this approach may be impractical for regional assessments that are computationally demanding. Methods have been developed to select climate model scenarios, generally consisting of selecting a model with the highest skill (validation), creating an ensemble, or selecting one or more extremes. Validation methods limit analyses to models with higher skill in simulating historical climate, ensemble methods typically take multi model means, median, or percentiles, and extremes methods tend to use scenarios which bound the projected changes in precipitation and temperature. In this paper a quantile regression based validation method is developed and applied to generate a reduced set of GCM-scenarios to analyze daily maximum streamflow uncertainty in the Upper Thames River Basin, Canada, while extremes and percentile ensemble approaches are also used for comparison. Results indicate that the validation method was able to effectively rank and reduce the set of scenarios, while the extremes and percentile ensemble methods were found not to necessarily correlate well with the range of extreme flows for all calendar months and return periods.
Keywords:
Climate Change, Uncertainty, Hydrologic Modelling, Extremes, Model Selection, Quantile Regression

1. Introduction
The process of regional climate change impact assessment with respect to water resources management typically involves the use of Global Climate Model (GCM) output to assess to the impact of a changing climate on river flow regimes. In this process, various bias correction and statistical or dynamic downscaling methods can be used to translate coarse scale GCM data to scales appropriate for regional impact analyses (e.g. hydrologic modeling). Uncertainty exists at all stages of regional climate change impact assessments of water resources. Alternate climate and hydrologic models, along with multiple methodologies for bias correction and downscaling all play a role. In previous studies the selection of climate models and future emission scenarios has been found to carry the highest uncertainty in this process which cannot be avoided [1] [2] [3] [4] [5] . Therefore, the process of climate model and scenario selection should be considered as an integral step in any regional analysis of vulnerability and adaptation to climate change.
The Fifth Coupled Model Intercomparison Project (CMIP5) provides a suite of GCMs consisting upwards of 35 models developed by 21 different modeling groups [6] . For each GCM there are multiple greenhouse gas emission scenarios known in the CMIP5 as Representative Concentration Pathways (RCPs). These pose a set of plausible pathways for the global radiative forcing associated with greenhouse gas emissions to the year 2100. The evolution of greenhouse gases in future emission scenarios is inherently uncertain, but because so many models exist to capture the same phenomena, there also exists a level of uncertainty associated with model structure between and within modeling groups, as well as from various model realizations due to the use of alternate initialization, and parameterization schemes. To deal with these sources of uncertainty, the IPCC recommends using as many GCM-scenario combinations as possible to generate a range of future climates when carrying out regional climate change impact analyses [7] . Depending on the computational nature of the analysis and available time and resources this approach may not be practical for management agencies and academic researchers [8] [9] [10] . As such, methods to select a subset of climate model outputs for a specific application are needed that can reasonably represent the range of predicted changes in future climate and their impacts.
Methods for selecting subsets of GCMs have been developed to reduce the number of GCM-scenarios required for impact assessments. [11] describes three general types of approaches consisting of the extreme combinations, ensemble, and validation methods. The method of extreme combinations approach is used to select models which re- present extreme combinations of climate variables, ensembles are used to aggregate GCM-scenarios, and validation can be used to limit the set of models to those with higher confidence. Hybrid selection approaches have been proposed consisting of a combination of two or more of these methods, while sensitivity-based methods have been used for generating climate impact response surfaces for which projected changes in climate variables can be directly translated into impacts [12] .
The ensemble approach selects a set of models that are aggregated using a multi- model mean. Although this approach lacks a physical basis, it has been shown to provide superior prediction capabilities with respect to historical climate, as the variability in the mean and variance of climate projections among multi-model sets have the ability to cancel each other out [13] . This suggests that the errors between models have an element of randomness [14] . While the ability to simply average all climate models and realizations can be a convenient selection method, it may not be applicable for analyzing hydro-climatic extremes. By taking an average, the variability in climate predictions on a daily scale is lost, and changes in different climate variables such as precipitation and temperature may no longer be physically consistent [15] . In addition, multi-model averages are not able to take into consideration the uncertainty in the timing of seasonal changes for precipitation and temperature, which is likely to alter the occurrence of extreme hydrologic events [8] . An alternative approach to developing multi-model ensembles can be made by selecting a set of GCM-scenarios corresponding to percentile changes in precipitation and temperature from the ensemble [11] [15] . In this way, changes in precipitation and temperature are obtained from the same models, making them physically consistent. Model runs are also kept separate in order to preserve the uncertainty in seasonal climate changes, and the loss in variance from averaging is eliminated.
Validation methods test the ability of climate models to capture various attributes of historical climate in an attempt to narrow the set of GCMs to those for which a higher level of confidence may be assigned in a particular region [11] . The assumption introduced here is that model skill in simulating historical climate attributes is indicative of projecting future climate. However, it is important to note that in previous studies model confidence or skill was not strongly correlated to the magnitude of future changes in precipitation and temperature on average [13] [14] . While the number of GCMs in the set to be used for evaluating climate impacts is reduced, this may not correspond with a reduction in the range of projected changes in climate. However, more importance may lie in the relationship of model skill and the projection of extremes. A wide range of metrics for the validation approach have been used based on the location, timescale, and variables of interest for a particular study. These metrics include; correlation and variance of mean statistics; comparisons of seasonal and diurnal fluctuations; prediction of regional meteorological phenomena (e.g. El-Nino Southern Oscillation (ENSO), Pacific Decadal Oscillation (PDO), cyclone development, etc.); robustness measures that take into account inter model spread; and methods of assessing model skill in reproducing probability density functions (PDFs) of specific climate variables [16] [17] [18] [19] . PDF methods that test the ability of climate models to simulate entire distributions of climate variables offer a tougher test than only comparisons of the mean and variance [19] ; however, they do not offer any indication of the GCMs ability to reproduce historical temporal trends. A common problem in using validation metrics is ranking the performance of each GCM, which range from arbitrarily selecting the top 50th percentile, averaging of ranks, or total Euclidean distance for a set of performance metrics with respect to historical climate [10] [13] [20] .
The method of extreme combinations involves the selection of GCM-scenario combinations in a way that aims to explore the full range of projected climate impacts. Previous studies have recommended using this method by calculating the maximum and minimum annual average changes in precipitation and temperature fields between a baseline and historical period for a set of GCMs [11] [15] [21] [22] . In this approach it is assumed that “extreme” combinations of projected changes in climate variables will generate the full range of projected climate impacts, however it many studies this is highly unlikely. In order to overcome this problem, studies have used simplified impact models to directly assess the sensitivity of changes in climate on specific impacts. Ntegeka et al. [8] used a simple lumped hydrologic model to select climate scenarios likely to generate extreme river flows. It was found that in order to replicate the upper and lower bounds of flow, combinations of climate perturbations from different models for both precipitation and evapotranspiration were needed. Vano et al. [9] used a Variable Infiltration Capacity model and dynamic general vegetation model to test the sensitivities of seasonally-averaged streamflow and vegetation carbon respectively, to changes in annual temperature and precipitation. Kay et al. [12] also used a sensitivity based method to estimate flood peaks for a range of river basins in the UK by generating a response surface dependent on the harmonic mean and amplitude of precipitation. The sensitivity metrics appear promising for quick selection of models to bound uncertainty with respect to extreme impacts. However, simplified impact models may not be able to capture the range of climate impacts projected by the full impact model, particularly in the case of extreme hydrologic events.
In this study three main selection methods (extreme combinations, ensemble, and validation) are applied to assess their effect on maximum daily streamflow uncertainty as a result of changes in daily precipitation and air temperature in the Upper Thames River Basin, Ontario, Canada. A quantile regression model validation methodology is proposed to assess the ability of GCMs to capture long-term changes in the distribution of hydrologically relevant climate variables. The proposed methodology is unique in that it considers the ability of GCMs to simulate the trajectory of observed climate across the distribution of a particular climate variable to gauge model skill. This is in contrast to methods which only simulate mean trends, or PDF methods which simply compare static GCM simulation of historical climate variable distributions to observations. This method is then used with a Compromise Programming multi-objective ranking method [23] to delineate the set of robust models with respect to the quantile regression results. This approach is then compared to an extreme combination and percentile ensemble scenario selection approach modified from [15] to gauge whether these selection methods are able to generate extreme and uniformly distributed maximum daily streamflow respectively.
In the following sections the details of the GCM-scenario selection methods are presented, along with the procedure used for the downscaling and hydrologic modeling of stream flow in the Upper Thames River Basin. Results of the selection process and its ability to capture daily maximum streamflow uncertainty are discussed, followed by concluding remarks and recommendations.
2. Methodology
2.1. Global Climate Model Evaluation and Scenario Selection
2.1.1. Validation Approach
Validation was used in this study to filter out the GCMs that under perform in comparison to the others with respect to their ability to represent the change in a climate variable’s distribution with time. The method used here is a linear quantile regression model to estimate the trajectory of a climate variable Y, for a given quantile,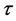 . The linear model, following Srivastav et al. [24] , adapted from Koenker and Bassett Jr. [25] is shown as a relationship between Y and time t, for a given quantile
. The linear model, following Srivastav et al. [24] , adapted from Koenker and Bassett Jr. [25] is shown as a relationship between Y and time t, for a given quantile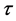 ,
,
 (1)
(1)
where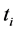 , and
, and 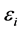 are the time index and error terms respectively for a given time step
are the time index and error terms respectively for a given time step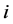 , while
, while 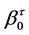 and
and 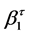 are the regression coefficients for a given quantile
are the regression coefficients for a given quantile . Regression coefficients can be obtained by minimizing,
. Regression coefficients can be obtained by minimizing,
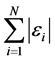
for a given value of , where the quantiles are defined by applying an asymmetric penalty function for values above and below the regression line as follows [25] ,
, where the quantiles are defined by applying an asymmetric penalty function for values above and below the regression line as follows [25] ,
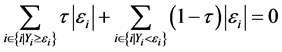 (2)
(2)
and the 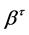 coefficients can be found for any value of
coefficients can be found for any value of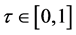 . By using quantile regression for this application as opposed to ordinary least squares, the temporal trend in varying quantiles of the distribution of Y can be compared between GCM and observed data as opposed to only the trend in the mean. The
. By using quantile regression for this application as opposed to ordinary least squares, the temporal trend in varying quantiles of the distribution of Y can be compared between GCM and observed data as opposed to only the trend in the mean. The 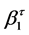 and
and 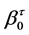 coefficients represent the slope and intercept of a particular climate variable for a given level of
coefficients represent the slope and intercept of a particular climate variable for a given level of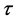 . Differences in the intercept between observed and GCM simulated historical climate re- present model bias, while differences in the slope can be considered as a disagreement in the long-term trajectory for a particular climate variable and quantile. Model bias is typically dealt with through the implementation of bias correction methods, and is already accounted for in the downscaling procedure described in the following section. Therefore, it is not considered for comparison to observations. In order to compare the quantile regression slopes between observed and GCM simulated historical climate, 95% confidence intervals are generated for
. Differences in the intercept between observed and GCM simulated historical climate re- present model bias, while differences in the slope can be considered as a disagreement in the long-term trajectory for a particular climate variable and quantile. Model bias is typically dealt with through the implementation of bias correction methods, and is already accounted for in the downscaling procedure described in the following section. Therefore, it is not considered for comparison to observations. In order to compare the quantile regression slopes between observed and GCM simulated historical climate, 95% confidence intervals are generated for 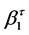 using the bootstrapping procedure described in Koenker and Hallock [26] . If there is no overlap in confidence intervals of
using the bootstrapping procedure described in Koenker and Hallock [26] . If there is no overlap in confidence intervals of 
Regional assessment of hydrologic extremes in response to climate change must target models that can more accurately simulate the changing statistical distributions of precipitation and air temperature for the purpose of hydrologic modeling. As such the analysis is applied to these variables; however, because the regional climate change impact assessment is directed towards changes in maximum daily flows, the extreme quantiles are given larger weight. With regards to precipitation, this signifies the ability to simulate higher magnitude events likely to cause flooding. To account for these effects, the number of failures in each quantile is weighted using a quadratic function with a heavier weight on the extremes. As such, the weighting for precipitation is assigned to be 0 when 


In order to rank and filter out models that under perform with respect to the others for precipitation and temperature variables, a compromise programming approach is taken to find the most robust set of models with respect to a set of distance metrics from the weighted mean failure rate to the ideal failure rate (0 percent weighted average failure rate for both precipitation and temperature variables). The distance metrics, 

where r is the number of climate variable skill scores (in this case r = 2 corresponding to the weighted average failure rate for precipitation and temperature), 






2.1.2. Extremes Approach
After the subset of GCMs have been selected from the validation method, a scatter plot method was used to select GCM-scenario combinations that are likely to generate hydro-climatic extremes. In the report from EBNFLO [15] , annual average temperature and precipitation change combinations from a baseline to future period were used to select 4 GCM-scenarios that represented the total range of uncertainty for future climate. This method assumes that extreme hydro-climatic events are linked to combinations of high temperature, low precipitation and vice versa for low and high stream flows respectively. In this study an intra-annual dimension is incorporated by using the N-day maximum annual adjusted precipitation change as a proxy for high flow events, where N corresponds to the time of concentration for the hydrologic model of the river basin under consideration. The use of adjusted precipitation takes into account the impact of snow accumulation and melt calculated using a degree day method.
2.1.3. Ensemble Approach
Due to the inherent uncertainty in future climate projections, it is essential to quantify the spread in climate related impacts using multi-model ensembles [27] . Using the same indicators for the selection of extreme GCM-scenario combinations, a range of scenarios within the 4 extreme precipitation and temperature combinations can be selected. This range corresponds to the 5th, 25th, 50th, 75th, and 95th percentile changes for the 5-day maximum annual precipitation and daily average air temperature. These combinations provide scenarios that cover the statistical range of future changes in precipitation and temperature. The impact of these GCM-scenario selection methods on the level of uncertainty in future stream flows for the basin is assessed in Section 4. Ideally, these methods should provide a way to limit the number of future climate scenarios that must be simulated, while retaining the uncertainty associated with future impacts of climate change on extreme daily flows.
2.2. Statistical Downscaling of Future Precipitation and Temperature Series
After the GCM-scenarios have been selected, future downscaled precipitation and temperature variables are generated using a Change Factor Methodology (CFM) combined with a non-parametric weather generator. CFMs consist of additive or multiplicative methods using single or multiple change factors for a given variable as seen fit for a particular analysis [28] . Typically CFMs allow for changes in the mean or variance projected by GCMs to be applied to historically observed data through additive and multiplicative change factors [29] . The factors can be calculated for the entire baseline period, or subdivided into calendar months to take into account seasonal variability for projected climate changes. Although monthly change factors take into account seasonal variability, they do not allow for accurate estimation of the changes in daily extreme climate data [30] .
In this study a monthly multiple change factor approach is used to scale future variables of daily precipitation and average air temperature. By using multiple change factors for each calendar month, the changes for a set of percentile ranges can be used to perturb the historical climate distributions, while taking into account seasonal climate changes. This allows for more accurate estimates of changes in extreme temperature and precipitation amounts. For this approach, Anandhi et al. [28] recommends a minimum of 25 change factors to reduce the difference in results obtained by using additive or multiplicative change factors. Additive change factors are used for air temperature, while multiplicative factors are used for precipitation. These are applied to the observed station data to generate a future scaled dataset. By using a multi CFM approach to perturb the historical climate record, bias correction is taken into account, as only the changes between GCM time slices are applied [8] .
The scaled climate series using CFM are then used with KNN-CADv4, a multi-site, multivariate weather generator developed by King et al. [31] . The main purpose of this step is to explore plausible temporal variability within the historical record through the process of bootstrap resampling, while generating a long climate series using the future scaled baseline period that will then be used for streamflow-frequency analysis. For this analysis, a total of 150 years of simulated weather is generated. Using this method, the spatial correlation among meteorological stations, as well as the temporal correlation of the generated variables will be preserved, as 10-day block periods are used for resampling among meteorological stations [31] .
3. Application
3.1. Description of Study Area
The area used for demonstration of GCM evaluation and scenario selection in this study is the Upper Thames River Basin (UTRB) located in Southern Ontario, Canada (Figure 1). The Thames River is composed of two main branches, the North and South, draining areas of 1750 km2 and 1360 km2 respectively. The climate can be considered as temperate, with mean annual precipitation of ~950 mm, an average air temperature of 8˚C, and a mean flow at the basin outlet of 42.6 m3∙s−1 (statistics calculated for 1975- 2005). At the basin outlet, a time of concentration of 5 days has been observed, and is used for scenario selection in this study [32] . The region is home to approximately 420,000 people mostly concentrated in the City of London located at the intersection of the North and South river branches. In early March, flooding as a result of snowmelt and spring rainfall on frozen ground constitutes one of the major hydrologic hazards in the basin [30] . In the past, flooding has resulted in extensive damage to the City of London, prompting construction of reservoirs and dykes for flood control.
Figure 1. Location of the Upper Thames River Basin in Southwestern Ontario, Canada.
3.2. Data Collection and Preparation
Meteorological data in the form of daily precipitation, as well as mean air temperature were obtained for 22 measurement stations in and around the UTRB for the period of 1950-2013. This data was obtained from the ANUSPLIN V4.3 dataset, constructed using a thin plate smoothing spline surface fitting method with Environment Canada climate station observations [33] [34] . This period was selected to be as long as possible in order to be able to detect longer term changes in the observed data using the linear quantile regression method for model validation.
GCMs used in the IPCC AR5 report that included climate variables corresponding to the selected meteorological variables for the historical scenario, as well as future emission scenarios RCP 2.6, RCP 4.5, and RCP 8.5 were selected for further analysis. These datasets were obtained from the CMIP5 through the Earth Surface Grid Federation data portal hosted by the Program for Climate Model Diagnosis and Intercomparison at the Lawrence Livermore National Laboratory. Information on each GCM’s name, affiliation and horizontal resolution are listed in Table 1. Each GCM grid was interpolated using the inverse distance method (IDM) for comparison with historically observed meteorological station data. Two 30-year future periods were selected for analysis centered on 2050 (2035-2065) and 2080 (2065-2095). The 2050 time period has been deemed to be appropriate for strategic planning, risk framing, and building resilience in water resources, while the 2080 time period can be used for longer term climate change impact assessments [15] .
3.3. Hydrologic Modeling in the Upper Thames River Basin
A calibrated, semi-distributed continuous hydrological model developed with HEC- HMS is used to estimate the impact of climate changes on streamflow at the basin
Table 1. Global climate models used in the selection process and maximum daily flow assessment.
outlet. In the model, precipitation data in combination with a soil moisture accounting algorithm, are used to generate baseflow and rainfall excess, which is then routed to streamflow in the river channel. Temperature data is used in the soil moisture accounting algorithm to determine evapotranspiration rates with the Thornthwaite equation. The Thornthwaite equation is used here for simplicity, as evapotranspiration effects were likely to be negligible when considering daily maximum flows, especially at larger return periods. The calibration and validation procedure for the model can be found in [32] . The focus of this study is limited to the effect of climate change on streamflow, and as such potential effects of changing land-use, reservoir operation, and water consumption and use were not included. The resulting flow series from the weather generated climate are used to compute flow-frequency curves with the Generalized Extreme Value (GEV) distribution. The GEV distribution was selected as it has been shown to perform well in comparison to other commonly used distributions in the UTRB [35] .
4. Results and Discussion
4.1. Selection of Global Climate Models Using the Validation Approach
Quantile regression slopes for both precipitation and temperature were calculated for the historically observed data (Figure 2).
The highest quantile regression slopes for wet-day precipitation were found for the largest precipitation events, to a maximum of 0.5 mm/decade (Figure 2(a)). The uncertainty however, is larger at the upper quantiles. This is expected as there is a greater amount of variability between events in this range. Below the 85th quantile the majority of regressions show slope parameters that are less than zero, signifying that in the UTRB there exists some evidence to say that small to medium daily precipitation amounts have been decreasing slightly while extreme daily precipitation amounts have increased over the observation period. With respect to air temperature, the changes are more pronounced. Significant trends across the distribution ranging from 0.07 to 0.36˚C/decade were found, with the largest changes concentrated at the lower quantiles (

Figure 2. All historically observed quantile regression slopes for (a) daily precipitation (mm/ decade) and (b) temperature (˚C/decade) variables for the period of 1950-2013. Shaded regions depict the 95% confidence interval for each regression slope.
Nearly all of the quantile regressions had positive slope parameters, most of which were significantly different from zero, with a maximum of approximately 0.35˚C/decade at the 30th quantile. The cumulative fraction of quantile regressions determined to be statistically significant are shown in Figure 3. Air temperature is shown to have statistically significant trends for 69% of all quantile regressions performed whereas precipitation has shown a total of 76%. The regions where the trends were not statistically significant are shown as flat regions in Figure 3, and shaded regions overlapping a slope of zero in Figure 2.
The underlying assumption comparing quantile regression trends between observed and modelled climate is that the models are capable of capturing historical levels of anthropogenic forcing, building confidence towards the climatic response to future forcing. The role of internal climate variability as opposed to historical anthropogenic forcing on the quantile regression slopes was tested by comparing the percentage difference in the quantile regression slopes when accounting for internal climate variability (in the form of ENSO and PDO) as additional endogenous components (Figure 4).
Figure 3. Cumulative fraction of quantile regressions determined to be statistically significant (p < 0.05).

Figure 4. Percentage difference of quantile regression slope parameters for precipitation (a) and temperature (b) with and without PDO and ONI as internal climate variability components. Dotted lines denote the regions of +/−20% difference.
The factors accounted for were the Oceanic Nino Index (ONI) and Pacific Decadal Oscillation (PDO) index. The results show that almost all of the precipitation slopes were largely unaffected by considering the effects of internal climate variability in the form of these indices. The temperature slopes however, are shown to be much lower at
With the proposed methodology, skill scores for each GCM, representing the weighted mean percentage of failures across model realizations and climate stations, for daily precipitation and average air temperature were calculated. It is assumed that models with a high failure rate may have a model structure or parameterization that is less applicable for the region of interest. With regards to precipitation it was found that the highest amount of failures were detected between the 15th and 80th quantiles, while the failure rate for smaller and more extreme events was much lower (Figure 5). This may be due to the fact that there is less variability across the distribution of precipitation at lower quantiles. For the largest events there were less regressions determined to be statistically significant and therefore could not be counted as failures.
Overall, HsdGEM2-AO and MIROC-ESM-CHEM had the highest weighted mean failure rates at 30% and 25% respectively, indicating that these models may be less applicable for projecting long-term changes in precipitation for the UTRB. With
Figure 5. Percentage of failures for precipitation by model for each quantile sorted top to bottom by weighted mean.
respect to average air temperature, it was found that the distribution of failure rates is opposite from that of precipitation, with more failures concentrated at the extremes (Figure 6). This may be in part due to the fact that there were fewer statistically significant quantile regression trends found between the 45th to 60th quantiles. BNU-ESM and HadGEM2-AO were shown to have the highest failure rate for air temperature, corresponding to 31% and 26% respectively. Although HadGEM2-AO performed poorly in both assessments of daily precipitation and air temperature, other models such as FGOALS-g2 had the lowest failure rate with regards to precipitation, and was in the top three for air temperature. It is because of this that both metrics should be considered for the overall ranking.
In order to select specific GCMs for further analysis, a subset is excluded in order to eliminate models which were found to be less capable in simulating historically observed climatic changes through the compromise multi-objective programming method. The remaining models in turn are deemed to be more robust. Rankings were first establishing using the distance metric p for values of 1, 2, and 100, with a equal to 0.5 for both temperature and precipitation from the ideal point (Figure 7).
Models are excluded by eliminating those that consistently rank in the bottom N. The relationship between N and the number of models selected is shown in Figure 8.
As the value of N increases, the selection criterion becomes more strict, and fewer models are included in the robust model set. In the UTRB a break-line appears at N = 12, where a decrease no longer eliminates GCMs from the analysis until N = 15. For this particular example, models that are below the dotted break line are deemed to be sufficiently robust in simulating the change in daily precipitation and air temperature distributions over the historical period for the UTRB, and are kept for further analysis.
Figure 6. Percentage of failures for average air temperature by model for each quantile sorted top to bottom by weighted mean.
Figure 7. Position of GCMs relative to the ideal point (0,0).
In other regions it may be possible to see a more distinct break line, to determine more specifically which models can be eliminated from the analysis. If a break line is not found, then it is up to the climate change impact modeler to justify how many models are feasible to include in subsequent analyses, and set the break line accordingly. It is important to note here that the compromise programming method of model ranking and selection can be extended to include more metrics of model skill as opposed to only those obtained from the quantile regression method proposed here, in order to obtain a more robust ranking of GCMs. In addition, the inclusion of more metrics may result in a clear break line with fewer models included in the robust model set.
4.2. Selection of Global Climate Model Scenarios Using the Extreme Combination and Percentile Ensemble Methods
Quantile regression was used to develop model skill scores, and the compromise programming method was used to rank and select a robust set of GCMs in simulating historical climate trends for the UTRB. The goal of the extremes and percentile ensemble methods are to select a set of GCM-scenarios in a way that preserves the range of uncertainty for future regional climatic changes. In Figure 9 the changes in annual average air temperature and 5-day maximum adjusted precipitation are shown for each GCM-scenario from the excluded models (those above the break line in Figure 8) and selected models.
Annual average temperature changes were shown to range from 0.8˚C to 4.4˚C, while the 5-day maximum annual adjusted rainfall had a range of −37.8% to 11.9%. The highest density of projected annual average temperature and 5-day annual maximum adjusted rainfall changes was shifted approximately −0.7˚C, and 8% respectively comparing the excluded to robust model sets. There do not appear to be any clear outlying scenarios. For the period of 2065-2095 the range and distribution of precipitation
Figure 8. Relationship between selection criterion denoting models that consistently appear in the bottom N, and the number of GCMs excluded from the analysis. The dotted break line highlights the point at which 9 models are excluded that consistently appear in the bottom 12.
Figure 9. Changes in annual average temperature and 5-day maximum annual adjusted rainfall from baseline to future (2035-2065), and their marginal distributions shown on the top and right axis respectively for both the robust and excluded model sets. GCM-scenarios selected by the extreme combinations and percentile ensemble methods are enclosed in circles and squares respectively.
changes remains approximately the same, while the changes in temperature are greatly skewed, as much higher temperature changes are projected to a maximum of 7.4˚C (Figure 10). In both future time slices it is noted that the excluded model set has higher projected maximum annual average temperature and 5-day maximum annual adjusted rainfall changes.
This cannot simply be justified by a lack of model skill on average using the quantile regression method to delineate the excluded and robust model sets. In future studies it may be possible to test the relationship between model skill and quantile regression slopes, however previous studies have not shown there to be a relationship between model skill and the magnitude of projected changes using mean statistics [13] [14] .
4.3. Characterizing Seasonal and Extreme Daily Flow Uncertainty with Respect to the GCM Selection Methods Used
The average monthly maximum daily stream flow in response to future climate perturbations from the periods of 2035-2065 and 2065-2095 are shown in Figure 11. In both time periods many of the GCM-scenarios used in this analysis project the timing of daily flow peaks to be shifted from March to February and January. This is due to the fact that increasing temperatures in late winter to early spring will shift the timing of
Figure 10. Changes in annual average temperature and 5-day maximum annual adjusted rainfall from baseline to future (2065-2095), and their marginal distributions shown on the top and right axis respectively for both the robust and excluded model sets. GCM-scenarios selected by the extremes and percentile ensemble methods are enclosed in circles and squares respectively.
Figure 11. Modelled maximum daily streamflow for all climate scenarios averaged across calendar months and divided into excluded and robust model sets for the validation method, as well as percentile ensemble and extreme combinations scatter-plot methods.
snowmelt contributions to streamflow. In the months that typically present the highest flow, the models that are part of the robust model set generally tend to preserve most of the uncertainty in maximum daily stream flows. In the months of June to September the excluded model set has a range that is greater than or equal to that of the robust model set, indicating that during the summer months the GCM uncertainty has been reduced.
The projected streamflow associated with the scenarios selected by the extremes method in most cases appears to underestimate the daily maximum streamflow range, especially during June to September where flows are generally lower. Similarly, the percentile ensemble scenarios do not provide good coverage of maximum daily streamflow ranges in most calendar months. It is likely that the annual average change in the 5-day maximum adjusted precipitation is not a good indicator for the lower range, as the lowest maximum daily flows may be associated with shorter duration rainfall. Additionally, it should be noted that summer flows are harder to reproduce in hydrologic models and include structural uncertainty as well. It is also important to note that the extreme combinations method does not generate the range of maximum daily flows for all months, as the metric used to select scenarios is not season specific. These two findings highlight the importance of using an appropriate metric to select GCM-scenarios that capture the range of a particular impact.
For the purpose of climate related impact frequency estimation, the quantile regression validation metrics could be useful for the selection of climate models for which the increase in extremes are of particular importance. Such cases could include selecting climate models for downscaled precipitation to be used in updating Intensity-Dura- tion-Frequency curves for storm water management design, or input to hydraulic models for the updating of floodplain maps. In this study flow-frequency curves are a useful tool for this type of analysis, as it allows for not only the magnitude of daily flows to be compared, but also the frequency of their occurrence. At the outlet of the UTRB the simulated historical flow corresponding to the 10 and 100 year return periods is 720 and 1215 m3∙s−1 respectively, while the impact of climate change on the historical flow frequency curve has a considerable amount of uncertainty (Figure 12). For the 2035 - 2065 time slice, ranges for the 10 and 100 year return period flows were simulated as 460 - 925 m3∙s−1 and 631 - 2160 m3∙s−1 respectively, while for the 2065 - 2095 time slice, the ranges of flow corresponding to these return periods were 486 - 860 m3∙s−1 and 665 - 1790 m3∙s−1. Based on these ranges there appears to be no consensus on the direction of change of the flow-frequency curve from the baseline period.
The use of the extreme combinations scenario selection method for this approach tends to underestimate the flow-frequency range at all return periods for both time slices. Similarly, the results from the percentile ensemble scenarios did not capture the range or distribution of flow-frequency at all return periods. This finding indicates that the scatter plot method used to “bound” the uncertainty in future climate projections does not necessarily capture the uncertainty in predicted extreme stream flows when considering the 5-day maximum annual precipitation and mean annual temperature changes as a proxy for high and low flow scenarios.
Comparing the range of predicted discharges between the set of robust and excluded model sets reveals that the range of projected flows are greater for both future time slices and all return periods in the excluded model set. This indicates that selecting models with higher skill in replicating the linear quantile trends has the potential to reduce GCM related uncertainty associated with daily maximum streamflow. If this were the case, then selecting a larger value of N in the compromise programming model ranking step should result in a lower range, as this would exclude only models ranking in the bottom N. In Figure 13 the effect of the selection of N on the uncertainty in the flow frequency distributions estimated for the UTRB is shown.
Figure 12. Modelled flow-frequency curves derived using the GEV distribution for all climate scenarios divided into excluded and robust model sets for the validation method, as well as percentile ensemble and extreme combinations scatter-plot methods.
Figure 13. Relationship between maximum daily flow-frequency uncertainty and the selection of N in the GCM ranking step. Flow-frequency ranges are shown as overlapping areas in ascending order of N, while the historically observed flow-frequency curve is shown as a solid black line.
With an increasing value of N, the range of flows are reduced for all return periods. Furthermore, the range tends to narrow around the historically observed results. This observation indicates that higher ranked models tend to give flow-frequency estimates that are more similar to the historically observed data in this case. This may be due to the inability of lower ranked models to simulate historical quantile trends, thus projecting excessive changes in precipitation and temperature variables. It is important to note that there may also be cases in alternate regions where lower ranked models could underestimate the range of projected maximum daily streamflow distributions. As such, the selection of N should be well justified in that a clear breakpoint between the robust set of models and those that will be excluded should be present. Otherwise, an arbitrary selection of N may leave out plausible climate model projections for regional impact analyses that could potentially influence the range of results. If a clear breakpoint is not present, alternative metrics for model skill could be used in the compromise programming ranking method such as those used in Rupp et al. [16] . This would add higher dimensionality to the model evaluation and likely result in a clear breakpoint with more models being eliminated from the analysis.
The focus of this study was on climate model selection for the assessment of climate change impacts on hydro-climatic extremes. As such the variables, impact model, selection methods, and weighting strategies (with reference to the proposed validation methodology) are all directed towards the assessment of daily maximum streamflow. In order to apply the selection methodologies discussed here to assess alternate streamflow conditions such as mean and low flow, it is likely that different variables and quantile weighting strategies would need to be selected as indicators of a particular impact. For example, in the case of low flow conditions, the quantile regression validation methodology would need to be adjusted by placing more weight on the upper quantiles of temperature for the weighted percentage of failure calculation, and precipitation amounts might be replaced by dry period durations. In addition, the analysis could be done at a seasonal time scale to deal more specifically with seasonal impacts.
5. Conclusions
Incorporating climate change in regional vulnerability and impact assessments can be challenging given the presence of alternate climate models, model realizations, and future emission scenarios, especially if the impact assessment is computationally demanding. In this study validation, extreme combinations, and ensemble GCM-scenario selection methods were used and applied to the assessment of maximum daily stream flows in the Upper Thames River Basin, Canada. The validation procedure proposed compared the regression coefficients from a linear quantile regression model to assign a model skill score representing the ability of models to simulate historical changes in a climate model’s daily distribution. Model skill scores for precipitation and temperature were ranked using Compromise Programming to generate a robust set of climate models for the UTRB, and the extreme combinations and percentile ensemble scenario selection methods were employed in an attempt to generate a representative set to capture uncertainty in maximum daily streamflow.
Results from the analysis indicate that the quantile regression methodology was able to detect statistically significant long term linear quantile trends in the precipitation and temperature variables in order to compare GCMs and observations for the assessment of model skill in this regard. However, it was noted that the trends for the temperature variable at the lowest quantiles were significantly affected by internal variability. As such more work is needed to be able to separate these effects when compared the modelled and observe results, especially in other regions where these effect will be more significant. The application of the validation model selection proposed captures most of the uncertainty with respect to daily maximum stream flows, but can also reduce the range of predicted flow-frequency curves. In the ranking of models with the compromise programming method, a small breakpoint was found to reduce the model set. It is expected that by including additional climate metrics to compare the models and observations that a clearer breakpoint will emerge. The method is also general enough that it can be extended to other climate variables and related impacts.
Both the extreme combinations and percentile ensemble selection methods were based on the scatter plot to bound the uncertainty with respect to future temperature and precipitation changes that are likely to produce hydro-climatic extremes. The 5-day maximum annual precipitation and annual average temperature change combinations were used as proxies for the range of high flow scenarios. It is recommended that when using scatter plot methods to select GCM-scenarios the precipitation and temperature metrics should be carefully considered based on the impact under consideration.
Acknowledgements
The authors would like to acknowledge the support from the NSERC Discovery Grant Program given to Professor Slobodan P. Simonovic, as well as collaborative grants provided by Western University, Canada, and the Institute for Water Resources and Hydropower Research, China. CMIP5 climate model data can be found through the Earth System Grid Federation data portal hosted by the Program for Climate Model Diagnosis and Intercomparison at the Lawrence Livermore National Laboratory
Cite this paper
Breach, P.A., Simonovic, S.P. and Yang, Z.Y. (2016) Global Climate Model Selection for Analysis of Un- certainty in Climate Change Impact Assess- ments of Hydro-Climatic Extremes. American Journal of Climate Change, 5, 502-525. http://dx.doi.org/10.4236/ajcc.2016.54036
References
- 1. Jung, I.W., Chang, H. and Moradkhani, H. (2011) Quantifying Uncertainty in Urban Flooding Analysis Considering Hydro-Climatic Projection and Urban Development Effects. Hydrology and Earth System Sciences, 15, 617-633.
http://dx.doi.org/10.5194/hess-15-617-2011 - 2. Kay, A.L., Davies, H.N., Bell, V. and Jones, R.G. (2009) Comparison of Uncertainty Sources for Climate Change Impacts: Flood Frequency in England. Climatic Change, 92, 41-63.
http://dx.doi.org/10.1007/s10584-008-9471-4 - 3. Kingston, D.G. and Taylor, R.G. (2010) Sources of Uncertainty in Climate Change Impacts on River Discharge and Groundwater in a Headwater Catchment of the Upper Nile Basin, Uganda. Hydrology and Earth System Sciences, 14, 1297-1308.
http://dx.doi.org/10.5194/hess-14-1297-2010 - 4. Wilby, R.L. and Harris, I. (2006) A Framework for Assessing Uncertainties in Climate Change Impacts: Low-Flow Scenarios for the River Thames, UK. Water Resources Research, 42, Article ID: W02419.
http://dx.doi.org/10.1029/2005wr004065 - 5. Eisner, S., Voss, F. and Kynast, E. (2012) Statistical Bias Correction of Global Climate Projections—Consequences for Large Scale Modeling of Flood Flows. Advances in Geosciences, 31, 75-82.
http://dx.doi.org/10.5194/adgeo-31-75-2012 - 6. Taylor, K.E., Stouffer, R.J. and Meehl, G.A. (2012) An Overview of CMIP5 and the Experiment Design. Bulletin of the American Meteorological Society, 93, 485-498.
http://dx.doi.org/10.1175/BAMS-D-11-00094.1 - 7. Carter, T.R. (2007) Guidelines on the Use of Scenario Data for Climate Impact and Adaptation Assessment: Version 2.
- 8. Ntegeka, V., Baguis, P., Roulin, E. and Willems, P. (2014) Developing Tailored Climate Change Scenarios for Hydrological Impact Assessments. Journal of Hydrology, 508, 307-321.
http://dx.doi.org/10.1016/j.jhydrol.2013.11.001 - 9. Vano, J., Kim, J.B., Rupp, D.E. and Mote, P.W. (2015) Selecting Climate Change Scenarios Using Impact-Relevant Sensitivities. Geophysical Research Letters, 42, 5516-5525.
http://dx.doi.org/10.1002/2015GL063208 - 10. Brekke, L.D., Dettinger, M.D., Maurer, E.P. and Anderson, M. (2008) Significance of Model Credibility in Estimating Climate Projection Distributions for regional Hydroclimatological Risk Assessments. Climatic Change, 89, 371-394.
http://dx.doi.org/10.1007/s10584-007-9388-3 - 11. Fenech, A., Comer, N. and Gough, B. (2002) Selecting a Global Climate Model for Understanding Future Projections of Climate Change. In: Linking Climate Models to Policy and Decision-Making, UPEI Climate Lab, Prince Edward Island, 133-145.
- 12. Kay, A.L., Crooks, S.M., Davies, H.N., Prudhomme, C. and Reynard, N.S. (2014) Probabilistic Impacts of Climate Change on Flood Frequency Using Response Surfaces I: England and Wales. Regional Environmental Change, 14, 1215-1227.
http://dx.doi.org/10.1007/s10113-013-0563-y - 13. Pierce, D.W., Barnett, T.P., Santer, B.D. and Gleckler, P.J. (2009) Selecting Global Climate Models for Regional Climate Change Studies. Proceedings of the National Academy of Sciences of the United States of America, 106, 8441-8446.
http://dx.doi.org/10.1073/pnas.0900094106 - 14. Knutti, R. (2008) Should We Believe Model Predictions of Future Climate Change? Philosophical Transactions Series A, 366, 4647-4664.
http://dx.doi.org/10.1098/rsta.2008.0169 - 15. EBNFLO Environmental AquaResource Inc (2010) Guide for Assessment of Hydrologic Effects of Climate Change in Ontario. The Ontario Ministry of Natural Resources and Ministry of the Environment.
- 16. Rupp, D.E., Abatzoglou, J.T., Hegewisch, K.C. and Mote, P.W. (2013) Evaluation of CMIP5 20th Century Climate Simulations for the Pacific Northwest USA. Journal of Geophysical Research: Atmospheres, 118, 10884-10906.
http://dx.doi.org/10.1002/jgrd.50843 - 17. Walsh, J.E., Chapman, W.L., Romanovsky, V., Christensen, J.H. and Stendel, M. (2008) Global Climate Model Performance over Alaska and Greenland. Journal of Climate, 21, 6156-6174.
http://dx.doi.org/10.1175/2008JCLI2163.1 - 18. Maloney, E.D., Camargo, S.J., Chang, E., Colle, B., Fu, R., Geil, K.L., et al. (2014) North American Climate in CMIP5 Experiments: Part III: Assessment of Twenty-First-Century Projections. Journal of Climate, 27, 2230-2270.
http://dx.doi.org/10.1175/JCLI-D-13-00273.1 - 19. Perkins, S.E., Pitman, A.J., Holbrook, N.J. and McAneney, J. (2007) Evaluation of the AR4 Climate Models’ Simulated Daily Maximum Temperature, Minimum Temperature, and Precipitation over Australia Using Probability Density Functions. Journal of Climate, 20, 4356-4376.
http://dx.doi.org/10.1175/JCLI4253.1 - 20. Pincus, R., Batstone, C.P., Patrick Hofmann, R.J., Taylor, K.E. and Glecker, P.J. (2008) Evaluating the Present-Day Simulation of Clouds, Precipitation, and Radiation in Climate Models. Journal of Geophysical Research, 113, Article ID: D14209.
http://dx.doi.org/10.1029/2007JD009334 - 21. Murdock, T.Q. and Spittlehouse, D.L. (2011) Selecting and Using Climate Change Scenarios for British Columbia. Pacific Climate Impacts Consortium, University of Victoria, Greater Victoria.
- 22. Eum, H.-I., Arunachalam, V. and Simonovic, S.P. (2009) Integrated Reservoir Management System for Adaptation to Climate Change Impacts in the Upper Thames River Basin. London, 53 p.
- 23. Simonovic, S.P. (2009) Managing Water Resources: Methods and Tools for a Systems Approach. UNESCO, Paris and Earthscan James & James, London.
- 24. Srivastav, R.K., Schardong, A. and Simonovic, S.P. (2014) Computerized Tool for the Development of Intensity-Duration-Frequency Curves under a Changing Climate. London, 62 p.
- 25. Koenker, R. and Bassett Jr., G. (1978) Regression Quantiles. Econometrica, 46, 33-50.
http://dx.doi.org/10.2307/1913643 - 26. Koenker, R. and Hallock, K. (2000) Quantile Regression: An Introduction. University of Illinois, Illinois.
- 27. Ehret, U., Zehe, E., Wulfmeyer, V., Warrach-Sagi, K. and Liebert, J. (2012) HESS Opinions “Should We Apply Bias Correction to Global and Regional Climate Model Data?” Hydrology and Earth System Sciences, 16, 3391-3404.
http://dx.doi.org/10.5194/hess-16-3391-2012 - 28. Anandhi, A., Frei, A., Pierson, D.C., Schneiderman, E.M., Zion, M.S., Lounsbury, D., et al. (2011) Examination of Change Factor Methodologies for Climate Change Impact Assessment. Water Resources Research, 47, Article ID: W03501.
http://dx.doi.org/10.1029/2010WR009104 - 29. Piani, C., Weedon, G.P., Best, M., Gomes, S.M., Viterbo, P., Hagemann, S., et al. (2010) Statistical Bias Correction of Global Simulated Daily Precipitation and Temperature for the Application of Hydrological Models. Journal of Hydrology, 395, 199-215.
http://dx.doi.org/10.1016/j.jhydrol.2010.10.024 - 30. Das, S. and Simonovic, S. (2012) Assessment of Uncertainty in Flood Flows under Climate Change Impacts in the Upper Thames River Basin, Canada. British Journal of Environment & Climate Change, 2, 318-338.
- 31. King, L.M., McLeod, A.I. and Simonovic, S.P. (2014) Simulation of Historical Temperatures Using a Multi-Site, Multivariate Block Resampling Algorithm with Perturbation. Hydrological Processes, 28, 905-912.
http://dx.doi.org/10.1002/hyp.9596 - 32. Cunderlik, J.M. and Simonovic, S.P. (2004) Calibration, Verification, and Sensitivity Analysis of the HEC-HMS Hydrologic Model. London, 113 p.
- 33. Hutchinson, M.F., McKenney, D.W., Lawrence, K., Pedlar, J.H., Hopkinson, R.F., Milewska, E., et al. (2009) Development and Testing of Canada-Wide Interpolated Spatial Models of Daily Minimum-Maximum Temperature and Precipitation for 1961-2003. Journal of Applied Meteorology and Climatology, 48, 725-741.
http://dx.doi.org/10.1175/2008JAMC1979.1 - 34. Hopkinson, R.F., McKenney, D.W., Milewska, E.J., Hutchinson, M.F., Papadopol, P. and Vincent, L.A. (2011) Impact of Aligning Climatological Day on Gridding Daily Maximum-Minimum Temperature and Precipitation over Canada. Journal of Applied Meteorology and Climatology, 50, 1654-1665.
http://dx.doi.org/10.1175/2011JAMC2684.1 - 35. Millington, N., Das, S. and Simonovic, S.P. (2011) The Comparison of GEV, Log-Pearson Type 3 and Gumbel Distributions in the Upper Thames River Watershed under Global Climate Models. Water Resources Research Report No. 81, Facility for Intelligent Decision Support, Department of Civil and Environmental Engineering, London, 81 p.













