American Journal of Climate Change
Vol.3 No.1(2014), Article ID:43633,10 pages DOI:10.4236/ajcc.2014.31005
An Assessment of Trends of Monthly Contributions to Seasonal Rainfall in South-Eastern Zimbabwe
Brain Mapurisa, David Chikodzi
Department of Physics, Geography and Environmental Science, Great Zimbabwe University, Masvingo, Zimbabwe
Email: bmapurisa@gzu.ac.zw, dchikodzi@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 24 May 2013; revised 27 June 2013; accepted 24 July 2013
ABSTRACT
Trends in the proportional contribution to the seasonal rainfall of each month were analyzed for the meteorological stations of Buffalo Range, Masvingo Airport and Zaka in South-Eastern Zimbabwe. Results found indicate the existence of some trends for all the stations and months. However, when subjected to a Mann-Kendel trend analysis, all the trends were found to be statistically not significant for all instances except for the month of October at the Zaka station. This month showed a significant trend of increasing proportional rainfall.
Keywords
Contribution to Seasonal Rainfall; Monthly Trends; Masvingo; South-Eastern Zimbabwe

1. Introduction
Africa is considered highly vulnerable to climate change [1] , largely because many socio-economic activities in Africa, particularly agriculture, depend on climate and especially rainfall. Climate Change in Zimbabwe and in Masvingo Province in particular manifests itself through a variety of ways such as increases in temperatures, extreme rainfall events, and increases in the proportion of low rainfall years, decreases in low intensity rainfall events and increases in droughts. Also climate change as perceived by farmers in the Province is causing a shift in the rainfall season of the country. The farmers allege that the onset of the rainfall season is coming later (around December instead of October) and ending earlier (in February instead of March), and this is accompanied by increased frequency and length of mid-season dry spells [2] [3] .
A major problem for any adaptation initiative, particularly at the local level, is insufficient information about what to adapt to. This often results from a lack of awareness of how the climate has changed in the past (and how social systems have responded), and how it is expected to change in the future.
This is further complicated by the need to interpret changes from meteorological analyses in terms of an impact on a particular sector. For the agricultural sector, which is the main source of livelihood for the majority of the population in Masvingo Province, it is crucial to understand how rainfall characteristics are changing, particularly those affecting planting dates and the crop growth cycle, e.g., the start of the rains or frequency and intensity of dry spells and daily rainfall, that can destroy crops if they occur at critical stages of plant growth [4] -[6] .
Climatic variations and change have an impact on the productivity of many socio-economic activities [7] . Within the agriculture sector, proper scheduling of planting dates with the start of the rainfall season is arguably the most important factor that has major impacts on yields.
Climate change is often recognized as a progressive trend. The trend analysis of rainfall series is of practical importance for the detection of the gradual trends over time in face of climate change and variability. Worldwide interest in global warming and climate change has led to numerous trend detection studies to determine if the values of a random variable generally increase or decrease over some period of time in statistical terms [8] -[11] .
Previous studies of climate change and trends in Zimbabwe have mainly focused on predicting future climates, determination of whether rainfall totals have changed over time, perceptions of farmers to climate change, relationships between climate change and farm productivity and analysis of dry spell activity [12] -[15] . Almost nothing has been done to test the validity of a common perception that the percentage contribution of each month of the rainfall season to the total seasonal rainfall has shifted.
The research therefore aims at determining whether the proportional contribution of each month in the rainy season to the annual rainfall shows any significant trend. The research hypothesis is that there is no significant trend in the contribution of each month’s rainfall to the seasonal total. The research outputs will help farmers and water resources’ planners to determine whether current problems of low agricultural yields and water availability are due to effects of natural climate change and variability or management practices.
2. Materials and Methods
2.1. Study Area
The area of study comprises the whole of Masvingo province. Masvingo Province is found in the south-eastern part of Zimbabwe comprising of seven districts, namely Bikita, Chiredzi, Chivi, Gutu, Masvingo, Mwenezi and Zaka. The province is 56,566 km² in area with a total population of 1,318,705 of which 616,243 are male and 702,462 are females. Figure 1 shows the study area [16] .
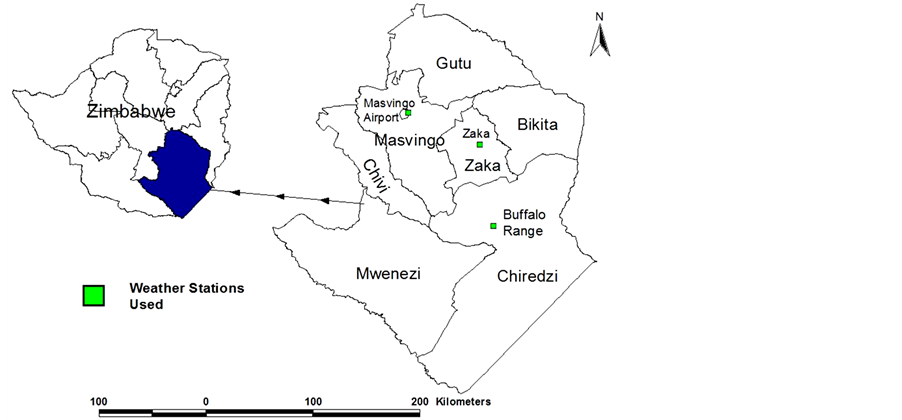
Figure 1. Study Area (south-eastern Zimbabwe).
The study area is located in the south-east low veld of the country where rainfall is minimal and uncertain. The southern parts of the province are drought prone and occur in agro-ecological region 5 of Zimbabwe. The province receives an average of 620 mm of rainfall per annum and has an average potential evapo-transpiration of between 600 - 1000 mm which by far exceeds the available water supply [2] .
2.2. Materials
• Rainfall Records for Masvingo Airport, Buffalo Range and Zaka weather stations run by the Zimbabwe Meteorological Services Department.
• Statistical Package for Social Scientist (SPSS).
• XLSTAT 2013 Excel plug-in.
2.3. Methods
For all the stations the raw mean monthly rainfall data for the rainfall seasons were acquired. Zimbabwe’s official rainfall season stretches for six months from October-March. The rainfall data obtained was for all the seasons since records began for each individual station. This was then followed by creating a time series of percentage contributions of rainfall for each month towards the annual total rainfall for each season.
The results showed a time series of percentage contributions of each rainfall month to the total seasonal rainfall since records began. These percentage contributions for each month over time were then subjected to normality tests using the Kolmogorov-Smirnov test in SPSS exploratory data analysis (EDA) in order to evaluate how well the data satisfies assumptions of parametric or non-parametric statistical analysis methods. Unless the assumption of normal distribution for parametric statistics is met, it is generally advisable to use nonparametric tests [17] [18] . Since the data was not normally distributed, non-parametric statistical methods were used in this study.
To examine whether the contribution of each month’s rainfall to the annual rainfall shows any significant trend, the Mann-Kendall (M-K) trend test was used. It was conducted for the rainy season months of OctoberMarch. If one were interested in detecting a trend in a particular month, the Mann-Kendall trend test for that particular month or group of months could be used [19] [20] . The Mann-Kendall trend test was used because it is simple, robust, can cope with missing values, and the data need not conform to any particular distribution [20] -[23] . Through the M-K test, the null hypothesis H0, that there is no significant trend, was tested, i.e. the observations are randomly ordered in time, against the alternative hypothesis, H1, where there is an increasing or decreasing monotonic trend.
Using the XLSTAT 2013 plug-in of Microsoft excel, the monthly percentage contributions of rainfall over years were subjected to the M-K trend test shown in Equation (1).
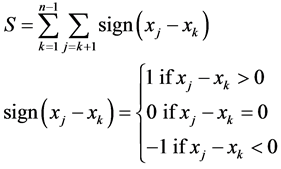 (1)
(1)
where: 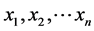 represent n data points, xj represents the data point at time j and S is the Mann-Kendall statistic.
represent n data points, xj represents the data point at time j and S is the Mann-Kendall statistic.
The results were then presented in the form of graphs and tables.
3. Results
Normality tests done on all sets of the three rainfall station data using the Kolmogorov-Smirnov test revealed that the data on percent contribution of each month to the total rainfall were randomly distributed (p = 0.000, α = 0.00 and p = 0.000, α = 0.05).
Figure 2 shows the trend of percentage rainfall distribution of monthly rainfall for the first three months of the rainfall season for Zaka Station. All the months show an increase in total rainfall contribution with time as shown by the positive trend lines on each month. The steepest increase is for the month of December.
Figure 3 shows the percent contributions of the second half of the rainfall season. In all the three months, there is a notable decline in their percentage contribution to the total. The steepest decline is for the month of March.
Figure 4 shows the percentage contribution of the first three months of the rainfall season at Masvingo Airport station. The trend shows so much fluctuations and variations with time but the month of December at the station shows a declining trend with time while October and November show slightly positive trends.
Figure 5 shows the percentage contribution of the last three months of the rainfall season at Masvingo Airport station. The months of January and February showed declining trends with time as evidenced by the negative trend line equations while March showed a slightly increasing trend.
Figure 6 shows the percentage contribution of the first three months of the rainfall season over time at Buffalo Range station. The onset of the season is beset by declining trends with October and November showing negative trend equations. December, however, shows an increasing trend from an average of less than 20% to an average of close to 30%.
Figure 7 shows the percentage contribution of the last three months of the rainfall season at Buffalo Range station. The month of February shows a declining trend while January and March show an increasing trend.
Figure 8 shows the long-term rainfall percent contribution of each rain season month at Masvingo station.
Figure 8 shows that for all the months, the percentage contributions are positively skewed towards the upper quartile of the distribution as indicated longer whiskers at the upper quarter of the data. The distribution shows that the percentage contribution of each month increases gradually until it peak in December and January and the starts to decline in February and March. In terms of rare events for Masvingo Station Figure 8 shows that
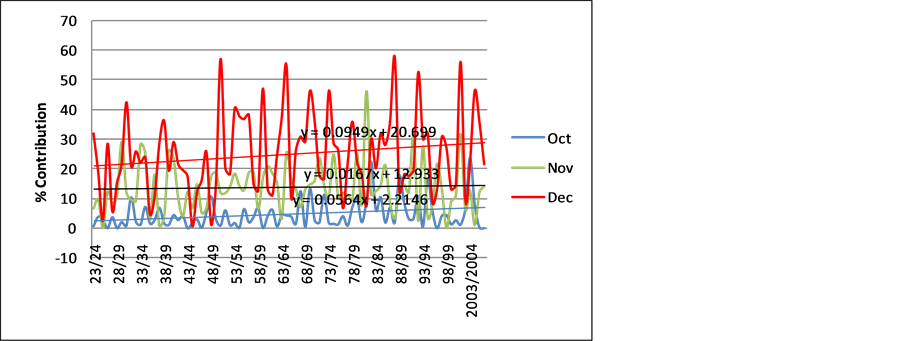
Figure 2. Zaka station monthly rainfall contribution trend for the first three months of the rainfall season.
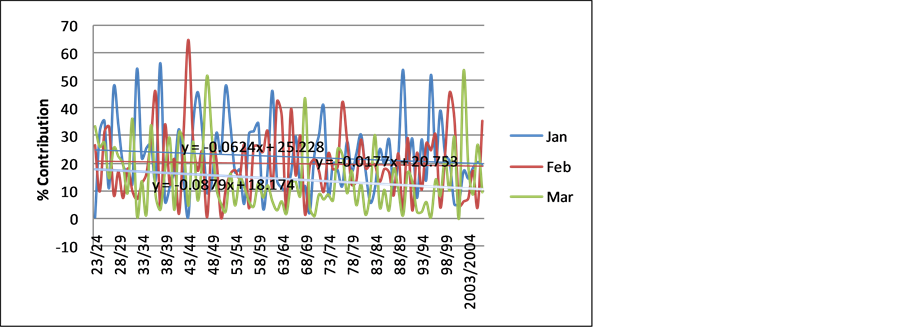
Figure 3. Zaka station monthly rainfall contribution trend for the last 3 months of the rainfall season.

Figure 4. Masvingo station monthly rainfall contribution trend for the first 3 months of the rainfall season.
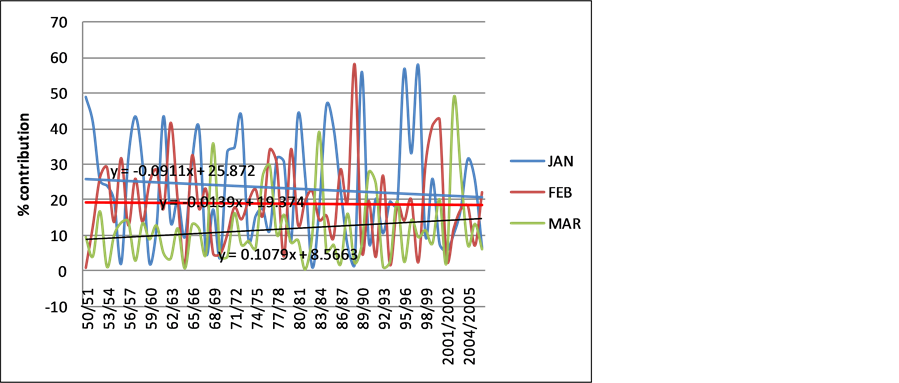
Figure 5. Masvingo station monthly rainfall contribution trend for the last 3 months of the rainfall season.
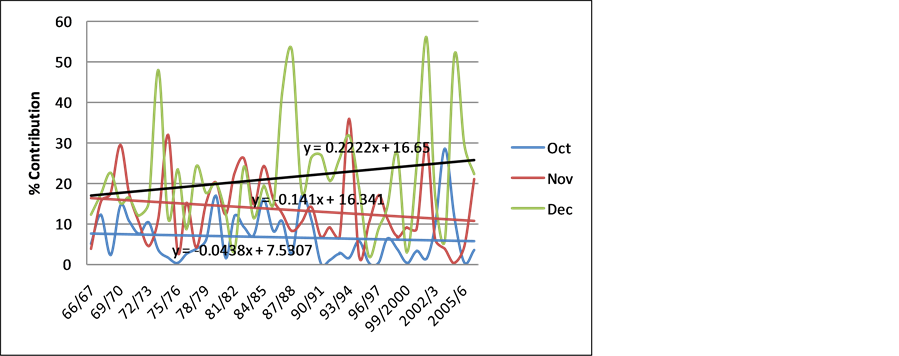
Figure 6. Buffalo range monthly rainfall contribution trend for the first 3 months of the rainfall season.
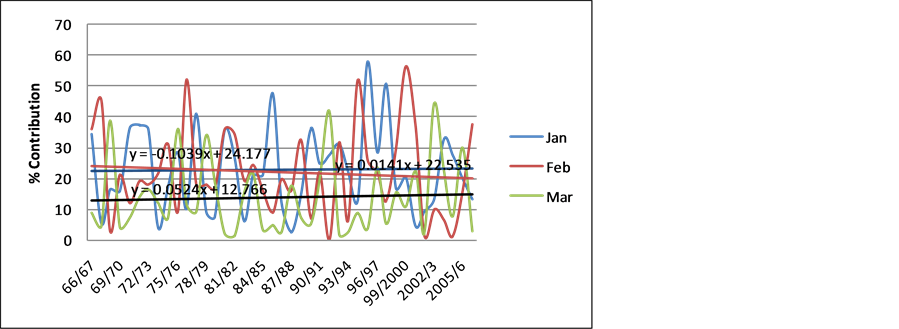
Figure 7. Buffalo range monthly rainfall contribution trend for the last 3 months of the rainfall season.

Figure 8. Percentage contribution of each month to total rainfall for Masvingo station.
they occur in the form of extremely high rainfall total contribution rather than low ones. The months of October, March and November have the highest number of outliers.
Figure 9 shows the long-term rainfall percent contribution of each rain season month at Buffalo Range station. At this station, the months of January and February contribute the most rainfall at the station. But their means are slightly below the median of the second and third quartile ranges indicating a declining mean over time. At Buffalo Range, it is mainly the month of December that has extreme high rainfall events. At the months have rainfall contributions which are positively skewed toward higher percentage contribution as shown by the longer whiskers on the upper quartiles on Figure 9.
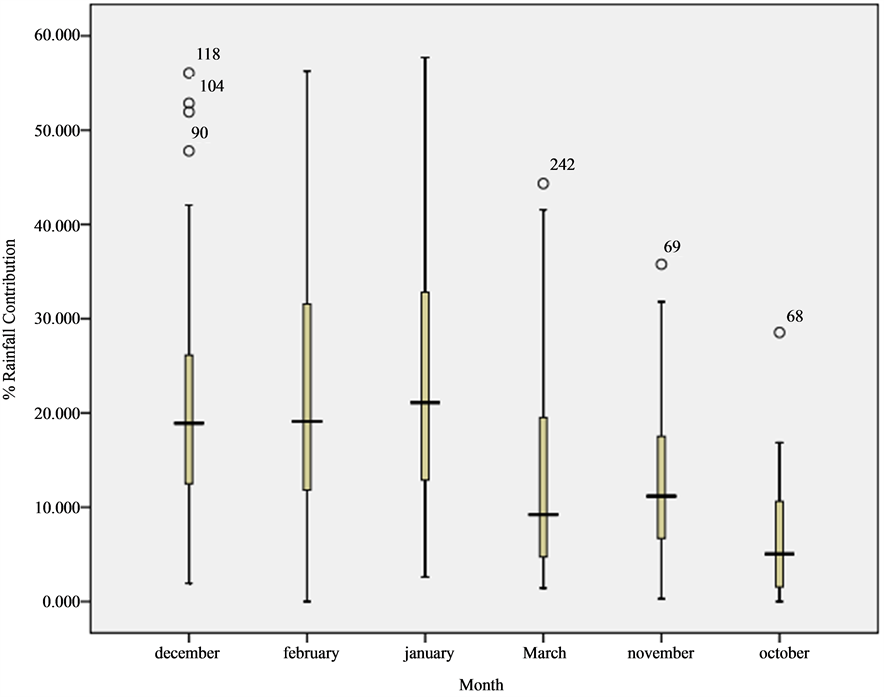
Figure 9. Percentage contribution of each month to total rainfall for Buffalo Range.
Figure 10 shows the long-term rainfall percentage contributions of each rain season month at Zaka station. The figure shows the months of October and March are the ones that on average receive uncharacteristic high rainfall events than expected. The months of December and January contribute most of the total rainfall received at the station.
A Mann-Kendall trend test was run for all the stations in order to determine if there was a month of the rainfall season whose contribution to total seasonal rainfall had significantly declined. Table 1 shows the results of the Mann-Kendall trend test for Zaka. The results for Zaka station show that the increase in rainfall contribution was statistically significant (p = 0.046, α = 0.05) only for the month of October.
The results imply that the onset of the rainfall season in Zaka had significantly shifted to increased rainfall contributions and that the contribution from the rest of the rainfall months remains the same.
Table 2 shows the Mann-Kendall trend test results for Buffalo Range station. The Mann-Kendall trend test was run Buffalo Range showed that there was no significant change in the contribution of each month to the total rainfall received at the station (no p-value less than 0.05, α = 0.05). Only the month of November shows a p-value close to significant.
Table 3 shows the Mann-Kendall trend test results for Masvingo station. Table 3 shows that the contribution of each rainfall month at Masvingo station to the seasonal total has not significantly changed.
4. Discussions and Conclusion
The results obtained show that for the stations considered in this study, only the month of October at Zaka station registered significant shift in rainfall contribution to the annual seasonal total. For this particular instance, an increase in contribution to the seasonal total has been recorded. This observation is in contrast to earlier work which asserts that the onset of the rainfall season was coming late at the station [12] .
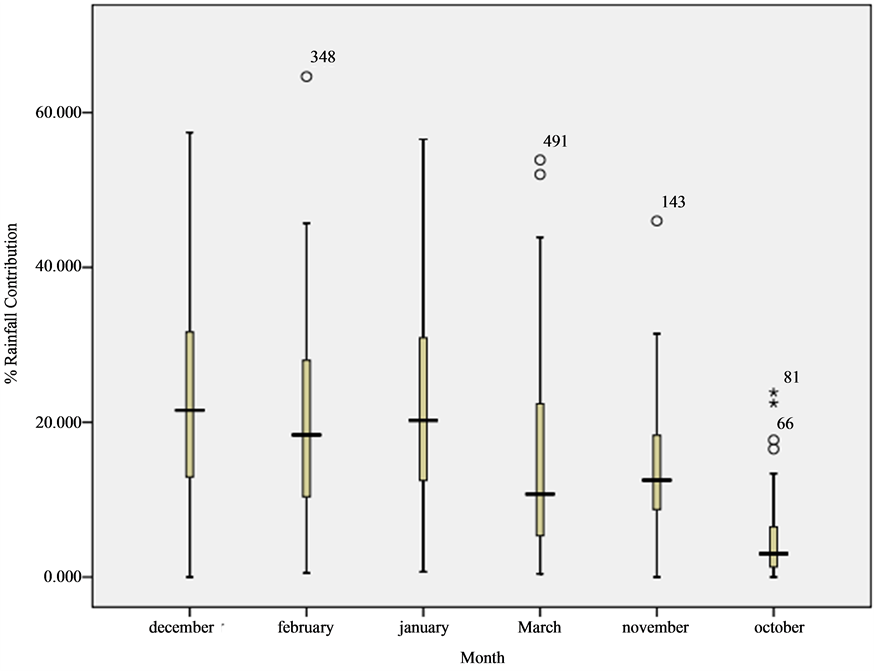
Figure 10. Percentage contribution of each month to total rainfall for Zaka station.
Table 1. Mann-Kendall trend test for Zaka station.
Table 2. Mann-Kendall trend test for Buffalo Range station.
Table 3. Mann-Kendall trend test for Masvingo station.
While the other months at all stations showed no significant trends in their contributions to the seasonal total rainfall, it does not necessarily imply that there is no trend, but rather the evidence presented in the available historical rainfall data is not sufficient to conclude that there is an effect of climate change on the rainfall pattern [24] . This can be attributed to the fluctuations in the trends for different months.
Similar results were obtained [25] that no significant trends in several rainfall indices derived from daily rainfall and that total annual precipitation at stations in Zimbabwe were found. Also it was found that there were no statistically significant trends in rainfall patterns for fourteen African countries [26] . Again no significant trend in rainfall from forty stations all over Zimbabwe was identified leading to a conclusion that there was no proof that the average rainfall in the country had changed for the period between 1892 to 2000 [27] .
The results of the study are in contrast with earlier findings which showed that precipitation in Zimbabwe, especially the Southern parts, has declined by up to 10% on average over the period 1900 to 1993, which is about 1% per decade [13] [15] [28] . Also the study contrasts the assertion that the magnitude of the reduced precipitation has increased and that the frequency of seasons recording below normal rainfall increased since 2002 [12] .
These differences could be attributed to earlier findings which identified an 18 - 20 years cycle in time series of annual rainfall for parts of Southern Africa including Zimbabwe [29] . In the same work, it was suggested that wet seasons of 9 - 10 years periods tend to occur together and that also seasons of below average rainfall cluster [29] .
The research concludes that all the rainfall season months have some form of change in their total contribution to total seasonal rainfall but only the changes for the month of October at Zaka station showed statistically significant change. The research recommends further studies to determine if statistical significance in terms of monthly precipitation contribution to seasonal falls is the same as environmental significance. This is because change seems to be occurring in the precipitation pattern but statistically not significant yet the challenges caused by these changes are visible.
References
- FAO (2004) Drought Impact Mitigation and Prevention in the Limpopo River Basin: A Situation Analysis. Land and Water Discussion Paper 4. Food and Agricultural Organisation of the United Nations, Rome.
- Chikodzi, D. (2012) Analysis of Monthly and Seasonal Ground Water Fluctuations in Zimbabwe: A Remote Sensing Perspective. Hydrology: Current Research, S1, 003.
- Unganai, L. (2009) Adaptation to Climate Change among Agro-Pastoral Systems: Case for Zimbabwe IOP Conf. Series: Earth and Environmental Science, 6, Article ID: 412045 http://dx.doi.org/10.1088/1755-1307/6/1/412045
- Ati, F.O., Stitger, C.J. and Oladipo, E.O. (2002) A Comparison of Methods to Determine the Onset of the Growing Season in Northern Nigeria. International Journal of Climatology, 22, 731-742. http://dx.doi.org/10.1002/joc.712
- Dennet, M.D. (987) Variation in Rainfall—The Background to Soil and Water Management in Dryland Regions. Soil Use and Management, 3, 47-57. http://dx.doi.org/10.1111/j.1475-2743.1987.tb00709.x
- Usman, M.T., Archer, E., Johnston, P. and Tadross, M. (2005) A Conceptual Framework for Enhancing the Utility of Rainfall Hazard Forecasts for Agriculture in Marginal Environments. Natural Hazards, 34, 29. http://dx.doi.org/10.1007/s11069-004-4349-x
- Obasi, G.O.P. (2005) The Impacts of ENSO in Africa Climate Change and Africa. Cambridge University Press, Cambridge.
- Diodato, N., Ceccarelli, M. and Bellocchi, G. (2008) Decadal and Century-Long Changes in the Reconstruction of Erosive Rainfall Anomalies in a Mediterranean Fluvial Basin. Earth Surface Processes and Landforms, 33, 2078-2093. http://dx.doi.org/10.1002/esp.1656
- Lana, X., Martínez, M.D., Serra, C. and Burgueño, A. (2004) Spatial and Temporal Variability of the Daily Rainfall Regime in Catalonia (Northeastern Spain), 1950-2000. International Journal of Climatology, 24, 613-641. http://dx.doi.org/10.1002/joc.1020
- Retalis, D., Hadjioannou, L., Nikolakakis, D. and Pashiardis, S. (1997) Time Series Analysis of Temperature and Precipitation over Greece and Cyprus. Final Report of a Program in Scientific and Technological Cooperation between Greece and Cyprus.
- WMO (1988) Analysing Long Time Series of Hydrological Data with Respect to Climate Variability. World Meteorological Organization, Geneva.
- Simba, F., Murwendo, T., Chikodzi, D., Mapurisa, B., Munthali, A. and Seyitini, L. (2012) Environmental Changes and Farm Productivity: An Assessment of Masvingo Region of the Zimbabwe. SACHA Journal of Environmental Studies, 2, 114-129.
- Makarau, A. (1995) Intra-Seasonal Oscillatory Models of the Southern Africa Summer Circulation. PhD Thesis, University of Cape Town, 324 p.
- Mazvimavi, D. (1989) Analysis of Annual Rainfall in Zimbabwe for Trends and Periodicities, 1891-1988. Geographical Journal of Zimbabwe, 20, 42-52.
- Unganai, L.S. (1996) Historic and Future Climatic Change in Zimbabwe. Climate Research, 6, 137-145. http://dx.doi.org/10.3354/cr006137
- Central Statistics Office (CSO) (2002) Zimbabwe Population Profile. http://www.zimstat.co.zw/dmdocuments/Census/Census.pdf
- Hirsch, R.M., Helsel, D.R., Cohn, T.A. and Gilroy, E.J. (1993) Statistical Analysis of Hydrologic Data. In: D. R. Maidment, Ed., Handbook of hydrology, McGraw-Hill Book Co., New York.
- Lettenmair, D.P. (1976) Detection of Tends in Water Quality Data from Records with Dependent Observations. Water Resources Research, 12, 1037-1046. http://dx.doi.org/10.1029/WR012i005p01037
- Hipel, K.W. and McLeod, A.I. (1994) Time Series Modelling of Water Resources and Environmental Systems. Elsevier, Amsterdam.
- Hirsch, R.M., Slack, J.R. and Smith, R.A. (1982) Techniques for Trend Assessment for Monthly Water Quality Data. Water Resources Research, 18, 107-121. http://dx.doi.org/10.1029/WR018i001p00107
- Dietz, E.J. and Killeen, T.J. (1981) A Non-Parametric Multivariate Test for Monotone Trend with Pharmaceutical Application. Journal of the American Statistical Association, 76, 169-174.
- Kendall, M.G. (1975) Rank Correlation Methods. 4th Edition, Charles Griffin, London.
- Mann, H.B. (1945) Non-Parametric Tests against Trend. Econmetrica, 13, 245-259. http://dx.doi.org/10.2307/1907187
- Helsel, D.R. and Hirsch, R.M. (1992) Statistical Methods in Water Resources. Elsevier, Amsterdam.
- Aguilar, E., Aziz Barry, E., Brunet, M., Ekang, L., Fernandes, A., Massoukina, M., Mbah, J., Mhanda, A., do Nascimento, D.J., Peterson, T.C., Thamba Umba, O., Tomou, M. and Zhang, X. (2009) Changes in Temperature and Precipitation Extremes in Western, Central Africa, Guinea Conakry, and Zimbabwe. Journal of Geophysical Research, 114, 1955-2006. http://www.agu.org/journals/ABS/2009/2008JD011010.shtml
- New, M., Hewitson, B., Stephenson, D.B., Tsiga, A., Kruger, A., Manhique, A., Gomez, B., Coelho, C.A.S, Masisi, D.N., Kululanga, E., Mbambalala, E., Adesina, F., Saleh, H., Kanyanga, J., Adosi, J., Bulane, L., Fortunata, L., Mdoka, M.L. and Lajoie, R. (2006) Evidence of Trends in Daily Climate Extremes over Southern and West Africa. Journal of Geophysical Research, 111, 1-11. http://dx.doi.org/10.1029/2005JD006289
- Mazvimavi, D. (2008) Investigating Changes over Time of Annual Rainfall in Zimbabwe. Hydrology and Earth System Sciences, 14, 2671-2679. http://dx.doi.org/10.5194/hess-14-2671-2010
- Mason, S.J. and Jury, M.R. (1997) Climatic Variability and Change over Southern Africa: A Reflection on Underlying Processes. Progress in Physical Geography, 21, 23-50. http://dx.doi.org/10.1177/030913339702100103
- Tyson, P.D. (1986) Climatic Change and Variability in Southern Africa. Oxford University Press, Cape Town.


