Received 30 November 2015; accepted 4 March 2016; published 7 March 2016

ABSTRACT

Convergence behaviors of solutions arising from certain system of third-order nonlinear differential equations are studied. Such convergence of solutions corresponding to extreme stability of solutions when 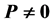relates a pair of solutions of the system considered. Using suitable Lyapunov functionals, we prove that the solutions of the nonlinear differential equation are convergent. Result obtained generalizes and improves some known results in the literature. Example is included to illustrate the result.

Keywords:

Nonlinear Differential Equations, Third Order, Convergence of Solutions, Lyapunov Method

1. Introduction

We shall consider here systems of real differential equations of the form

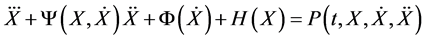(1)

which is equivalent to the system

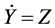
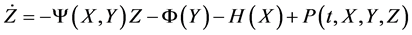(2)

where 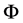and H are continuous vector functions and is an -positive definite continuous symmetric matrix function, for the argument displayed explicitly and the dots here as elsewhere stand for differentiation with respect to the independent variable t,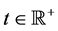; denote the real interval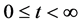. and 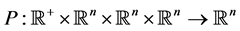in Equation (1).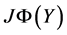, 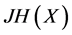are the Jacobian matrices corresponding to the vector functions and respectively exist and are symmetric, positive definite and continuous.

So far in the literature, much attention has been drawn to the boundedness of solutions of ordinary scalar and vector nonlinear differential equations of third order. The book of Reissig et al. [1] , the papers by Abou-El-Ela [2] , Afuwape [3] [4] , Chukwu [5] , Ezeilo [6] , Ezeilo and Tejumola [7] , Meng [8] , Omeike [9] , Omeike and Afuwape [10] , Tiryaki [11] , Tunc [12] [13] , Tunc and Ates [14] , Tunc and Mohammed [15] and the references cited therein have comprehensive treatment of the subject. Throughout the results present in the book of Reissig et al. [1] and the papers mentioned above, Lyapunov’s second (direct) method has been used as a basic tool to verify the results established in these works. Equations of the form (1) in which and have been studied by [16] [17] . They have obtained some results related to the convergence properties of solutions as well as Afuwape in [18] . Very recently, Tunc and Gozen [19] studied the convergence of solution of the equation

by extending the result of [17] to the special case of [17] . Also recently, Olutimo [20] studied the equation

a variant of (1), where c is a positive constant and obtained some results which guarantee the convergence of the solutions. With respect to our observation in the literature, no work based on (1) was found. The result to be obtained here is different from that in Olutimo [20] and the papers mentioned above. The intuitive idea of convergence of solutions also known as the extreme stability of solutions occurs when the difference between two equilibrium positions tends to zero as time increases infinitely is of practical importance. This intuitive idea is also applicable to nonlinear differential system. The Lyapunov’s second method allows us to predict the convergence property of solutions of nonlinear physical system. Result obtained generalizes and improves some known results in the literature. Example is included to illustrate the result.

Definition

Definition 1.1. Any two solutions, of (1) are said to converge if

If the relations above are true of each other (arbitrary) pair of solutions of (1), we shall describe this saying that all solutions of (1) converge.

2. Some Preliminary Results

We shall state for completeness, some standard results needed in the proofs of our results.

Lemma 1. Let D be a real symmetric matrices. Then for any.

where and are the least and greatest eigenvalues of D, respectively.

Proof of Lemma 1. See [3] [7] .

Lemma 2. Let be real symmetric commuting matrices. Then,

1) The eigenvalues of the product matrix are all real and satisfy

2) The eigenvalues of the sum of Q and D are all real and satisfy

where and are respectively the eigenvalues of Q and D.

Proof of Lemma 2. See [3] [7] .

Lemma 3. Subject to earlier conditions on the following is true

where and are the least and greatest eigenvalues of D, respectively.

Proof of Lemma 3. See [20] .

Lemma 4. Subject to earlier conditions on and that, then

1)

2)

Proof of Lemma 4. See [20] .

Lemma 5. Subject to earlier conditions on and that, then

1)

2)

Proof of Lemma 5. See [3] [7] [11] .

3. Statement of Results

Throughout the sequel are the Jacobian matrices corresponding to the vector

functions, respectively.

Our main result which gives an estimate for the solutions of (1) is the following:

Theorem 1. Assume that and, for all in are all symmetric. Jacobian matrices exist, positive definite and continuous. Furthermore, there are positive constants such that the following conditions are satisfied.

Suppose that and that

1) The continuous matrices, and are symmetric, associative and commute pairwise. Then eigenvalues of, of and of , satisfy

2) P satisfies

(3)

for any (i = 1, 2) in, and is a finite constant. Then, there exists a finite constant such that any two solutions of (2) necessarily converge if.

Our main tool in the proof of the result is the function defined for any in by

(4)

where

and is a fixed constant chosen such that

(5)

(6)

chosen such that.

The following result is immediate from (4).

Lemma 6. Assume that, all the hypotheses on matrix and vectors and in Theorem 1 are satisfied. Then there exist positive constants and such that

(7)

Proof of Lemma 6. In the proof of the lemma, the main tool is the function in (4).

This function, after re-arrangement, can be re-written as

Since

And

we have that

Since matrix is assumed symmetric and strictly positive definite. Consequently the square root exists which itself is symmetric and non-singular for all Therefore, we have

(8)

where stands for.

Thus,

(9)

From (9), the term

(10)

Since

by integrating both sides from to and because, then we obtain

But from

integrating both sides from to and because, we find

Hence, (10) becomes

combining the estimate for in (9), we have

By hypothesis (1) of Theorem 1 and lemmas 1 and 2, we have

where and by (5).

Similarly, after re-arrangement becomes

(11)

It is obvious that

also,

and

Combining all the estimates of and (11), we have

Now, combining and we must have

that is,

(12)

Thus, it is evident from the terms contained in (12) that there exists sufficiently small positive constants such that

where

The right half inequality in lemma 6 follows from lemma 1 and 2.

Thus,

where

Hence,

(13)

4. Proof of Theorem 1

Let, be any two solutions of (2), we define

By

where V is the function defined in (4) with replaced by respectively.

By lemma 6, (13) becomes

(14)

for and.

The derivative of with respect to t along the solution path and using Lemma 3, 4 and 5, after simplification yields

where, , and .

Using the fact that

and

where

Following (8),

and

Thus,

Note that

and

We have;

On applying Lemma 1 and 2, we have

If we choose, such that it satisfies (6), and using (3), we obtain

where

Thus,

with.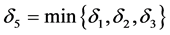

There exists a constants such that

In view of (14), the above inequality implies

(15)

Let be now fixed as. Thus, last part of the theorem is immediate, provided and on integrating (15) between and t, we have

which implies that

Thus, by (14), it shows that

From system (1) this implies that

This completes the proof of Theorem 1.

5. Conclusions

Analysis of nonlinear systems literary shows that Lyapunov’s theory in convergence of solutions is rarely scarce. The second Lyapunov’s method allows predicting the convergence behavior of solutions of sufficiently complicated nonlinear physical system.

Example 4.0.1. As a special case of system (2), let us take for such that is a function of t only and

Thus,

Clearly, and are symmetric and commute pairwise. That is,

and

Then, by easy calculation, we obtain eigenvalues of the matrices and as follows

It is obvious that, , , , and.

If we choose, we must have that

Thus, all the conditions of Theorem 1 are satisfied. Therefore, all solutions of (1) converge since (5) and (6) hold.

Cite this paper

Akinwale L.Olutimo, (2016) Result on the Convergence Behavior of Solutions of Certain System of Third-Order Nonlinear Differential Equations. International Journal of Modern Nonlinear Theory and Application,05,48-58. doi: 10.4236/ijmnta.2016.51005

References