International Journal of Modern Nonlinear Theory and Application
Vol.2 No.1A(2013), Article ID:29428,5 pages DOI:10.4236/ijmnta.2013.21A012
Chaotic Behavior of a Class of Neural Network with Discrete Delays
1Department of Mathematics, JIS College of Engineering, Kalyani, India
2Centre for Mathematical Biology and Ecology, Department of Mathematics, Jadavpur University, Kolkata, India
3Department of Mathematics, Jadavpur University, Kolkata, India
Email: ncmajee2000@yahoo.com
Received January 9, 2013; revised February 12, 2013; accepted February 21, 2013
Keywords: Neuronal Gain; Chaos; Lyapunov Exponent; Jacobian Matrix
ABSTRACT
In this paper, the effect of neuronal gain in discrete delayed neural network model is investigated. It is observed that such neural networks become highly chaotic due to the presence of high neuronal gain. On the basis of the largest Lyapunov exponent and largest eigenvalue of Jacobian matrix, chaos analysis has been done. Finally, some numerical simulations are presented to justify our results.
1. Introduction
Neuronal gain plays an important role for processing information in the brain [1]. At the single neuron level, gain modulation can arise if the two inputs are subject to a direct multiplicative interaction. Alternatively, these inputs can be summed in a linear manner by the neuron and gain modulation can arise, instead, from a nonlinear input-output relationship [2]. It was first observed in neurons of the parietal cortex of the macaque monkey that combine retinal and gaze signals in a multiplicative manner [3,4]. Gain modulation has also been seen in other cortical areas [5-7]. Higgs et al. [8] measured the effects of current noise on firing frequency-current f-I relationships in pyramidal neurons. In most pyramidal neurons, noise had a multiplicative effect on the steady-state f-I relationship, increasing gain. Aihara et al. [9] first introduced chaotic neural network models in order to simulate the chaotic behavior of biological neurons. Chaotic neural networks have been successfully applied in combinational optimization, parallel recognition, secure communication, and other areas [10,11]. Actually, such spatial networks as special complex networks can exhibit some complex dynamics including chaos [12,13]. Therefore the investigation of dynamics of chaotic neural networks is of practical importance and many interesting results have been obtained via different approaches in recent years [14,15].
In practice, due to the finite speeds of the switching and signals time delays exist in various delayed neural networks. Many research works have been done to investigate such dynamics of delayed neural network models considering neuron gain (the maximum slope of the sigmoidal activation function) as unity. Marcus and Westervelt [16] first introduced a single delay in Hopfield model and showed that symmetrically connected continuous time network oscillates as the delay crosses a critical value. Liu et al. [17] obtained sufficient conditions ensuring existence and global exponential stability of periodic solution for the BAM neural network with time varying delays. Sun et al. [18] studied global robust exponential stability of the periodic solution of interval-delayed neural networks. Majee [19] obtained sufficient conditions for asymptotic stability about the origin of the following gain modulated a class of n-neuron nonlinear delayed system:
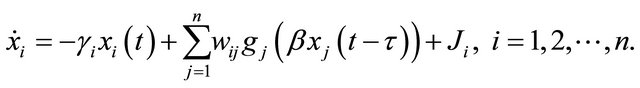 (1)
(1)
In this paper, the model (1) is again considered where gain parameter  is taken as greater than unity. The main motivation of this paper is to understand the role of neuronal gain in shaping the dynamics of a class of delayed n-neuron system. It also helps to detect chaotification of delayed system by easily varifiable conditions. It is shown that for a fixed small value of time delay the gradual increment of gain parameter may give rise to periodic solution then to chaos through period doubling. This chaotic dynamics are analyzed by means of largest Lyapunov exponent and largest eigenvalue of Jacobian matrix of the system. Sufficient conditions are verified by several numerical simulations.
is taken as greater than unity. The main motivation of this paper is to understand the role of neuronal gain in shaping the dynamics of a class of delayed n-neuron system. It also helps to detect chaotification of delayed system by easily varifiable conditions. It is shown that for a fixed small value of time delay the gradual increment of gain parameter may give rise to periodic solution then to chaos through period doubling. This chaotic dynamics are analyzed by means of largest Lyapunov exponent and largest eigenvalue of Jacobian matrix of the system. Sufficient conditions are verified by several numerical simulations.
2. Chaos Analysis
Main ingredients of chaos are sensitive dependence and transitivity. We will insist that the invariant set 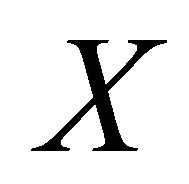 be bounded, so that the sensitivity is not simply due to escape to infinity. Finally, it is also necessary to require that
be bounded, so that the sensitivity is not simply due to escape to infinity. Finally, it is also necessary to require that 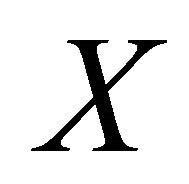 be closed to ensure that chaos is a topological invariant.
be closed to ensure that chaos is a topological invariant.
Definition 1. Chaos [20]: A flow  is chaotic on a compact invariant set
is chaotic on a compact invariant set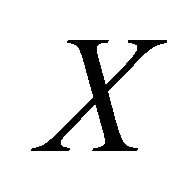 , if
, if  is transitive and exhibits sensitive dependence on
is transitive and exhibits sensitive dependence on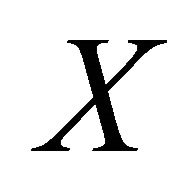 .
.
The concept of “sensitive dependence” requires that nearby orbits eventually separates; however, the rate of separation is not specified. Indeed, there appears to be a dichotomy between systems for which nearby orbits separate exponentially for truly chaotic system. Therefore we have 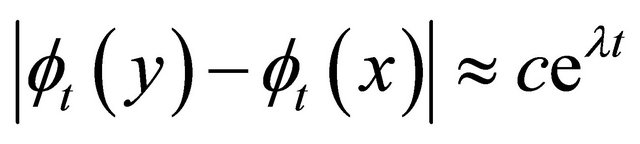 for
for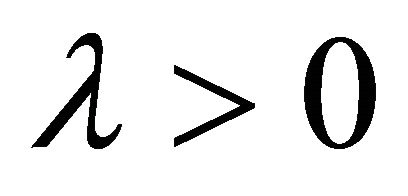 . This concept is familiar from our study of the linearization of equilibria: when the Jacobian matrix of the vector field at equilibrium has a positive eigenvalue, then the linearized system has trajectories that grow exponentially.
. This concept is familiar from our study of the linearization of equilibria: when the Jacobian matrix of the vector field at equilibrium has a positive eigenvalue, then the linearized system has trajectories that grow exponentially.
Therefore the sensitivity is always measured by the largest Lyapunov exponent at the initial conditions. Hence, when the Jacobian matrix is a parameter matrix, the Lyapunov exponents are equal to the eigenvalues of the jacobian matrix. If the largest Lyapunov exponent is positive, then the system is sensitive to the initial conditions. Science chaos is defined only for compact invariant sets, this bound is quite natural. Moreover, if jacobian is uniformly bounded on the orbit, it is easy to see that the growth of any vector is at most exponential.
The vector-matrix form of system (1) is
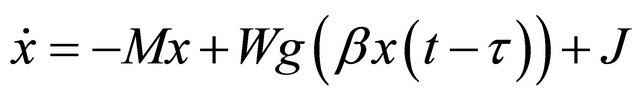 (2)
(2)
where,
 is the invariant set of the system (1).
is the invariant set of the system (1).
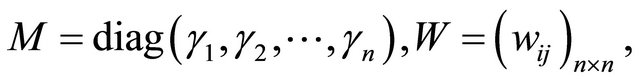
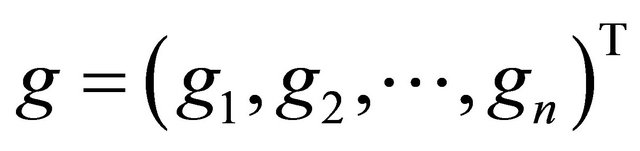
and
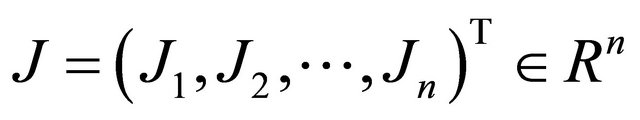 .
.
 is discrete delay parameter and
is discrete delay parameter and  is neuronal gain parameter which is a multiplicative factor not a function.
is neuronal gain parameter which is a multiplicative factor not a function.
 is continuous and differentiable nonlinear function.
is continuous and differentiable nonlinear function.
 is bounded function in
is bounded function in .
.
First we have to show the invariant set  is compact in the Euclidean space
is compact in the Euclidean space .
.
Lemma 1.
For the gain modulated delayed neural network model (1) satisfying  and
and , the invariant set
, the invariant set  remain compact for
remain compact for 
Proof.
As the following inequality
 (3)
(3)
satisfies system (1), it is obvious that all solutions of system (1) is closed and bounded for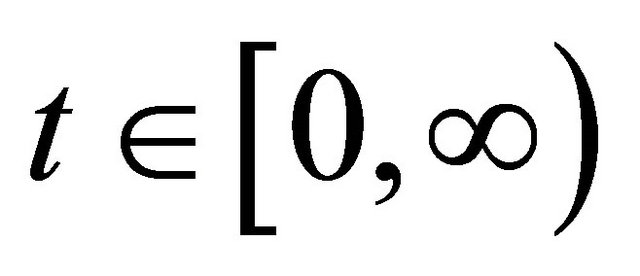 .
.
Therefore, it is easy to conclude that the invariant set , is compact for
, is compact for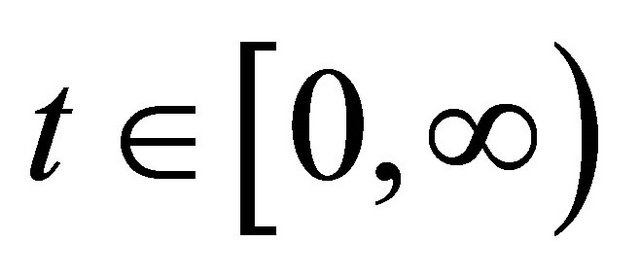 .
.
Let us take 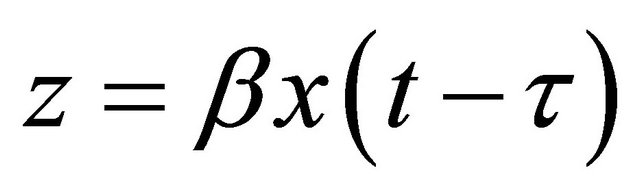 for small delay
for small delay .
.
Then
 (4)
(4)
Using (2) and (4) we have the Jacobian  of system (1) as follows:
of system (1) as follows:
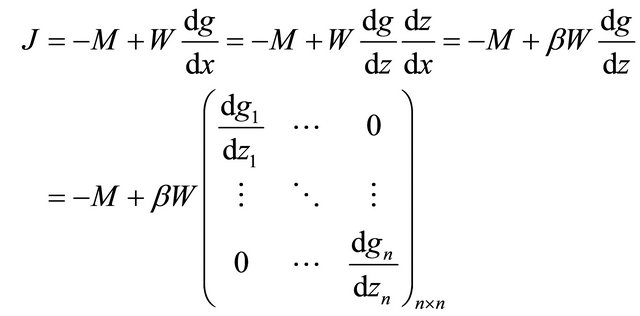
where, system (1) satisfies the initial conditions

Therefore the eigenvalues of  is similar to the values for Lyapunov exponent of system (1).
is similar to the values for Lyapunov exponent of system (1).
Theorem 1.
If 1) the activation function satisfies  and
and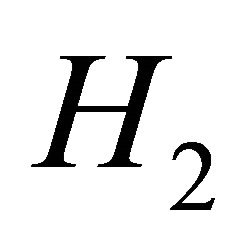 2) invariant set is compact3)
2) invariant set is compact3) 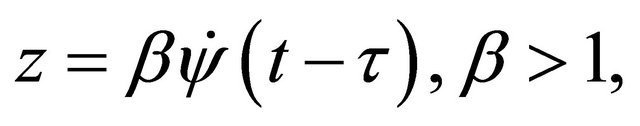
4) the largest eigenvalue of  is positive, then the system (1) is chaotic for the initial condition
is positive, then the system (1) is chaotic for the initial condition 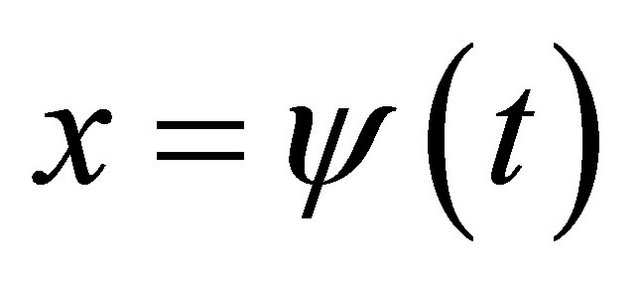 where
where 
3. Numerical Example
In this section we consider a system of three-neuron delayed network model:
 (5)
(5)
where,



It is shown in Figure 1(a) that without neuronal gain system (5) is oscillatory, but in presence neuronal gain , this system exhibits aperiodic behaviors (see Figures 1(b)-(e)) and ultimately becomes chaotic (as shown in Figures 1(f) and (i)). In Figure 2 bifurcation diagram depicts that system (5) become chaotic through periodic oscillation and then period-doubling as gain parameter
, this system exhibits aperiodic behaviors (see Figures 1(b)-(e)) and ultimately becomes chaotic (as shown in Figures 1(f) and (i)). In Figure 2 bifurcation diagram depicts that system (5) become chaotic through periodic oscillation and then period-doubling as gain parameter  varies. Chaotic behaviors are verified by different numerical simulation methodologies, which are shown in Figure 3.
varies. Chaotic behaviors are verified by different numerical simulation methodologies, which are shown in Figure 3.
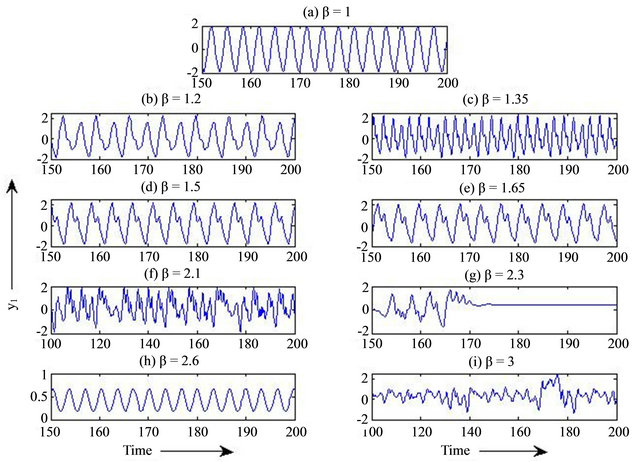
Figure 1. Time series evolution as  is gradually increasing for constat
is gradually increasing for constat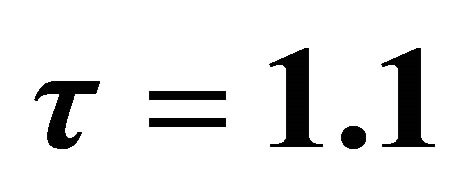 , shows the chaotic nature of system (5).
, shows the chaotic nature of system (5).

Figure 2. Bifurcation diagram of the system (5) with varying parameter  with constant
with constant 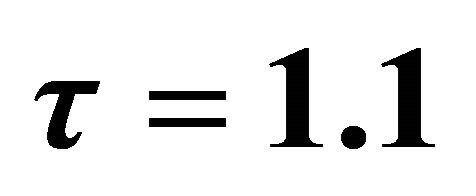 depicts that system becomes chaotic emanating from periodic oscillation through period-doubling.
depicts that system becomes chaotic emanating from periodic oscillation through period-doubling.

Figure 3. Diagnostic chaos test of system (5) for  and
and . (a) Lyapunov exponent; The largest positive value for Lyapunov exponent is deduced as 0.0845. Computational time for initiation of chaos in this L.E. is 1875 seconds calculated by a workstation (RAM 6 GB, 32 Bits), (b) Initial sensitivity, (c) Power spectral density and (d) Recurrence plot.
. (a) Lyapunov exponent; The largest positive value for Lyapunov exponent is deduced as 0.0845. Computational time for initiation of chaos in this L.E. is 1875 seconds calculated by a workstation (RAM 6 GB, 32 Bits), (b) Initial sensitivity, (c) Power spectral density and (d) Recurrence plot.
4. Conclusion
In this paper, it is shown that the gradual increment of maximum slope 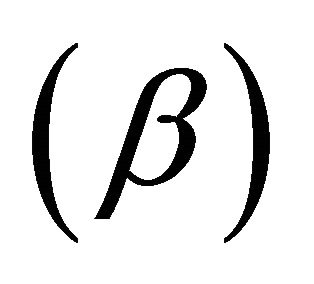 of the sigmoidal activation function for a system of a class of neural network (1) cause periodic oscillation, then to chaos through period-doubling. Numerical simulations are presented here to justify the obtained results. Moreover, largest Lyapunov exponent can be evaluated to verify that the system is sensitive to initial conditions.
of the sigmoidal activation function for a system of a class of neural network (1) cause periodic oscillation, then to chaos through period-doubling. Numerical simulations are presented here to justify the obtained results. Moreover, largest Lyapunov exponent can be evaluated to verify that the system is sensitive to initial conditions.
5. Acknowledgements
The first author acknowledges TEQIP-II (sub comp.1.2) grant of JIS College of Engineering, Kalyani, India for providing publication charges
REFERENCES
- S. Mitchell and R. A. Silver, “Shunting Inhibition Modulates Neuronal Gain during Synaptic Excitation,” Neuron, Vol. 38, No. 3, 2003, pp. 433-445. doi:10.1016/S0896-6273(03)00200-9
- M. Brozovic, L. F. Abbott and R. A. Andersen, “Mechanism of Gain Modulation at Single Neuron and Network Levels,” Journal of Computing Neuroscience, Vol. 25, No. 1, 2008, pp. 158-168. doi:10.1007/s10827-007-0070-6
- R. A. Andersen and V. B. Mountcastle, “The Influence of the Angle of Gaze upon the Excitability of the Light-Sensitive Neurons of the Posterior Parietal Cortex,” Journal of Neuroscience, Vol. 3, 1983, pp. 532-548.
- R. A. Andersen, G. K. Essick and R. M. Siegel, “The Encoding of Spatial Location by Posterior Parietal Neurons,” Science, Vol. 230, No. 4724, 1985, pp. 456-458. doi:10.1126/science.4048942
- M. Arsiero, C. Lüscher and G. Battaglini, “Gaze-Dependent Visual Neurons in Area V3A of Monkey Prestriate Cortex,” Journal of Neuroscience, Vol. 9, 1989, pp. 1112- 1125.
- F. Bremmer, U. J. Ilg, A. Thiele, C. Distler and K. P. Hoffmann,” Eye Position Effects in Monkey Cortex. I. Visual and Pursuit-Related Activity in Extrastriate Areas MT and MST,” Journal of Neurophysiology, Vol. 77, 1997, pp. 944-961.
- E. Salinas and T. J. Sejnowski, “Gain Modulation in the Central Nervous System: Where Behavior, Neurophysiology and Computation Meet,” The Neuroscientist, Vol. 7, No. 5, 2001, pp. 430-440. doi:10.1177/107385840100700512
- M. H. Higgs, S. J. Slee and W. J. Spain, “Diversity of Gain Modulation by Noise in Neocortical Neurons: Regulation by the Slow after Hyperpolarization Conductance,” The Journal of Neuroscience, Vol. 26, No. 34, 2006, pp. 8787- 8799. doi:10.1523/JNEUROSCI.1792-06.2006
- K. Aihara, T. Takabe and M. Toyoda, “Chaotic Neural Networks,” Physical Letter A, Vol. 144, No. 6-7, 1990, pp. 333-340. doi:10.1016/0375-9601(90)90136-C
- Y. Q. Zhang and Z.-R. He, “A Secure Communication Scheme Based on Cellular Neural Networks,” Proceedings of the IEEE International Conference on Intelligent Process Systems, Vol. 1, 1997, pp. 521-524.
- G. R. Chen, J. Zhou and Z. R. Liu, “Global Synchronization of Coupled Delayed Neural Networks and Applications to Chaotic CNN Models,” International Journal of Bifurcation and Chaos, Vol. 14, No. 7, 2004, pp. 2229- 2240. doi:10.1142/S0218127404010655
- H. T. Lu, “Chaotic Attractors in Delayed Neural Networks,” Physical Letters A, Vol. 298, No. 2-3, 2002, pp. 109-116. doi:10.1016/S0375-9601(02)00538-8
- M. Gilli, “Strange Attractors in Delayed Cellular Neural Networks,” IEEE Transactions on Circuits Systems I Fund Theory Applications, Vol. 40, No. 11, 2006, pp. 849- 853. doi:10.1109/81.251826
- Y. Q. Yang and J. D. Cao, “Exponential Lag Synchronization of a Class of Chaotic Delayed Neural Networks with Impulsive Effects,” Physica A, Vol. 386, No. 1, 2007, pp. 492-502. doi:10.1016/j.physa.2007.07.049
- X. D. Li and M. Bohner, “Exponential Synchronization of Chaotic Neural Networks with Mixed Delays and Impulsive Effects via Output Coupling with Delay Feedback,” Mathematical and Computer Modelling, Vol. 52, No. 5-6, 2010, pp. 643-653. doi:10.1016/j.mcm.2010.04.011
- C. M. Marcus and R. M. Westervelt, “Stability of Analog Neural Networks with Delay,” Physical Review A, Vol. 39, No. 1, 1989, pp. 347-359. doi:10.1103/PhysRevA.39.347
- Z. Liu, A. Chen, J. Cao and L. Huang, “Existence and Global Exponential Stability of Periodic Solution for BAM Neural Networks with Periodic Coefficients and TimeVarying Delays,” IEEE Transactions on Circuits and Systems-I: Fundamental Theory and Applications, Vol. 50, No. 9, 2003, pp. 1162-1172.
- C. Sun and C. Feng, “On Robust Exponential Periodicity of Interval Neural Networks with Delays,” Neural Processing Letters, Vol. 20, No. 1, 2004, pp. 53-61. doi:10.1023/B:NEPL.0000039426.58277.7e
- N. C. Majee, “Studies Convergent and Non-Convergent Dynamics of Some Continuous Artificial Neural Network Models with Time-Delay,” Thesis of Doctor of Philosophy, Jadavpur University, Kolkata, 1997.
- J. D. Meiss, “Differential Dynamical Systems,” 2007.

