International Journal of Modern Nonlinear Theory and Application
Vol. 2 No. 2 (2013) , Article ID: 33397 , 9 pages DOI:10.4236/ijmnta.2013.22018
Numerical Solution of Nonlinear Integro-Differential Equations with Initial Conditions by Bernstein Operational Matrix of Derivative
Department of Mathematics, Islamic Azad University of Birjand, Birjand, Iran
Email: behrooz.basirat@iaubir.ac.ir
Copyright © 2013 Behrooz Basirat, Mohammad Amin Shahdadi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 18, 2013; revised February 23, 2013; accepted March 25, 2013
Keywords: Bernstein Polynomial; Operational Matrix; Integro-Differential Equations
ABSTRACT
In this paper, we present a practical matrix method for solving nonlinear Volterra-Fredholm integro-differential equations under initial conditions in terms of Bernstein polynomials on the interval [0,1]. The nonlinear part is approximated in the form of matrices’ equations by operational matrices of Bernstein polynomials, and the differential part is approximated in the form of matrices’ equations by derivative operational matrix of Bernstein polynomials. Finally, the main equation is transformed into a nonlinear equations system, and the unknown of the main equation is then approximated. We also give some numerical examples to show the applicability of the operational matrices for solving nonlinear Volterra-Fredholm integro-differential equations (NVFIDEs).
1. Introduction
Some of the phenomena in physics, electronics, biology, and other applied sciences lead to nonlinear VolterraFredholm integro-differential equations. Of course, these equations can also appear when transforming a differential equation into an integral equation [1-7]. In these kinds of equations, the unknown function 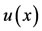 appears on both sides; it appears under the integral sign on one side, while it appears as an ordinary derivative on the other side. Investigating the results of nonlinear integrodifferential equations, we observe that no obvious algebraic method has been recognized to solve these equations, and thus, approximation methods are used to solve such equations [8-10]. Bernstein polynomials (B-plynomials) have many useful properties [11,12]. In this paper, we use Bernstein polynomials and their resulting operational matrices to solve the following nonlinear VolterraFredholm integro-differential equations with the initial conditions indicated as:
appears on both sides; it appears under the integral sign on one side, while it appears as an ordinary derivative on the other side. Investigating the results of nonlinear integrodifferential equations, we observe that no obvious algebraic method has been recognized to solve these equations, and thus, approximation methods are used to solve such equations [8-10]. Bernstein polynomials (B-plynomials) have many useful properties [11,12]. In this paper, we use Bernstein polynomials and their resulting operational matrices to solve the following nonlinear VolterraFredholm integro-differential equations with the initial conditions indicated as:
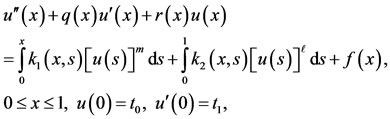 (1)
(1)
where the functions 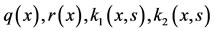 and
and 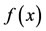 are known, whereas
are known, whereas 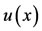 is unknown. We approximate phrases including derivative of unknown function by operational matrix of derivative
is unknown. We approximate phrases including derivative of unknown function by operational matrix of derivative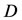 ; and approximate phrases including powers of unknown function by Bernstein polynomial matrix
; and approximate phrases including powers of unknown function by Bernstein polynomial matrix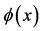 . This yields an equation based on the unknown
. This yields an equation based on the unknown 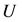 which is the approximation
which is the approximation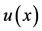 . To examine the accuracy of the formula, we present some examples. We will show the difference between the accurate and approximation solutions in these examples upon knowing.
. To examine the accuracy of the formula, we present some examples. We will show the difference between the accurate and approximation solutions in these examples upon knowing.
2. Bernstein Polynomials and Their Properties
2.1. Definition of Bernstein Polynomials Basis
The Bernstein basis polynomials of degree  are defined by:
are defined by:
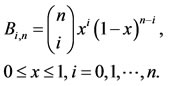 (2)
(2)
By using binomial expansion of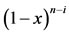 , one can show that
, one can show that
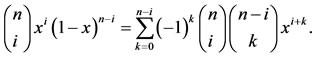 (3)
(3)
With the aid of Equation (3), the Bernstein vector
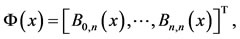 (4)
(4)
can be written in the form
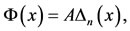 (5)
(5)
where
2.2. Function Approximation
A function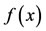 , square integrable in (0,1), may be expressed in terms of Bernstein basis [13]. In practice, only the first
, square integrable in (0,1), may be expressed in terms of Bernstein basis [13]. In practice, only the first 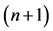 terms Bernstein polynomials are considered. Hence, if we write
terms Bernstein polynomials are considered. Hence, if we write
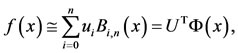 (7)
(7)
where
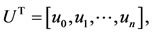 (8)
(8)
then
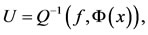 (9)
(9)
where 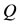 is said dual matrix of
is said dual matrix of 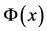 and is given in [13]. We can also approximate the function
and is given in [13]. We can also approximate the function 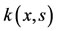
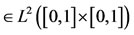 by double Fourier expansion as follows
by double Fourier expansion as follows
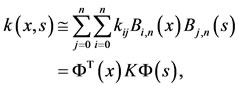 (10)
(10)
where

and 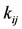 elements are given by
elements are given by
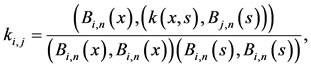 (11)
(11)
for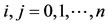 . Due of (9), we obtain
. Due of (9), we obtain
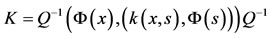 (12)
(12)
2.3. Operational Matrix of Integration
In performing arithmetic and other operations on Bernstein basis, we frequently encounter the integration of the vector 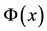 defined in Equation (4) by
defined in Equation (4) by
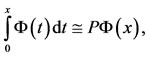 (13)
(13)
where 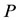 is the
is the 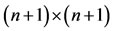 operational matrix for integration and is given in [13,14].
operational matrix for integration and is given in [13,14].
2.4. Product Operational Matrix
It is always necessary to evaluate the product of 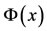 and
and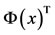 , which is called the product matrix of Bernstein polynomials basis. Let
, which is called the product matrix of Bernstein polynomials basis. Let
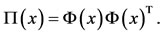 (14)
(14)
Then, multiplying the matrix 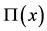 with the vector
with the vector 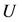 which is defined in Equation (8), we obtain
which is defined in Equation (8), we obtain
 (15)
(15)
where 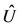 is an
is an 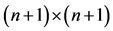 matrix and is called the coefficient matrix. The details of obtaining this matrix are given in [13].
matrix and is called the coefficient matrix. The details of obtaining this matrix are given in [13].
3. Operational Matrix of Derivative
The differentiation of vector 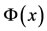 in Equation (4) can be expressed as:
in Equation (4) can be expressed as:
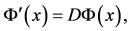 (16)
(16)
where 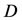 is the
is the 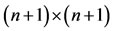 operational matrix of derivatives for Bernstein polynomials. From (5), we have
operational matrix of derivatives for Bernstein polynomials. From (5), we have 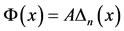 and then
and then
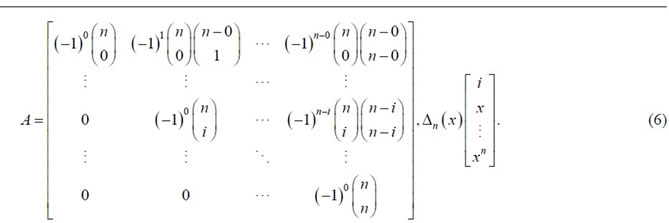
 (17)
(17)
Defining 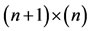 matrix
matrix 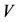 and vector
and vector  as
as
 (18)
(18)
Equation (17) may then be restated as
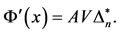 (19)
(19)
We now expand vector 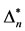 in terms of
in terms of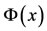 . We get
. We get 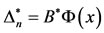 where
where
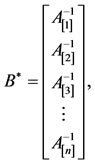 (20)
(20)
So
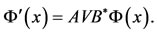 (21)
(21)
Therefore, we have the operational matrix of derivative as
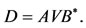 (22)
(22)
If we approximate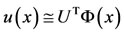 , then for
, then for 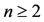 (
(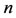 is the order of derivatives), we get
is the order of derivatives), we get
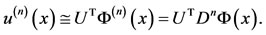 (23)
(23)
4. Operational Matrices for Numerical Solution of NVFIDE
To obtain the approximate solution of the (1) under the initial conditions, the following matrix method is used. Function 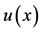 is approximated by using a finite number of terms in (7) as
is approximated by using a finite number of terms in (7) as
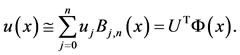 (24)
(24)
The approximate functions 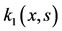 and
and  by Bernstein polynomials can be framed by:
by Bernstein polynomials can be framed by:
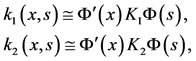 (25)
(25)
where 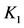 and
and 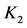 are defined with (12). For numerical implementation of the method explained in this section, we need to evaluate
are defined with (12). For numerical implementation of the method explained in this section, we need to evaluate 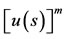 and
and 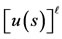 where
where 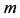 and
and 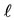 are positive integers, as follows
are positive integers, as follows
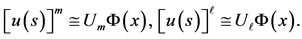 (26)
(26)
From (14) and (16), we have
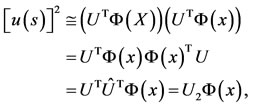 (27)
(27)
where the vector 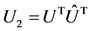 is an
is an 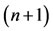 -vector;
-vector;
then, for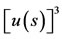 , we get
, we get
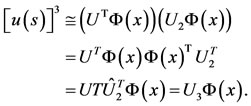 (28)
(28)
Therefore, with this method we can approximate 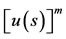 and
and  arbitrary
arbitrary  and
and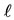 .
.
Suppose that this method holds for 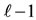 where
where
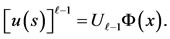 We obtain it for
We obtain it for 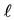 as follows
as follows
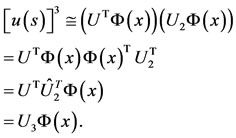 (29)
(29)
We have a similar relation for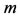 . So, the components of
. So, the components of 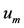 and
and 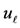 can be computed in terms of components of unknown vector
can be computed in terms of components of unknown vector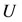 . In this case, for the Volterra and Fredholm part of (1), we have
. In this case, for the Volterra and Fredholm part of (1), we have
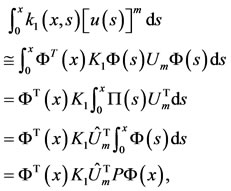 (30)
(30)
and
 (31)
(31)
Also, to approximate the differential part of Equation (1), making use of Equation (23) we have
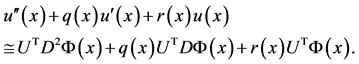 (32)
(32)
After substituting the approximate Equations (24)-(32) in (1), we get
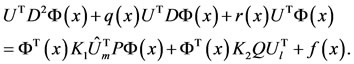 (33)
(33)
And also, for the initial conditions, we have
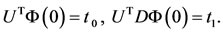 (34)
(34)
The initial conditions Equation (34) give two linear equations. Since the number of unknowns for a vector 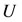 in (33) is
in (33) is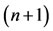 , then we collocate Equation (33) in
, then we collocate Equation (33) in 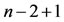 Newton-Cotes points as
Newton-Cotes points as
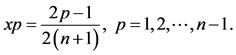 (35)
(35)
For collocating Equation (33), we have used the Newton-Cotes points because of their simplicity and their good utility in our implementation as regards the speed and accuracy of answers. However, we can use other points like the Gauss points, Clenshaw-Curtis points, Lobatto points, etc. Here we present the final system:
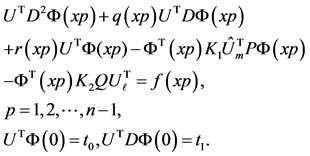 (36)
(36)
After solving nonlinear system (36), we get ; thenwe have the approximate solution of Equation (1).
; thenwe have the approximate solution of Equation (1).
5. Numerical Examples
To illustrate the effectiveness of the proposed method in the present paper, several examples are presented in this section.
Example 1. Consider the nonlinear Fredholm integrodifferential equation [15].
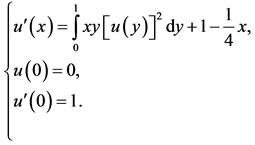 (37)
(37)
The exact solution is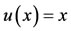 . The results of proposed method for this example are exhibited in Table 1 with 4 choices of
. The results of proposed method for this example are exhibited in Table 1 with 4 choices of . For this complicate NFIDE with a small number of Bernstein basis functions, we get acceptable results.
. For this complicate NFIDE with a small number of Bernstein basis functions, we get acceptable results.
By applying the method in Section 4, for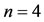 , we have
, we have


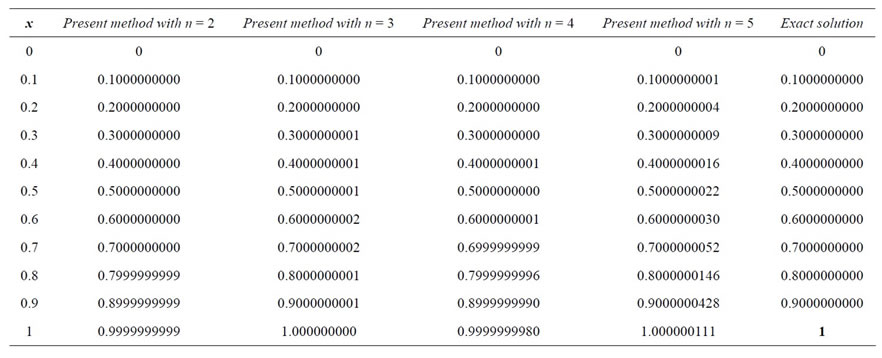
Table 1. Approximate and exact solutions for Example 1.

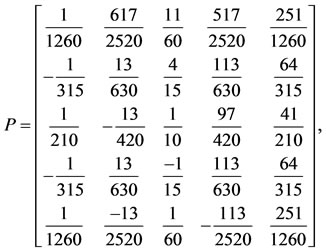

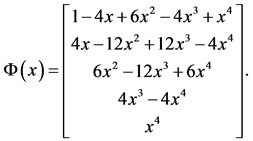
We obtain the approximate solutions of the problem for 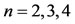 and
and 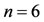 respectively,
respectively,

Example 2. Consider the nonlinear Fredholm integrodifferential equation, as follows [16]:
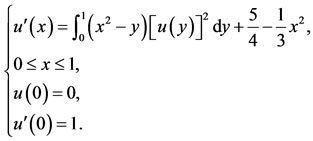 (38)
(38)
The exact solution is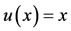 . Taking
. Taking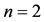 , we compare the obtained solution with exact solution and method [16] in Table 2.
, we compare the obtained solution with exact solution and method [16] in Table 2.
By applying the method in Section 4, we have for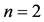 ,
,
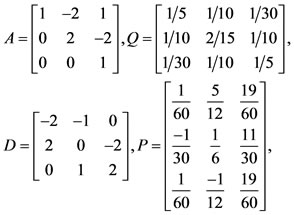
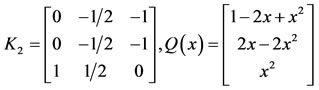 .
.
We obtain the approximate solutions of the problem  for
for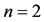 .
.
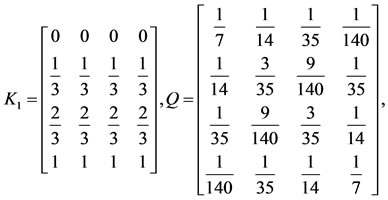
Example 3. Consider the nonlinear Volterra integrodifferential equation, as follows:
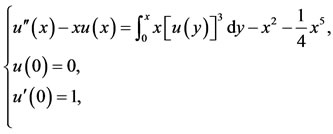 (39)
(39)
where the exact solution is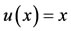 . Table 3 with 4 choices of
. Table 3 with 4 choices of 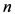 illustrates the numerical results for this example.
illustrates the numerical results for this example.
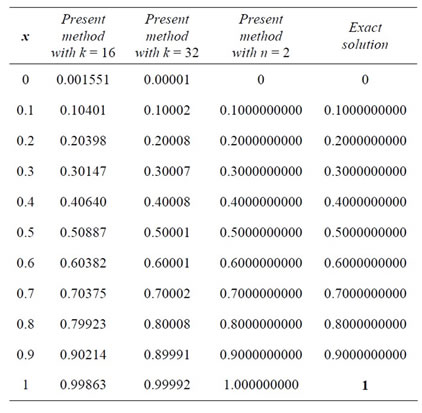
Table 2. Approximate and exact solutions for Example 2.
By applying the method in Section 4, we have for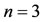 .
.
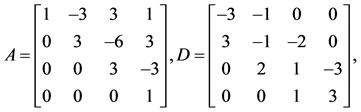

Example 4. Consider the nonlinear Volterra-Fredholm integro-differential equation
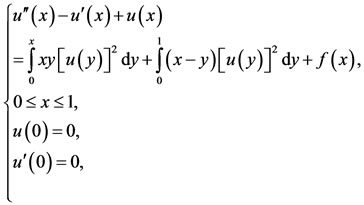 (40)
(40)
where 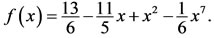
The exact solution is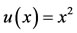 . The results of proposed method on this example are exhibited in Table 4 with 4 choices of
. The results of proposed method on this example are exhibited in Table 4 with 4 choices of . For this complicated NVFIDE, we get acceptable results with a small number of Bernstein basis functions. We obtain the approximate solutions of the problem for
. For this complicated NVFIDE, we get acceptable results with a small number of Bernstein basis functions. We obtain the approximate solutions of the problem for 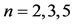 and
and 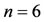 respectively,
respectively,

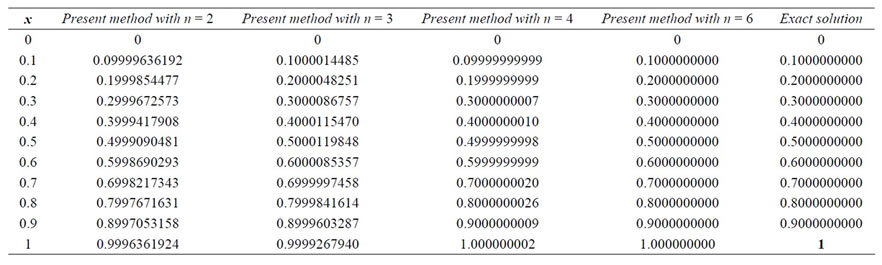
Table 3. Approximate and exact solutions for Example 3.
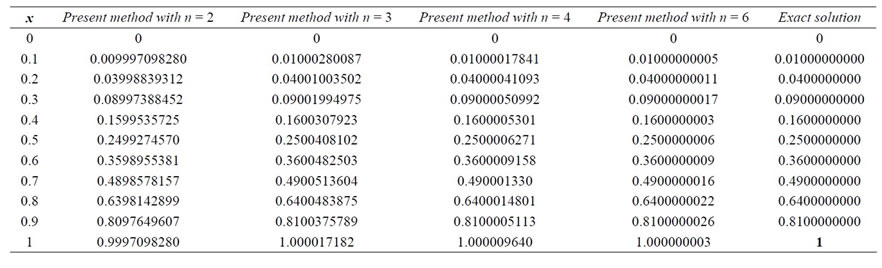
Table 4. Approximate and exact solutions for Example 4.
 In this regard, we have reported in figures and a table, the values of the exact solution
In this regard, we have reported in figures and a table, the values of the exact solution , the approximate solution
, the approximate solution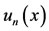 , and the absolute error function
, and the absolute error function 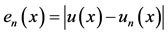 at the selected points of the given interval.
at the selected points of the given interval.
We have zoomed out Figures 1 and 2 to a great extent because the exact and approximate solutions are very close.
Example 5. Finally, consider the nonlinear VolterraFredholm integro-differential equation [17].
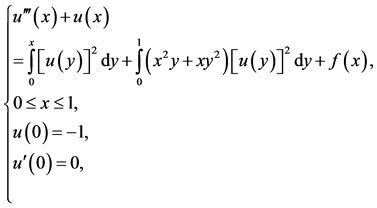 (41)
(41)
where,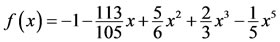 .
.
The exact solution is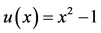 . The results of the proposed method for this example are exhibited in Table 5 with 4 choices of
. The results of the proposed method for this example are exhibited in Table 5 with 4 choices of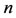 . For this complicated NVFIDE, we get acceptable results with a small number of Bernstein basis functions. We obtain the approximate solutions of the problem for
. For this complicated NVFIDE, we get acceptable results with a small number of Bernstein basis functions. We obtain the approximate solutions of the problem for 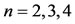 and
and 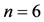 respectively,
respectively,


In this regard, we have reported in figures and a table, the values of the exact solution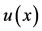 , the approximate solution
, the approximate solution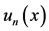 , and the absolute error function
, and the absolute error function 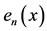
 at the selected points of the given interval.
at the selected points of the given interval.
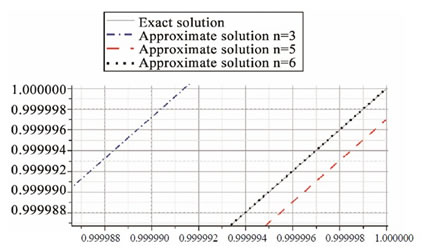
Figure 1. Comparison of the exact solution and the approximate solutions for Example 5.
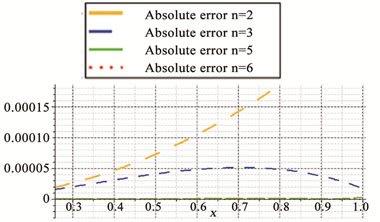
Figure 2. Comparison of the absolute error functions for Example 5.
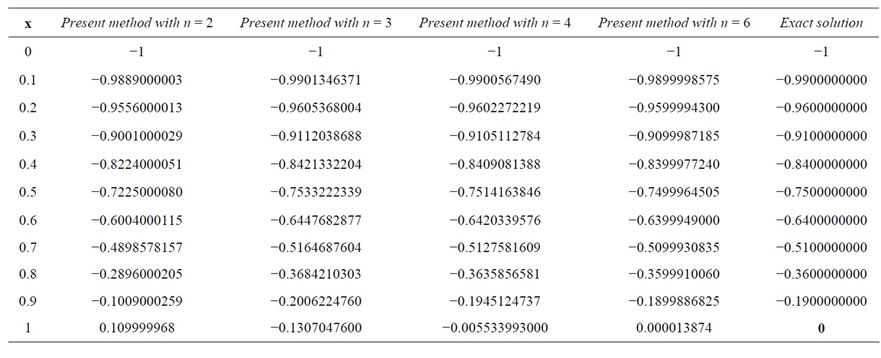
Table 5. Approximate and exact solutions for Example 5.
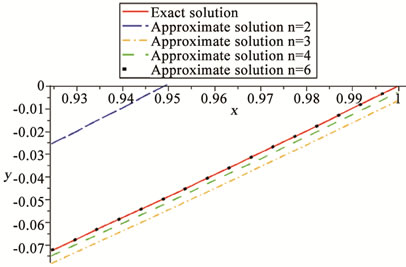
Figure 3. Comparison of the exact solution and the approximate solutions for Example 5.
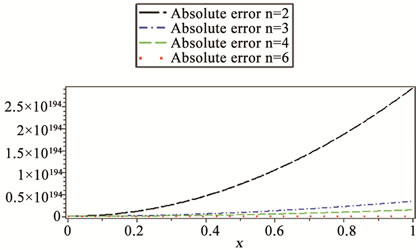
Figure 4. Comparison of the absolute error functions for Example 5.
We have zoomed out Figures 3 and 4 to a great extent because the exact and approximate solutions are very close. While in [17], the adopted method yields no solution for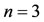 , takes time to give the approximate answer for
, takes time to give the approximate answer for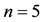 , and is proper only for
, and is proper only for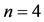 , our method is significant not only because it yeilds solutions for any n, but also because the approximate solutions it gives are very close to exact ones.
, our method is significant not only because it yeilds solutions for any n, but also because the approximate solutions it gives are very close to exact ones.
6. Conclusion
In this paper, we have proposed a numerical solution to solve nonlinear Volterra-Fredholm integro-differential equations with initial condition by Bernstein polynomials operational matrices and derived operational matrix. We use formula for numerical examples and it is obvious that the numerical solution coincides with the exact solution even with a few Bernstein polynomials used in the approximation. Finally, errors show that the approximation becomes more accurate when n is increased. Therefore, for better results, it is recommended to use a larger n.
REFERENCES
- M. A. Abdou, “On Asymptotic Methods for FredholmVolterra Integral Equation of the Second Kind in Contact Problems,” Journal of Computational and Applied Mathematics, Vol. 154, No. 2, 2003, pp. 431-446.
- F. Bloom, “Asymptotic Bounds for Solutions to a System of Damped Integro-Differential Equations of Electromagnetic Theory,” Journal of Mathematical Analysis and Applications, Vol. 73, 1980, pp. 524-542.
- M. A. Jaswon and G. T. Symm, “Integral Equation Methods in Potential Theory and Elastostatics,” Academic Press, London, 1977.
- S. Jiang and V. Rokhlin, “Second Kind Integral Equations for the Classical Potential Theory on Open Surface II,” Journal of Computational Physics, Vol. 195, No. 3, 2004, pp. 1-16.
- P. Schiavane and C. Constanda and A. Mioduchowski, “Integral Methods in Science and Engineering,” Birkhauser, Boston, 2002.
- B. I. Smetanin, “On an Integral Equation for AxiallySymmetric Problems in the Case of an Elastic Body Containing an Inclusion,” Journal of Applied Mathematics and Mechanics, Vol. 55, No. 3, 1991, pp. 371-375.
- N. N. Voitovich and O. O. Reshnyak, “Solutions of Nonlinear Integral Equation of Synthesis of the Linear Antenna Arrays,” BSUAE Journal of Applied Electromagnetism, Vol. 2, No. 1, 1999, pp. 43-52.
- L. M. Delves and J. Walsh, “Numerical Solution of Integral Equation,” Oxford University Press, London, 1974.
- G. Micula and P. Pavel, “Differential and Integral Equations through Practical Problems and Exercises,” Kluwer, 1992.
- R. K. Miller, “Nonlinear Volterra Integral Equations,” Menlo Park, 1967.
- E. H. Doha, A. H. Bhrawy and M. A. Saker, “Integrals of Bernestein Polynomials: An Application for the Solution of High Even-Order Differential Equations,” Applied Mathematics Letters, Vol. 24, No. 4, 2011, pp. 559-565.
- R. T. Farouki and V. T. Rajan, “Algorithms for Polynomials in Bernstein Form,” Computer Aided Geometric Design, Vol. 5, No. 1, 1988, pp. 1-26.
- K. Maleknejad, E. Hashemizadeh and B. Basirat, “Computational Method Based on Bernestein Operational Matrices for Nonlinear Volterra—Fredholm-Hammerstein Integral Equations,” Communications in Nonlinear Science and Numerical Simulation, Vol. 17, No. 1, 2012, pp. 52-61. doi:10.1016/j.cnsns.2011.04.023
- S. A. Yousefi and M. Behroozifar, “Operational Matrices of Bernstein Polynomials and Their Applications,” International Journal of Systems Science, Vol. 41, No. 6, 2010, pp. 709-716. doi:10.1080/00207720903154783
- Z. Avazzadeh, M. Heydari and G. B. Loghmani, “Numerical Solution of Fredholm Integral Equations of the Second Kind by Using Integral Mean Value Theorem,” Applied Mathematical Modelling, Vol. 35, No. 5, 2011, pp. 2374-2383.
- F. Mirzaee, “The RHFs for Solution of Nonlinear Fredholm Integro-Differential Equations,” Applied Mathematical Modelling, Vol. 5, No. 70, 2011, pp. 3453-3464.
- W. Wang, “An Algorithm for Solving the High-Order Nonlinear Volterra-Fredholm Integro-Differential Equation with Mechanization,” Applied Mathematics and Computation, Vol. 172, No. 1, 2006, pp. 1-23.

