International Journal of Modern Nonlinear Theory and Application
Vol.2 No.1(2013), Article ID:28826,12 pages DOI:10.4236/ijmnta.2013.21005
A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: heddinim@yahoo.com
Received November 16, 2012; revised December 22, 2012; accepted December 31, 2012
Keywords: Dark Energy; Homology of Fuzzy Kähler; Betti Numbers; Heterotic Strings; Revised Special Relativity; Speed of Light as a Probabilistic Expectation Value
ABSTRACT
Time dilation, space contraction and relativistic mass are combined in a novel fashion using Newtonian dynamics. In this way we can surprisingly retrieve an effective quantum gravity energy-mass equation which gives the accurate experimental value of vacuum density. Furthermore Einstein’s equation of special relativity E = mc2, where m is the mass and c is the velocity of light developed assuming smooth 4D space time is transferred to a rugged Calabi-Yau and K3 fuzzy Kähler manifolds and revised to become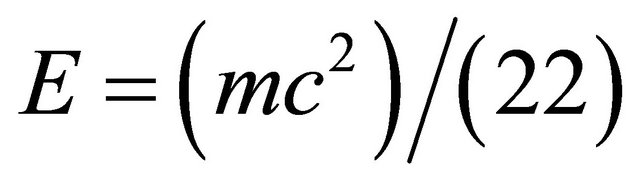 , where the division factor 22 maybe interpreted as the compactified bosonic dimensions of Veneziano-Nambu strings. The result is again an accurate effective quantum gravity energy-mass relation akin to the one found using Newtonian dynamics which correctly predicts that 95.4915028% of the energy in the cosmos is the hypothetical missing dark energy. The agreement with WMAP and supernova measurements is in that respect astounding. In addition different theories are used to check the calculations and all lead to the same quantitative result. Thus the theories of varying speed of light, scale relativity, E-infinity theory, M-theory, Heterotic super strings, quantum field in curved space time, Veneziano’s dual resonance model, Nash Euclidean embedding and super gravity all reinforce, without any reservation, the above mentioned theoretical result which in turn is in total agreement with the most sophisticated cosmological measurements which was deservingly awarded the 2011 Nobel Prize in Physics. Finally and more importantly from certain viewpoints, we reason that the speed of light is constant because it is a definite probabilistic expectation value of a variable velocity in a hierarchical fractal clopen, i.e. closed and open micro space time.
, where the division factor 22 maybe interpreted as the compactified bosonic dimensions of Veneziano-Nambu strings. The result is again an accurate effective quantum gravity energy-mass relation akin to the one found using Newtonian dynamics which correctly predicts that 95.4915028% of the energy in the cosmos is the hypothetical missing dark energy. The agreement with WMAP and supernova measurements is in that respect astounding. In addition different theories are used to check the calculations and all lead to the same quantitative result. Thus the theories of varying speed of light, scale relativity, E-infinity theory, M-theory, Heterotic super strings, quantum field in curved space time, Veneziano’s dual resonance model, Nash Euclidean embedding and super gravity all reinforce, without any reservation, the above mentioned theoretical result which in turn is in total agreement with the most sophisticated cosmological measurements which was deservingly awarded the 2011 Nobel Prize in Physics. Finally and more importantly from certain viewpoints, we reason that the speed of light is constant because it is a definite probabilistic expectation value of a variable velocity in a hierarchical fractal clopen, i.e. closed and open micro space time.
1. Introduction
The present work is mainly concerned with devising a theoretical explanation for the mystery of the so-called missing dark energy of the cosmos [1-4]. However this is all linked to quantum gravity [1-23] and we start here from special relativity and address the greatest puzzle of them all which we invariably took and rather wrongly as a given experiential fact of Nature which cannot be reduced or interrogated any further namely the constancy of the speed of light. As is well known Einstein’s special relativity presupposes a smooth space time with Lorentzian symmetry group invariance [1]. Quantum space time on the other hand is modeled via radically different geometrical visualization [1-8]. In string theory, M-theory and super gravity one uses various types of CalabiYau and complex Kähler manifolds for space time extra dimensions [9-17]. Consequently requiring the Poincaré
invariance in a complex space with such extra and compactified dimensions will most definitely lead to a different energy-mass relation than the classical famous Einstein equation of special relativity. On the other hand should the principle of scale relativity hold, then one would expect to retrieve Einstein’s familiar formula in a scaled form [3-5]. In a sense we expect a type of scale similarity close to that found between Newton’s kinetic energy and the famous energy-mass formula of relativity which differs by a factor of only 1/2 and changing the variable velocity v to the puzzlingly constant speed of light c. Noting that for a continuous manifold the Betti number 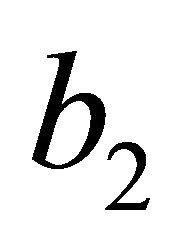 which counts the three dimensional holes in a manifold is given by
which counts the three dimensional holes in a manifold is given by 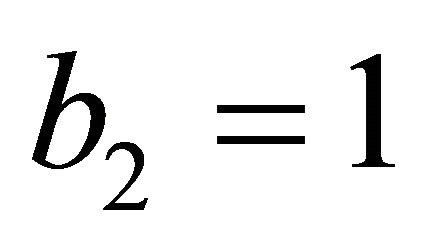 and that the same Betti number for a K3 Kähler is
and that the same Betti number for a K3 Kähler is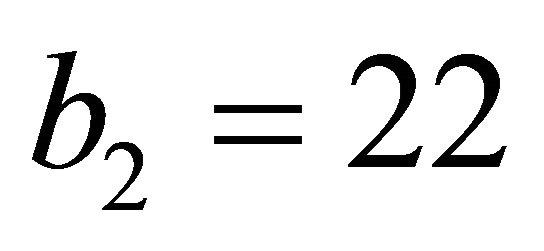 , it is possible to show that E = mc2 may be elevated to quantum relativity, i.e. an effective quantum gravity equation when scaled by
, it is possible to show that E = mc2 may be elevated to quantum relativity, i.e. an effective quantum gravity equation when scaled by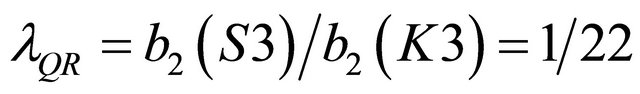 .
.
This prior intuitive mathematical expectation was confirmed on two counts, namely first experimentally using the WMAP and supernova cosmic measurements [4,19] and second theoretically using numerous sophisticated established theories, all leading to the same robust result, namely a scaling factor 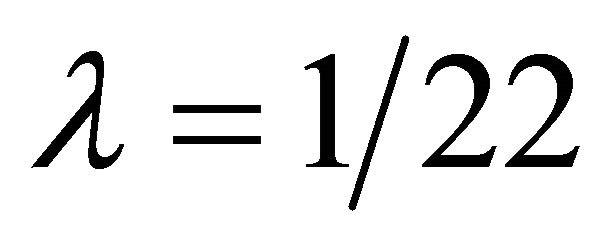 (see Table 1) [24-26].
(see Table 1) [24-26].
In this paper we start first from basic principles connected to special relativity then transform these principles back to Newtonian dynamics only to obtain quantum relativity results. Surprisingly that way we retrieve a highly non-classical equation indeed combining the quantum with relativity via a four dimensional Hilbert-He hypercube [7] (see Overview 3 and Table 2).
Subsequently we show that for a fuzzy Kähler [10,13] the scaling factor changes from 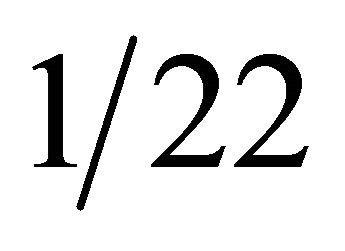 to
to 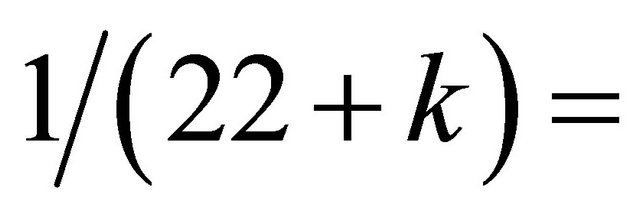
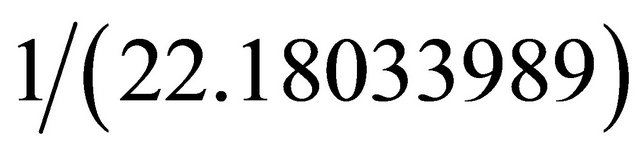 . In addition to giving a derivation of the new quantum relativity equation
. In addition to giving a derivation of the new quantum relativity equation 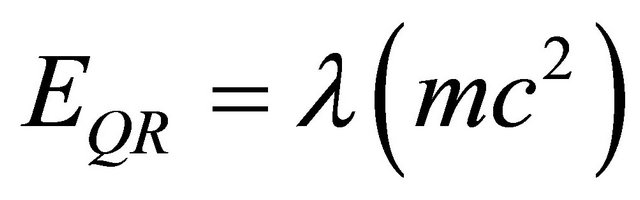 where m is the mass and c is the speed of light, we show that this result is in exquisite agreement with the cosmological measurement of COBE and WMAP as well as the analysis of certain supernovas which led to the award of last year’s 2011 Nobel Prize in Physics [4,18]. Based on our K3 fuzzy Kähler we can predict with very high precision that the percentage of hypothetical dark energy, supposedly missing, in the universe is 95.4915028%. This is a probably unprecedented agreement between theory and measurement in cosmology [4], if not in all of theoretical physics [1]. We will hopefully know with absolute certainty when the Planck measurement project [18] is completed.
where m is the mass and c is the speed of light, we show that this result is in exquisite agreement with the cosmological measurement of COBE and WMAP as well as the analysis of certain supernovas which led to the award of last year’s 2011 Nobel Prize in Physics [4,18]. Based on our K3 fuzzy Kähler we can predict with very high precision that the percentage of hypothetical dark energy, supposedly missing, in the universe is 95.4915028%. This is a probably unprecedented agreement between theory and measurement in cosmology [4], if not in all of theoretical physics [1]. We will hopefully know with absolute certainty when the Planck measurement project [18] is completed.
Last but as we mentioned above by no means least, noting that all real measurements are taken in the expectation dimensionality of spacetime 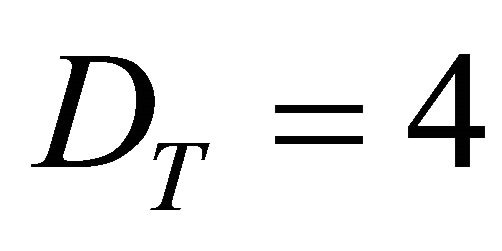 and
and 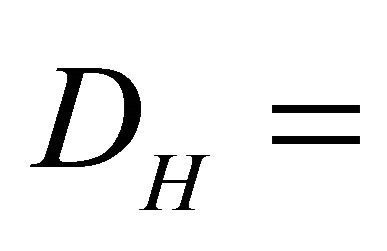
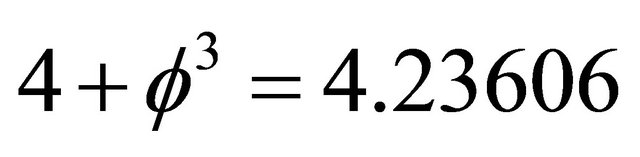 , we reason that the speed of light is constant because it is the probabilistic expectation value of variable speed in a fractal spacetime. In other words the constancy of the experimental value of the speed of light is the evidence that our spacetime manifold is highly complex non-classical fractal-Cantorian manifold on the quantum scale. Consequently this space must be topologically clopen i.e. closed and opened at the same time.
, we reason that the speed of light is constant because it is the probabilistic expectation value of variable speed in a fractal spacetime. In other words the constancy of the experimental value of the speed of light is the evidence that our spacetime manifold is highly complex non-classical fractal-Cantorian manifold on the quantum scale. Consequently this space must be topologically clopen i.e. closed and opened at the same time.
2. Motives for Revising Einstein’s Energy-Mass Equation—Combining Newtonian, Relativistic and Quantum Mechanics
2.1. General Remarks and Topological Considerations
An equation based entirely on the tacit assumption of a smooth space with Lorentzian space time invariance developed many years before the standard model of high energy particle physics and quantum field theory were discovered [1] could not possibly be expected not to break down at some quantum or intergalactic scales [1-3, 19]. The above is an accurate description of the circumstances surrounding the inception of A Einstein Iconic formula E = mc2 of special relativity in 1905. In the present paper we show that the supposedly missing dark energy in the cosmos, discovered through various accurate cosmological measurements [4] is in effect due to some basic fundamental inadequacies of applying Einstein’s celebrated equation E = mc2 (where E is the energy, m is the mass and c is the speed of light) outside its range of validity [5,6]. We thought for a long time and understandably so that gravity cannot have that crucial effect on elementary particle physics [1]. Similarly we thought that quantum mechanics also has very little effect on cosmology except maybe when it comes to incredibly shrinking objects such as black holes [1]. However when we started asking very deep questions regarding the unification of all fundamental interactions [7,8] we recognized suddenly that at the extreme small distances such as the Planck length (10−33 cm) the feeble gravity becomes as strong as the other three fundamental forces, i.e. the weak force, the strong force and the electromagnetic force [1,3,7]. On the other hand we have now just realized that quantum effects, such as quantum entanglement, have an equally huge impact on physics at extremely large intergalactic distances. It is so profound that the classical equation of Einstein E = mc2 is off the correct result by almost 95.5% [4,19]. Seen with the eyes of a particle physicist this should not be that astonishing because the only degree of freedom of special relativity is a single messenger particle, the photon [1]. By contrast the simplest model for high energy quantum physics, the standard model, requires 12 photon-like messenger particles equivalent to 12 degrees of freedom i.e. 12 generalized coordinates in the corresponding Lagrangian [1,7]. Special relativity therefore is highly confined by the Rayleigh theorem on Eigen values and is bound to over-estimate the energy levels.
In the present work we trace back the shortcoming in 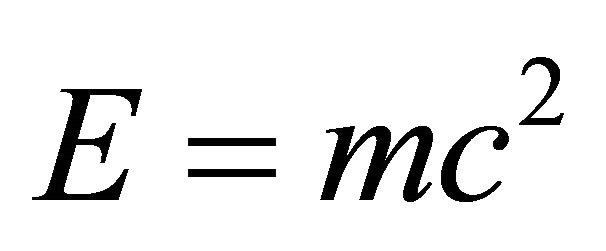 and prove that this is the case because of the real non-classical geometry and topology of the actual fabric of space time [2,7,8]. This non-classical topology is essentially the cause of amplifying what we perceive as quantum effect which screens the energy by as much as 95.5% in full agreement with measurements [4]. In particular we will show that the ratio of the two Betti numbers [9-12] fixes the homology of space time’s de Rham topology of smooth classical space time of relativity and the rugged K3 Kähler [11] based quantum space time of quantum gravity and give us a Weyl-Nottale scaling λ = b2 (smooth)/b2 (Kähler) equal to 1/22 which accounts for the 95.5% missing dark energy [4]. It is well known that the Betti numbers are topological invariants of a manifold [9,10] exactly as the dimensions and the
and prove that this is the case because of the real non-classical geometry and topology of the actual fabric of space time [2,7,8]. This non-classical topology is essentially the cause of amplifying what we perceive as quantum effect which screens the energy by as much as 95.5% in full agreement with measurements [4]. In particular we will show that the ratio of the two Betti numbers [9-12] fixes the homology of space time’s de Rham topology of smooth classical space time of relativity and the rugged K3 Kähler [11] based quantum space time of quantum gravity and give us a Weyl-Nottale scaling λ = b2 (smooth)/b2 (Kähler) equal to 1/22 which accounts for the 95.5% missing dark energy [4]. It is well known that the Betti numbers are topological invariants of a manifold [9,10] exactly as the dimensions and the
Table 1. The Energy mass relation of quantum relativity using various fundamental theory.


Continued


Continued

Euler characteristics [9-12] with the added advantage that b2 counts what we may call three dimensional holes (voids) [9] in the manifold which in this case is our real space time fabric. That way all the fractal-like fine structures of our space are taken into account [9,13]. How this actually is done is what we will explain next.
However before going ahead with the preceding outlined topological geometrical program, we will regress to reconsider relativity and Newtonian dynamics at the most possible basic level [1,20,21]. In the course of doing that, we will arrive at a far reaching conclusion with tremendous impact on the entire foundation of physics namely that the constancy of the speed of light and similar to 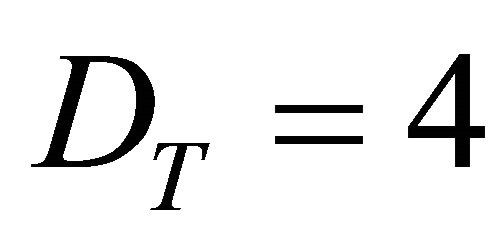 and
and 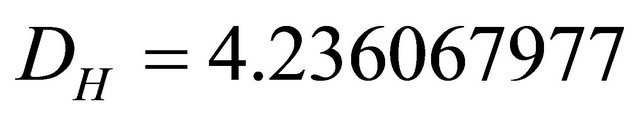 of space time (see Overview 1) is a consequence of the fractal Cantorian nature of the very fabric of space and time. Consequently the speed of Light is simply an expectation value in the sense of probability theory of an otherwise varying speed.
of space time (see Overview 1) is a consequence of the fractal Cantorian nature of the very fabric of space and time. Consequently the speed of Light is simply an expectation value in the sense of probability theory of an otherwise varying speed.
2.2. Basic Principles of Special Relativity Starting from Newtonian Dynamics and Leading to Quantum Mechanics and Quantum Relativity [20] (see Overview 2)
We will not start here from 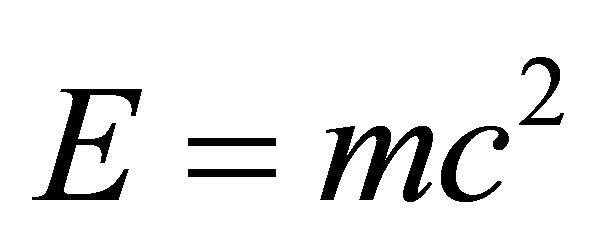 of relativity but rather from Newtonian kinetic energy
of relativity but rather from Newtonian kinetic energy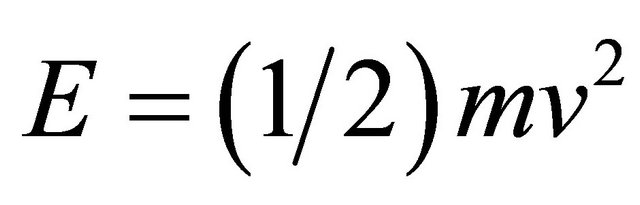 . Now we ponder the three well known relativistic effects, namely 1) time dilation which we introduce here by a simple factor
. Now we ponder the three well known relativistic effects, namely 1) time dilation which we introduce here by a simple factor 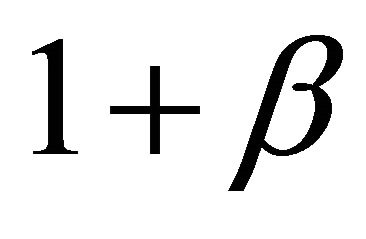 leading to
leading to 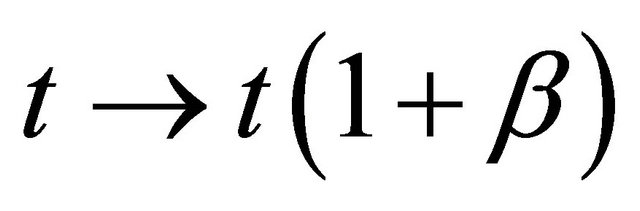 2) Then we have space contraction which is obviously
2) Then we have space contraction which is obviously 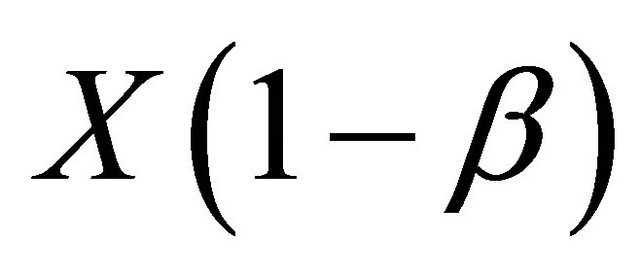
Space time dimensions and energy in the three fundamental theories: classical, relativistic and quantum gravity.
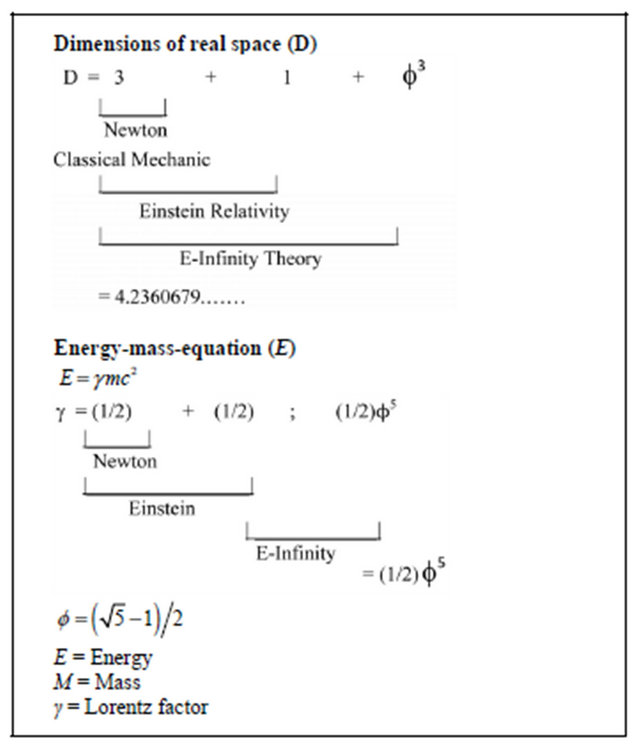
Overview 1.
where X is a space coordinate. Finally we have increased mass as ![]() and this leads to 3) relativistic mass
and this leads to 3) relativistic mass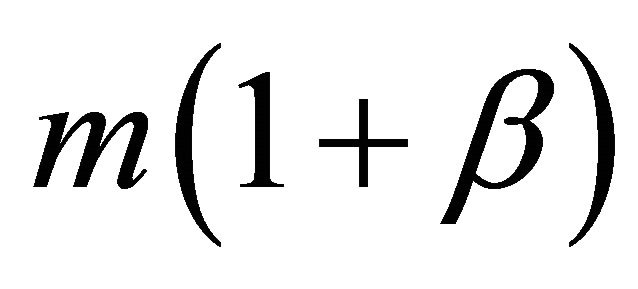 . Consequently our
. Consequently our 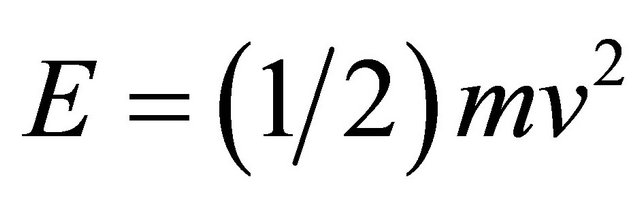 becomes (for details see Overview 3)
becomes (for details see Overview 3)
 (1)
(1)
The factor 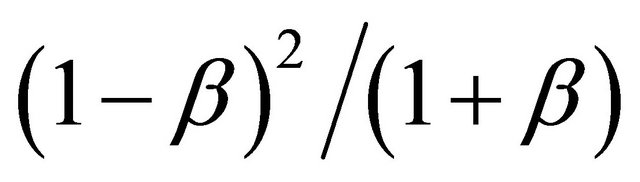 will play a crucial role in our theory leading to the inescapable conclusion that space time of special relativity is a random Cantorian Fractal with an average expectation value for the speed of Light.
will play a crucial role in our theory leading to the inescapable conclusion that space time of special relativity is a random Cantorian Fractal with an average expectation value for the speed of Light.
Let us see what value this twisted boost 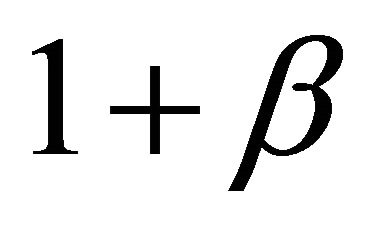 and anti-boost
and anti-boost 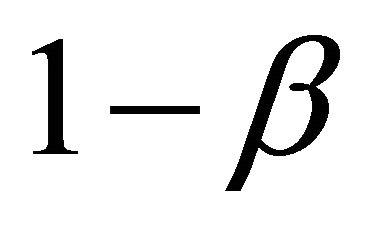 must take in order to retrieve Newton’s energy and Einstein’s energy. In the case of Newtonian energy, this is very simple because we must have
must take in order to retrieve Newton’s energy and Einstein’s energy. In the case of Newtonian energy, this is very simple because we must have
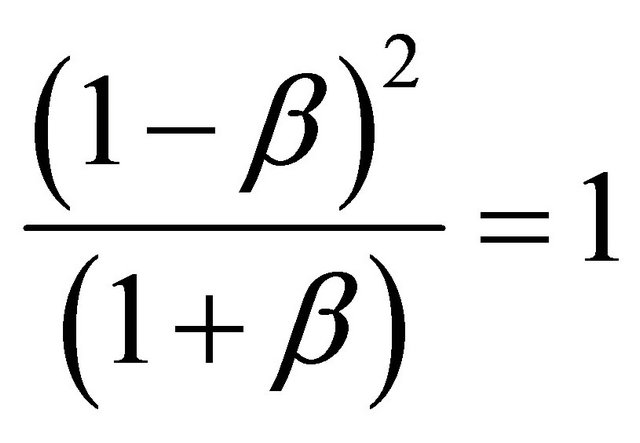 (2)
(2)
from which one finds that either 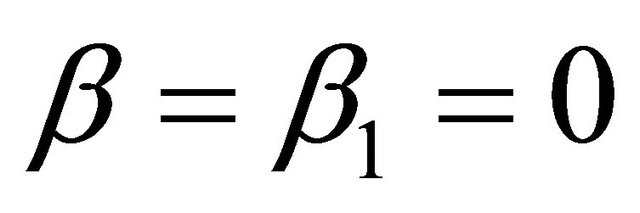 or
or 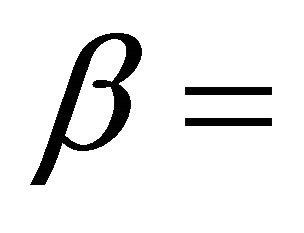
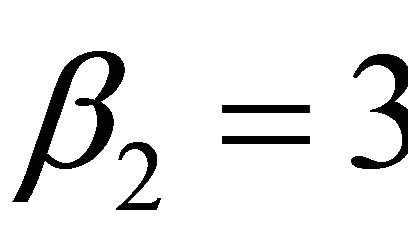 to obtain
to obtain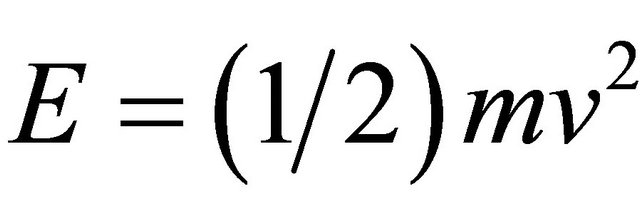 . Note that
. Note that 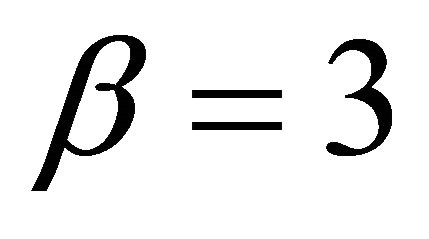 should be interpreted as the natural classical space which is not 4D but 3 + 1 dimensional space where time is now a simple parameter. For the relativistic case on the other hand, things are far more interesting and revealing because we must have
should be interpreted as the natural classical space which is not 4D but 3 + 1 dimensional space where time is now a simple parameter. For the relativistic case on the other hand, things are far more interesting and revealing because we must have
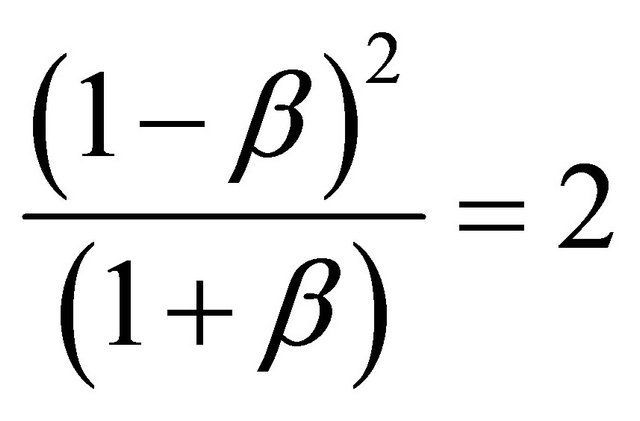 (3)
(3)
This leads to a quadratic equation
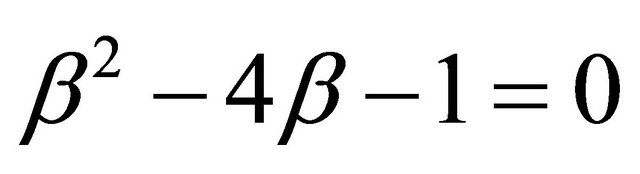 (4)
(4)
with two solutions [7,17]
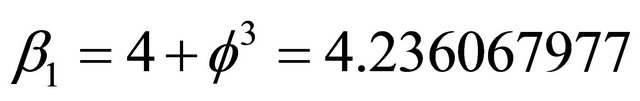 (5)
(5)
and [7]
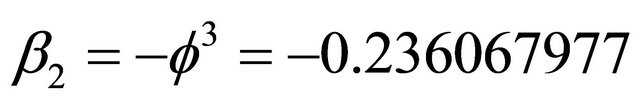 (6)
(6)
where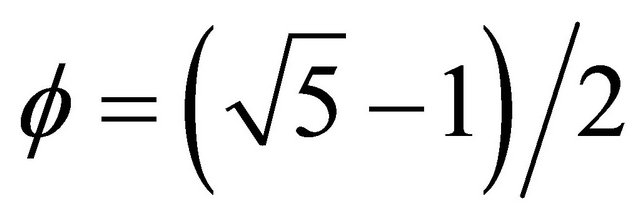 . Both
. Both 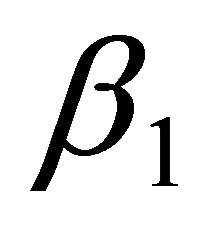 and
and 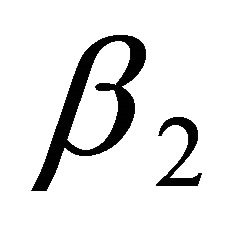 lead to E = mc2. On the other hand
lead to E = mc2. On the other hand 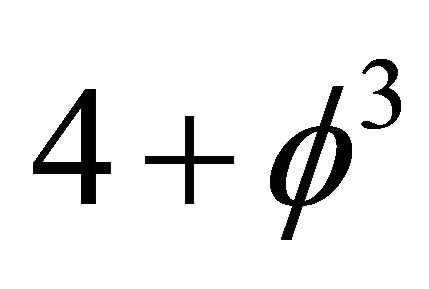 is the Hausdorff dimension of a Hilbert-fractal hyper cube discussed extensively by Ji-Huan He and the author [7]. This is indeed more than a remarkable result linking for the first time fractals in the form of a Hilbert-He 4 dimensional hypercube and
is the Hausdorff dimension of a Hilbert-fractal hyper cube discussed extensively by Ji-Huan He and the author [7]. This is indeed more than a remarkable result linking for the first time fractals in the form of a Hilbert-He 4 dimensional hypercube and

Overview 2.

Overview 3.
special relativity [7]. This implies indirectly that the speed of light varies between Zero and Infinity with the familiar experimental value being simply the probabilistic expectation value. In the rest of this paper we will show how the factor 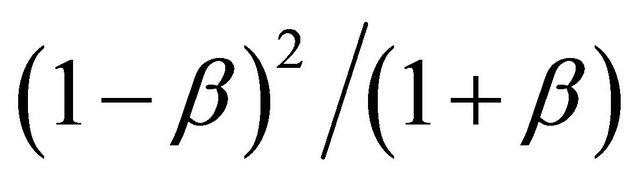 will lead to a quantum gravity-like equation combing relativity with quantum entanglement for the Sigalotti critical value
will lead to a quantum gravity-like equation combing relativity with quantum entanglement for the Sigalotti critical value 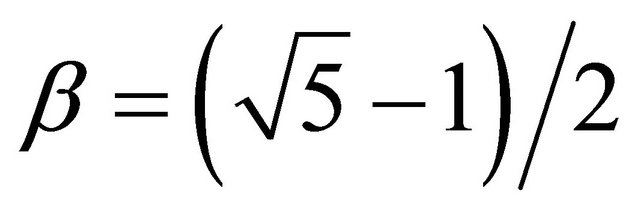 [17,22,27,28]. The preceding results are once more neatly summarized in Overview No. 3.
[17,22,27,28]. The preceding results are once more neatly summarized in Overview No. 3.
3. Homology of a Space Time Based on Crisp K3 Kähler Manifold [10]
Following super strings and related theories [12] we look first at the possibility of a quantum gravity spacetime based upon a K3 Kähler manifold [13]. We start with a non-fuzzy crisp Kähler then look at the fractal-like fuzzy case.
3.1. Classical Non-Fuzzy Kähler
We consider a K3 Kähler manifold with four complex dimensions used extensively in theories with hidden dimensions particularly super and Heterotic string theory [12,13]. The manifold is fixed by the Betti numbers which determine the Euler characteristic and the signature. In the case of non-fuzzy (crisp) K3 the Betti numbers are [10,13]
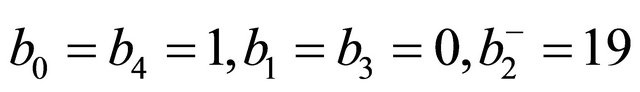 and
and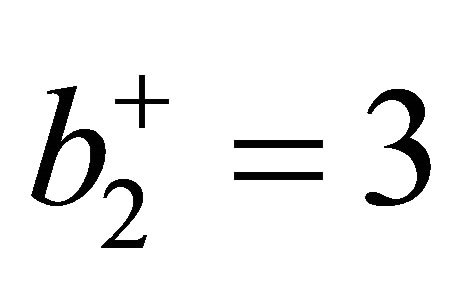 . (7)
. (7)
It follows then that the Euler characteristic is [10,13]
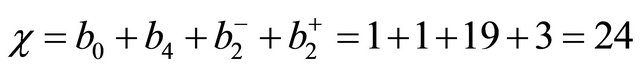 (8)
(8)
while [10,13]
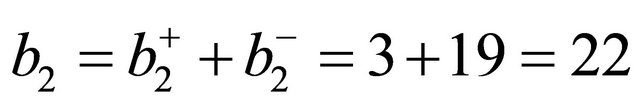 (9)
(9)
and the signature is [10,13]
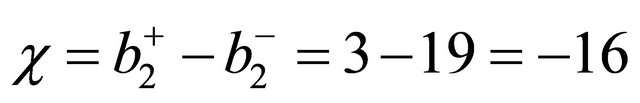 . (10)
. (10)
We stress once more that b2 counts the 3 dimensional holes in K3 and will play a crucial role in our derivation.
3.2. Fuzzy, Fractal-Like K3 Kähler
Now we look at an even more exotic version of K3 [13]. With that we mean fuzzy Kähler which we used in earlier studies in a slightly modified form [13,14]. The Kähler we construct here is a fuzzy version of the one considered above. The K3 Kähler in question is given by the same 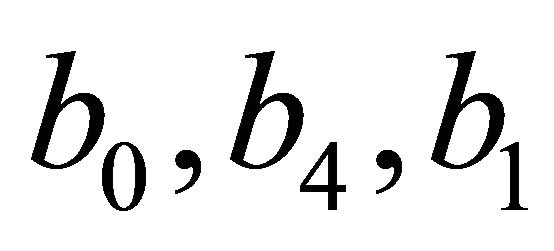 and b3 as the previous crisp Kähler. Only
and b3 as the previous crisp Kähler. Only 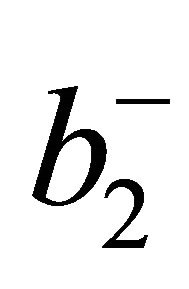 and
and 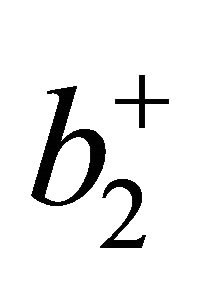 which measure a sort of average number of 3D fractal voids are given by [13,14,24-26].
which measure a sort of average number of 3D fractal voids are given by [13,14,24-26].
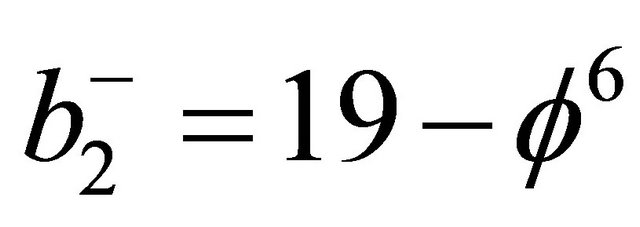 and
and 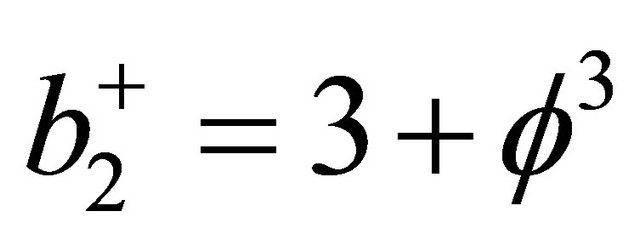 (11)
(11)
where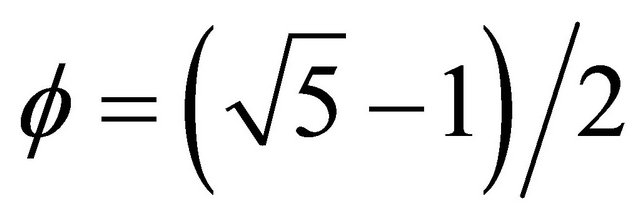 . It follows then that [13,14]
. It follows then that [13,14]
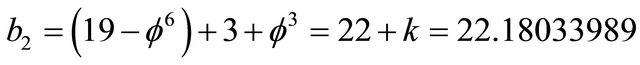 . (12)
. (12)
It is important to note the following. The small numbers 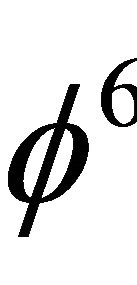 = 0.05572809014 as well as
= 0.05572809014 as well as  = 0.236067977 and
= 0.236067977 and 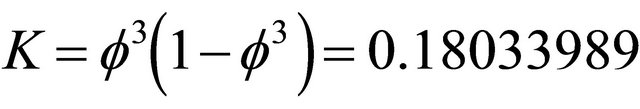 all have various physical, topological and geometrical interpretations. For instance
all have various physical, topological and geometrical interpretations. For instance 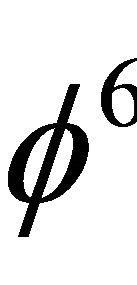 is the exact value of the vital Immirzi parameter of loop quantum gravity without which nothing would fit in this theory [15]. In addition
is the exact value of the vital Immirzi parameter of loop quantum gravity without which nothing would fit in this theory [15]. In addition 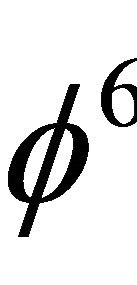 may be viewed as the probability for quantum entanglement of three quantum particles while
may be viewed as the probability for quantum entanglement of three quantum particles while  is the well known Hardy’s generic probability of quantum entanglement [16,17,22] for two particles which was also confirmed experimentally. Thus
is the well known Hardy’s generic probability of quantum entanglement [16,17,22] for two particles which was also confirmed experimentally. Thus  could be named the probability of Immirzi quantum entanglement. The
could be named the probability of Immirzi quantum entanglement. The  on the other hand is the generic probability of a Cantorian spacetime with a core Hausdorff dimension equal to
on the other hand is the generic probability of a Cantorian spacetime with a core Hausdorff dimension equal to 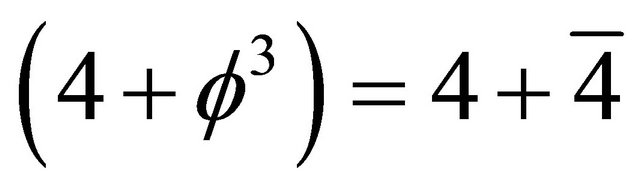 and is directly connected to the Unruh temperature [13] (see Overview 4).
and is directly connected to the Unruh temperature [13] (see Overview 4).
Finally,
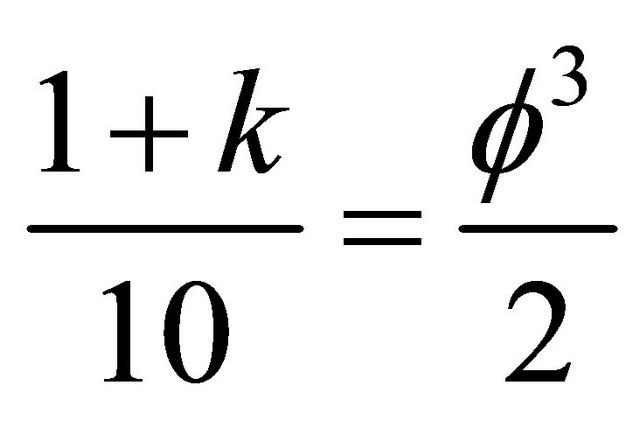 . (13)
. (13)
That means
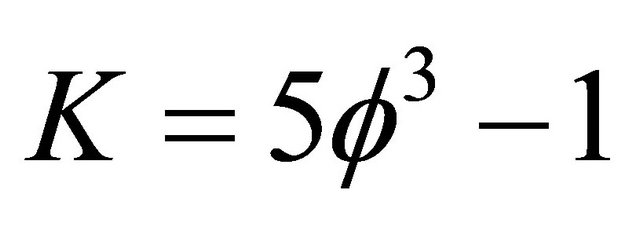 (14)
(14)
4. Elevating Einstein’s Relativistic Equation to a Quantum Gravity Energy-Mass Relation
We said that b2 is an important homological invariant of a manifold [9-11] and that it basically counts the 3 dimensional voids in the manifold [9,14]. For a two sphere S2 or any connected manifold b2 is equal to unity b2 = 1. On the other hand for our classical Kähler b2 = 3 + 19 = 22, and this number already indicates that this manifold is almost a Swiss cheese full of 3 dimensional holes [10, 13]. Compared to the smooth S2 manifold akin to the space time of Einstein, K3 has 22 times less space time and following general relativity, less energy [1]. Now following for instance Nottale’s scale relativity principle [24-26] we could define a scaling ![]() to account for fractal voids to be
to account for fractal voids to be
 (15)
(15)
and use it to scale 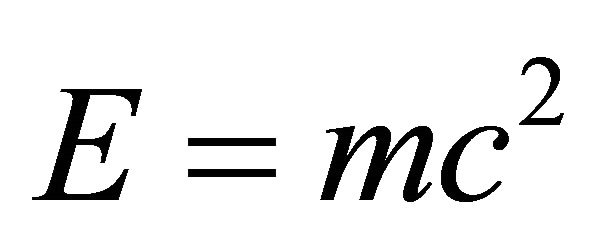 to
to
 (16)
(16)
This implies that the missing hypothetical dark energy is

Overview 4.
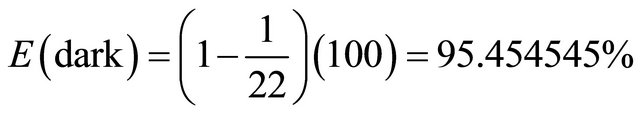 . (17)
. (17)
This is extremely close to the cosmological measurement [4]. Even better still, if we use the fuzzy version of K3 we arrive at a mathematically exact expression
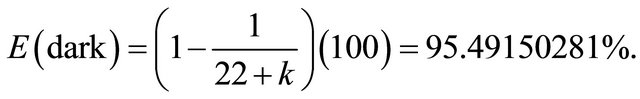 (18)
(18)
In fact when using the fuzzy Kähler, we notice immediately a quantum mechanical interpretation of the result because
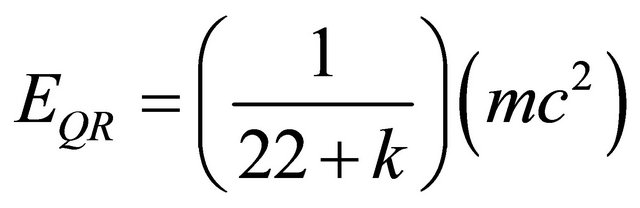 (19)
(19)
means that
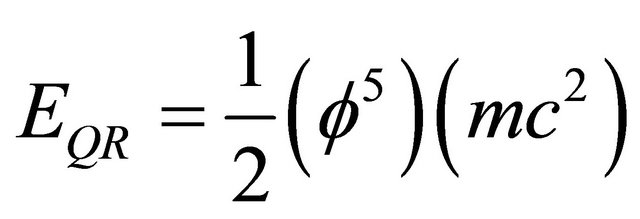 . (20)
. (20)
However  is nothing else but Hardy’s generic quantum entanglement of two quantum particles [16,17] so that our
is nothing else but Hardy’s generic quantum entanglement of two quantum particles [16,17] so that our  may be viewed as the screening of a substantial part of the energy in the cosmos by quantum entanglement reducing the Newtonian action at distance by as much as
may be viewed as the screening of a substantial part of the energy in the cosmos by quantum entanglement reducing the Newtonian action at distance by as much as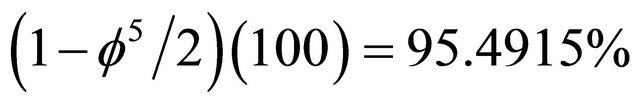 . Finally there is an even more immediate interpretation when we invoke string theory and M-theory as shown in Figures 1 and 2. In the case of string theory, we could argue our case as following: The largest number of dimensions in Heterotic string theory is 26 in the classical case and 26 + k in the transfinite fractal-fuzzy case. However we can make measurement only via 4 dimensions, 3 space dimensions and one time dimension. Thus we have 22 hidden dimensions [12]
. Finally there is an even more immediate interpretation when we invoke string theory and M-theory as shown in Figures 1 and 2. In the case of string theory, we could argue our case as following: The largest number of dimensions in Heterotic string theory is 26 in the classical case and 26 + k in the transfinite fractal-fuzzy case. However we can make measurement only via 4 dimensions, 3 space dimensions and one time dimension. Thus we have 22 hidden dimensions [12]
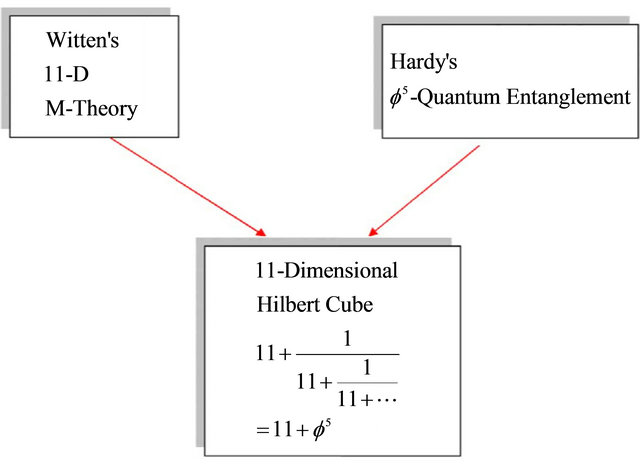
Figure 1. Combining M-theory and quantum entanglement to give a fractal M-theory.

Figure 2. Continued fraction representation of quantum relativity energy-mass equation.
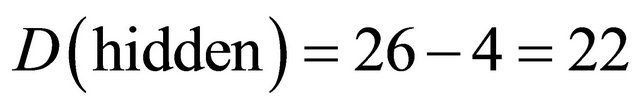 (21)
(21)
or more accurately [12,14]
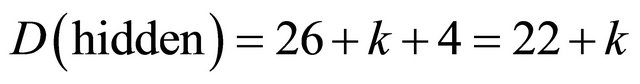 . (22)
. (22)
Thus our scaling exponent is
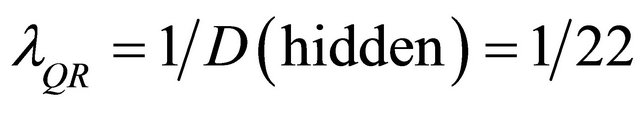 (23)
(23)
Or in the fuzzy case [13,14]
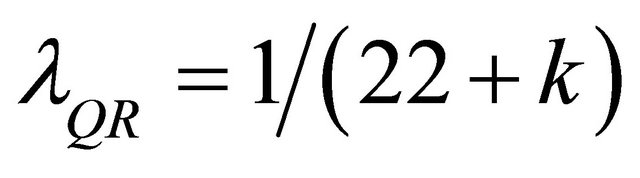 . (24)
. (24)
Within this mental picture we could say that the missing dark energy is concealed and hidden inside the dark extra dimension [7,12,14]. Now all what we need to do in order to see this unified picture of Newtonian, relativistic and quantum dynamics is to set following Sigalotti [27, 28] 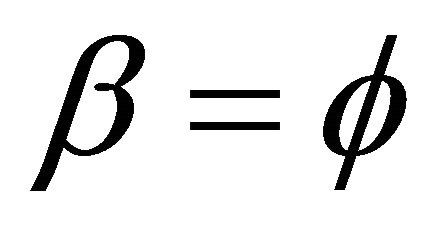 in our expression of Section 2.2 and find that
in our expression of Section 2.2 and find that 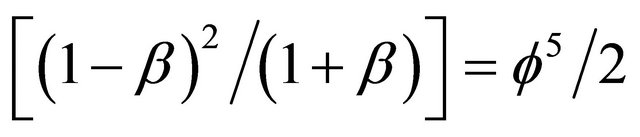 and that is exactly equal
and that is exactly equal 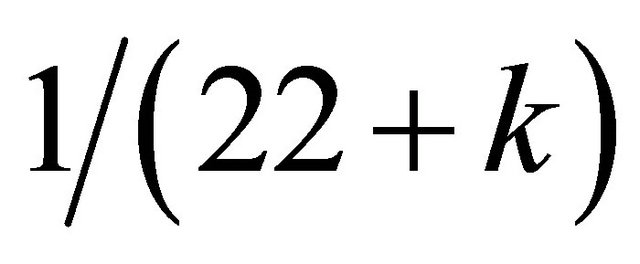 and in addition
and in addition 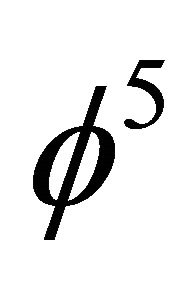 is Hardy’s generic probability of quantum entanglement [16,17,22].
is Hardy’s generic probability of quantum entanglement [16,17,22].
Incidentally 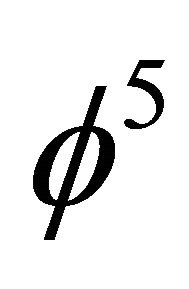 could be also interpreted as a dimensionless Planck energy equal to EP of the theory of varying speed of Light [5,6] while
could be also interpreted as a dimensionless Planck energy equal to EP of the theory of varying speed of Light [5,6] while  is corresponding to the Unruh temperature (See Overview 4) as mentioned earlier [29]. There is a fundamental connection between what we may call Witten Hyper cube and Witten Fractal M-Theory connecting quantum relativity with Hardy’s Quantum Entanglement. This is represented in a diagram and outlined in Figures 1 and 2. In Table 1 we summarized the result of applying 17 methods and theories to the problem at hand showing that the reduction factor in E is invariantly
is corresponding to the Unruh temperature (See Overview 4) as mentioned earlier [29]. There is a fundamental connection between what we may call Witten Hyper cube and Witten Fractal M-Theory connecting quantum relativity with Hardy’s Quantum Entanglement. This is represented in a diagram and outlined in Figures 1 and 2. In Table 1 we summarized the result of applying 17 methods and theories to the problem at hand showing that the reduction factor in E is invariantly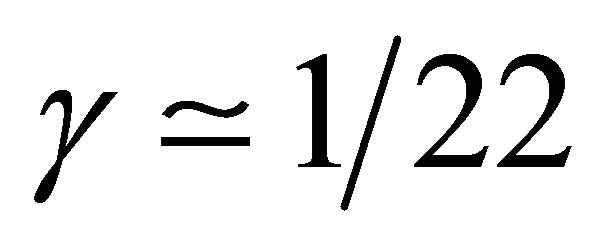 .
.
5. Special Relativity Gauged via Yang-Mills Theory Leads to Quantum Gravity
In what follows we show how to obtain the preceding result using a direct comparison between the field strength of Yang-Mills theory and that of special relativity [1]. In doing that we have de facto produced an effective quantum gravity equation [20]. Now special relativity spacetime is flat. The four types of photons namely 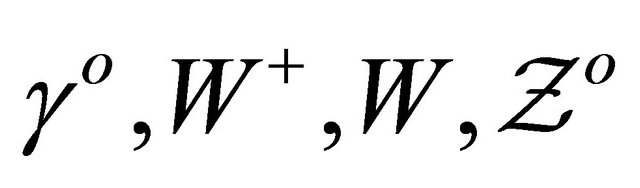 are assumed for the moment to be all massless and cannot curve space time [1]. By contrast the Yang-Mills field has a field strength [1] given by
are assumed for the moment to be all massless and cannot curve space time [1]. By contrast the Yang-Mills field has a field strength [1] given by 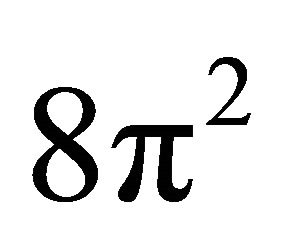 and can easily be shown to be at the point of grand unification energy scale
and can easily be shown to be at the point of grand unification energy scale 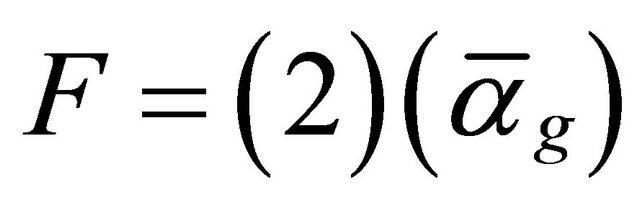 where
where 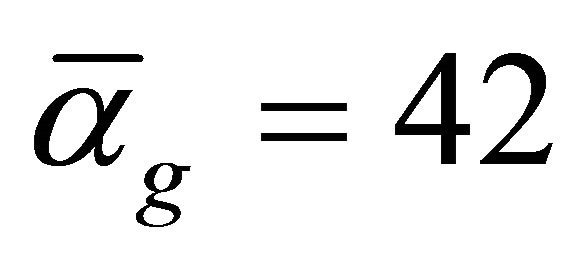 is the inverse common group coupling of GUT [1,7]. Field strength in the terminology of fiber bundle theory is simply the curvature [1]. Thus although the space of Einstein’s relativity is flat, it does have 4 photon-like gauge Bosons given by
is the inverse common group coupling of GUT [1,7]. Field strength in the terminology of fiber bundle theory is simply the curvature [1]. Thus although the space of Einstein’s relativity is flat, it does have 4 photon-like gauge Bosons given by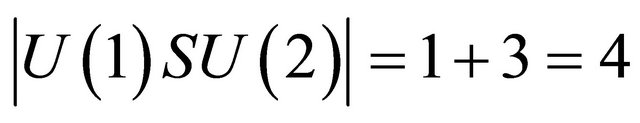 . Therefore we could ascribe a pseudo curvature to special relativity equal to 4. The ratio of the two curvatures or field strengths is thus given by
. Therefore we could ascribe a pseudo curvature to special relativity equal to 4. The ratio of the two curvatures or field strengths is thus given by
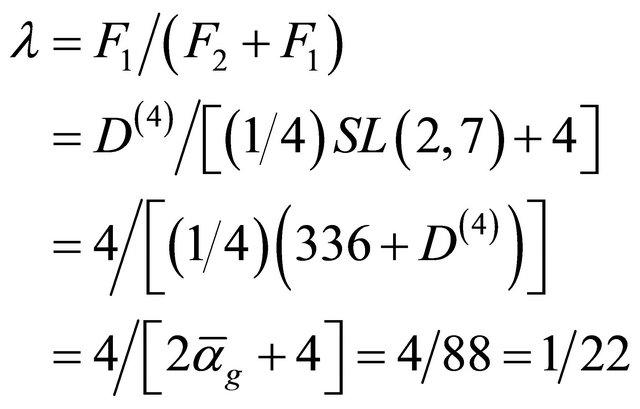 (25)
(25)
which is the same result found earlier on in this paper. To find the exact 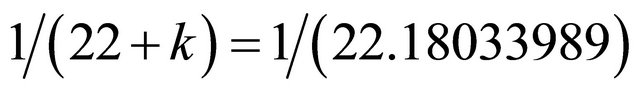 we must use the exact
we must use the exact 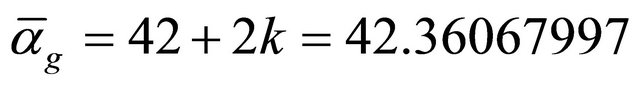 that is all [7]. The effective energy equation of quantum gravity is thus found from a quotient representing special relativity “field strength”
that is all [7]. The effective energy equation of quantum gravity is thus found from a quotient representing special relativity “field strength” 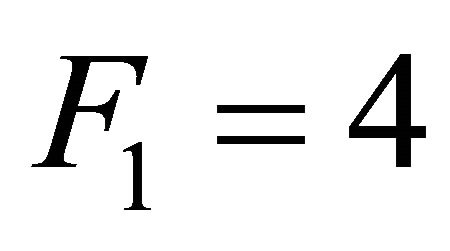 divided by the sum of the field strength of Yang-Mills theory and that of special relativity, i.e.
divided by the sum of the field strength of Yang-Mills theory and that of special relativity, i.e.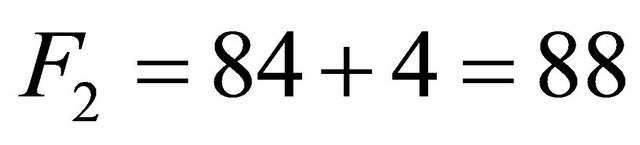 . The result is essentially a Lagrangian [30,31] multiplier equal
. The result is essentially a Lagrangian [30,31] multiplier equal 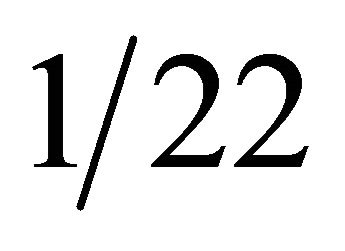 which is used as a scaling (see Table 1 No. 15).
which is used as a scaling (see Table 1 No. 15).
6. The Constancy of the Speed of Light as a Probabilistic Expectation Value Inseparably Linked to 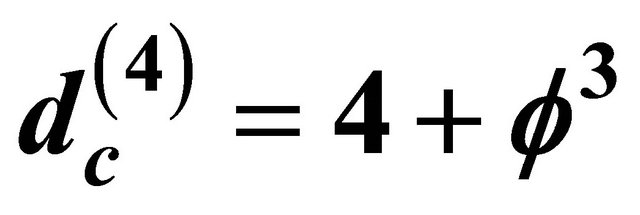 Expectation Value of the Dimensionality of Our Clopen Quantum Space Time
Expectation Value of the Dimensionality of Our Clopen Quantum Space Time
We know from Alain Connes’s work on non-commutative geometry that 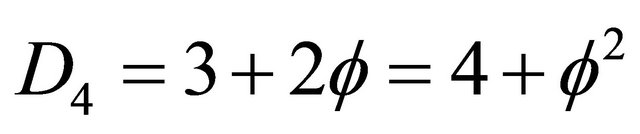 using E-Infinity this is
using E-Infinity this is 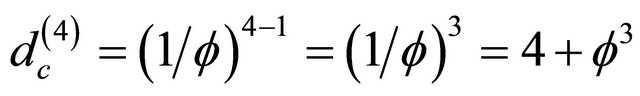 as well. This value is a probabilistic average or expectation value. This is easily proven from the following center of gravity theorem of probability theory:
as well. This value is a probabilistic average or expectation value. This is easily proven from the following center of gravity theorem of probability theory:
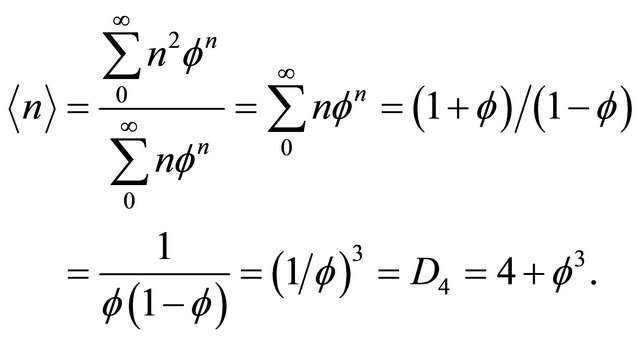 (26)
(26)
Here as everywhere else .
.
The constant speed of light is a similar expectation value. The “hidden” real speed of light varies between zero and infinity. In the topological dimension DT = 4 and Hausdorff dimension 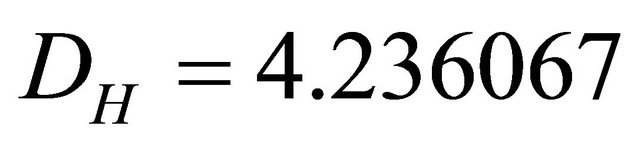 of a clopen i.e. closed and open universe, we can observe only the average using direct experiments. The other spectrum of velocities can be inferred only indirectly via quantum effects, such as Hardy’s entanglement.
of a clopen i.e. closed and open universe, we can observe only the average using direct experiments. The other spectrum of velocities can be inferred only indirectly via quantum effects, such as Hardy’s entanglement.
Thus when 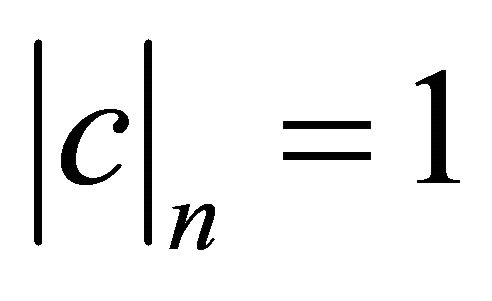 this corresponds to when
this corresponds to when![]() . this is similar to when
. this is similar to when 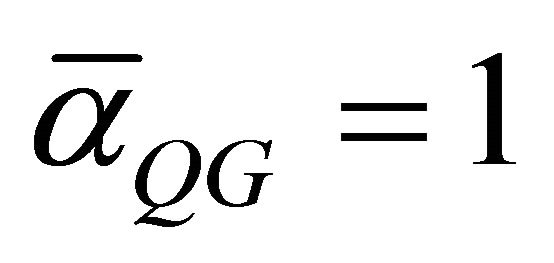 which corresponds to maximum quantum-Planck gravity coupling. Therefore for dimensionless light velocity, the expectation value will correspond to
which corresponds to maximum quantum-Planck gravity coupling. Therefore for dimensionless light velocity, the expectation value will correspond to  and thus
and thus 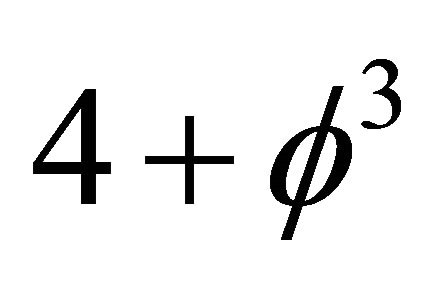 which means a topological dimension DT = 4 and consequently we can measure it only indirectly in
which means a topological dimension DT = 4 and consequently we can measure it only indirectly in  dimension of classical space time. A comparison reflecting the equivalence between A. Connes’ non-commutative geometry and E-Infinity Theory is given in Table 2.
dimension of classical space time. A comparison reflecting the equivalence between A. Connes’ non-commutative geometry and E-Infinity Theory is given in Table 2.
7. Conclusions
First we presented a unified Newtonian-relativisticquantum formula for quantum relativistic energy [20]. The homology of K3 Kähler and what we may call extra “dark” dimensions is the definite cause behind the supposedly missing dark energy [4,19]. To arrive at the correct quantitative result and reconcile theory with experiments and cosmological measurements we need to scale the classical  by a scale relativity factor
by a scale relativity factor  defined as the ratio of two second Betti numbers [10,11]. Since the Betti number of fuzzy Kähler
defined as the ratio of two second Betti numbers [10,11]. Since the Betti number of fuzzy Kähler 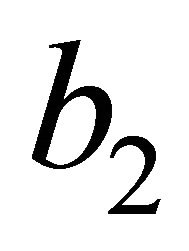 is 22 + k and since
is 22 + k and since 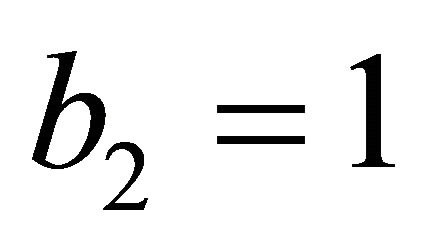 for Einstein space of special Relativity, our
for Einstein space of special Relativity, our  becomes equal to
becomes equal to 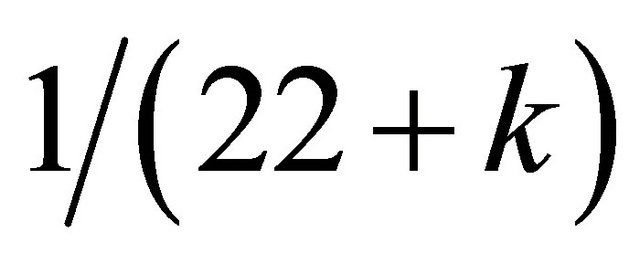 and one finds
and one finds
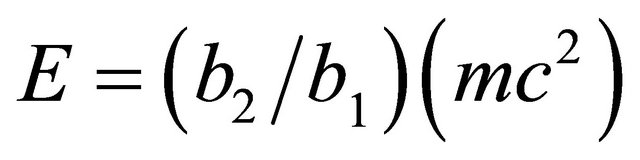 [9]. This means the missing dark energy of the cosmos is exactly equal to
[9]. This means the missing dark energy of the cosmos is exactly equal to 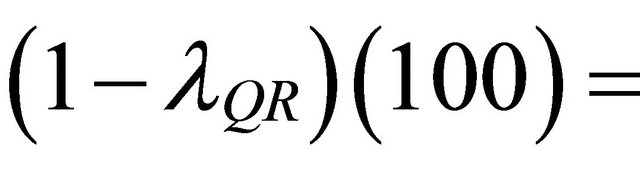 95.4915028%. It is almost a dream world how the results of cosmic measurement are close to this percentage [4]. Noting that
95.4915028%. It is almost a dream world how the results of cosmic measurement are close to this percentage [4]. Noting that 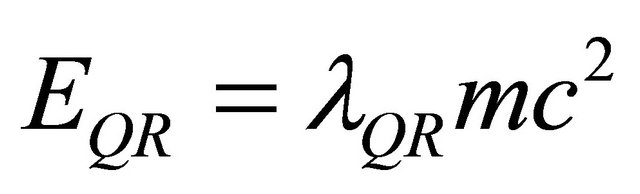 may also be written as
may also be written as 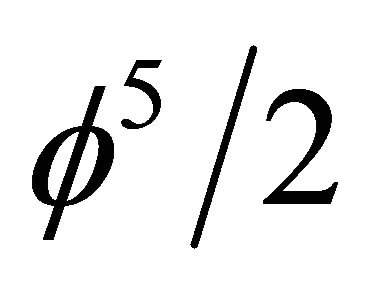 which means half of Hardy’s quantum entanglement probability found using orthodox quantum mechanics and confirmed through sophisticated quantum information experiments [16,17,22], we feel that the ordinary sharp non-fuzzy K3 Kähler manifold approximates quantum gravity space time geometry and topology to an astonishing extent and must be real. Seen that way, we must infer that the Creator is a mathematician [1] with a deep inclination towards topology, geometry and number theory [7]. From a purely intuitive view point however the result is not surprising when we remember that in terms of particle physics Einstein’s special relativity could in principle be found from a Lagrange with a single generalized coordinate, namely the photon [24-26]. A realistic theory of nature however must have a Lagrangian with a minimum of 12 generalized coordinates representing 12 massless gauge Bosons being the number of messenger particles of the standard model of high energy physics [1,7,14]. The fundamental similarity factor found here
which means half of Hardy’s quantum entanglement probability found using orthodox quantum mechanics and confirmed through sophisticated quantum information experiments [16,17,22], we feel that the ordinary sharp non-fuzzy K3 Kähler manifold approximates quantum gravity space time geometry and topology to an astonishing extent and must be real. Seen that way, we must infer that the Creator is a mathematician [1] with a deep inclination towards topology, geometry and number theory [7]. From a purely intuitive view point however the result is not surprising when we remember that in terms of particle physics Einstein’s special relativity could in principle be found from a Lagrange with a single generalized coordinate, namely the photon [24-26]. A realistic theory of nature however must have a Lagrangian with a minimum of 12 generalized coordinates representing 12 massless gauge Bosons being the number of messenger particles of the standard model of high energy physics [1,7,14]. The fundamental similarity factor found here 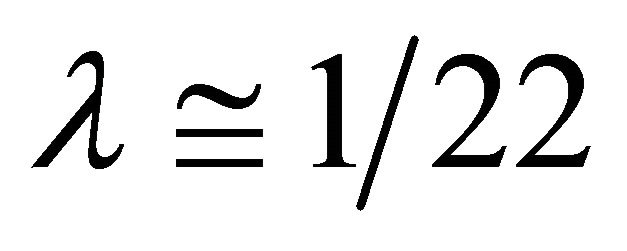 is mathematically the Lagrangian multiplier of an Isoperimetric variational problem when setting
is mathematically the Lagrangian multiplier of an Isoperimetric variational problem when setting 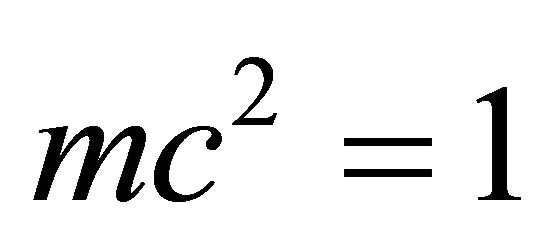 [30,31] and physically is the effect of quantum entanglement of the Hardy type on relativity for a single particle
[30,31] and physically is the effect of quantum entanglement of the Hardy type on relativity for a single particle 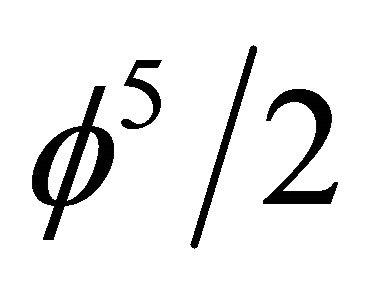 i.e. where
i.e. where  for two particle entanglement [22]. We checked our result using at least 24 different theories including Nottale’s scale relativity [3,25] Magueijo and Smolin’s varying speed of light theory [5,6], Witten’s M-theory [23], Veneziano’s dual resonance theory and quantum field Yang-Mills theory in curved space time [1] and obtained exactly the same robust result reported here (see Table 1). One striking point in the above analysis is the basic fundamental similarity of the energy equations of Newton, Einstein and quantum relativity. This can be explained as follows:
for two particle entanglement [22]. We checked our result using at least 24 different theories including Nottale’s scale relativity [3,25] Magueijo and Smolin’s varying speed of light theory [5,6], Witten’s M-theory [23], Veneziano’s dual resonance theory and quantum field Yang-Mills theory in curved space time [1] and obtained exactly the same robust result reported here (see Table 1). One striking point in the above analysis is the basic fundamental similarity of the energy equations of Newton, Einstein and quantum relativity. This can be explained as follows:
There is nothing more fundamental and abstract like the notion of energy [1]. That is why self similarity manifests itself here directly as simple scaling from Newton to Einstein and beyond all that, to quantum gravity [1,3,5,6, 12,15]. This point is taken few steps further in Table 3. This self-similarity or self-affinity is an important engineering concept in testing for instance Tsunami waves in small hydrodynamics laboratories [32]. It is also what made E. Witten discover that all the 5 different superstring theories are different facets of one theory [1,23]. Self-similarity exists in nature at all levels in the form of fractals [2,5]. Finally summing over all these self-similar objects and dimensions gives us a probabilistic constant value for the experimental speed of light exactly as it gave us the expectation value of the topological and Hausdorff dimension of spacetime namely DT = 4 and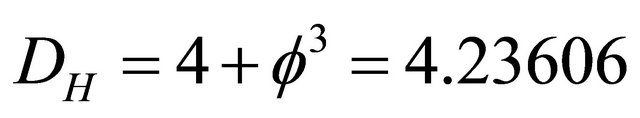 . Ontologically the speed of light varies from Zero to Infinity however in DT = 4, it is a constant expectation value and we should have suspected long ago that this alone is the clearest manifestation of
. Ontologically the speed of light varies from Zero to Infinity however in DT = 4, it is a constant expectation value and we should have suspected long ago that this alone is the clearest manifestation of
Table 2. The equivalence between non-commutative geometry and E-infinity formalism.

P.S.: ![]() is Hardy’s probability of quantum entanglement and corresponds to negative topological dimension
is Hardy’s probability of quantum entanglement and corresponds to negative topological dimension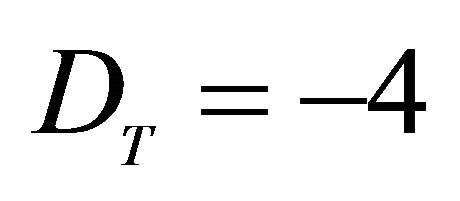 .
.
Table 3. Fundamental theories.

Note that in view of the above, Hardy’s entanglement represents a normalization of energy which is twice as large as the energy of a single particle according to the quantum relativity theory presented here with 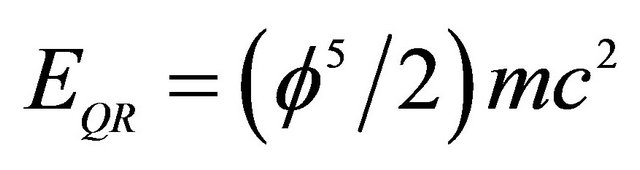 where
where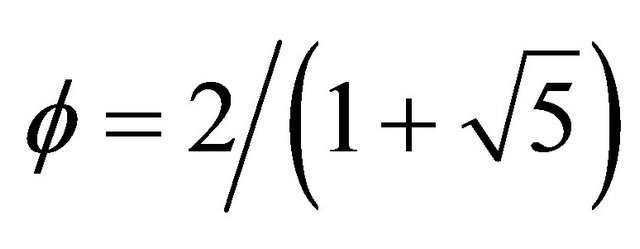 .
.
Table 4. Quantitative comparison between ordinary matter, dark matter and dark energy.

P.S.: One may loosely say dark energy to mean the sum of both dark matter (22.18033%) and dark energy (73.31117%) so that the total is 95.4915%.
the fractality of our real quantum space time [17,29]. In Table 4 we conclude by distinguishing between dark energy and dark matter and give the final results and percentages with hints about the method of analysis.
REFERENCES
- R. Penrose, “The Road to Reality,” Jonathan Cape, London, 2004.
- Y. Baryshev and P. Teerikorpi, “Discovery of Cosmic Fractals,” World Scientific, Singapore, 2002.
- L. Nottale, “Scale Relativity,” Imperial College Press, London, 2011.
- L. Amendola and S. Tsujikawa, “Dark Energy: Theory and Observations,” Cambridge University Press, Cambridge, 2010.
- J. Mageuijo and L. Smolin, “Lorentz Invariance with an Invariant Energy Scale,” 18 December 2001, arXiv:hepth/0112090V2.
- J. Mageuijo, “Faster Than the Speed of Light,” William Heinemann, London, 2003.
- M. S. El Naschie, “The theory of Cantorian Spacetime and High Energy Particle Physics (an Informal Review),” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2635-2646. doi:10.1016/j.chaos.2008.09.059
- M. S. El Naschie, “The Discrete Charm of Certain Eleven Dimensional Spacetime Theory,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, No. 4, 2006, pp. 477-481.
- C. Nash and S. Sen, “Topology and Geometry for Physicists,” Academic Press, San Diego, 1983.
- D. Joyce, “Compact Manifolds with Special Holonomy,” Oxford Press, Oxford, 2003.
- S. Yau and S. Nadis, “The Shape of Inner Space,” Perseus Book Group, New York, 2010.
- J. Polchinski, “String Theory,” Cambridge University Press, Cambridge, 1999.
- M. S. El Naschie, “On a Class of Fuzzy Kähler-Like Manifolds,” Chaos, Solitons & Fractals, Vol. 26, No. 2, 2005, pp. 257-261. doi:10.1016/j.chaos.2004.12.024
- M. S. El Naschie, “E-Infinity—Some Recent Results and New Interpretations,” Chaos, Solitons & Fractals, Vol. 29, No. 4, 2006, pp. 845-853. doi:10.1016/j.chaos.2006.01.073
- C. Rovelli, “Quantum Gravity,” Cambridge Press, Cambridge, 2004. doi:10.1017/CBO9780511755804
- M. S. El Naschie, “Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry,” Journal of Quantum Information Science, Vol. 1, 2011, pp. 50-53. doi:10.4236/jqis.2011.12007 http://www.SCRIP.org/journal/jqis
- J.-H. He, et al., “Quantum Golden Mean Entanglement Test as the Signature of the Fractality of Micro Spacetime,” Nonlinear Science Letters B, Vol. 1, No. 2, 2011, pp. 45-50.
- M. Planck, “Spacecraft,” Wikipedia, 2012. http://en.wikipedia.org/wiki/Planck
- R. Panek, “Dark Energy: The Biggest Mystery in the Universe,” The Smithsonian Magazine, 2010. http://www.smithsonianmagazine.com/science-nature/Dark-Energy
- D. R. Finkelstein, “Quantum Relativity,” Springer, Berlin, 1996. doi:10.1007/978-3-642-60936-7
- H. Saller, “Operational Quantum Theory,” Springer, Berlin, 2006.
- L. Hardy, “Non-Locality of Two Particles without Inequalities for Almost All Entangled States,” Physical Review Letters, Vol. 71, No. 11, 1993, pp. 1665-1668. doi:10.1103/PhysRevLett.71.1665
- M. Duff, “The World in Eleven Dimensions,” IOP Publishing, Bristol, 1999.
- M. S. El Naschie, “Revising Einstein’s E = mc2. A Theoretical resolution of the Mystery of Dark Energy,” Conference Program and Abstracts of the Fourth Arab International Conference in Physics and Material Sciences, Alexandria, 1-3 October 2012, p. 1.
- M. S. El Naschie and L. Marek-Crnjac, “Deriving the Exact Percentage of Dark Energy Using a Transfinite Version of Nottale’s Scale Relativity,” International Journal of Modern Nonlinear Theory and Application, in Press, 2012.
- J.-H. He, “A Historical Scientific Finding on Dark Energy,” Fractal Spacetime and Non-Commutatitve Geometry in Quantum and High Energy Physics, Vol. 2, No. 2, 2012. p. 154.
- L. Sigalotti and A. Mejias, “The Golden Mean in Special Relativity,” Chaos, Solitons & Fractals, Vol. 30, No. 3, 2006, pp. 521-524. doi:10.1016/j.chaos.2006.03.005
- S. Hendi and M. Sharif Zadeh, “Special Relativity and the Golden Mean,” Journal of Theoretical Physics, Vol. 1, IAU Publishing, 2012, pp. 37-45.
- L. Smolin, “Three Roads to Quantum Gravity,” Weindenfald & Nicolson, London, 2000.
- M. S. El Naschie, “Stress, Stability and Chaos in Structural Engineering,” McGraw Hill, London, 1990.
- C. Lanczos, “The Variational Principles of Mechanics,” 4th Edition, University of Toronto Press, Toronto, 1949.
- G. Barenblatt, “Scaling,” Cambridge University Press, Cambridge, 2003. doi:10.1017/CBO9780511814921

