International Journal of Modern Nonlinear Theory and Application
Vol.1 No.3(2012), Article ID:23087,9 pages DOI:10.4236/ijmnta.2012.13012
On the Need for Fractal Logic in High Energy Quantum Physics
1Department of Physics, Faculty of Science, University of Alexandria, Alexandria, Egypt
2College of Central Florida, Ocala, USA
3Nantong Textile Institute, National Engineering Laboratory for Modern Silk, College of Textile and Clothing, Soochow University, Suzhou, China
4Mathematics Department, Qatar University, Doha, Qatar
5Technical School Center of Maribor, Maribor, Slovenia
6Department of Mathematics, Faculty of Science, Cairo University, Giza, Egypt
Email: Chaossf@aol.com, olsens@cf.edu, hejihuan@suda.edu.cn, snada@qu.edu.qa, *leila.marek@guest.arnes.si, mahelal@yahoo.com
Received August 12, 2012; revised September 7, 2012; accepted September 17, 2012
Keywords: Fractal Fuzzy Logic; Hausdorff Dimension; Cantorian Space-Time; Golden Mean
ABSTRACT
Modern advances in pure mathematics and particularly in transfinite set theory have introduced into the fundamentals of theoretical physics many novel concepts and devices such as fractal quasi manifolds with non-integer (Hausdorff) dimension for its geometry as well as infinite dimensional wild topology and non classical fuzzy logic. In the present work transfinite fractal sets and fuzzy logic are combined to enable the introduction of a new theory termed fractal logic to the foundation of high energy particle physics. This leads naturally to a new look at quantum gravity. In particular we will show that to understand and develop quantum gravity we have to bring various fields together, particularly fractals and nonlinear dynamics as well as sphere packing, fuzzy set theory, number theory and quantum entanglement and irrationally q-deformed algebra.
1. Introduction and Background Information
There is a large body of literature on the application of fractals and deterministic chaos in quantum physics [1-69]. In particular, the present authors integrated Cantor sets and fractals as well as number theory into the foundation of quantum mechanics [5-22]. Modern transfinite set theory [6] has unraveled many undreamed of logical possibilities such as hierarchies of things and “numbers” larger than infinity [25] and smaller than zero in addition to non integer and even negative dimensions [1,2,4,5,7,8,10]. Some of these novel and particularly revolutionary mathematical notions have sometimes ago found their way into theoretical physics [1-16]. This is definitely the case with fractal-Hausdorff dimensions [11, 14,15] which led to the theory of fractal space time pioneered by G. Ord [7]. Other even more demanding concepts such as the empty set and negative topological dimensions form the basis of El Naschie’s Cantorian E-Infinity theory [5,10,31,32]. The present note continues this line of thinking by pointing out the urgent need for a new theory of general fractal logic in high energy quantum physics when counting and discovering new particles which is an essential part of the trade. The idea is related but not identical to Zadeh’s theory of fuzzy logic [33-38]. Our present main thrust is to reason that although counting which is at the basis of statistical mechanics may seem like the simplest thing in the universe, high energy physics calls for another form of fractal transfinite counting which is anything but straightforward in the traditional sense [5-10]. As a clear cut example of profound consequence we show that while the number of gauge bosons of the standard model is indeed 12 in the ordinary sense of counting using integer numbers [55-57], these 12 corresponding to only 11.7082394 bosons which have in turn the fractal weight of 14 rather than 12 gauge bosons [38-54]. In this sense we are asserting what on its face value is an absurdity namely the equality of 12 to 14 via 11.708294. This indicates that 2 more elementary particles are hidden allowing 14 particles to appear as if they were 12. We conjecture that these two extra particles may be the Higgs and the graviton. It is further concluded that this fractal nature which is inert even to the mere number of elementary quantum particles is in one way or another behind the enormous difficulties of discovering the Higgs and the graviton experimentally [55-57]. This is more than sufficient reason to call for the introduction of a new theory for fractal logic.
2. Radon Work and Transfinite Hardy Quantum Entanglement
In order to be able to analytically observe the transfinite irrational fingerprint of the golden mean entanglement [65-67], we must fulfill the following conditions:
a) First we must have an accurate mathematical model which can capture a substantial and relevant part of Reality.
b) Second we must solve the model exactly.
If we do not observe both of the above conditions, the golden mean fine structure, i.e. the fractal Cantorian structure disappears theoretically and would unlikely be observed experimentally [52].
Adding or subtracting small quantities with the objecttive of simplifying the corresponding field equation is a method which goes back to the work of F. John on the derivation of the equations of thin elastic shells using Taylor expansion from the 3D field equations of the classical theory of Elasticity [63]. Interestingly John based his method on the work of Radon and his theory of operators. In turn Radon’s work was extended by Von Neumann and later on by A. Connes in his theory of non-commutative geometry [10-63]. Finally all of this is strongly related to El Naschie’s E-Infinity theory [10,63]. It is thus understandable that E-Infinity extended and made extensive use of F. John’s method to make it applicable to quantum high energy physics [52,59]. The astonishing point is that the so-called transfinite correction corresponding to F. John’s method is almost entirely reducible to Hardy’s generic value f5 = 0.09016994393 which is the quantum probability of Hardy’s entanglement [30] where 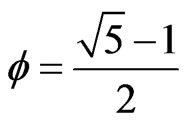
is the inverse of the golden mean. For instance 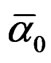 is simply the prime number 137 plus a function of f5 namely k0 = f5(1 – f5). We may thus write that [10,31,32]
is simply the prime number 137 plus a function of f5 namely k0 = f5(1 – f5). We may thus write that [10,31,32]
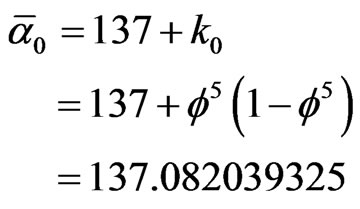 (1)
(1)
where 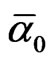 is the inverse electromagnetic fine structure constant [56,58].
is the inverse electromagnetic fine structure constant [56,58].
Now Measure Theory [29] gives us the tools to estimate the quantities needed to make things and equations “fit” harmonically together. In a manner of speaking transfinite corrections a la F. John and El Naschie is developed to make the rough or sharp edges of the equation and their geometrical shapes fit together like in Penrose’s golden mean fractal tiling [1] or a bathroom floor where transfinite “Mortel” fill the gaps between the edges the tiling to make for a smooth tiling similar to what we have in “Al Hambra” Islamic wallpaper groups, the 2 and 3 Stein spaces and the compactified Kleinian curve SL(2, 7) used for the Holographic boundary of E-Infinity [1-73]. Meantime it is well understood that this Holographic boundary manifold [2] is related to the bulk of E8E8 exceptional symmetry group via the fundamental equation B = H + G + E where B is the Bulk, H is the Holographic boundary, G is Einstein gravity and E is Electromagnetism. Since H = 339, G = 20 and E = 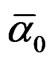 =137 one finds the integer value of B to be B = 496 = E8E8 exactly as should be [20,63]. However the exact transfinite-corrected value of B is found directly from the corresponding transfinite value of
=137 one finds the integer value of B to be B = 496 = E8E8 exactly as should be [20,63]. However the exact transfinite-corrected value of B is found directly from the corresponding transfinite value of 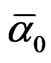 = 137 + k0 by the exact golden mean scaling which replaces the classical approximate logarithmic scaling of conventional quantum field theory [62]. The golden mean scaling exponent in this case is λ = 3 + f = 3.618033989 so that the exact B is found to be [10,63].
= 137 + k0 by the exact golden mean scaling which replaces the classical approximate logarithmic scaling of conventional quantum field theory [62]. The golden mean scaling exponent in this case is λ = 3 + f = 3.618033989 so that the exact B is found to be [10,63].
 (2)
(2)
where k = 2f5 = f3(1 – f3) and f5 is the probability of Hardy’s quantum entanglement [30].
The preceding result may be interpreted in terms of quasi particles as follows: We have an expectation average KAON [10] with mass equal 496 GeV meeting a virtual particle with negative mass equal –k2 = –0.032522475 GeV and producing 496 – k2 which in this unit-less form is the quasi dimension of the bulk. A similar interpretation may be given to 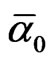 = 137 + k0 [10,63].
= 137 + k0 [10,63].
We may also note a very nice symmetry or rather anti-symmetry between the transfinite correction of E8E8 and that of 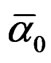 and
and .
.
This is obvious from contrasting k and k0 and remembering that, we subtract k2 from the exceptional 496 symmetry group dimension while we add k0 to the 137 of alfa:
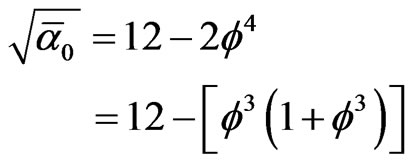 (3a)
(3a)
and
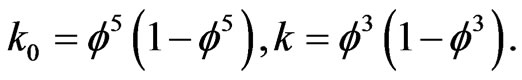 (3b)
(3b)
We recall that f3 is the contra factual or global probability of quantum entanglement [30-32] which together with the local two-particle quantum entanglement f2 gives us the Hardy generic value of the probability of quantum entanglement namely f5 = (f3)(f2). For readings on the method of adding and subtracting small quantities to smooth the given equation of classical field theories, we refer to the work of F. John and M. S. El Naschie [10,60-63].
3. Sphere Packing and Golden Mean Transfiniteness
The connection between “fractal” sphere packing and E-Infinity theory was considered in detail by L. MarekCrnjac and El Naschie [2,10]. Here we recall some remarkable observation which serves to deepen our understanding of transfinite golden mean corrections [30-32].
a) First we note that the density of sphere packing in four dimensions is Δ = 0.61685. This is very close to the golden mean f = 0.618033989.
b) In the case of ten dimensions i.e. the dimensionality of superstring theory, the lattice sphere packing has a density of Δ = 0.09202 ≈ 9%.
This is rather close to Hardy’s quantum entanglement probability.
c) Curiously, at this ten (10) dimensionality the central density is 0.03608. This is very close indeed to k0(exp) = 0.0359 which appears in the experimental determination of 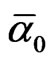
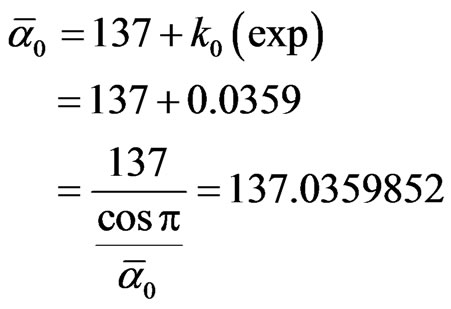
 (4)
(4)
We note that the theoretical value of k0 is k0 = f5(1 – f5) where f5 is Hardy’s quantum entanglement probability [30].
4. When the 12 Bosons of the Standard Model Become Equivalent to the 14 Bosons of Super Gravity via the New Theory of Fractal Logic
The classical standard model which is at the core of conventional quantum field theory relies and stems from 12 massless gauge bosons described by a 12 dimensional combined Lie symmetry group SU(3)SU(2)U(1). Apart from superstring theory which proceeds in an entirely different way with 496 massless bosons corresponding to the generator of E8E8 exceptional Lie group, there is a more conventional approach which is based on an eleven dimensional space-time similar to the acclaimed eleven dimensional M-theory of E. Witten [49,50]. This theory is known as super gravity and relies neither on E8E8 nor on SU(3)SU(2)SU(1) but rather on a less known group with 14 dimensions [55]. This is the ortho-symplectic group OSP(m/n) where [55,56]
 (5a)
(5a)
where
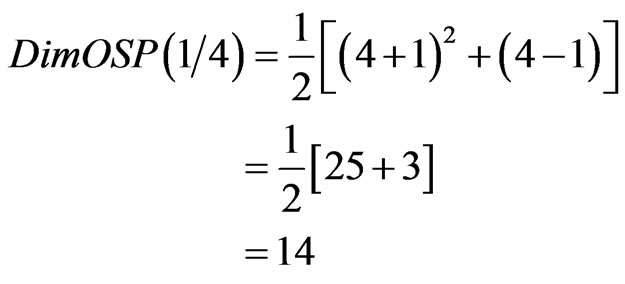 (5b)
(5b)
exactly as anticipated [55].
In what follows we will attempt to reason that the 12 bosons of the standard model are in reality 14 by virtue of a fractal number
 (6)
(6)
which give a real fractal weight to 12 bosons and make them equivalent to 14 in this fractal counting of fractal elementary particles using what we may call fractal logic. This is a notion related but not identical to fuzzy logic as mentioned earlier on [33,38].
Our next and most important novel task is to devise a fractal number to massless gauge bosons of the standard model. There is no automatic mechanistic way to do that at present but we are guided by intelligent guess work and the overriding principle of a harmonic number theoretical symphony which fits everything with everything else seamlessly [9,65]. This principle served us well in the past and as we will see shortly will lead us to also here astonishing undreamed of possibilities coupled with the utmost simplicity [36-53].
The first and may be the most important messenger particle of them all, the illusive photon (γ) will be given the fractal number weight not 1 but f. This f we recall is at the same time the Hausdorff dimension of a quantum particle whose cobordism [20,30] namely the quantum wave was given the Hausdorff dimension f2 [20]. We also recall that f corresponds to the zero set while f2 corresponds to the classical empty set with the MengerUhryson topological dimensions zero and minus 1 respectively [10,61].
Second the three bosons of the electro weak are given a priori an easily justifiable weighted number namely 16k = 32f5. Third the 8 gluons are given the fractal weight number 8 + (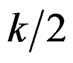 ) = 8 + f5. The total is now 11.5936411 weighed fractal particles corresponding to 12 particles. To this we add two new particles which we conjecture that they could be one Higgs and a graviton. The fractal number of the Higgs is k0 = f5(1 – f5) while that of the graviton is k2 = [f3(1 – f3)]2. The total is now 11.70820393 which happen to be
) = 8 + f5. The total is now 11.5936411 weighed fractal particles corresponding to 12 particles. To this we add two new particles which we conjecture that they could be one Higgs and a graviton. The fractal number of the Higgs is k0 = f5(1 – f5) while that of the graviton is k2 = [f3(1 – f3)]2. The total is now 11.70820393 which happen to be 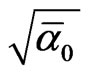 where
where 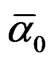 = 137 + k0 is the E-Infinity value of the inverse electromagnetic fine structure constant [10,63].
= 137 + k0 is the E-Infinity value of the inverse electromagnetic fine structure constant [10,63].
The  massless bosons correspond therefore to 14 particles when counting in the ordinary way using integers. Consequently they could be represented by the OSP(1/4) symmetry group of super gravity [55] and it is granted that this astonishing unexpected fact gives a feel similar to that of Alice in the Fractal Land of high-energy quantum physics [10,30-32]. The preceding result may be summarized in the following table:
massless bosons correspond therefore to 14 particles when counting in the ordinary way using integers. Consequently they could be represented by the OSP(1/4) symmetry group of super gravity [55] and it is granted that this astonishing unexpected fact gives a feel similar to that of Alice in the Fractal Land of high-energy quantum physics [10,30-32]. The preceding result may be summarized in the following table:

5. The Logarithmic Scaling of Quantum Field Theory as an Approximation of the Golden Mean Scaling of E-Infinity
The discovery of the logarithmic scaling of high energy physics was a major step forward for establishing quantum field theory [56,57]. Nonetheless logarithmic scaling as will be shown here is merely an excellent approximation of the exact golden mean scaling of E-Infinity golden field theory. As excellent as it is, this approximation masks Hardy’s golden mean quantum entanglement and makes algebraic manipulation of the governing equations unnecessarily heavy if not clumsy and sometime interactable and messy [55-57]. As a simple demonstration testifying for the above, let us consider the logarithmic scaling of the inverse fine structure constant of a Cooper Pair. This is clearly
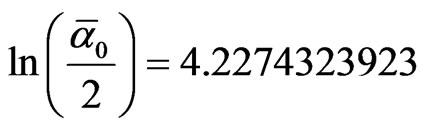
[58-64]. By comparison the golden mean scaling for 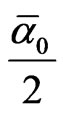 namely
namely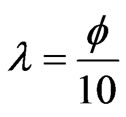 leads to
leads to
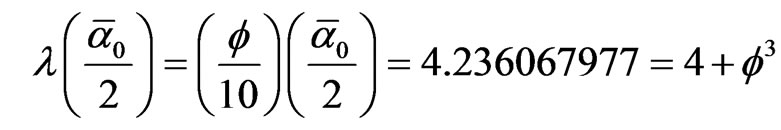 (7)
(7)
which is equal to the exact Hausdorff dimension of the core of E-Infinity Cantorian space-time.
The above result must make us wonder why not reconsider the famous renormalization equation of quantum gravity unification using golden mean scaling. Let us write the concerned renormalization equation in the logarithmic scaling form first. This is [61,62]
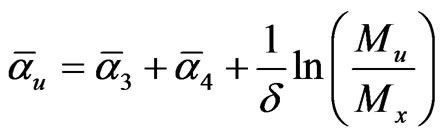 (8)
(8)
Let us replace in this equation the logarithmic scaling term by the golden mean scaling as follows [60-62]
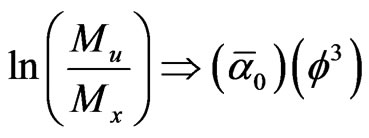 (9)
(9)
Then insert all the exact E-Infinity value of 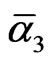 = 9 and
= 9 and 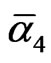 = 1,
= 1, 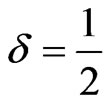
and  = 137.082039 in the renormalization equation of ordinary quantum field theory. That way we find [60-64]
= 137.082039 in the renormalization equation of ordinary quantum field theory. That way we find [60-64]
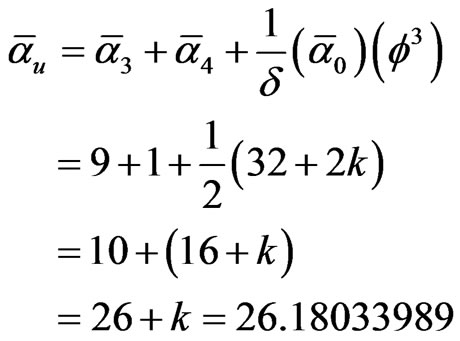 (10)
(10)
where k = f3(1 – f3).
This is the well known exact E-Infinity result [65,67].
To ascertain the high accuracy of the classical theory based on logarithmic scaling compared to our exact solution, we repeat the analysis and replace 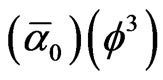 by what we have derived at the very beginning namely
by what we have derived at the very beginning namely
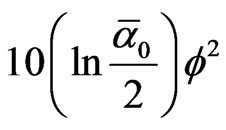
and find that [61-63]
 (11)
(11)
This is pretty close to the exact result of E-Infinity theory namely 26.18033989 [10,43,63]. Of course the above equation could have been performed without using  nor f2. We could have used the conventional purely logarithmic running of coupling by taking for instance Mu to be that of grand unification i.e. Mu(10)16 GeV while taking Mx = Mz = 91 GeV. This leads to [61-63]
nor f2. We could have used the conventional purely logarithmic running of coupling by taking for instance Mu to be that of grand unification i.e. Mu(10)16 GeV while taking Mx = Mz = 91 GeV. This leads to [61-63]
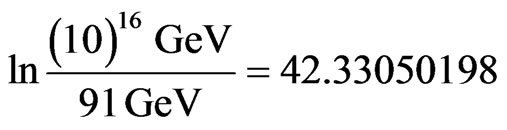 (12)
(12)
For non-super symmetric and super symmetric unification respectively, we found the values  = 42.33050198 and
= 42.33050198 and  = 26.16525099. Both values are very close to the exact results [48].
= 26.16525099. Both values are very close to the exact results [48].
6. Toward a Theory of Fractal Logic
Even today some would dispute that Fuzzy logic is a new theory [35]. We beg to differ and insist that Fuzzy logic [33-38] was and is still a radically novel theory with far reaching consequences which has played a significant role not only in running production lines of modern care industries but also in furthering and deepening understanding of fundamental theories such as quantum physics and deterministic chaos [61,62]. In what follows we list a large number of points and observations which when taken together indicate in our opinion that we are on the verge of discovering even more deep logical theories than Fuzzy Logic [33-38] which we have dubbed for the time being Fractal logic for want of a better name. Without much ado here are the points which we gathered for the purpose of the present article.
6.1. It is Currently a Widespread Belief that We Have 3 Different High Energy Theories Which Go beyond the Standard Model Namely
a) Super gravity [55];
b) Technicolor;
c) Extra dimensions [55].
However the point is that all the three theories are basically equivalent when pondered via the fractal fuzzy logic of E-Infinity theory [10,37,51]. The reason is simply the fractal fuzzy equivalence between particles, extra dimensions and color [41]. Within E-Infinity these concepts are fractally more or less logically the same [41,42,68]. In fact probability and dimension are in some E-Infinity sense the same [63].
6.2. Putting a Photon in a Fractal M-Theory Space-Time Leads to an Extended Standard Model and to 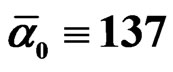
In a nutshell this could be explained as follows: A fractal 11D theory has a Hausdorff dimension [49,50,55]
 (13)
(13)
where 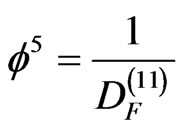 .
.
At the same time the fractal weighted number of the 14 = 12 + 2 particles of OSP(1/4) super gravity is
 (14)
(14)
where the photon γ is given the fractal number
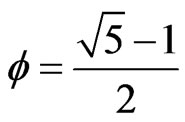
Consequently  is given by [49,50,55]
is given by [49,50,55]
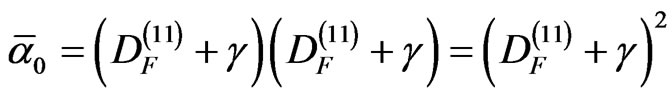 (15)
(15)
Noting that  is given by
is given by 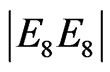 = (3 + f)(
= (3 + f)(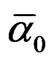 ) = 496 – k2 and that
) = 496 – k2 and that
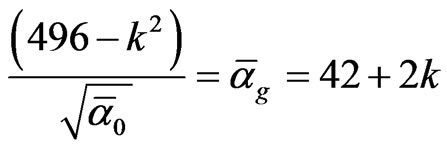 (16)
(16)
Then by analogy we have 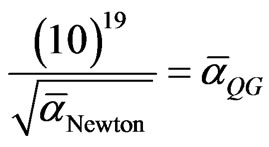
Here 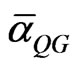 is the inverse of quantum gravity coupling which must evidently be unity because it is the coupling of Planck masses to the Planck Aether i.e. to itself and could therefore be maximally equal to unity
is the inverse of quantum gravity coupling which must evidently be unity because it is the coupling of Planck masses to the Planck Aether i.e. to itself and could therefore be maximally equal to unity 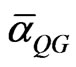 = 1. On the other hand (10)19 corresponds to the generator of E8E8. This is effectively a manifold with (10)19 degrees of freedom which may be interpreted as the number of nucleons in a plank mass [67,68]. Since a Plank mass is about (10)19 GeV and a nucleon is about 1000 GeV then we have nucleons corresponding to the degrees of freedom mentioned earlier on. The only unknown in the equation is thus
= 1. On the other hand (10)19 corresponds to the generator of E8E8. This is effectively a manifold with (10)19 degrees of freedom which may be interpreted as the number of nucleons in a plank mass [67,68]. Since a Plank mass is about (10)19 GeV and a nucleon is about 1000 GeV then we have nucleons corresponding to the degrees of freedom mentioned earlier on. The only unknown in the equation is thus  which we inserted by analogy to
which we inserted by analogy to  and which is the number of massless bosons in the standard model. Consequently by solving for
and which is the number of massless bosons in the standard model. Consequently by solving for 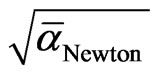 we find [58-63]
we find [58-63]
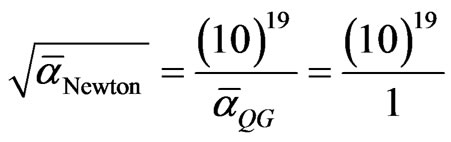 (17a)
(17a)
and therefore
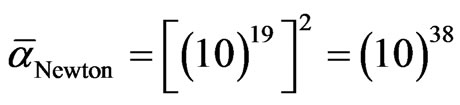 (17b)
(17b)
This is exactly the right order of magnitude expected for the unitless Newton gravity constant [67,68].
6.3. Why Ten Dimensional Superstrings and Why Fractal Eleven Dimensional M-Theory?
There is an excessively simple and elementary “fractal” way to persuade one at least intuitively that three should be an eleven dimensional M-like fractal space-time [49,50].
We know that bosons live in 3 + 1 = 4 dimensions, while fermions need a spin 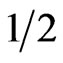 degree of freedom and need therefore 4 + 1 = 5 dimensions. Now what is the dimensionality of the space which combines both? A rather naive answer which turns to be the dimensionality of an 8D super space is to take (4 – 1)D and add (5 – 1)D to it and then add the time dimension and find (4 – 1) + (5 – 1) + 1 = 7 + 1 = 8D [55,63].
degree of freedom and need therefore 4 + 1 = 5 dimensions. Now what is the dimensionality of the space which combines both? A rather naive answer which turns to be the dimensionality of an 8D super space is to take (4 – 1)D and add (5 – 1)D to it and then add the time dimension and find (4 – 1) + (5 – 1) + 1 = 7 + 1 = 8D [55,63].
On the other hand arithmetic mean of the intersection of 4D and 5D gives us the dimensionality of superstrings because
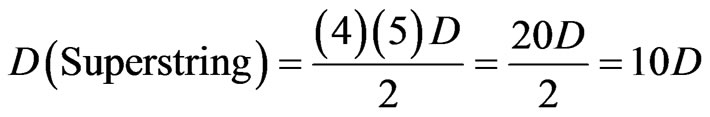 (18)
(18)
Now if we recall that the Hausdorff dimension of bosonic space is not 4 but 4 + f3 and that the Hausdorff dimension of the fermionic space is not 5 but 5 + f3 then we will realize that in this case the dimension corresponding to D(Superstring) = 10 is
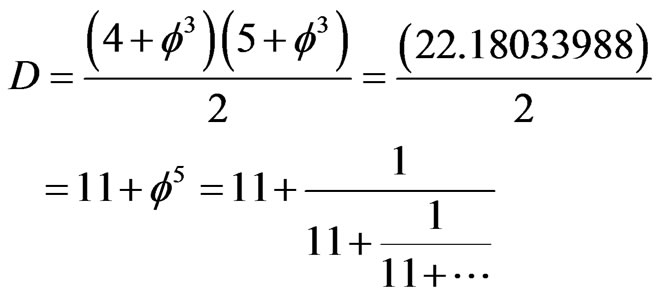 (19)
(19)
This is the dimensionality of the fractal M-theory as we may have surmised from the outset [49-51].
6.4. Quantum Dimension, Irrationally Deformed Algebra and the Golden Oscillator
As well known from the theory of quantum groups, the quantum dimension is given by [46]
 (20)
(20)
On the other hand we know that maximally irrationally deformed algebra for which n = 2 corresponds to two degrees of freedom oscillator which acquire for certain unitary parameters a frequency equal to
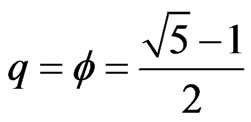 .
.
Inserting in D one finds [46]
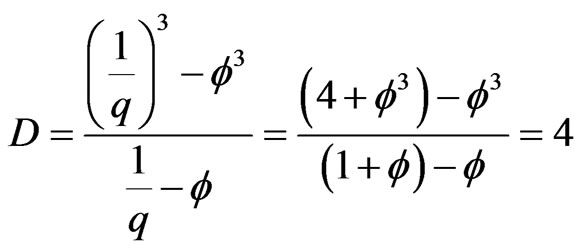 (21)
(21)
This is a remarkable result particularly when we recall the Hausdorff dimension of Cantorian space-time is given by [10]
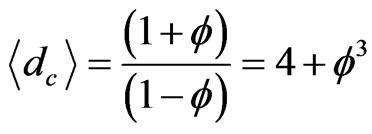 (22)
(22)
so that the two dimensions D and  are in dual relations [46]. The result shows indirectly that the golden mean number system used in our E-Infinity and fractal logic is naturally quantized and may be regarded as a generalization of the machinery of quantum groups [46]. This realization may be used advantageously in quantum mechanics and high energy physics as done in E-Infinity theory [10,63].
are in dual relations [46]. The result shows indirectly that the golden mean number system used in our E-Infinity and fractal logic is naturally quantized and may be regarded as a generalization of the machinery of quantum groups [46]. This realization may be used advantageously in quantum mechanics and high energy physics as done in E-Infinity theory [10,63].
6.5. An Infinite Hierarchy of Nothing
Research in set theory has revealed since sometime that there is a hierarchy of infinites with some that are larger than others [6,25]. In this section we show that there is an infinite hierarchy of empty sets i.e. Nothingness [62]. For this demonstration we use the formalism developed in non-commutative geometry of A. Connes which is in full agreement with the formalism and results of E-Infinity theory [63].
We start from the non-commutative geometry dimensional fraction of A. Connes namely [20,31,32]
 . (23a)
. (23a)
Thus we may write:
 (23b)
(23b)
where a, b represents classical Fibonacci numbers.
Consequently we have
 (24)
(24)
We note that while 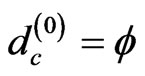 represents in E-Infinity theory a quantum particle, the empty set
represents in E-Infinity theory a quantum particle, the empty set 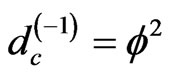 represents the quantum wave or the surface of the particle [20,31,32].
represents the quantum wave or the surface of the particle [20,31,32].
7. Discussion and Conclusions
The key to understanding the superficial inconsistency coupled with undreamed of possibilities which fractal logic and high energy particle physics offers is to understand the dual nature of the geometry and topology of random Cantor sets and its golden mean Hausdorff dimension [63].
Let us start by asking why random Cantor sets? The answer may be found in the following:
1) It has a zero measure i.e. a zero length as well as a zero topological dimension and yet it has a non-zero Hausdorff-fractal dimension. In a sense it is both there and not there at the same time [10,63].
2) A Cantor set has the cardinality of the continuum yet it is a totally disjointed discretuum [10,63].
3) It possesses the golden mean Hausdorff dimension which is the epitome of regularity and harmonic order, yet it is random [10,63].
4) Although its Lebesque measure is zero, its Hausdorff measure is 1 so that with certain fine print one could write for it an absurd looking equation namely that zero = one [31,32].
5) The geometry of a Cantor set is the reason behind quantum entanglement [30].
The next question to ask when seeking a deeper understanding of fractal logic is why the golden mean? This may be considered as follows:
1) It is the real solution for the simplest quadratic equation.
2) It is the most irrational number and thus belongs to most stable periodic orbit as shown in KAM theorems of non linear dynamics [45,62].
3) It preserves the simplicity of fractal tiling and symmetry groups such Penrose tiling [1].
4) It is the Eigen frequency of the simplest two degrees of freedom mechanical oscillators [10,18].
5) It has the simplest continued fraction and continued square root expansion representation [10,62,63].
6) It is found abundantly in philo texts of plants as well as in art, paintings and music being a bridge between art and science [9,10].
7) It is the raison d’etre for Hardy’s quantum entanglement.
8) Golden mean arithmetic and number system are a naturally quantized calculus with transition to zero at infinity [31,32].
For all of the above reasons and the other fundamental findings presented in the main body of this paper, it seems that fractal logic is unavoidable and in time it will become the standard tool of theoretical scientists who work in high energy particle physics [65]. We have reached a sophisticated level of our mathematical civilization moving from performing computations and counting using numbers to performing computations and counting using fractals and Cantor sets [65-69].
REFERENCES
- L. Marek-Crnjac, “The Hausdorff Dimension of the Penrose Universe,” Physics Research International, Vol. 2011, 2011, Article ID: 874302.
- L. Marek-Crnjac, “A Short History of Fractal Cantorian Space-Time,” Chaos, Solitons & Fractals, Vol. 41, 2009, pp. 2697-2705. doi:10.1016/j.chaos.2008.10.007
- J. Hocking and G. Young, “Topology,” Dover Publishing, New York, 1961.
- S. L. Lipscomb, “Fractals and Universal Spaces in Dimension Theory,” Springer, New York, 2009. doi:10.1007/978-0-387-85494-6
- M. S. El Naschie, “Complexity Theory Interpretation of High Energy Physics and Elementary Particle Mass Spectrum,” In: B. G. Sidharth, Ed., Frontiers of Fundamental Physics, Vol. 3, Universities Press, Hyderbad, 2007, pp. 1-32.
- M. Heller and W. H. Woodin, “Infinity: New Research Frontiers,” Cambridge University Press, Cambridge, 2011.
- G. N. Ord, “Fractal Space-Time a Geometric Analog of Relativistic Quantum Mechanics,” Journal of Physics A, Vol. 16, No. 9, 1983, pp. 1869-1884. doi:10.1088/0305-4470/16/9/012
- L. Nottale, “Fractal Space-Time and Micro Physics,” World Scientific, Singapore City, 1993.
- A. Stakhov, “The Mathematics of Harmony,” World Scientific, Singapore, 2009. doi:10.1142/6635
- M. S. El Naschie, “A Review of E-Infinity Theory and the Mass Spectrum of High Energy Particle Physics,” Chaos, Solitons & Fractals, Vol. 19, No. 1, 2004, pp. 209-236. doi:10.1016/S0960-0779(03)00278-9
- R. L. Devaney, “An Introduction to Chaotic Dynamical Systems,” Addison-Wesley, Redwood City, 1989.
- M. S. El Naschie, O. E. Rossler and I. Prigogine, “Quantum Mechanics, Diffusion and Chaotic Fractals,” Pergamon Press—Elsevier Publishing, Oxford, 1995.
- L. B. Crowell, “Quantum Fluctutations of Space Time,” World Scientific, Singapore City, 2005. doi:10.1142/5952
- L. Glass and M. Mackey, “The Rhythms of Life,” Princeton University Press, Princeton, 1988.
- B. B. Mandelbrot, “The Fractal Geometry of Nature,” Freeman, New York, 1983.
- J. H. He, E. Goldfain, L. D. G. Sigalotti and A. Mejias, “Beyond the 2006 Physics Nobel Prize for COBE,” China Culture and Science Publishing, Shanghai, 2006.
- C. Beck, “Spation-Temporal Chaos and Vacuum Fluctuations of Quantized Fields,” World Scientific, Singapore City, 2002. doi:10.1142/4853
- Y. Baryshev and P. Terrikorpi, “Discovery of Cosmic Fractals,” World Scientific, Singapore City, 2002. doi:10.1142/4896
- J. Nicolis, G. Nicolis and C. Nicolis, “Non Linear Dynamics and the Two Slit Delayed Experiment,” Chaos, Solitons & Fractals, Vol. 12, 2001, pp. 407-416. doi:10.1016/S0960-0779(00)00190-9
- M. S. El Naschie, “Quantum Collapse of Wave Interference Pattern in the Two-Slit Experiment: A Set of Theoretical Resolution,” Nonlinear Science Letter A, Vol. 2, No. 1, 2011, pp. 1-9.
- R. Elwes, “Ultimate Logic,” New Scientist, Vol. 211, No. 2183, 2011, pp. 30-33. doi:10.1016/S0262-4079(11)61838-1
- J. Ambjorn, J. Jurkiewicz and R. Loll, “The Self-Organizing Universe,” Scientific American, 2008, pp. 24-31.
- S. Kranz and H. Park, “Geometric Integration Theory,” Birkhauser, Boston, 2008. doi:10.1007/978-0-8176-4679-0
- T. Jech, “Set Theory,” Springer, Berlin, 2003.
- A. Kanamori, “The Higher Infinite,” Springer, Berlin, 2003.
- A. Kechris, “Classical Descriptive Set Theory,” Springer, New York, 1995. doi:10.1007/978-1-4612-4190-4
- L. Graham and J. Kantor, “Naming Infinity,” Harvard University Press, Cambridge, 2009.
- L. M. Wapner, “The Pea and the Sun,” A. K. Peters Ltd., Natick, 2005.
- F. Morgan, “Geometric Measure Theory,” Elsevier, Amsterdam, 2009.
- M. S. El Naschie, “Quantum Entanglement as a Consequence of a Cantorian Micro Space-time Geometry,” Journal of Quantum Information Science, Vol. 1, No. 2, 2011, pp. 50-53. doi:10.4236/jqis.2011.12007
- G. Ord, M. S. El Naschie and J. H. He, Fractal SpaceTime and Non Commutative Geometry in High Energy Physics, Asian Academic Publishing Ltd., Hong Kong, Vol. 1, No. 1, 2011, pp. 1-46.
- G. Ord, M. S. El Naschie and J. H. He, Fractal SpaceTime and Non Commutative Geometry in High Energy Physics, Asian Academic Publishing Ltd., Hong Kong, Vol. 2, No. 1, 2012, pp. 1-79.
- L. Zadeh, “Fuzzy Logic and Approximate Reasoning,” Synthese, Vol. 30, No. 3-4, 1975, pp. 407-428. doi:10.1007/BF00485052
- L. Zadeh, “Fuzzy Sets,” Information and Control, Vol. 8, 1965, pp. 338-353. doi:10.1016/S0019-9958(65)90241-X
- K. Kosko, “Fuzzy Thinking,” The New Science of Fuzzy Logic, Hyperion, New York, 1993.
- M. S. El Naschie, “Fuzzy Knot interpretation of YangMills Instantons and Witten’s 5 Brane Model,” Chaos, Solitons & Fractals, Vol. 38, No. 5, 2008, pp. 1349-1354. doi:10.1016/j.chaos.2008.07.002
- M. S. El Naschie, “From Experimental Quantum Optics to Quantum Gravity via a Fuzzy Kahler Manifold,” Chaos, Solitons & Fractals, Vol. 25, No. 5, 2005, pp. 969-977. doi:10.1016/j.chaos.2005.02.028
- M. S. El Naschie, “Fuzzy Dedochaedron Topology and E-Infinity Space-Time as a Model for Quantum Physics,” Chaos, Solitons & Fractals, Vol. 30, No. 5, 2006, pp. 1025-1033. doi:10.1016/j.chaos.2006.05.088
- N. M. Ahmed, “George Cantor: The Father of Set Theory,” The Post Graduate Magazine, 2007, pp. 4-14.
- M. S. El Naschie, “The Brain and E-Infinity”, International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, No. 2, 2006, pp. 128-131.
- M. S. El Naschie, “From Symmetry to Particle,” Chaos, Solitons & Fractals, Vol. 32, No. 2, 2007, pp. 427-430. doi:10.1016/j.chaos.2006.09.016
- M. S. El Naschie, “Kac-Moody Exceptional E12 from Simplectic Tiling,” Chaos, Solitons & Fractals, Vol. 41, No. 4, 2009, pp. 1569-1571. doi:10.1016/j.chaos.2008.06.020
- J. H. He, “Transfinite Physics,” China Culture and Science Publishing, Shanghai, 2005.
- M. S. El Naschie, “Knots and Exceptional Lie Groups as Building Blocks of High Energy Particle Physics,” Chaos, Solitons & Fractals, Vol. 41, No. 4, 2009, pp. 1799-1803. doi:10.1016/j.chaos.2008.07.025
- M. S. El Naschie, “Symmetry Group Prerequisite for E-Infinity in High Energy Physics,” Chaos, Solitons & Fractals, Vol. 35, No. 1, 2008, pp. 202-211. doi:10.1016/j.chaos.2007.05.006
- M. S. El Naschie, “Quantum Groups and Hamiltonian Sets on Nuclear Space-Time Cantorian Manifold,” Chaos, Solitons & Fractals, Vol. 10, No. 7, 1999, pp. 1251-1256. doi:10.1016/S0960-0779(99)00009-0
- M. S. El Naschie, “On a Class of Fuzzy Kahler-Like Manifold,” Chaos, Solitons & Fractals, Vol. 26, No. 2, 2005, pp. 257-261. doi:10.1016/j.chaos.2004.12.024
- M. S. El Naschie, “On a Class of General Theories for High Energy Particle Physics,” Chaos, Solitons & Fractals, Vol. 14, No. 4, 2002, pp. 649-668. doi:10.1016/S0960-0779(02)00033-4
- M. S. El Naschie, “On an Eleven Dimensional E-Infinity Fractal Space-Time,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, No. 4, 2006, pp. 407-409. doi:10.1515/IJNSNS.2006.7.4.407
- M. S. El Naschie, “The Discrete Charm of Certain Eleven Dimensional Space-Time Theory,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, No. 4, 2006, pp. 477-481.
- M. S. El Naschie, “On Fuzzy Kahler-Like Manifold Which Is Consistent with the Two-Slit Experiment,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 6, No. 2, 2005, pp. 8895-8898.
- M. S. El Naschie, “The Symplectic Vacuum, Exotic Quasi Particles and Gravitational Instanton,” Chaos, Solitons & Fractals, Vol. 22, No. 1, 2004, pp. 1-11. doi:10.1016/j.chaos.2004.01.015
- J. H. He, “Non Linear Dynamics and the Nobel Prize in Physics,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 8, No. 1, 2007, pp. 1-4. doi:10.1515/IJNSNS.2007.8.1.1
- L. Sigalotti and A. Mejias, “On El Naschie’s Conjugate Complex Time, Fractal E-Infinity Space-Time and Faster than Light Particles,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, No. 4, 2006, pp. 467-472. doi:10.1515/IJNSNS.2006.7.4.467
- M. Kaku, “Introduction to Superstrings and M-Theory,” Springer, New York, 1999.
- S. Weinberg, “The Quantum Theory of Fields,” Cambridge, Vol. II, 1996.
- S. Weinberg, “The Quantum Theory of Fields,” Cambridge, Vol. III, 2000.
- M. S. El Naschie, “Quantum Golden Field Theory—Ten Theorems and Various CONJECTURES,” Chaos, Solitons & Fractals, Vol. 36, No. 5, 2008, pp. 1121-1125. doi:10.1016/j.chaos.2007.09.023
- M. S. El Naschie, “An Outline for a Quantum Golden Field Theory,” Chaos, Solitons & Fractals, Vol. 37, No. 2, 2008, pp. 317-323. doi:10.1016/j.chaos.2007.09.092
- M. S. El Naschie, “Asymptotic Freedom and Unification in a Golden Field Theory,” Chaos, Solitons & Fractals, Vol. 36, No. 3, 2008, pp. 521-525. doi:10.1016/j.chaos.2007.09.004
- M. S. El Naschie, “A Guide to the Mathematics of E-Infinity Cantorian Space-Time Theory,” Chaos, Solitons & Fractals, Vol. 25, No. 5, 2005, pp. 995-964. doi:10.1016/j.chaos.2004.12.033
- M. S. El Naschie, “Elementary Prerequisites for E-Infinity,” Chaos, Solitons & Fractals, Vol. 30, No. 3, 2006, pp. 579-605. doi:10.1016/j.chaos.2006.03.030
- M. S. El Naschie, “The Theory of Cantorian Space-Time and High Energy Particle Physics (An Informal Review),” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2635-2646. doi:10.1016/j.chaos.2008.09.059
- K. Svozil, “Quantum Field Theory on Fractal SpaceTime,” Journal of Physics A, Vol. 20, No. 12, 1987, pp. 3861-3875. doi:10.1088/0305-4470/20/12/033
- M. S. El Naschie, “Transfinite Harmonization by Taking the Dissonance Out of the Quantum Field Symphony,” Chaos, Solitons & Fractals, Vol. 36, No. 4, 2008, pp. 781-786. doi:10.1016/j.chaos.2007.09.018
- M. S. El Naschie, “Extended Renormalization Group Analysis for Quantum Gravity and Newton’s Gravitational Constant,” Chaos, Solitons & Fractals, Vol. 35, No. 3, 2008, pp. 425-431. doi:10.1016/j.chaos.2007.07.059
- M. S. El Naschie, “Exact Non-Perturbative-Derivation of Gravity’s G4 Fine Structure Constant, the Mass of the Higgs and Elementary Black Holes,” Chaos, Solitons & Fractals, Vol. 37, No. 2, 2008, pp. 346-359. doi:10.1016/j.chaos.2007.10.021
- M. S. El Naschie, “Quantum E-Infinity Field Theoretical Gravitational Constant,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 8, No. 3, 2007, pp. 496-474.
- M. S. El Naschie, “Towards a Quantum Golden Field theory,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 8, No. 4, 2007, pp. 477-482. doi:10.1515/IJNSNS.2007.8.4.477
NOTES
*Corresponding author.

