Open Journal of Fluid Dynamics
Vol.08 No.04(2018), Article ID:88640,12 pages
10.4236/ojfd.2018.84026
Dynamics of Water Flow in the Atmosphere-Aerial Roots Continuum
Médéhouénou Enagnon Alexis1,2,3,4*, Kounouhéwa Bruno Basile1,2,3,4, Koutchadé Clément2,3,4
1Centre Béninoise de la Recherche Scientifique et de l’Innovation (CBRSI)-IRITESE
2Université d’Abomey-Calavi (UAC)
3Faculté des Sciences et Technique (FAST)
4Laboratoire de Physique du Rayonnement (LPR)

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 30, 2018; Accepted: November 18, 2018; Published: November 21, 2018
ABSTRACT
The study of the parameters influencing the absorption of atmospheric humidity not condensed by plants with aerial roots is a challenge in the current context of climatic disturbance where methods of adapting plants to water stress have become the concern of many scientific researchers. Based on Poiseuille and Fick laws, leaf water potential depending on solar radiation and atmospheric water potential around aerial roots; the influence of temperature, relative humidity, inclination angle of roots and solar radiation wavelength on the radial and axial water flow through a root segment is simulated. The various simulations show that a low temperature of the air surrounding the root favors a significant entry of water into the root as well as a relative humidity of the high air approaching 100%. The angle of inclination has an influence on the quantity of water entering the root and that rising in the xylem. These different streams of water are optimized for root tilting of 60˚. The wavelength of the red radiation received by the leaves favors more entry and rise of water in the root. Future studies for transgenes should be taken into account the influence of all these parameters.
Keywords:
Plant, Aerial Root, Absorption, Atmospheric Humidity

1. Introduction
Plants need water to grow. The water mobilization organs vary from one plant to another. Although many plants uptake water by underground roots, some of them absorb water by aerial roots. This is the case of Orchidaceae, Morgeniusae, Araceae, Liliaceae, Amaryllidaceae) [1] - [6] . The mechanism of water absorption by underground roots whose motor responsible is water potential gradient has been the subject of several studies [7] [8] [9] [10] [11] . The aerial root grows from the stems and branches of the plant and lives in the air [12] , it mobilizes atmospheric water i.e. rain, dew, fog, uncondensed moisture. This type of water mobilization has been the subject of several assertions and studies [13] - [18] . From these studies, it should be concluded that this mobilization is due to the spongy tissue consisting of dead cells called velamen that surrounds the aerial roots. Once waterlogged, the adjacent living cells allow this water to pass under a water potential gradient from the cortex to the leaves. The atmosphere is a reservoir of water in the form of humidity [19] . Plants with aerial roots mobilize this atmospheric water. In order to develop a sustainable agriculture in the current context of climate change, it is necessary to innovate in the search of solution to the mobilization of the water by the plants for the reduction of the water stress due to the delay or rupture of the rains. It is therefore imperative to study the mechanisms of mobilization of atmospheric humidity by taking as a model the aerial roots of plants. This paper aims to study the influence of certain parameters on the transport of atmospheric humidity in the atmosphere-root continuum. To carry out this study which aims to be the one of the bases of the development of new crop varieties, the data of radial and axial conductibility of corn will be used in the simulations.
2. Material and Method
2.1. Material
Figure 1 and Figure 2 are examples of plants with aerial roots. The roots are pendulous and absorb atmospheric humidity.
Figure 1. Example of plant with aerial roots: Epiphytic Orchid.
Figure 2. Plant with aerial roots.
2.2. Method
Velamen absorbs atmospheric humidity; it is supposed that a balance is established between the velamen and the atmospheric air in which the aerial root lives once the velamen is full of water. The water potential of the velamen can therefore be approached by the atmospheric water potential in this work.
Figure 3 is a schematic representation of a plant with an aerial root. This is the physical model used in this work.
The force responsible for the entry of water into the root is the water potential gradient. According to Fick’s law [10] , the flow of moisture entering the root is given by:
(1)
Thus,
(2)
with: : Radial conductibility; : Atmospheric water potential ; : Xylem water potential.
The atmospheric water potential is given by the relation:
(3)
The movement of water in the xylem is determined from the Navier Stokes equation for a circular tube.
(4)
In steady state, without convection:
(5)
Figure 3. Representation of a plant with aerial root.
Axial water flow in the xylem:
(6)
Replacing P by which takes into account water pressure, osmotic potential and gravitational potential; we have:
(7)
This axial flow of water in the xylem is Poiseuille’s law [8] .
Conservation of the water flow gives:
(8)
with:
According to [20] , the conservation of water flow in the xylem at the stem level is given by the relation:
(9)
Boundary conditions:
;
Continuity of flows and water potential:
et ;
;
The leaf water potential in this work is supposed to be related to photosynthesis. The sun, the plant are two thermodynamic systems (Figure 4). The sun energy is transferred to the plant this energy makes it possible to produce glucose.
To describe the energetic state of plant water, Slatyer and Taylor [21] introduced thermodynamics into plant physiology. Consider the following thermodynamic equation [22] .
(10)
(11)
U the internal energy, G Gibbs free energy, T the temperature, P the pressure, S the entropy, μ the chemical potential and n the number of moles. The sun is considered as thermal reservoir [23] , with constant pressure, volume and chemical composition [24] , Equation (10) and Equation (11) become:
(12)
(13)
The photosynthesis reaction is isothermal, the system (leaf) is assumed at constant pressure and volume [24] . Equation (10) and Equation (11) become:
(14)
(15)
Plants need 60 photon molecules to synthesize a molecule of glucose [25] ; thus for each molecule of synthesized glucose, the necessary solar energy is given by:
(16)
And the corresponding entropy is:
Figure 4. Principle of photosynthesis.
(17)
The part of energy released by the sun and absorbed by the leaves.
(18)
(19)
The solar energy absorbed by the leaf is the trigger fuel for the process of photosynthesis. This energy is supposed to be totally transformed into chemical energy in the synthesis of glucose; so:
(20)
The water potential is the variation of water potential per unit of molar volume of the water [10] .
(21)
Analytical solution:
(22)
(23)
The values in Table 1 are used for the various simulations.
3. Results and Analysis
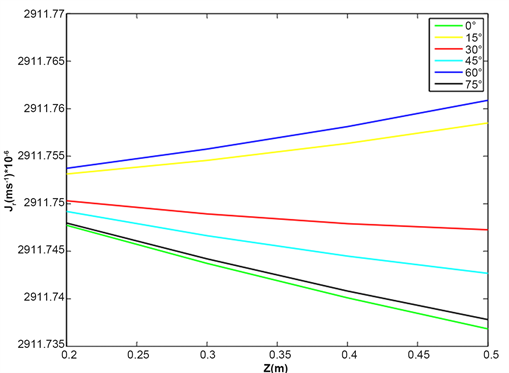
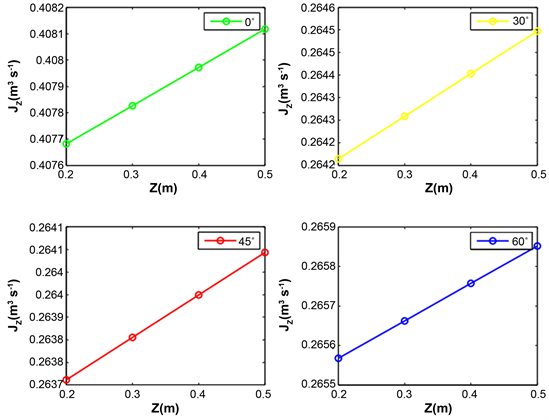
Figure 5 and Figure 6 reveal the evolution of radial water flow as a function of root length when chlorophyll reacts with visible blue radiation. For the 430 nm wavelength representing the lower bound of the blue radiation band, and the relative humidity of the air surrounding the roots equal to 100% at 30˚C, the flow of water entering the root depends on the root inclination. For inclinations of 0˚, 15˚, 30˚, 60˚, 45˚, 75˚; the water flow decreases along the length of the root. On the other hand for the inclinations of 15˚ and 60˚ this water flow increases and
Table 1. Values used in simulations.
Figure 5. Evolution of radial water flow in the root for various inclination angle of root, relative humidity HR = 100%, temperature T = 30˚C and wave length λ = 430 nm.
Figure 6. Evolution of radial water flow in the root for various inclination angle of root, relative humidity of the air HR = 100%, temperature T = 30˚C and wave length λ = 665 nm.
this is more remarkable for the inclination of 60˚. For the wavelength 665 nm of the band of the red radiation, the various curves keeps the same pace, however, the variation of the flow of water is more remarkable in each for each inclination.
It appears from this analysis that when chlorophyll reacts in the red radiation band, the flow of water entering the root is important for the inclination of 60˚.
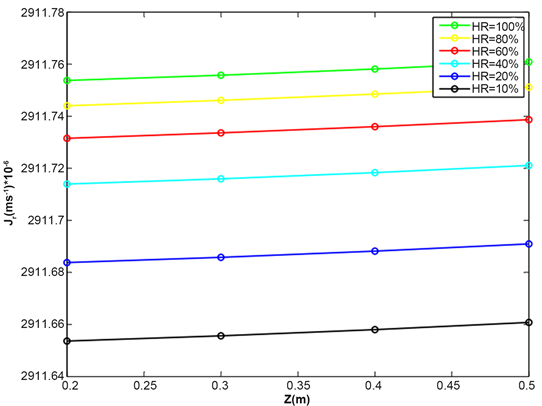
Figure 7 shows the evolution of the radial water flow as a function of wave length for various relative humidity of the air surrounding the roots. The various simulations show that the humidity of the surrounding air strongly influences water flow entering the root. This water flow increases with the humidity of the air and reaches 2911.762 × 10−6 m∙s−1 for 100% humidity for the various values of the simulation.
This analysis shows that the more water vapor in air surrounding aerial root, the more water enters the root.
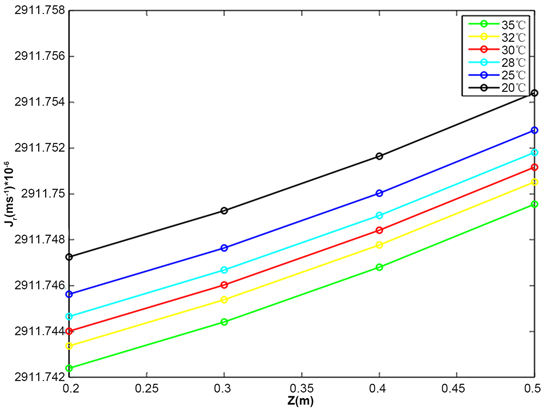
Figure 8 shows the evolution of the radial flow as a function of the length of the root for various values of the air temperature surrounding the root. For various temperature values, the water flow is important for low temperatures as for high temperatures.
This analysis shows that the entry of water into the root is favored by the low temperatures of the air surrounding the roots.
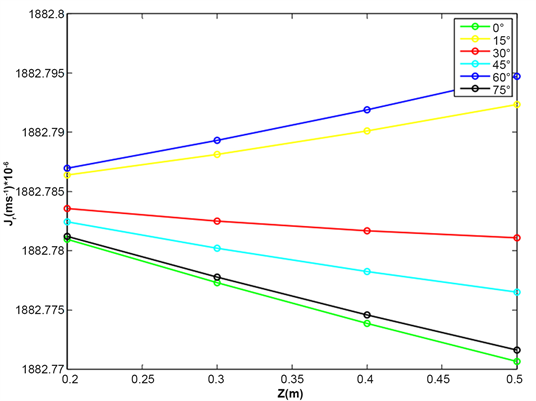
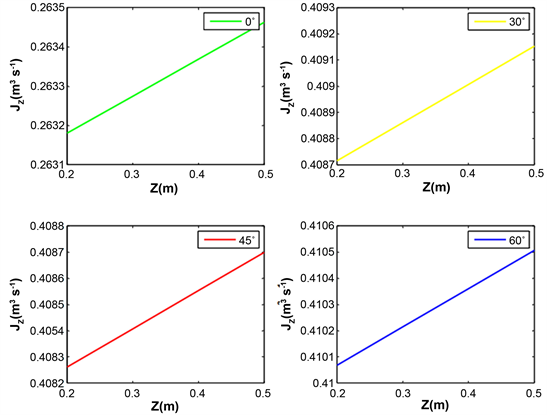
Figure 9 and Figure 10 reveal the water evolution in the xylem of the aerial roots of plants. The flow of water in xylem depends on the wave length. For each radiation, the maximum water flow is obtained with the inclination 60˚. After follows the inclination 30˚, 45˚ and finally 0˚.
Figure 7. Evolution of radial water flow in the root for various values of air relative humidity, temperature T = 30˚C, wavelength λ = 430 nm and inclination angle θ = 60˚.
Figure 8. Evolution of radial water flow in the root for various values of temperature, relative humidity HR= 80%, wavelength λ = 430 nm and inclination angle θ = 60˚.
It emerges from this analysis that the axial flow does not depend linearly on the angles of inclination of the roots. The roots at an angle of 60˚ or 30˚ favor the rise of water in the xylem of the roots. Taking into account the inclinations angles of roots is important in water mobilization from the root-atmosphere interface to the root xylem.
Figure 9. Evolution of axial water flow in the root for various values inclination angle of root, relative humidity HR = 80%, temperature T = 25˚C and wavelength λ = 430 nm.
Figure 10. Evolution of axial water flow in the root for various inclination angle of root, relative air humidity HR = 80%, temperature T = 25˚C and wavelength λ = 665 nm.
4. Conclusion
The aerial roots of plants such as Epiphytic orchids and Ficus microcarpa mobilize atmospheric water i.e. rain, dew, and uncondensed moisture. As non-condensed humidity is an available resource, its direct mobilization by aerial roots can reduce water stress in plants. This mobilization depends on the parameters including the inclination angle of roots, the temperature, the relative humidity of the air surrounding the roots, the wavelength of the light radiation received by the leaves. The results of the various simulations show that these parameters strongly influence the entry and the rise of water in the root. Thus, for studies within the framework of improving the mechanism of plants to directly mobilize uncondensed atmospheric humidity, it is important to take into account the influence of these parameters.
Acknowledgements
This work was supported by IRITESE/CBRSI.
Conflicts of Interest
We authors declare that we have no competing interests.
Cite this paper
Alexis, M.E., Basile, K.B. and Clément, K. (2018) Dynamics of Water Flow in the Atmosphere-Aerial Roots Continuum. Open Journal of Fluid Dynamics, 8, 404-415. https://doi.org/10.4236/ojfd.2018.84026
References
- 1. Benzing, D.H. (2000) Bromeliaceae—Profile of an Adaptive Radiation. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511565175
- 2. Augustus, M.D. and Lewis, K. (1957) The Role of the Velamen of the Aerial Roots of Orchids. International Journal of Plant Sciences, 119, 78-87. https://doi.org/10.1086/335966
- 3. Huggett, B. (2010) Aspects of Vessel Dimensions in the Aerial Roots of Epiphytic Araceae. International Journal of Plant Sciences, 171, 362-369. https://doi.org/10.1086/651230
- 4. Saifullah, S.M., Gul, S. and Rasool, F. (2004) Anomalous Aerial Roots in Grey Mangroves of an Arid Climate Lagoon. Pakistan Journal of Botany, 36, 463-466.
- 5. Benzing, D.H. (1996) Aerial Roots and Their Environments. In: Waisel, Y., Eshel, A. and Kafkafi, U., Eds., Plant Roots: The Hidden Half, Marcel Dekker, New York, 875-894.
- 6. Deb, C.R. and Pongener, A. (2012) Studies on the in Vitro Regenerative Competence of Aerial Roots of Two Horticultural Important Cymbidium Species. Journal of Plant Biochemistry and Biotechnology, 21, 235-241. https://doi.org/10.1007/s13562-011-0099-5
- 7. Doussan, C., Pierret, A., Garrigues, E. and Pagès, L. (2006) Water Uptake by Plant Roots: II-Modelling of Water Transfer in the Soil Root-System with Explicit Account of Flow within the Root System—Comparison with Experiments. Plant and Soil, 283, 99-117. https://doi.org/10.1007/s11104-004-7904-z
- 8. Frensch, J. and Steudle, E. (1989) Axial and Radial Hydraulic Resistance to Roots of Maize (Zea mays L.). Plant Physiology, 91, 719-726. https://doi.org/10.1104/pp.91.2.719
- 9. Molz, F. (1981) Models of Water Transport in the Soil-Plant System. Water Resources Research, 17, 1245-1260. https://doi.org/10.1029/WR017i005p01245
- 10. Molz, F.J. (1976) Water Transport in the Soil-Root System: Transient Analysis. Water Resources Research, 12, 805-808. https://doi.org/10.1029/WR012i004p00805
- 11. Landsberg, J.J. (1978) Water Movement through Plant Roots. Annals of Botany, 42, 493-508. https://doi.org/10.1093/oxfordjournals.aob.a085488
- 12. Bellini, C., Pacurar, D.I. and Perrone, I. (2014) Adventitious Roots and Lateral Roots: Similarities and Differences. Annual Review of Plant Biology, 65, 639-666. https://doi.org/10.1146/annurev-arplant-050213-035645
- 13. Schleiden, J.M. and Edwin, L. (1849) Principles of Botany. Green & Longman, London.
- 14. Went, F.W. (1940) Soziologie der Epiphyten eines tropischen Regenwaldes. Annales du Jardin botanique de Buitenzorg, 50, 1-98.
- 15. Benzing, D.H., Ott, D.W. and Friedman, W.E. (1982) Roots of Sobralia macrantha (Orchidaceae): Structure and Function of the Velamen-Exodermis Complex. American Journal of Botany, 69, 608-614. https://doi.org/10.1002/j.1537-2197.1982.tb13297.x
- 16. Lüttge, U. (1997) Physiological Ecology of Tropical Plants. Springer, Berlin. https://doi.org/10.1007/978-3-662-03340-1
- 17. Liu, L., Fu, X. and Chen, X. (2016) The Transpiration and Moisture Absorption Characteristics of Ficusmicrocarpa (L.) Aerial Roots in the South of China. Pakistan Journal of Botany, 48, 1473-1479.
- 18. Zotz, G. and Winkler, U. (2013) Aerial Roots of Epiphytic Orchids: The Velamen Radicum and Its Role in Water and Nutrient Uptake. Oecologia, 171, 733-741. https://doi.org/10.1007/s00442-012-2575-6
- 19. Clus, O. (2007) Condenseur radiatif de la vapeur d’eau (rosée) comme source alternative d’eau. Thèse de Doctorat, Université de Corse.
- 20. Payvandi, S., Daly, K.R., Jones, D.L., Talboys, P., Zygalakis, K.C. and Roose, T. (2007) A Mathematical Model of Water and Nutrient Transport in Xylem Vessels of a Wheat Plant. Society for Mathematical Biology.
- 21. Slatyer, R.O. and Taylor, S.A. (1960) Terminology in Plant-Soil-Water Relations. Nature, 187, 922-924. https://doi.org/10.1038/187922a0
- 22. Zemansky, M.W. and Dittan, R.H. (1981) Heat and Thermodynamic. McGraw Hill, New York, 212-244.
- 23. De vos, A. (1992) Enderversible Thermodynamic of Solar Energy Conservation. Oxford University Press, Oxford.
- 24. Albarran-Zavara, E. and Angulo-Broum, F. (2007) A Simple Thermodynamic Analysis of Phosynthesis. Etropy, 9, 152-168.
- 25. Andriess, C.D. and Hollestelle, M.J. (2001) Minimum Entropy Production in Photosynthesis. Biophysical Chemistry, 90, 249-253. https://doi.org/10.1016/S0301-4622(01)00146-6