Open Journal of Fluid Dynamics
Vol.05 No.03(2015), Article ID:60050,9 pages
10.4236/ojfd.2015.53028
Mechanism of Generation and Collapse of a Longitudinal Vortex System Induced around the Leading Edge of a Delta Wing
Shigeru Ogawa, Jumpei Takeda
Department of Mechanical Engineering, National Institute of Technology, Kure College, Hiroshima, Japan
Email: ogawa@kure-nct.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 September 2015; accepted 26 September 2015; published 29 September 2015
ABSTRACT
The purpose of the paper is to clarify the mechanism of generation and collapse of a longitudinal vortex system induced around the leading edge of a delta wing. CFD captured well characteristics of flow structure of the vortex system. It is found that the vortex system has a cone-shaped configuration, and both rotational velocity and vorticity have their largest values at the tip of the vortex and reduce downstream along the vortical axis. This resulted in inducing the largest negative pressure at the tip of the delta wing surface. The collapse of the vortex system was also studied. The system can still remain until the tip angle of 110 degrees. However, between 110 degrees and 120 degrees, the system becomes unstable. Over 120 degrees, the characteristics of the vortex are considered to have converted from the longitudinal vortex to the transverse one.
Keywords:
Delta Wing, Longitudinal Vortex, Vortex Breakdown, CFD

1. Introduction
The sound induced by turbulence in an unbounded fluid is generally called aerodynamic sound. With respect to aerodynamic sound, Lighthill [1] , Curle [2] and Howe [3] [4] have made their theoretical contributions to clarifying the relationship between turbulent flow and sound. Lighthill [1] transformed the Navier-Stokes and continuity equations to form an exact, inhomogeneous wave equation whose source terms were important only within the turbulent region. This equation is called Lighthill’s equation. In most applications of Lighthill’s theory, it is necessary to generalize the solution to account for the presence of solid bodies in the flow. Curle [2] has made an extension to Lighthill’s general theory of aerodynamic sound so as to incorporate the influence of solid boundaries upon the sound field. Howe [3] [4] recasts Lighthill’s equation in a form that emphasizes the prominent role of vorticity in the production of sound by taking the total enthalpy as the independent acoustic variable, which leads to the vortex sound equation. These theories have emphasized that unsteady motions of the vortex play a crucial role in the generation of aerodynamic sound.
Regarding the vortex, emphasis has been placed especially on longitudinal vortex which rotates on the axis whose direction coincides with the flow direction. In the automobile industry, the reduction of aerodynamic noise becomes more and more important for the comfortable vehicle since noises caused by engine, power train, tires, and other noise sources have been steadily reduced in recent years. It is well known that the front pillar of an automobile is regarded as one of the most dominant areas in generating aerodynamic noise due to strong longitudinal vortices. Separated flows behind the front pillar generate the longitudinal vortices. Based on the theories as mentioned above, many researchers have so far tried to reveal the generation mechanism of aerodynamic sound. Haruna, Nouzawa, Kamimoto and Sato [5] applied the Lighthill-Curle’s theory of aerodynamic sound to automobiles and experimentally estimated dipole noise emitted from the pressure fluctuations on the body surface. Recently Nouzawa, Li and Nakamura [6] have studied the mechanism of aerodynamic noise generated from front pillar and door mirror. Hamamoto, Okutsu and Yanagimoto [7] have investigated the effect of the external aerodynamic noise sources onto the interior noise around the front pillar where longitudinal vortices exist. Numerical approaches have also been conducted with delta wings and actual vehicles (Haruna, Hashiguchi, Kamimoto and Kuwahara [8] , Takeda and Ogawa [9] , Ogawa and Li [10] ). In addition to the aerodynamic engineering field, longitudinal vortex also has been focused in the heat transfer engineering field. Jacobi and Shah [11] reviewed enhancement of heat transfer through the use of longitudinal vortices. Recently Iwasaki, Hara and Honda [12] used longitudinal vortices for EGR (exhaust gas recirculation) system to cool down the temperature of exhaust gas from the engine.
There have been so many studies to reveal the generation mechanism of aerodynamic noise produced by longitudinal vortex. However, it has not yet been clarified that how the longitudinal vortex system has been generated and how this system produces the aerodynamic noise. The final objective of our study, therefore, is to simplify this specific aerodynamic noise problem to obtain a thorough understanding of how the longitudinal vortex is produced, and how the noise can be estimated quantitatively. As a first step, the present paper aims to reproduce the longitudinal vortex generated behind the front pillar of a vehicle by a simple delta wing model, and to clarify the mechanism of generation and collapse of the longitudinal vortex system.
2. Visualization of the Longitudinal Vortex System by Running Water Channel
Figure 1 shows the delta wing employed for reproduction of the longitudinal system. The wing model has three dimensions with 260 mm long, 160 mm wide and 3 mm thick. The model with attack of angles 15 degrees was immersed in the running water channel shown in Figure 2 whose uniform flow is 0.4 m/s. The test section is 1500 mm wide × 800 mm high × 4000 mm long which is large enough to visualize the flow around the delta wing. The delta wing has the tip angle of 90 degrees. Figure 3 depicts the longitudinal vortex visualized by the hydrogen bubble method in the running water channel. It was found that the separated flows around the leading edge are rotating upward. This method captured clearly the longitudinal vortex rotating in the form of a coned-shaped configuration shown in red line in the figure.
Figure 1. The delta wing employed.
Figure 2. Running water channel.
Figure 3. Longitudinal vortex system of the delta wing visualized by the hydrogen bubble method.
3. The Method of Numerical Simulation
As a next step, CFD will be employed to analytically investigate the structure of the longitudinal vortex. The study uses the software STAR-CCM+ with software V9.04.009. In the simulation, tip angles of the wing model vary from 40 degrees to 140 degrees in every 10 degrees step.
3.1. Numerical Method
This study employed RANS (Reynolds Averaged Navier-Stokes Simulation). This approach is valid when the maximum Mach number in the domain is less than 0.2 - 0.3, and when unsteady wake effects are not important.
Eddy viscosity models use the concept of a turbulent viscosity to model the Reynolds stress tensor as a function of mean flow quantities. K-ω model was used as the eddy viscosity model. It therefore follows that the flows are three-dimensionally calculated in steady state with turbulent model.
In the steady state analysis, the maximum step number is 3500. The speed of the water flow is 0.4 m/s as in the running water channel experiment. Reynolds number is defined in Equation (1), where U = 0.4 m/s, L = 0.26 m, and ν = 1.28 × 10−6 m2/s and results in Re = 8.1 × 104. This implies that the flow is turbulent and Mach number is 0.001.
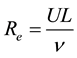 (1)
(1)
3.2. Mesh Generation Method
Figure 4 shows the wing model in numerical wind tunnel. The model employed in simulation has the tip angel 90 degrees with three dimensions shown in Figure 1. The scale of the numerical wind tunnel is 600 mm × 600 mm × 1260 mm. The wind scale was determined so that the uniform flows can be maintained around the delta wing model. The attack of angles for the model is 15 degrees the same as that used in the running water channel. Total number of mesh ranges from 7.48 million to 8.11 million, depending on the tip angles of the model. Minimum mesh size is 0.25 mm in closest vicinity to the leading edge of the model. In generating mesh, prism layer meshing method was adopted. This meshing method was used to optimize the mesh size in the boundary layer as shown in Figure 5. The prism layer mesh model is used with a core volume mesh to generate orthogonal prismatic cells next to wall surfaces or boundaries. This layer of cells is necessary to improve the accuracy of the flow solution. The prism layer mesh is defined in terms of its thickness, the number of cell layers, and the size distribution of the layers. In this study the thickness of prism layer is 3 mm and the number of cell layer is 5 and mesh size is 0.5 mm closest to the model surface.
4. Numerical Results and Discussion
4.1. Structure of Longitudinal Vortex
To investigate the longitudinal vortex in more detail, the numerical simulation was conducted. As shown in
Figure 4. The numerical wind tunnel and the delta wing model.
Figure 5. Mesh condition around a delta wing surface.
Figure 6, the longitudinal vortex was reproduced just as the experimental result. The longitudinal vortex system in Figure 6 was depicted so that incoming streamlines can go through the region with total pressure coefficient Cpt less than 0.8 in the section B. The streamlines of the vortex indicate the characteristics that the configuration is cone-shaped and the flow at the tip of the vortex is fastest, which is shown by red-colored streamlines. The flows are separating at the leading edge and rotating around the vortex axis upward. At the place of the tip flows firstly separate due to the wing configuration and flows are going upward with the flow rotating around the vortical axis. The fastest flow velocity decreases their velocity along the vortical axis. This is because there are strong interactions between flows and the wing body. As a result, fluid particles dissipate their energy due to viscosity and convection.
Vorticity in the longitudinal axis was investigated in each section of A, B, and C as shown in Figure 7. The red shows a stronger vorticity whereas the dark blue shows a weaker vorticity. The vorticity is the strongest at the tip of the vortex at the section A, and the vorticity becomes weaker downstream along the vortical axis at the section B and C. It is found that there exists a pair of vortices whose rotating directions are opposite. Basically, firstly flows separated at the leading edge generate the clockwise vortex, which secondly induces counterclockwise one due to viscosity of the flows. Although the current numerical simulation does not reveal all the vortices, it is considered that a pair of vortices whose rotating directions are opposite exists infinitely at the each section. The properties of the vortices distribution shown in Figure 7 showed good agreement with the experimental results obtained by hot wire anemometers for an actual vehicle by Ogawa [13] [14] .
Figure 6. Streamlines of the longitudinal vortex generated behind the leading edge of the delta wing with the tip angle of 90 degrees.
Figure 7. Vortices distribution of each section A, B, and C for the tip angle of 90 degrees.
Figure 8 shows equi-contour lines of pressure coefficients. The definition of pressure coefficients is described in Equation (2).
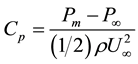 (2)
(2)
This Cp coefficient shows how the pressure on the wing indicates, compared with the pressure in the uniform flows. It, therefore, follows that if Cp has negative value, the pressure on the wing surface is lower than one in the uniform flows.
Characteristics of the longitudinal vortex are well reflected by pressure coefficients on the wing surface. The fast flows at the wing tip are rapidly separated, but the rotational radius is small. Since the centrifugal force has the property that it is proportional to the square of the velocity and is in inverse proportion to the rotational radius, this causes the tip of the longitudinal vortex to induce the largest negative pressure. As a result, the wing tip has the lowest pressure coefficients as shown in Figure 8. The pressures in the longitudinal vortex gradually tend to recover due to the diffusion of the vorticity and convection of flows. In addition, the existence of two vortices is confirmed by distribution of pressure coefficients as shown in red chain lines of Figure 8. These two red chain lines have much to do with a pair of vortices shown in Figure 7. The characteristics of equi-contour lines of pressure coefficients in Figure agree well with the experimental results of actual vehicle by Ogawa [13] [14] .
4.2. Collapse Phenomena of Longitudinal Vortex
In order to clarify the collapse phenomena of the longitudinal vortex, tip angles of the wing model were varied from 40 degrees to 140 degrees at every 10 degrees. Vorticity was used as a physical quantity for evaluating the transformation of the vortex. The vorticity will be described in Equation (3) to Equation (7) with respect to X, Y, Z coordinate axes and velocity vector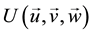 . Three components
. Three components ,
,
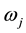 , and
, and
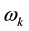 express the vorticity in X, Y, Z axial directions respectively, and
express the vorticity in X, Y, Z axial directions respectively, and
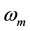 expresses the magnitude of the vorticity.
expresses the magnitude of the vorticity.
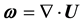 (3)
(3)
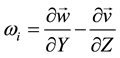 (4)
(4)



Figure 8. Equi-contour lines of pressure coefficients. Two red chain lines are considered the existence of the vortex axes for two different vortices.
In evaluating the transformation of the vortex, time-averaged vorticity was employed for the extracted region where total pressure coefficient Cpt is less than 0.8 in each section A, B, and C. Cpt was used as a physical quantity for identifying the region where the vortex exists.
Figure 9 shows the relationship between vorticities and tip angles in each section of A, B, and C. In each section three quantities (













The longitudinal vortex can still remain until the tip angle of 110 degrees. However, between 110 degrees and
Figure 9. Relationship between vorticities and tip angles. (a) Section A, (b) Section B, (c) Section C.
Figure 10. Streamlines of the longitudinal vortex whose tip angle change from 100 degrees to 140 degrees. (a) Tip angle of 100 degrees, (b) Tip angle of 110 degrees, (c) Tip angle of 120 degrees, (d) Tip angle of 130 degrees, (e) Tip angle of 140 degrees.
120 degrees the longitudinal characteristics become unstable. Over 120 degrees the characteristics of the vortex are considered to have converted from the longitudinal to the transverse one. It follows, therefore, that the longitudinal characteristics of the vortex are converted to the transverse vortex.
In order to investigate qualitatively the configuration of the vortex generated behind the leading edge, the streamlines of the vortex were investigated for tip angles from 100 degrees to 140 degrees at every 10 degrees.
Figure 10 shows the streamlines of the longitudinal vortex generated behind the leading edge of the delta
wing with the tip angle from 100 degrees to 140 degrees. The depicted region where a threshold value of Cpt less than 0.8 in section B is established in order to extract the streamlines at the region which exists the vortex. The configuration of the vortex still remains cone-shaped until 100 degrees. At 110 degrees the vortex system becomes unstable. Over 120 degrees, the rotational radius of the vortex increases and the configuration of the vortex begins to shift from cone-shaped to elliptical-shaped. That is, the vortex generated behind the leading edge changed from the longitudinal to the transverse vortex which rotates on the Y axis lying at right angles to flow direction. After the shift from the longitudinal vortex to the transverse vortex,

It follows, therefore, that the longitudinal vortex can remain until the tip angle of 100 degrees, and undergoing the transient region around 110 degrees, the longitudinal vortex has been changed to the transverse vortex over 120 degrees.
5. Conclusions
The mechanism of generation and collapse of a longitudinal vortex system induced around the leading edge of a delta wing was investigated. The results obtained are summarized as follows.
1) CFD captured well characteristics of flow structure of the longitudinal vortex system. It is found that the longitudinal vortex has a cone-shaped configuration, and both rotational velocity and vorticity have their largest values at the tip of the vortex and reduce downstream along the vertical axis. This resulted in inducing the largest negative pressure at the tip of the delta wing surface.
2) With respect to the vortical characteristics, the following was clarified. The longitudinal vortex can still remain until the tip angle of 110 degrees. However, between 110 degrees and 120 degrees, the longitudinal characteristics become unstable. Over 120 degrees, the characteristics of the vortex are considered to have converted from the longitudinal to the transverse one.
Cite this paper
ShigeruOgawa,JumpeiTakeda, (2015) Mechanism of Generation and Collapse of a Longitudinal Vortex System Induced around the Leading Edge of a Delta Wing. Open Journal of Fluid Dynamics,05,265-274. doi: 10.4236/ojfd.2015.53028
References
- 1. Lighthill, M.J. (1952) On Sound Generated Aerodynamically I. General Theory. Proceedings of the Royal Society A, 211, 564-587.
http://rspa.royalsocietypublishing.org/content/211/1107/564 - 2. Curle, N. (1955) The Influence of Solid Boundaries upon Aerodynamic Sound. Proceedings of the Royal Society A, 231, 505-514.
http://rspa.royalsocietypublishing.org/content/231/1187/505.short
http://dx.doi.org/10.1098/rspa.1955.0191 - 3. Howe, M.S. (2003) Theory of Vortex Sound: Cambridge Texts in Applied Mathematics. Cambridge University Press, Cambridge.
- 4. Howe, M.S. (2014) Acoustics and Aerodynamic Sound. Cambridge University Press, Cambridge.
- 5. Haruna, S., Nouzawa, T., Kamimoto, I. and Sato, H. (1990) An Experimental Analysis and Estimation of Aerodynamic Noise Using a Production Vehicle. SAE Transactions: Journal of Passenger Cars, 99.
http://papers.sae.org/900316/ - 6. Nouzawa, T., Li, Y. and Nakamura, T. (2011) Mechanism of Aerodynamic Noise Generated from Front-Pillar and Door Mirror of Automobile. Journal of Environment and Engineering, 6, 615-626.
http://dx.doi.org/10.1299/jee.6.615 - 7. Hamamoto,N., Okutsu,Y. and Yanagimoto, K. (2013) Investigation for the Effect of the External Noise Sources onto the Interior Aerodynamic Noise. Proceedings of SAE 2013 World Congress & Exhibition, Detroit, 16-18 April 2013.
http://papers.sae.org/2013-01-1257/ - 8. Haruna, S., Hashiguchi, M., Kamimoto, I. and Kuwahara, K. (1992) Numerical Study of Aerodynamic Noise Radiated from a Three-Dimensional Wing. SAE Transactions: Journal of Passenger Cars, 101.
http://papers.sae.org/920341/ - 9. Takeda, J. and Ogawa, S. (2014) Prediction of Aerodynamic Noise Radiated from a Delta Wing. Proceedings of the 4th International Symposium on Technology for Sustainability, Taipei, 19-21 November 2014.
- 10. Ogawa, S. and Li, Y. (2014) Control of Longitudinal Vortex Generated around Front Pillar of Vehicles, Based on Clarification of the Vortex Generation Mechanism Using a Delta-Wing. Proceedings of the 12th International Conference on Motion and Vibration Control, Hokkaido, 3-7 August 2014.
- 11. Jacobi, A.M. and Shah, R.K. (1995) Heat Transfer Surface Enhancement through the Use of Longitudinal Vortices, A Review of Recent Progress. Experimental Thermal and Fluid Science, 11, 295-309.
http://www.sciencedirect.com/science/article/pii/089417779500066U
http://dx.doi.org/10.1016/0894-1777(95)00066-U - 12. Iwasaki, M., Hara, J. and Honda, I. (2014) Development of Vortex Generator for EGR Cooler. Proceedings of FISITA 2014 World Automotive Congress, Maastricht, 2-6 June 2014.
- 13. Ogawa, S. (1995) Aerodynamic Noise of a Body with Separated and Reattached Flow by Longitudinal Vortices. PhD Thesis, University of Tokyo, Tokyo.
- 14. Ogawa, S. (1995) Generation Mechanism of Aerodynamic Noise by Interference between Longitudinal Vortex and Body. Proceedings of the Japan National Congress for Applied Mechanics, 44, 215-220.
Nomenclature
Re: Reynolds Number
U: Flow Velocity (m/s)
L: Representative Length (m)
ν: Kinematic Viscosity (m2/s)
ω: Vorticity (1/s)
θ: Tip Angle of the Delta Wing (degree)
Cpt: Total Pressure Coefficient
Cp: Pressure Coefficient
Pm: Pressure of Measuring Point on the Wing (Pa)
P∞: Pressure in the Uniform Flow (Pa)
ρ: Density of Fluid (kg/m3)











