ABSTRACT

The dynamics of steady, two-dimensional magnetohydrodynamics (MHD) free con- vective flow of micropolar fluid along a vertical porous surface embedded in a thermally stratified medium is investigated. The ratio of pressure drop caused by liquid-solid interactions to that of pressure drop caused by viscous resistance are equal; hence, the non-Darcy effect is properly accounted for in the momentum equation. The temperature at the wall and at the free stream which best accounts for thermal stratification are adopted. Similarity transformations are used to convert the non- linear partial differential equation to a system of coupled non-linear ordinary differ- rential equation and also to parameterize the governing equations. The approximate analytical solution of the corresponding BVP are obtained using Homotopy Analysis Method (HAM). The effects of stratification parameter, thermal radiation and other pertinent parameters on velocity, angular velocity and temperature profiles are shown graphically. It is observed that increase in the stratification parameter leads to decrease in both velocity and temperature distribution and also makes the micro- rotation distribution to increase near the plate and decrease away from the plate. The influence of both thermal stratification and exponential space dependent internal heat source on velocity, micro-rotation and temperature profiles are presented. The comparison of the solutions obtained using analytical techniques (HAM) and MATLAB package (bvp4c) is shown and a good agreement is observed.

Keywords:

Porous Medium, Thermal Stratification, Homotopy Analysis Method, Free Convection, Micropolar

1. Introduction

The study and structure of a fluid as it flows over a surface results in vertical density variations which is of great importance in industry due to its vast application in industry. Dake and Harleman [1] extensively discussed distribution of temperature across a deep lake and further explained the applications of thermal stratification in real life situation. Thermal stratification is a natural process that describes the layering of bodies of water based on their temperature. It occurs mainly because of temperature variations due to the presence of different fluids of different density. This natural process creates a transition zone of temperature gradient between cold and hot fluid zones. In a case of natural convection and boundary layer analysis, thermal stratification plays an important role in vertical temperature distribution. The concept of thermal stratification is based on the division of water bodies about a surface/plate into three layers known as epilimnion, metalimnion and hypolimnion. Animasaun [2] explained that all the three divisions exists within the thin boundary layer and at each division the nature of velocity and temperature may vary. Dynamics of thermally stratified fluid has attracted the attention of researchers and and it has become an important topic for scientific enquiry because of its wide spread applications in a number of industrial engineering and environmental applications. Madhu et al. [3] studied effects of viscous dissipation and ther- mal stratification on chemical reacting fluid flow over a vertical stretching surface with heat source. Hayat et al. [4] investigated thermal and concentration stratifications effects in radiative flow of a Jeffery fluid over a stretching sheet; it was observed that an increase in the thermal stratification parameter leads to reduction in fluid velocity, temperature field and thermal boundary layer thickness. Mixed convection flow along a stretching cylinder in a thermally stratified medium was carried out by Mukhopadhyay [5] . Murthy [6] studied thermo-diffusion effect on free convection heat and mass transfer in a thermally linearly stratified non-Darcy porous media. Recently, Omowaye et al. [7] investigated heat and mass transfer of upper convected maxwell fluid flow with variable thermo-physical properties over a horizontal melting surface, it was reported that increase in the magnitude of thermal stratification parameter corresponds to a systematic way of decreasing the heat energy entering into the fluid domain from the free stream.

Micropolar fluids are fluids with internal structures or micro-structures which belong to a class of fluids with nonsymmetric stress tensor that can be called polar fluids. The theory of micropolar fluids introduced by Eringen [8] takes into account the microscopic effect arising from the local structure and micro-rotation of fluid particles and is expected to provide a mathematical model for the non-Newtonian fluid behavior and studies have also shown that the model can be successfully applied to a wide range of applications which is able to describe the behavior of the polymeric additives, blood flow, lubricants, porous media, turbulent shear flows, liquid crystals, dirty oils and solutions of colloidal suspension etc. The resulting equations in this fluid involve a micro-rotation parameter and a gyration parameter in addition to a classical velocity field. A thorough review of the subject of the application of micropolar fluid have also been discussed by Lukaszewicz [9] . The study of free convection heat transfer in the boundary layer flow along a vertical surface in a micropolar fluid has been studied by many researchers. Mohammad et al. [10] investigated MHD viscous flow of micropolar fluids due to a shrinking sheet. Mohammad [11] investigated Soret and Dufour effects on steady free convection in MHD micropolar fluid flow, together with hall current, heat and mass transfer. Umavathi [12] studied mixed convection flow of a micropolar fluid with concentration in a vertical channel in the presence of heat source or sink. Thia- garajan [13] considered a semi analytical investigation on MHD micropolar fluid and heat transfer in a permeable porous channel. MHD flow and heat transfer near the stagnation point of a micropolar fluid over a stretching surface with heat generation/ absorption was carried out by Jat et al. [14] . Ravi et al. [15] studied transient free convective flow of a micropolar fluid between two vertical walls. Recently, steady mixed convection micropolar fluid flow towards stagnation point formed on horizontal linearly stretchable melting surface is presented in Ref. [16] . The vortex viscosity of micropolar fluid along a melting surface was considered as a constant function of temperature while dynamic viscosity and thermal conductivity are temperature dependent due to the influence of internal heat source on the fluid.

Porous medium is a very important aspect in Science and Engineering which is described as a medium or material that contains pores or spaces between solid materials or solid matrix through which liquids or gases can pass. Common examples of naturally occurring porous medium include sand, soil, sandstone, sponges, ceramics and foams. Fluid flow in porous media is an important dimension in many areas of reservoir engineering, such as petroleum, environmental and groundwater hydrology. A number of studies have been reported in the literature focusing on the problem of combined heat and mass transfer in porous media and the analysis of convective transport in a porous medium with the inclusion of non-Darcian effects has also been a matter of study in recent years. Non-Darcy behavior is important for describing fluid flow in porous media in situations where high velocity occurs. Hence, due to its important applications in many fields, a full understanding of heat transfer by non-Darcy natural convection from a heated vertical surface embedded in fluid saturated porous medium is meaningful. Mohammed et al. [17] examined thermal radiation effects on MHD free convection flow of a micropolar fluid past a stretching surface embedded in a non-Darcian porous medium. Emad et al. [18] studied flow and heat transfer of a micropolar fluid past a stretching surfaced embedded in a non-Darcian porous medium with uniform free stream. RamReddy et al. [19] considered influence of viscous dissipation on free convection in a non-Darcy porous medium saturated with nanofluid in the presence of magnetic field. Natural convection heat and mass transfer in a micropolar fluid-saturated non-Darcy porous regime with radiation and thermophoresis effects was carried out by Bakier [20] .

In the literatures above, little attention has been given to investigate free convective micropolar fluid flow along a vertical surface embedded in non-Darcian thermally medium. In addition, no attempt has been made to investigate the behaviour of micro- polar fluid in the presence of exponential space dependent and temperature dependent internal heat source along a vertical surface embedded in non-Darcian thermally stratified porous medium using Homotopy Analysis Method. In view of this, it is imperative to highlight that, the present study will offer helpful information to scientists and engineers in industry.

2. Mathematical Formulation

We consider steady two-dimensional free convective boundary layer flow of an incompressible, electrically conducting micropolar fluid along a vertical surface embedded in non-Darcian thermally stratified porous medium. Keeping the origin fixed, the sheet is then stretched with a velocity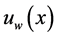, varying linearly with the distance from the slit. The flow is assumed to flow in x-direction which is along vertical surface and y-axis is normal to it. Fluid suction/injection is imposed at the plate surface. The temperature of the surface is held uniform at which is higher than the ambient temperature i.e.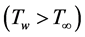. In this study, the thermal stratification is properly accounted for by modifying both and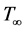. The uniform magnetic field of magnitude 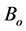is applied normal to the plate. Also the magnetic Reynolds number is assumed to be small so that the induced magnetic field is negligible in comparison to the applied magnetic field. The viscous dissipation term in the energy equation is assumed to be negligible (since the fluid model is characterized with a higher velocity). Under the foregoing assumptions with the Boussinesq approximation, the governing equations of the MHD free convection flow are:

Continuity Equation

(1)

Momentum Equation

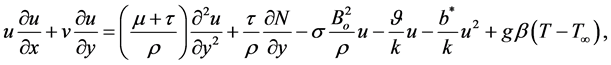(2)

Angular Momentum Equation

(3)

Energy Equation

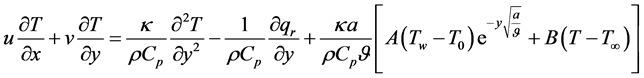(4)

Subject to boundary conditions

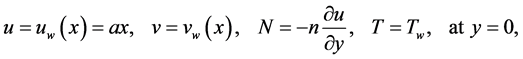(5)

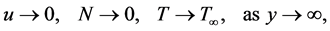(6)

In this study, wall temperature and free stream temperature are defined as

(7)

where u and v are components of velocity in x and y directions respectively, is the wall shrinking or stretching velocity, (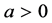) for stretching, (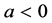) for shrinking and () for static wall, is the wall mass flux velocity, is the fluid density, is the dynamic viscosity, is the kinematic viscosity, is the electrical conductivity, j is the micro-inertial density, is the spin gradient viscosity, is the vortex viscosity, T is the fluid temperature in the boundary layer, is the free

stream temperature, is the thermal expansion coefficient, is the thermal

diffusivity, is the thermal conductivity, is the wall heat flux, n is a constant such that. When, we have the vanishing of anti-symmetric part of the stress tensor and denotes weak concentration of microelements, the case is used for the modeling of turbulent boundary layer flows. This study reports that the case we consider is when (called strong concentration) which represents concentrated particle flows in which the microelements close to the wall are unable to rotate, then, near the wall and N is the micro-rotation or angular velocity whose direction of rotation is in the plane. In this study, a case when is considered.

The Micropolar parameter or material parameter is, for micropolar

fluid and for classical Newtonian fluid. Any of these assumptions is invoked to allow the field of equations that predicts the correct behaviour in the limiting case when the microstructure effects become negligible and the total spin N reduces to the angular velocity Adhikari and Maiti [21] . By the Rosseland approximation the radiative heat flux can be reduced in the form:

(8)

where is the Stefan-Boltzmann constant and is known as the mean absorption coefficient. It should be noted that by using Rosseland approximation, the present study is limited to optically thick fluids. Expanding in a Taylor series about as:

(9)

and then neglecting higher order terms beyond the first degree in, we get

(10)

In view of the Equations (8) and (10), Equation (4) becomes;

(11)

The continuity Equation (1) is satisfied by introducing a stream function such that

(12)

The momentum, angular momentum and energy equations can be transformed into the corresponding ordinary differential equations by the following transformation

(13)

where is the independent dimensionless similarity variable. Thus u and v are given by, substituting variables (13) into Equations (2), (3) and (11), we obtain the following ordinary differential equations:

(14)

(15)

(16)

subject to the boundary conditions (5) and (6) which become;

(17)

(18)

In the above equations, primes denote differentiation with respect to. The dimensionless velocity, angular velocity and temperature are represented as,

and respectively, the characteristic length (Rees and Bassom), the Prandtl number, the magnetic parameter, the constant mass flux with for suction and for injection, the Local Forchheimer parameter, Local Darcy parameter, Porosity parameter, the Modified Local Grashof number, the Stratification parameter, the Radiation parameter. The physical quantities of in-

terest are the skin friction coefficient and the local Nusselt number are defined as;

(19)

where the wall shear stress and the heat flux are given by

(20)

where being the thermal conductivity. Using the similarity variables (13), we get

(21)

3. Homotopy Analysis Method (HAM)

Nonlinear differential equations are usually arising from mathematical modeling of many physical systems. Some of them are solved using numerical methods and some are solved using the analytic methods such as perturbation techniques, Adomian Decomposition and d-expansion method. Generally speaking, it is still difficult to obtain analytical solutions of nonlinear problems. In this research, Homotopy analysis method is considered as a method of solution because of its efficiency as an approximate solution of linear and nonlinear differential equations and also; HAM is valid for strongly nonlinear problems even if a given nonlinear problem does not contain any small/large parameters. Animasaun et al. [22] explained that Homotopy theory was first introduced by Hilton [24] and Homotopy Analysis Method (HAM) was proposed by Liao [23] to obtain better approximate solution of non-linear differential equation if compared with Adomian decomposition. Logically, HAM is believed to contain some analytic techniques such as Adomian’s decomposition method, Lyapunov’s artificial small parameter, and the d-expansion method, which can still be considered as generalized theory of the aforementioned techniques. Unlike the previously mentioned analytic techniques, HAM offers a great freedom to express solutions of a given non-linear problem by means of different base functions. Hence, non-linear problem can be approximated more efficiently by choosing a proper set of base functions, mainly because, the convergence region and rate of a series are determined by the base functions used to express the solution. Furthermore, the HAM provides extremely large freedom to choose initial guess and equation-type of linear sub-problems. It is found in Liao [23] that lots of nonlinear BVPs in science, engineering and finance can be solved conveniently by means of the HAM, no matter whether the interval is finite or not. Let consider a differential equation

(22)

where N is a nonlinear operator, denote independent variable and is an approximate solution of (22) which is an unknown function. Let denote an initial approximation of, is known as auxiliary function and L denote an auxiliary linear operator with the property

(23)

Instead of using the traditional Homotopy

we considered a nonzero auxilary parameter and a nonzero auxilary function to construct a new kind of Homotopy of the form;

(24)

is an embedding parameter and is a function of and q.

When, Equation (24) becomes

(25)

Next step is to find solution of. Making use of (23), RHS of Equation (25) becomes

(26)

Equation (26) is the solution of

When, Equation (24) becomes

(27)

Consider the solution of

Equating to Equation (22)

Algebrically,

(28)

In many cases, by mean of analyzing the physical background and the initial/ boundary conditions of the nonlinear differential problem, we might know what kinds of base functions are proper to represent the solution, even without solving the given nonlinear problem. In view of the boundary conditions (17) and (18), , and can be expressed by the set of base functions of the form

(29)

The solutions, and can be represented in a series form as

(30)

(31)

(32)

In which, and are the coefficients. As long as such a set of base functions are determined, the auxiliary function, the initial approximation, and, and the auxiliary linear operator, and must be chosen in such a way that all solutions of the corresponding high-order deformation of Equations (65), (66) and (67) exist and can be expressed by this set of base functions. This provides us with a fundamental rule on how to choose the auxiliary function, the initial approximation, and, and the auxiliary linear operator, and; this is called the rule of solution expression. This rule plays an important role in the frame of the Homotopy analysis method, as shown in this research. As mentioned above, a real function might be expressed by many different base functions. Thus, their might exist some different kinds of rule of solution expressions and all of them might give accurate approximations for a given nonlinear problem. In this case we might gain the best one by choosing the best set of base functions. As mentioned above, in Homotopy Analysis method we have great freedom to choose the auxiliary linear operator L, the initial approximation, and, and the auxiliary function to construct the zero-order deformation equation. Invoking the rule of solution expressions above for, and on (14), (15) and (16) together with boundary conditions (17) and (18), the initial guesses, and which satisfies both the initial and boundary con- ditions (17) and (18) are;

(33)

Linear operators, and are

(34)

(35)

(36)

The operators, and have the following properties

(37)

In which, , , , , and are constants.

3.1. Zero Order of Deformation

(38)

(39)

(40)

Subject to boundary conditions

(41)

(42)

where the nonlinear operators are defined as

(43)

(44)

(45)

(46)

(47)

when, zero order of deformation Equations (38) to (40) leads to

(48)

With the property

(49)

(50)

(51)

Subject to

(52)

(53)

when, the zero order of deformation Equations (38) to (40) leads to

Based on the fact that and but,

(54)

(55)

(56)

Equating Equations (54) to (56) with Equations (22), we have

(57)

(58)

(59)

Subject to

(60)

(61)

3.2. High Order of Deformation

Expanding, and in Taylor series with respect to the embedding parameter q,

(62)

(63)

(64)

The auxiliary parameters are so properly chosen that the series (62), (63) and (64) converge at. Hence,

(65)

(66)

(67)

For the mth order deformation, differentiate (38) to (40) m times with respect to q, divide by and set, then we have;

(68)

(69)

(70)

Subject to

(71)

(72)

where

(73)

(74)

(75)

And

The general solutions of equations are given by

Here, , and are the particular solutions of Equations (66)- (68). Following the rule of solution expression, the rule of coefficient ergodicity and the rule of solution existence as discussed in [21] we choose auxiliary functions as

(76)

4. Results and Discussion

In order to gain an insight into the behavior of the fluid as it flows, analytic approximate solution of the dimensionless governing equation described in the previous section has been carried out using various values of stratification parameter, Magnetic parameter M, temperature dependent heat source A and B. The accuracy of the adopted method of solution (Homotopy Analysis Method) is achieved by comparing the values of, and at various values of stratification parameter () with the solution of MATLAB package (bvp4c).

Table 1 reveals the comparison and it is important to remark that good agreement is observed. It is noticed from the table that the magnitude of skin friction decreases with an increase in. The magnitude of couple stress increases with an increase in.

In addition, it is also noticed from the table that the magnitude of the local heat transfer rate increases with an increase in.

Pertinent to inquire the effects of variation of, , M and A & B, the numerical results are thus presented in the form of velocity profiles, micro-rotation profiles and temperature profiles in Figures 1-15 for the different values of each parameter. It is very important to remark that the local skin friction coefficient is denoted by, Nusselt number is proportional to local heat transfer rate while couple stress is denoted by. Table 2 shows the convergence of HAM solutions for different order of approximations when, , , , , , , , , , and.

Figures 1-3 represent the velocity, micro-rotation and temperature profiles with variation in the magnitude of thermal stratification parameter. Figure 1 depicts the effects of variation of thermal stratification parameter on velocity profiles of Mi- cropolar fluid in the presence of internal heat source (i.e.), in the pre- sence of magnetic field () and uniform suction (); it is observed that velocity profile decreases with an increase in stratification parameter. It is worth mentioning that increase in the magnitude of stratification parameter corresponds to a decrease in temperature distribution. This can be confirmed in Figure 3. In addition,

this can be traced to the fact that, as increases, the surface temperature within thermally stratified medium ranges from epilimnion to hypolimnion. Physically, this decrease of temperature distribution as the Micropolar fluid flows along a vertical surface may accounts for an increase in the viscosity of the fluid. Consequently, intermolecular forces between the bond of Micropolar fluid becomes stronger and hence account for the decrease in velocity profiles. Infact, it is noticed that the influence of increasing stratification parameter dominates the likely influence of both space- and temperature dependent heat source. This may be traced to the fact that the magnitudes assigned to A & B are 0.4 & 0.2 respectively. In addition, with an increase in stratification parameter, the decrease in temperature profile is more significant near the wall. This result is true since the heat energy around the porous vertical wall is substantial and even greater than that of freestream. This result actually complements the one reported in Ref. [7] . It is also noticed from Figure 2 that increase in the magnitude of stratification parameter makes the micro-rotation distribution to increase near the vertical wall and decrease thereafter as. The increment we noticed near the wall can be traced to the fact that a case () is considered in this study; the micro-elements close to the wall are unable to rotate. Nevertheless, it is noticed that when the maximum value of micro-rotation is estimated as 0.094 (i.e. the micro-rotation increases negligible with an increase in). Figure 4 depicts the effect of micropolar parameter K on micro-rotation profile. It is observed that increase in the magnitude of micropolar parameter K leads to increase in the micro-rotation profile. Likewise, an increase in the magnitude of K corresponds to a decrease in temperature and micro-rotation distributions within the fluid domain (see Figure 5, Figure 6).

Figure 7 reveals the effect of Porosity parameter () on the temperature profiles. It is noticed from Figure 7 that increase in the magnitude of the porosity parameter corresponds to an increase in the temperature of the fluid and thermal boundary layer thickness. It is noted that large values of porosity parameter corresponds to high porosity in porous medium, obviously, increase in the magnitude of the porosity parameter implies that the porous medium is offering more resistance to the fluid flow

and this results in reduction in the velocity distribution and likewise micro-rotation distribution and this also corresponds to reduction in the thickness of velocity boundary layer.

The variation of the dimensionless velocity, micro-rotation, temperature profiles for different values of magnetic parameter M is illustrated in Figures 8-10 respectively. It is observed from Figure 8 that, the velocity distribution decreases as the magnetic parameter increases. This is due to the fact that, the application of a transverse magnetic field normal to the flow direction induces an electric field which gives rise to a resistive force or dragline force called Lorentz force. This force has the tendency to slow down

the velocity of the fluid and angular velocity of micro-rotation in the boundary layer and to increase its temperature. It is observed from Figure 9 that the micro-rotation component increases negligibly near the surface and decreases far away from the surface with an increasing values of magnetic parameter. Figure 10 shows the effect of M on the temperature profile, from this figure, we observe that the temperature increases with the increase in magnetic parameter M.

Figures 11-13 depicts the effect of space-dependent and temperature-dependent heat source parameters A and B. It is shown that increase in A and B leads to an increase in

velocity, micro-rotation and temperature profiles respectively. The presence of the exponential term in the space-dependent heat source is to produce additional heat energy across the fluid region, leading to increase in velocity and temperature of the fluid and also the thickness of the velocity and thermal boundary layer increase. It is revealed in Figure 12 that heat source parameters A and B have noticeable effect on the micro-rotation profile in such a way that, as the value of heat source parameters A and B increases, micro-rotation distribution reduces near the surface and increases away from

the surface. In other words, we can still say that when heat source parameters A and B have increasing positive values, it is observed that substantial heat source will be generated within the fluid domain and hence influence the thermal boundary layer.

Convergence of the Homotopy Solution

It is obvious that the series Equations (65)-(67) consists of the non-zero auxiliary parameters, and which can adjust and control the convergence. The interval on h-axis for which the h-curve becomes parallel to the h-axis is recognized as the

set of admissible values of, and for which the solution series converges. For this purpose, the h-curves are plotted for the 10th-order of approximations in Fig- ures 14-16 when, , , , , , , , , , ,. These figures show that the ranges for the acceptable values of, and are, and. Obviously, from the h-curves for this problem, we obtained the

approximate optimal values of, and at 10th-order of approximation as, and.

5. Conclusions

The study describes free convective boundary layer flow of a conducting micropolar fluid in the presence of exponential space and temperature dependent heat source is analyzed, the set of non-linear ordinary differential equations are then solved by an analytic approximate techniques (Homotopy Analysis Method) and the behaviours of embedded parameters are investigated. The following conclusions are drawn from the

analysis:

1) Velocity profiles and micro-rotation profiles are strongly influenced by the magnetic field in the boundary layer, which decreases with increase in the Magnetic parameter M.

2) Increase in the stratification parameter leads to decrease in both velocity profile and temperature profile. In the presence of space- and temperature-dependent internal heat source and thermal stratification, the micro-rotation profile negligibly increases within the thin layer near the wall.

3) Increasing the value of Micropolar parameter results in increase in micro-rotation profile.

4) Micro-rotation profile has a parabolic distribution when micro-gyration para- meter.

5) Micropolar fluids reduce the shear stresses and enhance couple stress as compared to Newtonian fluids.

6) Variation of stratification parameter result in decrease in the local skin friction coefficient and increase the couples stress and local heat transfer rate respectively.

Cite this paper

Koriko, O.K., Ore- yeni, T., Omowaye, A.J. and Animasaun, I.L. (2016) Homotopy Analysis of MHD Free Convective Micropolar Fluid Flow along a Vertical Surface Embedded in Non- Darcian Thermally-Stratified Medium. Open Journal of Fluid Dynamics, 6, 198-221. http://dx.doi.org/10.4236/ojfd.2016.63016

References