Open Journal of Fluid Dynamics Vol.05 No.01(2015), Article ID:54333,4
pages
10.4236/ojfd.2015.51005
Possibility of a Straightening Flow-Meter by Using Woven Screen
Takahiro Tsuchiya, Yota Koishi, Mitsuo Iwamoto, Hidemi Yamada
Department of Mechanical and Energy Systems Engineering, Oita University, Oita, Japan
Email: yamada@oita-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 February 2015; accepted 23 February 2015; published 28 February 2015
ABSTRACT
In this paper, the possibility of the flow rate measurement for a circular pipe flow by using a woven screen with the property of straightening un-uniform flows is discussed. The resistance coefficient and the flow rate coefficient are estimated from the pressure difference caused by the woven screen under the experiment ranges of the wire Reynolds number, Red = 2.2 × 102 - 1.8 × 103, and of the open area ratio, β = 0.28 - 0.65. As a result, the resistance coefficient decreases and the flow rate coefficient increases as the wire Reynolds number Red or the open area ratio β increases. In addition, both coefficients are not affected by the difference between uniform and turbulent pipe flows approaching the woven screen. Therefore, the possibility of a flow-meter having the property to straighten the un-uniform flow is expected.
Keywords:
Flow Rate Measurement, Woven Screen, Flow-Straightening, Resistance Coefficient

1. Introduction
It is a significant assignment to measure the flow rate exactly in engineering fields using pipe line flows. A flow- meter generally requires a long runway approaching it and/or a straightening device, such as perforated plates, honeycombs or woven screens upstream of it. As for a woven screen, often used to straighten un-uniform flows such as a prejudice flow and a turbulent flow in many engineering fields [1] [2] , there have been a lot of studies on resistance thus far [3] - [10] . In recent years, the requirements of downsizing the apparatus have appeared.
Therefore, an idea of measuring the flow rate by using a woven screen is proposed in this paper, because it is expected that it could play both the role of straightening the flow as well as measuring the flow rate. The possibility as a flow-meter having the ability to straighten an un-uniform flow from the measurements of the flow rate coefficient and resistance coefficient of a woven screen for two different pipe flow fields is discussed.
2. Experimental Approach
Figure 1 shows a summary of this experiment and nomenclature. The experimental apparatus is composed of the entrance nozzle and a straight circular pipe with an inner diameter of D = 42 mm. On the inner wall of the pipe, there are many pressure measurement holes (diameter 0.5 mm) along the flow direction. The woven screen is set at the position L = 210 mm or 1080 mm downstream from the tip of the entrance nozzle. The woven screen is made of stainless steel wires of 1.0 mm diameter and has four open area ratios. The wire Reynolds number, Red, is defined in Equation (1) based on the wire diameter, the velocity averaged in the pipe’s cross section and the kinematic viscosity of the air was varied from 2.2 × 102 to 1.8 × 103.
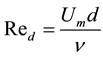 (1)
(1)
Table 1 shows the geometric parameters of woven
screen models used in this study. M is number of the meshes, and β is the open area
ratio defined as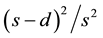 .
Figure 2 shows the velocity distribution in the
pipe’s cross section measured at the positions of L = 1080 mm and 210 mm under the
Reynolds number based on the circular pipe diameter, ReD = 8.3 ×
103 − 8.7 × 104, before the woven screens is set. The
velocity in the pipe is obtained from the pressure difference between total pressure
measured by a small handmade total pressure tube and static pressure taken from
a pressure hole in the position nearest to the tip of the total pressure tube.
.
Figure 2 shows the velocity distribution in the
pipe’s cross section measured at the positions of L = 1080 mm and 210 mm under the
Reynolds number based on the circular pipe diameter, ReD = 8.3 ×
103 − 8.7 × 104, before the woven screens is set. The
velocity in the pipe is obtained from the pressure difference between total pressure
measured by a small handmade total pressure tube and static pressure taken from
a pressure hole in the position nearest to the tip of the total pressure tube.
It is understood that the velocity distributions obtained at the pipe’s cross section in the case of L = 1080 mm are almost consistent with the 1/6-power law as shown in Figure 2(a). Because the inner flow in the case of L = 1080 mm can be regarded as a developed turbulent pipe flow, thereafter it is called “the turbulent pipe flow”. On the other hand, the velocity distributions in the case of L = 210 mm are almost uniform, except in the vicinity of the pipe wall as shown in Figure 2(b). Because the constant velocity region occupies about 70% in the pipe’s cross section, thereafter the inner flow is called “the uniform pipe flow”. For all pressure measurements, a Gottingen type manometer (minimum scale 0.05 mm) is used.
3. Experimental Results and Discussions
3.1. Wall Pressure Distribution
Figure 3 shows a typical example of the x direction distribution of a wall pressure coefficient Cp upstream and downstream of the woven screen. The wall pressure coefficient is defined as
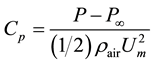 (2)
(2)
Figure 1. Experimental apparatus and coordinate system.
Table 1. Geometric parameters of woven screen models.


Figure 2. Velocity profiles in circular pipe flow. (a) Turbulent pipe flow; (b) Uniform pipe flow.
Figure 3. Wall pressure distribution in circular pipe (β = 0.65, Turbulent pipe flow, Red = 990).
where P is the wall pressure, P∞ is the atmospheric pressure and ρair
is the density of the air. It is noted that the wall pressure varies linearly over
the wide range of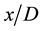 ,
and that a difference in the wall pressure coefficient,
,
and that a difference in the wall pressure coefficient,
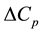 , occurs between
the regions upstream and downstream of the woven screen.
, occurs between
the regions upstream and downstream of the woven screen.
3.2. Resistance Coefficient
Figure 4(a) shows the relationship between the resistance coefficient K and the wire Reynolds number Red. The resistance coefficient K is defined as
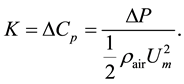 (3)
(3)
The resistance coefficient K decreases as the wire Reynolds number Red and the open area ratio β increase. Although the resistance coefficients K for each β is obtained under two different pipe flow approaching the woven screen, the turbulent flow and the uniform flow, they agree very well. Then, it is noted that the resistance coefficient is not affected by the difference of flow approaching the woven screen. This may be because two approaching-flows become similar to each other by the damming effect which occurs in front of the woven screen. Therefore, it is expected that the woven screen has a property which could straighten the turbulent pipe flow as well as the uniform pipe flow. The black-lines in Figure 4(a) exhibit the approximation of the obtained resistance coefficient K and are given by the following Equation (4), depending on the wire Reynolds number Red and the open area ratio β. They approximate the resistance coefficient K very well.
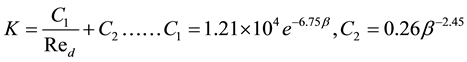 (4)
(4)
3.3. Flow Rate Coefficient
Figure 4(b) shows the variation of the flow rate
coefficient α for the wire Reynolds number Red and the open area ratio
β. The flow rate coefficient α is derived from general formulas,
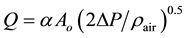 , where Ao
is the open area of the woven screen. The flow rate coefficient α increases as the
wire Reynolds number Red and the open area ratio β increases. In addition,
it was noticed that the flow rate coefficient α obtained in two different pipe flows,
the turbulent pipe flow and the uniform pipe flow, are close to each other. On the
other hand, the flow rate coefficient α can be calculated from the wall pressure
difference based on the following Equation (5), where A is the pipe cross-sectional
area.
, where Ao
is the open area of the woven screen. The flow rate coefficient α increases as the
wire Reynolds number Red and the open area ratio β increases. In addition,
it was noticed that the flow rate coefficient α obtained in two different pipe flows,
the turbulent pipe flow and the uniform pipe flow, are close to each other. On the
other hand, the flow rate coefficient α can be calculated from the wall pressure
difference based on the following Equation (5), where A is the pipe cross-sectional
area.
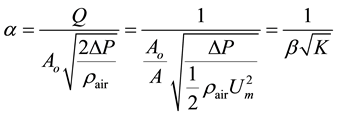 (5)
(5)
The black-lines in Figure 4(b) are converted from the black-lines in Figure 4(a), and agree with the experimental results of the flow rate coefficient α.
3.4. Reconfirmation from Direct Pressure Drop
Generally, in the case of the flow rate measurement using the pressure difference,
the pressure difference
 is decided as the wall pressure drop between the front and the back of a device’s
position. Therefore, the measurement of the pressure drop in the case of the transient
pipe flow was attempted in the vicinity of the woven screen as shown in Figure 5. Because the pressure drop coefficient
is decided as the wall pressure drop between the front and the back of a device’s
position. Therefore, the measurement of the pressure drop in the case of the transient
pipe flow was attempted in the vicinity of the woven screen as shown in Figure 5. Because the pressure drop coefficient
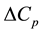 measured between two positions nearest to the woven screen, x = −1.05 D and 0.10
D, is fairly larger than the
measured between two positions nearest to the woven screen, x = −1.05 D and 0.10
D, is fairly larger than the

4. Conclusion
The resistance coefficient K and the flow rate coefficient α of the woven screen placed in the circular pipe were experimentally investigated. As a result, although the flow rate coefficient α varies depending on the wire Reynolds number Red and the open area ratio β increases, both coefficients is not affected by the difference between


Figure 4. Influence of Reynolds number and open area ratio. (a) Resistance coefficient; (b) Flow rate coefficient.
Figure 5. Wall pressure distribution in circular pipe (β = 0.65, Transient pipe flow, Red = 880).
a uniform and a turbulent pipe flows approaching the woven screen. Therefore, the possibility of a flow-meter having the ability of straightening an un-uniform flow can be expected. Furthermore, considering the pressure measurement points, the numbers of woven screens and/or combination with perforated plates and honeycombs, its ability as a straightening flow-meter will rise.
References
- Makita, H. (2002) Turbulence Wind Tunnel (Wind Tunnel Experiments). Journal of Japan Society of Fluid Mechanics, 21, 409-418. (In Japanese) http://dx.doi.org/10.11426/nagare1982.21.409
- Masaki, D., Futamura, H. and Nishizawa, T. (2010) Design of JAXA TechClean Fan Stage (Base Configuration). JAXA (Japan Aerospace Exploration Agency) Research and Development Report, 10, 1-16. (In Japanese)
- Wieghardt, K.E.G. (1953) On the Resistance of Screens. The Aeronautical Quarterly, 4, 186-192.
- Armour, J.C. and Cannon, J. (1968) Fluid Flow through Woven Screens. AIChE Journal, 14, 415-420.
- Sodré, J.R. and Parise, J.A.R. (1997) Friction Factor Determination for Flow through Finite Wire-Mesh Woven-Screen Matrices. Journal of Fluids Engineering, 119, 847-851.
- Hamaguchi, K., Magara, Y. and Yamashita, I. (2004) Effects of Stacking Method on Pressure Loss and Heat Transfer Characteristics in Stacked Wire Gauze. The Japan Society of Mechanical Engineers, 70, 187-194. (In Japanese)
- Shiozaki, T., Maruyama, S., Mohri, T. and Hosumi, Y. (2005) Fluid Flow Characteristics through a Wire Mesh at Low Reynolds Number for High Temperature Air Combustion Furnace. The Japan Society of Mechanical Engineers, 71, 163-166. (In Japanese)
- Wu, W.T., Liu, J.F. and Hsieh, W.H. (2005) Measurement and Correlation of Hydraulic Resistance of Flow through Woven Metal Screens. International Journal of Heat and Mass Transfer, 48, 3008-3017. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2005.01.038
- Kołodziej, A., Łojewska, J., Jaroszy?ski, M., Gancarczyk, A. and Jodłowski, P. (2012) Heat Transfer and Flow Resistance for Stacked Wire Gauzes: Experiments and Modelling. International Journal of Heat and Fluid Flow, 33, 101- 108. http://dx.doi.org/10.1016/j.ijheatfluidflow.2011.11.006
- Fischer, A. and Gerstmann, J. (2013) Flow Resistance of Metallic Screens in Liquid, Gaseous and Cryogenic Flow. 5th European Conference for Aero-Space Science, München, 1-5 July 2013, 1-12.





