Open Journal of Fluid Dynamics
Vol.04 No.04(2014), Article ID:52651,11 pages
10.4236/ojfd.2014.44030
Dynamics of Drainage of Power-Law Liquid into a Deformable Porous Material
Javed I. Siddique1, Forrest A. Landis2, Muhammad R. Mohyuddin3,4
1Department of Mathematics, Pennsylvania State University, York Campus, York, USA
2Department of Chemistry, Pennsylvania State University, York Campus, York, USA
3Department of Mathematics, FAST University, Islamabad, Pakistan
4NCBA & E, Gujrat, Pakistan
Email: jis15@psu.edu, fal100@psu.edu, m_raheel@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 October 2014; revised 22 November 2014; accepted 20 December 2014
ABSTRACT
In this study we explore the one-dimensional drainage of a power-law fluid into a deformable porous material. Initially, the fluid is imbibed into the dry undeformed material due to capillary suction which in turn deforms the porous material and forms liquid and solid interfaces. Mixture theory is employed to study the movement of the liquid and solid phases. The zero-gravity model contains the similarity solution that is solved numerically. The stress gradient within the deformable porous material is induced from a pressure gradient that produces an evolving solid fraction and hence deformation. In the absence of gravity effects, the deformation of the solid seems in the same direction of imbibition. This is because of attraction of gravity. Note that these liquid and solid dynamics depend on both the power-law indexes n and m. We performed the experiments to measure the drainage and deformations of deformable porous materials for two samples of silicon oil (polydimethylsiloxane) in a polyurethane foam. Our experiments show that the silicon with high viscosity drains slower than silicon oil with low viscosity. The theoretical and experimental results show the same qualitative trend.
Keywords:
Power Law Fluid, Mixture Theory, Deformable Porous Material

1. Introduction
In this study we develop a model for the drainage of a power law liquid into deformable porous materials. The motivation of this work is connected to many scientific fields, such as oil recovery, inkjet printing, textile engineering, soil consolidation, reservoir engineering and biomechanics. The movement of fluid through the porous materials swells the porous material which in turn affects the flow of fluid. This alteration in fluid flow and deformation of the porous material identifies the complexity and importance of these flows. Interestingly enough, most of the fluids involved in these processes are not Newtonian in nature and hence should be incorporated in the complex dynamics of deformation. To accommodate this need, we present a coupled model for deformation of porous material and drainage of power law fluids.
An overview of literature shows that the deformation of porous materials couple with fluid flow goes back to Terzaghi [1] . This idea was later extended by Biot [2] [3] to study soil consolidation. Later on, mixture theory [4] [5] was introduced to enhance the understanding of material deformation causes by fluid imbibition. Some of the biological applications that use the mixture theories include articular cartilage [6] - [12] , arterial tissue [13] - [16] and skin [17] . Note that most of the fluids involved in the above referenced biological studies possess non- Newtonian properties and therefore, non-Newtonian properties must be incorporated with the mixture theory in future studies.
Most industrial applications (e.g. composite materials, paper and inkjet printing, and dyeing of colored fabrics) involve fluids that are non-Newtonian. In an effort to address this behavior, Sommer and Mortensen [18] studied a forced unidirectional infiltration of deformable porous materials. They considered a constant pressure driven flow in an initially dry sponge like material and an agreement between theory and experiment was reported. A similar model of an infiltration of an incompressible liquid into an initially dry porous material was developed by Preziosi et al. [19] , where they allowed the porous material to deform and relax. Another study that uses mixture theory to model the imbibition of a liquid droplet on a deformable substrate in a one dimensional setting was presented by Anderson [20] . In the absence of gravity effects, the imbibition causes swelling, swelling relaxation and shrinking of a porous material.
The history of capillary rise into porous media goes back to the classical model first presented by Washburn [21] . This model shows that the amount of liquid imbibed into a porous material is proportional to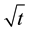 . To validate the Washburn model, Zhmud et al. [22] and Lago and Araujo [23] presented an experimental and theoretical model of capillary rise into porous materials. Their results are consistent with the Washburn model for initial times and deviate from this trend for long times. Following these studies, Siddique et al. [24] presented an analog of the Washburn model of capillary rise. Mixture theory has been used to take into account the deformation of porous materials.
. To validate the Washburn model, Zhmud et al. [22] and Lago and Araujo [23] presented an experimental and theoretical model of capillary rise into porous materials. Their results are consistent with the Washburn model for initial times and deviate from this trend for long times. Following these studies, Siddique et al. [24] presented an analog of the Washburn model of capillary rise. Mixture theory has been used to take into account the deformation of porous materials.
The non-Newtonian modeling along with the mixture theory was studied by Siddique and Anderson [25] . In particular, they studied the capillary rise of a power law fluid into a deformable porous material, where they assumed imbibition occurring from an infinite bath of power law fluid. When gravity effects are present, both liquid and solid interface positions reach equilibrium heights depending upon the power law index n. This study mimics only one particular aspect of capillary rise; however the need is to extend the current power law model along with mixture theory to explore many other physical settings. In this study we explore the drainage of a finite amount of liquid into deformable porous materials in the presence and absence of gravity effects.
There are many types of non-Newtonian fluid models, e.g. Herschel-Bulkley fluid, power law and differential fluid type, etc. These fluid models have been widely used in a variety of settings to analyze various physical aspects. Most relevant ones are Christopher and Middleman [26] , Sadowski [27] and Hayes et al. [28] . These studies explained some of the important aspects of porous medium flow based on power law model but there are still important phenomena to explain and clarify. The current study is an effort to model the power law fluid with mixture theory (for details see [25] ).
In this paper, we study the drainage of a power law fluid into deformable porous material. The initial height  of fluid is modeled via an Equation. Our experiments of drainage of silicon oil with low and high viscosity into deformable porous material encouraged us to present a mathematical model that can be used to predict the similar dynamics of drainage. We do this by following Siddique et al. [24] [25] . We hope that our preliminary efforts in this regard may lead to further investigate the additional features of flows in complex porous media.
of fluid is modeled via an Equation. Our experiments of drainage of silicon oil with low and high viscosity into deformable porous material encouraged us to present a mathematical model that can be used to predict the similar dynamics of drainage. We do this by following Siddique et al. [24] [25] . We hope that our preliminary efforts in this regard may lead to further investigate the additional features of flows in complex porous media.
2. Experiment
A sample of polyurethane foam (pore size ca. 50 - 150 mm (Figure 1)) was cut into a 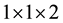 cm piece. The foam was then inserted into a 1 cm2 plastic cuvette with a hole drilled in the bottom to allow for drainage. The foam fit just snuggly in the cuvette so that liquid could not flow around the foam, but little compression of the
cm piece. The foam was then inserted into a 1 cm2 plastic cuvette with a hole drilled in the bottom to allow for drainage. The foam fit just snuggly in the cuvette so that liquid could not flow around the foam, but little compression of the
Figure 1. Optical micrograph of a cross-section of the polyurethane foam.
foam occurred which would alter the drainage of the liquid (Figure 2). Two samples of silicon oil (polydimethylsiloxane) were used as the drainage fluid: a low viscosity sample (10 cPs) and a high viscosity sample (1000 cPs). Since these non-Newtonian silicon oils have identical chemical structure, their molecular interaction with the foam should also be identical; however, they have different molar masses, which is manifested in their differences in viscosity. Only these differences in viscosity should affect their drainage through the foam. A single grain of solid iodine was dissolved in both silicon oils to provide contrast with the foam and aid in the determination of the movement of the oils through the foam. It is not expected that the presence of the iodine will alter the drainage of the oils. 1 mL of the dyed silicon oil was injected into the top of the cuvette and it began to drain into the foam. A digital camera operating at 30 frames per second and a resolution of 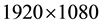 pixels was used to record the flow of the silicon oils through the foam. Using the images produced by the camera, the position (in pixels) of the oil above the foam,
pixels was used to record the flow of the silicon oils through the foam. Using the images produced by the camera, the position (in pixels) of the oil above the foam, 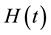 , the foam interface position,
, the foam interface position, 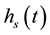 , and the liquid interface,
, and the liquid interface, 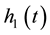 , were determined as a function of time (Figure 2). The distance in pixels was converted to distance in mm using the length of the cuvette (1 cm) as a scale. The experiment was concluded when the level of the silicon above the foam reached the level of the foam.
, were determined as a function of time (Figure 2). The distance in pixels was converted to distance in mm using the length of the cuvette (1 cm) as a scale. The experiment was concluded when the level of the silicon above the foam reached the level of the foam.
Experimental Results
Figure 2 shows a representative drainage experiment using the high viscosity silicon oil as the fluid. The beginning point (0 s in Figure 2) was chosen as the image where all of the 1 mL volume of silicon oil had been added to the cuvette. As the experiment continued, the height of the liquid above the foam, 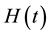 , and the liquid interface position,
, and the liquid interface position, 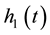 , both dropped as the oil absorbed into the foam (10 s and 30 s in Figure 2). This experiment was terminated when all of the silicon oil had penetrated into the foam (when
, both dropped as the oil absorbed into the foam (10 s and 30 s in Figure 2). This experiment was terminated when all of the silicon oil had penetrated into the foam (when 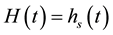 at ca. 100 s). The positions of each of the three interfaces are plotted as a function of time in Figure 3 for both the low and high viscosity silicon oils. It took approximately 4 s for the low viscosity oil to completely drain into the foam while the higher viscosity oil took significantly longer at 100 s.
at ca. 100 s). The positions of each of the three interfaces are plotted as a function of time in Figure 3 for both the low and high viscosity silicon oils. It took approximately 4 s for the low viscosity oil to completely drain into the foam while the higher viscosity oil took significantly longer at 100 s.
It should be noted that no measurable expansion of the foam was observed (i.e., 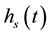 was constant) for these foams when imbibed with either silicon oil. This is in contrast to drainage experiments where low molar
was constant) for these foams when imbibed with either silicon oil. This is in contrast to drainage experiments where low molar
Figure 2. Representative photographs showing the drainage of the high viscosity silicon oil into the polyurethane foam at different time intervals. The liquid height above the foam, the foam height, and the liquid interface are labeled (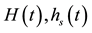 , and
, and , respectively).
, respectively).
Figure 3. This figure shows the dynamics behavior where the curves are shown in dimensional form. The dashed curves shows the initial height as a function of time


mass alcohols such as ethanol were used. While ethanol has similar rapid drainage characteristics to the low viscosity silicon oil, it differed in that it also caused a significant expansion of the foam. Ethanol is a polar liquid that can interact strongly with the polyurethane foam causing expansion. In contrast, the silicon oil is essentially nonpolar and will not interact strongly with the foam resulting in little expansion. Clearly the expansion of the foam is very dependent on the nature of the intermolecular interactions between the foam and the liquid and will be examined in future research efforts.
Figure 3 shows the dynamics behavior of the low and high viscosity silicon oils into the polyurethane foam. Here the curves are shown in dimensional form. The dashed curves shows the initial height as a function of time


3. Mathematical Modeling
The basic geometrical description for our problem is shown in Figure 4. We consider a finite amount of a non- Newtonian liquid with an initial height defined as 







The above dimensionless quantities suggest the following time and length scales after balancing the terms in
both momentum equations 

law index 







Figure 4. Problem configuration at 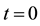

and 

where
Note, setting 






where 




Equations (3) and (4) represent mass balances and Equations (5) and (6) are momentum balances for the solid and liquid phases (see [25] ). The set of parameters in these Equations can be divided into two categories, first set of parameters inside the wet material regions such as the solid volume fraction






We follow the same procedure as was followed in Anderson (2005), Siddique et al. [24] , and Siddique and Anderson [25] to obtain the partial differential equation for the solid volume fraction 

The appropriate boundary conditions for the solid volume fraction are


In the derivation of boundary condition (8), we integrate Equation (6) after substituting 

where 
The boundary conditions at the liquid-wet material interface 



where 
The kinematic and pressure boundary conditions at wet-material-dry material interface 


where 
Boundary conditions (11) and (14) transform to ordinary differential Equations for the solid and liquid interfaces


where

If we take 


4. Gravity Independent Solution
In the absence of gravity effects, Equation (7) admits the solution in terms of a similarity variable


subject to the boundary conditions 











The non-linear ODE (19) along with the non-linear Equations (20) and (21) is solved numerically. The ODE and non-linear Equations are discretized using finite difference and midpoint rule yielding a system of non-linear Equations. This coupled system of non-linear Equations is solved numerically. We will present the solution of zero gravity case in the results section. It is worthwhile highlighting that this numerically computed zero gravity solution will be used as an initial condition for non-zero gravity case which we will discuss in the section below.
5. Non-Zero Gravity Solution
In the presence of gravity effects, we will first transform the moving domain problem given by (7) along with (16) and (17) to fixed domain using the following transformation

This helps transforming the moving domain problem 





6. Results
Our results are based on a specific set of test fluids for which power-law index 













In the beginning of the process, a finite amount of liquid is supplied, whose height is shown by 











Figure 5. The plots show the drainage of Newtonian and non-Newtonian liquids. Top left shows the comparison between 











index 










In order to connect our theoretical predictions with experiments, we performed drainage of silicon oil of two different viscosities with identical chemical structure into deformable sponge like materials. Our experimental predictions show a similar trend for drainage and deformation of deformable porous materials. The drainage of water into deformable porous material follow approximately 




Figure 6. This plot shows the comparison of drainage of Newtonian fluid with non-Newtonian fluid for different power-law index. The curves as labeled


7. Discussion
In this present work we have presented a basic model for predicting the drainage of a power law liquid into a deformable porous material. More specifically, we transform the capillary rise theory developed for power law liquids into deformable porous materials [24] to the drainage setting by specifying liquid height [25] via an equation based on conservation of liquid argument. In addition to theoretical predictions, this work includes a set of experiments showing the similar behavior as shown in our numerically simulations. In this study we use the mixture theory [15] [16] [18] - [20] [24] [25] to model the problem of drainage of power law liquid into deformable porous material.
In the absence of gravity effects, the deformation of the porous material and the penetration of liquid follows
a different power law behavior 
both 






The present study is preliminary, but suggests some interesting possibilities in the theory of drainage of power law fluid. An interesting area to explore in future investigations would be the use of a more generalized function for solid stress 



Acknowledgements
The author J. I. Siddique greatly appreciate the support of Simons Foundation Grant No. 281839.
References
- Terzaghi, K. (1925) Erdbaumechanik auf Bodenphysikalischen Grundlagen. Deuticke, Wien.
- Biot, M.A. (1955) Theory of Elasticity and Consolidation for a Porous Anisotropic Solid. Journal of Applied Physics, 26, 182-185. http://dx.doi.org/10.1063/1.1721956
- Biot, M.A. (1962) Mechanics of Deformation and Acoustic Propogation in Porous Media. Journal of Applied Physics, 33, 1482-1498.
- Atkin, R.J. and Crain, R.E. (1976) Continuum Theories of Mixture: Basic Theory and Historical Development. Quarterly Journal of Mechanics and Applied Mathematics, 29, 209-244. http://dx.doi.org/10.1093/qjmam/29.2.209
- Bowen, R.M. (1980) Incompressible Porous Media Models by Use of the Theory of Mixtures. International Journal of Engineering Science, 18, 1129-1148. http://dx.doi.org/10.1016/0020-7225(80)90114-7
- Lai, W.M. and Mow, V.C. (1980) Drag Induced Compression of Articular Cartilage during a Permeation Experiment. Biorheology, 17, 111-123.
- Holmes, M.H. (1983) A Nonlinear Diffusion Equation Arising in the Study of Soft Tissue. Quarterly of Applied Mathematics, 41, 209.
- Holmes, M.H. (1984) Comparison Theorems and Similarity Solution Approximations for a Nonlinear Diffusion Equation Arising in the Study of Soft Tissue. SIAM Journal on Applied Mathematics, 44, 545-556. http://dx.doi.org/10.1137/0144037
- Holmes, M.H. (1985) A Theoretical Analysis for Determining the Nonlinear Hydraulic Permeability of a Soft Tissue from a Permeation Experiment. Bulletin of Mathematical Biology, 47, 669-683. http://dx.doi.org/10.1007/BF02460132
- Holmes, M.H. (1986) Finite Deformation of Soft Tissue: Analysis of a Mixture Model in Uni-Axial Compression. Journal of Biomechanical Engineering, 108, 372-381. http://dx.doi.org/10.1115/1.3138633
- Holmes, M.H. and Mow, V.C. (1990) The Nonlinear Characteristic of Soft Gels and Hydrated Connective Tissue in Ultrafiltration. Journal of Biomechanics, 23, 1145-1156. http://dx.doi.org/10.1016/0021-9290(90)90007-P
- Hou, J.S., Holmes, M.H., Lai, W.M. and Mow, V.C. (1989) Boundary Conditions at the Cartilage-Synovial Fluid Interface for Joint Lubrication and Theoretical Verifications. Journal of Biomechanical Engineering, 111, 78-87. http://dx.doi.org/10.1115/1.3168343
- Kenyon, D.E. (1976) The Theory of an Incompressible Solid-Fluid Mixture. Archive for Rational Mechanics and Analysis, 62, 131-147.
- Klanchar, M. and Tarbell, J.M. (1987) Modelling Water Flow through Arterial Tissue. Bulletin of Mathematical Biology, 49, 651-669. http://dx.doi.org/10.1007/BF02481766
- Barry, S.I. and Aldis, G.K. (1992) Flow Induced Deformation from Pressurized Cavities in Absorbing Porous Tissues. Bulletin of Mathematical Biology, 54, 977-997. http://dx.doi.org/10.1007/BF02460662
- Barry, S.I., Parker, K.H. and Aldis, G.K. (1991) Fluid Flow over a Thin Deformable Porous Layer. Journal of Applied Mathematics and Pysics (ZAMP), 42, 633-648.
- Oomens, C.W.J., Van Campen, D.H. and Grootenboer, H.J. (1987) A Mixture Approach to the Mechanics of Skin. Journal of Biomechanics, 20, 877-885. http://dx.doi.org/10.1016/0021-9290(87)90147-3
- Sommer, J.L. and Mortensen, A. (1996) Forced Unidirectional Infiltration of Deformable Porous Media. Journal of Fluid Mechanics, 311, 193-217. http://dx.doi.org/10.1017/S002211209600256X
- Preziosi, L., Joseph, D.D. and Beavers, G.S. (1996) Infiltration of Initially Dry, Deforamable Porous Media. International Journal of Multiphase Flow, 22, 1205-1222. http://dx.doi.org/10.1016/0301-9322(96)00035-3
- Anderson, D.M. (2005) Imbibition of a Liquid Droplet on a Deformable Porous Substrate. Physics of Fluids, 17, Article ID: 087140. http://dx.doi.org/10.1063/1.2000247
- Washburn, E.W. (1921) The Dynamics of Capillary Flow. Physical Review, 17, 273-283. http://dx.doi.org/10.1103/PhysRev.17.273
- Zhmud, B.V., Tiberg, F. and Hallstensson, K. (2000) Dynamic of Capillary Rise. Journal of Colloid and Interface Science, 228, 263-269. http://dx.doi.org/10.1006/jcis.2000.6951
- Lago, M. and Araujo, M. (2001) Capillary Rise in Porous Media. Journal of Colloid and Interface Science, 234, 35-43. http://dx.doi.org/10.1006/jcis.2000.7241
- Siddique, J.I., Anderson, D.M. and Bondarev, A. (2009) Capillary Rise of Liquid into Deformable Porous Material. Physics of Fluids, 21, Article ID: 013106. http://dx.doi.org/10.1063/1.3068194
- Siddique, J.I. and Anderson, D.M. (2011) Capillary Rise of Non-Newtonian Liquid into Deformable Porous Material. Journal of Porous Media, 14, 1087-1102. http://dx.doi.org/10.1615/JPorMedia.v14.i12.40
- Christopher, R.H. and Middlemen, S. (1965) Power-Law Flow through a Packed Tube. Industrial & Engineering Chemistry Fundamentals, 4, 422-426. http://dx.doi.org/10.1021/i160016a011
- Sadowski, T.J. (1963) Non-Newtonian Flow through Porous Media. Ph.D. Thesis, University of Winconsin, Madison.
- Hayes, R.E., Afacan, A., Boulanger, B. and Shenoy, A.V. (1996) Modeling the Flow of Power Law Fluids in a Packed Bed Using a Volume-Averaged Equations of Motion. Transport in Porous Media, 41, 175-196.
- Missirlis, K.A., Assimacopoulos, D., Mitsoulis, E. and Chhabra, R.P. (2001) Wall Effects for Motion of Spheres in Power-Law Fluids. Journal of Non-Newtonian Fluid Mechanics, 96, 459-471.


















