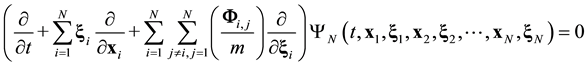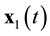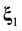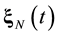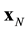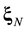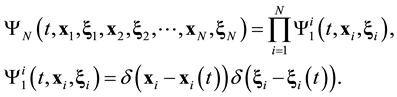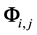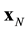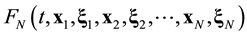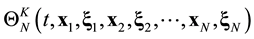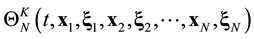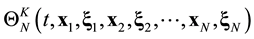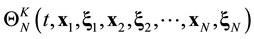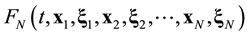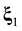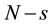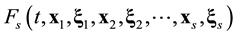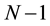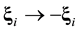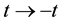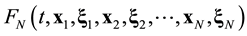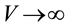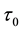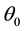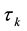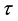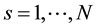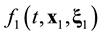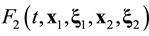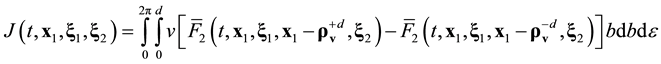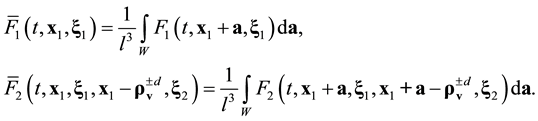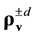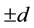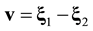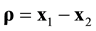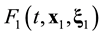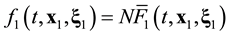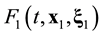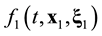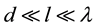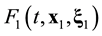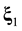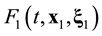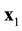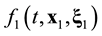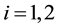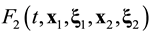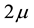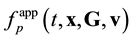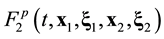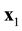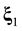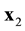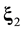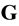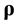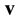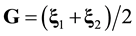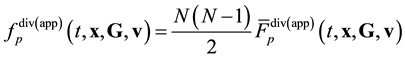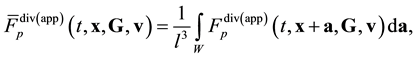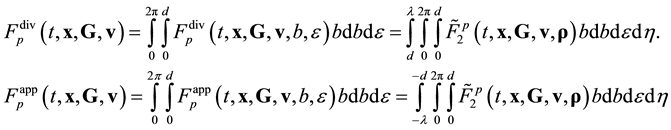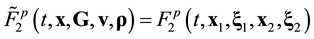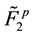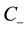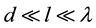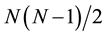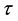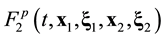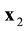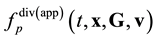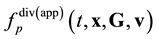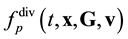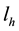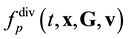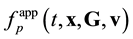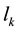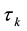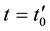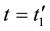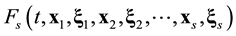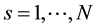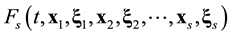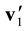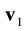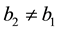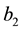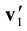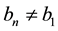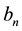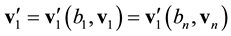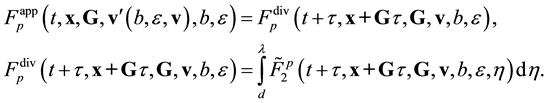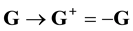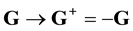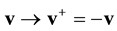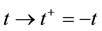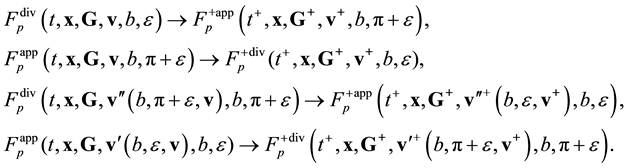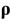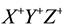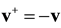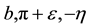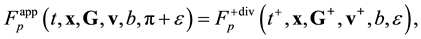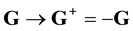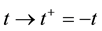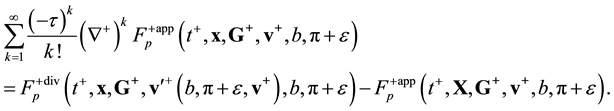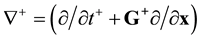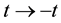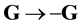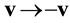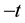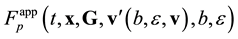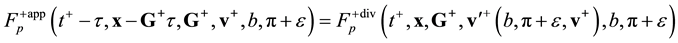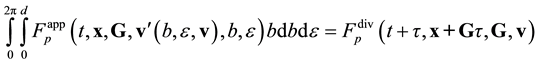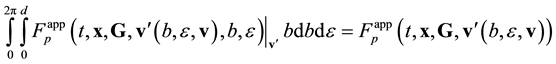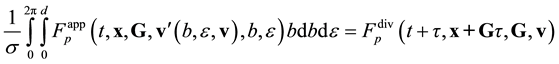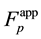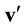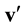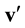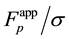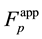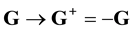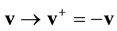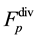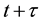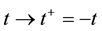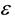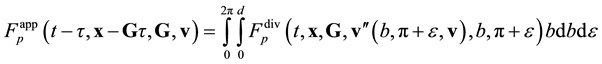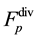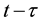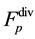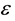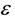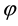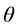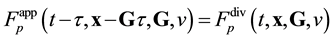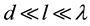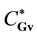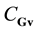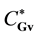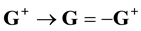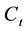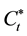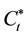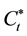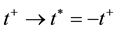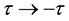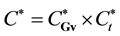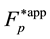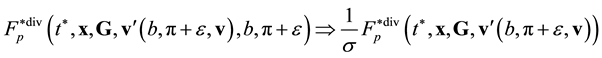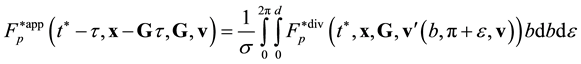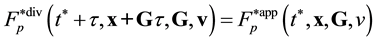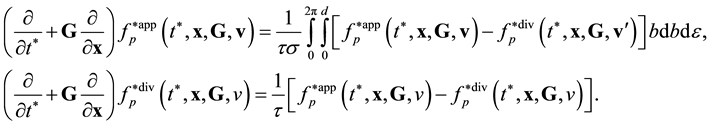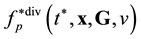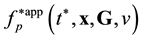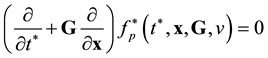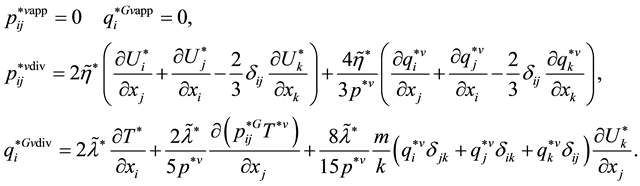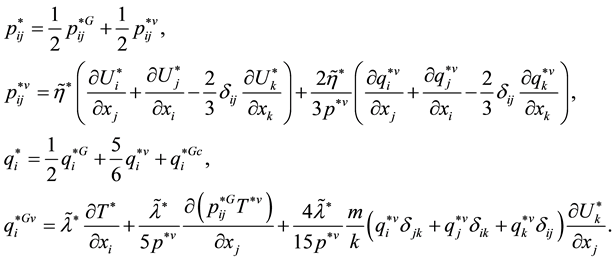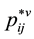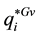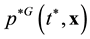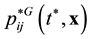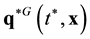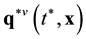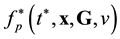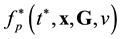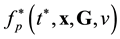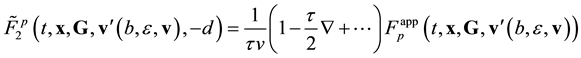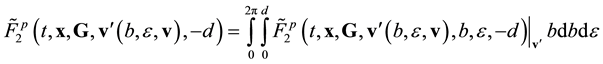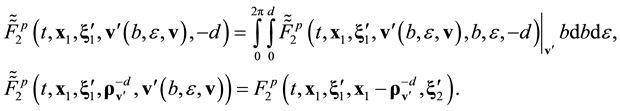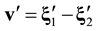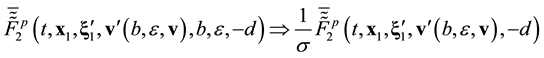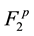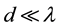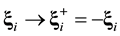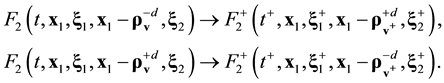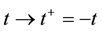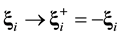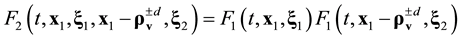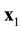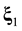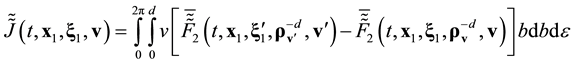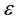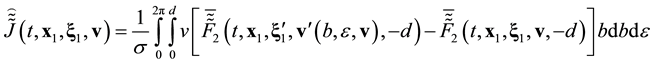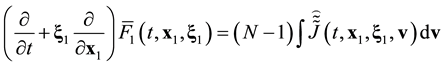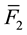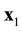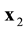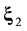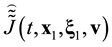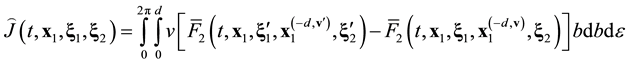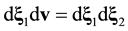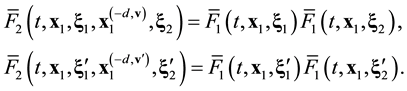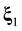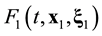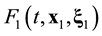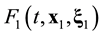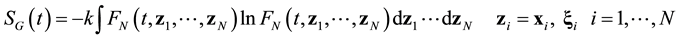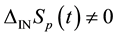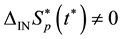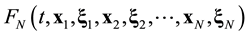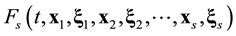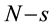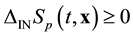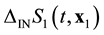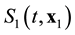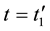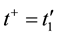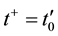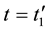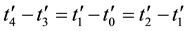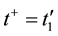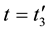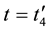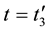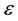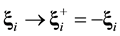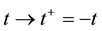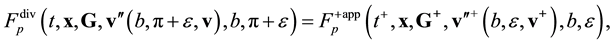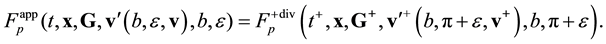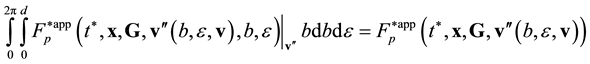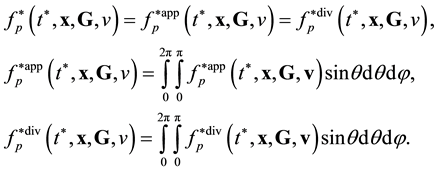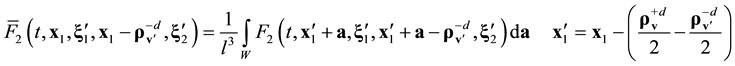Open Journal of Fluid Dynamics
Vol.04 No.03(2014), Article ID:49697,23 pages
10.4236/ojfd.2014.43023
About Appearance of the Irreversibility
Igor
V.
Lebed
Zhukovsky Central Institute of Aerohydrodynamics, Moscow, Russia
Email: lebed-i@newmail.ru
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 July 2014; revised 24 August 2014; accepted 10 September 2014
ABSTRACT
The inevitability of arising in equations of kinetics and hydrodynamics irreversibility not contained in original equations of classic mechanics is substantiated. It is established that transfer of information about the direction of system evolution from initial conditions to resulting equations is the consequence of losing information about the position of an individual particle in space, which takes place at roughening description. It is shown that the roughening with respect to impact parameters of colliding particles is responsible for appearance of the irreversibility in resulting equations. Direct equations of kinetics and hydrodynamics are the result of roughening distribution functions with respect to impact parameters of particles, which have not yet reached the domain of their interaction. The direct equations are valid for the progressive direction of timing on the time axis pointing from the past to the future. Reverse equations of kinetics and hydrodynamics are the result of roughening distribution functions with respect to impact parameters of particles, which have already left the domain of their interaction. The reverse equations are valid for the progressive direction of timing on the time axis pointing from the future to the past.
Keywords:
Irreversibility, Direct Equations, Reverse Equations, Instability, Multimoment Hydrodynamics

1. Introduction
The detailed comparison of the results of direct numerical integration of the Navier-Stokes equations with the experimental data in the problem on flow around a sphere is given in [1] . The comparison demonstrated that the solutions to the classic hydrodynamics equations interpret successfully the experiment until a first critical
Reynolds
number value is reached. However, after passing first critical
Reynolds
number value, these solutions become inapplicable to interpreting the instability [1] . In accordance with ideas given in [1] -[3] the solutions to the classic hydrodynamics equations attain successfully the boundary of the instability field. However, these solutions are unable to cross this boundary and, consequently, enter the instability field.
The problems encountered by classic hydrodynamics when interpreting observed evolution of unstable process, are proposed to be solved on the way toward an increase in the number of principle hydrodynamic values [4] . In [5] -[8] , the multimoment hydrodynamics equations are used to study the phenomena of instability appearance and development in problem on flow around a solid sphere at a wide range of
Reynolds
number values.
The studies [5] -[8] demonstrated that when interpreting each of unstable regimes in problem on flow around a sphere the need emerges to involve the so-called reverse multimoment hydrodynamics equations [9] . The evolution of the system after losing its stability that is described by the direct hydrodynamics equations advances in direction of the system departure from the statistical equilibrium state. The evolution of the system after losing its stability that is described by the reverse hydrodynamics equations advances in direction of the system approaching the statistical equilibrium state.
Both the direct and the reverse multimoment hydrodynamics equations are irreversible. The main purpose of the present work is to elucidate the physical meaning of appearance of the irreversibility in equations of kinetics and hydrodynamics.
A.
Einstein
believed that irreversibility is not a fundamental law of nature, as far as it is not incorporated in the basic laws of physics represented by original equations. He saw no reasons for emergence of the irreversibility in the resulting equations as a result of any transformation of original equations because the initial conditions are responsible for one or another direction of evolution. Thus,
A.
Einstein
believed that appearance of the irreversibility in resulting equations is not sufficiently substantiated [10] . Unlike
A.
Einstein
, I. Prigogine treated, the irreversibility, as a fundamental law of nature. I.
Prigogine
introduced the irreversibility into original equation, thereby, like
A.
Einstein
, he denied the feasibility of achieving the irreversibility when starting with the original equations [11] .
The present work shows that during transition from the classic mechanics equations to equations of kinetics and hydrodynamics the irreversibility is incapable not to appear, it must appear. By another words, the present work substantiates appearance of the irreversibility in resulting equations. Section 2 recounts the ideas on levels and stages that specify the degree of accuracy for medium description. Section 3 represents the only roughening operation, which is responsible for appearance of the irreversibility in kinetics and hydrodynamics equations. The necessity to introduce this roughening operation is substantiated.
2. Medium Description Levels and Stages
Suppose that some physical system consists of N structureless particles. Let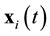 ,
,  ,
, 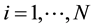 , represent respectively the coordinates and velocities of the particles, i.e., the point in 6N-dimensional phase space. The evolution of the variables
, represent respectively the coordinates and velocities of the particles, i.e., the point in 6N-dimensional phase space. The evolution of the variables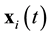 ,
, 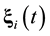 ,
, 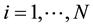 , is calculated in the frameworks of the equations of classic mechanics. Let us carry out at some time t the inversion in velocity space and in time,
, is calculated in the frameworks of the equations of classic mechanics. Let us carry out at some time t the inversion in velocity space and in time, 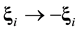 ,
, 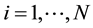 ,
,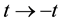 . It turns out that the classic mechanics equations are invariant with respect to this operation, that is, the equations of classic mechanics are reversible. This means the following. Let at time t0 the initial conditions
. It turns out that the classic mechanics equations are invariant with respect to this operation, that is, the equations of classic mechanics are reversible. This means the following. Let at time t0 the initial conditions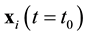 ,
, 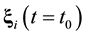 ,
, 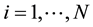 , are specified. Let by the time
, are specified. Let by the time 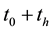 the equations of classic mechanics transfer them into
the equations of classic mechanics transfer them into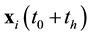 ,
, 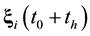 ,
, 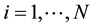 , respectively. Then, after inversion at time
, respectively. Then, after inversion at time![]() , the equations of classic mechanics transfer the conditions
, the equations of classic mechanics transfer the conditions![]() ,
, ![]() ,
, ![]() , into the conditions
, into the conditions![]() ,
, ![]() ,
, ![]() , by the time t0. Having once more the operation of inversion, make sure that the equations of classic mechanics returned the system to the same point of the phase space from which they took her.
, by the time t0. Having once more the operation of inversion, make sure that the equations of classic mechanics returned the system to the same point of the phase space from which they took her.
Having described by classic mechanics equations the motion of each system particle, we will be able to calculate any macroscopic characteristic of system at any time moment, i.e., to describe the evolution of system as a whole. This description corresponds to the dynamic deterministic level. This level is the most complete and overly detailed. As a rule, the necessity in such a detailed description does not occur. When solving practical tasks we need information not about the velocities and coordinates of individual particles but about the macroscopic properties of a system. It is therefore advisable to switch from the equations of classic mechanics, which describes the motion of each system particle, to equations for macroscopic characteristics.
The first step on this way is the transition from the dynamic deterministic level of description to the statistical deterministic one, see Figure 3 from [3] . Let us choose the Liouville formalism among the famous formalisms of classic mechanics equations (Newton,
Hamilton
,
Lagrange
, and Liouville) [12] . In terms of the Liouville formalism, the classic mechanics equations have the form:
![]() (2.1)
(2.1)
The ![]() dynamic distribution function has a meaning of reliability at some time t to find the particle that occupies the trajectory
dynamic distribution function has a meaning of reliability at some time t to find the particle that occupies the trajectory![]() ,
, ![]() in phase space point
in phase space point![]() ,
, ![]() ,
, ![]() , and the particle that occupies the trajectory
, and the particle that occupies the trajectory![]() ,
, ![]() , in phase space point
, in phase space point![]() ,
, ![]() ,
,
![]() (2.2)
(2.2)
In (2.1), m is the mass of the particle, ![]() is the force of action of the i-particle on the j-particle. From the point of view of dynamics one scalar Equation (2.1) for function
is the force of action of the i-particle on the j-particle. From the point of view of dynamics one scalar Equation (2.1) for function ![]() is equivalent to 6N Newton (
Hamilton
,
Lagrange
) equations [12] .
is equivalent to 6N Newton (
Hamilton
,
Lagrange
) equations [12] .
To reach the statistical deterministic level at some time t it is necessary to describe the set of systems (
Gibbs
ensemble) rather than single concrete system. The systems in ensemble differ from each other by values of coordinates and velocities of particles that form the system. The variables![]() ,
, ![]() ,
, ![]() , of an arbitrary K-system of ensemble,
, of an arbitrary K-system of ensemble, ![]() , possess such values, under which the macroscopic characteristics of the K-system of ensemble differ from the corresponding characteristics of any other ensemble system within the order of magnitude of fluctuations typical for time t:
, possess such values, under which the macroscopic characteristics of the K-system of ensemble differ from the corresponding characteristics of any other ensemble system within the order of magnitude of fluctuations typical for time t:
![]() (2.3)
(2.3)
The ![]() statistical distribution function has a meaning of probability to find at some time t one of medium particles within the unit element of phase space near point
statistical distribution function has a meaning of probability to find at some time t one of medium particles within the unit element of phase space near point![]() ,
, ![]() , another particle near point
, another particle near point![]() ,
, ![]() ,
, ![]() , and the last particle near point
, and the last particle near point![]() ,
, ![]() [12] . The
[12] . The ![]() statistical distribution function is a linear combination of the
statistical distribution function is a linear combination of the![]() ,
, ![]() , dynamic distribution functions. The
, dynamic distribution functions. The ![]() distribution function is invariant with respect to permutation of any pair of arguments
distribution function is invariant with respect to permutation of any pair of arguments![]() ,
, ![]() ,
,![]() . It is the cardinal difference between
. It is the cardinal difference between ![]() and
and ![]() dynamic distribution functions. The distribution functions
dynamic distribution functions. The distribution functions ![]() and
and ![]() are governed by the Liouville Equation (2.1). The difference between the
are governed by the Liouville Equation (2.1). The difference between the ![]() function and the
function and the ![]() function described specifically the K-system of ensemble constitutes the fluctuation of the N-particle distribution function.
function described specifically the K-system of ensemble constitutes the fluctuation of the N-particle distribution function.
The ![]() function contains statistical information about all N particles of the system. The reduction of the ordinal number of the particle distribution function accompanies by the loss of information about the position in phase space of the particle in turn. The s-particle distribution function
function contains statistical information about all N particles of the system. The reduction of the ordinal number of the particle distribution function accompanies by the loss of information about the position in phase space of the particle in turn. The s-particle distribution function ![]() has a meaning of the probability that at some time t one particle, say particle 1, finds itself within unit element of phase space near point
has a meaning of the probability that at some time t one particle, say particle 1, finds itself within unit element of phase space near point![]() ,
, ![]() , another particle, say particle 2, within unit element near point
, another particle, say particle 2, within unit element near point![]() ,
, ![]() ,
, ![]() , and particle s-near point
, and particle s-near point![]() ,
, ![]() , regardless of the position in phase space of the remaining
, regardless of the position in phase space of the remaining ![]() particles. The
particles. The ![]() function obeys the s-equation of the BBGKY hierarchy [12] :
function obeys the s-equation of the BBGKY hierarchy [12] :
![]() (2.4)
(2.4)
The ![]() function obeys the first equation of the hierarchy (2.4). The
function obeys the first equation of the hierarchy (2.4). The ![]() function contains statistical information about particle 1 regardless of the position in phase space of the remaining
function contains statistical information about particle 1 regardless of the position in phase space of the remaining ![]() particles. Every equation of the BBGKY hierarchy (2.4) is invariant with respect to inversion of velocities and time,
particles. Every equation of the BBGKY hierarchy (2.4) is invariant with respect to inversion of velocities and time, ![]() ,
, ![]() ,
, ![]() , that is, every equation of the BBGKY hierarchy is reversible. The BBGKY hierarchy is closed by the Liouville equation for
, that is, every equation of the BBGKY hierarchy is reversible. The BBGKY hierarchy is closed by the Liouville equation for![]() . In the thermodynamic limit,
. In the thermodynamic limit, ![]() ,
, ![]() , yet
, yet ![]() is a finite, V is the volume of the system.
is a finite, V is the volume of the system.
Analyzing the hierarchy (2.4),
N.
Bogolyubov
[13] introduced a concept of characteristic intervals (scales) in gas medium. Three temporal intervals were distinguished in [13] :![]() ,
, ![]() , and
, and![]() . Interval
. Interval ![]() is equivalent to the characteristic time of particle collisions
is equivalent to the characteristic time of particle collisions![]() . The spatial scale l0 corresponding to it is identical to the characteristic particle size d. Interval
. The spatial scale l0 corresponding to it is identical to the characteristic particle size d. Interval ![]() is the characteristic time between collisions
is the characteristic time between collisions![]() . The spatial interval lk corresponding to it is identical to the characteristic free path length
. The spatial interval lk corresponding to it is identical to the characteristic free path length![]() . Temporal interval
. Temporal interval ![]() and spatial interval lh corresponding to it are equivalent to the characteristic temporal scale of flow
and spatial interval lh corresponding to it are equivalent to the characteristic temporal scale of flow ![]() and the characteristic spatial scale of flow L correspondently. The above three intervals specify three Bogolyubov accuracy stages of gas description: initial l0 scale, kinetic lk scale, and hydrodynamic lh scale. Initial stage equations are the most detailed. The solutions to these equations describe the system at the finest initial stage as well as at the kinetic and hydrodynamic stages. Passage to less detailed kinetic description stage is implemented by neglecting the information about a sharp change of the distribution functions on the initial scale. Namely, the distribution function governed by the equations of kinetic description stage, varies slightly on l0 scale. After transition to the most coarse hydrodynamic description stage the distribution function varies strongly on lh scale only.
and the characteristic spatial scale of flow L correspondently. The above three intervals specify three Bogolyubov accuracy stages of gas description: initial l0 scale, kinetic lk scale, and hydrodynamic lh scale. Initial stage equations are the most detailed. The solutions to these equations describe the system at the finest initial stage as well as at the kinetic and hydrodynamic stages. Passage to less detailed kinetic description stage is implemented by neglecting the information about a sharp change of the distribution functions on the initial scale. Namely, the distribution function governed by the equations of kinetic description stage, varies slightly on l0 scale. After transition to the most coarse hydrodynamic description stage the distribution function varies strongly on lh scale only.
The BBGKY hierarchy (2.4) describes the medium with accuracy that satisfies the initial stage. The ![]() ,
, ![]() , distribution functions contain the excessively detailed information about the system under consideration.
, distribution functions contain the excessively detailed information about the system under consideration.
At the kinetic and hydrodynamic stages, the gas is described by the one-particle distribution function ![]() governed by the
Boltzmann
equation. The
Boltzmann
equation is direct corollary to the reversible first equation of the BBGKY hierarchy (2.4) for the
governed by the
Boltzmann
equation. The
Boltzmann
equation is direct corollary to the reversible first equation of the BBGKY hierarchy (2.4) for the ![]() distribution function. The first equation of the BBGKY hierarchy is not closed. The integral term contains two-particle distribution function
distribution function. The first equation of the BBGKY hierarchy is not closed. The integral term contains two-particle distribution function ![]() responsible for interaction of particle 1 with some particle 2. There are several variants of the derivation of the
Boltzmann
equation directly from the first equation of the BBGKY hierarchy [12] . Each of them reaches inevitably the equation:
responsible for interaction of particle 1 with some particle 2. There are several variants of the derivation of the
Boltzmann
equation directly from the first equation of the BBGKY hierarchy [12] . Each of them reaches inevitably the equation:
![]() (2.5)
(2.5)
The collision integral ![]() assumes the form:
assumes the form:
![]() (2.6)
(2.6)
Equations (2.5), (2.6) are valid for a rarefied gas medium, where![]() ,
,
![]() (2.7)
(2.7)
In (2.6), (2.7), vector ![]() has the cylindrical coordinates b,
has the cylindrical coordinates b, ![]() ,
, ![]() in reference frame with the Z axis parallel to
in reference frame with the Z axis parallel to![]() ,
,![]() . If the
. If the ![]() function varies slightly on the l0 scale, the
function varies slightly on the l0 scale, the ![]() product differs by the negligibly small value from:
product differs by the negligibly small value from:
![]() (2.8)
(2.8)
Otherwise, let the ![]() function varies strongly on the l0 scale. Then, in order to transit from the initial description stage to the kinetic one, namely, in order to obtain the equation for
function varies strongly on the l0 scale. Then, in order to transit from the initial description stage to the kinetic one, namely, in order to obtain the equation for ![]() from the first equation of BBGKY hierarchy, it is necessary to carry out additionally the spatial averaging (2.7). The integration (2.7) with respect to a within domain W having the characteristic linear size
from the first equation of BBGKY hierarchy, it is necessary to carry out additionally the spatial averaging (2.7). The integration (2.7) with respect to a within domain W having the characteristic linear size ![]() removes strong spatial dependence of the
removes strong spatial dependence of the ![]() function on the l0 scale. Therefore, when passing the kinetic and hydrodynamic description stages, information about spatial position of an individual particle is lost. The
function on the l0 scale. Therefore, when passing the kinetic and hydrodynamic description stages, information about spatial position of an individual particle is lost. The ![]() distribution function has a meaning of a probable number of particles, which are concentrated in a unit volume element near x1 and velocities, in unit interval near
distribution function has a meaning of a probable number of particles, which are concentrated in a unit volume element near x1 and velocities, in unit interval near ![]() at time t. The x1 argument of the
at time t. The x1 argument of the ![]() distribution function is the coordinate of particle 1. The
distribution function is the coordinate of particle 1. The ![]() argument of the
argument of the ![]() distribution function is not the coordinate of individual particle. The x1 argument of the
distribution function is not the coordinate of individual particle. The x1 argument of the ![]() function marks the place in space in the vicinity of which a set of particles is concentrated within init volume. The
Boltzmann
equation is not invariant with respect to inversion of velocities and time:
function marks the place in space in the vicinity of which a set of particles is concentrated within init volume. The
Boltzmann
equation is not invariant with respect to inversion of velocities and time:![]() ,
, ![]() ,
, ![]() , that is, the
Boltzmann
equation is irreversible. The operation responsible for appearance of the irreversibility is represented in Section 3.
, that is, the
Boltzmann
equation is irreversible. The operation responsible for appearance of the irreversibility is represented in Section 3.
The second equation of the BBGKY hierarchy (2.4), like the first one, is not closed. The integral term of the second hierarchy equation contains a three-particle distribution function responsible for the interaction of particles 1 and 2 with some third particle. The absence of closeness of the second hierarchy equation prevents us from the transition to the hydrodynamic stage from the phase space of two particles. It was, however, found that in the gas medium without the triple collisions of particles![]() , the necessity of taking the third particle into account can be obviated. This possibility opens up prospects for the transition to the hydrodynamic description stage without invoking additional hypotheses.
, the necessity of taking the third particle into account can be obviated. This possibility opens up prospects for the transition to the hydrodynamic description stage without invoking additional hypotheses.
If the ![]() partial distribution function obeying the second equation of BBGKY hierarchy (2.4) described two particles occupying positions in the
partial distribution function obeying the second equation of BBGKY hierarchy (2.4) described two particles occupying positions in the ![]() -space arbitrary with respect to each other, the
-space arbitrary with respect to each other, the ![]() partial distribution function describes two particles occupying quite definite positions with respect to each other. The reversible equation for
partial distribution function describes two particles occupying quite definite positions with respect to each other. The reversible equation for ![]() has the form:
has the form:
![]() (2.9)
(2.9)
The idea that leads to the concept of a pair of particles is given in [14] [15] . In [15] , Equation (2.9) describing the evolution of a pair of particles is derived directly from the main statistical mechanics postulates. The heuristic derivation of Equation (2.9) was given in [3] .
The ![]() and
and ![]() pair distribution functions are implemented based on the
pair distribution functions are implemented based on the ![]() function. Let us pass from the 12-dimensional phase space of particles 1 and 2 constructed on the
function. Let us pass from the 12-dimensional phase space of particles 1 and 2 constructed on the![]() ,
, ![]() ,
, ![]() ,
, ![]() vectors to the 12-dimensional space constructed on the
vectors to the 12-dimensional space constructed on the![]() ,
, ![]() ,
, ![]() ,
, ![]() vectors, where
vectors, where![]() ,
, ![]() ,
, ![]() ,
,![]() . Then,
. Then,
![]() (2.10)
(2.10)
![]() (2.11)
(2.11)
![]() (2.12)
(2.12)
In (2.12),![]() . The integration of
. The integration of ![]() with respect to
with respect to ![]() (2.12) within cylindrical volume
(2.12) within cylindrical volume ![]() limits
limits ![]() collects all the positions of particles 1 and 2 with respect to each other in which they turn out to be after a collision with each other. The integration of
collects all the positions of particles 1 and 2 with respect to each other in which they turn out to be after a collision with each other. The integration of ![]() with respect to
with respect to ![]() (2.12) within cylindrical volume
(2.12) within cylindrical volume ![]() limits
limits ![]() collects all the positions of particles 1 and 2 with respect to each other in which they turn out to be before a collision with each other, see Figure 3 from [2] . The integration of
collects all the positions of particles 1 and 2 with respect to each other in which they turn out to be before a collision with each other, see Figure 3 from [2] . The integration of ![]() (2.11) with respect to a within region W having the characteristic linear size
(2.11) with respect to a within region W having the characteristic linear size ![]() removes strong spatial dependence of the functions on the initial scale having the particle size d. The multiplication of
removes strong spatial dependence of the functions on the initial scale having the particle size d. The multiplication of ![]() by the number of methods for selecting a pair from a set of N particles,
by the number of methods for selecting a pair from a set of N particles, ![]() , (the permutation of particles does not create a new pair) leads to pair distribution functions. It follows that operations (2.10) - (2.12) collect all pairs of particles which either inevitably collide during an interval that does not exceed the characteristic time between collisions
, (the permutation of particles does not create a new pair) leads to pair distribution functions. It follows that operations (2.10) - (2.12) collect all pairs of particles which either inevitably collide during an interval that does not exceed the characteristic time between collisions![]() , or fly apart after a collision during an interval not longer than
, or fly apart after a collision during an interval not longer than![]() . The
. The ![]() pair function has the meaning of a probable number of pairs flying apart (approaching each other) the centers of mass of which are concentrated in a unit volume element near x and velocities, in a unit interval near G, v at time t. The arguments of the
pair function has the meaning of a probable number of pairs flying apart (approaching each other) the centers of mass of which are concentrated in a unit volume element near x and velocities, in a unit interval near G, v at time t. The arguments of the ![]() distribution function are
distribution function are ![]() and
and![]() , which are spatial coordinates of particles 1 and 2. The x argument of the
, which are spatial coordinates of particles 1 and 2. The x argument of the ![]() distribution function is the coordinate of the center of mass of particles 1 and 2.
distribution function is the coordinate of the center of mass of particles 1 and 2.
The x argument of ![]() pair distribution functions is not the coordinate of the center of mass of some pair. Indeed, the centers of mass of all the pairs described by the
pair distribution functions is not the coordinate of the center of mass of some pair. Indeed, the centers of mass of all the pairs described by the ![]() functions have the coordinate x. The x argument of
functions have the coordinate x. The x argument of ![]() functions marks the place in space in the vicinity of which a set of centers of mass of pairs of particles is concentrated in unit volume. It follows that operations (2.10) - (2.12) remove the dependence of pair distribution functions on the coordinates of individual particles. The
functions marks the place in space in the vicinity of which a set of centers of mass of pairs of particles is concentrated in unit volume. It follows that operations (2.10) - (2.12) remove the dependence of pair distribution functions on the coordinates of individual particles. The ![]() and
and ![]() pair distribution functions obey the irreversible equations obtained in [15] . The
pair distribution functions obey the irreversible equations obtained in [15] . The ![]() and
and ![]() are the characteristic scales for changing the
are the characteristic scales for changing the ![]() and
and ![]() functions. Why the irreversibility is appeared in equations for pair functions is investigated in Section 3.
functions. Why the irreversibility is appeared in equations for pair functions is investigated in Section 3.
At the hydrodynamic stage, the description of gas medium may be carried out not in terms of distribution function but in terms of hydrodynamic values that are the moments of distribution functions. In order to derive the hydrodynamics equations from the equations for the distribution functions it is necessary to refuse the study of behavior of the distribution function on the kinetic scale, ![]() ,
, ![]() kinetic scale. Under the hydrodynamic description, the
Knudsen
layers, the initial layers and the shock waves, where the scale of the change of the distribution function is
kinetic scale. Under the hydrodynamic description, the
Knudsen
layers, the initial layers and the shock waves, where the scale of the change of the distribution function is![]() ,
, ![]() , are excluded from consideration.
, are excluded from consideration.
3. Inevitability of Appearance of the Irreversibility
To understand the physical meaning of appearance of the irreversibility in equations of kinetics and hydrodynamics, two concepts discussed above should be compared. First, since the time of
L.
Bolzmann
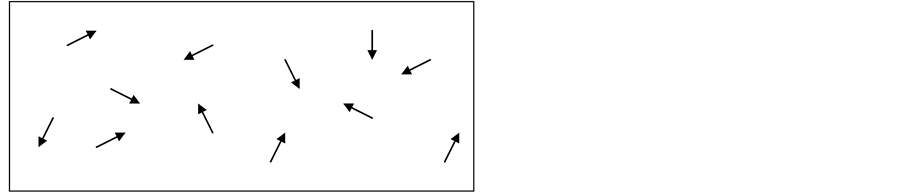
, the responsibility for direction of evolution of the system rests with the initial conditions, namely, the set of initial values of coordinates and velocities of all the particles [16] . At a certain mutual arrangement of the particles, the system evolves in the direction that we see everywhere and every second. However, there exist such arrangements of particles that send the system along an extremely unlike, rarely realized direction. Refer to the example. Let after removal of partition at the time ![]() isolated system of
isolated system of ![]() particles,
particles, ![]() relaxes from non-equili- brium state (Figure 1(a)) to the state of statistical equilibrium (Figure 1(b)) that is achieved by the time
relaxes from non-equili- brium state (Figure 1(a)) to the state of statistical equilibrium (Figure 1(b)) that is achieved by the time![]() . The mutual arrangement of particles at the time
. The mutual arrangement of particles at the time ![]() sends the system along the usually observed direction that corresponds to approaching the state of statistical equilibrium. However, mutual arrangement of the particles at the time
sends the system along the usually observed direction that corresponds to approaching the state of statistical equilibrium. However, mutual arrangement of the particles at the time ![]() after inversion in velocity space (Figure 1(c)) sends the system along extremely unlike direction that corresponds to departure from the state of statistical equilibrium. Even a negligible change in mutual arrangement of the particles (on distance much smaller than particle size d) can change the direction of evolution [17] .
after inversion in velocity space (Figure 1(c)) sends the system along extremely unlike direction that corresponds to departure from the state of statistical equilibrium. Even a negligible change in mutual arrangement of the particles (on distance much smaller than particle size d) can change the direction of evolution [17] .
Secondly, after transition from the initial to the kinetic and hydrodynamic description stages the distribution functions lose the information about spatial position of individual particle and hence, about mutual arrangement of particles. The variables xi, ![]() both in the s-particle distribution function
both in the s-particle distribution function![]() ,
, ![]() , and in the initial conditions of the initial description stage are the spatial coordinates of separate particles. It means that the functions
, and in the initial conditions of the initial description stage are the spatial coordinates of separate particles. It means that the functions![]() ,
, ![]() , contain the information about direction of evolution. The x1 variable in distribution functions and initial conditions of the kinetic and hydrodynamic stages specifies the location in space. It means that distribution functions and initial conditions of kinetic and hydrodynamic stages lose the information about the direction of evolution. If the roughening operations, transforming the equations and the initial conditions of the initial stage into equations and the initial conditions of the kinetic and hydrodynamic stages, are performed correctly, the information about direction of evolution of the system must somehow be preserved. And this information preserved, it disappeared from the coarse distribution functions and the initial conditions, but appeared in the coarse equations of the kinetic and hydrodynamic stages. The equations of the kinetic and hydrodynamic stages acquired a new characteristic property that is not contained in the classic mechanics equations as well as in the BBGKY hierarchy equations. The irreversibility identified with the direction of the system evolution appeared there.
, contain the information about direction of evolution. The x1 variable in distribution functions and initial conditions of the kinetic and hydrodynamic stages specifies the location in space. It means that distribution functions and initial conditions of kinetic and hydrodynamic stages lose the information about the direction of evolution. If the roughening operations, transforming the equations and the initial conditions of the initial stage into equations and the initial conditions of the kinetic and hydrodynamic stages, are performed correctly, the information about direction of evolution of the system must somehow be preserved. And this information preserved, it disappeared from the coarse distribution functions and the initial conditions, but appeared in the coarse equations of the kinetic and hydrodynamic stages. The equations of the kinetic and hydrodynamic stages acquired a new characteristic property that is not contained in the classic mechanics equations as well as in the BBGKY hierarchy equations. The irreversibility identified with the direction of the system evolution appeared there.
To clear up the mechanism of appearance of the irreversibility in equations of kinetics and hydrodynamics let us carry out the roughening the reversible Equation (2.9) that describes the motion and interaction of two particles of pair. Suppose that ![]() is the velocity of relative motion of particles which after an elastic collision with the impact parameter b and azimuth angle
is the velocity of relative motion of particles which after an elastic collision with the impact parameter b and azimuth angle ![]() acquire velocity v. Trajectories of relative motion of
acquire velocity v. Trajectories of relative motion of
two particles in the interaction domain at a fixed ![]() are illustrated in Figure 2. The particles with parameters
are illustrated in Figure 2. The particles with parameters ![]() and
and ![]() pursue trajectory 1 and leave the interaction domain with parameters
pursue trajectory 1 and leave the interaction domain with parameters ![]() and
and![]() ,
,![]() . In order to leave the interaction domain with the same velocity
. In order to leave the interaction domain with the same velocity![]() , and parameter
, and parameter![]() , particles should enter it with
, particles should enter it with ![]() and
and![]() , (trajectory
2 in
Figure 2). If the particles have velocity
, (trajectory
2 in
Figure 2). If the particles have velocity ![]() and
and ![]() at the point of entry, they will emerge from the interaction domain with parameters
at the point of entry, they will emerge from the interaction domain with parameters ![]() and
and![]() , such that
, such that
![]() .
.
Let us recast Equation (2.9) in the trajectory form. The newly obtained equation is then integrated with respect to ![]() between the limits of variation of two-particle distribution functions
between the limits of variation of two-particle distribution functions ![]() and
and![]() . These limits are represented in Equation (2.12):
. These limits are represented in Equation (2.12):
![]() (
3.1a
)
(
3.1a
)
![]() (3.1b)
(3.1b)
Here,![]() . Velocities of relative motion of particles appearing in Equation (3.1) are displayed in Figure 3,
. Velocities of relative motion of particles appearing in Equation (3.1) are displayed in Figure 3,![]() . Equation (3.1) convey distinct physical meaning. They imply that after a
. Equation (3.1) convey distinct physical meaning. They imply that after a
lapse of time![]() , all pairs of approaching particles, indiscriminately, become the pairs of diverging particles. Let us pass on from trajectory Equation (3.1) to differential equations,
, all pairs of approaching particles, indiscriminately, become the pairs of diverging particles. Let us pass on from trajectory Equation (3.1) to differential equations,
![]() ( 3.2a )
( 3.2a )
![]() (3.2b)
(3.2b)
Here,![]() . Reversibility of the equations for pair functions will be examined in the seven- dimensional space
. Reversibility of the equations for pair functions will be examined in the seven- dimensional space![]() . The seven-dimensional space is a combination of the
. The seven-dimensional space is a combination of the ![]() six-dimensional space of velocities defined by vectors G and v and the
six-dimensional space of velocities defined by vectors G and v and the ![]() one-dimensional time space. The positive direction of the time axis runs from the past to the future.
one-dimensional time space. The positive direction of the time axis runs from the past to the future.
Suppose that at some instant of time, we have a chance to reverse the directions of the velocities of all the particles, ![]() ,
, ![]() , without changing the directions of the reference axes in space
, without changing the directions of the reference axes in space![]() . In space
. In space![]() , time t may be reckoned in the direction of its increase:
, time t may be reckoned in the direction of its increase:![]() , while time
, while time![]() , in the return di-
, in the return di-
rection:![]() , so that
, so that![]() . Inverting the velocities,
. Inverting the velocities, ![]() ,
, ![]() , we reverse the direction of motion of particles which, according to the laws of classic mechanics, retreat to their starting positions. Now let us alter orientation of the time axis, directing it from the future to the past. Reckoning time in the new frame of reference
, we reverse the direction of motion of particles which, according to the laws of classic mechanics, retreat to their starting positions. Now let us alter orientation of the time axis, directing it from the future to the past. Reckoning time in the new frame of reference ![]() in the direction:
in the direction:![]() , we, as previously, move from the past to the future.
, we, as previously, move from the past to the future.
Let us reverse the signs of particle velocities, ![]() ,
, ![]() , and reckon time in the direction of its decrease,
, and reckon time in the direction of its decrease,![]() . As the velocities are inverted, pairs of approaching particles become the pairs of diverging particles, and vice versa. For every pair function cylindrical coordinates of vector
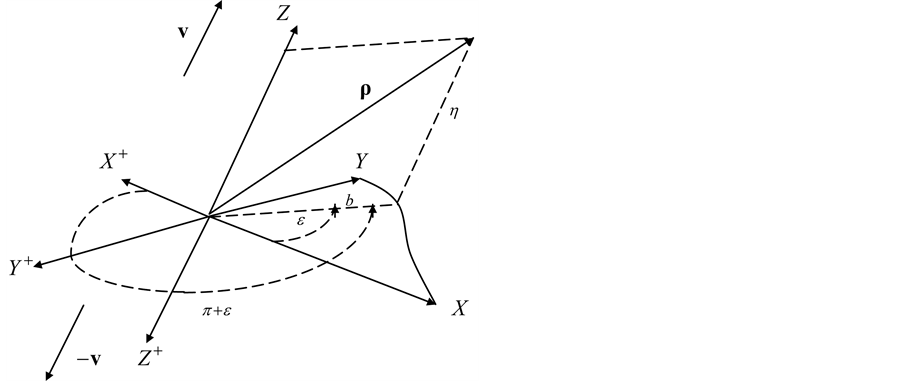
. As the velocities are inverted, pairs of approaching particles become the pairs of diverging particles, and vice versa. For every pair function cylindrical coordinates of vector ![]() are specified in the frame of reference with Z-axis oriented in the direction of vector v (Figure 4),
are specified in the frame of reference with Z-axis oriented in the direction of vector v (Figure 4),
![]() (
3.3a
)
(
3.3a
)
![]()
Figure 3. Velocities of relative motion of two particles at the inlet and outlet of their interaction domain, appearing in Equation (3.1). Velocities are displayed in the frame of reference![]() ,
,![]() .
.
Superscript + marks the pair distribution functions ![]() and
and![]() , which evolve with regressive direction
, which evolve with regressive direction
of timing along the time axis pointing from the past to the future. Inversion of time and velocities fails to alter the number of pairs of diverging particles which at time t start approaching each other and the number of pairs of approaching particles which at time t start diverging each other,
![]()
![]() (3.3b)
(3.3b)
![]()
![]()
Now substitute operations (
3.3a
) into Equation (3.2). Let us take Equation (3.3b) into account. These actions reduce Equation (
3.2a
) to Equation (3.2b) and Equation (3.2b) to Equation (
3.2a
). Hence, Equation (3.2) are invariant with respect to the change of variables![]() ,
, ![]() ,
,![]() :
:
![]() ( 3.4a )
( 3.4a )
![]() (3.4b)
(3.4b)
Here,![]() . The formal criterion [12] of reversibility of Equation (3.2) is thus established.
. The formal criterion [12] of reversibility of Equation (3.2) is thus established.
Let us go beyond the scope of formal analysis and examine Equation (3.la). Inversion of time and velocities, ![]() ,
, ![]() ,
, ![]() , yields:
, yields:
![]() ( 3.5a )
( 3.5a )
Inversion of time and velocities fails to alter the number of pairs of diverging particles, which at time ![]() start approaching each other,
start approaching each other,
![]() (3.5b)
(3.5b)
Now substitute operations (
3.5a
) into Equation (
3.1a
). Let us take Equation (3.5b) into account. From the resulting equation it follows that the number of pairs ![]() that reverted to unit volume around point x by time
that reverted to unit volume around point x by time ![]() equals the number of pairs
equals the number of pairs ![]() that left this volume at time t. It turned out that Equation (3.la) is reversible. Reversibility of Equation (3.lb) can be proved in the same way.
that left this volume at time t. It turned out that Equation (3.la) is reversible. Reversibility of Equation (3.lb) can be proved in the same way.
Let us pass on from differential Equation (3.4) to trajectory equations,
![]() ( 3.6a )
( 3.6a )
![]() (3.6b)
(3.6b)
The sets (3.1) and (3.2) are written for the progressive direction of timing along the time axis pointing from the past to the future. The sets (3.4) and (3.6) are written for the regressive direction of timing along the same time axis.
To comply with the physical scenario by which the system attains the kinetic and hydrodynamic stages and the peculiarities of this stage, let us dispose of the variables defining the mutual arrangement of particles. To this end, integrate Equation (3.la) with respect to b and![]() :
:
![]() (3.7)
(3.7)
Integration “collects” all the trajectories of types 1 and 2 (Figure 2) differing by their b and ![]() values at the outlet of the interaction domain at a fixed v. However, integration with respect to b and
values at the outlet of the interaction domain at a fixed v. However, integration with respect to b and ![]() failed to eliminate these parameters, because the distribution function on the left hand side of Equation (3.7) depends on b and
failed to eliminate these parameters, because the distribution function on the left hand side of Equation (3.7) depends on b and ![]() both explicitly and implicitly (via
both explicitly and implicitly (via![]() ).
).
Let us next integrate ![]() with respect to b and
with respect to b and ![]() at a fixed
at a fixed![]() ,
,
![]() (3.8)
(3.8)
Here, integration is over the trajectories of types 1 and n (Figure 2) differing by their b and ![]() values at the entry of the interaction domain at a fixed
values at the entry of the interaction domain at a fixed![]() . Now replace
. Now replace ![]() in Equation (3.7) by its average over b and
in Equation (3.7) by its average over b and ![]() (3.8),
(3.8),
![]() (3.9)
(3.9)
Equation (3.7) assumes therewith the following form:
![]() (3.10)
(3.10)
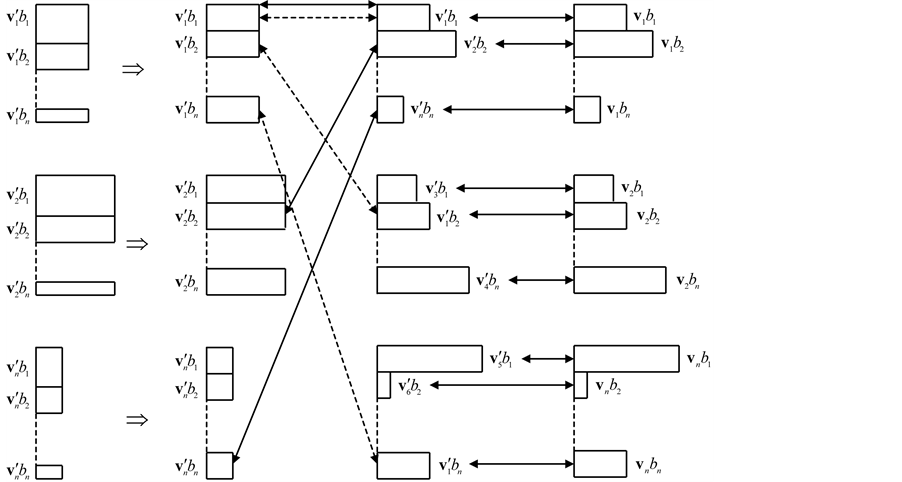
Figure 5 is a pictorial representation of operations (3.7)-(3.10). Column A portrays the integrand function on the left hand side of Equation (3.7) modeling pairs of approaching particles at fixed G and![]() . Each rectangle in A corresponds to
. Each rectangle in A corresponds to ![]() with some particular values of b and
with some particular values of b and![]() . Rectangles have different areas, each area being proportional to the number of pairs with the appropriate values of b and
. Rectangles have different areas, each area being proportional to the number of pairs with the appropriate values of b and![]() . Replacing (3.9) translates A into B. The
. Replacing (3.9) translates A into B. The ![]() transition is equivalent to replacing
transition is equivalent to replacing ![]() with given b and
with given b and ![]() by its average over all b values at a fixed
by its average over all b values at a fixed![]() ,
, ![]() (3.8). The result of this transition is that rectangles in column B, corresponding to different values of b and identical values of
(3.8). The result of this transition is that rectangles in column B, corresponding to different values of b and identical values of ![]() have equal areas. Thus, the
have equal areas. Thus, the ![]() transition brings us to a less accurate description of the system.
transition brings us to a less accurate description of the system.
The ![]() transition in Figure 5 is mediated by integration of the left hand side of Equation (3.10). The solid arrows connecting columns B and C correspond to the trajectories of types 1 and 2 (Figure 2) along which the left hand side of Equation (3.10) is integrated. The “collected” trajectories then experience the
transition in Figure 5 is mediated by integration of the left hand side of Equation (3.10). The solid arrows connecting columns B and C correspond to the trajectories of types 1 and 2 (Figure 2) along which the left hand side of Equation (3.10) is integrated. The “collected” trajectories then experience the ![]() transition to yield pairs of diverging particles with identical velocities v. Column D depicts pairs of diverging
transition to yield pairs of diverging particles with identical velocities v. Column D depicts pairs of diverging
particles ![]() modelled by the right hand side of Equation (3.10). It is worth emphasizing that each rectangle in column D derives from the isometric triangle in column B, corresponding to an approximate value of
modelled by the right hand side of Equation (3.10). It is worth emphasizing that each rectangle in column D derives from the isometric triangle in column B, corresponding to an approximate value of![]() .
.
Dashed arrows between B and C are the trajectories of types 1 and n (Figure 2). It is these trajectories that were “collected” by integrating (3.8) to switch from the exact value of ![]() with some b and
with some b and ![]() (depicted by the appropriate rectangle in column A) to its average
(depicted by the appropriate rectangle in column A) to its average ![]() having the same
having the same ![]() and appearing in column B as a rectangle of a different area.
and appearing in column B as a rectangle of a different area.
Reversibility of Equation (3.10) will be analyzed in the same informal manner as that of Equation (3.la). Let us reverse the signs of particle velocities and reckon time in the direction of its decrease:![]() ,
,
![]() (A) (B) (C) (D)
(A) (B) (C) (D)
Figure 5. Graphic representation of operations (3.7)-(3.10).
![]() ,
,![]() . Variation of the left and right hand sides of Equation (3.10) is given by operations (
3.5a
) from which the explicit dependence on G and
. Variation of the left and right hand sides of Equation (3.10) is given by operations (
3.5a
) from which the explicit dependence on G and ![]() is omitted. Substituting Equation (3.5b) independent explicitly of G and
is omitted. Substituting Equation (3.5b) independent explicitly of G and ![]() into Equation (3.10) yields the equation for transition from column D at time
into Equation (3.10) yields the equation for transition from column D at time ![]() to column B at time
to column B at time ![]() in the direction of decreasing time. Equation (3.10) fails to account for the reverse transition to column A and therefore is irreversible.
in the direction of decreasing time. Equation (3.10) fails to account for the reverse transition to column A and therefore is irreversible.
Thus, at time t, we replace the exact initial functions modeling pairs of particles which have not collided yet (left hand side of Equation (3.7)) by their approximations. From these approximations ![]() to the true func- tions at time t we derive the functions
to the true func- tions at time t we derive the functions ![]() modeling already collided particles at time
modeling already collided particles at time ![]() (Equation (3.10)).
(Equation (3.10)).
Operation (3.9) eliminated all information about the initial functions (left hand side of Equation (3.7)) from the left hand side of Equation (3.10). This information cannot be replenished by inverting time and particle velocities:![]() ,
, ![]() ,
,![]() . Equation (3.10) is irreversible and valid only in the direction of increasing time. Note that operations (3.8) and (3.9) are by no means a sort of manipulation with impact parameters b and
. Equation (3.10) is irreversible and valid only in the direction of increasing time. Note that operations (3.8) and (3.9) are by no means a sort of manipulation with impact parameters b and![]() . They are a logical and consistent means of deriving the approximation that contains no information unnecessary in the kinetic stage of gas medium modeling.
. They are a logical and consistent means of deriving the approximation that contains no information unnecessary in the kinetic stage of gas medium modeling.
Let us integrate Equation (3.lb) with respect to b and![]() ,
,
![]() (3.11)
(3.11)
By analogy with operation (3.9) we replace the initial function by its average,
![]() (3.12)
(3.12)
where
![]()
In Equation (3.11), function ![]() models pairs of particles which have collided by time t and depends exclusively on function
models pairs of particles which have collided by time t and depends exclusively on function ![]() modeling pairs of particles approaching each other at time
modeling pairs of particles approaching each other at time![]() . Replacing the exact function
. Replacing the exact function ![]() on the right hand side of Equation (3.11) by its average over b and
on the right hand side of Equation (3.11) by its average over b and![]() ,
, ![]() (3.12), is inadmissible with progressive direction of timing. Really, after replacing (3.12), function
(3.12), is inadmissible with progressive direction of timing. Really, after replacing (3.12), function ![]() at time
at time ![]() depends exclusively on average function
depends exclusively on average function ![]() at time t. Hence, Equation (3.11) with its right hand side re-
at time t. Hence, Equation (3.11) with its right hand side re-
placed by operation (3.12) is unsuitable for modeling evolution of distribution functions in the direction of increasing time. Thus, an attempt to do away with the explicit dependence of distribution functions on b and ![]() in Equation (3.11) has not met with success with the progressive direction of timing. Let
in Equation (3.11) has not met with success with the progressive direction of timing. Let ![]() and
and ![]() be the spherical coordinates of vector v. Integration of Equation (3.11) with respect to
be the spherical coordinates of vector v. Integration of Equation (3.11) with respect to ![]() and
and ![]() spares us the information useless in the kinetic stage of description,
spares us the information useless in the kinetic stage of description,
![]() (3.13)
(3.13)
Equation (3.13) is reversible. This inference stems from an informal analysis similar to analysis of Equation (3.la).
Following the procedure proposed in [15] , we average Equation (3.10) and (3.13) over x within domain W of linear size![]() , Equation (2.11), multiply two-particle distribution functions by the number of ways in which a pair of particles can be chosen among N panicles, and switch from the trajectory form of the equations to their differential form,
, Equation (2.11), multiply two-particle distribution functions by the number of ways in which a pair of particles can be chosen among N panicles, and switch from the trajectory form of the equations to their differential form,
![]() (3.14)
(3.14)
Equation (3.14) were previously derived heuristically in [14] and immediately from the Liouville equation in [15] . The functions ![]() and
and ![]() were defined by Equations (2.10), (2.11), and (2.12).
were defined by Equations (2.10), (2.11), and (2.12).
Now we switch from space ![]() to space
to space![]() ,
,![]() . All the axes of the six-dimensional frame of reference
. All the axes of the six-dimensional frame of reference ![]() are in opposition to the axes of
are in opposition to the axes of![]() . Inversion of the reference axes of the velocity space
. Inversion of the reference axes of the velocity space ![]() has no effect on the physical pattern: particles keep moving. In going to
has no effect on the physical pattern: particles keep moving. In going to![]() , the superscript of pair distribution functions remains invariant. However, in frame of reference
, the superscript of pair distribution functions remains invariant. However, in frame of reference![]() , the arguments of distribution functions G and v reverse their signs:
, the arguments of distribution functions G and v reverse their signs:![]() ,
, ![]() , Figure 6,
, Figure 6,![]() . Now we switch from space
. Now we switch from space ![]() to space
to space![]() . The time axis in space
. The time axis in space ![]() points towards the past. In space
points towards the past. In space![]() ,
, ![]() ,
,![]() . The set (3.6) assumes the following form in frame of reference
. The set (3.6) assumes the following form in frame of reference![]() :
:
![]() (3.l 5a )
(3.l 5a )
![]() (3.l5b)
(3.l5b)
Superscript * marks the pair distribution functions ![]() and
and![]() , which evolve with progressive direction of timing along the time axis pointing from the future to the past. Let us integrate Equation (3.l
5a
) with respect to b and
, which evolve with progressive direction of timing along the time axis pointing from the future to the past. Let us integrate Equation (3.l
5a
) with respect to b and![]() ,
,
![]() (3.16)
(3.16)
Let us carry out the replacing,
![]() (3.17)
(3.17)
where
![]() (3.18)
(3.18)
Equation (3.16) with replacing (3.17) assumes the form:
![]() (3.19)
(3.19)
In Equation (3.19), average function ![]() models pairs of particles which have collided by time
models pairs of particles which have collided by time![]() .
.
![]()
Figure 6. Velocities of relative motion of two particles at the inlet and outlet of their interaction domain, appearing in Equation (3.15). Velocities are displayed in the frame of reference![]() ,
,![]() .
.
Function ![]() models pairs of particles approaching each other at time
models pairs of particles approaching each other at time ![]() and depends exclusively on average function
and depends exclusively on average function ![]() at time
at time![]() . Replacing (3.17) the exact function
. Replacing (3.17) the exact function ![]() on the right hand side of Equation (3.16) by its average over b and
on the right hand side of Equation (3.16) by its average over b and![]() ,
, ![]() (3.18), is responsible for the irreversibility of Equation (3.19). Equation (3.19) is suitable for modeling evolution of distribution functions in the direction of increasing time along the time axis pointing from the future to the past. Let us carry out the replacing,
(3.18), is responsible for the irreversibility of Equation (3.19). Equation (3.19) is suitable for modeling evolution of distribution functions in the direction of increasing time along the time axis pointing from the future to the past. Let us carry out the replacing,
![]() (3.20)
(3.20)
where
![]()
Let us integrate Equation (3.l5b) with respect to b and![]() , and use the replacing (3.20),
, and use the replacing (3.20),
![]() (3.21)
(3.21)
In Equation (3.21), function ![]() models pairs of particles which have collided by time
models pairs of particles which have collided by time ![]() and depends exclusively on average function
and depends exclusively on average function ![]() modeling pairs of particles approaching each other at time
modeling pairs of particles approaching each other at time![]() . Hence, replacing the exact function
. Hence, replacing the exact function ![]() by its average over b and
by its average over b and![]() ,
, ![]() (3.20), is inadmissible with
(3.20), is inadmissible with
the progressive direction of timing on the time axis pointing from the future to the past. So, Equation (3.21) is unsuitable for modeling evolution of distribution functions in the direction of increasing time along the same time axis. Integration of Equation (3.15b) with respect to b and![]() ,
, ![]() and
and![]() , spares us the information useless in the kinetic stage of description:
, spares us the information useless in the kinetic stage of description:
![]() (3.22)
(3.22)
As previously in [15] , we average Equations (3.19) and (3.22) over x within domain W of linear size![]() , Equation (2.11), multiply the distribution functions by the number of ways in which a pair of particles can be selected from an ensemble of N particles, and switch from the trajectory form of equations to their differential form:
, Equation (2.11), multiply the distribution functions by the number of ways in which a pair of particles can be selected from an ensemble of N particles, and switch from the trajectory form of equations to their differential form:
![]() (3.23)
(3.23)
Equation (3.23) are valid in the direction of increasing time along the time axis pointing from the future to the past. Equation (3.23) are called the reverse equations for pair distribution functions. In [9] , Equation (3.23) are derived directly from the Equation (3.14) by means of inversion of velocities and time supplemented with inversion of the reference axes of the velocities and time space.
The basic property of pair functions ![]() and
and ![]() is also good for the reverse functions. Hence, pair functions
is also good for the reverse functions. Hence, pair functions ![]() and
and ![]() remain unchanged at time along the trajectory of the center of mass of the pair for progressive direction of timing on the time axis pointing from the future to the past,
remain unchanged at time along the trajectory of the center of mass of the pair for progressive direction of timing on the time axis pointing from the future to the past,
![]() (3.24)
(3.24)
here,
![]()
Reverse multimoment hydrodynamics equations can be derived from Equation (3.23) within the formalism of [4] . It turned out that the form of the resulting equations of conservation (55) and (56) from [4] is invariant with respect to the direction of the time axis,
![]() (3.25)
(3.25)
However, expressions for the non-principal hydrodynamic values (52) and, hence, (53) from [4] undergo transformations:
![]() (3.26)
(3.26)
Then,
![]() (3.27)
(3.27)
Thus, the reverse Equation (3.23) give the expressions for the stress tensor ![]() and heat flux vector
and heat flux vector ![]() differ from their counterparts (Equation (53) in [4] ) stemming from direct Equation (3.14) by their sign. Principal hydrodynamic values
differ from their counterparts (Equation (53) in [4] ) stemming from direct Equation (3.14) by their sign. Principal hydrodynamic values![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are the moments of pair function
are the moments of pair function![]() . Expressions for the moments of the reverse pair function
. Expressions for the moments of the reverse pair function ![]() are identical to expressions for the moments of the pair function
are identical to expressions for the moments of the pair function ![]() presented in [4] .
presented in [4] .
Let us recast replacing (3.9) in terms of two-particle distribution functions. Invoking relationship (
10a
) from [4] , we obtain:
![]() (3.28)
(3.28)
Let us integrate Equation (3.28) first with respect to b and![]() ,
,
![]() (3.29)
(3.29)
and then with respect to b and ![]() at a fixed
at a fixed![]() ,
,
![]() (3.30)
(3.30)
where
![]() (3.31)
(3.31)
Let us next apply operation (3.9) to Equation (3.29). From Equations (3.30) and (3.31) we obtain that operation (3.9) is equivalent to:
![]() (3.32)
(3.32)
Invoking relationships between two-particle distribution functions [4] , let us recast replacing (3.32) in terms of functions![]() , written in the
, written in the ![]() variables,
variables,
![]() (3.33)
(3.33)
here,
![]() (3.34)
(3.34)
In Equation (3.34)![]() ,
, ![]() ,
,![]() . Following to Equation (2.11), let us eliminate strong spatial dependence of the distribution functions from replacing (3.33) on the initial scale,
. Following to Equation (2.11), let us eliminate strong spatial dependence of the distribution functions from replacing (3.33) on the initial scale,
![]() (3.35)
(3.35)
In accordance with Equation (10) from [15] , two-particle distribution functions ![]() and
and ![]() have identical physical meaning within interaction domain and governed by the same equations when triple collisions are neglected,
have identical physical meaning within interaction domain and governed by the same equations when triple collisions are neglected,![]() . Hence,
. Hence,
![]() (3.36)
(3.36)
Boundary condition (3.36) remains valid for functions ![]() and
and![]() .
.
To analyze reversibility of Equation (2.5) with collision integral (2.6) let us reverse the signs of velocities, ![]() ,
, ![]() , and reckon time in the direction of its decrease,
, and reckon time in the direction of its decrease,![]() . As the velocities are inverted, pairs of particles at the inlet of the interaction domain become the pairs of particles at the outlet of this domain, and vice versa,
. As the velocities are inverted, pairs of particles at the inlet of the interaction domain become the pairs of particles at the outlet of this domain, and vice versa,
![]() (3.37)
(3.37)
Inversion of time and velocities fails to alter the number of pairs of diverging particles which at time t start approaching each other and the number of pairs of approaching particles which at time t start diverging each other. In this case, operations (3.37) remain true with respect to replacement of the symbol ® by the symbol =. As a result, Equation (2.5) with collision integral (2.6) is invariant with respect to inversion:![]() ,
, ![]() ,
, ![]() , that is, Equation (2.5) with collision integral (2.6) is reversible. The reversibility of Equation (2.5) is true for any analytical representation of two-particle distribution functions in the collision integral (2.6). Hence, the Bogolyubov boundary condition for correlation failure [13] ,
, that is, Equation (2.5) with collision integral (2.6) is reversible. The reversibility of Equation (2.5) is true for any analytical representation of two-particle distribution functions in the collision integral (2.6). Hence, the Bogolyubov boundary condition for correlation failure [13] ,
![]() (3.38)
(3.38)
does not eliminate the reversibility of Equation (2.5) with collision integral (2.6). The second component of collision integral (2.6) corresponds to pair of particles at the entrance to their interaction domain. The first component of collision integral (2.6) describes pair of particles at the exit from this domain. Let us express function ![]() in terms of the two-particle distribution function at the entrance to interaction domain. Invoking relationships derived in [18] , we obtain:
in terms of the two-particle distribution function at the entrance to interaction domain. Invoking relationships derived in [18] , we obtain:
![]() (3.39)
(3.39)
here,
![]()
Let us recast collision integral (3.39) in terms of two-particle distribution functions![]() , written in
, written in![]() ,
, ![]() ,
, ![]() , v variables,
, v variables,
![]() (3.40)
(3.40)
here,
![]()
Equation (2.5) with collision integral (3.39) remains invariant with respect to inversion of time and velocities, ![]() ,
, ![]() ,
, ![]() , that is, Equation (2.5) with collision integral (3.39) is reversible. Equa-
, that is, Equation (2.5) with collision integral (3.39) is reversible. Equa-
tion (2.5) with collision integral (3.40) is also reversible. Invoking boundary condition (3.36) for the ![]() dis-
dis-
tribution function, let us replace the first component in the collision integral (3.40) by its average over b and ![]() (3.35). Then,
(3.35). Then,
![]() (3.41)
(3.41)
here,
![]() (3.42)
(3.42)
Let us invoke replacing (3.41) to obtain Equation (2.5) with collision integral (3.40) in the form:
![]() (3.43)
(3.43)
In terms of two-particle distribution functions![]() , written in
, written in![]() ,
, ![]() ,
, ![]() ,
, ![]() variables, collision integral
variables, collision integral ![]() (3.42) assumes the form:
(3.42) assumes the form:
![]() (3.44)
(3.44)
here,
![]()
In Equation (3.43),![]() . Equation (3.43) with collision integral (3.42) is irreversible. Replacing
. Equation (3.43) with collision integral (3.42) is irreversible. Replacing
(3.32) is equivalent to replacing (3.9). Operations (3.9) and (3.32) are true for particles of pair which have not collided yet. That is why Equation (3.43) with collision integral (3.42) is valid for the progressive direction of timing along the time axis pointing from the past to the future. Analogously, Equation (3.43) with collision integral (3.44) is also valid with progressive timing along the same time axis. Following to
Boltzmann
, let us
factorize two particle distribution functions in the ![]() collision integral (3.44),
collision integral (3.44),
![]() (3.45)
(3.45)
The factorization of two particle distribution functions, that is, their representation in the form of product of two one-particle functions, closes Equation (3.43) with collision integral (3.44). The obtained classic kinetic equation for the ![]() one-particle function is called the
Boltzmann
equation:
one-particle function is called the
Boltzmann
equation:
![]() (3.46)
(3.46)
Boltzmann
hypothesis (“Stosszahlansatz”) (3.45) transforms irreversible Equation (3.43) with collision integral (3.44) into irreversible Boltzmann Equation (3.46). So,
Boltzmann
hypothesis (3.45) is not responsible for appearance of the irreversibility in the kinetic equation. Let us factorize two particle distribution functions in the ![]() collision integral (3.39),
collision integral (3.39),
![]() (3.47)
(3.47)
The factorization (3.47) transforms the reversible Equation (2.5) with collision integral (3.39) also into the irreversible Boltzmann Equation (3.46). It follows that the factorization (3.47) masks the true cause for appearance of the irreversibility in the kinetic Equation (3.46).
The stated ideas about the transition of information from initial conditions to resulting equations allow submitting additional argument in favor of strong spatial dependence of the one-particle distribution function ![]() on the scale of particle size. Suppose that the
on the scale of particle size. Suppose that the ![]() function weakly varies upon x1 on l0 scale. In this case, the
function weakly varies upon x1 on l0 scale. In this case, the ![]() function can be identified with number of
function can be identified with number of ![]() -particles in unit volume element near point x1. Then, it will be impossible to distinguish one direction of evolution from another by means of initial conditions for the
-particles in unit volume element near point x1. Then, it will be impossible to distinguish one direction of evolution from another by means of initial conditions for the ![]() function, because, in accordance with the assumption, the
function, because, in accordance with the assumption, the ![]() function will not contain the information on mutual arrangement of particles. The
function will not contain the information on mutual arrangement of particles. The ![]() one-particle distribution function obeys the first reversible equation of BBGKY hierarchy (2.4). Thus, having disappeared from the initial conditions, direction of evolution identified with irreversibility does not appear in the equation. That is why, the assumption made will not allow for a description of both directions of evolution in the terms of the
one-particle distribution function obeys the first reversible equation of BBGKY hierarchy (2.4). Thus, having disappeared from the initial conditions, direction of evolution identified with irreversibility does not appear in the equation. That is why, the assumption made will not allow for a description of both directions of evolution in the terms of the ![]() function. Appearance of this possibility as a result of further roughening, which ensures the transition to the kinetic stage, is excluded because the roughening able to lose, but not to introduce new information about the system. Thus, the loss of the possibility of interpretation of both directions of evolution in terms of the
function. Appearance of this possibility as a result of further roughening, which ensures the transition to the kinetic stage, is excluded because the roughening able to lose, but not to introduce new information about the system. Thus, the loss of the possibility of interpretation of both directions of evolution in terms of the ![]() function disproves the assumption was made.
function disproves the assumption was made.
4. Discussion
Evolution of function called entropy is the indicator of reversibility of equation. Every function presented above, Equations (2.3), (2.8), (2.10), allows to form own entropy. At the dynamic description level the system is characterized by the dynamic entropy,
![]() (4.1)
(4.1)
The ![]() function corresponds to the K-system of
Gibbs
ensemble, k is the
Boltzmann
constant. At the initial description stage of the statistical level the system is characterized by the
function corresponds to the K-system of
Gibbs
ensemble, k is the
Boltzmann
constant. At the initial description stage of the statistical level the system is characterized by the ![]() Gibbs
entropy,
Gibbs
entropy,
![]() (4.2)
(4.2)
At the kinetic and hydrodynamic description stages the system is characterized by the ![]() Boltzmann
entropy. Besides the
Boltzmann
entropy. Besides the ![]() entropy, the
entropy, the![]() ,
, ![]() pair entropy may also characterize the system,
pair entropy may also characterize the system,
![]() (4.3)
(4.3)
![]() (4.4)
(4.4)
![]() (4.5)
(4.5)
Evolution of the ![]() function,
function, ![]() is defined by two factors, by the
is defined by two factors, by the ![]() entropy production in the system and the
entropy production in the system and the ![]() entropy outflow through the surface confining the system [12] [19] ,
entropy outflow through the surface confining the system [12] [19] ,
![]() (4.6)
(4.6)
The system does not produce the dynamic entropy, ![]() , regardless of characteristic features of processes within it. The
Gibbs
entropy also is not produced by the system,
, regardless of characteristic features of processes within it. The
Gibbs
entropy also is not produced by the system,![]() . Therefore, in accordance with (4.6), the absence of entropy outflow through the surface confining the system ensures conservation in time both the
. Therefore, in accordance with (4.6), the absence of entropy outflow through the surface confining the system ensures conservation in time both the ![]() dynamic entropy and the
dynamic entropy and the ![]() Gibbs
entropy [12] . The absence of production of the dynamic entropy is the indicator of reversibility of the classic mechanics equations. The absence of production of the
Gibbs
entropy is the indicator of reversibility of equations of the BBGKY hierarchy.
Gibbs
entropy [12] . The absence of production of the dynamic entropy is the indicator of reversibility of the classic mechanics equations. The absence of production of the
Gibbs
entropy is the indicator of reversibility of equations of the BBGKY hierarchy.
The irreversible equations of kinetics and hydrodynamics demonstrate qualitatively different behavior. Depending on the characteristic features of processes within non-equilibrium system the binary collisions of particles either generate or absorb the entropy, ![]() ,
, ![]() ,
,![]() . Both the
. Both the ![]() Boltzmann
entropy (4.3) and the
Boltzmann
entropy (4.3) and the![]() ,
, ![]() pair entropy (4.4), (4.5) have quite definite physical sense; they meet the volume which system occupies in the G-space [6] [19] . Thus, the system evolution is accompanied by change of its volume in the G-space.
pair entropy (4.4), (4.5) have quite definite physical sense; they meet the volume which system occupies in the G-space [6] [19] . Thus, the system evolution is accompanied by change of its volume in the G-space.
The temporal conservation of entropy for system that evolves to the state of statistical equilibrium at its detailed description (at high accuracy level) is noted by
J.
Gibbs
on the classical example with dye [20] . According to
Gibbs
, the temporal change of entropy is possible only when a coarse description.
Among other things, the entropy specifies the degree of smearing system macroscopic state upon acceptable microscopic states. At the dynamic description level the microscopic state that corresponds to given macroscopic state is quite concrete. At the initial stage of the statistical level, the absence of entropy outflow through the surface confining the system ensures the conservation of the degree of smearing system macroscopic state upon acceptable microscopic states. At the kinetic and hydrodynamic stages, the system evolution is accompanied by change of the degree of smearing due to non-zero entropy production.
The transition from the classic mechanics equations to the hydrodynamics equations is a successive multistep process of loss of excess information about the system. During this transition a set of roughening operations is performed but only one of these operations transforms the reversible equations into the irreversible ones. At the first step of roughening the description of an individual system is replaced by description of the ensemble of systems. The ![]() ensemble distribution function (2.3) obeys the Liouville equation (2.4). The Liouville equation is reversible, that is, the first roughening step does not lead to appearance of the irreversibility.
ensemble distribution function (2.3) obeys the Liouville equation (2.4). The Liouville equation is reversible, that is, the first roughening step does not lead to appearance of the irreversibility.
The second roughening step reduces the ordinal number of partial distribution functions. The second step is accompanied by loss of information about the position in phase space of the particles in turn. If the ![]() distribution function contains the information about the position of all N particles in the phase space, then the
distribution function contains the information about the position of all N particles in the phase space, then the ![]() function contains such information only about s particles of the system regardless of the position in phase space of the remaining
function contains such information only about s particles of the system regardless of the position in phase space of the remaining ![]() particles. Every equation of the BBGKY hierarchy (2.4) is reversible, that is, the second step of roughening also does not lead to appearance of the irreversibility.
particles. Every equation of the BBGKY hierarchy (2.4) is reversible, that is, the second step of roughening also does not lead to appearance of the irreversibility.
The irreversibility appears at the next roughening step after transition from the initial description stage to the kinetic and hydrodynamic stages. Equation (3.7) is invariant with respect to inversion of time and velocities. Replacing the exact function on the left hand side of Equation (3.7) by its average over impact parameters (3.9) eliminates the reversibility of Equation (3.7), that is, Equation (3.10) becomes irreversible. Replacing (3.9) closes one of two directions for time reckoning. It means that both Equation (3.10) and the direct set (3.14) are valid for the progressive direction of timing on the time axis pointing from the past to the future.
Equation (3.16) is invariant with respect to inversion of time and velocities. Replacing the exact function on the right hand side of Equation (3.16) by its average over impact parameters (3.17) eliminates the reversibility of Equation (3.16), that is, Equation (3.19) becomes irreversible. Replacing (3.17) closes one of two directions for time reckoning. It means that both Equation (3.19) and the reverse set (3.23) are valid for the progressive direction of timing on the time axis pointing from the future to the past. Note that solutions to the set (3.23) are also suitable for modeling observed system evolution with regressive timing along the time axis pointing from the past to the future.
The local pair entropy corresponding to the direct equations for pair distribution functions (3.14) and the multimoment hydrodynamics equations they yield can only be produced in the system due to binary collisions at any space point x and at any instant t, ![]() [6] . Thus, at any instant t binary collisions merely rise the pair entropy of the system,
[6] . Thus, at any instant t binary collisions merely rise the pair entropy of the system,![]() . Such behavior of the entropy is in full accordance with the second law of thermodynamics. The solutions to the direct multimoment hydrodynamics equations describe the direction of evolution of the system that is everywhere and every second is found in nature.
. Such behavior of the entropy is in full accordance with the second law of thermodynamics. The solutions to the direct multimoment hydrodynamics equations describe the direction of evolution of the system that is everywhere and every second is found in nature.
The local pair entropy corresponding to the reverse equations for the pair distribution functions (3.23) and the reverse multimoment hydrodynamics equations they yield can only be absorbed in the system due to binary collisions at any space point x and at any instant![]() ,
, ![]() [6] [9] . Thus, at any instant
[6] [9] . Thus, at any instant ![]() binary col-
binary col-
lisions absorb the pair entropy of the system,![]() . The solutions to the reverse multimoment hydro-
. The solutions to the reverse multimoment hydro-
dynamics equations describe the evolution of the system in the opposite direction, which, as is commonly believed, is extremely rare in nature.
In [6] , it is shown that production of the
Boltzmann
local entropy![]() , generally speaking, is not a strictly positive value. The growth of the
Boltzmann
entropy due to binary collisions takes place only at a weak deviation of system state from the state of statistical equilibrium. In the problem on flow around a sphere [6] , the space regions were discovered where the
Boltzmann
local entropy was absorbed due to binary collisions. The entropy absorption appeared in stable system at rather high values of
Reynolds
number. This property of the
, generally speaking, is not a strictly positive value. The growth of the
Boltzmann
entropy due to binary collisions takes place only at a weak deviation of system state from the state of statistical equilibrium. In the problem on flow around a sphere [6] , the space regions were discovered where the
Boltzmann
local entropy was absorbed due to binary collisions. The entropy absorption appeared in stable system at rather high values of
Reynolds
number. This property of the ![]() function is the main reason why the pair entropy should be preferred to the
Boltzmann
entropy when interpreting highly non-equilibrium phenomena.
function is the main reason why the pair entropy should be preferred to the
Boltzmann
entropy when interpreting highly non-equilibrium phenomena.
Let us refer again to the example, Figure 1. Suppose that at the time ![]() the direction of the velocities of all the particles are reversed without changing the positions of particles (Figure 1(c)). This inversion is a hardly probable event. Then, by the time
the direction of the velocities of all the particles are reversed without changing the positions of particles (Figure 1(c)). This inversion is a hardly probable event. Then, by the time![]()
![]() , in accordance with the laws of classic mechanics, all the particles will return to the left side of the vessel. Since the time
, in accordance with the laws of classic mechanics, all the particles will return to the left side of the vessel. Since the time![]() , let us reckon the time in the regressive direction along the time axis pointing from the past to the future,
, let us reckon the time in the regressive direction along the time axis pointing from the past to the future, ![]() within
within![]() . Beginning from the time
. Beginning from the time ![]() up to the time
up to the time![]() , let some solution to direct set (3.14) describes the process of filling of the vessel. The inversion of velocities and time supplemented with inversion of the reference axes of the velocities and time space transforms the direct Equation (3.14) into the reverse Equation (3.23) [9] . Then, beginning from the time
, let some solution to direct set (3.14) describes the process of filling of the vessel. The inversion of velocities and time supplemented with inversion of the reference axes of the velocities and time space transforms the direct Equation (3.14) into the reverse Equation (3.23) [9] . Then, beginning from the time ![]() up to the time
up to the time![]() , the corresponding solution to the reverse Equation (3.23) will describe the process of returning the gas into the left side of the vessel. Generally speaking, the process of returning the gas from the state realized at the time
, the corresponding solution to the reverse Equation (3.23) will describe the process of returning the gas into the left side of the vessel. Generally speaking, the process of returning the gas from the state realized at the time ![]() (Figure 1(c)) into the state achieved by the time
(Figure 1(c)) into the state achieved by the time ![]() (Figure 1(a)) has no relation with the choice of direction of timing. This process is determined exclusively by the system initial conditions.
(Figure 1(a)) has no relation with the choice of direction of timing. This process is determined exclusively by the system initial conditions.
Let in closed vessel, by the time ![]() the conditions completely identical to those, which occurred at the time
the conditions completely identical to those, which occurred at the time ![]() after inversion in velocities space (Figure 1(c)), are established by itself. In principle, such an event is real, as it does not contradict the conservation laws. However, it is extremely unlike at a sufficiently large number of particles within the vessel. The durability of time interval
after inversion in velocities space (Figure 1(c)), are established by itself. In principle, such an event is real, as it does not contradict the conservation laws. However, it is extremely unlike at a sufficiently large number of particles within the vessel. The durability of time interval ![]() is no importance in this case. Then, by the time
is no importance in this case. Then, by the time ![]() all the particles of gas will be concentrated in left side of the vessel,
all the particles of gas will be concentrated in left side of the vessel,![]() . The process of returning the gas occurs for the progressive direction of timing on the time axis pointing from the past to the future. This process is absolutely identical to that one, which occurred within time interval between
. The process of returning the gas occurs for the progressive direction of timing on the time axis pointing from the past to the future. This process is absolutely identical to that one, which occurred within time interval between ![]() and
and ![]() for the regressive direction of timing on the same time axis. Two identical processes should be described by the same equations. Therefore, returning the gas into the left side of the vessel occurred within time interval between
for the regressive direction of timing on the same time axis. Two identical processes should be described by the same equations. Therefore, returning the gas into the left side of the vessel occurred within time interval between ![]() and
and ![]() for the progressive direction of timing on the time axis pointing from the past to the future should also be described by the reverse Equation (3.23). So, the reverse Equation (3.23) are suitable for description of processes occurring with progressive timing on the time axis pointing from the past to the future.
for the progressive direction of timing on the time axis pointing from the past to the future should also be described by the reverse Equation (3.23). So, the reverse Equation (3.23) are suitable for description of processes occurring with progressive timing on the time axis pointing from the past to the future.
This example returns us to the days of
L.
Boltzmann
, when there were controversial debates about the correctness of the
Boltzmann
equation and the H-theorem it yields. Opponents of L. Boltzmann, E. Zermelo and J. Loschmidt, gave examples of processes that are not described by the Boltzmann equation [21] [22] . Namely,
J.
Loschmidt
proposed to reverse the sign of velocities of all the particles at the time![]() , (Figure 1(c)), and
E.
Zermelo
proposed to wait until the time
, (Figure 1(c)), and
E.
Zermelo
proposed to wait until the time ![]() when the condition shown in Figure 1(c) will be established by itself.
L.
Boltzmann
was unable to refute the arguments of the opponents. He was forced to acknowledge the existence of processes that can not be described in the frameworks of his theory. However,
L.
Boltzmann
noticed that his theory predicts the direction of evolution for overwhelming majority of processes occurred in nature. At the same time, the processes that the opponents cited are extremely unlikely, i.e., almost unreal [16] [23] [24] .
when the condition shown in Figure 1(c) will be established by itself.
L.
Boltzmann
was unable to refute the arguments of the opponents. He was forced to acknowledge the existence of processes that can not be described in the frameworks of his theory. However,
L.
Boltzmann
noticed that his theory predicts the direction of evolution for overwhelming majority of processes occurred in nature. At the same time, the processes that the opponents cited are extremely unlikely, i.e., almost unreal [16] [23] [24] .
Indeed, at low deviation of the system state from the state of statistical equilibrium, as
L.
Boltzmann
predicted, the conditions directed the system along the unlikely path arise extremely rarely. However, with the increase of departure from the state of statistical equilibrium the probability of occurrence of such conditions is growing. Penetration into the instability field confirmed this assumption. It turned out that in the instability field the probability of the occurrence of conditions that forces the system to move in the unlikely direction is about the value of basic order. The movement of unstable system in the unlikely direction becomes a regular event. The reverse movement provides the periodicity of unstable processes occurring in the system. It prevents the disintegration of the system losing its stability [8] .
5. Conclusions
The original equations of classic mechanics do not contain information about the direction of system evolution. This information is enclosed in the initial conditions and the direction of evolution is defined by the mutual arrangement of system particles. Roughening the original equations together with the initial conditions is a successive process to exclude the excessively detailed information and obtain coarse equations suitable for use. The information on the spatial position of an individual particle is lost at one of the roughening steps. Therefore, at this roughening step the initial conditions lost the information about the direction of system evolution. At the same time, at this roughening step the direction of evolution identified with the irreversibility appears in the equations. Therefore, the irreversibility did not appear from nothing in the coarse equations, it transited from initial conditions to equations by means of the roughening process. The substitutions (3.9) and (3.17) are responsible for appearance of the irreversibility in the kinetics and hydrodynamics equations. These substitutions are by no means a sort of manipulation with impact parameters b and![]() . They are a logical and consistent means of deriving the approximation that contains no information unnecessary in kinetic and hydrodynamic description stages. The averaging (3.8) is carried out with respect to collision parameters of two particles, which are approaching each other before their collision. The direct equations of kinetics and hydrodynamics are the result of this roughening. These equations are true for the progressive direction of timing on the time axis pointing from the past to the future. The averaging (3.18) is carried out with respect to collision parameters of two particles, which are diverging after collision with each other. The reverse equations of kinetics and hydrodynamics are the result of this roughening. These equations are true for the progressive direction of timing on the time axis pointing from the future to the past. Solutions to the reverse equations of kinetics and hydrodynamics are also applicable to interpret observed system evolution with regressive timing along the time axis pointing from the past to the future.
. They are a logical and consistent means of deriving the approximation that contains no information unnecessary in kinetic and hydrodynamic description stages. The averaging (3.8) is carried out with respect to collision parameters of two particles, which are approaching each other before their collision. The direct equations of kinetics and hydrodynamics are the result of this roughening. These equations are true for the progressive direction of timing on the time axis pointing from the past to the future. The averaging (3.18) is carried out with respect to collision parameters of two particles, which are diverging after collision with each other. The reverse equations of kinetics and hydrodynamics are the result of this roughening. These equations are true for the progressive direction of timing on the time axis pointing from the future to the past. Solutions to the reverse equations of kinetics and hydrodynamics are also applicable to interpret observed system evolution with regressive timing along the time axis pointing from the past to the future.
Suppose that each system in ensemble consists of N particles. Let the evolution of ensemble systems be described by the direct set (3.14). At some time t, let us reverse the sign of velocities of all N particles of all the systems in ensemble, ![]() ,
, ![]() , and reckon time in the direction of its decrease,
, and reckon time in the direction of its decrease,![]() . As a result of this inversion, in accordance with the laws of classic mechanics, all the particles of all the systems in ensemble will move in the opposite direction. The reverse Equation (3.23) should describe the reverse movement of particles. Indeed, reverse Equation (3.23) can be obtained from direct Equation (3.14) also by the inversion of velocities and time. However, to implement the reverse movement in system, it is not necessary to change the direction of timing. It is enough to change the direction of velocities of all the particles of system, then, the system will move back with progressive direction of timing.
. As a result of this inversion, in accordance with the laws of classic mechanics, all the particles of all the systems in ensemble will move in the opposite direction. The reverse Equation (3.23) should describe the reverse movement of particles. Indeed, reverse Equation (3.23) can be obtained from direct Equation (3.14) also by the inversion of velocities and time. However, to implement the reverse movement in system, it is not necessary to change the direction of timing. It is enough to change the direction of velocities of all the particles of system, then, the system will move back with progressive direction of timing.
Processes occurring in nature are objective events, while the choice of the direction of timing on the time axis is a subjective process. Time is reckoned by an observer, while processes occurring in nature are absolutely insensitive to the direction in which the observer counts the time. Therefore, if the reverse Equation (3.23) are capable to describe the reverse motion of systems in ensemble for progressive direction of timing on the time axis pointing from the future to the past, then the same equations must describe the reverse movement of systems in ensemble for progressive direction of timing on the time axis pointing from the past to the future.
This means the followings. Let us reckon the time in progressive direction both along the time axis pointing from the future to the past and along the time axis pointing from the past to the future. Let us begin to observe some phenomenon, agreeing upon the origin for two directions of timing. On finding solution to the reverse Equations (3.23), we obtain the distribution of hydrodynamic values, their spatial and temporal derivatives. Let the calculated values agree well with the values observed in the direction of increasing time on the time axis pointing from the future to the past. Then, we also find the agreement between the calculated reverse distributions of hydrodynamic values, their spatial and temporal derivatives and the values observed in the direction of increasing time on the time axis pointing from the past to the future. However, there exist no direct equations that would satisfy the distributions of reverse hydrodynamic values, their spatial and temporal derivatives.
Cite this paper
Igor V.Lebed, (2014) About Appearance of the Irreversibility. Open Journal of Fluid Dynamics,04,298-320. doi: 10.4236/ojfd.2014.43023
References
- 1. Lebed, I.V. and Umanskii, S.Y. (2007) The Appearance and Development of Turbulence in a Flow Past a Sphere: Problems and the Existing Approaches to Their Solution. Russian Journal of Physical Chemistry B, 1, 52-73.
- 2. Lebed, I.V. and Umanskii, S.Y. (2012) On the Possibility of Improving Classic Hydrodynamics Equations by an Increase in the Number of Hydrodynamic Values. Russian Journal of Physical Chemistry B, 6, 149-162.
- 3. Lebed, I.V. (2013) About the Prospects for Passage to Instability. Open Journal of Fluid Dynamics, 3, 214-229.
http://dx.doi.org/10.4236/ojfd.2013.33027
- 4. Lebed, I.V. (1996) Method of Two-Particle Distribution Functions. Hydrodynamic Equations. Chemical Physics Reports, 15, 861-883.
- 5. Lebed, I.V. (1997) The Method of Pair Functions as Applied to the Problem of a Flow around a Quiescent Solid Sphere. Chemical Physics Reports, 16, 1263-1301.
- 6. Lebed, I.V. (1998) About the Behavior of the Entropy of a Gas Flow Losing Its Stability. Chemical Physics Reports, 17, 411-439.
- 7. Lebed, I.V. (2014) Development of Instability in the Problem of Flow around a Sphere. Russian Journal of Physical Chemistry B, 8, 240-253.
- 8. Lebed, I.V. (2014) Multimoment Hydrodynamics in Problem on Flow around a Sphere: Entropy Interpretation of the Appearance and Development of Instability. Open Journal of Fluid Dynamics, 4, 163-206.
http://dx.doi.org/10.4236/ojfd.2014.42015
- 9. Lebed, I.V. (1996) Hydrodynamic Equations Stemming from Two Particle Distributions in the Limit of Weak Non-equilibrium. Analysis of Invertibility of Equations. Chemical Physics Reports, 15, 1725-1750.
- 10. Einstein, A. and Besso, M. (1972) Correspondence 1903-1955. Hermann, Paris.
- 11. Prigogine, I. (1999) Laws of Nature, Probability and Time Symmetry Breaking. Physica A: Statistical Mechanics and Its Applications, 263, 528-539.
http://dx.doi.org/10.1016/S0378-4371(98)00527-5
- 12. Liboff, R.L. (1969) Introduction to the Theory of Kinetic Equations. Willey, New York/London/Sydney/Toronto.
- 13. Bogolubov, N.N. (1946) The Problems of Dynamic Theory in Statistical Physics. Gostechizdat, Moscow-Leningrad.
- 14. Lebed, I.V. (1990) Equations of Pair Distribution Functions. Chemical Physics Letters, 165, 226-228.
http://dx.doi.org/10.1016/0009-2614(90)85433-D
- 15. Lebed, I.V. (1995) Derivation of the Equations for Pair Distribution Functions. Chemical Physics Reports, 14, 599-615.
- 16. Boltzmann, L. (1896) Entgegnung auf die Warmetheoretischen Betrachtungen des Hrn. Zermelo. Annalen der Physik, 57, 773-784.
- 17. Orban, J. and Bellemance, A. (1967) Velocity-Inversion and Irreversibility in a Dilute Gas of Hard Discs. Physics Letters A, 24, 1132-1140.
- 18. Lebed, I.V. (1995) Equations for a One-Particle Distribution Function. Chemical Physics Reports, 13, 1132-1140.
- 19. Ferziger, J.H. and Kaper, H.G. (1972) Mathematical Theory of Transport Processes in Gases. North-Holland Publishing Company, Amsterdam.
- 20. Gibbs, J.W. (1982) Thermodynamics. Statistical Mechanics. Nauka, Moscow.
- 21. Zermelo, E. (1896) Uber einen Satz der Dynamik and die mechanische Warmetheorie. Annalen der Physik, 57, 485-494.
- 22. Loschmidt, J. (1876) Uber den Zustand des Warmegleichgewichtes eines Systems von Korpern mit Rücksicht auf die Schwerkraft. Wien. Ber., 73, 128-142.
- 23. Boltzmann, L. (1894-1895) On Certain Question of the Theory of Gases. Nature, 51, 413-415.
http://dx.doi.org/10.1038/051413b0
- 24. Boltzmann, L. (1897) Zu Hrn. Zermelo’s Abhandlung “Uber die mechanische Erklarung Irreversibler Vorgangre”. Annalen der Physik, 60, 392-398.




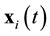 ,
,  ,
, 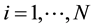 , represent respectively the coordinates and velocities of the particles, i.e., the point in 6N-dimensional phase space. The evolution of the variables
, represent respectively the coordinates and velocities of the particles, i.e., the point in 6N-dimensional phase space. The evolution of the variables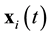 ,
, 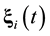 ,
, 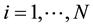 , is calculated in the frameworks of the equations of classic mechanics. Let us carry out at some time t the inversion in velocity space and in time,
, is calculated in the frameworks of the equations of classic mechanics. Let us carry out at some time t the inversion in velocity space and in time, 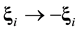 ,
, 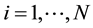 ,
,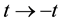 . It turns out that the classic mechanics equations are invariant with respect to this operation, that is, the equations of classic mechanics are reversible. This means the following. Let at time t0 the initial conditions
. It turns out that the classic mechanics equations are invariant with respect to this operation, that is, the equations of classic mechanics are reversible. This means the following. Let at time t0 the initial conditions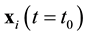 ,
, 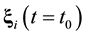 ,
, 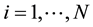 , are specified. Let by the time
, are specified. Let by the time 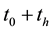 the equations of classic mechanics transfer them into
the equations of classic mechanics transfer them into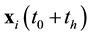 ,
, 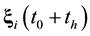 ,
,  , respectively. Then, after inversion at time
, respectively. Then, after inversion at time