Open Journal of Fluid Dynamics
Vol.04 No.02(2014), Article ID:46243,13 pages
10.4236/ojfd.2014.42013
Novel Power Law of Turbulent Spectrum
Chusak Osonphasop1, Takeo R. M. Nakagawa2
1Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Australia
2Pan-Asian Center for the Independent Liberal Study of Science Technology and the Humanities, Jusup Balasagyn Kyrgyz National University, Bishkek, Kyrgyz Republic
Email: mummykat@hotmail.com, npo.hakusan@kjc.biglobe.ne.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2014; revised 24 April 2014; accepted 2 May 2014
ABSTRACT
This paper is concerned with novel power law of turbulent energy spectrum and the relevant experiment in tidal current. The power law in the inertial sub-range has been proposed in such a way that the power of the one-dimensional turbulent energy spectrum varies from 0 to −2 approximately, but it is accompanying the small oscillation with increasing the wave number. The well-known Kolmogorov −5/3 power law is merely one facet, to appear within the present proposed novel power law. The turbulent energy spectra (Su, Sv, Sw) in x-, y- and z-directions, respectively oscillate with the wave number. It is found that the turbulent in the tidal currents is three dimensional, and the intermittence of momentum transport is a predominant and characteristic feature in tidal current.
Keywords:
Energy Spectrum, Kinetic Theory, Tidal Current, Inertial Sub-Range, Turbulence Measurement, Power Law

1. Introduction
Late Dr. Shunichi Tsugé (1932.4.1-2003.6.21) has elaborated a new theory of turbulence on the basis of Newton mechanics and mathematical probability or statistical mechanics so at to elucidate the motion of a system consisting of N particles with mathematics and computer [1] - [4] . So far, his theory has been successfully applied to boundary layer flow [5] , turbulent combustion [6] - [9] , mixing layer flow [10] , grid-produced turbulence [11] - [14] , Bénard convection [15] [16] , turbulent energy spectrum [17] . Most crucial feature of Tsugé’s theory is that it includes no empirical constant, contrary to almost all the other existing turbulent theories such as Prandtl mixing length theory and k - ε Model. In this sense, Tsugé’s theory is only one true turbulent theory among the many, for soundness and usefulness of his theory have been well confirmed by the relevant experiments [7] - [19] . Major Tsugé’s papers on turbulence research have been collected by the senior author [18] [19] , which are accessible at National Diet Library in Tokyo.
Intermittency in turbulence is an essential feature in laboratory [20] [21] , so measurements of turbulence have been also conducted in geophysical flow to examine it [22] - [26] . However, even so tremendous efforts to clarify the turbulence phenomena have been continued by many researchers in the world since the end of 19 century by Reynolds [27] , still relatively little is known about this. Only success known in this research field except for Tsugés achievements is made by Kolmogorov [28] , who obtain a power law of turbulent energy spectrum in the inertial sub-range in terms of dimensional analysis, this is known as −5/3 law widely.
It is, therefore, natural to examine what law can be derived by Tsugé’ theory, if it is rigorous theory of turbulence currently existing in this globe. Indeed, this prompts us to conduct this study.
The structure of this paper is as follows:
1) Introduction, 2) Liouville equation and BBGKY hierarchy, 3) Navier-Stokes equation is only valid for laminar flow, but not for turbulent flow, 4) Experimental (4.1 Velocity probes, 4.2 Underwater tower, 4.3 Experimental procedure and technique, 4.4 Location and site conditions, 4.5 Results of turbulence measurements, 4.6 Turbulence statistics), 5) Proposition of novel power law of turbulent energy spectrum and its comparison with the experiment, and 6) Conclusion.
The main purpose of the present paper is to derive the novel power law of turbulent energy spectrum, based on the theory and experiment.
2. Liouvill Equation and BBGKY Hierarchy
It is well known that the Liouville equation describes the motion of N particles, and it is 6 N Dimensions. However, problem is that number of particles involved is too many to trace their trajectories. For example, order of 1020 molecules is contained in the air of 1 cm3 or in a water droplet of radius of 1mm. Because information to specify position (x, y, z) and velocity (u, v, w) for each the molecule is required, one must know the position and velocity for N molecules.
There is no question that if we could obtain the solution of Liouville equation completely, it is said that motion of particles is solved, so that turbulence may not be problem anymore. However, this task is so difficult that no genius and no computer have not ever succeeded. Non the less, there is still some room that human beings would solve the Liouville equation describing motion of N (⇢∞) particles some day in future.
Bogoliubov [29] has proposed so-called “Synchronization Principle” as a practical mathematical idea to overcome the forgoing despairing situation. According to this principle, “since any particle is considered to be equal to each other, except for objective particles, one is allowed to smear out the rest particles by integrating with respect to the position as well as velocity”. For example, integration to smear the unnecessary particles ranging from (s + 1)th to Nth may be done in order to obtain the distribution function for s-molecules, and we get it as follows,

with
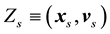
In this way, the smeared particles now form the background for the objective particles. Surprisingly, this method has succeeded to reduce number of objective particles from N to 1. This whole procedure is called BBGKY hierarchy theory. BBGKY hierarchy is summarized in Table 1, where N is total number of particles.
Tsugé [1] has rigorously proven based on the kinetic theory that two-particle level of Liouville equation is reduced to Kármán-Howarth equation [30] , which was derived by them heuristically or phenomenologically. In another words, this means that Kármán-Howarth equation has acquired kinetic theoretical background.
The kinetic theoretical base for Reynolds averaged Navier-Stokes equation, 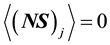 has been given by
has been given by
Tsugé & Sagara [3] . It is realized that Liouville equation for N = 1 particle, D(f) = J(f2) in the kinetic theory corresponds to Reynolds averaged Navier-Stokes equation in fluid mechanics.
The kinetic theoretical base for Navier-Stokes equation, 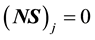 has been provided by Chapman [31] and Enskog [32] independently in 1917. It has been proven mathematically that Liouville equation for N = 1 particle with binary molecular chaos, D(f) = J(ff) with f2 = ff, in the kinetic theory corresponds to Navier-Stokes equation in fluid mechanics. That is, Navier-Stokes equation never includes two-point, or double correlation, so that this equation is not even relevant to turbulence in general. This statement is also supported by the isotropic assump-
has been provided by Chapman [31] and Enskog [32] independently in 1917. It has been proven mathematically that Liouville equation for N = 1 particle with binary molecular chaos, D(f) = J(ff) with f2 = ff, in the kinetic theory corresponds to Navier-Stokes equation in fluid mechanics. That is, Navier-Stokes equation never includes two-point, or double correlation, so that this equation is not even relevant to turbulence in general. This statement is also supported by the isotropic assump-
Table 1. BBGKY hierarchy.
Note 1: Boltzmann equation and Navier-Stokes equation D(f) = J(ff) ⇒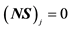 ; with f2 = ff: binary molecular chaos hypothesis
; with f2 = ff: binary molecular chaos hypothesis
(Bolzmann equation) (Navier-Stokes equation),
where f is the Bolzmann function, and f2 is distribution function for two particles. Note 2: Symbol < > in this Table denote ensemble average. Note 3: In Kármán-Howarth equation [30] , 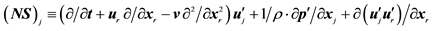 , and
, and  is the Klimontovich microscopic velocity, where microscopic density
is the Klimontovich microscopic velocity, where microscopic density  [33] is defined by
[33] is defined by  where Z(x, v) stands for a point in μ space, Z(s)(t) the trajectory of the sth particle in this space, δ Dirac’s delta function in six-dimensional space, and the summation is over all particle of N.
where Z(x, v) stands for a point in μ space, Z(s)(t) the trajectory of the sth particle in this space, δ Dirac’s delta function in six-dimensional space, and the summation is over all particle of N.
tion adopted when this equation was derived [34] .
The above sketch of Navier-Stokes equation would infer its severe limitation to the application for turbulence, to be also discussed in the next section.
3. Navier-Stokes Equation Is Only Valid for Laminar Flow, But Not for Turbulent Flow
Tsugé equation or Kármán-Howarth equation retains the binary molecular correlation or two-point correlation. though Boltzmann equation or Navier-Stokes equation has not this correlation. This denotes that Navier-Stokes equation has no potential to describe turbulence, for which two-point correlation is essential and so it must be taken into consideration. Hence, It is impossible to exaggerate that Navier-Stokes equation is only valid for laminar flow, but not for turbulent flow. It is, therefore, necessary for us to break away from the current turbulent theory based on Boltzmann equation, or Navier-Stokes equation (NS)j = 0.
Even though we have Kármán-Howarth equation since 1938, it must be noted that all of the previous turbulent theories are limited only to homogeneous and isotropic turbulence, so that such a theory is useless not only from engineering point of view, but also from physical point of view. In the history of turbulent researches, one exception in which Navier-Stokes equation may be useful is in the inertial sub-range, for here turbulence itself is homogeneous and isotropic approximately. It is considered that this is the reason why Kolmogorov’s concept of inertial sub range has made some success to describe turbulent behaviors [28] . Another example is chaos [35] [36] , though it is not turbulence actually. Since chaos appears just before the flow becomes turbulent, Navier- Stokes equation could capture the motion of fluid.
Tsugé equation is concisely expressed by
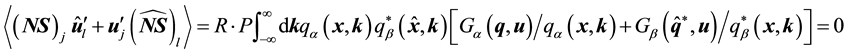
with
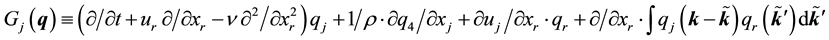
where Einstein’s rule for tensor notation is used. Note this rule has been adopted without mentioning through the paper.
Tsugé equation can be solved by the method of variable separation at two points x, and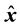 , so that this equation is divided into two independent separate equations through the separation constant λ = ik.
, so that this equation is divided into two independent separate equations through the separation constant λ = ik.
As the closure condition at the tertiary molecular chaos, q2 = q3 (or q2 ≠ 0, q3 = 0) is used. Note that the conventional approach of turbulent theory has adopted the binary molecular chaos exclusively, so Tsugé’s approach with the tertiary molecular chaos has wider freedom in turbulence and thus it must be promising and attractive.
Observable quantity is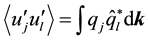 , so that qj and
, so that qj and 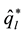 must be obtained at two points x, and
must be obtained at two points x, and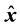 , respectively.
, respectively.
It may be worth noting that uncertainty in the solution is indiscernible, for in future an advanced super-com- puter may solve the series of differential equations governing N particles directly; that is the Liouville equation for N particles in 6 N dimensions must be solved. However, such an enormous information may be not useful, but we should concentrate to provide people in the society necessary and sufficient concise information.
4. Experimental
To obtain turbulent velocity statistics over the depth in a real tidal flow, an experimental data collection program was conducted in Westernport Bay, a large tidal inlet in Victoria, Australia [22] - [24] . This Section describes the methodology and presents the results relevant to the present research.
4.1. Velocity Probes
While an array of electro-magnetic current meters would have given two and possibly three-component data, the cost would have been several times the budget for the entire project. Because no other commercially available devices within the budget range were suitable, an existing velocity probe was redesigned especially for this study in order to measure the three-components of turbulent velocity fluctuations. It was a drag-type probe in which the flowing water creates a drag force on a perforated sphere (a practice golf ball), mounted at the free end of a cantilever as depicted in Figure 1.
Figure 1. Schematic diagram of the 3-component velocity probe.
The diameter of the sphere is of 42 mm and in a current of 0 - 1.00 m/s it is capable of resolving velocity component fluctuations from 0 to better than 4 HZ. The shape of the probe is shown in this figure.
For a turbulence intensity of 0% - 20%, the effect of inertia on the probe is found, by experiments in a calibration rig, to be insignificant compared to the drag. Assuming the effect of inertia force on the probe is negligible, the voltage readouts from the component strain bridges are proportional to the components of drag force on the sphere. The threshold velocity of the mean velocity component is 0.02 m/s, and for the transverse and vertical components is 0.004 and 0.006 m/s, respectively. The voltages are amplified and low pass filtered to prevent aliasing errors. The velocity probe was calibrated using a reference flow meter that had been calibrated in the laboratory by volumetric measurement. The departure from the theoretical calibration was found to be less than 5%.
4.2. Underwater Tower
The underwater tower [23] which was developed to support the probes is sketched in Figure 2.
It consisted of a column formed of two 4 m lengths of 102 mm diameter steel pipe, mounted on a base of three radial arms, each of which was made of two steel angles 127 × 76 × 10 mm, with spikes for stabilizing the legs in position on the sea bed. The outer end of each leg was tied to the top of the column with a cable tensioned by a hand winch. The lower part of the tower had a universal joint for the vertical alignment of the column on different sea bed configurations. Ropes wrapped around the column were used to minimize the vibration due to vortex shedding in flowing water. The damped natural frequency of the tower was about 10 Hz, which was much higher than that of the energy containing eddies. Thus, the effect due to the vibration of the column is considered to be negligibly small.
4.3. Experimental Procedure and Technique
During this study, the field experiments were conducted from “Triton”, an 8 m cabin launch, “Hydraulics”, a 4.3 m aluminium runabout, and a raft, of the Mechanical Engineering Department, Monash University. Triton housed the minicomputer, power supplies and the other electronic equipment for the data recording system. Hydraulics was used to carry out the topographic survey around the site for the tidal cycle during the data collection, and for transportation between site to site. The raft was made of four 0.2 m3 petrol drums with a small wooden deck and equipped with one-ton hand winch. This raft was used to lift and lower down the three steel legs, which were used to stand and stabilize the underwater column at the site.
4.4. Location and Site Conditions
A total of 15 cruises were conducted in North Arm, a tidal channel in Westernport Bay, Victoria, Australia, as shown in Figure 3. These cruises were undertaken over 3 years, viz., from May 1978 and to November 1981,
Figure 2. Schematic diagram of the instrument tower.
Figure 3. Location of the experimental study. Base map from Google Maps.
following loss of an earlier tower with all equipment. Full utilization of this period was prevented by severe weather, instrument failure and damage, and staff availability.
Four cruises were made in the tidal channel: three in a section of channel with small sand dunes and one in a very rough bed consisting of big and steep sand dunes. Measurements were made of the turbulent velocity fluctuations, bottom topography, wave height, temperature and salinity at different depths. In particular, velocity fluctuation data were collected throughout the tidal cycle of 12.4 hours. Altogether ten 910-second long simultaneous records of the three velocity components (u, v, w) at 6 depths (1, 2, 3, 4, 5 and 6 m above the bed) and thirteen 910-second long records of the three velocity components at respective, 3 depths (1, 2 and 3 m above the bed). Additionally, several 1820-second long records were used to examine the fluctuations having longer period. Mean flow velocities determined from the records at 1, 2, 3, 4, 5, and 6 m above the sea bed.
The effects of wind and surface waves on the flow are negligible, for the channel is protected from the effects of the predominant strong winds and days of data collection were chosen such that the sea was calm and the wind speed less than 5 m/s. Wave height was measured at the instrument tower using a staff gauge, and never exceeded a few centimeters, with wave periods being generally less than 1.0 second. It is quite unlikely that such small waves would cause detectable velocities at the depth of measurement.
Temperature and salinity profiles were made over the depth. In general, the variations of temperature and salinity were found to be random with ranges of 0.2˚C and less than 0.1 ppt, respectively. There was no evidence of a thin surface layer having different temperature or salinity. The lack of such gradients precludes the existence of internal waves.
The sea bed at both locations was sandy, with small dunes at one site and large dunes at the other slightly different results were obtained at the two sites, but only the results from the latter site are presented here. In some measurements over a large dune bed there is evidence that the velocity meter fixed 1m above the bed was in the lee of the upstream dune for part of the measurement time.
It is possible that some error may be introduced into the mean flow due to the zero drift of the instruments, mainly due to thermal effects, but it is estimated that the combined error should be less than 5%. This would not affect the measurement of the turbulence.
4.5. Results of Turbulence Measurements
Figure 4 shows a typical time record of the velocity fluctuation components (u, v, w), together with the Reynolds stress uw at 2 m above the sea bed.
Fluctuations of u, v, and w are distributed around zero with intermittent events, while those of uw indicate much larger instantaneous values changing from a positive value to negative one, and vice versa, where u, v, and w are turbulent velocities in the main, transverse and vertical flow directions, respectively. It is worth noting that the present result for the Reynolds stress in this figure adds another piece of evidence that the intermittent phenomena observed in wind tunnel and laboratory boundary layers can be scaled up to dimensions of geophysical interest [37] .
Figure 4. Typical time records of the velocity fluctuation components (u, v, w), together with the Reynolds stress uw at 2 m above the sea bed.
4.6. Turbulence Statistics
The probability distributions, not shown, of the turbulent velocity fluctuations, together with the turbulent intensity and the turbulent scales in the component directions were determined at the six depths of the measurement in the tidal channel. It was found that the probability distributions of each of the velocity components (u, v, w) were approximately Gaussian, while those of the cross product u∙w were far from Gaussian having large skewness and kurtosis [23] .
It is, therefore, suggested that the intermittency of momentum transport is a predominant and characteristic feature of most geophysical boundary layers, as to be also demonstrated in the present turbulent velocities and energy spectra.
The scatter between records is quite considerable, so no strong systematic variations of turbulent intensity
σu/U, σv/U, σw/U, and 
range of 1 - 6 m above the sea bed, though a weak trend towards higher turbulence intensity at locations closer to the sea bed is shown. It must be noted that somewhat higher turbulence intensities are found in case of the rough bottom configuration comparing with the smooth one. The 95% confidence interval for the normalized turbulence intensities for each component are:
and,
These results indicate that the turbulent intensity in the main flow direction is largest, while that in the vertical direction is the smallest, but only by a very small margin.
4.7. Spectral Analysis
In obtaining a statistically accurate spectral analysis of a turbulence record, an ensemble of time series would be necessary to estimate the spectra by averaging all together. Under controlled conditions such as in the laboratory, any long time series under a steady flow condition can be established relatively easily, and thus by dividing it into shorter ones an ensemble of time series can be obtained. However, in case of tidal flow in the tidal channel as the present study, it is very difficult to obtain even a shorter time series under steady condition. The change in the mean velocity of two successive 910second long records, during three hours of peak flow, is normally within 3 cm/s. The sphere current probes are sometimes fouled by seaweed, for a short time series, even though it is not frequent, but for a long time series the chance of being interrupted by seaweed is much higher.
In this analysis, the spectra are presented as wave number spectra S(k) on log-log plots in order to identify the wave number k dependence clearly. Note this plot is convenient to compare the present results with the existing ones. The wave number spectra S(k) may be transformed from the frequency spectra S(f) by adopting Taylor’s hypothesis, in which the relation of L = UT stands, where L is the length scale, U the local mean flow velocity, and T the period. The wave number k is equal to 1/L, so this is different from the radian wave number 2π/L. The wave number spectrum is thus given as S(k) = S(f)U.
Figure 5 and Figure 6, respectively, show typical turbulence spectrum for each of the components (Su, Sv, Sw) at 1 m and 2 m from the sea bed. It is evident that in the low wave number range Su is the largest, while Sw is the
Figure 5. Three components of turbulent energy spectra (Su, Sv, Sw) at 1 m above the big and steep dunes on the sea bed.
Figure 6. Three components of turbulent energy spectra (Su, Sv, Sw) at 2 m above the big and steep dunes on the sea bed.
smallest. However, at higher wave numbers, the component spectra do not show this trend, but, despite the data scatter of each the measurement, it suggests anisotropy as depicted in these figures.
The magnitude of each of the spectral components decreases slightly with increasing the elevation from the sea bed, but increases with increasing the mean flow velocity U. These spectra never follow −5/3 power law due to Kolmogrorov [28] , but decrease intermittently and/or periodically with wave number, though in average they follow a power law between −5/3 and −2, as predicted by Tsugé [17] and others. Thus, any sound power law of turbulent energy spectrum must express these basic characteristics properly, as to be proposed in the next section.
5. Proposition of Novel Power Law of Turbulent Energy Spectrum and Its Comparison with the Experiment
As early as in 1941, Kolmogorov [28] derived −5/3 power law of turbulent energy spectrum, which looks to have been supported by experiments at least “partially” in later years. It is, however, rather surprising that this law is based on purely dimensional analyses by imposing an intuitive hypothesis of “local homogeneity” for small-scale turbulence. It is more surprising that this famous law has little to do with the dynamic equations of fluid.
Proposed is a novel power law of turbulent energy spectrum in the inertial sub-range based on Tsugé turbulent equation [1] [6] governing turbulent flow: A correction term Ζ is added to the well-known one-dimensional Kolmogorov power law
with
where n is the mode number of fluid vibrations, and coefficients αn and βn are small compared with α0. This new power law has been discovered heuristically, based on the theoretical results by Tsugé [17] , together with the turbulent measurements in the tidal current by Osonphasop [23] and. Osonphasop & Hinwood [22] [24] .
The comparison of the present power law with the experiment suggests us the wide flexibility of this law, and indeed it is realized that this law can interpret any data in principle. It should be noted that the Kolmogorov power law of 
Because turbulence is highly complicated motion of fluid particles in general, it must be time dependent and three dimensional. This is why the Kolmogorov power law has been inquired critically in the light of the sound theoretical and experimental facts.
Figure A2 illustrates Tsugé’s theoretical result on the power law (see Appendix). This figure illustrates how the power law depends on the initial conditions and oscillates with increasing the wave number k1. Whereas Figure 6 delineates Osonphasop’s turbulent energy power spectrum for u, v, and w, respectively, obtained by turbulent measurements at 2 m above the sea bed in the tidal current [23] . This figure indicates that the power spectrum in x-, y-, and z-directions, respectively, neither follow the Kolmogorov power law nor draws straight line, but oscillates depending on each the wavenumber as being captured by the proposed universal power law of the turbulent energy spectrum. The infinite trigonometric series in Z-term will be used as approximate to any oscillation appearing in the energy spectrum.
The present proposed power law of turbulent energy spectrum is of significance for the practical point of view, for it is expressed by a simple mathematical form to be used by engineers. It is believed that discovery of the present law is an essential contribution to the progress of science if one recalls its wide applicability, covering many engineering professional fields such as fluid mechanics, hydraulics, oceanography, geophysical fluid dynamics, astrophysics, and many others.
6. Conclusions
New insights and new knowledge obtained through this study are summarized as follows:
1. It has been confirmed that Navier-Stokes equation has no potential to describe turbulence except for isotropic and homogeneous one.
2. Kolmogorov’s −5/3 power law appears in the small region of k1 in the inertial sub-range, but −2 power law prevails in larger region of k1. It is, therefore, inferred that neither −5/3 power law of the turbulent energy spectrum nor the −2 power law is universal in the inertial sub-range.
3. It is found that though numeral power laws in the inertial sub-range exist, but no law is adequate, so that novel power law of turbulent energy spectrum has been proposed as
with
where n is the mode number of fluid vibrations, and coefficients αn and βn are small compared with α0.
It is clear that this parameter Z is not constant, but depends on the wave number k1, for the spectra oscillate with it. This fact has been confirmed both by Tsugé’ theory and the present experiment in the tidal current.
4. The time records and spectra for the turbulent velocities have clearly demonstrated that the turbulence in the tidal current is highly three-dimensional.
5. It is reassured that the intermittence of momentum transport is a predominant and characteristic feature of geophysical boundary layer.
6. Tsugé equation or Kármán-Howarth equation retains the two-point or double correlation, but Navier-Stokes equation does not: It is, therefore, absolutely necessary for us to use the former equation to solve any problem on turbulence in order not to waste our time.
Acknowledgements
This paper is cordially dedicated to Dr. Shunichi Tsugé (1932.4.1-2003.6.21). The authors are grateful to Senior Research Associate, Dr. Jonathan B. Hinwood, Department of Mechanical and Aerospace Engineering, Monash University, Australia for his permanent support from the very beginning to the current stage in every respects leading to this publication. He has been directing this study as the supervisor for the both authors between 1977 and 1983, so it is certain that this paper never appear without his contribution.
References
- Tsugé, S. (1974) Approach to the Origin of Turbulence on the Basis of Two-Point Kinetic Theory. Physics of Fluids, 17, 22-33. http://dx.doi.org/10.1063/1.1694592
- Tsugé, S. and Sagara, K. (1975) A New Hierarchy System on the Basis of Master Boltzmann Equation for Microscopic Density. Journal of Statistical Physics, 12, 403-425. http://dx.doi.org/10.1007/BF01012885
- Tsugé, S. and Sagara, K. (1976) Kinetic Theory of Turbulent Compressible Flows and Comparison with Classical Theory. Physics of Fluids, 19, 1478-1485. http://dx.doi.org/10.1063/1.861350
- Tsugé, S. (1979) Separation of Variables in Two-Point Kinetic Equations. Physics Letters, 70A, 266-268. http://dx.doi.org/10.1016/0375-9601(79)90118-X
- Tsugé, S. (1970) On the Divergent Growth of Molecular Fluctuations in Classical Shear Flow. Physics Letters, 33A, 145-146. http://dx.doi.org/10.1016/0375-9601(70)90699-7
- Sagara, K. and Tsugé, S. (1976) A Kinetic Theory of Turbulent and Thermal Fluctuations in Compressible Flows. Nielsen Engineering & Research.
- Sagara, K. and Tsugé, S. (1982) A Bimodal Maxwellian Distribution as the Equilibrium Solution of the Two-Particle Regime. Physics of Fluids, 25, 1970-1977. http://dx.doi.org/10.1063/1.863673
- Sagara, K. (1980) Exact Turbulence Correction to Arrhenius Law in the Asymptotic Limit of High Activation Energy. Science & Technology, 21, 191-197.
- Tsugé, S. and Ogawa, S. (1993) Molecular and Turbulent Transports Competing in Premixed Flames. In: Takeno, T., Ed., Turbulent and Molecular Processes in Combustion, Elsevier, 35-50.
- Bai, B. (1995) Solitary Wave Solution of Turbulent Mixing Layer by the Method of Pseudo-Compressibility. Ph.D. Thesis, Institute of Engineering and Mechanics, University of Tsukuba, Tsukuba.
- Nakagawa, T. (1979) A Theory of Decay of Grid-Produced Turbulence. Zeitschrift für Angewandte Mathematik und Mechanik, 59, 648-651. http://dx.doi.org/10.1002/zamm.19790591111
- Nakagawa, T. (1979) On Decay of Grid Produced Turbulence. Department of Mechanical Engineering, Monash Uni- versity, Clayton.
- Nakagawa, T. (1981) The Comparison of a New Theory of Grid-Produced Turbulence with an Experiment. Zeitschrift für Angewandte Mathematik und Mechanik, 62, 6-8.
- Nakagawa, T. and Iida, H. (2012) Statistical Theory of Turbulence by the Late Lamented Dr. Shunichi Tsugé―Case Study on Flow through a Grid in Wind Tunnel. Open Journal of Applied Sciences, 2, 18-21.
- Ishibashi, K. (1991) Solitary Wave Solution of Turbulent Bénard Convection. Ph.D. Thesis, Institute of Mechanics, University of Tsukuba, Tsukuba.
- Ishibashi, K., Tsugé, S. and Nakagawa, T.M.S. (1998) Solitary-Wave Solution of Turbulence with Application to Bénard Convection. In: Bainov, D., Ed., Proceedings of 8th International Colloquium on Differential Equations, Plov- div, 18-23 August 1997, 227-236.
- Tsugé, S. (2013) The Kolmogorov Turbulence Theory in the Light of Six-Dimensional Navier-Stokes’ Equation. In: Nakagawa, T.R.M, Ed., Philosophy of Flow, Vol. 10, Supplement, Royal White Mountains Academia Press, 19.
- Tsugé, S. (2004) Scientific Papers on Turbulence by Dr. Shunichi Tsugé. In: Nakagawa, T.M.S., Ed., Philosophy of Flow, Columbus University Press, Hakusan, 10.
- Tsugé, S. (2004) Scientific Papers on Combustion by Dr. Shunichi Tsugé. In: Nakagawa, T.M.S., Ed., Philosophy of Flow, Columbus University Press, Hakusan, 11.
- Sreenivasan, K.R. (1985) On the Fine-Scale Intermittency of Turbulence. Journal of Fluid Mechanics, 151, 81-103. http://dx.doi.org/10.1017/S0022112085000878
- Antonia, R.A. and Pearson, B. (2000) Effect of Initial Conditions on the Mean Energy Dissipation Rate and the Scaling Exponent. Flow, Turbulence and Combustion, 64, 95-117.
- Osonphasop, C. and Hinwood, J.B. (1983) Turbulence Measurements for the Whole Depth of Water in a Tidal Channel. 8th Australasian Conference of Fluid Mechanics, University of Newcastle, 5 September 1983, 10-14.
- Osonphasop, C. (1983) The Measurements of Turbulence in Tidal Currents. A Thesis Submitted to the Faculty of En- gineering in Partial Fulfillment of the Requirement for the Degree of Doctor of Philosophy, Department of Mechanical Engineering, Monash University, Clayton.
- Osonphasop, C. and Hinwood, J.B. (1984) On Measurement of Turbulence and Shear Stresses in Tidal Currents. APD-IAHR 4th Conference of the International Association for Hydraulic Research, Chiangmai, 25 May 1984, 1-5.
- Trevethan, M. and Chanson, H. (2010) Turbulence and Turbulent Flux Events in a Small Estuary. Environmental Fluid Mechanics, 10, 345-368. http://dx.doi.org/10.1007/s10652-009-9134-7
- Chanson, H., Brown, R. and Trevethan, M. (2012) Turbulence Measurements in a Small Subtropical Estuary under King Tide Condition. Environmental Fluid Mechanics, 12, 265-289. http://dx.doi.org/10.1007/s10652-011-9234-z
- Reynolds, O. (1883) An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels. Philosophical Transactions of the Royal Society of London, 174, 935-982. http://dx.doi.org/10.1098/rstl.1883.0029
- Kolmogorov, A.N. (1941) The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Rey- nolds Numbers. Doklady Akademii Nauk SSSR, 30, 301-304.
- Bogoliubov, N.N. (1959) Problems of Dynamical Theory in Statistical Physics. AFCRC-TR-59-235.
- De Kármán, Th. and Howarth, L. (1938) On the Statistical Theory of Isotropic Turbulence. Proceedings of the Royal Society A, 164, 192-215. http://dx.doi.org/10.1098/rspa.1938.0013
- Chapman, S. (1917) On the Kinetic Theory of a Gas II. Philosophical Transactions of the Royal Society A, 217, 115- 197.
- Enskog, D. (1917) Kinetische Theorie der Vorgange in Messigverdünnten Gasen. Dissertation, Uppsala University, Uppsala.
- Klimontovich, Yu.L. (1967) The Statistical Theory of Non-Equilibrium Processes in a Plasma. MIT Press, Cambridge.
- Lamb, H. (1932) Hydrodynamics. 6th Edition, Cambridge University Press, Cambridge, 1-8.
- Lorenz, E.N. (1963) Deterministic Nom-Periodic Flow. Journal of the Atmospheric Sciences, 20, 130-141. http://dx.doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
- Ueda, Y. (1992) Strange Attractors and the Origin of Chaos. In: Ueda, Y., Ed., The Road to Chaos, Aerial Press, Cali- fornia, 185-216.
- Nakagawa, T. and Hinwood, J.B. (1978) On Measurement of Turbulence in Tidal Currents. Monash University, Clay- ton, MMEL34.
Appendix: Brief Introduction How to Derive the Present Power Law of Turbulent Energy Spectrum
The complete account of this Appendix is discussed in Tsugé’s paper [17] , so that only a brief introduction on the paper will be made here.
The actual form of q1(s) written in axially isotropic form 


Note that there is no contribution from qs to q1. For

which is no more than a quadruple field.
Figure A1 depicts streamlines of the fictitious flow generated by a pair of dipoles, which are given by the following potentials,

This axially-symmetric flow can be alternatively represented by using stream function ψ as

from which we have the following relation,

The flow pattern ψ = constant, shows quadruple-like structure at far field, 
Let us obtain the power spectrum for inertial sub-range. The actual form of the pseudo-singularity enables us to calculate power spectrum for one-dimensional wave number k1 in the inertial sub-range. This spectrum function P11(k1) is written by definition,
Figure A1. Pseudo-singularity formed by a pair of dipoles in the inertial sub-range of the eddy space. The shaded part represents the dissipation region. After Tsugé [17] .

The Kolmogorov’s consequence of the similitude analysisis that P11, having the dimension of v2l ~ ε2/3l5/3, where v is the velocity, l the eddy size, and ε the dissipation, leads in the language of wave number space as

with

The present view into the existing formula for the power spectrum is rather straightforward: The concrete form of P11 can be derived by comparing expressions for the observable quantity of fluctuation correlation

which results in

where used is made of the definition of power spectrum function (6). The above integral (10) is transformed into the one in s-space as follows,

Since the integration spans over the whole s-space, we have yet to have solution q1 inside the dissipation
range

present purpose:
to be integrated over its own region. Then, the integral can be converted into a double one as follows,

with

where the boundary contour 

The one-dimensional power spectrum (10) is depicted in Figure A2. The parameter δ corresponds to the slenderness ratio of the worm as detected by the direct numerical simulation [10] , which is estimated as the order of O(10N)−1, where N is number in the order from 1 to 3. For a certain range of this parameter, the power spectrum shows k1−5/3 dependence, then with increase in the value of δ, it changes to 
It may be worth noting that the power spectrum P11 is not straight, but sinuous, depending on the wave number k1. This clearly suggests us that the power spectrum possesses intrinsic oscillatory character.
Figure A2. One-dimensional power spectrum P11 against one- dimensional wave number k1 with the slenderness ratio of worm δ as the parameter. The calculated spectrum is averaged over five neighboring points to make the comparison with −5/3 and or −2 power law easier. After Tsugé [17] .
Figure A2 indicates the following points.
1. For δ ≤ 0.01, P11 is almost independent of k1, but oscillates.
2. For 0.01 < δ < 0.1, the greater δ is, the more P11 rapidly decreases. Note −5/3 power law appears in this range of δ.
3. At δ ≈ 0.1, P11 decreases with increasing k1, following −2 power, if >40.
4. For δ > 0.1, there exists a region of k1, following −2 power law. It may be worth noting that with increasing δ, the range of k1 following −2 power law becomes wider than otherwise.
5. For δ >> 0.1, P11 decreases with k1, following a negative power law having slightly greater than −2 of the slope in almost all region of k1.
Note that the one-dimensional power spectrum P11 is oscillatory, but not steady if k1 is smaller than a certain value.


















