Open Journal of Fluid Dynamics
Vol.2 No.3(2012), Article ID:22526,10 pages DOI:10.4236/ojfd.2012.23009
Dufour and Soret Effect on Steady MHD Flow in Presence of Heat Generation and Magnetic Field past an Inclined Stretching Sheet
1Department of Mathematics, Comilla University, Comilla, Bangladesh
2Department of Mathematics, University of Dhaka, Dhaka, Bangladesh
Email: ekarim_du@yahoo.com
Received April 25, 2012; revised May 30, 2012; accepted June 18, 2012
Keywords: Dufour Effect; Magnetic Field; MHD; Nusselt Number and Soret Number
ABSTRACT
An analysis of two-dimensional steady magneto-hydrodynamic free convection flow of an electrically conducting, viscous and incompressible fluid past an inclined stretching porous plate in the presence of a uniform magnetic field and thermal radiation with heat generation is made. Both the Dufour and Soret effects are considered for a hydrogen-air mixture as the non-chemically reacting fluid pair. The equations governing the flow, temperature and concentration fields are reduced to a system of joined non-linear ordinary differential equations by similarity transformation. Non-linear differential equations are integrated numerically by using Nachtsheim-Swigert shooting iteration technique along with sixth order Runge-Kutta integration scheme. Finally the significance of physical parameters which are of engineering interest are examined both in graphical and tabular form.
1. Introduction
Laminar boundary layer flow, a significant type of flow, in presence of magnetic field and radiation over a moving continuous and linearly stretched surface has been receiving wide attention due to its applications in engineering, electro-chemistry, Gorla [1], Chin [2] and polymer processing, Erickson [3]. For examples, materials manufactured by aerodynamic extrusion processes and heat-treated materials traveling between a feed roll and a wind-up roll or on a conveyor belt possess the characteristics of a moving continuous stretching surface. Moreover lots of metallurgical processes occupy the system of cooling of continuous strips or filaments by drawing them through a quiescent fluid and that in the process of drawing, these strips are sometimes stretched. Another important matter is that the final product depends to a great extent on the rate of cooling. By drawing such strips in an electrically conducting fluid subjected to a magnetic field, the rate of cooling can be controlled and a final product of desired characteristics can be achieved. The study of heat and mass transfer is necessary for determining the quality of the final product, Samad and Mohebujjaman [4].
Sakiadis [5] analyzed the boundary layer flow over a solid surface moving with a constant velocity. Cess [6] examined the effect of thermal radiation on absorbing emitting gray fluids with black vertical plate. The above investigations having a definite bearing on the problem of a polymer sheet extruded continuously from a dye. It is usually assumed that the sheet is inextensible, but situations may arise in the polymer industry in which it is necessary to deal with a stretching plastic sheet, as noted by Crane [7]. Sparrow [8] explained a parameter named Rosseland approximation to describe the radiation heat flux in the energy equation in his book. Soundalgekar et al. [9] made analytical study on the MHD forced and free convection flow past a vertical porous plate. The flow field of a stretching wall with a power-law velocity variation was discussed by Banks [10]. McLeod and Rajagopal [11] investigated the uniqueness of the flow of a Navier Stokes fluid due to a linear stretching boundary. Chen and Char [12] studied the suction and injection on a linearly moving plate subject to uniform wall temperature and heat flux. By using the Rosseland diffusion approximation [8], a study of the unsteady mixed convection flow of an optically dense viscous incompressible fluid past a heated vertical plate with a free uniform stream velocity and surface temperature was made by Hossain and Takhar [13].
The thermal-diffusion (Soret) effect, for instance, has been utilized for isotope separation, and in mixtures between gases with very light molecular weight (Hz, He) and of medium molecular weight (Nz, air) the diffusion-thermo (Dufour) effect was found to be of a considerable magnitude such that it cannot be ignored, described by Eckert and Drake [14] in their book. Alabraba et al. [15] studied the interaction of mixed convection with thermal radiation in laminar boundary layer flow taking into account the binary chemical reaction and Soret-Dufour effects. Postelnicu [16] studied numerically the influence of a magnetic field on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effects. Alam and Rahman [17] discovered the Dufour and Soret effect on unsteady MHD flow in a porous medium. Very recently Karim et al. [18] discussed the thermal effect on MHD flow.
The present paper is the investigation of the Dufour and Soret effects of an electrically conducting viscous incompressible fluid interaction with thermal radiation on the flow over an inclined linearly stretched sheet in the presence of heat and mass transfer permitted by a transversely applied uniform magnetic field with heat generation taking into account the Rosseland diffusion approximation. The investigation is based on known similarity analysis and the local similarity solutions are obtained numerically.
2. Mathematical Analysis
A steady-state two-dimensional heat and mass transfer flow of an electrically conducting viscous incompressible fluid along an isothermal stretching permeable inclined sheet with an angle 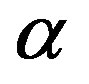 to the vertical embedded in a porous medium with heat generation/absorption is considered. A strong magnetic field is applied in the y-axis direction. Here the effect of the induced magnetic field is neglected in comparison to the applied magnetic field. The electrical current flowing in the fluid gives rise to an induced magnetic field if the fluid were an electrical insulator, but here we have taken the fluid to be electrically conducting. Hence, only the applied magnetic field of strength B0 plays a role which gives rise to magnetic forces
to the vertical embedded in a porous medium with heat generation/absorption is considered. A strong magnetic field is applied in the y-axis direction. Here the effect of the induced magnetic field is neglected in comparison to the applied magnetic field. The electrical current flowing in the fluid gives rise to an induced magnetic field if the fluid were an electrical insulator, but here we have taken the fluid to be electrically conducting. Hence, only the applied magnetic field of strength B0 plays a role which gives rise to magnetic forces  in x-direction,
in x-direction,  where is the electrical conductivity assumed to be directly proportional to the x-translational velocity (u) of the fluid found by Helmy [19] and
where is the electrical conductivity assumed to be directly proportional to the x-translational velocity (u) of the fluid found by Helmy [19] and 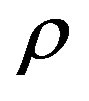 is the density of the fluid. We also bring into account the effect of temperature dependent volumetric heat generation (W/m3), in the flow region that is given by Vajravelu and Hadjinicolaou [20] as
is the density of the fluid. We also bring into account the effect of temperature dependent volumetric heat generation (W/m3), in the flow region that is given by Vajravelu and Hadjinicolaou [20] as
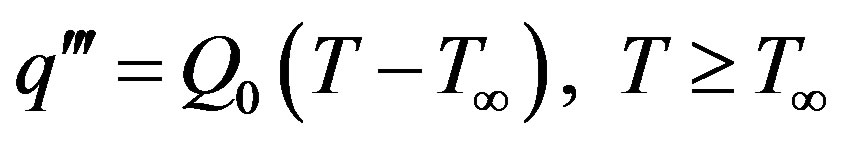
where Q0 is the heat generation. Two equal and opposite forces are introduced along the x-axis so that the sheet is stretched keeping the origin fixed as shown in Figure 1.
The fluid is considered to be gray, absorbing emitting radiation but non-scattering medium and the Rosseland approximation is used to describe the radiation heat flux in the energy equation. The radiative heat flux in the x-direction is negligible to the flux in the y-direction. The plate temperature and concentration are initially raised to Tw and Cw respectively which are thereafter maintained constant. The ambient temperature of the flow is T¥ and the concentration of the uniform flow is C¥.

Figure 1. Flow configuration and coordinate system.
Under the usual boundary layer and Boussinesq approximations and using the Darcy-Forchhemier model, the flow and heat transfer in the presence of radiation are governed by the following equations.
Continuity Equation
 (1)
(1)
Momentum Equation
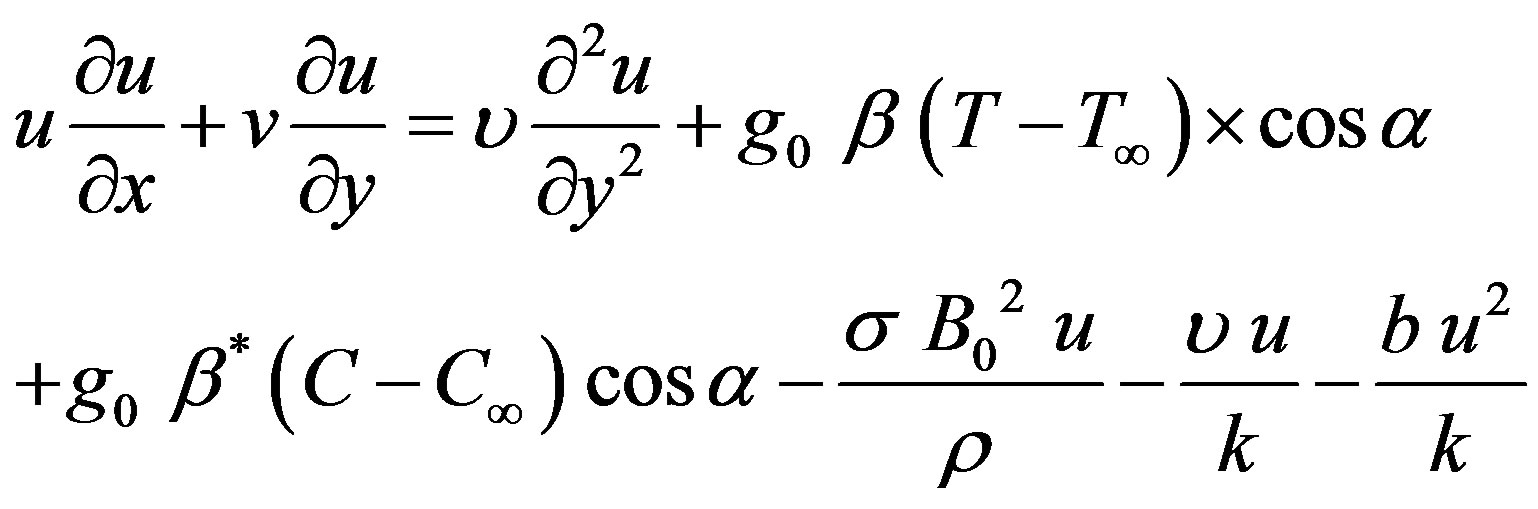 (2)
(2)
Energy Equation
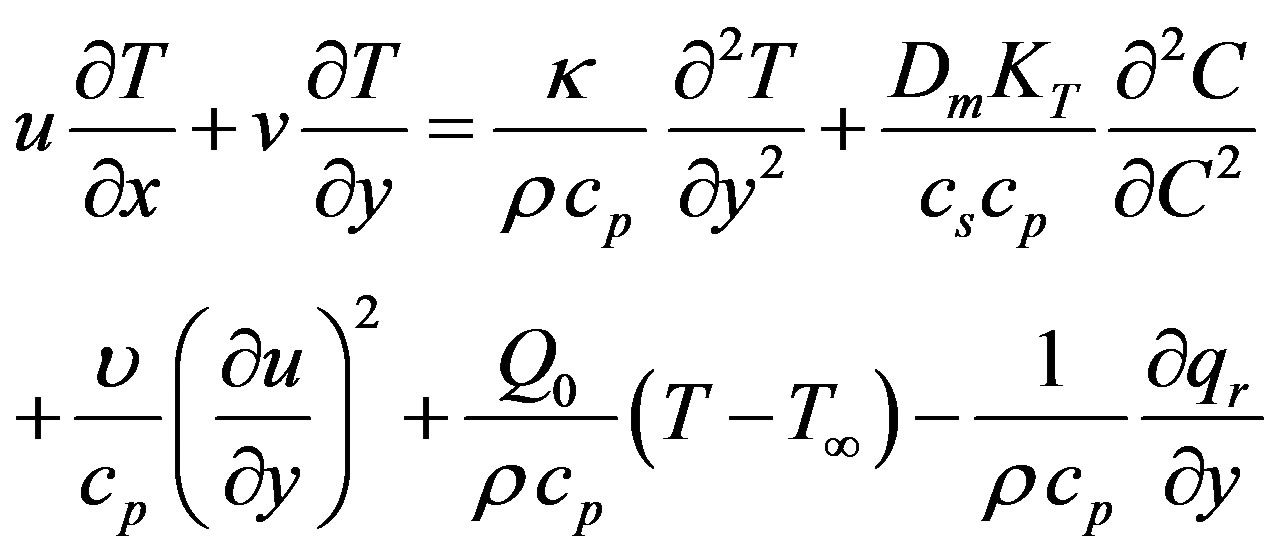 (3)
(3)
Concentration equation
 (4)
(4)
where  and
and  are the velocity components in the xand y-directions respectively,
are the velocity components in the xand y-directions respectively, 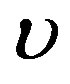 is the kinematic viscosity, g0 is the acceleration due to gravity,
is the kinematic viscosity, g0 is the acceleration due to gravity, 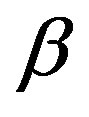 is the volumetric coefficient of thermal expansion,
is the volumetric coefficient of thermal expansion,  and T¥ are the fluid temperature within the boundary layer and in the free-stream respectively, while C is the concentration of the fluid within the boundary layer,
and T¥ are the fluid temperature within the boundary layer and in the free-stream respectively, while C is the concentration of the fluid within the boundary layer,  is the electric conductivity, B0 is the uniform magnetic field strength (magnetic induction),
is the electric conductivity, B0 is the uniform magnetic field strength (magnetic induction), 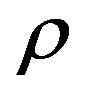 is the density of the fluid,
is the density of the fluid,  is the thermal conductivity of the fluid, cp is the specific heat at constant pressure, Q0 is the volumetric rate of heat generation/absorption and Dm is the chemical molecular diffusivity.
is the thermal conductivity of the fluid, cp is the specific heat at constant pressure, Q0 is the volumetric rate of heat generation/absorption and Dm is the chemical molecular diffusivity.
The corresponding boundary conditions for the model are
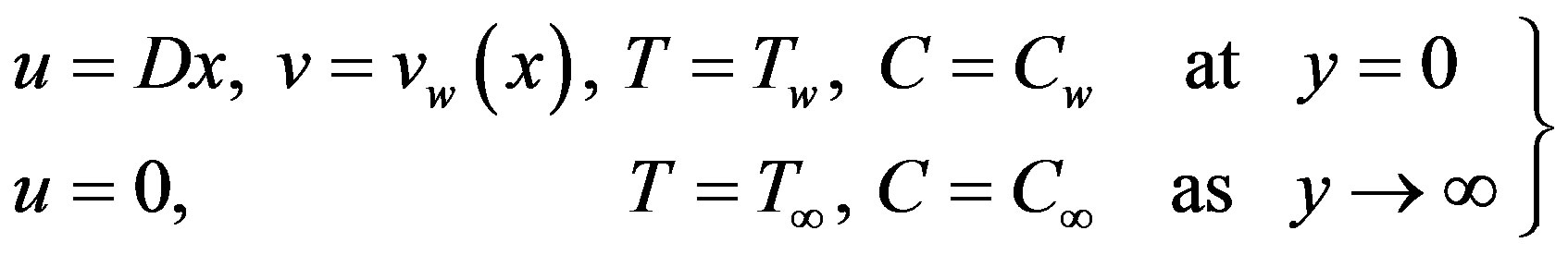 (5)
(5)
where D (>0) is a constant, vw(x) is a velocity component at the wall having positive value to indicate suction, Tw is the uniform sheet temperature and Cw is the concentration of the fluid at the sheet.
By using Rosseland approximation 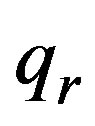 takes the form
takes the form
 (6)
(6)
where 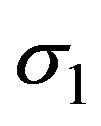 is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and 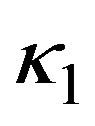 is the mean absorption coefficient. It is assumed that the temperature differences within the flow are sufficiently small such that T4 may be expressed as a linear function of temperature. This is accomplished by expanding T4 in a Taylor series about T¥ and neglecting higher order terms, thus
is the mean absorption coefficient. It is assumed that the temperature differences within the flow are sufficiently small such that T4 may be expressed as a linear function of temperature. This is accomplished by expanding T4 in a Taylor series about T¥ and neglecting higher order terms, thus
 . (7)
. (7)
Using Equations (6) & (7), Equation (3) takes the form
 (8)
(8)
Similarity Analysis
In order to obtain similarity solution for the problem under consideration, we may take the following suitable similarity variables
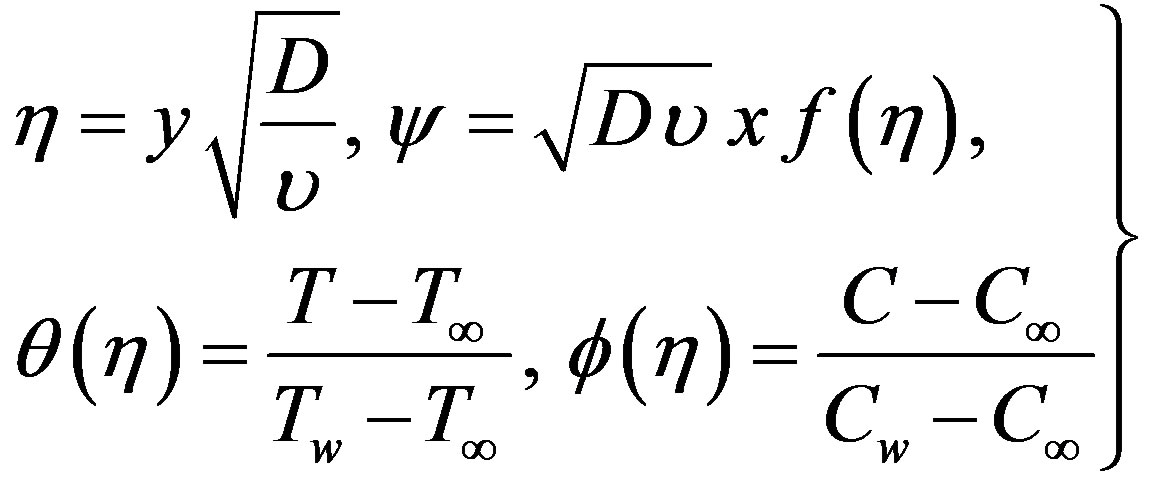 (9)
(9)
where 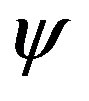 is the stream function,
is the stream function, 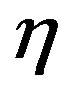 is the dimensionless distance normal to the sheet, f is the dimensionless stream function,
is the dimensionless distance normal to the sheet, f is the dimensionless stream function,  is the dimensionless fluid temperature and
is the dimensionless fluid temperature and  is the dimensionless concentration.
is the dimensionless concentration.
Since  and
and 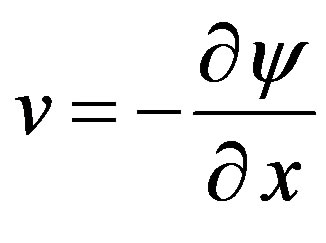 we have the velocity components from equation (6) given by
we have the velocity components from equation (6) given by
 and
and  (10)
(10)
where prime denotes the derivative with respect to .
.
Now introducing the similarity variables from Equation (9) and using equation (10), equations (2) to (4) are reduced to the dimensionless equations given by
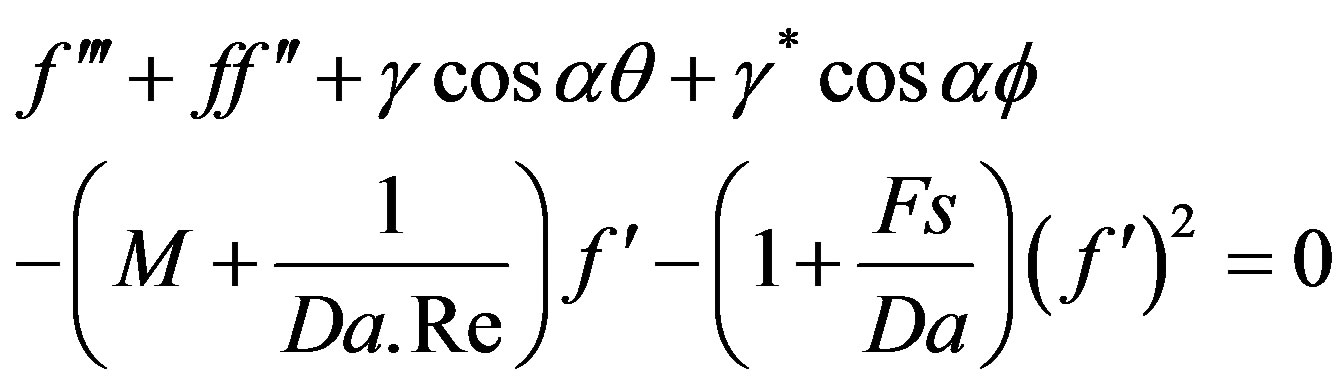 (11)
(11)
 (12)
(12)
 (13)
(13)
where  is the local buoyancy parameter,
is the local buoyancy parameter, 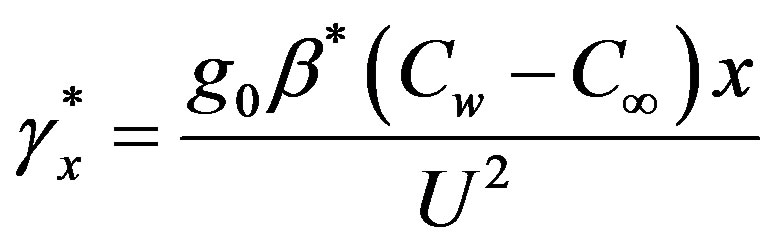 is the modified local buoyancy parameter,
is the modified local buoyancy parameter, 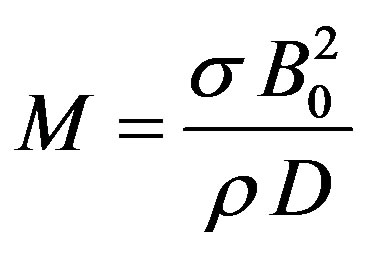 is the magnetic field parameter,
is the magnetic field parameter,  is the local Darcy number,
is the local Darcy number,  is the Reynolds number,
is the Reynolds number,  is the Forchhemier number,
is the Forchhemier number,  is the Prandtl number,
is the Prandtl number,  is the radiation parameter and
is the radiation parameter and ,
,  is the heat source
is the heat source  parameter,
parameter, 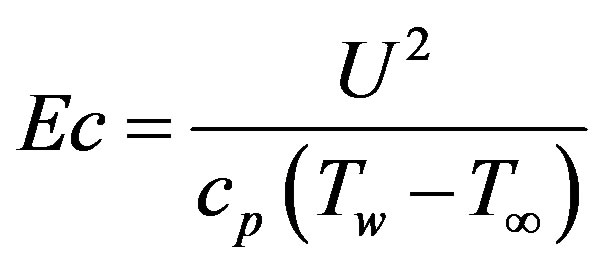 is the Eckert number,
is the Eckert number, 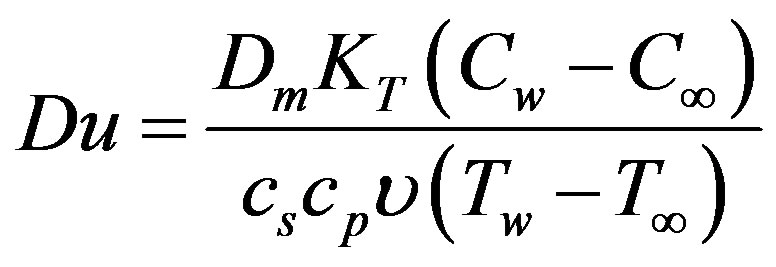 is the Dufour number,
is the Dufour number,  is the Schmidt number and
is the Schmidt number and  is the Soret number.
is the Soret number.
The transformed boundary conditions are
 (14)
(14)
where 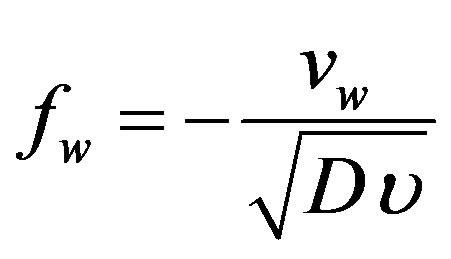 is the suction parameter. The nonlinear ordinary differential Equations (8), (9) and (10) under the boundary conditions (11) are solved numerically for various values of the parameters entering into the problems.
is the suction parameter. The nonlinear ordinary differential Equations (8), (9) and (10) under the boundary conditions (11) are solved numerically for various values of the parameters entering into the problems.
Skin friction, rate of heat and mass transfer: The parameters of engineering interest for the present problem are the skin friction coefficient (cf), local Nusselt number (Nu) and Sherwood number (Sh) which indicate physically the wall shear stress, the rate of heat transfer and the local surface mass flux respectively. The dimensionless skin-friction coefficient, Nusselt number and Sherwood number for impulsively started plate are given by
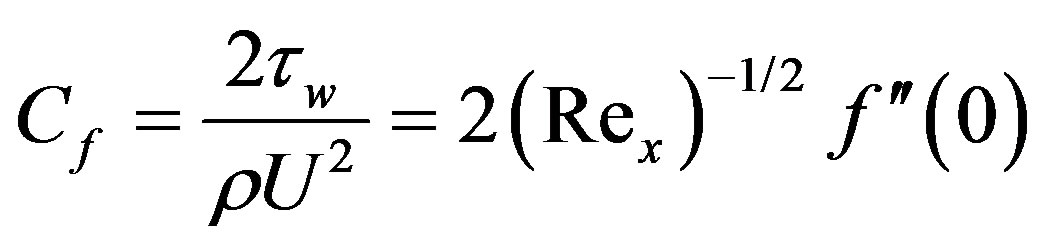 (15)
(15)
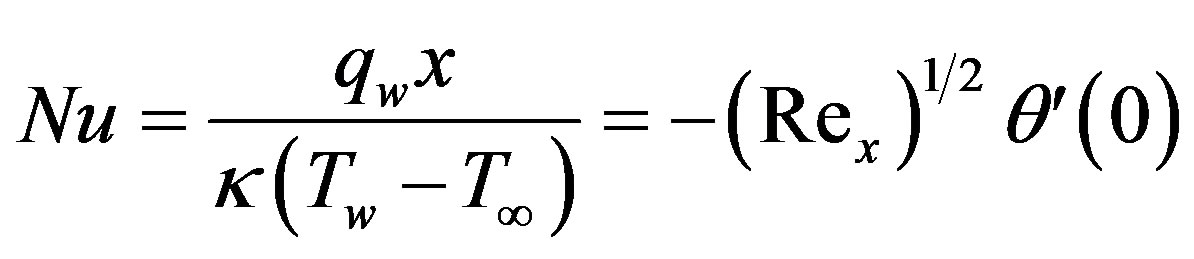 (16)
(16)
 (17)
(17)
where 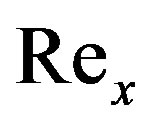 is the Reynolds number. And hence the values proportional to the skin-friction coefficient, Nusselt number and Sherwood number are
is the Reynolds number. And hence the values proportional to the skin-friction coefficient, Nusselt number and Sherwood number are ,
, 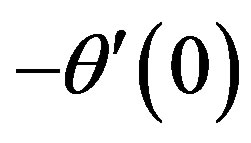 and
and 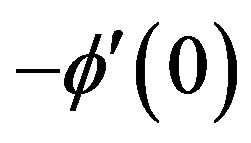 respectively.
respectively.
3. Numerical Computation
The numerical solutions of the non-linear differential equations (11) to (13) under the boundary conditions (14) have been performed by applying a shooting method namely Nachtsheim and Swigert [21] iteration technique (guessing the missing values) along with sixth order Runge-Kutta iteration scheme. We have chosen a step size  to satisfy the convergence criterion of 10–6 in all cases. The value of
to satisfy the convergence criterion of 10–6 in all cases. The value of 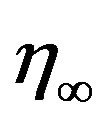 has been found to each iteration loop by
has been found to each iteration loop by . The maximum value of
. The maximum value of 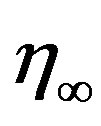 to each group of parameters
to each group of parameters 
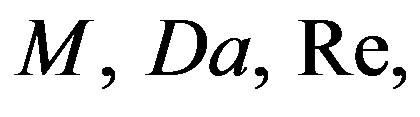 Fs, Pr, N, Ec, Sr, Du, Q, Ec, Pn and
Fs, Pr, N, Ec, Sr, Du, Q, Ec, Pn and 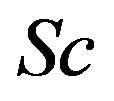 has been determined when the values of the unknown boundary conditions at
has been determined when the values of the unknown boundary conditions at 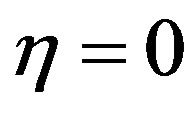 not change to successful loop with error less than 10–6. In order to verify the effects of the step size
not change to successful loop with error less than 10–6. In order to verify the effects of the step size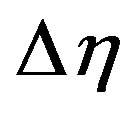 , we have run the code for our model with three different step sizes as
, we have run the code for our model with three different step sizes as 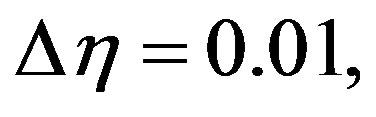
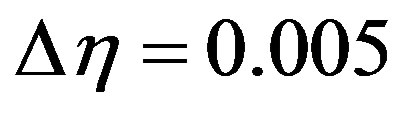 and
and 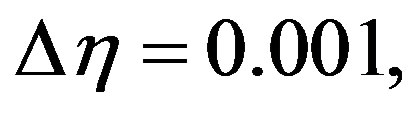 and in each case we have found excellent agreement among them shown in Figures 2 to 4.
and in each case we have found excellent agreement among them shown in Figures 2 to 4.
To assess the accuracy of the present numerical method, we have compared our surface mass flux with Samad and Mohebujjaman [4] for viscous fluid when Da = 1000, N = 0, 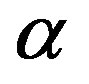 = 00, Fs = 0,
= 00, Fs = 0, 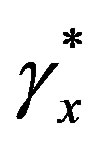 = 0, Du = 0, Ec = 0 and Sr = 0 and we have found excellent agreement among the results shown in Table 1. Therefore, the developed code can be used with great confidence to study the problem considered in this paper.
= 0, Du = 0, Ec = 0 and Sr = 0 and we have found excellent agreement among the results shown in Table 1. Therefore, the developed code can be used with great confidence to study the problem considered in this paper.
4. Results and Discussion
For the purpose of discussing the results of the flow field
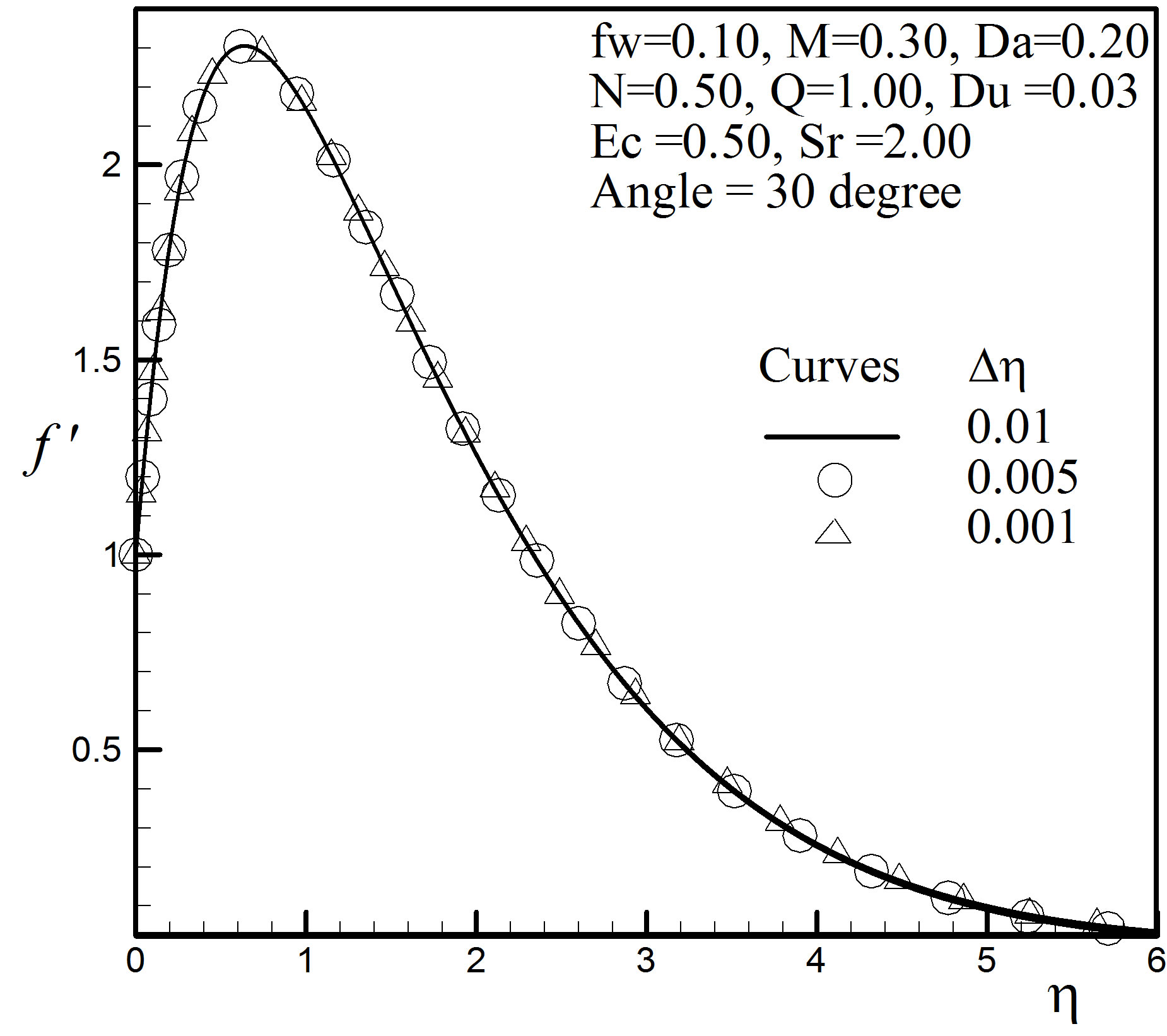
Figure 2. Velocity profiles for different step size.
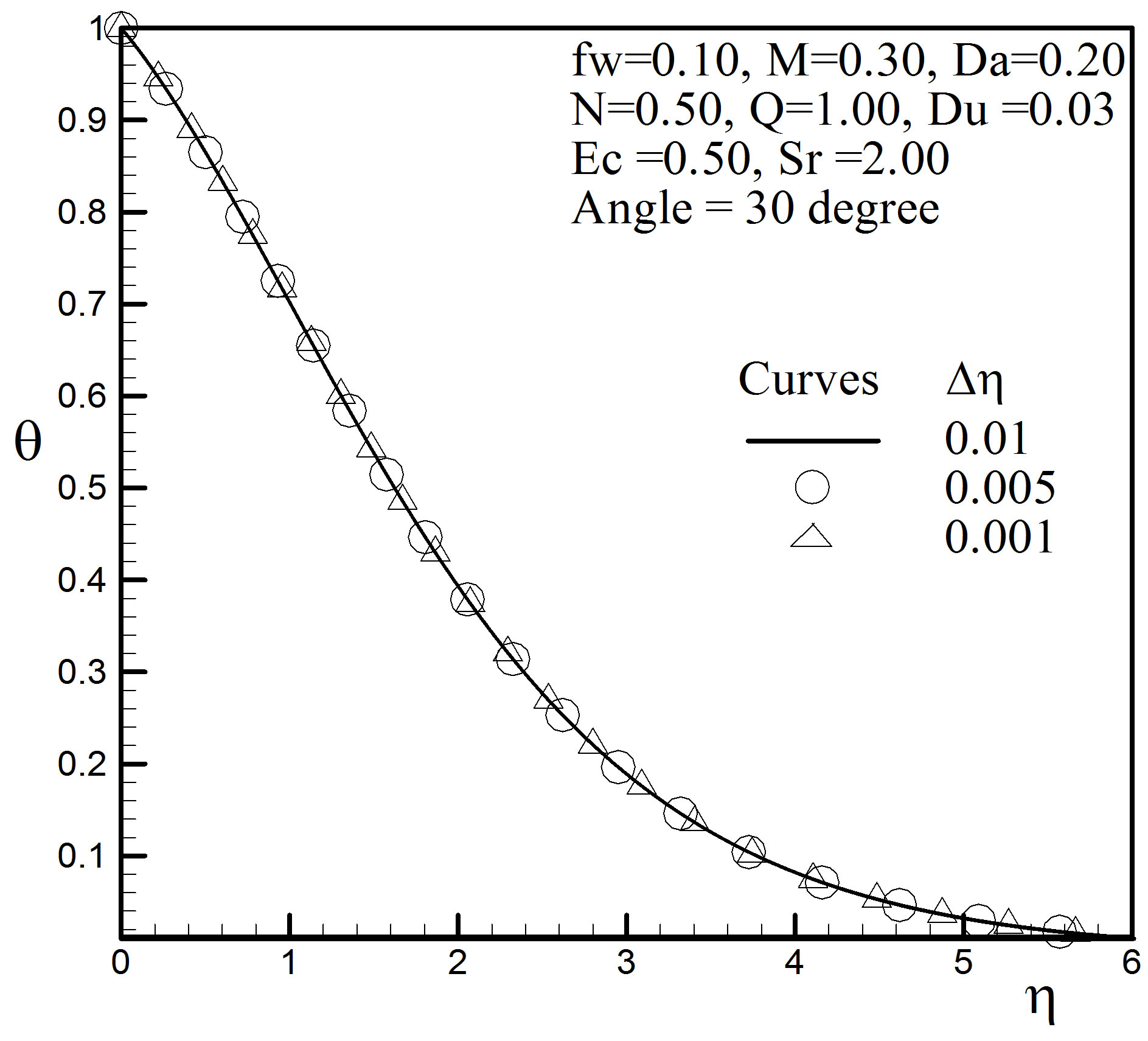
Figure 3. Temperature profiles for different step size.
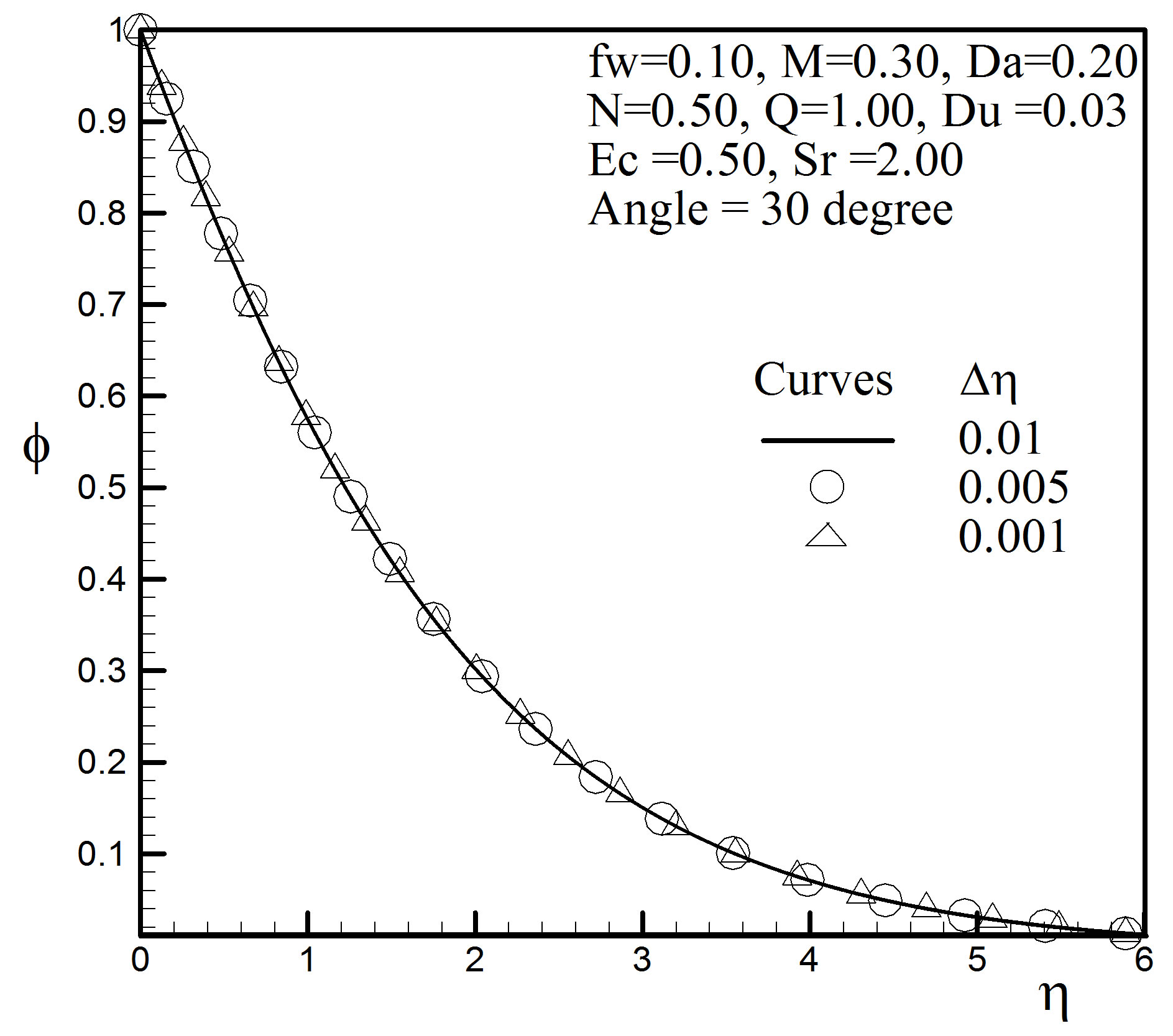
Figure 4. Concentration profiles for different step size.
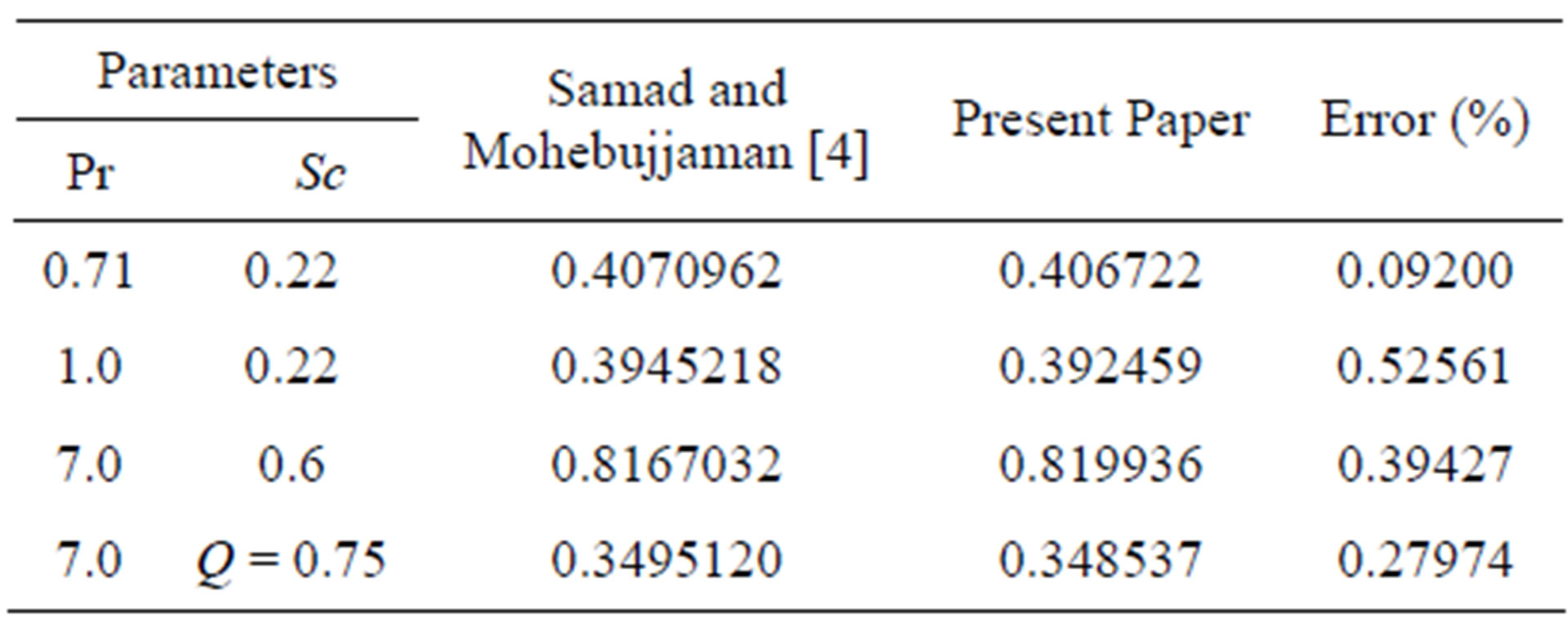
Table 1. Comparison of the values of Sherwood number (Sh).
represented in the Figure 1, the numerical calculations are presented in the form of non-dimensional velocity, temperature and concentration profiles. The values of buoyancy parameter  and modified buoyancy parameter
and modified buoyancy parameter  are taken to be both positive to represent cooling of the plate. The parameters are chosen arbitrarily where Pr = 0.71 corresponds physically to air at 20˚C, Pr = 1.0 corresponds to electrolyte solution such as salt water and Pr = 7.0 corresponds to water, and Sc = 0.22, 0.6 and 1.0 corresponds to hydrogen, water vapor and methanol respectively at approximate 25˚C and 1 atmosphere. The values of Dufour number and Soret number are chosen in such a way that their product is constant provided that the mean temperature Tm is kept constant as well.
are taken to be both positive to represent cooling of the plate. The parameters are chosen arbitrarily where Pr = 0.71 corresponds physically to air at 20˚C, Pr = 1.0 corresponds to electrolyte solution such as salt water and Pr = 7.0 corresponds to water, and Sc = 0.22, 0.6 and 1.0 corresponds to hydrogen, water vapor and methanol respectively at approximate 25˚C and 1 atmosphere. The values of Dufour number and Soret number are chosen in such a way that their product is constant provided that the mean temperature Tm is kept constant as well.
Due to free convection problem positive large values of  = 12 and
= 12 and  = 6 are chosen. The value of Re is kept 100, Fs equal to 0.09, Da = 0.2, Ec = 0.5, fw = 0.1 and N = 0.5. However, numerical computations have been carried out for different values of the magnetic field parameter (M), angle of inclination (
= 6 are chosen. The value of Re is kept 100, Fs equal to 0.09, Da = 0.2, Ec = 0.5, fw = 0.1 and N = 0.5. However, numerical computations have been carried out for different values of the magnetic field parameter (M), angle of inclination ( ), heat source/ sink parameter (Q), Dufour number (Du) and Soret number (Sr). The numerical results for the velocity, temperature and concentration profiles are displayed in Figures 5-19.
), heat source/ sink parameter (Q), Dufour number (Du) and Soret number (Sr). The numerical results for the velocity, temperature and concentration profiles are displayed in Figures 5-19.
Figures 5 to 7 display the effects of the Soret number Sr on the velocity, temperature and concentration profiles. It is observed that, when Sr increases, the velocity increases slightly while temperature decreases to a small extent. Figure 7 reveals that the Soret number Sr has influence on concentration profiles to a great extent. The concentration decreases near the wall first and after that starts to increase from  = 0.59, due to the effect of Sr on the stretching sheet.
= 0.59, due to the effect of Sr on the stretching sheet.
From Figure 8, we observe that first the velocity decreases rapidly and after  = 2.74 starts to increase slowly with the increase of M. This is due to the effect of magnetic field on the stretching sheet. In addition, the temperature field as well as concentration increases with the increase of magnetic field. The magnetic field lines
= 2.74 starts to increase slowly with the increase of M. This is due to the effect of magnetic field on the stretching sheet. In addition, the temperature field as well as concentration increases with the increase of magnetic field. The magnetic field lines
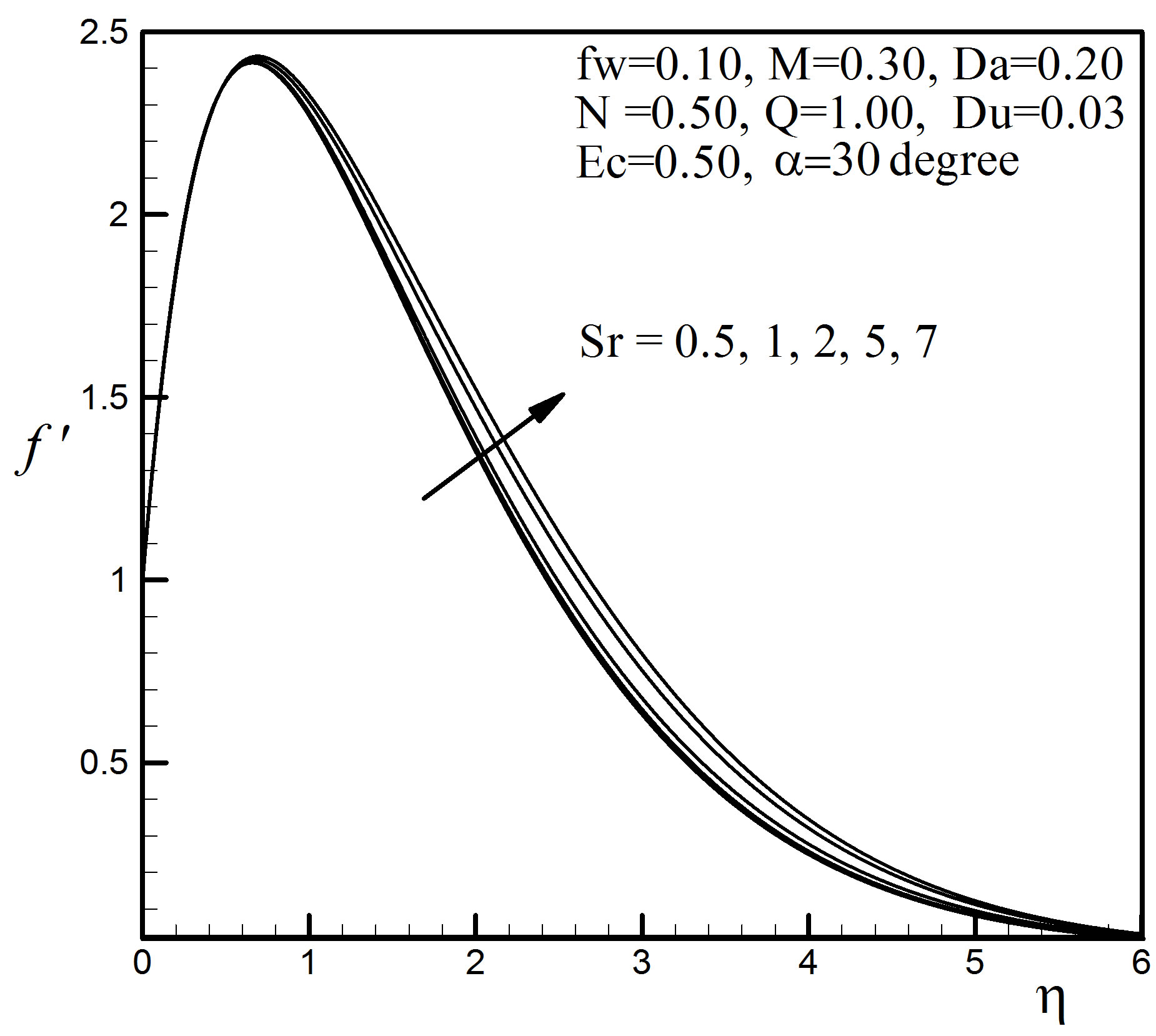
Figure 5. Velocity profiles for different values of Sr.
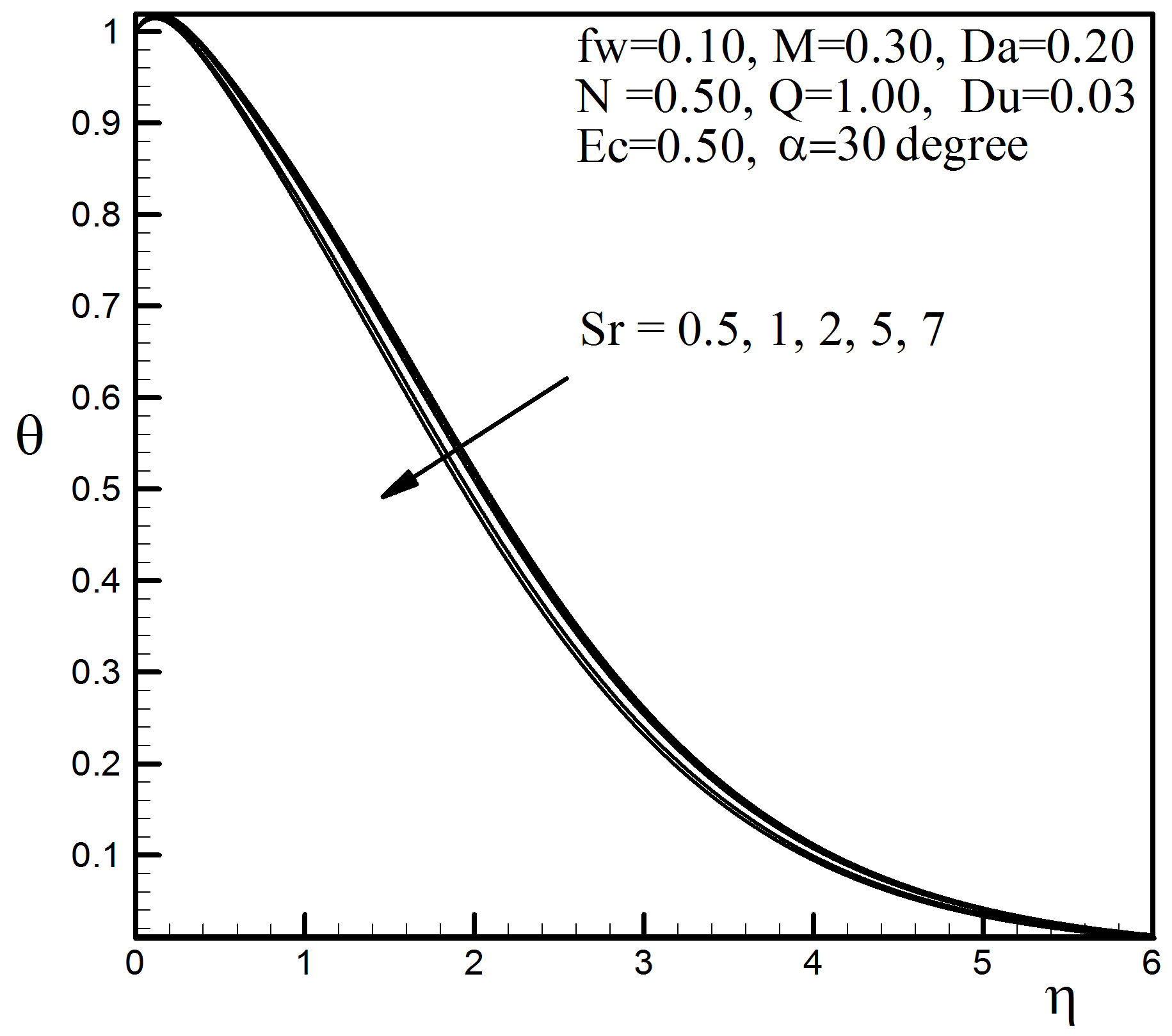
Figure 6. Temperature profiles for different values of Sr.
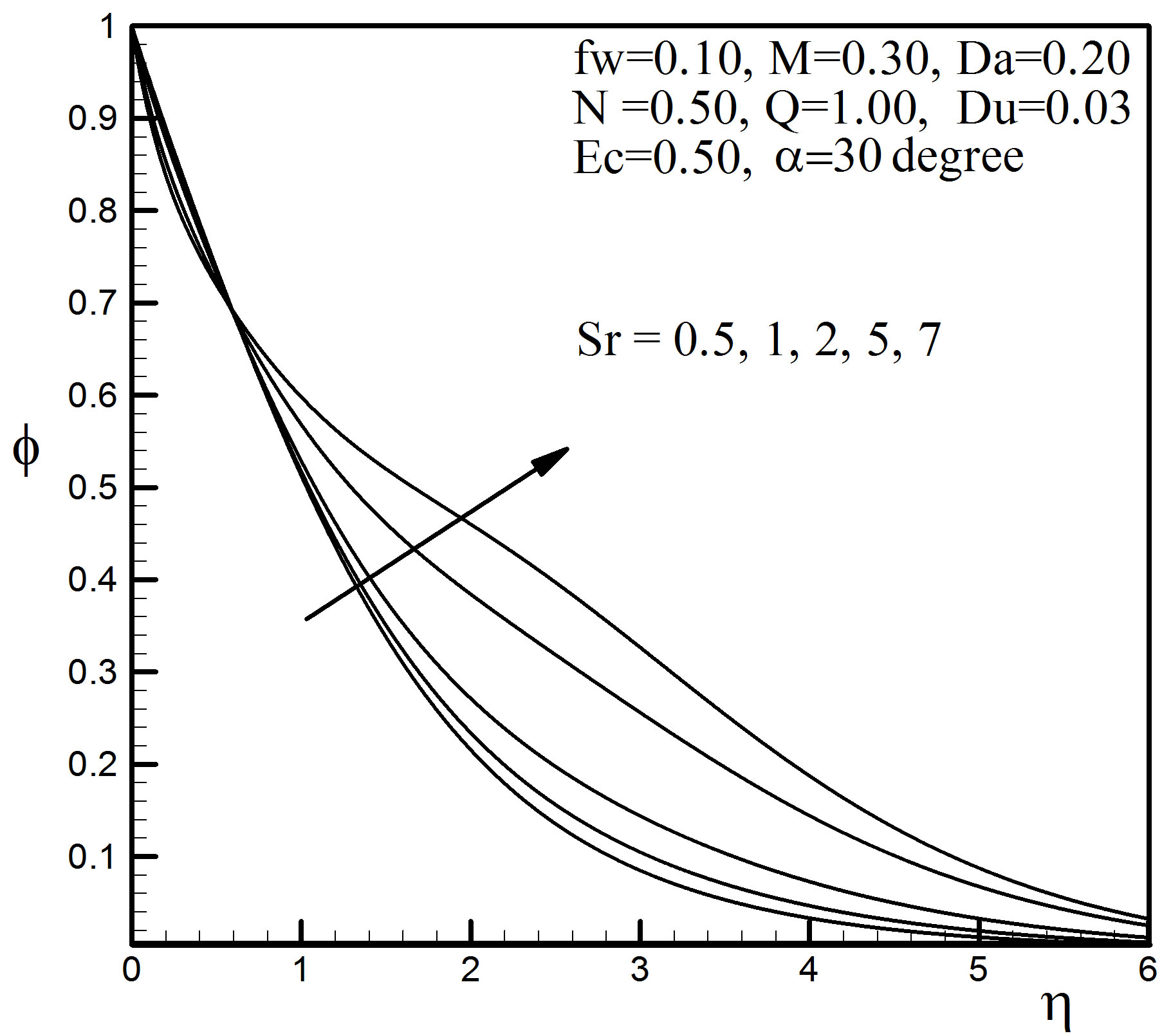
Figure 7. Concentration profiles for different values of Sr.

Figure 8. Velocity profiles for different values of M.

Figure 9. Temperature profiles for different values of M.
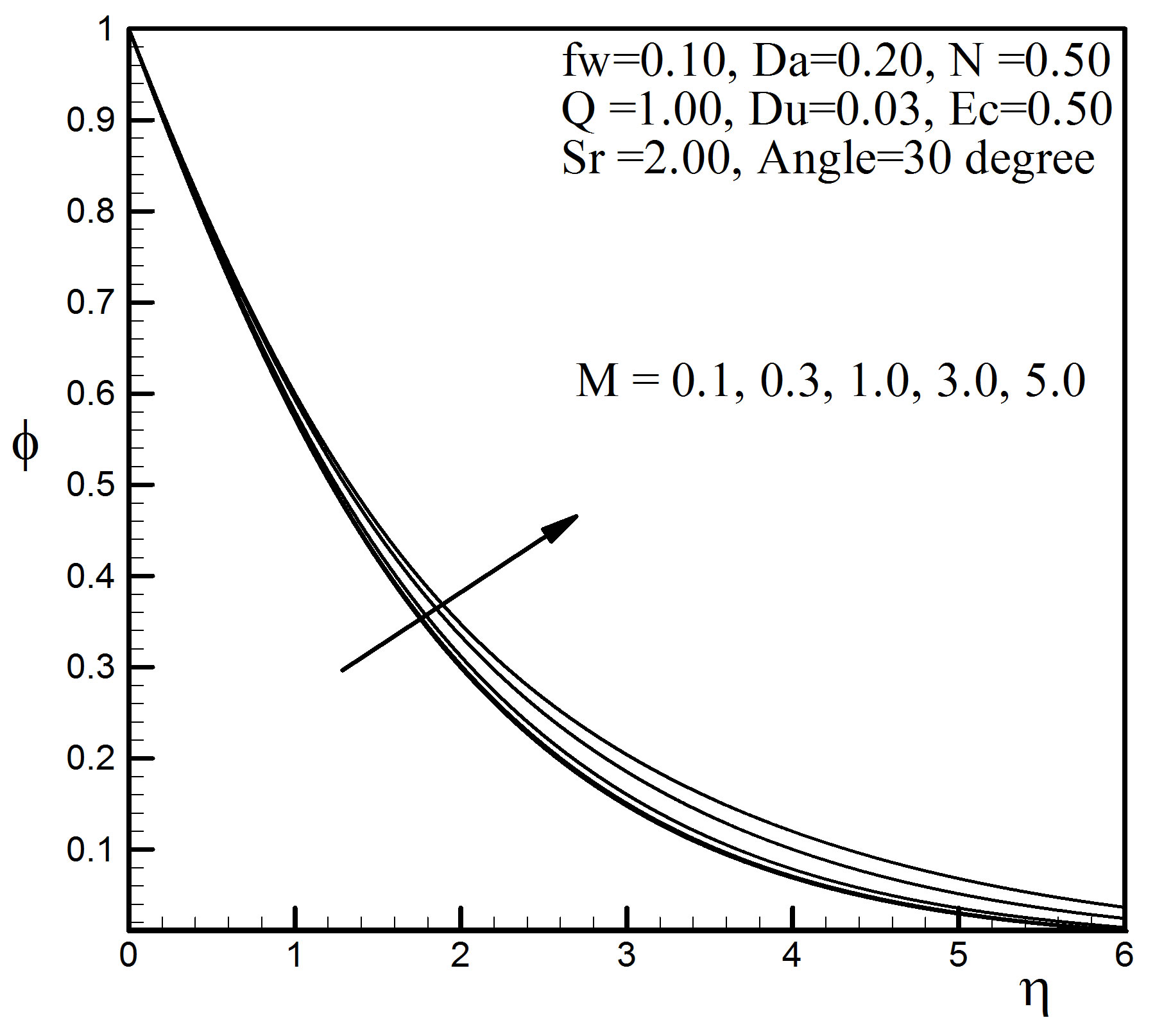
Figure 10. Concentration profiles for different values of M.
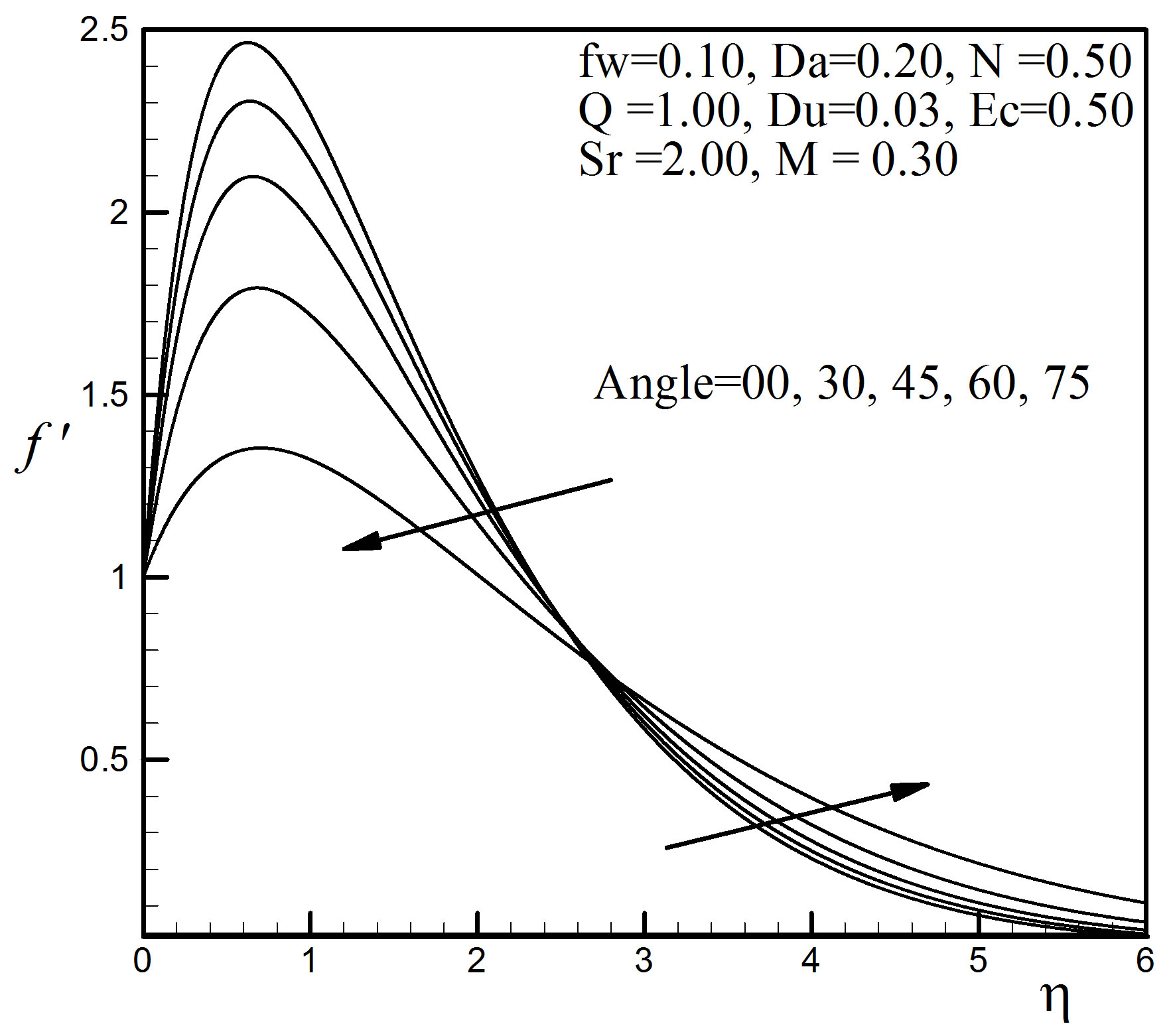
Figure 11. Velocity profiles for different values of angle a.
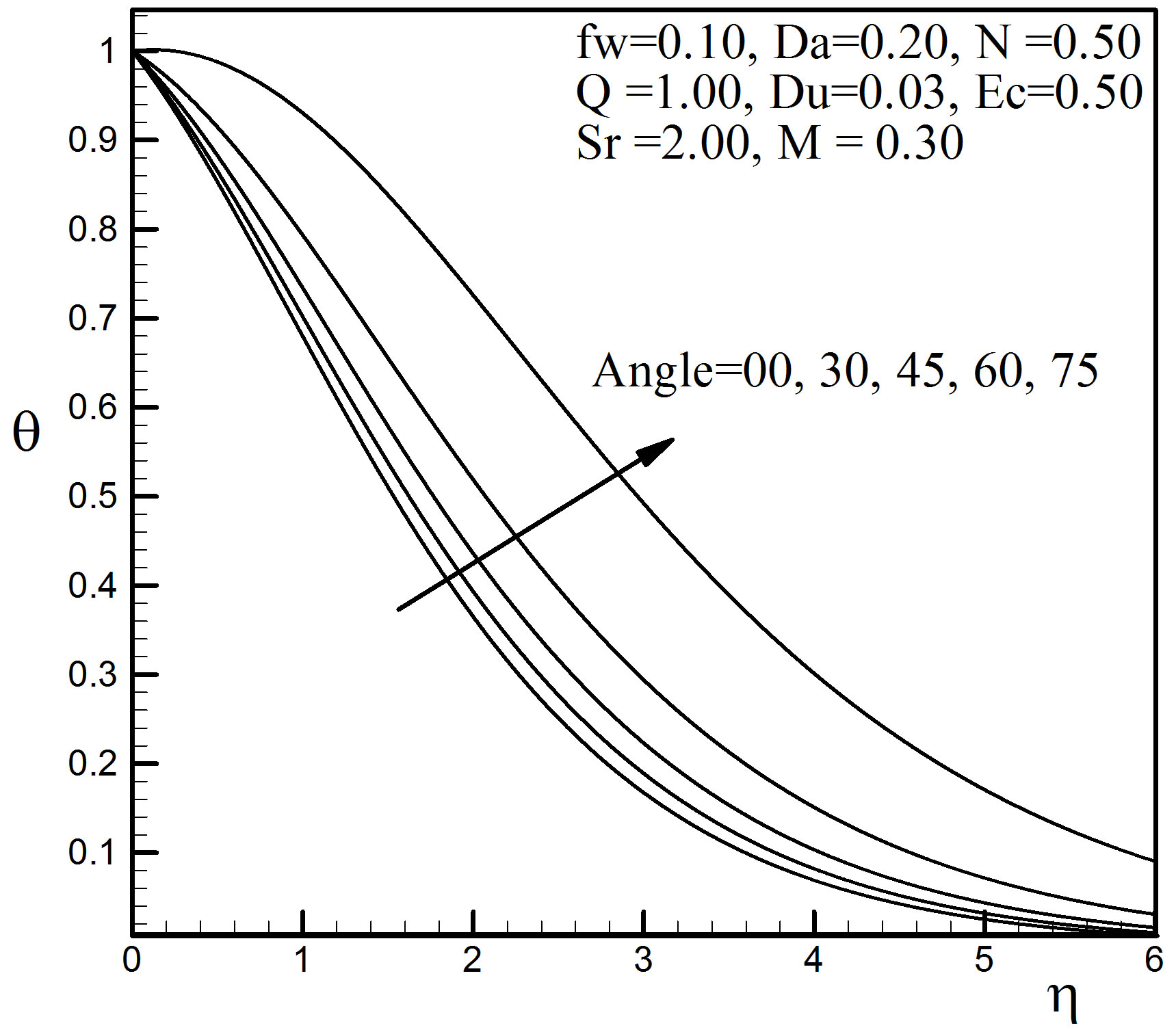
Figure 12. Temperature profiles for different values of angle a.
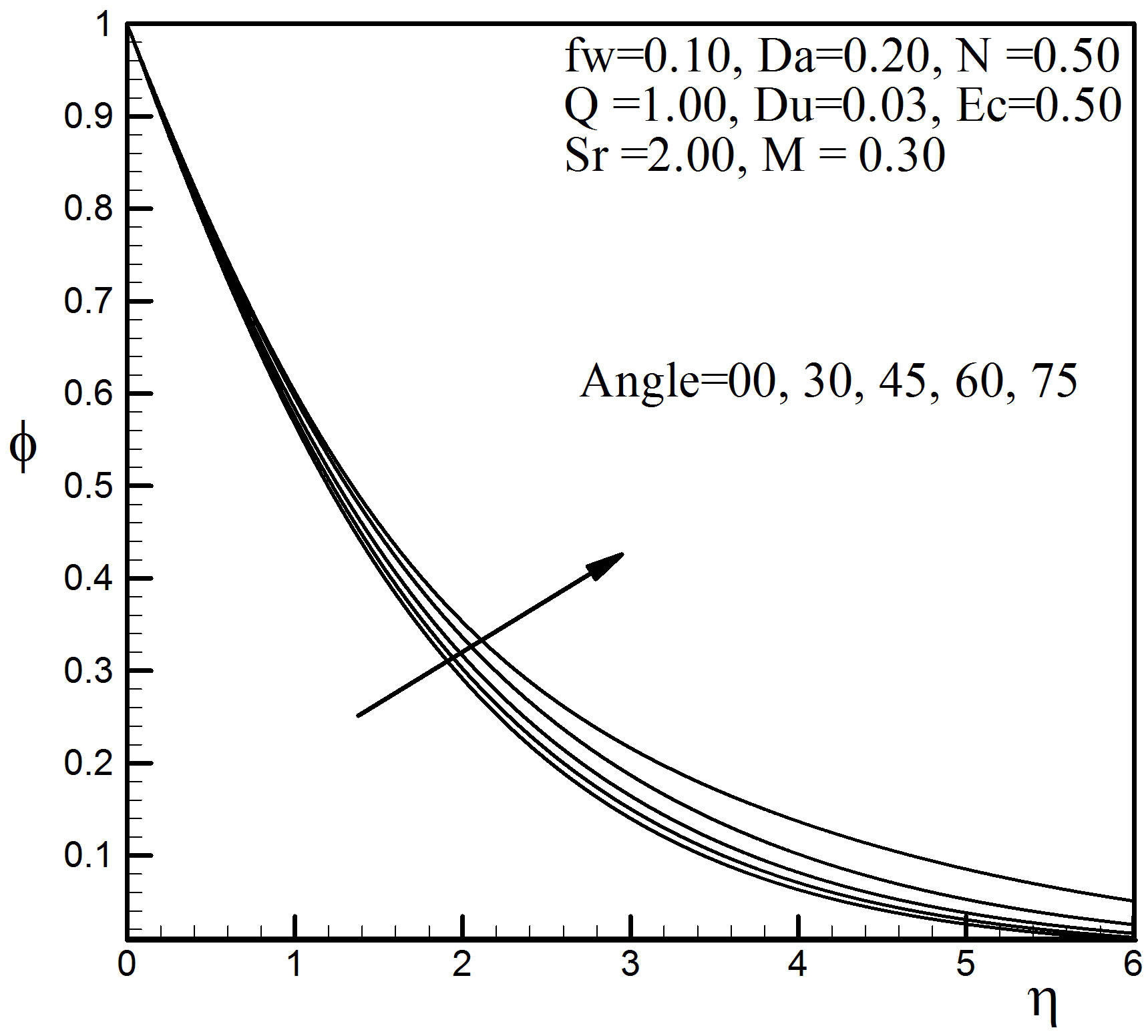
Figure 13. Concentration profiles for different values of angle a.
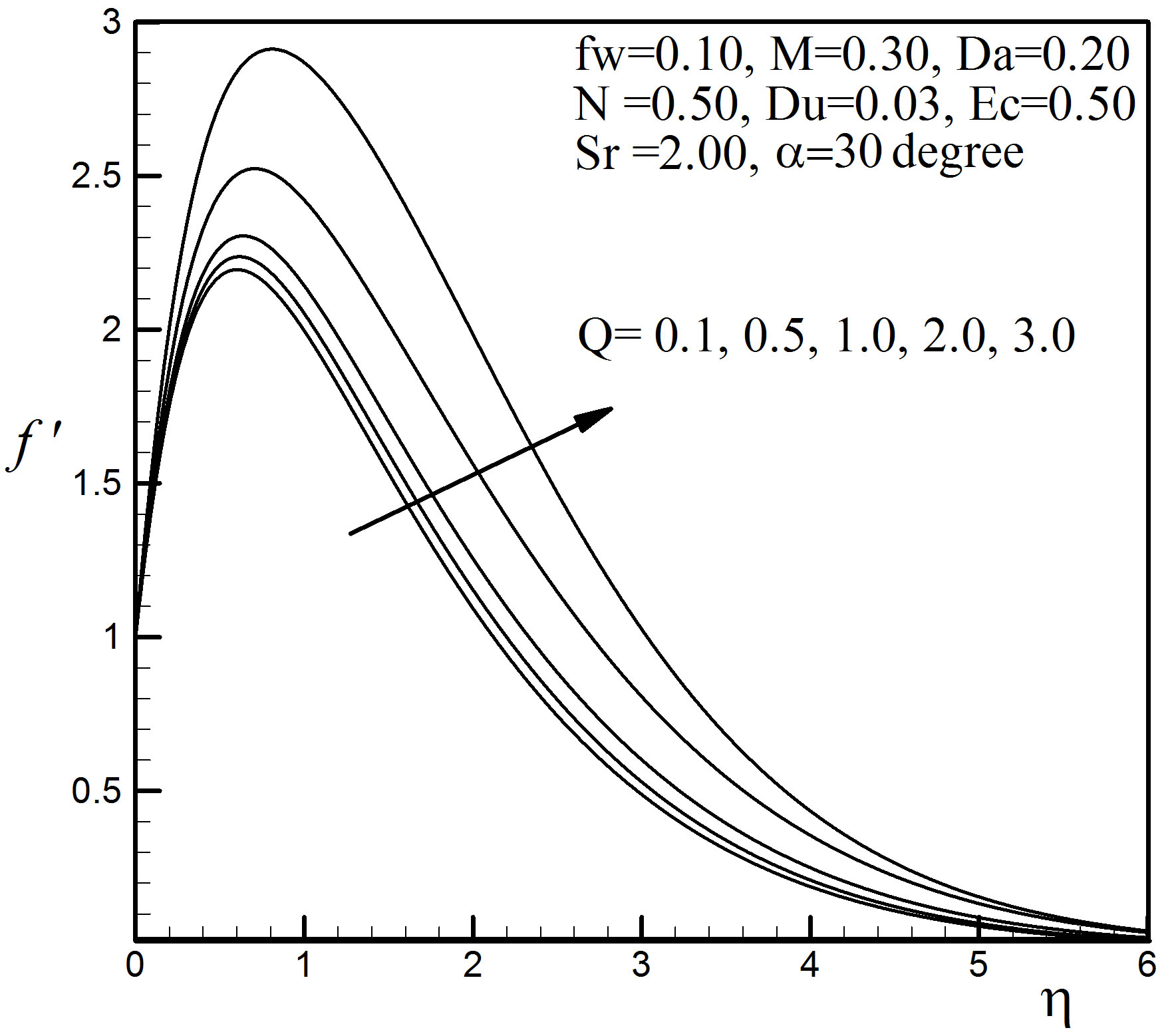
Figure 14. Velocity profiles for different values of Q.

Figure 15. Temperature profiles for different values of Q.
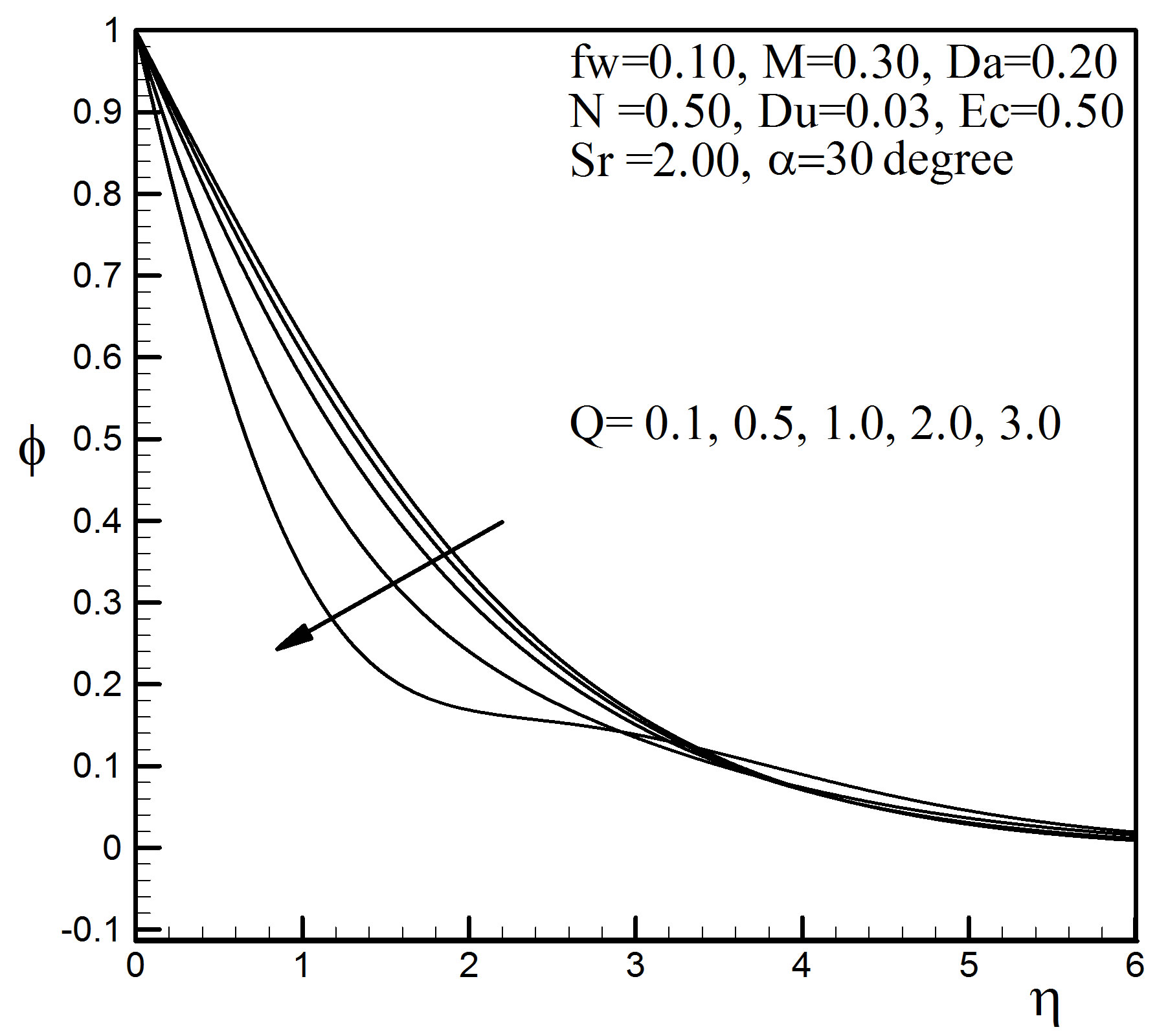
Figure 16. Concentration profiles for different values of Q.
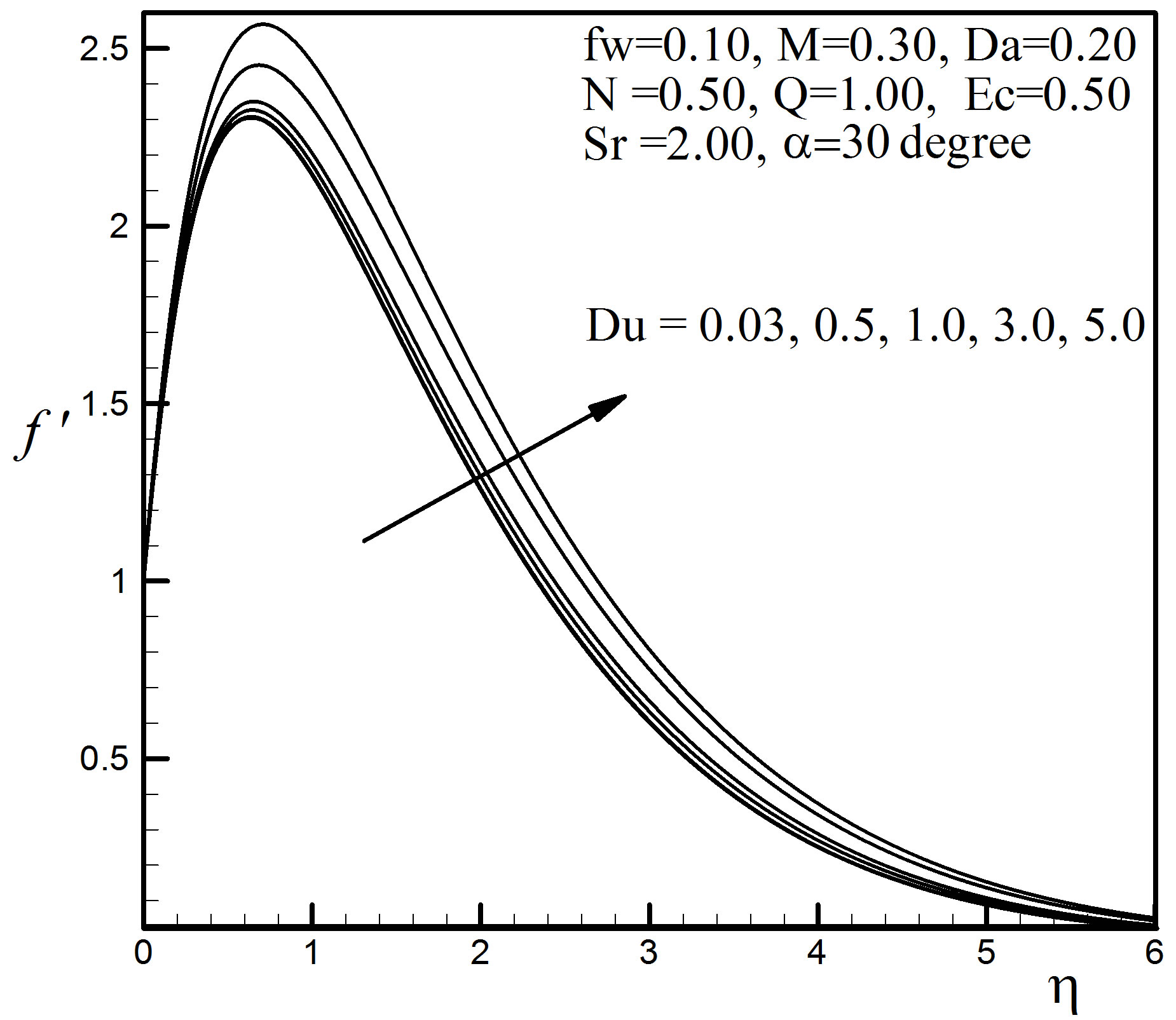
Figure 17. Velocity profiles for different values of Du.
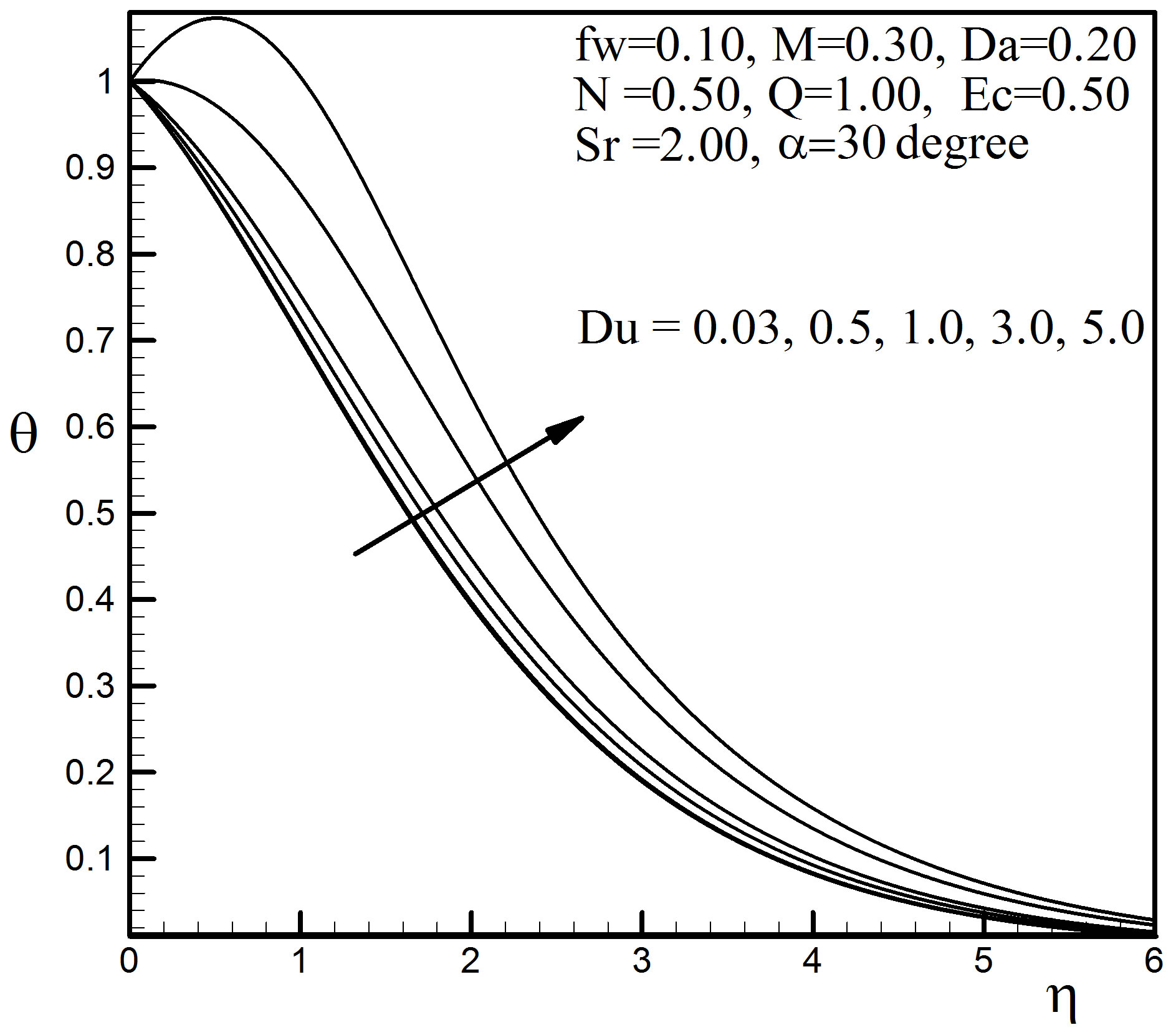
Figure 18. Temperature profiles for different values of Du.
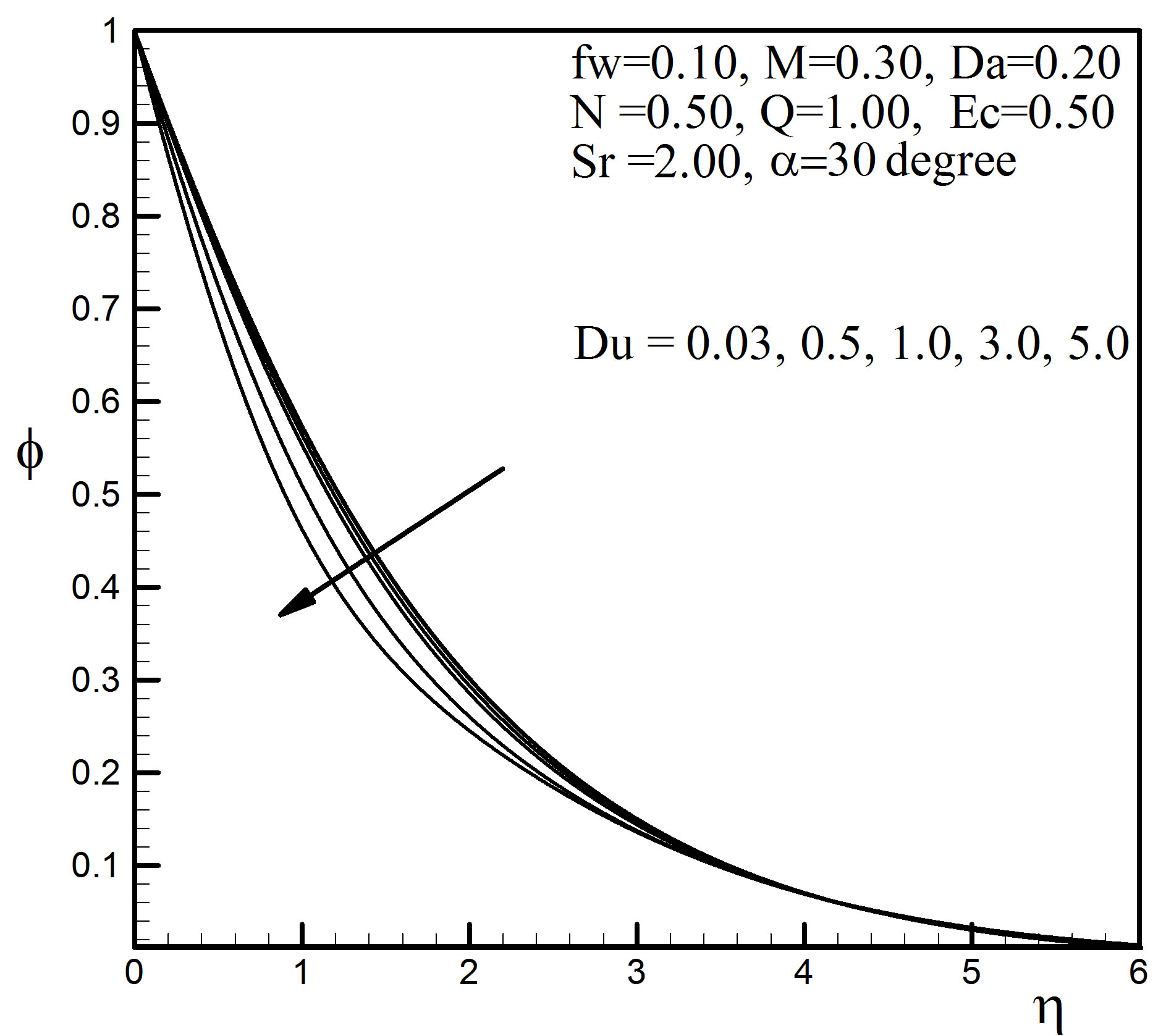
Figure 19. Concentration profiles for different values of Du.
act like a string and tend to retard the motion of the fluid. The consequence of which is to increase the rate of heat transfer temperature variation is prominent as seen in Figure 9.
The effect of the angle of inclination 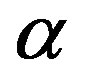 of the stretching sheet on the velocity field is shown in Figure 11. From this figure we see that the velocity decreases with the increase of
of the stretching sheet on the velocity field is shown in Figure 11. From this figure we see that the velocity decreases with the increase of 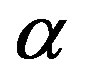 swiftly up to
swiftly up to 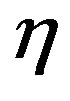 = 2.69. As
= 2.69. As 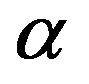 increases, the effect of the buoyancy force decreases because of the multiplication factor
increases, the effect of the buoyancy force decreases because of the multiplication factor  and the velocities decrease. But after
and the velocities decrease. But after 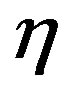 = 2.69 it is seen that the velocity is increasing with the raise of
= 2.69 it is seen that the velocity is increasing with the raise of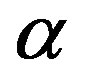 . Figure 12 shows that the thermal boundary layer thickness and the temperature rise hastily with grow up of
. Figure 12 shows that the thermal boundary layer thickness and the temperature rise hastily with grow up of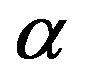 . Finally, we observe that the angle of inclination affects the concentration very slowly near the plate surface in Figure 13. Away from the plate, however, the effect on the concentration profiles is significant.
. Finally, we observe that the angle of inclination affects the concentration very slowly near the plate surface in Figure 13. Away from the plate, however, the effect on the concentration profiles is significant.
For different values of heat source parameter Q the velocity, temperature and concentration profiles are exposed in Figures 14 to 16. We have illustrated non-dimensional velocity, temperature and concentration profiles against 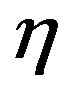 for some representative values of the heat source parameter Q = 0.1, 0.5, 1.0, 2.0, 3.0. The positive value of Q represents source i.e. heat generation in the fluid. From Figure 14, it is observed that due to the generation of heat the buoyancy force increases which in turn gives higher velocity in the boundary layer. For heat generation, the peak velocity occurs near the surface of the stretching plate. This is corroborated by Figure 15 where it is seen that the temperatures do indeed rapid increase as Q increases. The temperature gradient at the surface is decreasing from negative to positive as we increase Q. This means that when Q = 0.1 the temperature is transferred from the sheet, but for increasing Q, the heat transfer rate is decreasing, when
for some representative values of the heat source parameter Q = 0.1, 0.5, 1.0, 2.0, 3.0. The positive value of Q represents source i.e. heat generation in the fluid. From Figure 14, it is observed that due to the generation of heat the buoyancy force increases which in turn gives higher velocity in the boundary layer. For heat generation, the peak velocity occurs near the surface of the stretching plate. This is corroborated by Figure 15 where it is seen that the temperatures do indeed rapid increase as Q increases. The temperature gradient at the surface is decreasing from negative to positive as we increase Q. This means that when Q = 0.1 the temperature is transferred from the sheet, but for increasing Q, the heat transfer rate is decreasing, when 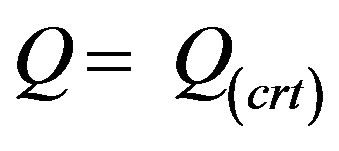 = 1.644035 the temperature gradient at the sheet is zero, if we further increase Q, the temperature gradient increases to positive value, that is, the stretching sheet gains temperature from the environment. The hydrodynamic and thermal boundary layers thickness increase but the concentration boundary layer thickness reduces with the increase of Q for
= 1.644035 the temperature gradient at the sheet is zero, if we further increase Q, the temperature gradient increases to positive value, that is, the stretching sheet gains temperature from the environment. The hydrodynamic and thermal boundary layers thickness increase but the concentration boundary layer thickness reduces with the increase of Q for 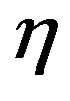 < 2.87. After this there is no variation but for large value of Q there exist some fluctuations in the concentration profiles shown in Figure 16.
< 2.87. After this there is no variation but for large value of Q there exist some fluctuations in the concentration profiles shown in Figure 16.
It is observed that with the increase of the value of Du the velocity profiles occur higher. From Figure 18, it is seen that Du has remarkable effect on temperature profiles; quantitatively when  = 1.5 Du increases from 0.03 to 0.5 and there is 5.11% increase in the temperature value, whereas the corresponding increase is 16.53%, when Du increases from 3.0 to 5.0. The Dufour number has a falling effect on the concentration field shown in Figure 19. Quantitatively when
= 1.5 Du increases from 0.03 to 0.5 and there is 5.11% increase in the temperature value, whereas the corresponding increase is 16.53%, when Du increases from 3.0 to 5.0. The Dufour number has a falling effect on the concentration field shown in Figure 19. Quantitatively when  = 1.5 and Du increases from 0.03 to 0.5, there is 2.45% decrease in the concentration value, whereas the corresponding decrease is 8.840% when Du increases from 3.0 to 5.0.
= 1.5 and Du increases from 0.03 to 0.5, there is 2.45% decrease in the concentration value, whereas the corresponding decrease is 8.840% when Du increases from 3.0 to 5.0.
Finally, the effects of various parameters on the skin friction Cf, local Nusselt number Nu and local Sherwood number Sh are shown in the Tables 2 to 5.
5. Conclusions
From the present study we can make the following conclusions:
1) Using magnetic field we can control the heat and mass transfer flow characteristics;
2) The effect of heat source parameter is very noteworthy;
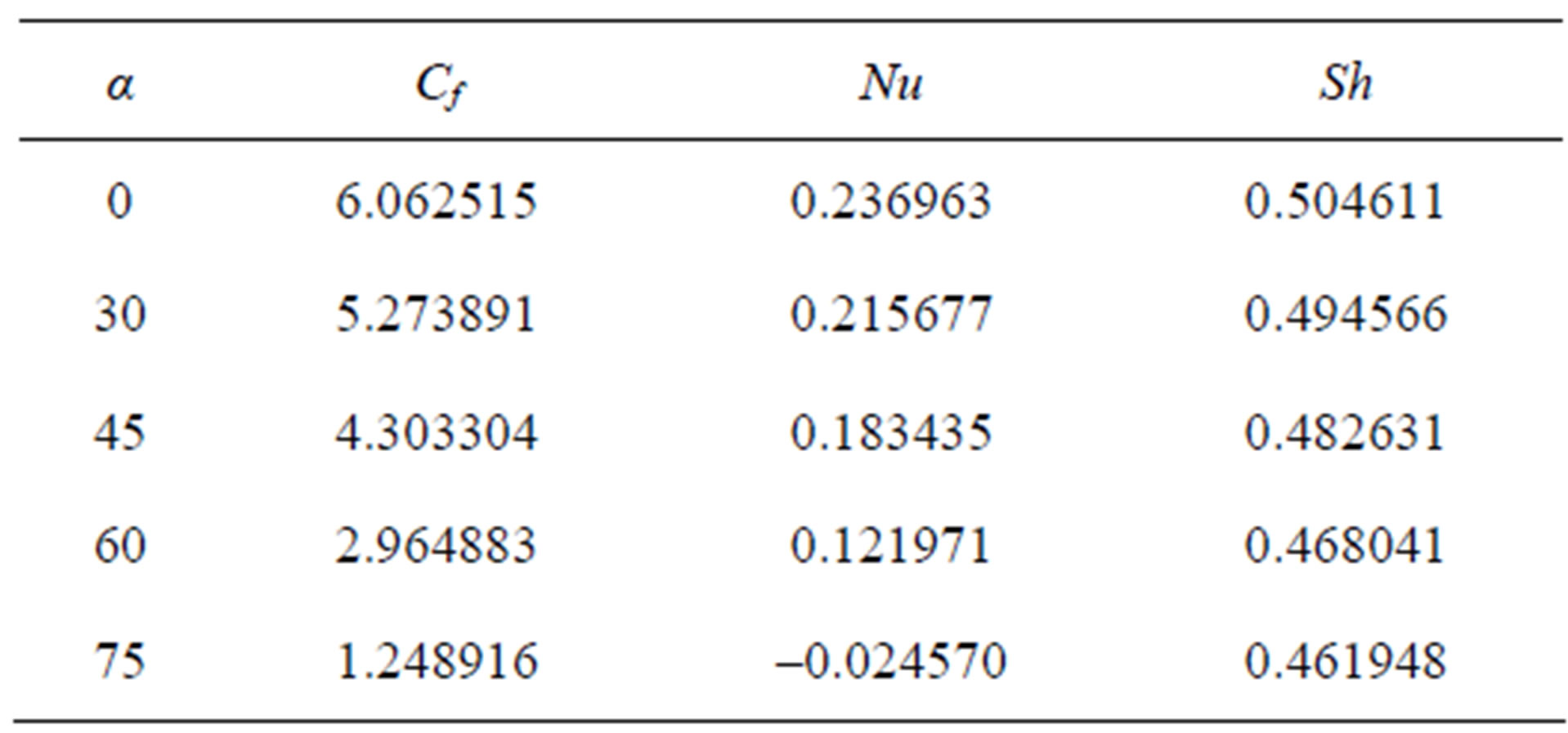
Table 2. Cf, Nu and Sh for different values of α.

Table 3. Cf, Nu and Sh for different values of Q.

Table 4. Cf, Nu and Sh for different values of Du.
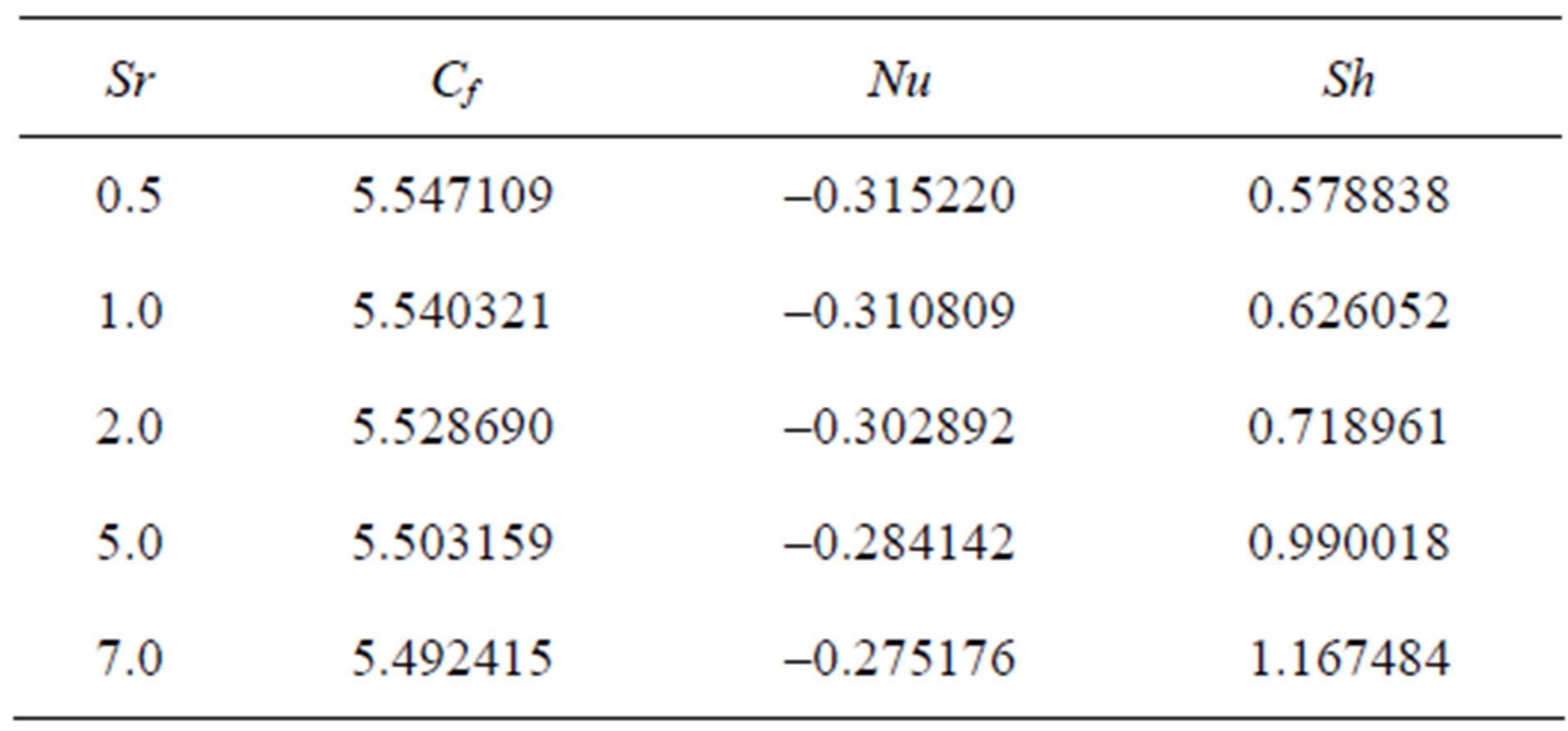
Table 5. Cf, Nu and Sh for different values of Sr.
3) The inclination of plate has remarkable effect on temperature;
4) The Dufour effect is significant;
5) The Soret number plays a role on concentration.
REFERENCES
- R. S. R. Gorla, “Unsteady Mass Transfer in the Boundary Layer on a Continuous Moving Sheet Electrod,” Journal of the Electrochemical Society, Vol. 125, No. 6, 1978, pp. 865-869. doi:10.1149/1.2131569
- D. T. Chin, “Mass Transfer to a Continuous Moving Sheet Electrode,” Journal of the Electrochemical Society, Vol. 122, No. 5, 1975, pp. 643-646. doi:10.1149/1.2134281
- L. E. Erickson, L. T. Fan and V. G. Fox, “Heat and Mass Transfer on a Moving Continuous Flat Plate with Suction or Injection,” Industrial Engineering and Chemical Fundamentals, Vol. 5, 1966, pp. 19-25. doi:10.1021/i160017a004
- M. A. Samad and M. Mohebujjaman, “MHD Heat and Mass Transfer Free Convection Flow along a Vertical Stretching Sheet in Presence of Magnetic Field with Heat Generation,” Research Journal of Applied Science, Engineering and Technology, Vol. 1, No. 3, 2009, pp. 98-106.
- B. C. Sakiadis, “Boundary-Layer Behavior on Continuous Solid Surfaces: I. Boundary-Layer Equations for TwoDimensional and Axisymmetric Flow,” AIChE Journal, Vol. 7, No. 1, 1961, pp. 26-28. doi:10.1002/aic.690070108
- R. D. Cess, “The Interaction of Thermal Radiation with Free Convection Heat Transfer,” International Journal of Heat Mass Transfer, Vol. 9, No. 11, 1966, pp. 1269-1277. doi:10.1016/0017-9310(66)90119-0
- L. J. Crane, “Flow Past a Stretching Sheet,” Zeitschrift für Angewandte Mathematik und Physik (ZAMP), Vol. 21, No. 4, 1970, pp. 645-647. doi:10.1007/BF01587695
- E. M. Sparrow, “Radiation Heat Transfer,” Augmented Edition, Hemisphere Publishing Corp., Washington DC, 1978.
- V. M. Soundalgekar, N. V. Vighnesam and I. Pop, “Combined Free and Forced Convection Flow Past a Vertical Porous Plate,” International Journal of Energy Research, Vol. 5, No. 3, 1981, pp. 215-226. doi:10.1002/er.4440050303
- W. H. H. Banks, “Similarity Solutions of the Boundary Layer Equation for a Stretching Wall,” Journal de Mecanique Theorique et Appliquee, Vol. 2, No. 3, 1983, pp. 375-392.
- J. B. McLeod and K. R. Rajagopal, “On the Uniqueness of Flow of a Navier-Stokes Fluid Due to a Stretching Boundary,” Archive for Rational Mechanics and Analysis, Vol. 98, No. 4, 1987, pp. 386-395. doi:10.1007/BF00276915
- C. K. Chen and M. I. Char, “Heat Transfer of a Continuous, Stretching Surface with Suction or Blowing,” Journal of Mathematical Analysis and Applications, Vol. 135, No. 2, 1988, pp. 568-580. doi:10.1016/0022-247X(88)90172-2
- M. A. Hossain and H. S. Takhar, “Radiation Effect on Mixed Convection along a Vertical Plate with Uniform Surface Temperature,” Heat and Mass Transfer, Vol. 31, No. 4, 1996, pp. 243-248. doi:10.1007/BF02328616
- E. R. G. Eckert and R. M. Drake, “Analysis of Heat and Mass Transfer,” McGraw-Hill, New York, 1972.
- M. A. Alabraba, A. R. Bestman and A. Ogulu, “Laminar Convection in Binary Mixed of Hydromagnetic Flow with Radiative Heat Transfer,” Astrophysics and Space Science, Vol. 195, No. 2, 1992, pp. 431-439. doi:10.1007/BF00646774
- A. Postelnicu, “Influence of a Magnetic Field on Heat and Mass Transfer by Natural Convection from Vertical Surfaces in Porous Media Considering Soret and Dufour Effects,” International Journal of Heat Mass Transfer, Vol. 47, No. 6-7, 2004, pp. 1467-1472. doi:10.1016/j.ijheatmasstransfer.2003.09.017
- M. S. Alam and M. M. Rahman, “Dufour and Soret Effects on Mixed Convection Flow Past a Vertical Porous Flat Plate with Variable Suction,” Nonlinear Analysis: Modelling and Contral, Vol. 11, No. 1, 2006, pp. 3-12.
- M. Enamul Karim, M. A. Samad and Md. Abdus Sattar, “Steady MHD Free Convection Flow with Thermal Radiation Past a Vertical Porous Plate Immersed in a Porous Medium,” Research Journal of Mathematics and Statistics, Vol. 3, 2011, pp. 141-147.
- K. A. Helmy, “MHD Boundary Layer Equations for Power Law Fluids with Variable Electric Conductivity,” Meccanica, Vol. 30, No. 2, 1995, pp. 187-200. doi:10.1007/BF00990456
- K. Vajravelu and A. Hadjinicolaou, “Heat Transfer in a Viscous Fluid over a Stretching Sheet with Viscous Dissipation and Internal Heat Generation,” International Communications in Heat Mass Transfer, Vol. 20, No. 3, 1993, pp. 417-430. doi:10.1016/0735-1933(93)90026-R
- P. R. Nachtsheim and P. Swigert, “Satisfaction of the Asymptotic Boundary Conditions in Numerical Solution of the Systems of Non-Linear Equations of Boundary Layer Type,” Ph.D. Thesis, NASA TN D-3004, Washington DC, 1965.

