ABSTRACT

In this article, variational iteration method (VIM) and homotopy perturbation method (HPM) solve the nonlinear initial value problems of first-order fractional quadratic integro-differential equations (FQIDEs). We use the Caputo sense in this article to describe the fractional derivatives. The solutions of the problems are derived by infinite convergent series, and the results show that both methods are most convenient and effective.

Keywords:

Fractional Quadratic Integro-Differential Equations, Variational Iteration Method, Homotopy Perturbation Method

1. Introduction

The fractional calculus has appeared in many areas during the recent decades. Some scientists use approximation and numerical methods because there are almost no exact solutions of the fractional differential equations. He has pro- posed the VIM and HPM to solve the problems of linear and nonlinear [1] [2] [3] [4] . VIM is based on Lagrange multiplier. The another method is HPM which defines as a coupling of the traditional perturbation method and homotopy in topology. Many authors successfully apply these methods to find the solutions of functional equations which arise in scientific and engineering problems [1] [5] [6] [7] [8] [9] . The Adomian decomposition method presents solution of functional equations but perhaps we find some difficulties that will arise during the computation of Adomian polynomials, the VIM and HPM overcome it is difficulties [7] . Fractional differential equations have diverse applications of physical phenomena [10] [11] [12] [13] , for instance, acoustics, electromag- netism, control theory, robotics, viscoelastic materials, diffusion, edge detection, turbulence, signal processing, anomalous diffusion and fractured media [14] . In literature, Momani and Noor [15] used the Adomian decomposition method for solving the fourth order fractional integro-differential Equation. Elbeleze et al. [16] [17] , Kadem and Kilicman [18] applied the HPM and VIM methods for integro-differential Equation of fractional order with initial-boundary con- ditions. Recently, Gaafar [19] studied the existence and nondecreasing solution for the initial value problem of a quadratic integro-differential equations. How- ever, there is little work on nonlinear fractional quadratic integro-differential equations.

Our goal for this article is extending the analysis of VIM and HPM to construct the approximate solutions of the following nonlinear initial value problems for first-order fractional quadratic integro-differential equations.

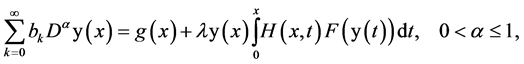(1)

subject to the following initial condition:

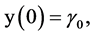(2)

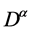is the fractional derivative in the caputo sense, is any nonlinear function, 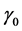is real constant and g is given and can be approximated by taylor polynomials.

2. Basic Definitions

In this section, we intend to present some basic definitions and properties of fractional calculus theory which are further used in this article.

Definition 1.

Areal function 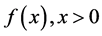is said to be in space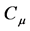, 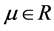if there exists a real number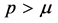, such that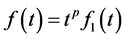, where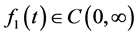, and it is said to be in the space 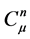if and only if,.

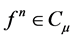Definition 2.

The Riemann-Liouville fractional integral operator of order 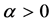of a function, is defined as

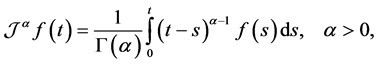(3)

Some properties of the operator can be found in [11] , which are needed here, as follows:

for and:

1.

2.

3.

Definition 3. The fractional derivative of in the caputo sense is defined as

(4)

for.

Lemma 1.

If the the following two properties hold:

1.

2.

3. Analysis of VIM

The basic concept of the VIM is constructing the correction functional for the fractional quadratic integro-differential equation sees Equation (1) with initial conditions,

(5)

(6)

is the Rieman-Liouville fractional integral operator of order, is a general Lagrange multiplier and refers to the restricted variation (i.e.) to identify the approximate Lagrange multiplier, construct the correctional function (6) which can be approximately expressed as:

(7)

taking the variation of Equation (7) to the independent variable we find

(8)

to make the previous equation stationary, we gain the following stationary conditions:

(9)

finally, the Lagrange multiplier is:

(10)

We achieve the following iteration formula by substitution of (10) into the functional (6)

(11)

(12)

the initial approximation can be selected by the following way which satisfies initial conditions

(13)

4. Analysis of HPM

The main concept of the HPM is constructing the homotopy for fractional quadratic integro-differential equation sees Equation (1),

(14)

(15)

is an embedding parameter. If, then Equation (15) turns into a linear Equation

and when, then Equation (15) becomes to be the original problem.

The solution of Equation (1) can be considered as a power series in p which is the basic assumption of HPM :

(16)

when in (16) the approximate solution of Equation (1) can be as following

First, substitute the relation (16) in the Equation (15). Second, equate the terms which have the same power’s of p which yield to the following series of equations:

(17)

(18)

(19)

(20)

and so on, the functions satisfy the following condition:

5. Applications

n this section, we apply VIM and HPM to first-order nonlinear (FQIDEs).

Example 1.

Consider the following nonlinear first-order (FQIDEs):

(21)

subject to the following initial condition

(22)

According to VIM, the expression of the iteration formula (12) for Equation (21) can be observed in the following form:

(23)

To avoid the difficulty of fractional integration, for the exponential term we

take the truncated taylor expansion in (23), e.g., to sa-

tisfy the initial condition (22), we assume that the initial approximation has the following form first-order approximation takes the following form by using iteration Formula (23):

(24)

(25)

Table 1 and Figure 1 presents the approximate solution for the different values of a, we have noticed that the accuracy is improving. First, by computing more terms of the approximate solutions. The second way is taking more terms in the taylor expansion of the exponential term.

According to HPM, we build the following homotopy:

(26)

First, substitute the relation (16) in the Equation (26).

Second, equate the terms which have the same power’s of p which yield to the following series of Equations:

(27)

and so on, apply the operator to the previous equations, and use the initial condition (22), to gain the following equations:

(28)

(29)

(30)

and so on, by taking the truncated taylor expansions for the exponential term in

(29, 30): e.g., to avoid the difficulty of fractional integra-

tion, thus by solving Equations (28, 29, 30), we obtain

(31)

(32)

The two terms approximation are formed as the following Equation

(33)

Table 2 and Figure 2 shows the approximate solutions of (33) for and for some values of.

Figure 3 represent a comparison between two approximate solutions by using VIM and HPM methods.

Example 2.

Consider the following (FQIDEs):

(34)

According to VIM, the expression of the iteration Formula (12) for Equation (34) can be observed in the following form:

(35)

To avoid the difficulty of fractional integration, for the exponential term we

take the truncated taylor expansion in (35), e.g., to satisfy

the initial condition, we assume that the initial approximation has the following form first-order approximation takes the following form by using iteration Formula (35):

(36)

Table 3 and Figure 4 presents the approximate solution for the different values of a, we have noticed that the accuracy is improving. First, by computing more terms of the approximate solutions. The second way is taking more terms in the taylor expansion of the exponential term.

According to HPM, we build the following homotopy:

(37)

First, substitute the relation (16) in the Equation (37).

Second, equate the terms which have the same power’s of p which yield to the following series of Equations:

(38)

and so on, applying the operator to the previous Equations, and use the initial condition (34), to gain the following Equations:

(39)

(40)

(41)

and so on, by taking the truncated taylor expansions for the exponential term in

(40, 41): e.g.,.

To avoid the difficulty of fractional integration, thus by solving Equations (39, 40, 41), we obtain

(42)

(43)

(44)

the two terms approximation are formed as the following Equation

(45)

Table 4 and Figure 5 shows the approximate solutions of (34) for and for some values of.

Figure 6 represent a comparison between two approximate solutions by using VIM and HPM methods.

Example 3.

Consider the following nonlinear (FQIDEs)

(46)

For with exact solution. By using VIM, the iteration formula for Equation (46) is,

(47)

We can take an initial approximation

The first two iterations are easily obtained from (47) and are given by:

(48)

(49)

Therefore, we obtain the exact solution,.

According to HPM, we construct the following homotopy:

(50)

and continuously trace an implicity defined curve from starting point to a solution function substituting (16) into (50). Also, we have to equate the terms with the same identical power’s of p, then, we gain these components

(51)

(52)

(53)

(54)

and so on, we obtain therefore, the approximate solution is

obtained readily by which is the exact solution.

6. Conclusion

In this paper, we have applied the VIM and HPM to find the solution of nonlinear initial value problem of fractional quadratic integro-differential equations for the first order. The methods do not require any linearization, perturbation or restrictive assumptions, we have observed that the VIM and HPM is a very powerful and effective tool for finding the solutions of the fractional quadratic integro-differential Equation. We use the Maple package (2015) in calculations.

Cite this paper

Alhendi, F., Shammakh, W. and Al-Badrani, H. (2017) Numerical Solutions for Quadratic Integro- Differential Equations of Fractional Or- ders. Open Journal of Applied Sciences, 7, 157-170. https://doi.org/10.4236/ojapps.2017.74014

References