Open Journal of Applied Sciences
Vol.05 No.12(2015), Article ID:62187,14 pages
10.4236/ojapps.2015.512075
A Variational Model for Removing Multiple Multiplicative Noises
Xuegang Hu, Yan Hu*
Chongqing University of Posts and Telecommunications, Chongqing, China

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 November 2015; accepted 21 December 2015; published 24 December 2015
ABSTRACT
The problem of multiplicative noise removal has been widely studied in recent years. Many methods have been used to remove it, but the final results are not very excellent. The total variation regularization method to solve the problem of the noise removal can preserve edge well, but sometimes produces undesirable staircasing effect. In this paper, we propose a variational model to remove multiplicative noise. An alternative algorithm is employed to solve variational model minimization problem. Experimental results show that the proposed model can not only effectively remove Gamma noise, but also Rayleigh noise, as well as the staircasing effect is significantly reduced.
Keywords:
Noise Removal, Staircase Effect, Rayleigh Noise, Gamma Noise

1. Introduction
Image noise removal is one of fundamental problems of image processing and computer version. A real recorded image may be disturbed by some random factors, which is an unavoidable. Additive noise model [1] -[3] is always assumed as
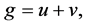 where
where
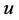 is the original image and
is the original image and
 is the noise. The denoising problem is to recover
is the noise. The denoising problem is to recover
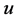 from the observed image
from the observed image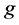 . Removing additive noise, however, is already quite maturing now. Multiplicative noise widespread in our lives, such as: Ultrasound imaging, synthetic aperture radar imaging [4] [5] , has more significance and challenging for us to remove. Rayleigh noise commonly occurs in ultrasound imaging.
. Removing additive noise, however, is already quite maturing now. Multiplicative noise widespread in our lives, such as: Ultrasound imaging, synthetic aperture radar imaging [4] [5] , has more significance and challenging for us to remove. Rayleigh noise commonly occurs in ultrasound imaging.
Classical variational model for multiplicative noise removal is aiming at Gaussian distribution [6] . But when the noise is disobedience Gaussian distributed, the effect of denoising is not very satisfactory. To solve the problem that assuming multiplicative noise model is more reasonable and representative, in 2008, Aubert and Aujol [7] assumed the noise with Gamma distribution with mean 1. A variational model, named AA, used the distribution characteristics of Gamma multiplicative noise and maximizing a posterior (MAP) has been proposed,
and its fidelity term expresses as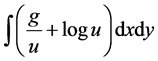 . Aiming at solving the problem of the fidelity term sick, a
. Aiming at solving the problem of the fidelity term sick, a
series of variation models have taken logarithmic transformation
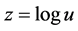 [8] [9] , and then get a new fidelity
[8] [9] , and then get a new fidelity
term written as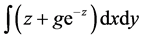 .
.
For solving problem that AA is not strictly convex, Huang, Ng and Wen [8] used a logarithmic transformation and proposed a new model (Named HNW model):
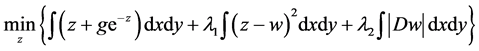
Numerical results show that noise removal ability of HNW is better than AA, but it produces “staircase effect”. Alternative iterative algorithm ensures that the solution of the model is unique, and the iterative sequence also converges to optimal solution of it.
After, a body of variation models [7] -[13] of multiplicative noise removal has been proposed, and removing multiplicative noise abilities made considerable progress. Models not only can effectively remove the noise, but also to better protect the image edge and texture. When we get a model, and then must need a good algorithm to solve it. Numerical algorithm of variation model, today, includes ADMM [14] [15] , ALM [16] [17] , Newton iterative method [8] [9] [18] [19] and dual algorithm [20] -[22] and so on. HNW model has used adaptive alternating iterative algorithm. That is to say, the model can be divided into two parts: one uses Newton iterative method, and the other uses dual algorithm. Iterative sequence obtained converges to the optimal value of the model.
The rest of this paper is organized as follows. In Section 2, we introduce the proposed model how constructs it. Next section will give a new numerical algorithm. Convergence proof of the model will be launched in Section 4. In Section 5, we will show the experiments and its specific analysis. Finally, concluding remarks are given.
2. The Proposed Model
The difference between additive noise and multiplicative noise is whether the noise signal and the original image signal are independent or not. Multiplicative noise, however, is not independent. In paper [23] , multiplicative noise model is assumed . Inspired by it, assuming the noise model:
. Inspired by it, assuming the noise model:
 (2.1)
(2.1)
In which g is the observed image, u is the original image, n is multiplicative noise under Rayleigh distribution, and the probability density function of n is denoted as follows
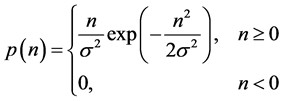 (2.2)
(2.2)
where
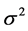 is a constant. The smaller
is a constant. The smaller
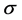 is, the greater the intensity of the added noise. On the contrary, it is smaller. g and u are two independent random variables, so that, for any
is, the greater the intensity of the added noise. On the contrary, it is smaller. g and u are two independent random variables, so that, for any , there is
, there is

To realize the estimate of the original image u, the estimate can be computed by
Applying Bayes’s rule, it becomes

Based on (2.4), minimize post mortem energy of its MAP method
Logarithmic energy equation

We can know the truth from the reference [24]

Combining (2.2), (2.3), (2.5) with (2.6), we can get


From (2.1), we can derive that

If


where D is a two-dimensional bounded open domain of R2 with Lipschitz boundary, then image can be interpreted as a real function defined on D.
With using a logarithmic transformation


An unconstrained optimization problem can be solved by a composition function

Variable splitting [17] is a very simple procedure that consists in creating a new variable, say v, to serve as the argument of


which is apparently equivalent to formula (2.11), and the Lagrange function can be written as follows
where
We denote
To solve its minimum value, it is equivalent to this constrained optimization problem

3. Algorithms
Inspired by the iterative algorithm of reference [8] and [18] , in this paper, I will propose a new algorithm to solve (2.13). Starting from initial guess
Such that

To solve the problem (3.1), we need to divide it into the following three steps.
The first step of the method is to solve a part of the optimization problem. The minimizer of this problem

Its discretization
Now, letting

Since f is continuous and derivable in the specified range, this function is equitant to solving the regular with

We use CSM [25] to replace Newton iteration method [8] [9] .
And then, we can get

The second step of the method is to apply a TV denoising scheme to the image generated by the previous multiplicative noise removal step. The minimizer of the optimization problem

Denoting
Its corresponding Euler-Lagrange equation of the variational problem (3.5) as follows
where
and
In this paper,



where
and
Using gradient descent method to obtain (3.5) the optimization numerical solution as follows:

where
and iterative formula
The third step is to analysis the condition to stop iterative.

4. The Convergence Analysis
In this section, we will discuss the convergence of the iterative algorithm. First, we know that


Theorem 1. For any given initial value


To prove this theorem, we will give the following lemmas, and the appropriate proof.
Lemma 1. Sequence

Proof. It follows from the alternating iterative process in algorithm that

It is obvious that sequence






Lemma 2.The function

Proof. Let

The matrix S is not a full-rank. The discrete total variation of regularization term of model (2.13) as follows
Denote

Next we will discuss two cases: 1)




For (i), we note that

to z. therefore we obtain

By using the above inequality, we have
Considering


We can get that

For (ii), considering



So

Definition 3. Let





Proof of theorem 1. Since sequence


function and strictly convex function, the set of fixed points are just minimizers of
one and only one minimizer of

Moreover, we have, for any

Let us denote by


We can get conclusion that






So


5. Experimental Results
In this section, we will experiment on Lena and Cameraman. Different strength Gamma and Rayleigh noises are added to the original image, and then comparing effects of the proposed model proposed model denosing with HNW. In our experiments, Figure 1(a) is original image of Lena; Figure 1(b) is Cameraman. Figures 2-5 are noised images distorted by Rayleigh and Gamma noise with different strength.
In Figure 3 and Figure 4, denosing results of Lena obtained by the proposed model and HNW model are including noise removal image―The clearer image is, the well model is; residual plot-More image’ signal has been kept, more bad experimental results; gray value curve figure―The blue color represents the original image of the selected signal, and red signal represents denoised part. If red and blue colors are fitting well, we could say that the denosing effect is better. From Figure 3, we can clearly see that the proposed model has more effective

Figure 1. Original images. (a) Lena. (b) Cameraman.

Figure 2. Noisy images for Lena. (a) L = 20 Gamma. (b)

than HNW for Lena with Gamma L = 20, because gray distribution is reasonable and fitting degree of denoised image is stronger than HNW model. The result of denosed aiming at the noise under the Rayleigh distributed multiplicative noise

In Figure 6 and Figure 7, experimental results for Cameraman destroyed by L = 10 and
In order to better illustrate the effectiveness ofthe proposed model, this paper will use the additional data to show it. These are iteration time (T), signal to noise ratio (SNR), mean square error (MSE), peak signal to noise ratio (PSNR), and relative error rate (ReErr). T is time to work-the smaller timeis, the well model is. For SNR or PSNR, the larger the value, the smaller noise. For MSE or ReErr, the value is smaller, indicating that denoising effect is positive. Table 1 and Table 2 show the experimental data. Datasshow that whether for Gamma noise or Rayleigh noise, or simple or a little texture detail-rich images, the proposed model is better than NHW model to obtain considerable experimental data.



Figure 3. Restored images for Lena L = 20.



Figure 4. Restored images for Lena



Figure 6. Restored images for Cameraman L = 10.



Figure 7. Restored images for Cameraman
Table 1. Data for lena.
Table 2. Data for cameraman.
6. Conclusion
In this paper, we propose a variational method for removing multiple multiplicative noises, and give a new numerical iterative algorithm. We proved the sequence obtained converges to the optimal solution of the model. Final experiments show that whether Gamma noise or Rayleigh noise, denoising and edge-protection ability of the proposed model are stronger than HNW model, at the same time, staircasing effect (image has the same gray in some regions) is greatly suppressed. But, proposed model has only dealt with two noises. Next work, we wish that we can find a model to remove many more kinds of multiplicative noises and make sure it has unique solution!
Cite this paper
XuegangHu,YanHu, (2015) A Variational Model for Removing Multiple Multiplicative Noises. Open Journal of Applied Sciences,05,783-796. doi: 10.4236/ojapps.2015.512075
References
- 1. Hou, Y.Q., Zhang, H., Zhang, H. and Zhang, L.Y. (2008) An Improved Adaptive Image Denoising Model Based on Total Variation. Journal of Northwest University (Natural Science Edition), 38, 371-373.
- 2. Guo, X.L., Wu, C.S., et al. (2011) Improved Adaptive Image Denoising Total Variation Regularization Model. Journal of WUT (Information &Management Engineering), 33, 200-202.
- 3. Peng, L., Fang, H., Li, G.Q. and Liu, Z.W. (2012) Remote-Sensing Image Denoising Using Partial Differential Equations and Auxiliary Images as Priors. IEEE Geoscience and Remote Sensing Letters, 9, 358-362. http://dx.doi.org/10.1109/LGRS.2011.2168598
- 4. Zheng, M.J. and Xiao, P.Y. (2010) Analysis of a New Variational Model for Multiplicative Noise Removal. Journal of Mathematical Analysis and Applications, 362, 415-426. http://dx.doi.org/10.1016/j.jmaa.2009.08.036
- 5. Shih, Y., Rei, C. and Wang, H. (2009) A Novel PDE Based Image Restoration: Convection-Diffusion Equation for Image Denoising. Journal of Computational and Applied Mathematics, 231, 771-779. http://dx.doi.org/10.1016/j.cam.2009.05.001
- 6. Rudin, L., Lions, P.L. and Osher S. (2003) Multiplicative Denoising and Deblurring: Theory and Algorithms. Geometric Level Set Methods in Imaging, Vision, and Graphics. Springer, New York, 103-119. http://dx.doi.org/10.1007/0-387-21810-6_6
- 7. Aubert, G. and Aujol, F. (2008) A Variational Approach to Removing Multiplicative Noise. SIAM Journal on Applied Mathematics, 68, 925-946. http://dx.doi.org/10.1137/060671814
- 8. Huang, Y.-M., Ng, M.K. and Wen, Y.-W. (2009) A New Total Variation Method for Multiplicative Noise Removal. SIAM Journal on Imaging Sciences, 2, 20-40. http://dx.doi.org/10.1137/080712593
- 9. Hu, X.G. and Lou, Y.F. (2014) A Novel Total Variational Model for Gamma Multiplicative Noise Removal. Journal of Sichuan University (Engineering Science Edition), 46, 59-65.
- 10. Shi, J. and Osher, S. (2008) A Nonlinear Inverse Scale Space Method for a Convex Multiplicative Noise Model. SIAM Journal on Imaging Sciences, 1, 294-321. http://dx.doi.org/10.1137/070689954
- 11. Rodrigues, I.C. and Sanches, J.M.R. (2011) Convex Total Variation Denoising of Poisson Fluorescence Confocal Images Anisotropic Filtering. IEEE Transactions on Image Processing, 20, 146-160. http://dx.doi.org/10.1109/TIP.2010.2055879
- 12. Bioucas-Dias, J.M. and Figueiredo, M.A.T. (2010) Multiplicative Noise Removal Using Variable Splitting and Constrained Optimization. IEEE Transactions on Image Processing, 19, 1720-1730. http://dx.doi.org/10.1109/TIP.2010.2045029
- 13. Afonso, M. and Sanches, J.M. (2015) Image Reconstruction under Multiplicative Speckle Noise Using Total Variation. Contents List at Science Direct, 15, 200-213.
- 14. Eckstein, J. and Bertsekas, D. (1992) On the Douglas-Rachford Splitting Method and the Proximal Point Algorithm for Maximal Monotone Operators. Mathematical Programming, 55, 293-318. http://dx.doi.org/10.1007/BF01581204
- 15. Bioucas, J. and Figueiredo, M. (2010) Multiplicative Noise Removal Using Variable Splitting and Constrained Optimization. IEEE Transactions on Image Processing, 19, 1720-1730. http://dx.doi.org/10.1109/TIP.2010.2045029
- 16. Yin, W., Osher, S., Goldfarb, D. and Drabon, J. (2008) Bregman Iterative Algorithms for -Minimization with Applications to Compressed Sensing. SIAM Journal on Imaging Sciences, 1, 143-168. http://dx.doi.org/10.1137/070703983
- 17. Bonnans, J. and Jean, C.G. (2006) Numerical Optimization: Theoretical and Practical Aspects. Springer Press.
- 18. Seabra, J. and Sanches, J. (2008) Modeling Log-Compressed Ultrasound Images for Radio Frequency Signal Recovery. 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, 20-25 August 2008, 426-429. http://dx.doi.org/10.1109/iembs.2008.4649181
- 19. Cheng, W.B. and Cheng, J. (2011) Image Processing and Analysis. Science Press, Beijing.
- 20. Hao, Y. and Xu, J.L. (2014) An Effective Dual Method for Multiplicative Noise Removal. Journal of Visual Communication and Image Representation, 25, 306-312. http://dx.doi.org/10.1016/j.jvcir.2013.11.004
- 21. Chen, H.Z., Song, J.P. and Tai, X.C. (2009) A Dual Algorithm for Minimization of the LLT Model. Advances in Computational Mathematics, 31, 115-130. http://dx.doi.org/10.1007/s10444-008-9097-0
- 22. Chambole, A. (2004) An Algorithm for Total Variation Minimization and Applications. Journal of Mathematical Imaging and Vision, 20, 133-146. http://dx.doi.org/10.1023/B:JMIV.0000011321.19549.88
- 23. Zheng, M.J. and Xiao, P.Y. (2011) A Variational Model to Remove the Multiplicative Noise in Ultrasound Images. Journal of Mathematical Imaging and Vision, 39, 62-74. http://dx.doi.org/10.1007/s10851-010-0225-3
- 24. Grimmett, G. (1986) Probability: An Introduction. Oxford University Press, Oxford.
- 25. Zheng, J.M. and Zhu, W. (2000) Numerical Calculation Method. Chongqing University Press, Chongqing.
- 26. Byne, C.L. (2012) Alternating Minimization as Sequential Unconstrained Minimizations: A Survey. Journal of Optimization Theory and Applications, 156, 554-566.
- 27. Lv, X.G., Le, J., Huang, J. and Jun, L. (2013) A Fast High-Order Total Variation Minimization Method for Multiplicative Noise Removal. Mathematical Problems in Engineering, 2013, Article ID: 834035. http://dx.doi.org/10.1155/2013/834035
NOTES
*Corresponding author.












































 Rayleigh
Rayleigh






