Open Journal of Applied Sciences
Vol.05 No.07(2015), Article ID:57976,12 pages
10.4236/ojapps.2015.57036
Decision Theory and Analysis: An Optima Value Creation Precursor for Organizations
Cephas A. Gbande1, Paul T. Akuhwa2
1Faculty of Administration, Department of Business Administration, Nassarawa State University, Keffi, Nigeria
2OTIJOSH Resources Limited, Abuja, Nigeria
Email: Cgbande3@gmail.com, akuhwa.paul@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 June 2015; accepted 12 July 2015; published 15 July 2015
ABSTRACT
Organizations make many informed decisions such as increasing production capacity, improving human capital, entering a new market etc. This paper shows that executives take either of the two major types of decisions: programmed (structured) and nonprogrammed (unstructured) decisions. While the programmed decisions are for perfectly stable situations, the nonprogrammed decisions are for the real world situation surrounded by uncertainties, risks and ambiguities. For an optima value creation, this paper is succinct that a robust decision theory and analysis serve as a precursor. The environment of decision-making keeps changing and it takes decision-making for organizations to change proportionately to these environmental changes if they must survive. The decision-maker uses probability values to convert uncertainties and risks into perfect knowledge poles so as to make informed decisions. Models are veritable decision making tools and are deterministic and probabilistic (or stochastic) for programmed and nonprogrammed decisions respectively. Real-world value optimization in this paper centres on decisions under pure uncertainty and risky situations generating model fits for an optima value creation. Finally, the optima value creation models under the uncertainty and risk are suggested and organizations advised to use professional decision theorists and analysts as the need arise.
Keywords:
Decision-Making, Decision Environment, Programmed and Nonprogrammed Decisions, Optimization

1. Introduction
Almost all human endeavours involve decisions, and consequently, success in business and industry is the sole preserve of the quality of decision-making. This quality of decision-making and the technical progress amongst societies are inextricable and diametrically symbiotic. Theorizing about decision-making is almost the same as theorizing about human endeavours. Concomitantly, a Hegelian approach about decision-making discourse is same as Hegelian approach with human endeavour discourses. However, decision theory and analysis are not quite as all-embracing as it focuses only on some aspects of human endeavours. In particular, it focuses on how the decision-maker (or executive) uses his/her freedom among the myriad of decision choices [1] . In situations encountered by decision theorists and analysts, there are options to choose, and the decision-maker chooses in a non-random way. The choices of the decision-maker, in these situations, are goal-directed activities. Hence, decision theory and analysis are concerned with the goal-directed behaviour in the presence of options [1] . Decision making is central to the corporate existence, operational excellence, effective performance and productivity of businesses and organizations. To the intent that organizations today are a function of decisions and subsequently, organizations tomorrow are subjects of decisions to make today.
Decision-making is not an endless process but a discontinuous one. In the history of almost any endeavours, there are periods of decision-making being crafted and other periods in which most of the decision-making implementation takes place. Decision theory and analysis try to throw some light, in various ways, on the former type of period (i.e. the period of crafting decision-making) [1] . Organization as a system emphasizes the need for good information and channels of communication in order to assist the effective decision making. The systems approach to organization, involves the isolation of these functions most directly concerned with the achievement of objectives and identification of main decision areas. Recognition of the need for decision-making and the attainment of goals draw attention to a sub-division of the systems approach and the decision theory. The decision theory focuses on managerial decision-making and how organizations process and use information in making decisions [2] [3] . Modern decision theory and analysis have developed since the middle of the 20th century through contributions from several academic disciplines. Although, being clearly an academic subject of its own right now, decision theory is typically pursued by scholar-practitioners and seminal researchers who identify themselves as economists, statisticians, engineers, psychologists, operations research scientists, political and social scientists, management scientists and other philosophers.
As organizations responds to diverse environmental changes, the decision-making process involves the clarification of objectives, the specification of problems and the search for implementation of solutions. Thus, the organization is seen as an information-processing network with numerous decision points. An understanding of how decisions are made helps in understanding behaviour in organizations with mechanisms by which conflict is resolved and choices are made [2] . The decision making in each functional areas of management under probabilistic situation is a complex process. For such decisions, the study of the experiences of the executives using experience survey research is required. Consequently, conclusive decision researches tests hypotheses to draw definite conclusions for implementation and after the validation of the hypotheses, a decision-making framework can be formulated [4] .
The understanding of the operation of decision theory and analysis in shaping behavior in organizations and society’s decision process is very crucial. Also, the critical synthesis of theoretical and conceptual foundations of decision theory and analysis considering their differences and common grounds for decision approaches in a wide range of corporate and public spheres is invaluable. The act of decision making, whether under certainty, uncertainty, risk and ambiguity is founded on both subjective and objective realms of human behavior. Thus, the key theoretical issues of decisions under certainty, uncertainty and risky conditions dealing with deterministic and probabilistic (stochastic) outcomes together are very necessary a precursor for optimal value creation in organizations and business. The theoretical views from the foundational theories as they relate to the factors that influence organizational abilities for decision-making based on modeling, alternative choices, and past occurrences in the decision environment are brought to bear in this study. The in-depth synthesis of these theoretical issues directed to management theory and organizations with respect to why, what, how and when issues of planned (structured) and unplanned (unstructured) decisions for optimal value creation are also explained in this study.
Finally, decision-making for optimal value creation in organizations requires answers to questions, such as; what are the key issues and decision variables interacting that should be considered? What are the situational and environmental variables that form the domain of decision-making for optimal value creation in organizations? How can organizations formulate direct functions (or models) for optimal value creation of their resources? These above posted questions represent the knowledge gaps calling for this research study. Since the real world issues are masterminds of uncertainty and risk challenging executives and managers decision-making, decision analysis for optima value creation are detailed in this study for probable decision solutions. Lastly, the study is arranged into five sections with the first foregoing section highlighting the study’s overview. The second section discusses the problems of the study while the third section deals with theoretical framework and reviews. The fourth section discusses methodology and analysis, with the fifth section closing the study with discussions, conclusion, and recommendations.
2. Problem of the Study
Organizations are living organisms existing as bio-corporate ecological units in the global business ecosystem. The business ecosystems economy is controlled by many factors such as population size, industrial activities, agriculture, government policies, culture, educational system, infrastructure and etc. The process of need satisfaction in the business ecosystem constrains people and government to engage in various socioeconomic activities for production of goods and services. Policies and guidelines of the central and state governments facilitate the integration, coordination and control of all activities with the main objective of optimizing (maximizing or minimizing) socioeconomic growth and development. Suffice it to say that, the entity of the economy, at every point in time, is influenced by certain forces to have competitive role in order to maximize its productivity for its sustenance, continuity, growth and survival [4] . Thus, the productivity of different organizations in the business ecosystems economy can be optimized (i.e. improved and enhanced) through several research studies deploying decision theory and analysis as a precursor (or blueprint).The productivity of any business system being a decision-objective function, is the ratio between its output and input. Where the output corresponds to annual total income of the business system and the input corresponds to the annual total cost of the different resources consumed and services utilized by the business system to realize the annual production [4] . Optimization is a state of affair that maximizes or minimizes the decision-objective function to enhance effectiveness or make use of its best. In other words,
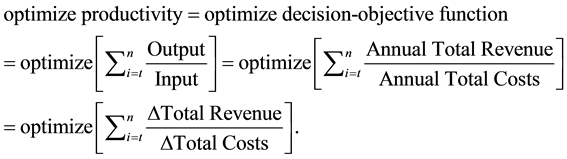
where; n = total period in consideration, in this case, n = 1 year (12 months); t = (0, 1, 2, ××× n),  = increase or difference, and Ʃ = summation.
= increase or difference, and Ʃ = summation.
This is a general form of decision-objective function for optimizing productivity. Decision analysis and theory is the heart of it as it assesses all combinations of variables and criteria for optimization. In any business ecosystem, this productivity is affected by many ecological and environmental factors that are of quantitative and qualitative characteristics. Thus, the development of models using the data of these factors augmented with a detailed survey analysis is the decision theory and analysis which is largely informed by the logic of rationality and the mathematical/statistical theory of probability.
Decision-making in business and organization is not an easy task and hardly follow any consistent procedure. where decisions are to be made abound. Changing times and environment evolve situations which business and industrial problems are becoming more and more complex [5] . The varying degrees of certainty and uncertainty define the type of decision managers are to make and differentiate between programmed and nonprogrammed decisions. In a perfect world, organizations would have all the information necessary for making decisions. In reality, however, some things are unknowable, thus; some decisions will fail to solve the problem or attain the desired outcome [3] [6] .
Organizations today face major business crises and human-accelerated environmental changes worldwide. Arguably, there is a critical need for evidence based information to guide business policy. Most times, business decisions are taken with certainty and/or uncertainty and are pivotal to the future survival of the organization. In most cases, the managers who take these decisions will not know whether they have the right choices. They have to take these decisions against the backdrop of uncertainty or risk [7] . Also, it is the background of afore mentioned reasons that this study tries to answer the following questions representing the problem of the study:
1) How do people make decisions under certainty and uncertainty and what do they consider desirable or the subjective element in their decision process?
2) What objective and subjective probabilities do decision making assign to the occurrences of different desirable outcomes in business and organizations?
3) What are the best methods of rationalization and designing decision models to inform effective decision process?
3. Objectives of the Study
This study’s intention is to provide answers to the manner, style and what situational variables influences in decision-making. Many a managers would wish organizations to operate a perfectly stable environment which they can easily make informed decisions. This is a perfect and utopian business ecosystem with a fixed organizational environment. The real world however presents a different business ecosystem which change is continuous and the only constant with challenges that dreads the corporate existence of business and organizations requiring managers and executives to make hard and right-fast decisions. This study explored decision-making situations and the corresponding strategies to clone a fit and congruence in decision-making and decision-objective function for organizational superior performance (optima value creation).
4. Theoretical Framework and Reviews
Seminal research pointed that, “a theory is an organized body of concepts and principles intended to explain a particular phenomenon” [8] . Also, it was stressed that theorizing is the process of systematically formulating and organizing ideas to understand a particular phenomenon, and concludes that, a theory is the set of interconnected ideas that emerges from this process [9] . Thus,the focus of this paper makes literature inevitable to address the problem, questions, and objectives [10] [11] . More so, a growing and increasingly important trend in the social and behavioral sciences is to think about and attempt to understand specific research problems from an interdisciplinary perspective. One way to do this is to not rely exclusively on the theories in a particular discipline, but to think about how an issue might be informed by theories developed in other disciplines. Building theoretical frameworks based on the postulates and hypotheses developed in other disciplinary contexts can be both invaluably enlightening and an effective way to be fully engaged in this particular study [12] . A theoretical framework of this nature consists of concepts and, together with their definitions and reference to relevant scholarly literature, existing theory that is used for a particular study. This theoretical framework demonstrates an understanding of theories and concepts that are relevant to the topic of this study and that relate to the broader areas of knowledge being considered. These theories are formulated to explain, predict, and understand phenomena and, in many cases, to challenge and extend existing knowledge within the limits of critical bounding assumptions. Therefore, this theoretical framework is the structure supporting theory of this research study, introduces and describes the theory that explains why the research problem under study exists [13] .
The theoretical framework for this study is shown below in Figure 1 with all major related variables. The main objective is to optimize value creation in organizations as shown in the framework, which requires inputs from decision theory and analysis as a precursor. The decision theory and analysis takes place in a decision environment to clone a decision-making approach for the executives aiding a model building for decision model analytic. Alternatives are developed for selection of one best fit to maximize value as the optima value creation criterion in the organization with feedback on model fit and objective realization. Thus, literature review for this study is below and only for concepts of variables shown in the theoretical framework in Figure 1.
4.1. Decision Theory and Analysis
Decision theory and analysis is the combination of descriptive and prescriptive business modelling approach to classify the degree of knowledge. The degree of knowledge is usually classified in order from ignorance-uncer- tainty-risk-certainty. The complete knowledge (or certainty) is on the far right and complete ignorance is on the far left. Between the two are risk and uncertainty. Decision theory and analysis provides an analytical and systematic approach to depict the expected result of a situation, when alternative managerial actions and outcomes are compared [14] . The study of the best possible outcomes for decisions made under varying conditions is decision theory or decision analysis. It involves procedures for choosing optimal decisions in the face of uncertainty,
Figure 1. Theoretical framework for organizations value creation optimization.
risk and ambiguity. These are situations in which a decision is made, an event occurs, another decision is made, another event occurs, and so on.
In a perfect world, organizations would have all the information necessary for making decisions. In reality, however, some things are unknowable, thus; some decisions will fail to solve the problem or attain the desired outcome [3] [6] . Decision theory and analysis provides the decision maker a meaningful conceptual framework for improved decision making. It is a body of methods employed by the decision maker to select one course of action amongst the alternative plans of action available [5] .
Every decision situation can be organized on a scale according the availability of information and possibility of failure. These four positions on the scale are certainty, risk, uncertainty, and ambiguity. Whereas programmed or structured decisions can be made in situations involving certainty, many decisions that managers’ deal with everyday involve at least some degree of uncertainty and require nonprogrammed or unstructured decisions making. From the foregoing, it can be generalized that; decision theory is a continuum and the central part of decision science with programmed decisions and nonprogrammed decisions at the continuum extreme ends for effective decision problem solutions.
4.2. Decision Environment
It is desirable to know the details about resources (such as managers, employees, equipment, finance and etc.) that are required to carry out policies of the organization and at the same time keeping in mind the social and ecological environments in which the organization functions. Knowledge of such factors will help in modifying the initial set of decision-makers’ objectives. The decision environment is the situational framework within which the decision is taken [3] [6] [14] . These situations can be certain, uncertain, risking and ambiguous.
Certainty―This is the situation where the outcome of a specified system of decision can be predetermined with exactness or certainty. It is a determinate situation which each action will lead to only one or same outcome. In this type of decision situation, the decision maker knows without doubt the outcome of every alternative courses of action because all the information the decision maker needs is fully available [5] -[7] [14] -[16] .
Risk―This means that a decision has clear-cut goals and that good information is available, but the future outcomes associated with each alternative are subject to chance. However, enough information is available to allow the probability of a successful outcome for each alternative to be estimated [5] -[7] [15] -[17] . Statistical analysis may be used to calculate the probabilities of success or failure. Thus, the decision maker knows the likelihood that each various states of nature will occur―each action will lead to one outcome, each with a known probability. In other words, it is a stochastic situation where there are many state of affairs and the decision maker knows the probability of occurrence of each state of affair.
Uncertainty―Managers know which goals they wish to achieve, but the information about alternatives and future events in incomplete. Managers may have to make assumptions from which to forge the decision even though it will be wrong if the assumptions are incorrect. Some of the questions concerning decision maker under uncertainty include: Will the product catch up with the market? Will the new branch of business be successful? [5] This perspective made Robert Robin, former US Treasury Secretary to define uncertainty as a situation that even a good decision might produce a bad outcome [6] .
Ambiguity and Conflict―Ambiguity is by far the most difficult decision situation. Ambiguity means that the goals to be achieved or the problem to be solved is unclear, alternatives are difficult to define, and information about outcomes is unavailable [6] . It is a situation in which something (decision alternative course) can be understood in more than one way and it is not clear which meaning is intended. In some situations presented by business and industry, managers involved in a decision create ambiguity because they see things differently and disagree about what they want. A highly ambiguous situation can create what is sometimes called a wicked decision problem. Sometimes managers will come up with a decision “solution” only to realize that they hadn’t clearly defined the real problem to begin with [3] [6] .
4.3. The Decision-Making Approach
The approach managers use to make decisions usually falls into one of the three types: the classical model, the administrative model or the political model. These models and their various characteristics descriptions and differences are as shown in Table 1 below. The choice of model depends on manager’s preference, whether the decision is programmed or nonprogrammed, and the degree of uncertainty associated with the decision [2] [6] .
4.4. Decision Modeling
The end-point of decision theory and analysis is model-building as it is both quantitative, quantitative and mixed-method (i.e. quantitative-qualitative). With respect to organizations objectives, alternative strategies and decision-making environment, there are basic theoretical constructs that are premises in decision theory for decision model-building to aid effective management decision-making. Through modeling, the assumed real world is abstracted from the real situation by concentrating on the dominant variables that control the behavior of the real system. The model expresses in an amenable manner the mathematical functions that represent the behavior of the assumed real world. In other words, effective model must be representative of reality that is being investigated and have major impact on the decision [4] [14] -[17] . The key to model-building lies in abstracting only the relevant variables that affect the criteria of the measures-of-performance of the given system and in expressing the relationship in a suitable form. Model enrichment is accomplished through the process of changing constants into variables, adding variables, relaxing linear and other assumptions, and including randomness [14] . The top three qualities of any model are:
1) Validity―How the model will represent the critical aspects of the system or problem under study;
2) Usability―Whether the model can be used for the specific purposes;
3) Value―Attain value expectation of the user.
The conditional characteristics and dimensions of decision theory models are classified into eight different but interacting variables. These are: function, structure, dimensionality, and degree of certainty, time reference, and degree of generality, degree of closure, and degree of quantification. However, this study discusses models
Table 1. Characteristics of Decision-Making Models (Daft, 2010; p. 221).
based on degree of certainty and are basically two types: the deterministic models and probabilistic or stochastic models.
Deterministic Models―If all the parameters, constants and functional relationship are assumed to be known with certainty when the decision is made, the model is said to be deterministic. Thus, in such a case where the outcome associated with a particular course of action is known, i.e. for a specific set of input values, there is a uniquely determined output which represents the solution of the model under conditions of certainty. The results of this model assume a single value. Examples of this model include linear programming models, input-output models, and activity models, Transportation and assignment models, etc. [5] [14] .
Probabilistic (Stochastic) Models―These are models in which at least one parameter or decision variable is a random variable. Since at least one decision variable is random, the independent variable(s), will also be random. This means consequences or payoff due to certain changes in the independent variable cannot be predicted with certainty. However, it is possible to predict a pattern of values of both the variables by their probability distribution. Stochastic programming models and Bayesian models are examples of probabilistic models [5] .
4.5. The Decision Objective.
The objective of decision making takes priority in the decision making process (or decision theory). Thus, it is very important to define clearly and explicitly the objectives involved in the decision process. Managers are expected to be rational (i.e. able to choose worthwhile in the light of cost-benefit analysis), and are required to possess acceptable value systems necessary for effective decision making [5] . That is, either the decision-maker has already obtained some solution of the problem and wants to retain it, or he/she wants to improve it to a higher degree. If there are conflicting objectives, he/she may be advised to rank the objectives in order of preference; overlapping among several objectives may be eliminated [14] .
4.6. Model Analysis
Most decision problems in real life are probabilistic (or stochastic) in nature due to changing environment that makes information incomplete, scarce and uncontrollable to the decision-maker. Thus, their models contains at least one parameter or decision variable that is a random variable. Since at least one decision variable is random, the independent variable(s), will also be random. That means consequences or payoff due to certain changes in the independent variable cannot be predicted with certainty. This requires a critical search for best-fit decisions centers on optima plan of action.
Alternative Plans of Actions (Strategies)―The problem arises only when there are several courses of action available for a solution. An exhaustive list of courses of action can be prepared in the process of going through problem formulation. Courses of action that are not feasible with respect to the objectives and resources may be ruled out [14] . The alternative plans of action are strategy options open to the decision maker’s choice if there is only one course of action. There are limited and unlimited strategies for decision making, so an explanation list of all feasible alternative plans of action or strategies should be prepared in advance, since the object of decision making is to pick up the best out of these limited or unlimited strategies [5] . The starting point is in formulation of decision pay-off in which the results or pay-offs of all the different possibilities or strategies that could be chosen are arranged according to the conditions or states of nature affecting the pay-off that might prevail [7] .
Decision Payoff―A numerical value (outcome) resulting from each possible combination of alternatives and states of nature is called payoff. The payoff values are always conditional because of unknown states of nature. Payoff is measured within a specified period (e.g. after one year). This period is sometimes called the decision horizon and the tabular arrangement of these conditional outcome (payoff) values is known as payoff matrix [14] . Decision payoff is an indication of the effectiveness of the strategies. It is measured in terms of money but in many situations, it is not possible to give a realistic value of money. In such a case, the executive decides in accordance with the skills and experience he/she has as to what the outcome of a decision worth to the organization. Payoffs may be fixed (i.e. determinate in nature) or can be random (i.e. probabilistic in nature). A probabilistic payoff is determined by chance the strategy is chosen [5] [7] .
Selection of Desired Alternative―Once feasible alternatives are developed, one must be selected. The decision choice is the selection of the most promising of several alternative courses of action. The best alternative is one in which the solution best fits the overall goals and values of the organization and achieves the desired results using the fewest resources. Executives try to select the choice with least risk and uncertainty. Choosing among alternatives also depends on manager’s personal factors and willingness to accept risk and uncertainty. Risk propensity is the willingness to undertake risk with the opportunity of gaining increased payoff. Payoff is always shown in a table form known as the payoff matrix, as shown in Table 2 below. The table shows the states of nature with their probabilities of occurrence but uncontrollable by the decision maker, and their corresponding courses of actions. The decision-maker is expected to choose the best alternative from the list that result into the optima value (utility). The level of risk a manager is willing to accept will influence the analysis of cost and benefits to be derived from the decision [6] .
Implementation of Decision Solution (Alternative)―This involves the use of managerial, administrative, and persuasive abilities to ensure that the chosen alternative is carried out. The decision-maker not only has to identify good decision alternative to select but also to select the alternatives that are capable of being implemented. It is important to ensure that any decision implemented is continuously reviewed and updated in the light of changing environment. The behavioral aspects of change are exceedingly important to the successful implementation of decision. Studies show that when employees see that managers follow up on their decisions by tracking implementation success, they are more committed to positive actions [6] . In any case the decision-maker, who is in the best position to implement the decision, must be aware of the objective, assumption, omissions and limitation of the decision model [14] .
Evaluation and Feedback―In the evaluation stage of the decision process, decision makers gather information that tells them how well the decision was implemented and whether it was effective in achieving its goals. Feedback is important because decision making is not a continuous and never-ending process [6] Feedback provides decision makers with information that can precipitate a new decision cycle. It is also part of monitoring that assesses whether a new decision needs to be made. The dynamic environment and changes have significant implications regarding the continuing validity of models and their solutions. Thus, a control procedure has to be established for detecting significant changes in decision variables of the problem so that the suitable adjustments can be made in the solution [14] .
5. Methodology and Analysis of the Study
The methodology of this study considers existing works of various seminal researchers and theoretical foundations of decisions-making using probabilities as a measure of risk and uncertainty. The models developed with their respective analyses are carefully examined toward value creation optimization. Globally, decisions are most often taken under conditions of uncertainty and risk to arrive at optima value creation in organizations [5] [6] [14] . This paper synthesized these models and evaluated how optimization of value creation could be understood and deployed in organizations. In deterministic models, a good decision is judged by the outcome alone, while in probabilistic models, the decision maker is concerned not only with the outcome value but also with the amount of risk each decision carries. As an example of deterministic versus probabilistic models, consider the past and the future. Nothing can be done to change the past, but everything done presently influences and changes the future, although the future has an element of uncertainty. Managers are captivated much more by shaping the future than the history of the past [18] .
Probability Theory in Decision Analysis
Uncertainty is the fact of life and business, whilst probability is the guide for a “good” life and successful busi-
Table 2. General form of Pay-off Matrix Table.
ness. The concept of probability occupies an important place in the decision making process, whether the problem is one faced in business, in government, in the social sciences, or just in one's own everyday personal life. In very few decisions making situations is perfect information that all the needed facts are available, as most decisions are made in the face of uncertainty [6] [14] [18] . Probability enters into the process by playing the role of a substitute for certainty (i.e. complete knowledge). Probabilistic modelling is largely based on application of statistics for probability assessment of uncontrollable events (or factors), as well as risk assessment of decisions.
Probability is derived from the verb to probe meaning to “find out” what is not too easily accessible or understandable. The word “proof” has the same origin that provides necessary details to understand what is claimed to be true. Probabilistic models are viewed as similar to that of a game; actions are based on expected outcomes. The centre of interest moves from the deterministic to probabilistic models using subjective statistical techniques for estimation, testing and predictions. In probabilistic modelling, risk means uncertainty for which the probability distribution is known. Therefore risk assessment means a study to determine the outcomes of decisions along with their probabilities [18] . As decision makers often face a severe lack of information, probability assessment quantifies the information gap between what is known, and what needs to be known for an optimal decision. The probabilistic models are used for protection against adverse uncertainty, and exploitation of propitious uncertainty. Difficulty in probability assessment arises from information that is scarce, vague, inconsistent or incomplete. Business decision making as earlier posited is almost always accompanied by conditions of uncertainty.
Clearly, the more information the decision maker has, the better the decision will be. Treating decisions as if they were gambles is the basis of decision theory. This means that we have to trade off the value of a certain outcome against its probability. To operate according to the canons of decision theory, we must compute the value of a certain outcome and its probabilities; hence, determining the consequences of our choices. The origin of decision theory is derived from economics by using the utility function of payoffs. It suggests that decisions be made by computing the utility and probability, the ranges of options, and also prescribes strategies for good decisions. Probability assessment is nothing more than the quantification of uncertainty. In other words, quantification of uncertainty allows for the communication of uncertainty between persons. There can be uncertainties regarding events, states of the world, beliefs and so on. Probability is the tool for both communicating uncertainty and managing it.
Lastly, as succinctly positioned by [18] , there are different types of probabilistic or stochastic decision models that help to analyse the different scenarios for optima value creation in the real business world. In their view,the three most widely used types decision-making depending on the amount and degree of knowledge are:
1) Decision making under pure uncertainty;
2) Decision making under risk;
3) Decision making by buying information.
6. Decision-Making under Uncertainty
In decision making under pure uncertainty, the decision maker has absolutely no knowledge, not even about the likelihood of occurrence for any state of nature. In such situations, the decision maker’s behaviour is purely based on his/her attitude toward the unknown [18] . Decision making under uncertainty places the decision- maker in the position of being unable to specify the probabilities of occurrence of the various states of nature (future), though the possibilities of states of nature are known. Thus, decisions under uncertainty are carefully taken even with less information. In absence of knowledge about the probability of any state of nature (future) occurring, the decision-maker must arrive at a decision only on the actual payoff values, together with policy (attitude). There are several theoretical criteria of decision making in this situation of uncertainty. Some of these theoretical criteria include [14] -[16] :
1) Optimism (Maximax or Minimim) criterion;
2) Pessimism (Maximin or Minimax) criterion;
3) Equal probabilities (Laplace) criterion;
4) Coefficient of optimism (Hurwiez) criterion;
5) Regret (Salvage) criterion.
Optimism (Maximum and Minimum) Criterion―The decision-maker ensures that the opportunity to miss the largest possible profit (maximax) or the lowest possible cost (minimin). This is called the “best of best” criterion [16] . Thus, he selects the alternative (decision choice or course of action) that represents the maximum of the maxima (or minimum of the minima) payoffs (consequences or outcomes). This is called optimistic decision theory since the criterion requires the decision-maker to select an alternative that has the largest (or lowest) possible payoff.
Pessimism (Maximin or Minimax) Criterion―The decision-maker requires in this theoretical criterion to earn no less (or pay no more) than some specified amount. This is achieved by selection of the alternative that represents the maximum of the minima (or minimum of the maxima in case of loss) payoffs in case of profits. It is called the “best of worst” criterion [16] . This theoretical criteria is known as Wald’s criterion and popularly called pessimistic decision theory as the decision-maker is conservative about the future and always anticipates the worst possible outcome (minimum for profit and maximum for cost or loss).
Equal Probabilities (Laplace) Criterion―This is a situation that the probabilities of the states of nature are not known, so, an assumption is generated that all the states of nature will have equal probability of occurrence (that is assigning equal probability to each state of nature). Given that states of nature are mutually exclusive and collectively exclusive, the probability of each of the state must be 1/(number of states of nature). This theoretical criterion is known as the theory of insufficient reason, because except in few cases, some information about the likelihood of occurrence of states of nature is available.
Coefficient of Optimism (Hurwiecz) Criterion―This criterion is based on the theoretical premise that a rational decision-maker should be neither optimistic nor pessimistic and, therefore, must display a mixture of both. Hurwiecz in this theory, introduced a coefficient of optimism (denoted by α) to measure the decision-makers degree of optimism. This coefficient takes values between 0 and 1, where; 0 represents complete pessimistic attitude about the future, and 1 a complete optimistic attitude about the future. Thus, α is a coefficient of optimism, then (1?α) will be the coefficient of pessimism. Hurwiecz suggested that the decision maker must select an alternative that maximizes, thus;
 .
.
In other words, Hurwiecz theory is based on the weighted average of the best and worst payoffs of each action and is calculated thus: Weighted payoff = α × worst payoff + (1 ? α) × best payoff.
The Regret (Savage) Criterion―This is the opportunity loss decision criterion or minimax regret decision criterion because the decision-maker regrets the fact that he/she has adopted a wrong course of action (or alternative) resulting in an opportunity loss of payoff. Thus, he/she always intend to minimize this regret.
7. Decision-Making under Risk
Decision-making under risk is a probabilistic decision situation in which more than one state of nature exists and the decision-maker has sufficient information to assign probability values to the likely occurrence of each of the states. Knowing the probability distribution of the states of nature, the best decision is to select that course of action which has the largest expected payoff value. The expected (average) payoff of an alternative is the sum of all possible payoffs of that alternative, weighted by the probabilities of the occurrence of those payoffs. Some of the most widely used criteria for evaluating various courses of action (alternatives) under risk are [14] -[16] :
1) Expected Monetary Value (EMV);
2) Expected Opportunity Loss (EOL);
3) Expected Value of Perfect Information (EVPI);
4) Posterior Probabilities and Bayesian Analysis.
Expected Monetary Value (EMV)―The expected monetary value (EMV) for a given course of action is the weighted sum of all possible payoffs for each alternative. The expected (or mean) value is the long-run average value that would result if the decision were repeated a large number of time. Mathematically EMV is stated as follows:
EMV (Course of action, Sj) = 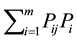
where m = number of possible states of nature;
Pi = probability of occurrence of states of nature, Ni;
Pij = payoff associated with state of nature Ni and course of action, Sj.
Expected Opportunity Loss (EOL)-An alternative approach to maximizing expected monetary value (EMV) is to maximize the expected opportunity loss (EOL), also called expected value of regret. The EOL is defined as the difference between the highest profit (OR payoff) of a state of nature and the actual profit obtained by the particular course of action taken. In order words, EOL is the amount of payoff that is lost by not selecting that course of action which has the greatest payoff for the state of nature that actually occurs. The course of action due to which EOL is minimum is recommended. Since EOL is an alternative decision criterion for decision making under risk, therefore, the results will always be the same as these obtained by EMV criterion discussed earlier. Thus, only one of the two methods should be applied to reach a decision. Mathematically, it is stated as follows.
EOL (state of nature, Ni) = 
where Iij = opportunity loss due to state of nature, Ni and course of action, Sj;
Pi = probability of occurrence of state of nature, Ni.
Expected Value of Perfect Information (EVPI)―In the decision-making under risk, each state of nature is associated with the probability of its occurrence. However, if the decision maker can acquire perfect (complete and accurate) information about the occurrence of various states of nature, then he would be able to select a course of action that yields the desired payoff for whatever state of nature that actually occurs. It has been seen that the EMV or EOl criterion helps the decision maker select a particular course of action that optimizes the expected payoff, without the need of any additional information. Expected value of perfect information (EVPI) represents the maximum amount of money the decision maker has to pay in order to get this additional information about the occurrence of various states of nature, before a decision has to be made. Mathematically it is stated as:
EVPI = (Expected profit with perfect information)-(Expected profit without perfect information).
EVPI = 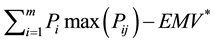
where, Pij = best payoff when action, Sj is taken in the presence of state of nature, Ni;
Pi = probability of state of nature, Ni;
EMV* = maximum expected monetary value.
Posterior Probabilities and Bayesian Analysis―The search and evaluation of decision alternatives often reveal new information. If such information is regarding the effects of alternatives, the consequences are restated. When the uncontrollable factors are involved, either the states of nature themselves are reconsidered or their likelihoods are revised. The value of new information is evaluated in terms of its impact on the expected payoff. The expected value and the cost of the new information are compared to determine whether it is worth acquiring. An initial probability statement to evaluate expected payoff is called a prior probability distribution, the one which has, been revised in the light of new information called a posterior probability distribution. It will be evident that what is a posterior to one sequence of state of nature becomes the prior to others that are yet to happen. The method of computing posterior probabilities from prior probabilities is by using a called Bayes’ theorem. A further analysis of problems using these probabilities, with respect to new expected payoffs with additional information, is called prior-posterior analysis. The Bayes’ theorem, in general terms, can be stated as follows: Let 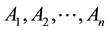 be mutually exclusive and collectively exhaustive outcomes. Their probabilities
be mutually exclusive and collectively exhaustive outcomes. Their probabilities 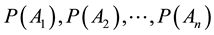 are known. Given the information that outcome B has occurred, the revised conditional probabilities of outcomes Ai, i.e.
are known. Given the information that outcome B has occurred, the revised conditional probabilities of outcomes Ai, i.e. ,
,  are determined by using the following conditional probability relationship:
are determined by using the following conditional probability relationship:
 where;.
where;.
Since each joint probability can be expressed as the product of a known marginal (prior) and conditional probability, 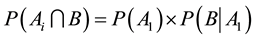 , thus;
, thus;
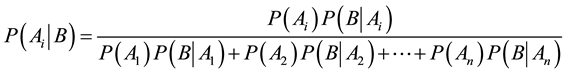
Finally, the big advantage of Bayes’ decision rule is that it incorporates all the available information including all the payoffs and the best available estimates of the probabilities of the respective states of nature [15] .
8. Discussions, Conclusion and Recommendations
All organizations face the challenge of decision-making about outcomes that maximizes their expected utilities respectively. But these decisions hardly are taken with perfect knowledge and information by the decision- maker, because the business environment is fluid and portends tsunami changes. These changes create decision-making environments of uncertainty, risk and ambiguity whilst, the organizations objective sign posts for the optima value creation (utility maximization) have not shifted. In order to achieve the decision objective function optimally, organizations deploy decision theory and analysis approach as a premise for taking informed decisions within the confine of utility function maximization. The absence of effective decision theory and analysis makes many faults and failures in decision-making and consequent failure in organizational performance leading to subsequent survival challenges. The emergence of decision theory as a systematic study and a multidimensional field of knowledge in the late 20th century make it a definite precursor for decision-making effectiveness in organizations.
Decision theory and analysis show that based on the objective function maximization quest and the fast changing environment of the decision-maker, programmed decisions are not obvious business solutions but non- programmed decision types. And because nonprogrammed decisions are often characterized by uncertainty, risk and ambiguity, the decision maker takes on approaches of administrative (to satisfice) and sometimes political (to build alliances for coalition and scenario analysis) approaches. The classical and normative approaches are not applicable due to problems of boundary rationality in the decision-making process. Mostly, intuition based on executive’s experiential surveys plays a better role in the objective utility optimization. This humanistic decision approach to decision-making holds the sway for an optimum value creation in presence of Simon’s theorem on decision-making.
Decision theory and analysis also argue that since there is no one way and hit method managers codify to take all decisions, it is very important to clone a decision-making model contingent to the decision issues at hand. The models then abstract the real world situations of the decision variables. Top on the list of these models are the deterministic and probabilistic (or stochastic) models. The dynamic models put the decision-maker in the position of perfect knowledge and information, but not prevalent in real world. Whilst, the stochastic models use probability as a substitute for knowledge and information (i.e. risks and uncertainties) to mould optima value creation decisions, representing the real world.
This study analyses decision models under pure uncertainty and risk and find that for organizations to realize the optima value creation in pure uncertainty environments, decision theory and analysis must be their precursor for decision-making process and must deploy either of the following models for effective decision-making:
a) Optimism (Maximax or Minimim) criterion;
b) Pessimism (Maximin or Minimax) criterion;
c) Equal probabilities (Laplace) criterion;
d) Coefficient of optimism (Hurwiez) criterion;
e) Regret (Salvage) criterion.
Concomitantly, in risky environments, this study succinctly recommends either of the following models for effective decision-making process if organizations crave optima value creation:
1) Expected Monetary Value (EMV);
2) Expected Opportunity Loss (EOL);
3) Expected Value of Perfect Information (EVPI);
4) Posterior Probabilities and Bayesian Analysis.
Finally, this paper wonders why with the availability of these real world models for uncertainty and risky environments of decision-making, organizations still strives hard with issues of decisions-making. It is also generally held that entrepreneurs are risk aversive in business venturing and avoids uncertainties. However, risks and uncertainties are the real world business environment that is the domain of entrepreneurship venturing. Is entrepreneurship excluded in decision theory and analysis? In other words, are entrepreneurs not needed to deploy decision theory and analysis in their business venturing? Therefore, this paper recommends specific decision theory and analysis research in entrepreneurship venturing to answer the question directed at entrepreneurship decision-making. Also, a cross-sectional research to be conducted on executives and managers regarding their attitudinal capacity to engage in decision theory and analysis, if not, they should engage decision-making services from consultants and specialists.
Cite this paper
Cephas A.Gbande,Paul T.Akuhwa, (2015) Decision Theory and Analysis: An Optima Value Creation Precursor for Organizations. Open Journal of Applied Sciences,05,355-367. doi: 10.4236/ojapps.2015.57036
References
- 1. Hansson, S.O. (2005) Decision Theory: A Brief Introduction. Department of Philosophy and the History of Technology Royal Institute of Technology (KTH), Stockholm.
- 2. Mullins, L.J. (2010) Management and Organizational Behavior. 9th Edition, England Pearson Education Limited, London.
- 3. Jones, R.G. and George, J.M (2008) Contemporary Management. 5th Edition, McGraw-Hill International Edition, McGraw-Hill/Irwin, New York.
- 4. Pannneerselvan, P. (2013) Research Methodology. PHI learning Private Limited, Delhi.
- 5. Ihemeje, J.C. (2006) Quantitative Business Decision Management Theories and Techniques. Onaivi Printing, Keffi- Nigeria.
- 6. Daft, R.L. (2010) New Era of Management. 9th Edition, International Edition, CENGAGE Learning, Boston.
- 7. Buglear, J. (2005) Quantitative Methods for Business. The A-Z of QM, 1st Publishing, Elsevier Butterworth-Heine- mann, Oxford.
- 8. Leedy, P.D. and Armrod, J.E. (2005) Practical Research and Design. 8th Edition, Pearson Education, London.
- 9. Boss, P., Doherty, W.J., LaRoss, R., Schumm, W. and Steimetz, S.K. (1994) Sourcebook of Family Theories and Methods: A Contextual Approach. Springer, New York.
- 10. Cooper, R.D. and Schindlier, P.S. (2003) Business Research Methods. 8th Edition, McGraw-Hill/Irwin, New York.
- 11. Saunders, M., Lewis, P. and Thornhill, A. (1997) Research Methods for Business Students. Pitman Publishing, London.
- 12. Robert, F. (2010) The Oxford Handbook of Interdisciplinarity. Oxford University Press, New York. http://libguides.usc.edu/c.php?g=235034&p=1561763
- 13. Richard, S.A. (2013) Importance of Theory. Theory Building in Applied Disciplines. Berrett-Koehler Publishers, San Francisco. http://libguides.usc.edu/c.php?g=235034&p=1561763
- 14. Sharma, J.K. (2010) Operations Research Theory and Practice. 4th Edition, Macmillan Publishers India Limited, Chennai.
- 15. Taha, H.M. (2008) Operations Research an Introduction. 8th Edition, Prentice-Hall of India Private Limited, New- Delhi.
- 16. Lucey, T. (1999) Quantitative Techniques. 5th Edition, Letts Educational, London.
- 17. Field, A. (2009) Discovering Statistics Using SPSS. 3rd Edition, SAGE Publications Ltd., London.
- 18. Taghavifard, M.T., Damghani, K.K. and Moghaddam, T.R. (2009) Decision Making under Uncertainty and Risky Situ- ations. Copyright 2009 by the Society of Actuaries.



