Open Journal of Applied Sciences
Vol.05 No.06(2015), Article ID:57175,8 pages
10.4236/ojapps.2015.56028
Clustering Algorithm of Quantum Self-Organization Network
Ziyang Li1*, Panchi Li2
1School of Earth Science, Northeast Petroleum University, Daqing, China
2School of Computer and Information Technology, Northeast Petroleum University, Daqing, China
Email: *liziyangemail@126.com, lipanchi@vip.sina.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 May 2015; accepted 13 June 2015; published 16 June 2015
ABSTRACT
To enhance the clustering ability of self-organization network, this paper introduces a quantum inspired self-organization clustering algorithm. First, the clustering samples and the weight values in the competitive layer are mapped to the qubits on the Bloch sphere, and then, the winning node is obtained by computing the spherical distance between sample and weight value. Finally, the weight values of the winning nodes and its neighborhood are updated by rotating them to the sample on the Bloch sphere until the convergence. The clustering results of IRIS sample show that the proposed approach is obviously superior to the classical self-organization network and the K-mean clustering algorithm.
Keywords:
Quantum Bits, Bloch Spherical Rotation, Self-Organization Network, Clustering Algorithm

1. Introduction
Since Kak [1] firstly proposed the concept of quantum inspired neural computation in 1995; quantum neural network (QNN) has attracted great attention by the international scholars during the past decade, and a large number of novel techniques have been studied for quantum computation and neural network. For example, Gopathy et al. [2] proposed the model of quantum neural network with multilevel hidden neurons based on the superposition of quantum states in the quantum theory. Michail et al. [3] attempted to reconcile the linear reversible structure of quantum evolution with nonlinear irreversible dynamics of neural network. Michiharu et al. [4] presented a novel learning model with qubit neuron according to quantum circuit for XOR problem and described the influence to learning by reducing the number of neurons. Gupta et al. [5] defined a new mathematical model of quantum neural network, building on Deutsch’s model of quantum computational network, which provides an approach for building scalable parallel computers. Fariel [6] proposed the neural network with the quantum gated nodes, and indicated that such quantum network may contain more advantageous features from the biological systems than the regular electronic devices. In our previous works [7] , we proposed a quantum BP neural network model with learning algorithm based on the single-qubit rotation gates and two qubits controlled-rotation gates. Next, we proposed a neural network model with quantum gated nodes and a smart algorithm for it [8] , which shows superior performance in comparison with a standard error back propagation network. Adenilton et al. [9] proposed a weightless model based on quantum circuit. It is not only quantum-in- spired but also actually a quantum NN. This model is based on Grover’s search algorithm, and it can both perform quantum learning and simulate the classical models. At present, the fusion of quantum computation and neural computation is gradually becoming a new research direction.
In all of the above models, the fusion of quantum computing and supervised neural networks has been widely studied. However the fusion of quantum computing and unsupervised self-organizing neural network is relatively few. In the classical clustering algorithms, Cai et al. [10] proposed a new algorithm called K-Distributions for Clustering Categorical Data, and Huang [11] investigated clustering problem of large data sets with mixed numeric and categorical values. As it is known to all, unsupervised clustering is the only function of the self- organizing network. For self-organizing network, unsupervised clustering process, in essence, is the application process of the network. This is very different from BP network which must perform a supervised training process before application. Although we proposed quantum self-organizing networks with quantum inputs and quantum weights [12] , this model applied the supervised mode to training, which severely reduces its generalization ability. In addition, although quantum computing effectively enhances the performance of the traditional self-organizing networks, the fusion research of quantum computation and neural computation is still far from mature. It is necessary to further research a new way of integration between them, in order to further improve the performance of neural computation. Hence, we proposed a quantum self-organization network based on Bloch spherical rotation (BQSON), and designed its clustering algorithm in detail. In our approach, both the samples and the weights are denoted by qubits described in Bloch sphere; the weights of the competition winning node and its neighbourhood nodes are adjusted by rotating these qubits to corresponding sample qubit about rotation axis. The experimental results of a benchmark of IRIS clustering show that our approach is superior to the traditional clustering methods such as common self-organizing networks, K-mean clustering, and the adjacent clustering.
2. The Spherical Description and Rotation of Qubits
2.1. The Spherical Description of Qubit
In the quantum computing, a qubit is a two-level quantum system which could be described in two-dimension complex Hilbert space. According to principle of superposition, a qubit can be defined as
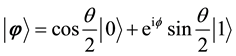 (1)
(1)
where ,
, 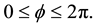
Notation like  is called the Dirac notation, and we will see it often in the following paragraphs, as it is the standard notation for states in quantum mechanics. Therefore, unlike the classical bit, which can only equal 0 or 1, the qubit resides in a vector space parameterized by the continuous variables
is called the Dirac notation, and we will see it often in the following paragraphs, as it is the standard notation for states in quantum mechanics. Therefore, unlike the classical bit, which can only equal 0 or 1, the qubit resides in a vector space parameterized by the continuous variables 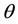 and
and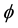 . The normalization condition means that the qubit’s state can be represented by a point on a sphere of unit radius, called the Bloch sphere. The Bloch sphere representation is useful as it provides a geometric picture of the qubit and of the transformations that can be applied to its state. This sphere can be embedded in a three-dimensional space of Cartesian coordinates (
. The normalization condition means that the qubit’s state can be represented by a point on a sphere of unit radius, called the Bloch sphere. The Bloch sphere representation is useful as it provides a geometric picture of the qubit and of the transformations that can be applied to its state. This sphere can be embedded in a three-dimensional space of Cartesian coordinates (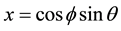 ,
,  ,
,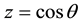 ). Thus, the state
). Thus, the state 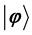 can be written as
can be written as
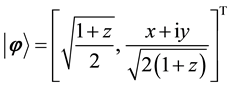 (2)
(2)
By definition, a Bloch vector is a vector whose components 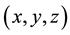 represent a point on the Bloch sphere. We can say that the angles
represent a point on the Bloch sphere. We can say that the angles 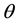 and
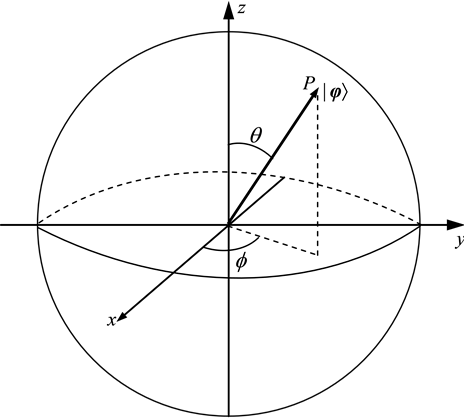
and  define a Bloch vector, as shown in Figure 1.
define a Bloch vector, as shown in Figure 1.
2.2. The Rotation of Qubit about an Aaxi on the Bloch Sphere
In this work, we adjust the weights of competition layer by rotating them around an axis towards the target qubit on the Bloch sphere. This rotation can simultaneously change two parameters 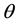 and
and  of a qubit and can automatically achieve the best matching out of two adjustments, which can better simulate the quantum behaviour. To achieve this rotation, it is crucial to determine the rotation axis, as it can directly impact the convergence speed and efficiency of algorithm. To determine the rotation axis, we propose the following method.
of a qubit and can automatically achieve the best matching out of two adjustments, which can better simulate the quantum behaviour. To achieve this rotation, it is crucial to determine the rotation axis, as it can directly impact the convergence speed and efficiency of algorithm. To determine the rotation axis, we propose the following method.
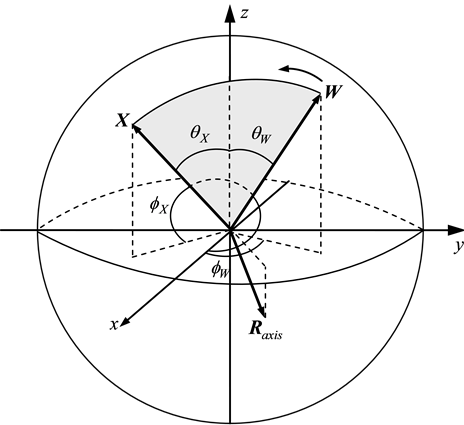
Let 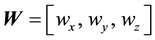
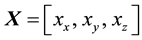
Let the Bloch coordinates of 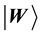
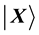
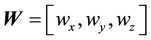
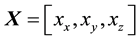
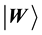
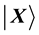
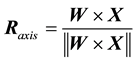
Figure 1. Qubit description on the Bloch sphere.
Figure 2. The rotation axis of a qubit on the Bloch sphere.
From the principles of quantum computing, on the Bloch sphere a rotation through an angle 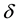
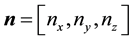
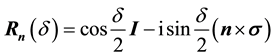
where 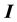
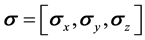
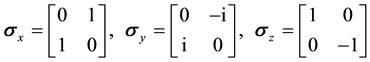
Hence, on the Bloch sphere, a rotation through an angle 

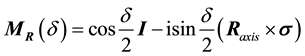
and the rotation operation can be written as
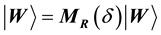
2.3. The Measurement of Qubits
From the principles of quantum computing, the coordinates x, y, and z of a qubit on the Bloch sphere can be measured by the Pauli operators using the following equations.
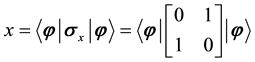
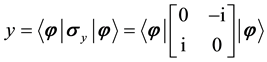
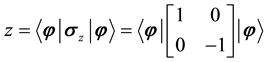
3. Quantum Self-Organization Neural Networks Model
We propose the quantum self-organization neural networks model based on the Bloch spherical rotation are shown in Figure 3, where both inputs and weight values are qubits described on the Bloch sphere.
Let 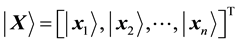
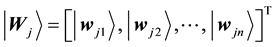
values of the jth node in competition layer. By the projection measuring, the Bloch coordinates of 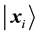
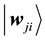
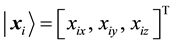
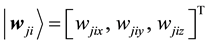
Figure 3. The quantum self-organization neural networks model.
to 1, the spherical distance between 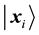
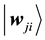
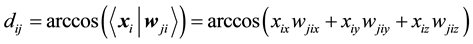
Hence, the distance between 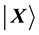
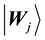
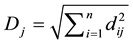
4. Quantum Self-Organization Neural Networks Algorithm
4.1. Quantum State Description of the Samples
First, all samples data are converted to [0, 1]. Let 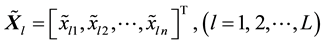
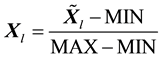
where 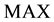
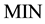
Let sample after normalization be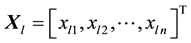
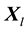

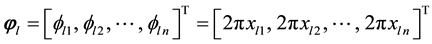
At this point, 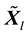
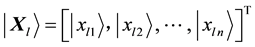
where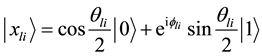
4.2. Competitive Learning Rules
Let 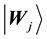
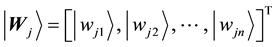
For the lth sample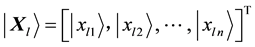
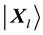
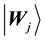
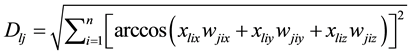
Suppose that the competition layer has C nodes, and that the node with a minimum distance is defined as the winning one. Hence, the winning node should satisfy the following equation
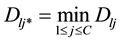
4.3. Network Clustering Algorithm
The self-organizing network is a typical unsupervised clustering model; it is suitable for solving the problem of don’t know the class number of clustering beforehand. Its training is completely different from the traditional BP neural networks. If a self-organizing network must apply supervised information in clustering, it is powerless for clustering problems with no supervision information available. The training process of our model does not contain any prior knowledge about samples classification results; otherwise will lose its generalization ability, which is the shortcoming of Ref. [12] . Our approach can be summarized as follows.
Step 1 Quantum state description of the sample. Convert the samples to qubit states by Equations (13)-(16). Measure the quantum samples by Equations (8)-(10) to obtain their Bloch coordinates.
Step 2 The weights of networks initialization. Initialize all the networks weights to randomly distribution of qubits on the Bloch sphere, as shown below.
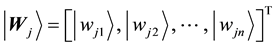
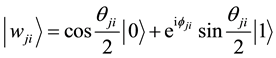
where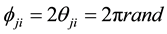
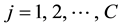
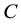
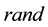
Step 3 The parameters of networks initialization. Include: the maximum iterative steps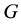
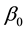
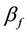
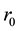
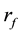
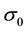
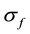
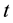
Step 4 Compute the current learning rate, neighborhood radius, and variance by the following equations.
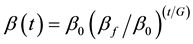
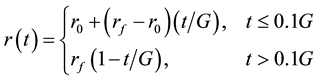
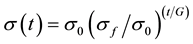
Step 5 Measure all quantum weights in competition layer by Equations (8)-(10) to obtain their Bloch coordinates. For the lth sample 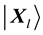
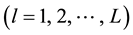
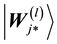
Step 6 For the lth sample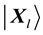
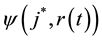
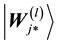
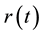
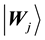
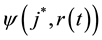
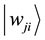
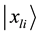
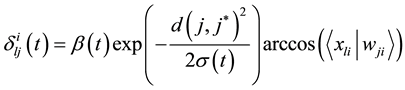
where 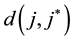
According to theorem, the rotation axis and rotation matrix of rotating 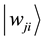
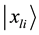
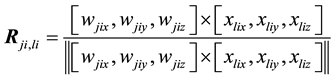
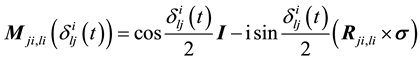
Then, the rotation operation can be written as
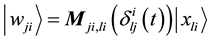
where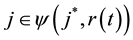
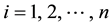
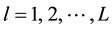
Step 7 If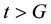
5. Simulations
In order to experimentally illustrate the effectiveness of the proposed BQSON, the IRIS samples are used to compare it with the Classical Self-Organization Network (CSON ), the K-mean clustering, the Nearest Neighbor Clustering (NNC) in this section. In these experiments, we perform and evaluate the BQSON in Matlab (Version
5.1. Parameter Settings
Both BQSON and CSON have 4 input nodes and 100 competition nodes arranged in square matrix. Other parameters are set as follows: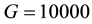
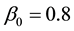

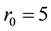
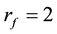
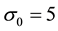
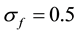
If the clustering results do not change in 100 consecutive steps, we call algorithm reach convergence. For K-mean clustering, the K is set to 3, and if each of variations of class centers is less than 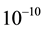
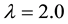
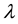
5.2. Clustering Result Contrasts
Considering the log likelihood function is more used in evaluation of the performance of the Bayesian classification network, and less used in clustering algorithm, therefore, we don’t use this index in our work. To facilitate comparison, two relevant concepts are defined as follows:
Precision Ratio Let the correct number of samples in the kth class after clustering be NPR, and the total number of samples in the kth class after clustering be NA. Precision Ratio is defined as follows
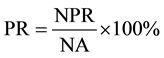
Recall Ratio Let the correct number of samples in the kth class after clustering be NPR, and the total number of samples in the kth class before clustering be NB, Recall Ratio is defined as follows
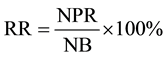
After 9797 iterative steps, the BQSON reaches convergence. All samples are divided into three classes, and each class contains 50 samples. The first class contains 50 “setosa” samples. The second class contains 48 “versicolor” samples and 2 “virginica” samples. The third class contains 48 “virginica” samples and 2 “versicolor” samples. The Precision Ratio and Recall Ratio of three class samples reach 100%, 96%, 96%, respectively.
After 10,000 iterative steps, the CSON does not reach convergence, where the first class contains 50 “setosa” samples, and for the rest of the 100 samples, the model is powerless. In addition, we running until 30000 iterative steps, the CSON is still not convergence.
For K-mean clustering, after 11 iterative steps, convergence is reached. The first class contains 50 “setosa” samples, the second class contains 61 samples where 47 samples are correct, and the third class contains 39 samples where 36 samples are correct. The Precision Ratio of three class samples reach 100%, 77.05%, 92.31%, respectively, and the Recall Ratio of three class samples reach 100%, 94%, 72%, respectively.
For NNC, All samples are divided into three classes. The first class contains 50 “setosa” samples, the second class contains 62 samples where 50 samples are correct, and the third class contains 38 samples where all 38 samples are correct. The Precision Ratio of three class samples reach 100%, 80.65%, 100%, respectively, and the Recall Ratio of three class samples reach 100%, 100%, 76%, respectively.
5.3. Clustering Results Analysis
From the experimental results, it is clear that both Precision Ratio and Recall Ratio of BQSON are the highest in four algorithms. These results show that the BQSON is obviously superior not only to the CSON but to the K-mean and the NNC as well.
Next, we theoretically explain the above experimental results. First, BQSON adopted a new way to calculate the distance of nodes between input layer and competition layer. In the existing clustering algorithms, the distance measurement is generally taken the Euclidean distance, which this distance is calculated based on coordinates. In BQSON, however, the distance is obtained by calculating the Bloch spherical distance of each dimension between input samples and competition nodes. Let 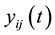
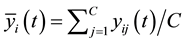
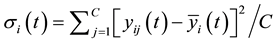
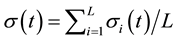
where C denotes the number of nodes in competition layer, and L denotes the total number of samples.
For the normalized samples, in CSON, the difference of each dimension between sample and weight 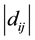
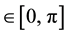
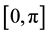
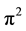
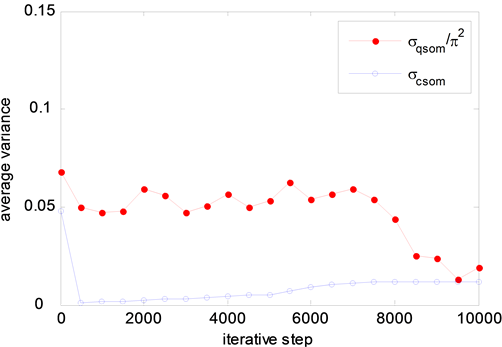
The Figure 4 shows that the average variance of BQSON is obviously greater than that of CSON, which suggests that the spherical distance have better distinguish ability than Euclidean distance for intensive samples. The “setosa” samples are relatively independent, which lead four algorithms to obtain the ideal clustering results. Both “versicolor” and “virginica” samples present overlapping intensive distribution, where the BQSON have also obtained the ideal clustering results. However, the clustering effect is not ideal for both K-mean and NNC based on the Euclidean distance, the CSON is completely unable to separate these two classes of samples.
Secondly, the BQSON adopted a new way of weight adjustment. In CSON, the vector differences between samples and weights are directly used to adjust the weighs, which is strongly influenced by learning rate, not easy to achieve fine adjustment. In BQSON, however, the weighs are adjusted by rotating them to a sample so as to approximate this sample. Due to the rotation is performed on the Bloch sphere, so, it may conduct a subtle adjustment of weights, which enhance the clustering ability of BQSON.
6. Conclusion
In this work, a quantum self-organization network clustering algorithm is proposed. In our approach, the weights of nodes in competition layer are updated by rotating qubits on the Bloch sphere. The comparative experiments of IRIS show that the clustering ability of proposed approach is significantly higher than the classic self-orga- nizing network. The Precision Ratio and Recall Ratio of BQSON increased by 7.5467% and 8.6667% more than those of K-mean and increased by 3.7833% and 5.3333% more than those of NNC. In addition, the BQSON is inefficient. It is also worth pointing out that, BQSON increases computing operations, such as the axis of rotation, rotation matrix and projection measurement, which lead to the increasing amount of calculation, prolonging running time, and reducing efficiency of clustering. However, the increase of these operations greatly improves
Figure 4. The average variance contrasts of BQSON and CSON.
the clustering ability of BQSON. In other words, BQSON is at the cost of computing efficiency for enhancing clustering ability, which is consistent with no free lunch theorem. Hence, how to enhance the computing efficiency of BQSON is the subject of further research.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 61170132), Natural Science Foundation of Heilongjiang Province of China (Grant No. F2015021), Science Technology Research Project of Heilongjiang Educational Committee of China (Grant No. 12541059), and Youth Foundation of Northeast Petroleum University (Grant No. 2013NQ119).
References
- Kak, S. (1995) On Quantum Neural Computing. Information Science, 83, 143-160. http://dx.doi.org/10.1016/0020-0255(94)00095-S
- Gopathy, P. and Nicolaos, B.K. (1997) Quantum Neural Network (QNN’s): Inherently Fuzzy Feed forward Neural Network. IEEE Transactions on Neural Networks, 8, 679-693. http://dx.doi.org/10.1109/72.572106
- Michail, Z. and Colin, P.W. (1998) Quantum Neural Nets. International Journal of Theory Physics, 37, 651-684. http://dx.doi.org/10.1023/A:1026656110699
- Michiharu, M., Masaya, S. and Hiromi, M. (2007) Qubit Neuron According to Quantum Circuit for XOR Problem. Applied Mathematics and Computation, 185, 1015-1025. http://dx.doi.org/10.1016/j.amc.2006.07.046
- Gupta, S. and Zia, R.K.P. (2001) Quantum Neural Network. Journal of Computer System Sciences, 63, 355-383. http://dx.doi.org/10.1006/jcss.2001.1769
- Fariel, S. (2007) Neural Network with Quantum Gated Nodes. Engineering Application of Artificial Intelligence, 20, 429-437. http://dx.doi.org/10.1016/j.engappai.2006.09.004
- Li, P.C. and Li, S.Y. (2008) Learning Algorithm and Application of Quantum BP Neural Network Based on Universal Quantum Gates. Journal of Systems Engineering and Electronics, 19, 167-174. http://dx.doi.org/10.1016/S1004-4132(08)60063-8
- Li, P.C., Song, K.P. and Yang, E.L. (2010) Model and Algorithm of Neural Network with Quantum Gated Nodes. Neural Network World, 11, 189-206.
- Adenilton, J., Wilson, R. and Teresa, B. (2012) Classical and Superposed Learning for Quantum Weightless Neural Network. Neurocomputing, 75, 52-60. http://dx.doi.org/10.1016/j.neucom.2011.03.055
- Cai, Z.H., Wang, D.H. and Jiang, L.X. (2007) K-Distributions: A New Algorithm for Clustering Categorical Data. Proceedings of the 3rd International Conference on Intelligent Computing (ICIC’07), Qingdao, August 2007, 436-443. http://dx.doi.org/10.1007/978-3-540-74205-0_48
- Huang, Z.X. (1997) Clustering Large Data Sets with Mixed Numeric and Categorical Values. Proceedings of the First Pacific Asia Knowledge Discovery and Data Mining Conference, Singapore, World Scientific, 21-34.
- Li, P.C. and Li, S.Y. (2007) A Quantum Self-Organization Feature Mapping Networks and Clustering Algorithm. Chinese Journal of Quantum Electronics, 24, 463-468.
NOTES
*Corresponding author.