Open Journal of Applied Sciences
Vol.3 No.4(2013), Article ID:35008,4 pages DOI:10.4236/ojapps.2013.34041
Nonlinear Oscillations Current Carry Orthotropic Shell in a Magnetic Field
Samarkand Branch of Tashkent University of Information Technologies, Samarkand, Uzbekistan
Email: r_indiaminov@mail.ru
Copyright © 2013 Ravsan Sh. Indiaminov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 17, 2013; revised January 4, 2013; accepted January 14, 2013
Keywords: shell; magnetic field; magneto elasticity
ABSTRACT
A two-dimensional variant of connected nonlinear equations of electrodynamics of the current—carrying orthotropic rotation shells, under no stationary loads is presented. A procedure for solution of asymmetrical problems of magneto elasticity of flexible current-carrying orthotropic rotation shells under no stationary actions of mechanical and electromagnetic forces is plotted. A stress-strained state of flexible current-carrying orthotropic rotation shells is geometrically nonlinear statement.
1. Introduction
The development of the theory of conjugate fields, and in particular the theory of electromagnetic interaction with deformable medium is considered as one of the main directions of development of modern solid mechanics. The mechanism of interaction of elastic medium with the electromagnetic field due to various and geometrical characteristics and physical properties of the body is in question. In particular, this mechanism gets some special features when considering the problem of relative thin shells having anisotropic conductive. Often the interaction of electromagnetic fields with a resilient body occurs in the presence of an external electric current (e.g., elasticcarrying body) in a magnetic field, or in its absence. In this case, we have a problem electro-magneto-elasticity.
In modern technology rational constructions and components used shell. They are in most cases naturally or structurally anisotropic. The problem of interaction of structural elements such as shells and plates with the electromagnetic field can arise in many areas of modern technology. The impact of time-dependent magnetic fields on the metal structures causes the bulk of electrodynamics forces. Particularly significant impacts on the electrodynamics forces are thin-walled elements, plates and shells. This in turn requires the study of the stressstrain state of plates and shells to take into account the geometric nonlinearity. Therefore, the study of unsteady problems of deformation of flexible current-carrying plates and shells in a magnetic field on the basis of a nonlinear system of magneto elasticity represents actual scientific task.
2. Nonlinear Formulation of the Problem
We will consider flexible current-carrying conical shell with variable thickness along the meridian under the influence of transient electromagnetic and mechanical fields. Neglecting the influence of the processes of polarization and magnetization, and thermal stresses believe that the shell is brought to the edge of an alternating electrical current from an external source. Presupposes that the electric current in the unperturbed state is evenly distributed throughout the body (current density does not depend on the origin). The elastic properties of the coating material are considered orthotropic, the main directions of elasticity which coincide with the corresponding coordinate lines, the electromagnetic properties of the material are characterized by tensors of electrical conductivity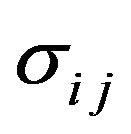 , magnetic permeability
, magnetic permeability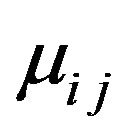 , dielectric constant
, dielectric constant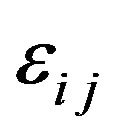 . Thus, on the basis of crystal physics, for the class of conducting orthotropic media with orthorhombic crystal structure believe that the tensors
. Thus, on the basis of crystal physics, for the class of conducting orthotropic media with orthorhombic crystal structure believe that the tensors ,
,  and
and 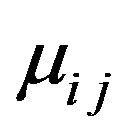 take diagonal. In this case, any second-order surface has three mutually perpendicular axes of the second order, and you can position the axes are parallel to the crystallographic axes of the second order and second order characteristic surface has all the elements of symmetry, which can be a class orthorhombic system. Assume that the geometrical and mechanical characteristics of the body such that the description of the deformation process is applicable version of the geometrically nonlinear theory of thin shells in the quadratic approximation. Also assume that the relative strength of the electric field
take diagonal. In this case, any second-order surface has three mutually perpendicular axes of the second order, and you can position the axes are parallel to the crystallographic axes of the second order and second order characteristic surface has all the elements of symmetry, which can be a class orthorhombic system. Assume that the geometrical and mechanical characteristics of the body such that the description of the deformation process is applicable version of the geometrically nonlinear theory of thin shells in the quadratic approximation. Also assume that the relative strength of the electric field  and magnetic field are
and magnetic field are  performed electromagnetic hypothesis [1]:
performed electromagnetic hypothesis [1]:
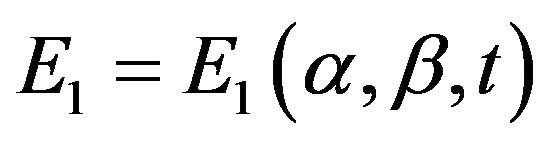 ,
,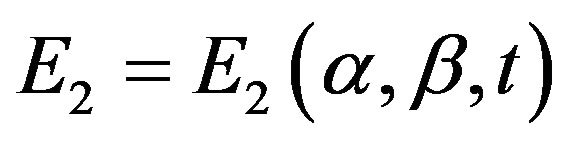 ,
,
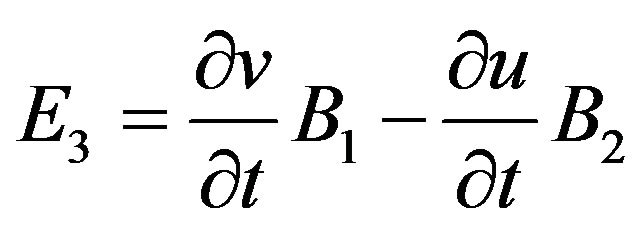 ,
,
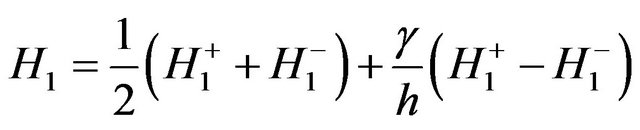
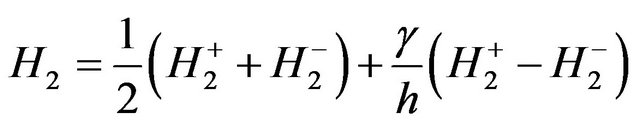
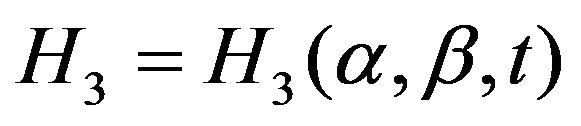 (1).
(1).
These assumptions are somewhat analogous to the electrodynamics hypothesis of no deformable normals and together with the latter hypothesis are magneto elasticity thin bodies. The adoption of these hypotheses can reduce the problem of three-dimensional deformation of the body to the problem of deformation chosen arbitrarily coordinate surface. Coordinate surface in the unreformed state belongs to the curvilinear orthogonal coordinate system ![]() and
and , where
, where —the length of the arc generator (meridian), measured from a fixed point, a central angle in a parallel circle, measured from the selected plane. Coordinate lines
—the length of the arc generator (meridian), measured from a fixed point, a central angle in a parallel circle, measured from the selected plane. Coordinate lines 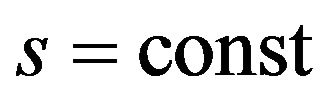 and
and 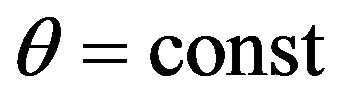 are the lines of the principal curvatures of the coordinate surface. Choosing the coordinate
are the lines of the principal curvatures of the coordinate surface. Choosing the coordinate ![]() normal to the coordinate surface of revolution shell refer to the coordinate system of spatial coordinates
normal to the coordinate surface of revolution shell refer to the coordinate system of spatial coordinates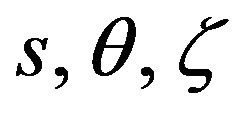 . We assume that the surface of a conical shell known vector of magnetic induction, as well as surface mechanical strength.
. We assume that the surface of a conical shell known vector of magnetic induction, as well as surface mechanical strength.
Upon receipt of the resolution of the system in the normal Cauchy form chosen as the basic functions of selecting these functions in the future

you can choose different combinations of fixing the cone.
Differential system of equations in core functions, describing the stress-strain state of the current-carrying shells in a magnetic field, taking into account the geometric nonlinearity and orthotropic conductivity, solved for the first derivative of the required functions for one of the coordinates. We assume that all the components of the excited electromagnetic field and the displacement field in the equations of the problem magneto elasticity is independent coordinates , believe that the elastic properties of the material and electromagnet elasticity mechanical shells do not vary along the parallels. After some transformations [2], we obtain a complete system of nonlinear differential equations magneto elasticity in the Cauchy form, which describes the stress-strain state of a current-carrying orthotropic conical shell under unsteady effects of mechanical and magnetic fields.
, believe that the elastic properties of the material and electromagnet elasticity mechanical shells do not vary along the parallels. After some transformations [2], we obtain a complete system of nonlinear differential equations magneto elasticity in the Cauchy form, which describes the stress-strain state of a current-carrying orthotropic conical shell under unsteady effects of mechanical and magnetic fields.
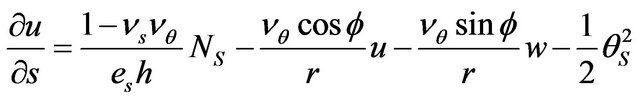
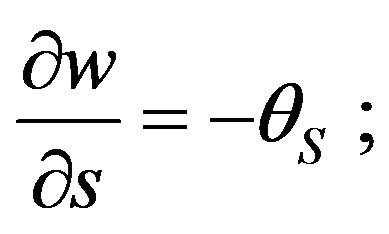
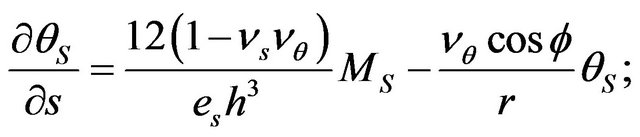
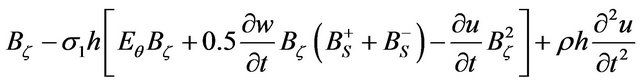 (2)
(2)
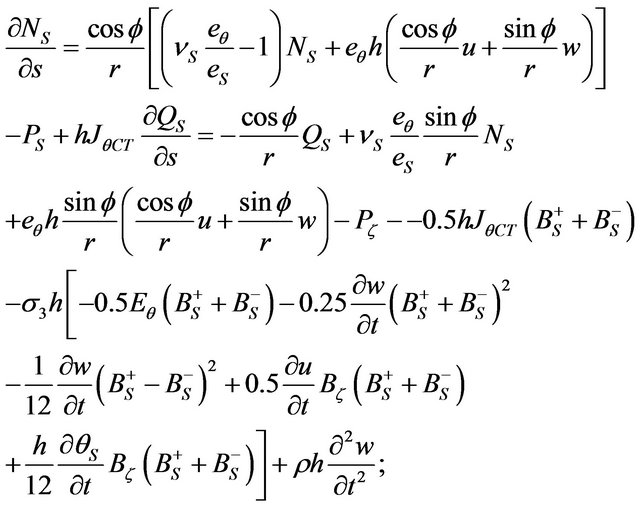

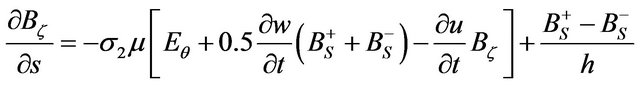

Used in the conventional (1), (2) shell theory and the theory of electromagnet elasticity notation. In addition, the following notation is introduced: —the tangential components of the magnetic field on the surface of the current-carrying conical shell. The solution of boundary value problems magneto elasticity associated with certain difficulties. This is because the resolution of the system (2) is a system of differential equations of hyperbolicparabolic type of the eighth order with variable coefficients. Ponder motive Lorentz force components include nonlinear terms, taking into account the displacement caused by the shell when it is deformed.
—the tangential components of the magnetic field on the surface of the current-carrying conical shell. The solution of boundary value problems magneto elasticity associated with certain difficulties. This is because the resolution of the system (2) is a system of differential equations of hyperbolicparabolic type of the eighth order with variable coefficients. Ponder motive Lorentz force components include nonlinear terms, taking into account the displacement caused by the shell when it is deformed.
Developed methods to the numerical solution of the new class of related problems magneto elasticity theory of orthotropic conical shells of revolution having orthotropic conductivity, based on the consistent application of the finite-difference scheme of Numark, quasilinearization method and discrete orthogonalization [2-5].
For effective use of the proposed method suggest that the appearance of the external magnetic field does not appear sharp skin effect on the shell thickness and the electromagnetic process is moving fast to coordinate ![]() mode close to steady. Note that, using the scheme of Numark, the entire range of variation of the time will be divided into separate small time intervals and trace the history of deformation, consistently solving the problem at each time step.
mode close to steady. Note that, using the scheme of Numark, the entire range of variation of the time will be divided into separate small time intervals and trace the history of deformation, consistently solving the problem at each time step.
As an example, consider the nonlinear behavior of the current-carrying orthotropic conical shell of variable thickness
 .
.
We believe that the shell of beryllium is exposed to mechanical force
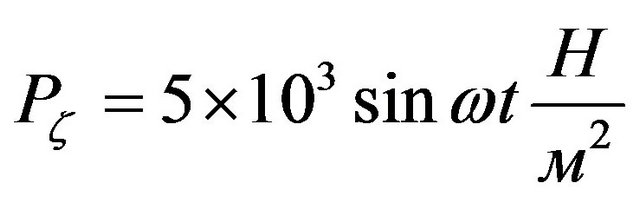
of an external electric current
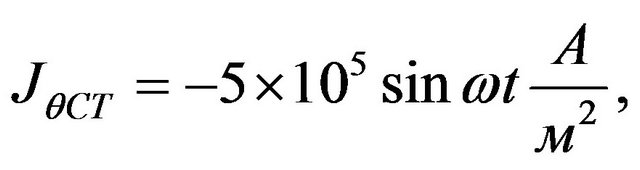
and magnetic field
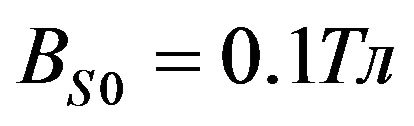 and that the shell has a finite orthotropic electrical conductivity
and that the shell has a finite orthotropic electrical conductivity
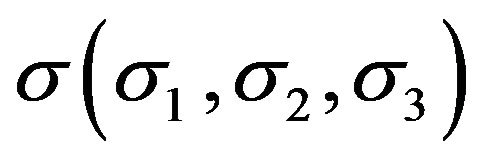 .
.
Investigate the behavior of orthotropic shell of variable thickness depending on the alteration of the electric current, which is changed as follows (5 versions):
1)  ;
;
2)  ;
;
3) 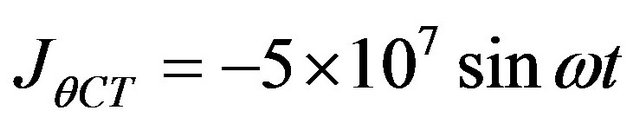 ;
;
4) 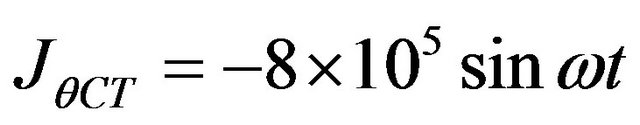 ;
;
5) 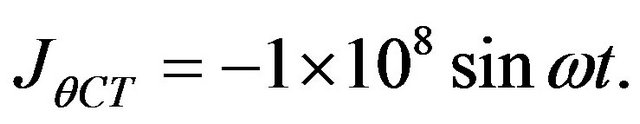
Boundary conditions:

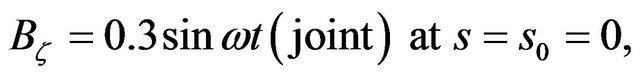
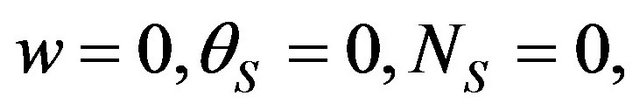

Shell parameters and accept the following materials:
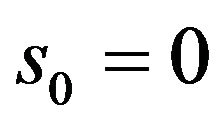 ,
, 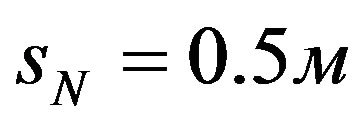 ,
,
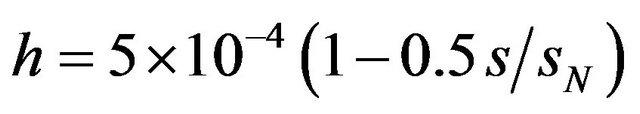 ,
,
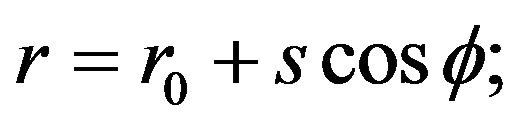 ,
, 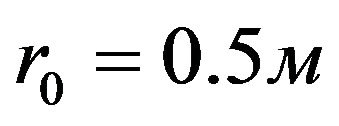 ,
,
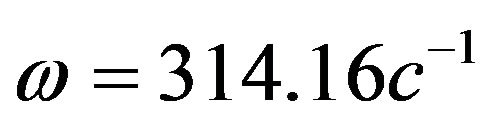 ,
, 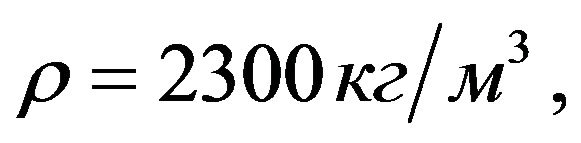
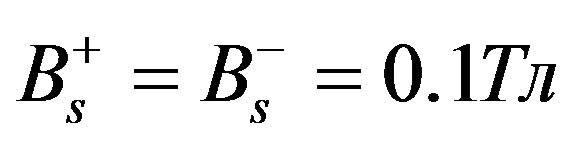 ,
, 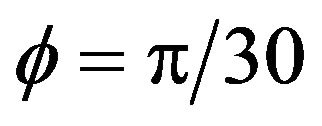 ,
, 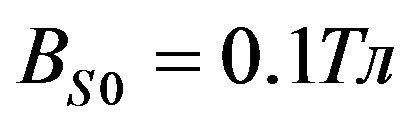 ,
,
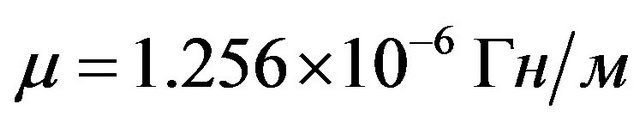 ,
, 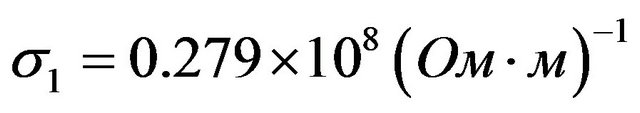
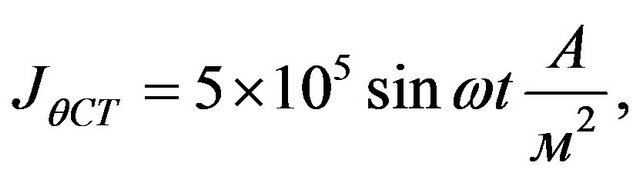 ,
,
 ,
,
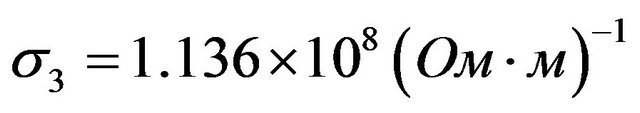 ,
, 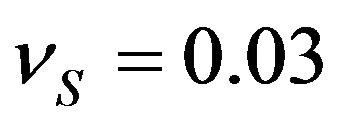 ,
,
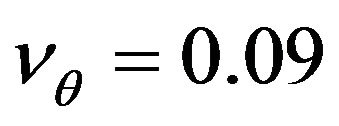 ,
, 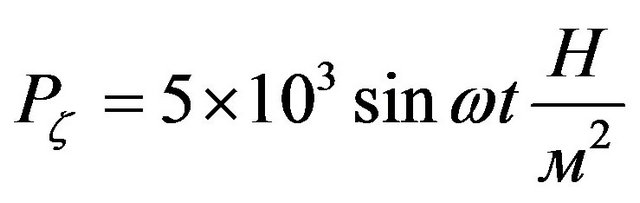 ,
,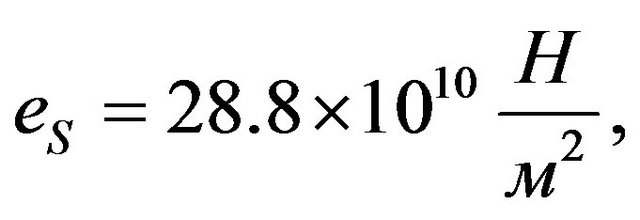
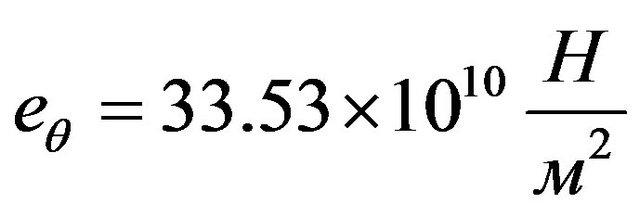
Solution of the problem is defined on a time interval of time 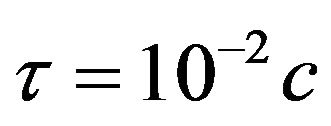 integration step was chosen equal
integration step was chosen equal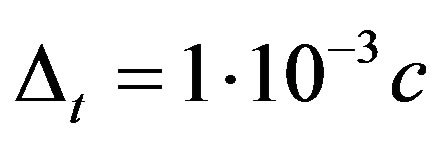 . Maximum values obtained at time step
. Maximum values obtained at time step . Note that in this case, the anisotropy of the electrical resistance is
. Note that in this case, the anisotropy of the electrical resistance is .
.
In Figures 1 and 2, respectively, given the distribution of the maximum values of the tangential 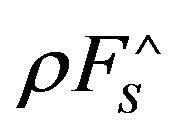 and normal components
and normal components  of the Lorentz force as a function of time
of the Lorentz force as a function of time  at all options for changing the external current
at all options for changing the external current . As can be seen from the figures, with an increase in value of an external electric current value of the tangential and normal components of the Lorentz force increases, the normal component of the Lorentz force for Options 2 and 3 changes symmetrically on time and has about the same absolute values (Figure 2).
. As can be seen from the figures, with an increase in value of an external electric current value of the tangential and normal components of the Lorentz force increases, the normal component of the Lorentz force for Options 2 and 3 changes symmetrically on time and has about the same absolute values (Figure 2).
3. Conclusions
We note that the numerical example illustrates the possibility of using our methods for solution of geometrically nonlinear problems on magneto-elastisity of shells. The above equations together with the solution procedure are capable of describing the anisotropy of the material, the anisotropy of the internal electromagnetic field of the shell, and the effect of strains on the electromagnetic properties of the body.
The above results make it possible to evaluate the im-

Figure 1. The change of the tangential component of the Lorentz force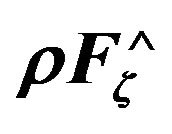 depending on the time when
depending on the time when 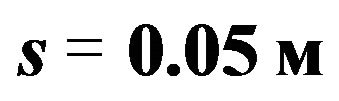 all options for changing the external electric current
all options for changing the external electric current : 1)
: 1)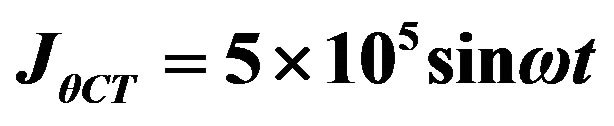 ; 2)
; 2)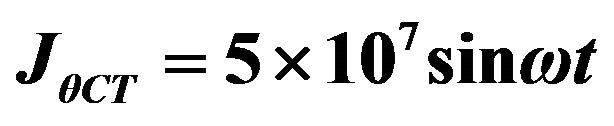 ; 3)
; 3) ;4)
;4) ; 5)
; 5)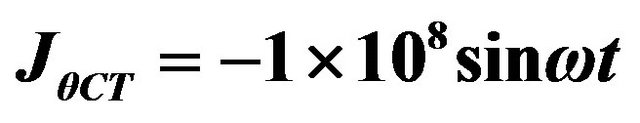 .
.
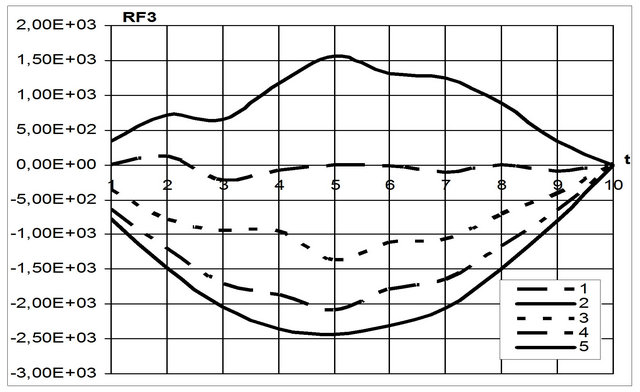
Figure 2. Change in the normal component of the Lorentz force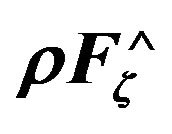 depending on the time when
depending on the time when 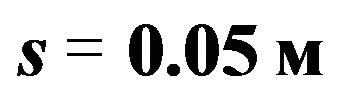 all options for changing the external electric current
all options for changing the external electric current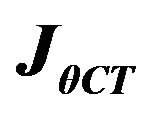 : 1)
: 1)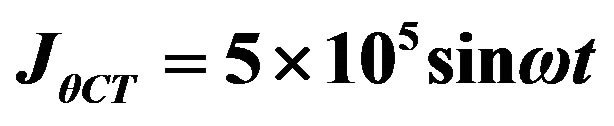 ; 2)
; 2)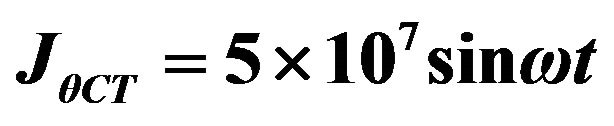 ; 3)
; 3)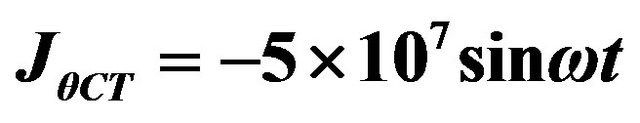 ; 4)
; 4)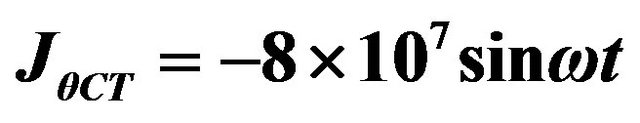 ; 5)
; 5)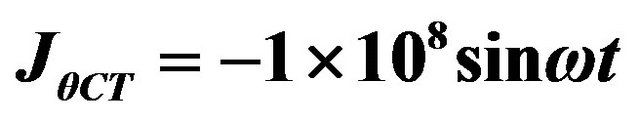 .
.
pact on the external shell of the electric current and the magnetic induction, and their combined effects. Thus, by choosing the direction and magnitude of external electric current density, it is possible to optimize the stress state of the shell.
REFERENCES
- S. A. Ambartsumian, G. E. Bagdasarian and M. Belubekyan, “Magnetoelasticity Thin Shells and Plates [in Rusian],” Nauka, Moscow City, 1977.
- L. V. Mol’chenko, I. I. Loss and R. Sh. Indiaminov, “The Magnetoelastisity of Conical Shells Mith Ortotropic Elektroconductivity in Nonlinear Position,” Bulletin of the University of Kiev, Series: Physics & Mathematics, No. 2, 2007, pp. 85-90.
- L. V. Mol`chenko, I. I. Loss and R. Sh. Indiaminov, “Determining the Stress State of Flexible Orthotropic Shells of Revolution in Magnetic Field,” International Applied Mechanics, Vol. 44, No. 8, 2008, pp. 882-891. doi:10.1007/s10778-008-0102-6
- R. Sh. Indiaminov, “On the Absence of the Tangential Projection of the Lorenz Force on the Ax Symmetrical Stressed State of Current-Carrying Conic Shells,” International Journal Computational Technologies, Vol. 13, No. 6, 2008, pp. 65-77.
- R. Sh. Indiaminov, “Solution of Dynamic Problems Associated Magnetoelasticity Current Carrying Orthotropic Conical Shells,” Collection of Article Eleventh International Scientific and Practical Conferences “Fundamental and Applied Research, Development and Application of High Technology in the Industry”, St. Petersburg, 27-29 April 2011, pp. 152-158.

