Received 12 March 2016; accepted 11 June 2016; published 14 June 2016

ABSTRACT

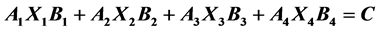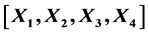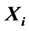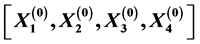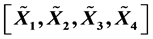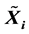In this paper, an iterative method is constructed to find the least-squares solutions of generalized Sylvester equation, where is real matrices group, and satisfies different linear constraint. By this iterative method, for any initial matrix group within a special constrained matrix set, a least squares solution group with satisfying different linear constraint can be obtained within finite iteration steps in the absence of round off errors, and the unique least norm least-squares solution can be obtained by choosing a special kind of initial matrix group. In addition, a minimization property of this iterative method is characterized. Finally, numerical experiments are reported to show the efficiency of the proposed method.

Keywords:

Least-Squares Problem, Centro-Symmetric Matrix, Bisymmetric Matrix, Iterative Method

1. Introduction

A matrix is said to be a Centro-symmetric matrix if 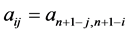for all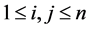. A matrix 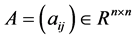is said to be a Bisymmetric matrix if 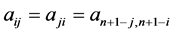for all. Let

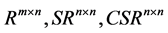and 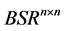denote the set of 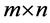real matrices, real symmetric matrices, real Centro-symmetric matrices and real Bisymmetric matrices, respectively. where denotes ith column of unit matrix. For a matrix, we denote its transpose, traced by respectively. In space, we define inner product as: for all, then the norm of a matrix A generated by this inner product is, obviously, Frobenius norm and denoted by.

Denote

Obviously, K, i.e., is a linear subspace of real number field.

In this paper, we mainly consider the following two problems:

Problem I. Given matrices, , find matrix group such that

Problem II. Denote by the solution set of Problem I. Find matrix group, such that

In fact, Problem II is to find the least norm solution of Problem I.

There are many valuable efforts on formulating solutions of various linear matrix equations with or without linear constraint. For example, Baksalary and Kala [1] , Chu [2] [3] , Peng [4] , Liao, Bai and Lei [5] and Xu, Wei and Zheng [6] considered the nonsymmetric solution of the matrix equation

(1)

by using Moore-Penrose generalized inverse and the generalized singular value decomposition of matrices, while Chang and Wang [7] considered the symmetric conditions on the solution of the matrix equations

(2)

Zietak [8] [9] discussed the -solution and Chebyshev-solution of the matrix equation

(3)

Peng [10] researched the general linear matrix equation

(4)

with the bisymmetric conditions on the solutions. Vec operator and Kronecker product are employed in this paper, so the size of the matrix is enlarged greatly and the computation is very expensive in the process of solving solutions. Iterative algorithms have been received much attention to solve linear matrix equations in recent years. For example, by extending the well-known Jacobi and Gauss-seidel iterations for, Ding, Liu and Ding in [11] derived iterative solutions of matrix equations and generalized Sylvester matrix equations. By absorbing the thought of the conjugate gradient method, Peng [12] presented an iterative algorithm to solve Equation (1). Peng [13] , Peng, Hu and Zhang [14] put forward an iterative method for bisymmetric solution of Equation (4). These matrix-form CG methods are based on short recurrences, which keep work and storage requirement constant at each iteration. However, these iteration methods are only defined by the Galerkin condition, but lack of a minimization property, which means that the algorithm may exhibit a rather irregular convergence, and often results in a very slow convergence. Lei and Liao [15] presented that a minimal residual algorithm could remedy this problem, and this algorithm satisfies a minimization property, which ensures that this method possesses a smoothly convergence.

However, to our best knowledge, the unknown matrix with different linear constraint of linear matrix equations, such as Equations ((1)-(4)), has not been considered yet. No loss of generality, we research the following case

(5)

which has four unknown matrices and each is required to satisfy different linear constraint. We should point out that the matrices are experimentally occurring in practices, so they may not satisfy solvability conditions. Hence, we should study the least squares solutions, i.e. Problem I. Noting that it is obvious difficulties to solve this problem by conventional methods, such as matrix decomposition and ver operator, hence iterative method is considered. Absorbing the thought of the minimal residual algorithm presented by Lei and Liao [15] , and combing the trait of problem, we conduct an iterative method for solving Problem I. This method can both maintain the short recurrence and satisfy a minimization property, i.e. the approximation solution minimizes the residual norm of Equation (5) over a special affine subspace, which ensures that this method converges smoothly.

The paper is organized as follows. In Section 2, we first conduct an iterative method for solving Problem I, and then describe the basic properties of this method; we also solve Problem II by using this iterative method. In Section 3, we show that the method possesses a minimization property. In Section 4, we present numerical experiments to show the efficiency of the proposed method, and use some conclusions in Section 5 to end our paper.

2. The Iterative Method for Solving Problem I and II

In this section, we firstly introduce some lemmas which are required for solving Problem I, we then conduct an iterative method to obtain the solution of Problem I. We show that, for any initial matrix group , the matrix group sequences generated by the iterative method converge to a solution of Problem I within finite iteration steps in the absence of roundoff errors. We also show that the unique least norm solution of Problem I can be obtained by choosing a special kind of initial matrix group.

Lemma 1. [16] [17] . A matrix if and only if.

A matrix if and only if.

Lemma 2. Suppose that a matrix, then.

Suppose that a matrix, then.

Proof: Its proof is easy to obtain from Lemma 1. W

Lemma 3. Suppose that, , , then

Proof: It is easy to verify from direct computation. W

Lemma 4. (Projection Theorem) [18] . Let X be a finite dimensional inner product space, M be a subspace of X, and be the orthogonal complement subspace of M. For a given, there always exists an such that

where is the norm associated with the inner product defined in X. Moreover, is the unique minimization vector in M if and only if

Lemma 5. Suppose is the residual of matrix group corresponding to Equation (5), i.e., if the following conditions are satisfied simultaneously,

(6)

then the matrix group is a solution of Problem I.

Proof: Let

obviously, Z is a linear subspace of. For matrix group, denote

then. Applying to Lemma 4, we know that is a solution of Problem I if and only if

i.e. for all,

By Lemma 3, it is easy to verify that if the equations of (6) are satisfied simultaneously, the expression above holds, which means is a solution of Problem I. W

Lemma 6. Suppose that matrix group is a solution of Problem I, then arbitrary matrix group can be express as where matrix group satisfies

(7)

Proof: Assume that matrix group is a solution of Problem I. If , then by Lemma 5 and its proof process, we have

which implies matrix group satisfies (7).

Conversely, if matrix group

where matrix group satisfies (7), then

which means matrix group W

Next, we develop iterative algorithm for the least-squares solutions with satisfies different linear constraint of matrix equation

where, and C are given constant matrices, and is the unknown matrices group to be solved.

Algorithm 1. For an arbitrary initial matrix group, compute

Step 1.

Step 2. If, then stop; else, , and compute

Step 3.

Step 4. Go to step 2.

Remark 1. 1) Obviously, matrices sequence generated by Algorithm 1 satisfies

2) is the residual of Equation (5), when

3) Algorithm 1 implies that if, then the corresponding matrix group is the solution of Problem I.

In the next part, we will show the basic properties of iteration method by induction. First for convenience of discussion in the later context, we introduce the following conclusions from Algorithm 1. For all

Lemma 7. For matrices, (r = 1, 2, 3, 4) and generated by Algorithm 1, if there exist a positive integer k such that, , and for all, then we have

1)

2)

3)

Proof: For, it follows that

Assume that the conclusions

hold for all, then

By the assumption of Equation (3), we have

Then for j = s,

Then the conclusion and the assumption show that

for all. By the principal of induction, we know that Eq.(3) holds for all, and Equation (1) and Equation (2) hold for all due to the fact that holds for all matrices A and B in. W

Lemma 7. shows that the matrix sequence

generated by Algorithm 1 are orthogonal each other in the finite dimension matrix space. Hence the iterative method will be terminated at most steps in the absence of roundoff errors.

It is worth to note that the conclusions of Lemma 7 may not be true without the assumptions and. Hence it is necessary to consider the case that or.

If, which implies, it follows that.

If, which implies, then we have, making inner product with by both side, yields

So the discussions above show that if there exist a positive integer i such that the coefficient or, then the corresponding matrix group is just the solution of Problem I.

Together with Lemma 7 and the discussion about the coefficient, we can conclude the following theorem.

Theorem 1. For an arbitrary initial matrix group, the matrix group sequence generated by Algorithm 1 will converge to a solution of Problem I at infinite iteration steps in exact arithmetic.

By choosing a special kind of initial matrix group, we can obtain the unique least norm of Problem I. To this end, we first define a matrix set as follows

where. Evidently, S is a linear subspace of K.

Theorem 2. If we choose the initial matrix group, especially, let , we can obtain the least norm solution of Problem I.

Proof: By the Algorithm 1 and Theorem 1, if we choosing initial matrix group, we can obtain the solution of Problem I with finite iteration steps and there exist a matrix such that the solution can be represented that

By Lemma 6 we know that arbitrary solution of Problem I can be express as

where matrix group satisfies (7).

Then

So we have

which implies that matrix group is the least norm solution of Problem I. W

Remark 2. Since the solution of Problem I is no empty, so the is a closed convex linear subspace, hence it is certain that the least norm solution group of Problem I is unique, and . If matrix group is a solution of Problem I, then it just be the unique least norm solution of Problem I, i.e..

3. The Minimization Property of Iterative Method

In this section, the minimization property of Algorithm 1 is characterized, which ensures the Algorithm 1 converges smoothly.

Theorem 3. For an arbitrary initial matrix group, the matrix group generated by Algorithm 1 at the kth iteration step satisfies the following minimization problem

where F denote a affine subspace which has the following form

Proof: For arbitrary matrix group, there exist a set of real number such that

Denote

by the conclusion Equation (2) in Lemma 7, we have

where is the corresponding residual of initial matrix group. Algorithm 1 show that the matrix can be express as

Because is a continuous and differentiable function with respect to the k variable , we easily know that

if and only if

It follows from the conclusion in Lemma 7 that

By the fact that

We complete the proof. W

Theorem 3 shows that the approximation solution minimizes the residual norm in the affine subspace F for all initial matrix group within K. Furthermore, by the fact

, then we have

which shows that the sequence

is monotonically decreasing. The descent property of the residual norm of Equation (5) ensures that the Algorithm 1 possesses fast and smoothly convergence.

4. Numerical Examples

In this section, we present numerical examples to illustrate the efficiency of the proposed iteration method. All the tests are performed using Matlab 7.0 which has a machine precision of around 10⁻¹⁶. Because of the error of calculation, the iteration will not stop within finite steps. Hence, we regard the approximation solution group

as the solution of Problem I if the corresponding satisfies.

Example 1. Given matrices and C as follows:

Choose the initial matrices where 0 denotes zero matrix in appropriate dimension. Using Algorithm 1 and iterating 74 steps, we have the unique least norm solution as follows:

with

And

If we let the initial matrix, noting that within K but not within S, then we have

with

And

Example 2. Suppose that the matrices are the same as Example 1, let , where, , , , that is to say, Equation (5) is consistent over set K. Then similarly Algorithm 2.1 in Peng [14] we can conduct another iteration algorithm as follows:

Algorithm 2. For an arbitrary initial matrix group, compute

Step 1.

Step 2. If, then stop; else, , and compute

Step 3.

Step 4. Go to step 2.

The main differences of Algorithm 1 and Algorithm 2 are: in Algorithm 1 the selection of coefficient make, and such that but in Algorithm 2, the choosing of such that, and such that. Noting that Algorithm 2 satisfies

the Galerkin condition, but lacks of minimization property. Choosing the initial matrix where 0 denotes zero matrix in appropriate dimension, by making use of Algorithm 1 and Algorithm 2, we can

obtain the same least norm solution group, and we also obtain the convergence curves of residual norm shown in Figure 1. The results in this figure show clearly that the residual norm of Algorithm 1 is monotonically decreasing, which is in accordance with the theory established in this paper, and the convergence curve is more smooth than that in Algorithm 2.

Acknowledgements

We thank the Editor and the referee for their comments. Research supported by the National Natural Science Foundation of China (11301107, 11261014, 11561015, 51268006).

Cite this paper

Xuelin Zhou,Dandan Song,Qingle Yang,Jiaofen Li, (2016) Least-Squares Solutions of Generalized Sylvester Equation with Xi Satisfies Different Linear Constraint. Advances in Linear Algebra & Matrix Theory,06,59-74. doi: 10.4236/alamt.2016.62008

References

NOTES

^*Corresponding author.