Advances in Linear Algebra & Matrix Theory
Vol.05 No.03(2015), Article ID:59559,19 pages
10.4236/alamt.2015.53011
A Direct Transformation of a Matrix Spectrum
Albert Iskhakov1, Sergey Skovpen2
1VNIIEM Corporation’ JSC, Moscow, Russia
2Northern (Arctic) Federal University, Severodvinsk, Russia
Email: asimath@bk.ru, skovpensm@mail.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 July 2015; accepted 11 September 2015; published 14 September 2015
ABSTRACT
A method is presented for calculating a matrix spectrum with a given set of eigenvalues. It can be used to build systems with different spectrums with the aim of choosing desired alternative. It enables a practical implementation of control algorithms without resorting to transformation of variables.
Keywords:
Matrix Spectrum, Frobenius Matrix, Frobenius Transformation, Spectral Equation

1. Introduction
In algebra, the problems dealing with eigenvalues belong to spectral ones. A matrix spectrum is changed via its elements. This procedure can be implemented in various ways. For example, in computing mathematics, a matrix is multiplied by other matrix for solving systems of linear algebraic equations.
The problem of target transforming a spectrum is the subject of control theory. It is called as the method of characteristic equation setting, arrangement of eigenvalues, spectrum control, and modal control [1] -[4] . To change a spectrum, the relationships between coefficients of characteristic polynomial and its roots are used. They are known as Vieta’s formulas.
Such spectrum transformation, which is pertinently called Frobenius, has a clear theoretical basis; moreover, it specifies an obvious way for its practical application, which implies supplementing the elements of the row of Frobenius matrix to the values making a matrix spectrum equal to a given set of numbers.
The reason for searching a new method of a spectrum transformation is the requirement for obtaining a desired spectrum for concrete technical systems using real-time control algorithms. A more detailed explanation of the necessity of other approach for solving this problem is given in Appendix 1.
The method for calculating a desired spectrum, for which the authors find possible to use the definition in the headline, is not based on a Frobenius matrix.
It can be used to calculate the feedback coefficients of a control system with the aim to obtain a desired spectrum of closed-loop system without resorting to transformation of variables. This allows practical problems of control to be solved at the design phase of the system. By simulating the system behavior with different spectrums, it is possible to find a suitable alternative, which can be further implemented as a direct digital control algorithm. The paper is an outgrowth of the work [5] .
2. Informal Reasoning
In the matrix, a Frobenius transformation forms the row of elements reflecting the coefficients of the characteristic polynomial. An additive influence of the feedback onto these elements varies a spectrum. The feedback elements are calculated in the obvious way as the differences of the row elements and the coefficients of the polynomial with roots that equal to the values of a given spectrum.
The proposed method is based on the relationships between the elements and the spectrum not for the transformed matrix but the original one. These relations represent another kind of Vieta’s formulas, where the sums of the main minors of the matrix appear instead of characteristic polynomial coefficients. In contrast to the Frobenius form and Vieta’s formulas these minors contain all of the matrix elements.
In order to change a spectrum by a given set of eigenvalues, the matrix elements are replaced by unknowns, and then the corresponding elements of minors and combinations of the matrix eigenvalues are replaced by the same combinations of numbers from a given set. In this case, the identities are transformed into a system of equations for the unknowns. As a result, after the unknown will be replaced by the solution of the obtained system of equations, the matrix gains a desired spectrum. Feedback elements can also be calculated in obvious way as the differences between replaced matrix elements and elements of solution.
3. Aim of the Work
Suppose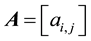 ,
,
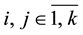 is a given k ´ k real matrix, s(А) is its spectrum, and
is a given k ´ k real matrix, s(А) is its spectrum, and
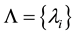 is a set of real numbers. By Ax denote the matrix A with k replaced elements by unknowns.
is a set of real numbers. By Ax denote the matrix A with k replaced elements by unknowns.
The objective is to consider a range of issues related to evaluation of the unknowns, which are substituted into the matrix Ax, such that the condition
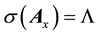 is satisfied.
is satisfied.
4. Definitions
1) Replacement is a replacing the elements of the matrix A (replaced elements) by other elements (replacing elements). Replacing matrix Ax (matrix with replacement) is a matrix with replacing elements.
2) Spectral equations of matrix A (replacement system) are k equations that was formed by replacing the coefficients of Vieta’s formulae by the sums of main minors of the matrix Ax and by replacing the roots by the elements from a given set L.
3) Replacement of the i-th order is a replacement leading to spectral equations of the i-th order. Linear replacement is a replacement of the first order. Non-linear replacement is a replacement of the second order or higher.
4) Spectral transformation of the matrix A is a replacing the elements of the matrix Ax by the solution of spectral equations.
5. Frobenius Transformation of a Spectrum and Its Alternative
For a matrix
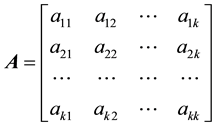 , (1)
, (1)
it is known Vieta’s formulas
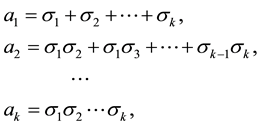 (2)
(2)
where σi and ai are the i-th root of the characteristic polynomial and the result of summation in the i-th row, which are the coefficients of the characteristic polynomial considering the sign.
Frobenius transformation of a spectrum is based on obtaining the elements on the left-hand side (taking into account the sign) by non-singular transformation of the matrix A and by supplementing them to the values that satisfy a given set. This corresponds to the fact that the sum on the right-hand side (2) are replaced by the same relationships between the numbers of a given set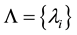 , and the elements on the left-hand side are supplemented by unknowns xi. This leads the system to the equations
, and the elements on the left-hand side are supplemented by unknowns xi. This leads the system to the equations
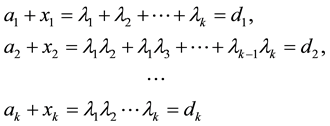 (3)
(3)
with an obvious solution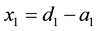 , where di is a sum in the i-th row. Substituting the solution into Frobenius matrix one forms its spectrum with the values from a given set Λ.
, where di is a sum in the i-th row. Substituting the solution into Frobenius matrix one forms its spectrum with the values from a given set Λ.
The possibility to change a matrix spectrum by supplementing the matrix elements to the values that satisfy a given set provides an alternative to Frobenius transformation of a matrix.
To perform this procedure, we use the system (2) in the form of sums of main minors on the left-hand side. The example of such system for a matrix of the 3-rd order is given by
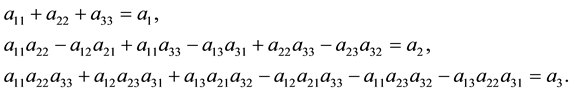
In this case, all of the matrix elements are in the system. In particular, this system enables one to evaluate how each element influences on the spectrum. This can’t be done with the help of Frobenius transformation.
Now, we supplement arbitrary elements of A, for example, the main diagonal elements by unknowns x1, x2, and x3. As a result, the matrix A takes the form
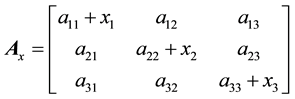 ,
,
and we obtain the system of equations for supplements the same as (3):
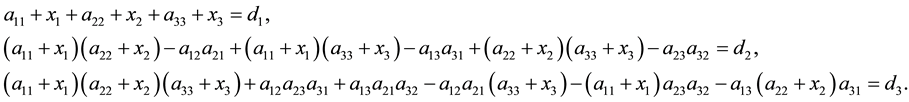 (4)
(4)
By solving (4), we consider the goal has been achieved. Indeed, substituting the solutions into the matrix Ax one makes it equal to a given set without resort to transforming the matrix.
Further efforts are aimed to simplifying the method of solving, since just the solving this particular system, after opening the brackets, is very complicated, and the solving complexity increases many-fold when the dimension increases. Difficulties in solving a particular system can be even more enhanced when we need to solve multivariate problems associated with a choice of complementary elements. The above example is illustrated by supplementing diagonal elements. Besides this embodiment, other variants can be used, the number of which also extremely increases with increasing a size of the matrix. Frobenius transformation of a spectrum does not have the variety of alternatives, as it has the unique solution to (3) when an appropriate condition is satisfied.
6. Spectral Equations
The above computational difficulties can be significantly reduced by choosing as the unknowns the elements together with its supplements instead of just the supplements. After solving the equations, we can determine the supplements as easy as in the Frobenius transformation.
For this purpose, the k arbitrary elements of A are replaced by unknowns, which are denoted for presentation by the capital letter X with the same indexes. For example, instead of the matrix
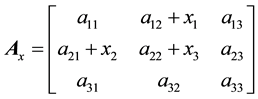
with unknown supplements to the elements a12, a21, a22 it is assumed the replacing matrix
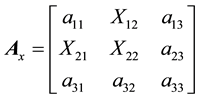
where instead of the elements a12, a21, a22 called in definition 4.1 as replaced, the replacing elements X12, X21, X22 considered as the unknowns are located.
The result is the system of equations for X12, X21, X22 of the form
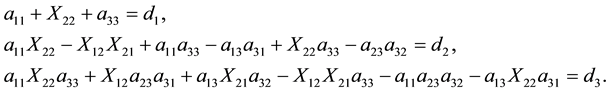 (6)
(6)
In general case, replacement of k elements of A with combining the replacing elements Xi,j into the vector Xi,j and building Ax gives the system of equations
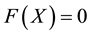 , (7)
, (7)
where F is the non-linear vector function with size of k called by the spectral equation.
In a similar way, we can choose

different replacing sets of elements and obtain replacing matrices in the form of (5) and equations in the form of (7). The number N very rapidly increases with the size of A. For small values of k, it is given in Table 1.
7. Types of Spectral Equations
The type of the system (7) depends on the arrangement of replacing elements in Ax. If we allocate the replacing elements in different rows and columns, as it is shown for the matrix (5), the system can takes the linear or
Table 1. The growth rate in the number of replacing sets, inconsistent equations, and solvable systems for the different values of k.
non-linear form of degree from 2 to k. However, not all of the systems have a solution. Using a particular matrix, we can at once determine a group of systems that do not have a solution.
Further, for the sake of simplicity, we will denote the replacing and non-replaced elements of matrices by the numbers that equal to the indexes and dots, respectively.
The right-hand side of the first equations of the system (6) is the fixed sum, and the left-hand side has the unknown, therefore, the equation is consistent with arbitrary values of а11, а33, and d1. But, for the other matrix

there are no unknowns on the left-hand side of

so, the last expression is inconsistent.
It is straightforward to make the following generalization. The matrix (9) belongs to the family of matrices, which is formed by replacing k elements of A that lie outside of the main diagonal in the two triangle areas containing k2 − k elements. This means that a necessary condition to solve (7) is that at least a one replacing element must be located on the main diagonal. It follows that the number of inconsistent Equation (7) is equal to the number of combinations

The dependence (10) is also given in Table 1.
Subtracting (10) from (8), we obtain

(given in Table 1) that is the number of solvable systems (7). Under appropriate conditions, this number is the sum

where Mi is the number of the i-th order equations.
Determining the terms in (12) for a general case as functions of k is the problem that needs to be solved. Even calculating M1, i.e. determining the number of the linear systems (7), is unobvious procedure that requires an analysis of equations of the form (6). We can say definitely (or, rather, we can suggest, since there is no rigorous proof) about only the single term Mi for i = k. It is equal to 1. In other words, there is only one way to replace k elements of matrix that allows a spectral equation of order k to be obtained by replacing the elements on the main diagonal.
We consider next a particular case for a matrix of the third order. By analyzing 64 consistent Equation (7), we establish 18, 45 and 1 variants to replace 3 elements according to (11). Replacements are described by two types of the first order equations, six types of the second order equations, and one type of third order equation. Equations of all types are resulted.
8. Linear Replacements
At first, we discuss the variants with evident solving the problem of choosing elements for linear replacement associated with a replacement of rows and columns of A.
There is only one element of replacing rows and columns in the summands of minors. Each of summand contains one unknown, and the multipliers obtained from the remaining elements give the coefficient at the summand. Assembly of these coefficients forms a matrix denoted by R. These equations belong to the type 1.1.
Some summands on the left-hand side, as it can be seen from the system (6), do not have replacing elements. We combine these elements in the row i into the element bi. Then, after combining the elements bi and di into the vectors b and d respectively, we can represent the Equation (7) in the linear form

by replacing rows and columns.
The solution to (13) exists under condition

The number of Equation (13) is

They do not describe all of possible linear systems but determine only obvious ones.
If replacing elements are not rows or columns, we can also get the linear system (7). In this case, the summands of minors can contain a product of replacing elements. Indeed, for example, for the matrix

the replacement system is

In the third row, we obtain the summand with a product of unknowns X11 and X32. In this case, we have a formal reason to assign (17) to the second order system. However, we can find X11 from the first equation (i.e. X11 is known), and the system becomes linear. These equations belong to the type 1.2. The given types of equations exhaust linear replacements.
9. The Second Order Replacements
9.1. Replacing a Single Diagonal Element
Replacements with a single diagonal elements lead to different types of the second order equations. Consider the matrix

which differs from (16) in a single element. The second and third equations for (18) is given by

The last equation of (19) is like (17) only externally. In the product, there is no variable expressed from the first equation. This type of replacement is denoted as 2.1.
The matrix

differs from (18) in a single element and contains by a single product of elements in two equations:

This type of replacement is denoted as 2.2.
The matrix

differs from (16) in a single element and also contains the product of elements in two equations

but the third equations has the product of three elements. This type is denoted as 2.3.
The matrix

which differs from (16) in a single element, is characterized by the equations

with two products of two unknowns in the third row. This type is denoted as 2.4.
9.2. Replacement of Two Diagonal Elements
When two diagonal elements are replaced the type of equations depends on a choosing the third element. Consider two matrices

with identical replaced diagonal elements and common first equation

differ from 2.2 in the first equation. They are denoted as 2.5. For the matrix b), the equations

with a single product in the second row and two products in the third row are denoted as 2.6.
9.3. Replacement of the k Order
The last equation of (7) contains the k! summands with products of k elements while the single summand has all unknown multipliers. Replacement of k elements using variants of (10) gives spectral equations of the k order only for unique case when the main diagonal of a matrix is replaced. Other variants of replacement lead to equations of the lower order. This conclusion is done without proving due to analysis of all spectral equations of the third order matrix.
10. Spectral Transformation of the Second Order Matrix
For the matrix

we write the system (2) as
Two of fore elements can be replaced in six ways. Only one of those with replacing the elements a12, а21 leads to incompliance equations in the form (6). From five remaining ways, fore are replacements of rows and columns and lead to linear spectral equations. Replacing the main diagonal elements a12, а21 leads to the second order equation.
10.1. Linear Equations
Replacement of rows and columns gives the replacing matrices

and linear equations
We present them in the form of (13) as

where











For the matrices (29), the conditions (14) are given by
If these conditions are satisfied, the equations take the form
Substituting the equations into (29) one gives the matrices

with a spectrum that equal to a given set
10.2. The Second Order Equation
Replacing the diagonal elements a11, а22 gives the matrix
with the equation
Its solution

where


with a given spectrum.
Example 1. Given a set


After calculating the matrices (31), we obtain
They have the spectrum that contains the elements from the given set.
With these results, the solution (32)
as well as the matrices (33)
are complex.
11. Spectral Transformation of the Third Order Matrix
From Table 1, we have the 84 variants for choosing three elements. Among them, the 20 variants lead to incompliant systems. The remaining 64 variants represent systems of the first, second and third order. These systems are described by equations of tow, six and one types respectively. Each value Mi in (12) is found via analysis of equations.
11.1. Linear Spectral Equations
Replacing rows and columns one gives the matrices

with appropriate equations. For example, for the matrix 1), we obtain the following equations

They can be presented in the form (13) as

where




























As it mentioned above, choice of replacing elements in different rows leads to leaner equations of the type 1.2. Matrices and equations for all of remaining variants for such types are resulted in Appendix 2. The first equation is not cited because it remains identical for replacements with other elements.
11.2. Matrices with the Second Order Replacement
In Appendix 2, we consider matrices and equations of the types 2.1 - 2.4 when a single diagonal element is replaced. In addition, we result equations of the type 2.5 and 2.6 when two diagonal elements are replaced.
11.3. Matrix with the Third Order Replacement
For the third order matrix, 63 of 64 variants for choosing three elements lead to equations of the first and second order. The remaining matrix

is characterized by the third order equation

The result obtained can be generalized for an arbitrary order matrix.
Example 2. With a set
The matrix 1). Let’s calculate
























The matrices are non-singular, hence, there are all the solutions:
With these solutions, replacing matrices (34)
take the spectrum
that is equal to a given set with calculating accuracy.
The matrix 2). Omitting intermediate calculations, here and further, we find matrices
Among all the matrices, only R5 is singular and hence the solution Х5 does not exist.
With the remaining matrices, the solutions to the systems (36) are
Substituting them into the matrices (34)
one forms the spectrum
that is equal to a given set.
The matrix 3). Let’s evaluate the matrices
The matrices R2 and R5 are singular and hence the solutions Х2 and Х5 do not exist. With the remaining solutions
the matrices
take the given spectrum
The matrix 4). Among the matrices
R1 and R6 are non-singular. With them, the solutions are

For replacing matrices
these solutions provide a given spectrum.
Example 3. This example describes a spectrum transformation with linear replacement of elements located in different rows and columns. Consider the matrix and Equation (12) given in Appendix 2. From the first equation, we define the unknown
at once. Two others are reduced to an equation for Х13 and Х23 with the matrix
and the vector

With the set and matrix 1) from example 2, the solution
for the matrix 15)
forms the given spectrum
All calculations were made in MathCAD.
12. Conclusions
A method for obtaining a matrix spectrum equal to a given set of numbers without transformation to a Frobenius form is stated. Calculating tool is a system of equations, which has been obtained by replacement of arbitrary matrix elements by unknowns. Their number is equal to the size obtained from relationships between matrix elements in the form of main minors and elements of a given set.
The method has many variants for choosing replacing elements and equations to calculate replacing elements from linear to non-linear with an order equal to the size.
Cite this paper
AlbertIskhakov,SergeySkovpen, (2015) A Direct Transformation of a Matrix Spectrum. Advances in Linear Algebra & Matrix Theory,05,109-128. doi: 10.4236/alamt.2015.53011
References
- 1. Leonov, G.A. and Shumafov, M.M. (2005) The Methods for Linear Controlled System Stabilization. St.-Petersburg University Publisher, St.-Petersburg.
- 2. Kuzovkov, N.T. (1976) Modal Control and Observe Devices. Mashinostroenie, Moscow.
- 3. Krasovsky, A.A. (1987) Control Theory Reference Book. Nauka, Moscow.
- 4. Islamov, G.G. (1987) On the Control of a Dynamical System Spectrum. Differential Equations, 8, 1299-1302.
- 5. Iskhakov, A., Pospelov, V. and Skovpen, S. (2012) Non-Frobenius Spectrum-Transformation Method. Applied Mathematics, 1, 1471-1479.
http://dx.doi.org/10.4236/am.2012.330206
Appendix 1. Proving the Method of a Direct Spectrum Transformation
In technical systems, variables having a certain physical sense are used. These variables characterize energy stores such that a speed of moving mass, a solenoid current, a capacity voltage and similar parameters, which are measured by sensors. To obtain a Frobenius matrix it is required both direct and reverse transformation of variables in the feedback loop. The reverse transformation is explained by the fact that a combination of physical variables must enter into the system input. Firmware implementing the transformation needs additional hardware expenses, and software realization needs expenditure of time. This leads to delay in the feedback loop and to deteriorate dynamical properties of system. As a result, the advantage of a control method based on the variation of system spectrum is used not to the full owing to the features of the method using to implement a spectrum transformation.
Appendix 2. Replacing Matrices and Spectral Equations for the Third Order Matrix
A.2.1. Linear Replacements
For the type 1.2, replacement of the element а11 (number 7) refers to the matrix (16) and Equation (17):
8)
9)
10)
Replacing the element a22 gives
11)
12)
13)
14)
Replacing the element а33 gives
15)
16)
17)
18)
A.2.2. The Second Order Replacement with a Single Diagonal Element
For the type 2.1, replacement of the element а11 (number 1) refers to the matrix (18) and Equation (19):
2)
2)
Replacing the element а22 gives
3)
4)
Replacing the element а33 gives
5)
6)
For the type 2.2, replacement of the element а11 (number 7) refers to the matrix (20) and Equation (21):
8)
8)
Replacing the element а22 gives
9)
10)
Replacing the element а33 gives
11)
12)
The type 2.3 (number 13) refers to the matrix (22) and Equation (23):
14)
15)
For the type 2.4, replacement of the element а11 (number 16) refers to the matrix (24) and Equation (25):
17)
18)
19)
Replacing the element а22 gives
20)
21)
22)
23)
Replacing the element а33 gives
24)
25)
26)
27)
A.2.3. The Second Order Replacement with Two Diagonal Elements
For the type 2.5, replacement of the elements a11, a22 (number 28) refers to the matrix (a) (26) and Equation (27)
29)
29)
Replacing the elements a11, a33 gives
30)
31)
Replacing the elements a22, a33 gives
32)
33)
For the type 2.6, replacement of the element a11, a22 (number 34) refers to the matrix (b) (26) and Equation (28):
35)
36)
37)
Replacing the elements a11, a33 gives
38)
39)
40)
41)
Replacing the elements a22, a33 gives
42)
43)
44)
45)































































































