Advances in Linear Algebra & Matrix Theory
Vol.04 No.04(2014), Article ID:52892,8 pages
10.4236/alamt.2014.44020
First Review of Articles on Rhotrix Theory Since Its Inception
A. Mohammed, M. Balarabe
Department of Mathematics, Ahmadu Bello University, Zaria, Nigeria
Email: abdulmaths@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 September 2014; revised 11 October 2014; accepted 20 October 2014
ABSTRACT
This paper presents an up-to-date review of the developments made in the field of rhotrix theory for a decade, starting from the year 2003, when the concept of rhotrix was introduced, up to the end of 2013. Over forty articles on rhotrix theory have been published in journals since its inception, indicating the need for a first review.
Keywords:
Rhotrix, Matrix, Rhotrix Theory, Matrix Theory

1. Introduction
In the year 2003, a relatively new paradigm of science, now known as rhotrix theory was initiated by Ajibade [1] , as an extension of ideas, on matrix-tertions and matrix-noitrets proposed by Atanassov and Shannon [2] . Since the publication of the article titled as “the concept of rhotrix for mathematical enrichment” in [1] , many researchers have shown interest in the improvement of the theories and applications of rhotrices for the past one decade.
In the literature of rhotrix theory, starting from 2003, over forty articles have been published, thereby requiring the need for a first review. Before going further, it is pertinent to mention that two methods for multiplication of rhotrices having the same size are currently available in literature. The first one is “the heart based method for rhotrix multiplication” defined in [1] , where the initial algebra and analysis of rhotrices were presented. The second alternative method is the row-column based method for rhotrix multiplication proposed by Sani [3] [4] , in an attempt to answer the question of “finding a transformation for conversion rhotrix to matrix and vice versa” posed by Ajibade in the concluding section of his article. However, each method provides enabling environment to explore the usefulness of rhotrices as tools for carrying out mathematical research.
The objective of this article is to give a comprehensive literature survey of all published articles on rhotrix theory, since the introduction of the concept in 2003, up to the end of 2013. To achieve this, we classify all the over fourty articles in the literature of rhotrix theory into two classes. We term one class of the articles in the literature of rhotrix theory as commutative rhotrix theory, while the other class as non-commutative rhotrix theory. The reason behind this classification is due to the fact that, contributory author(s) of a single article on rhotrix theory adopted either Ajibade’s heart-based method for multiplication of rhotrices or Sani’s row-column me- thod for multiplication of rhotrices in carrying out the work.
The choice of the two class names: commutative rhotrix theory and non-commutative rhotrix theory arise, respectively, from the commutative property inherent with the heart-based method for rhotrix multiplication, and the non-commutative property associated with row-column based method for rhotrix multiplication.
In line with this, articles on rhotrix theory can be broadly categorized according to the method of rhotrix multiplication used in presenting the work as follows:
1) Commutative rhotrix theory, i.e. Ajibade’s article and all other articles using the Ajibade’s heart-based method for rhotrix multiplication.
2) Non-commutative rhotrix theory, i.e. singularly authored articles by Sani and all other articles using Sani’s row-column based method for rhotrix multiplication.
This survey paper contains three other sections after the introductory section. Section 2 presents the survey of developments in rhotrix theory. Section 3 analyzes these developments and then Section 4 presents the conclusion.
2. Survey of Developments on Rhotrix Theory
This section presents a review of developments on rhotrix theory in a systematize form, starting with the review of commutative rhotrix theory in Subsection 2.1 and then followed by the review of non-commutative rhotrix theory in Subsection 2.2.
2.1. Class of Commutative Rhotrix Theory
Table 1 illustrates the title list of all journal articles that used Ajibade’s heart based method for rhotrix multiplication, available in the literature of rhotrix theory, starting from 2003 and to the end of 2013. Thus, articles in Table 1 belong to the class of commutative rhotrix theory. Now, we start a systemic review of these works in Table 1 as follows:
In [1] Ajibade introduced the concept of rhotrix of size three as
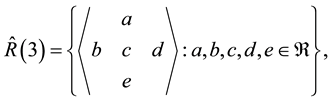
where 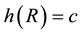 is called the heart of any rhotrix
is called the heart of any rhotrix . The operations of addition, scalar multiplication and multiplication
. The operations of addition, scalar multiplication and multiplication  are defined for rhotrices of size three in [1] . These rhotrix operations defined for rhotrix set of size three in [1] were thereafter, extended to rhotrix set of size
are defined for rhotrices of size three in [1] . These rhotrix operations defined for rhotrix set of size three in [1] were thereafter, extended to rhotrix set of size  in the Ph.D. thesis of Mohammed [5] , and recorded as follows: let
in the Ph.D. thesis of Mohammed [5] , and recorded as follows: let
 (1)
(1)
Table 1. List of titles in journals published from 2003 to 2013 that belong to the class of commutative rhotrix theory.
be the set of all real rhotrices of size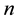 , where
, where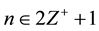 ,
, 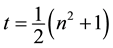 ,
, 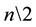 is the integer value obtained
is the integer value obtained
on division of 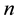 by 2, and
by 2, and 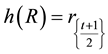 is the heart of any rhotrix
is the heart of any rhotrix 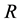 in
in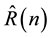 . Let
. Let 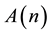 and
and 
any two rhotrices in 



(4)
where 



The extended rhotrix multiplication (4) was named in [5] as “Ajibade’s heart-based method for multiplication of rhotrices”. The rhotrix operations defined in [1] was adopted by [6] to present various classifications of rhotrices and their expressions as abstract structures of groups, semigroups, monoids, rings and Boolean algebras. The theorem for rhotrix exponent rule was first proposed without proof in [6] , thereafter, [7] established and characterized the theorem for rhotrix exponent rule and extended the result to systemization of expressing special series and polynomial equations over rhotrices.
A remark on classifications of rhotrices as abstract structures was proposed by [8] over rhotrices. In the work, rhotrix ring was characterized; rhotrix integral domain and rhotrix field were constructed with certain conditions. Construction of certain field of fractions over rhotrices was presented by [9] as an extension to [8] . It was made known in [10] that the rhotrix field in [8] [9] holds only if the set of all hearty rhotrices of size three given in [6] is used as the underlying set.
The generalization of Ajibade’s heart based method for rhotrix multiplication in [5] was algorithmatized for computing machines by [11] . A simplification of rhotrix expression generalization in [5] was presented by [12] . Construction and analysis of metric topological spaces using rhotrix set as the underlying set were considered in [13] .
The concept of tree in graph theory was extended to rhotrix theory by [14] through their introduction of
rhomtrees of order 


was shown in their work that these rhomtrees have connection to known real world models such as topology of computing network, methane compound and certain product of sets.
In [15] , the algebraic properties of singleton, coiled and modulo rhotrices were presented. Investigations of various constructions of finite fields over rhotrices were carried out in both [16] [17] . The cardinality of these finite fields was calculated through concrete examples. A study of the structure of rhotrices having entries from the set of integers modulo 

2.2. Class of Non-Commutative Rhotrix Theory
Table 2 illustrates the title list of all journal articles that used row-column based method for rhotrix multiplication, available in the literature of rhotrix theory from 2003 to 2013. Thus, articles in Table 2 belong to the class of non-commutative rhotrix theory. Now, we start a systemic review of works in Table 2 as follows:
Sani [3] proposed (5) as an alternative method for multiplication of rhotrices of size three as an attempt to answer the question of “how can one convert a rhotrix to matrix and then vice versa”, posed in the concluding
Table 2. List of titles published from 2003 to 2013 that belong to the class of non-commutative rhotrix theory.
section in [1] .

This multiplication was later generalized by [4] to multiplication of rhotrices of size n as:

where 

This (6) was presented in [5] as extended row-column based method for rhotrix multiplication.
In [24] , a presentation of the concept of Hilbert rhotrix and its relationship with well known Hilbert matrix was done. A special rhotrix termed as “Hilbert rhotrix” of size 5 was shown as a couple of two Hilbert matrices of sizes 

A method of converting rhotrix to a special form of matrix called “coupled matrix” was given in [25] . This was achieved through rotating the rhotrix 



where 



This is a rhotrix 




Two coupled matrices 

2.3. Theorem
If a coupled matrix 
the matrices 


This result on coupled matrix is very significant because it can be applied to solve problems involving two different systems of linear equations simultaneously, where one is a 



Sani [26] presented the solution of two coupled matrices by extending the idea of a coupled matrix in [25] to a general case involving 

A one-sided system of the form




The rhotrix addition and scalar multiplication defined in [1] was expressed in form of coupled matrices in [4] . The ideas were used by [28] to generalize and characterize the rhotrix vector space of size 3 initiated in [1] to rhotrix vector space of size n, through expression of rhotrices as coupled matrices.
Following this, [29] presented the concept of linear mapping to rhotrices and present its properties. It was shown in the work that the proposed method of converting a rhotrix to a “coupled matrix” (8) as defined in [25] is also a linear mapping.
In [30] an algorithm design for Sani’s row-column based method for rhotrix multiplication (6) was proposed. As an extension to [3] [4] [25] , various method of representing an arbitrary rhotrix was identified by [31] . One of the methods is the row-wise method, observed in the article to be flexible in analyzing rhotrices for mathematical enrichment. The flexibility of the representation has paved way for two formulae, one for row-column based method for arbitrary rhotrix multiplication and the other for heart-based method for arbitrary rhotrix multiplication.
The Cayley-Hamilton theorem for matrix is one of the well-known results in linear algebra. In 2012, the equivalence of this result was considered for rhotrix Cayley-Hamilton theorem in both [32] [33] . A note on relationship between invertible rhotrices and associated invertible matrices was proposed by [34] . A study of adjoint of a rhotrix and its basic properties was presented by [35] . The concept of inner product and bilinear forms over real rhotrices was considered in [36] . A determinant method for solving rhotrix system of linear equations was presented by [37] .
It is well known that an involutory matrix is a matrix that is its own inverse. Such matrices are of great im- portance in matrix theory and algebraic cryptography. In [38] a method for constructing involutory rhotrices and their properties was given. Thereafter, an extension to [38] was given by [39] through the development of some
Table 3. Number and percentage of articles on rhotrix theory per rhotrix theory class.
theorems on involution in the context of rhotrices. Also, the description of Pascal rhotrices and their related properties was also considered. In [40] , the theory of graph was extended to consider adjacent rhotrix of a complete, simple and undirected graph. A consideration of parallel multiplication of rhotrices using systolic array architecture was presented by [41] . Thereafter, a rhotrix multiplication on two-dimensional process grid topologies was carried out by [42] . The concept of rhotrix linear transformation with a number of theorems was presented by [43] . An investigation of rhotrices and its elementary row operations was carried out in [44] .
3. Analysis
In this section, we present two tables for the analysis of articles in the literature review of rhotrix theory. In Table 3, we specify the number and percentage of articles on rhotrix theory from 2003 to the end of 2013 per rhotrix theory class.
The remarkable aspect of this literature review of articles on rhotrix theory is that authors following the class of commutative rhotrix theory enjoy the commutative property associated with the heart based method for rhotrix multiplication. For this reason, a number of abstract structures such as rhotrix groups, rhotrix semigroups, rhotrix rings, rhotrix Boolean algebra, rhotrix topological spaces, rhotrix metric spaces, rhotrix graphical trees called rhomtrees were developed. Furthermore, rhotrix finite fields, rhotrix exponent rule and their applications to special series, polynomial equations and polynomial rings over rhotrices were developed.
On the other hand, the contributory authors working on non-commutative rhotrix theory focus their researches majorly on extending the properties of matrices to rhotrices. Their inspirations came from the works of Sani [25] [26] in his papers on conversion of rhotrix to a special matrix termed as coupled matrix. These articles made several authors to study analogous properties of matrices to rhotrices.
Now, it is also pertinent for us to mention here that authors use the same symbol “


In over all, we can say that from 2003 to 2013, the class of non-commutative rhotrix theory has more than 9% of articles in the literature of rhotrix theory than the class of commutative rhotrix theory.
4. Conclusion
In conclusion, we have presented a survey of articles on rhotrix theory starting from the year 2003 when the concept was initiated up to 2013. We have also classified the articles on rhotrix theory into two classes as commutative rhotrix theory and non-commutative rhotrix theory. It was shown in our analysis that the class of non- commutative rhotrix theory possessed 54.46% of articles in the literature of rhotrix theory while the class of commutative rhotrix theory possessed 45.24% of the articles.
Acknowledgements
We wish to thank the unknown reviewers for their helpful suggestions. We also wish to thank Ahmadu Bello University, Zaria, Nigeria for funding this relatively new area of research.
References
- Ajibade, A.O. (2003) The Concept of Rhotrix in Mathematical Enrichment. International Journal of Mathematical Education in Science and Technology, 34, 175-179. http://dx.doi.org/10.1080/0020739021000053828
- Atanassov, K.T. and Shannon, A.G. (1998) Matrix-Tertions and Matrix-Noitrets: Exercises in Mathematical Enrichment. International Journal of Mathematical Education in Science and Technology, 29, 898-903.
- Sani, B. (2004) An Alternative Method for Multiplication of Rhotrices. International Journal of Mathematical Education in Science and Technology, 35, 777-781. http://dx.doi.org/10.1080/00207390410001716577
- Sani, B. (2007) The Row-Column Multiplication of Higher Dimensional Rhotrices. International Journal of Mathematical Education in Science and Technology, 38, 657-662. http://dx.doi.org/10.1080/00207390601035245
- Mohammed, A. (2011) Theoretical Development and Applications of Rhotrices. Ph.D. Thesis, Ahmadu Bello University, Zaria.
- Mohammed, A. (2007) Enrichment Exercises through Extension to Rhotrices. International Journal of Mathematical Education in Science and Technology, 38, 131-136. http://dx.doi.org/10.1080/00207390600838490
- Mohammed, A. (2007) A Note on Rhotrix Exponent Rule and Its Applications to Special Series and Polynomial Equations Defined over Rhotrices. Notes on Number Theory and Discrete Mathematics, 13, 1-15.
- Mohammed, A. (2009) A Remark on the Classifications of Rhotrices as Abstract Structures. International Journal of Physical Sciences, 4, 496-499.
- Usaini, S. and Tudunkaya, S.M. (2011) Certain Field of Fractions. Global Journal of Science Frontier Research, 11, 4-8.
- Usaini, S. and Tudunkaya, S.M. (2012) Note on Certain Field of Fractions. Global Journal of Science Frontier Research, 12, 74-81.
- Mohammed, A., Ezugwu, E.A. and Sani, B. (2011) On Generalization and Algorithmatization of Heart-Based Method for Multiplication of Rhotrices. International Journal of Computer Information Systems, 2, 46-49.
- Absalom, E.A., Junaidu, S.B. and Sani, B. (2011) The Concept of Heart-Oriented Rhotrix Multiplication. Global Journal of Science Frontier, 11, 35-46.
- Mohammed and Tijjani (2011) Rhotrix Topological Spaces. International Journal of Advances in Science and Technology, 3.
- Mohammed, A. and Sani, B. (2011) On Construction of Rhomtrees as Graphical Representation of Rhotrices. Notes on Number Theory and Discrete Mathematics, 17, 21-29.
- Tudunkaya and Makanjuola (2010) Algebraic Properties of Singleton, Coiled and Modulo Rhotrices. African Journal of Mathematics and Computer Sciences.
- Tudunkaya, S.M. and Makanjuola, S.O. (2010) Rhotrices and the Construction of Finite Fields. Bulletin of Pure and Applied Sciences, 29e, 225-229.
- Usaini, S. and Tudunkaya, S.M. (2011) Note on Rhotrices and the Construction of Finite Fields. Bulletin of Pure and Applied Sciences, 30e, 53-59.
- Tudunkaya, S.M. and Makanjuola, S.O. (2012) On the Structure of Rhotrices. National Association of Mathematical Physics, 21, 271-280.
- Tudunkaya, S.M. and Makanjuola, S.O. (2012) Certain Quadratic Extensions. National Association of Mathematical Physics, 21, 271-280.
- Tudunkaya, S.M. (2013) Rhotrix Polynomial and Polynomial Rhotrices. Pure and Applied Mathematics Journal, 2, 38-41. http://dx.doi.org/10.11648/j.pamj.20130201.16
- Mohammed, A. and Tella, Y. (2012) Rhotrix Sets and Rhotrix Spaces Category. International Journal of Mathematics and Computational Methods in Science and Technology, 2, 21-25.
- Aminu, A. (2009) On the Linear System over Rhotrices. Notes on Number Theory and Discrete Mathematics, 15, 7-12.
- Aminu, A. (2012) A Note on the Rhotrix System of Equation. Journal of the Nigerian Association of Mathematical Physics, 21, 289-296.
- Kaurangini, M.L. and Sani, B. (2007) Hilbert Matrix and Its Relationship with a Special Rhotrix. Journal of the Mathematical Association of Nigeria, 34, 101-106.
- Sani, B. (2008) Conversion of a Rhotrix to a Coupled Matrix. International Journal of Mathematical Education in Science and Technology, 39, 244-249. http://dx.doi.org/10.1080/00207390701500197
- Sani, B. (2009) Solution of Two Coupled Matrices. Journal of the Mathematical Association of Nigeria, 32, 53-57.
- Aminu, A. (2010) The Equation Rnx = b over Rhotrices. International Journal of Mathematical Education in Science and Technology, 41, 98-105. http://dx.doi.org/10.1080/00207390903189187
- Aminu, A. (2010) Rhotrix Vector Spaces. International Journal of Mathematical Education in Science and Technology, 41, 531-578. http://dx.doi.org/10.1080/00207390903398408
- Aminu, A. (2010) An Example of Linear Mappings: Extension to Rhotrices. International Journal of Mathematical Education in Science and Technology, 41, 691-698. http://dx.doi.org/10.1080/00207391003605213
- Absalom, E.E., Ajibade, A.O. and Sahalu, J.B. (2011) Algorithm Design for Row-Column Multiplication of N-Di- mensional Rhotrices. Global Journal of Computer Science and Technology, 11, 22-30.
- Chinedu, M.P. (2012) Row-Wise Representation of Arbitrary Rhotrix. Notes on Number Theory and Discrete Mathematics, 18, 1-27.
- Sharma, P.L. and Kanwar, R.K. (2012) The Cayley-Hamilton Theorem for Rhotrices. International Journal of Mathematics and Analysis, 4, 171-178.
- Aminu, A. (2012) Cayley-Hamilton Theorem in Rhotrices. National Association of Mathematical Physics, 20, 289- 296.
- Sharma, P.L. and Kanwar, R.K. (2011) A Note on Relationship between Invertible Rhotrices and Associated Invertible Matrices. Bulletin of Pure and Applied Sciences: Mathematics and Statistics, 30e, 333-339.
- Sharma, P.L. and Kanwar, R.K. (2012) Adjoint of a Rhotrix and Its Basic Properties. International Journal of Mathematical Sciences, 11, 337-343.
- Sharma, P.L. and Kanwar, R.K. (2012) On Inner Product Spaces and Bilinear Forms of Rhotrices. Bulletin of Pure and Applied Sciences, 31e, 109-118.
- Aminu, A. (2012) A Determinant Method for Solving Rhotrix System of Equation. Journal of the Nigerian Association of Mathematical Physics, 21, 281-288.
- Usaini, S. (2012) On the Construction of Involutory Rhotrices. International Journal of Mathematical Education in Science and Technology, 43, 510-515. http://dx.doi.org/10.1080/0020739X.2011.599875
- Sharma, P.L. and Kanwar, R.K. (2013) On Involutory and Pascal Rhotrices. International Journal of Mathematical Sciences and Engineering Applications, 7, 133-146.
- Aminu, A. and Michael, O. (2013) Adjacent Rhotrix of a Complete, Simple and Undirected Graph. National Association of Mathematical Physics, 25, 267-274.
- Absalom, E.A., Abdullahi, M., Ibrahim, K., Mohammed, A. and Junaidu, S.B. (2011) Parallel Multiplication of Rhotrices Using Systolic Array Architecture. International Journal of Computer Information Systems, 2, 68-73.
- Absalom, E.E. and Sahalu, J.B. (2012) Rhotrix Multiplication of Two-Dimensional Process Grid Topologies. International Journal of Grid and High Performance Computing, 4, 21-36. http://dx.doi.org/10.4018/jghpc.2012010102
- Mohammed, A., Balarabe, M. and Imam, A.T. (2012) Rhotrix Linear Transformation. Advances in Linear Algebra & Matrix Theory, 2, 43-47. http://dx.doi.org/10.4236/alamt.2012.24007
- Usaini, S. (2012) Rhotrices and Elementary Row Operation. Journal of the Nigerian Association of Mathematical Physics, 20, 37-42.



