Advances in Linear Algebra & Matrix Theory
Vol.3 No.4(2013), Article ID:40922,5 pages DOI:10.4236/alamt.2013.34010
 Solution to a System of Matrix Equations
Solution to a System of Matrix Equations
School of Mathematics and Science, Shijiazhuang University of Economics, Shijiazhuang, China
Email: dongchangzh@sina.com, yuping.zh@163.com
Copyright © 2013 Changzhou Dong et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 29, 2013; revised October 29, 2013; accepted November 5, 2013
Keywords:  Matrix; Matrix Equation; Moore-Penrose Inverse; Approximation Problem; Least Squares Solution
Matrix; Matrix Equation; Moore-Penrose Inverse; Approximation Problem; Least Squares Solution
ABSTRACT
A square complex matrix  is called
is called  if it can be written in the form
if it can be written in the form  with
with 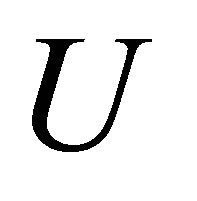 being fixed unitary and
being fixed unitary and  being arbitrary matrix in
being arbitrary matrix in . We give necessary and sufficient conditions for the existence of the
. We give necessary and sufficient conditions for the existence of the  solution to the system of complex matrix equation
solution to the system of complex matrix equation 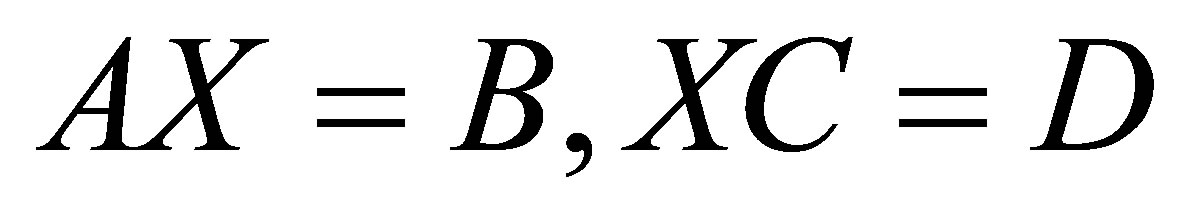 and present an expression of the
and present an expression of the 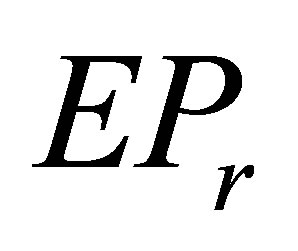 solution to the system when the solvability conditions are satisfied. In addition, the solution to an optimal approximation problem is obtained. Furthermore, the least square
solution to the system when the solvability conditions are satisfied. In addition, the solution to an optimal approximation problem is obtained. Furthermore, the least square 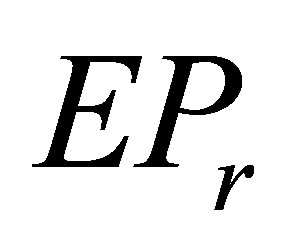 solution with least norm to this system mentioned above is considered. The representation of such solution is also derived.
solution with least norm to this system mentioned above is considered. The representation of such solution is also derived.
1. Introduction
Throughout we denote the complex 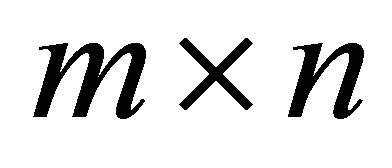 matrix space by
matrix space by 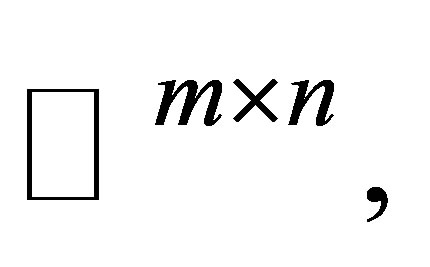 the real
the real  matrix space by
matrix space by 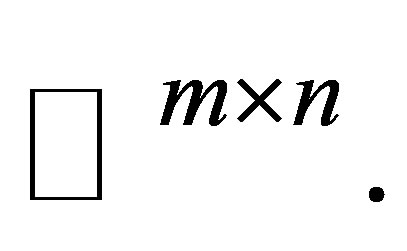 The symbols
The symbols  and
and  stand for the identity matrix with the appropriate size, the conjugate transpose, the range, the null space, and the Frobenius norm of
stand for the identity matrix with the appropriate size, the conjugate transpose, the range, the null space, and the Frobenius norm of  respectively. The Moore-Penrose inverse of
respectively. The Moore-Penrose inverse of 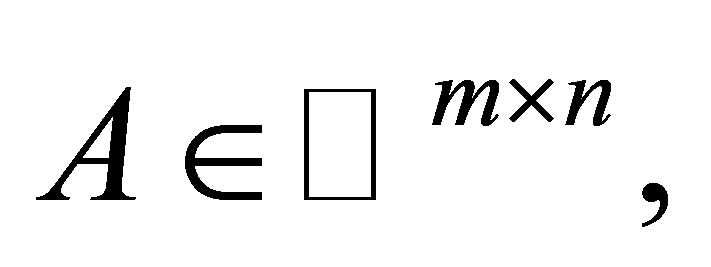 denoted by
denoted by  is defined to be the unique matrix
is defined to be the unique matrix 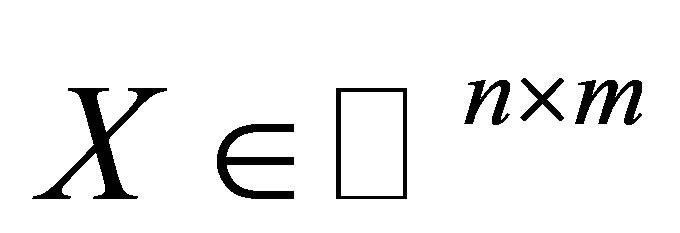 of the following matrix equations
of the following matrix equations

Recall that an 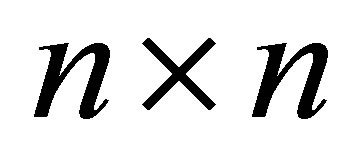 complex matrix
complex matrix  is called
is called  (or range Hermitian) if
(or range Hermitian) if 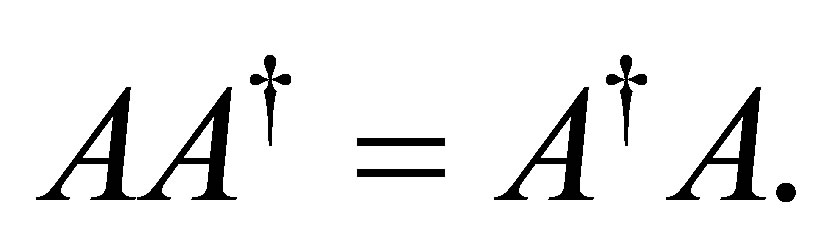
 matrices were introduced by Schwerdtfeger in [1], ever since many authors have studied
matrices were introduced by Schwerdtfeger in [1], ever since many authors have studied  matrices with entries from complex number field to semigroups with involution and given various equivalent conditions and many characterizations for matrix to be
matrices with entries from complex number field to semigroups with involution and given various equivalent conditions and many characterizations for matrix to be  (see, [2-5]).
(see, [2-5]).
Investigating the matrix equation
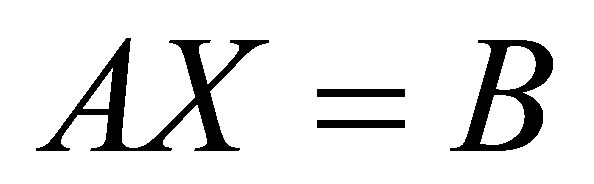 (1)
(1)
with the unknown matrix 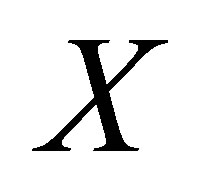 being symmetric, reflexive, Hermitian-generalized Hamiltonian and re-positive definite is a very active research topic (see, [6-9]). As a generalization of (1), the classical system of matrix equations
being symmetric, reflexive, Hermitian-generalized Hamiltonian and re-positive definite is a very active research topic (see, [6-9]). As a generalization of (1), the classical system of matrix equations
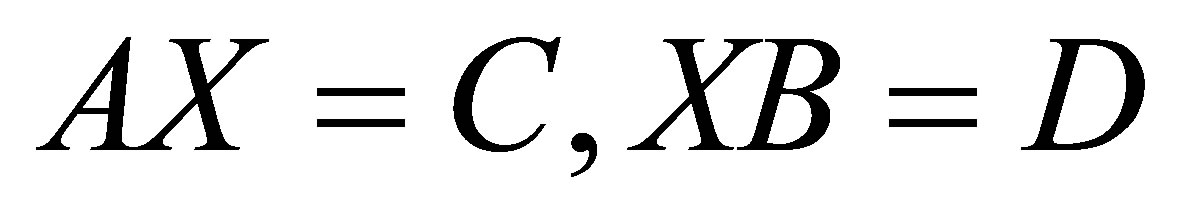 (2)
(2)
has attracted many people’s attention and many results have been obtained about system (2) with various constraints, such as bisymmetric, Hermitian, positive semidefinite, reflexive, and generalized reflexive solutions, and so on (see, [9-12]). It is well-known that  matrices are a wide class of objects that include many matrices as their special cases, such as Hermitian and skewHermitian matrices (i.e.,
matrices are a wide class of objects that include many matrices as their special cases, such as Hermitian and skewHermitian matrices (i.e., ), normal matrices (i.e.,
), normal matrices (i.e., ), as well as all nonsingular matrices. Therefore investigating the
), as well as all nonsingular matrices. Therefore investigating the  solution of the matrix Equation (2) is very meaningful.
solution of the matrix Equation (2) is very meaningful.
Pearl showed in ([2]) that a matrix  is
is  if and only if it can be written in the form
if and only if it can be written in the form 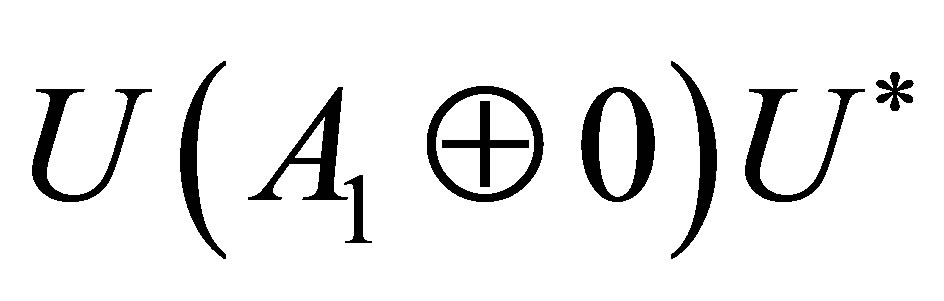 with
with 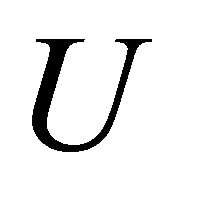 unitary and
unitary and  nonsingular. A square complex matrix
nonsingular. A square complex matrix  is called
is called  if it can be written in the form
if it can be written in the form  where
where 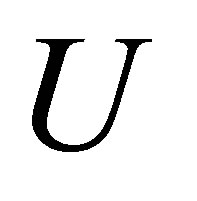 is fixed unitary and
is fixed unitary and  is arbitrary matrix in
is arbitrary matrix in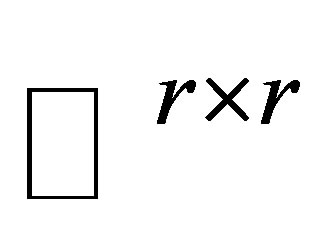 . To our knowledge, so far there has been little investigation of this
. To our knowledge, so far there has been little investigation of this  solution to (2).
solution to (2).
Motivated by the work mentioned above, we investigate 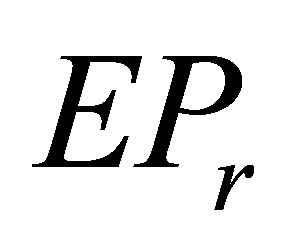 solution to (2). We also consider the optimal approximation problem
solution to (2). We also consider the optimal approximation problem
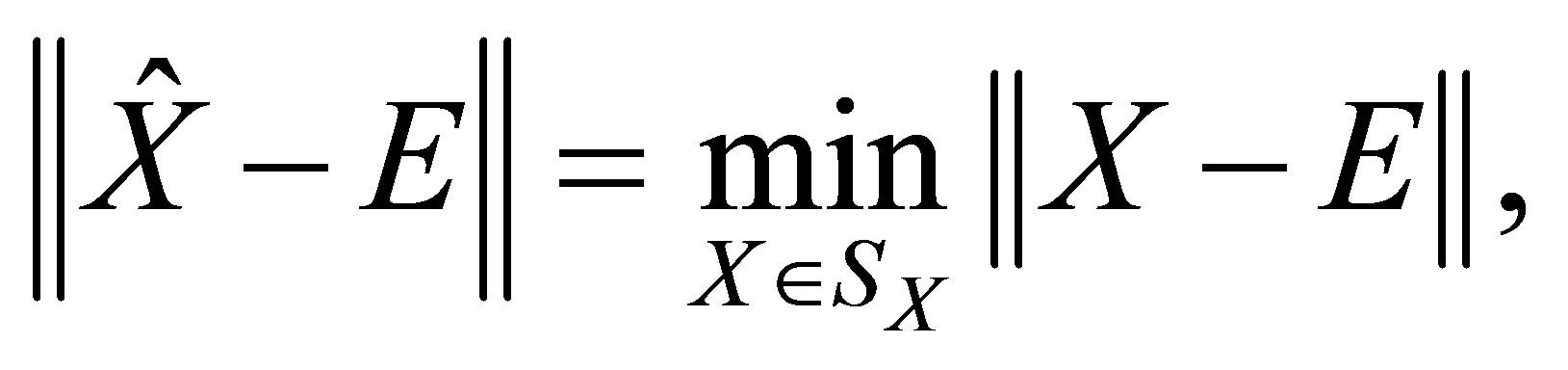 (3)
(3)
where 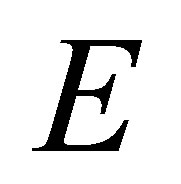 is a given matrix in
is a given matrix in 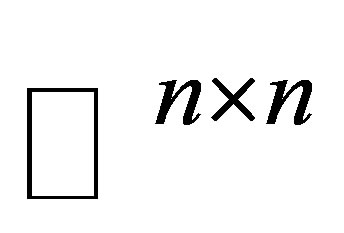 and
and 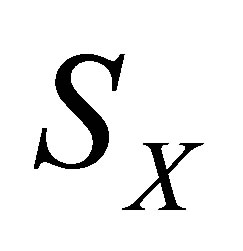 the set of all
the set of all  solutions to (2). In many case Equation (2) has not an
solutions to (2). In many case Equation (2) has not an  solution. Hence we need to further study its least squares solution, which can be described as follows: Let
solution. Hence we need to further study its least squares solution, which can be described as follows: Let 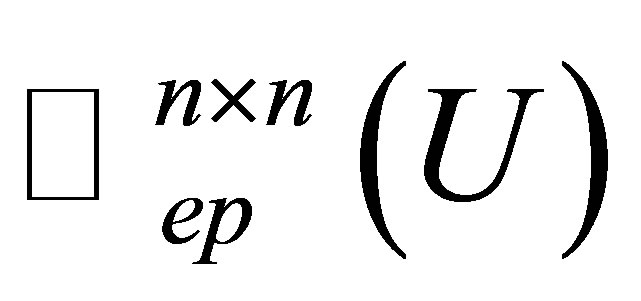 denote the set of all
denote the set of all  matrices with fixed unitary matrix
matrices with fixed unitary matrix  in
in 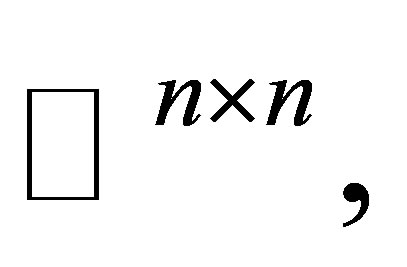

Find  such that
such that
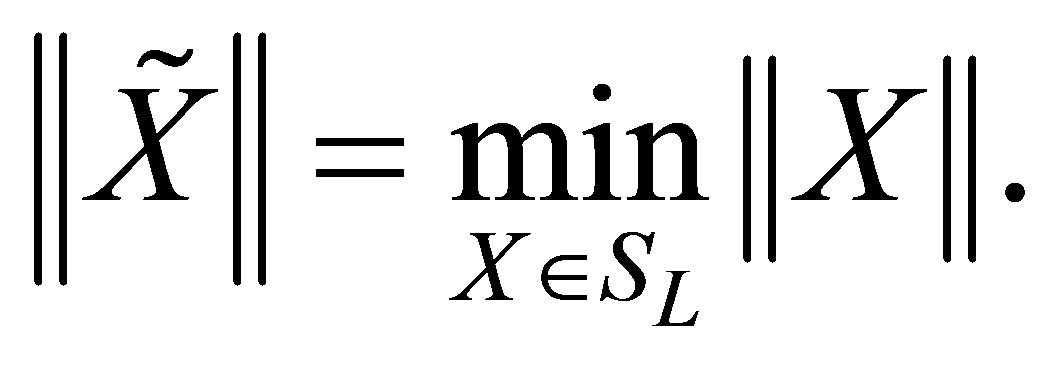 (4)
(4)
In Section 2, we present necessary and sufficient conditions for the existence of the 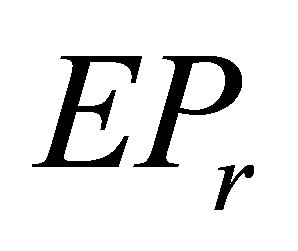 solution to (2), and give an expression of this solution when the solvability conditions are met. In Section 3, we derive an optimal approximation solution to (3). In Section 4, we provide the least squares
solution to (2), and give an expression of this solution when the solvability conditions are met. In Section 3, we derive an optimal approximation solution to (3). In Section 4, we provide the least squares 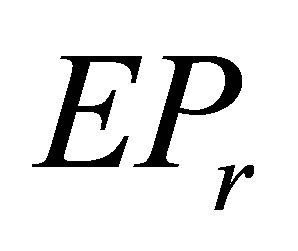 solution to (4).
solution to (4).
2.  Solution to (2)
Solution to (2)
In this section, we establish the solvability conditions and the general expression for the 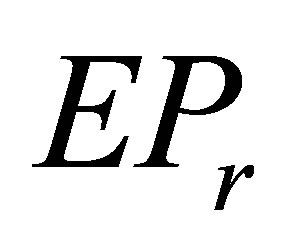 solution to (2).
solution to (2).
Throughout we denotes 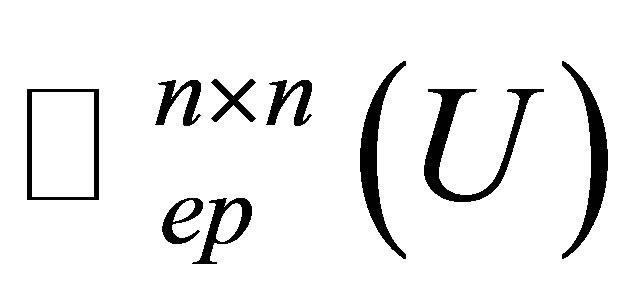 the set of all
the set of all  matrices with fixed unitary matrix
matrices with fixed unitary matrix  in
in  i.e.,
i.e.,
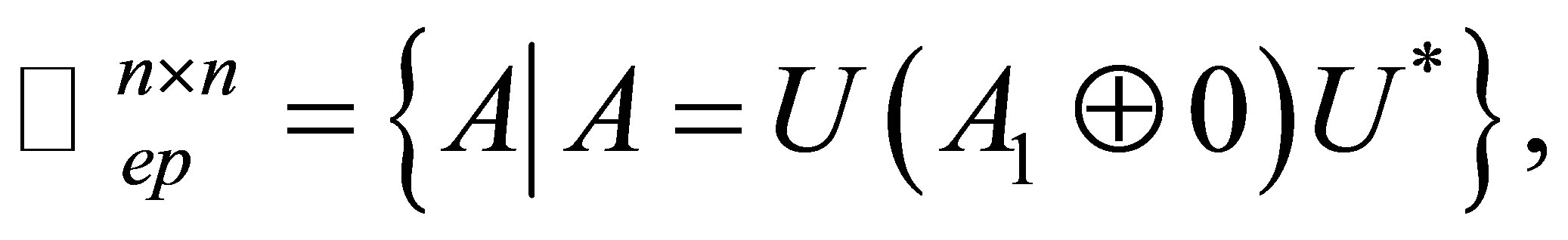
where 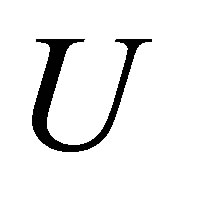 is fixed unitary and
is fixed unitary and  is arbitrary matrix in
is arbitrary matrix in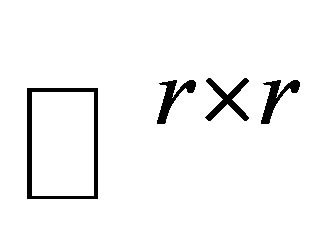 .
.
Lemma 2.1. ([3]) Let 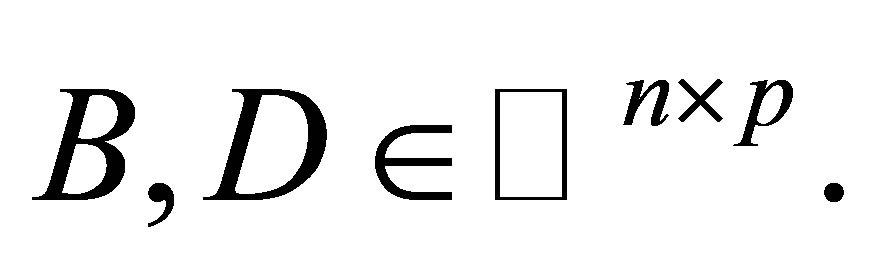
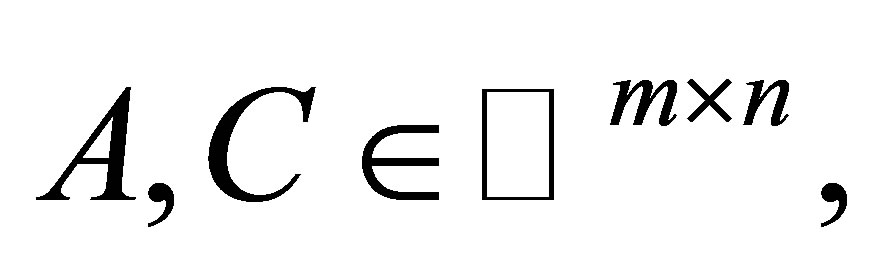 Then the system of matrix equations
Then the system of matrix equations 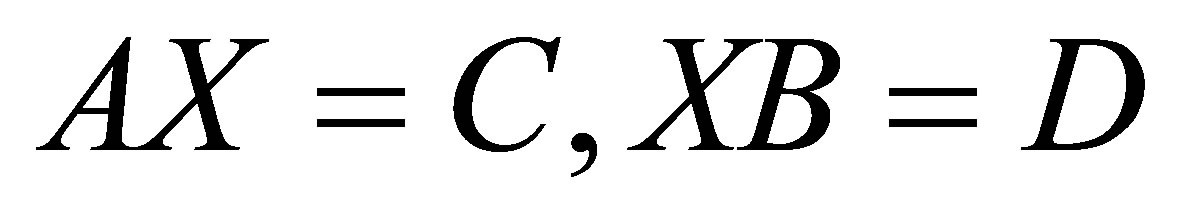 is consistent if and only if
is consistent if and only if

In that case, the general solution of this system is
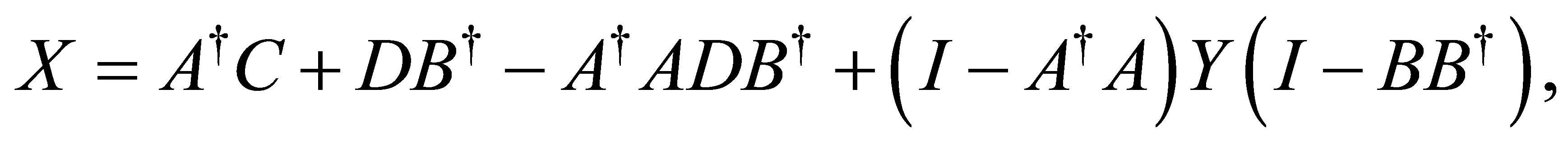
where 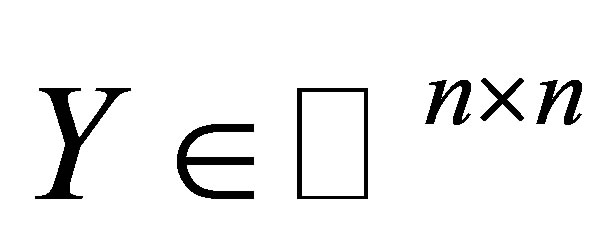 is arbitrary.
is arbitrary.
Now we consider the 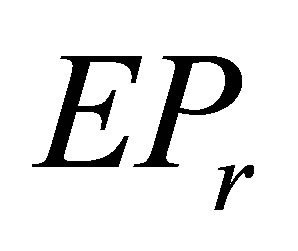 solution to (1). By the definition of
solution to (1). By the definition of  matrix, the solution has the following factorization:
matrix, the solution has the following factorization:
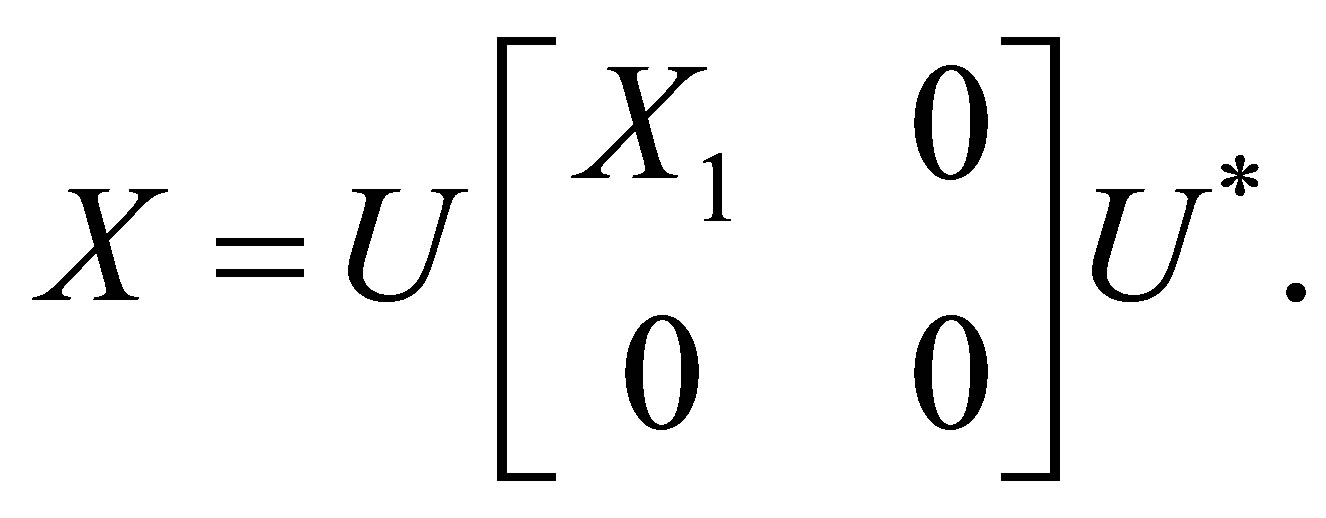
Let
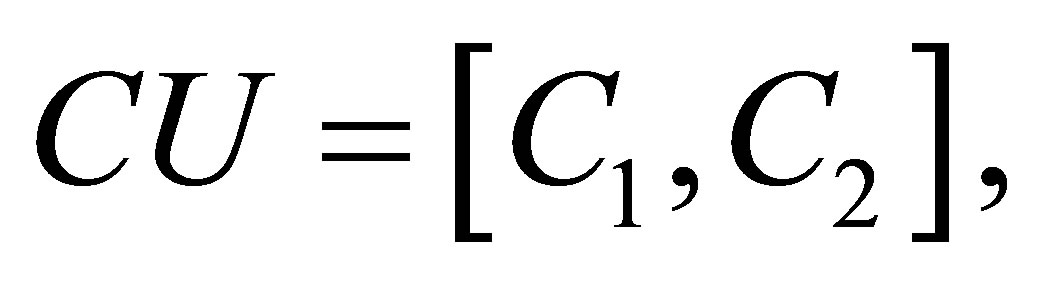
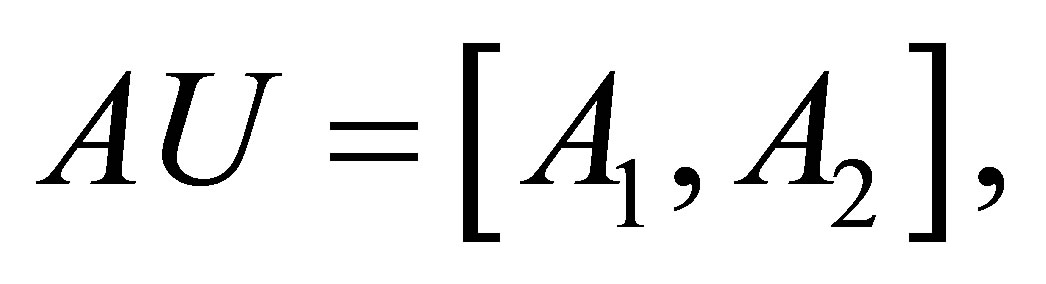

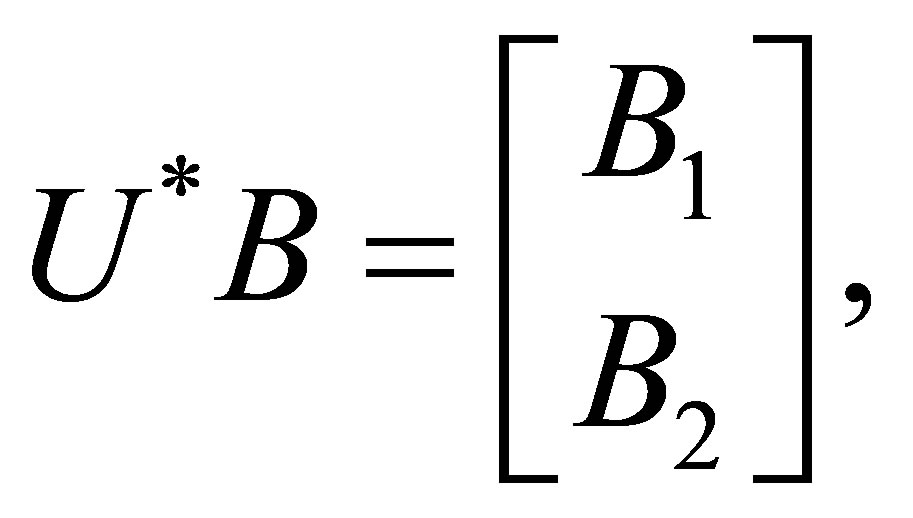
where 
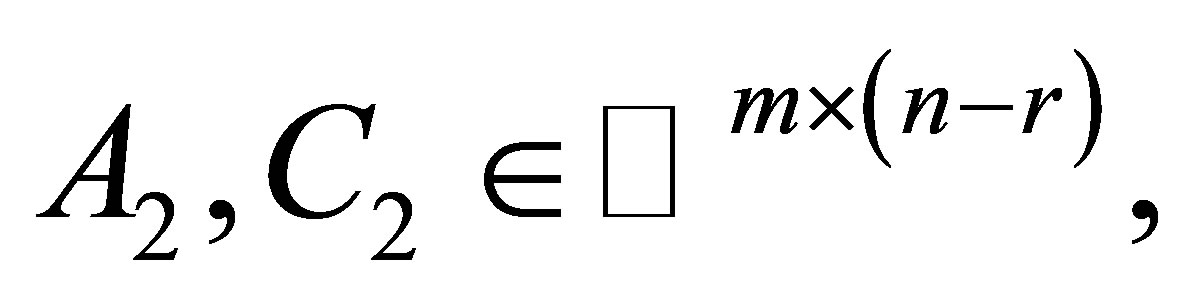
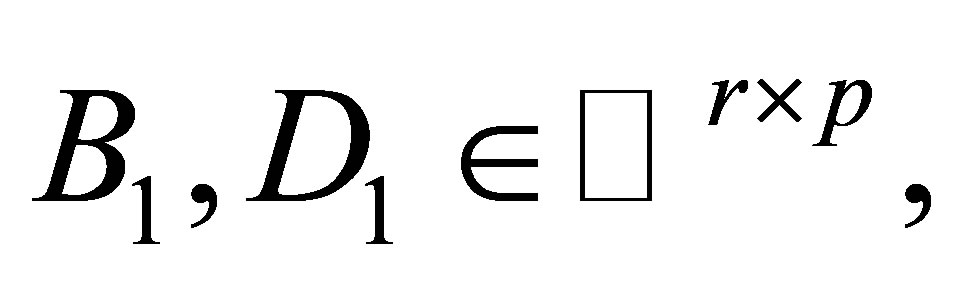
 then (2) has
then (2) has 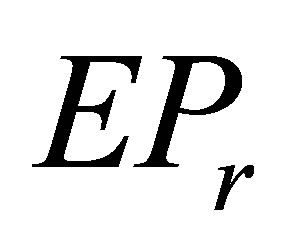 solution if and only if the system of matrix equations
solution if and only if the system of matrix equations

is consistent. By Lemma 2.1, we have the following theorem.
Theorem 2.2. Let 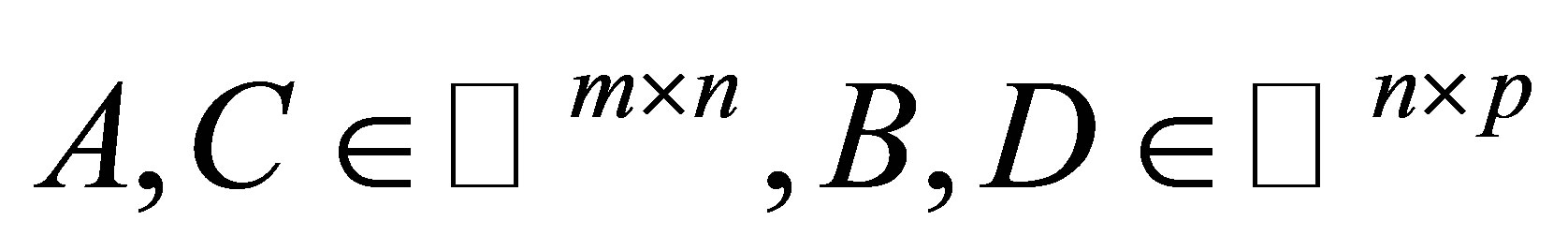 and
and

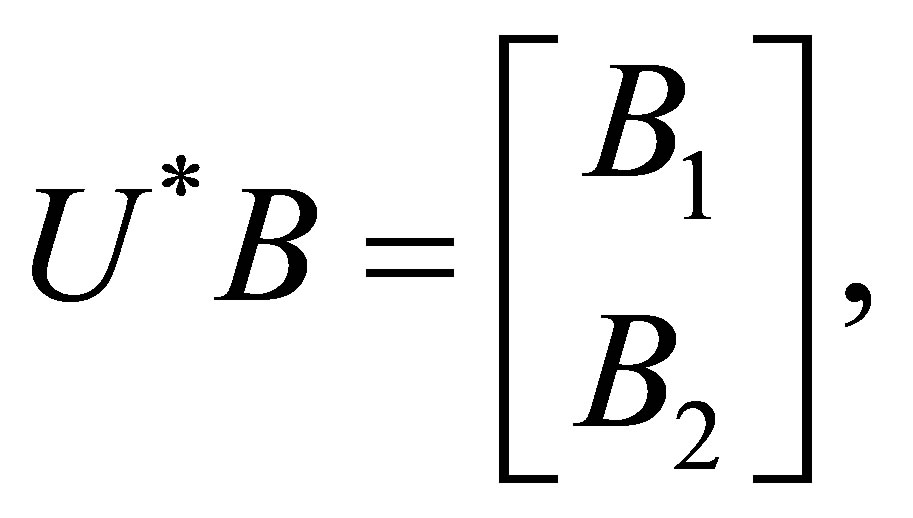
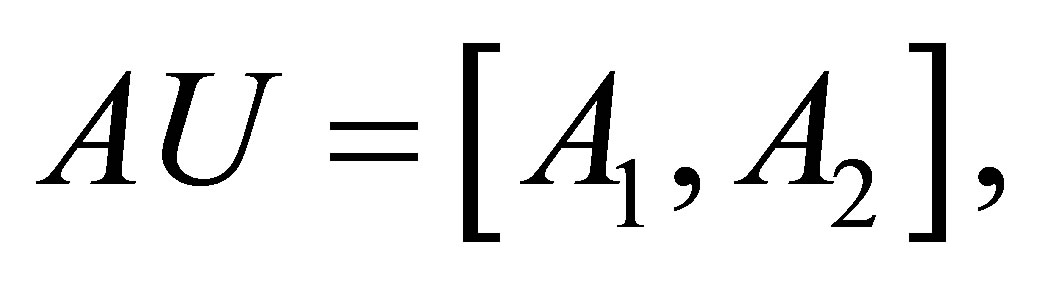
where 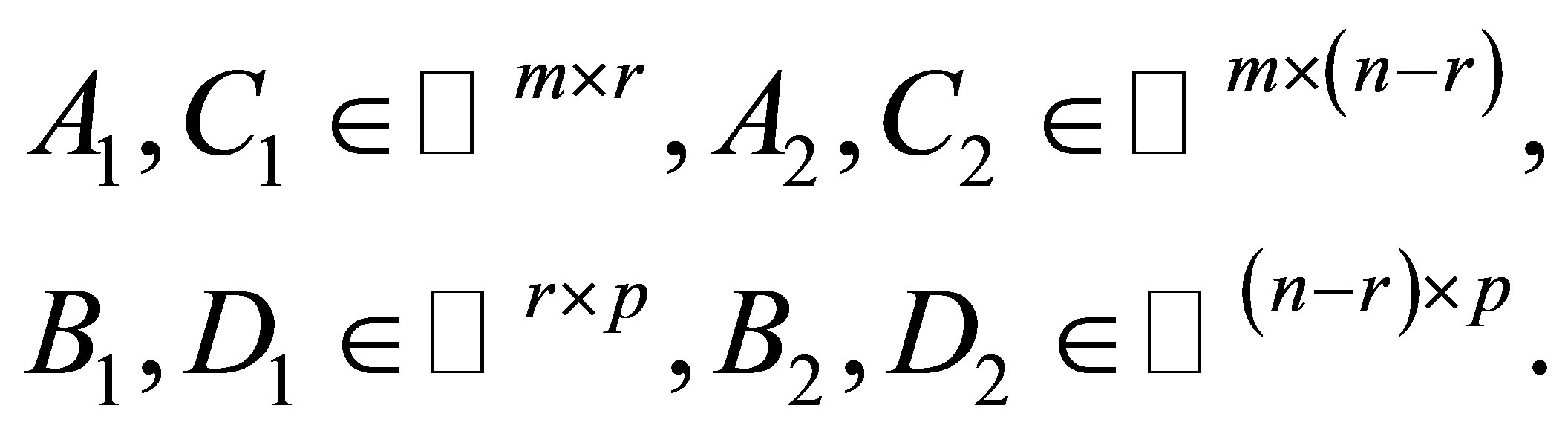
Then the matrix Equation (2) has a  solution in
solution in  if and only if
if and only if
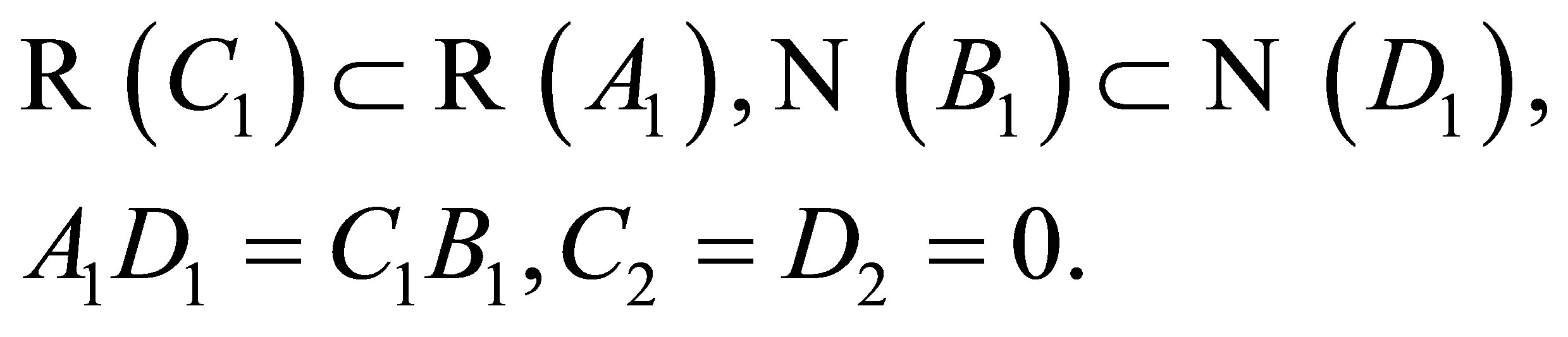 (5)
(5)
In that case, the general  solution of (1) is
solution of (1) is
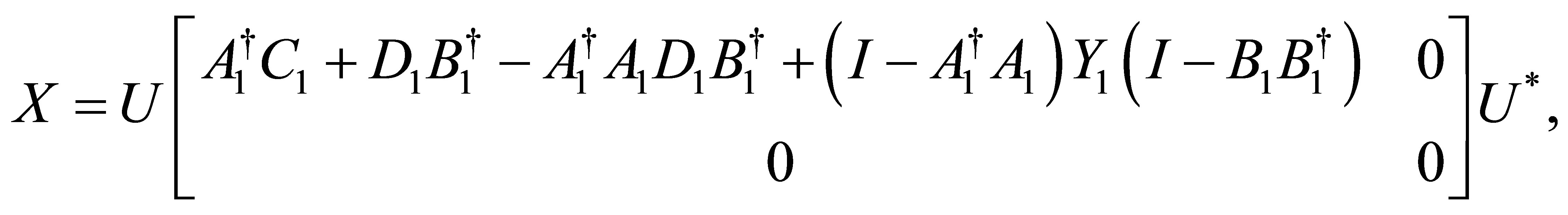 (6)
(6)
where 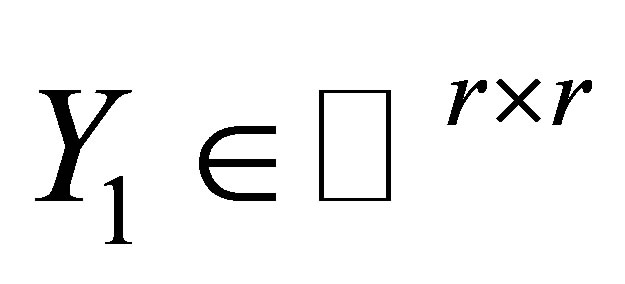 is arbitrary.
is arbitrary.
3. The Solution of Optimal Approximation Problem (3)
When the set  of all
of all 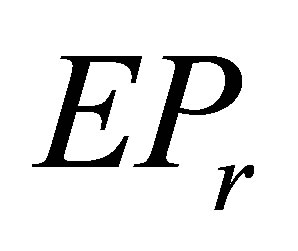 solution to (2) is nonempty, it is easy to verify
solution to (2) is nonempty, it is easy to verify 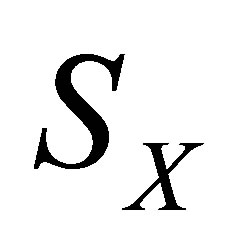 is a closed set. Therefore the optimal approximation problem (3) has a unique solution by [13]. We first verify the following lemma.
is a closed set. Therefore the optimal approximation problem (3) has a unique solution by [13]. We first verify the following lemma.
Lemma 3.1. Let  Then the procrustes problem
Then the procrustes problem

has a solution which can be expressed as
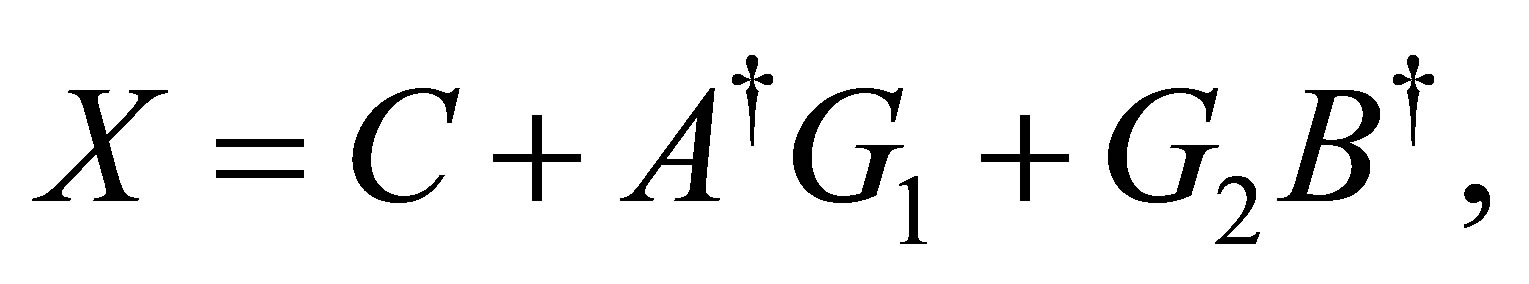
where 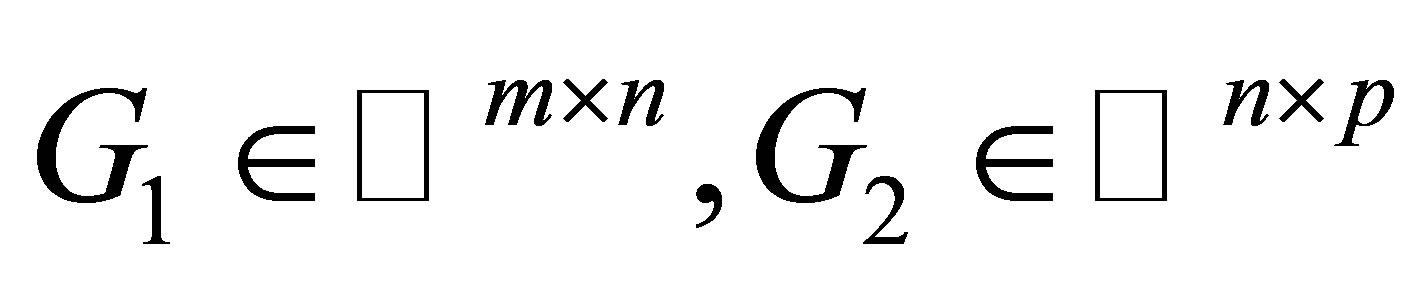 are arbitrary matrices.
are arbitrary matrices.
Proof. It follows from the properties of Moore-Penrose generalized inverse and the inner product that
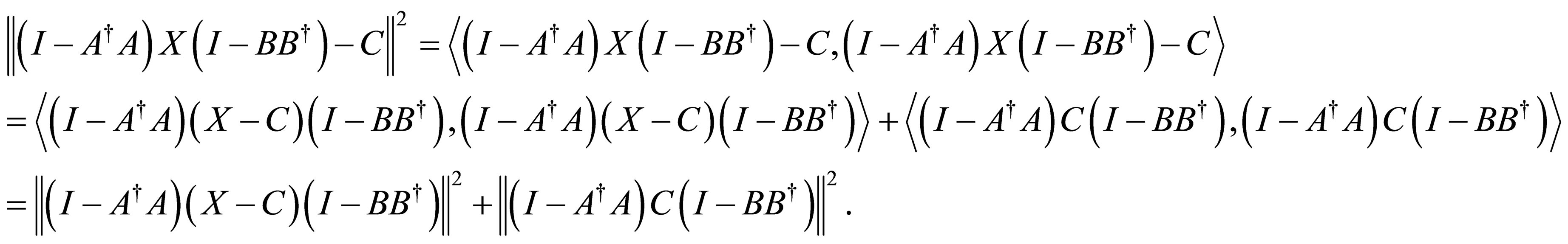
Hence,
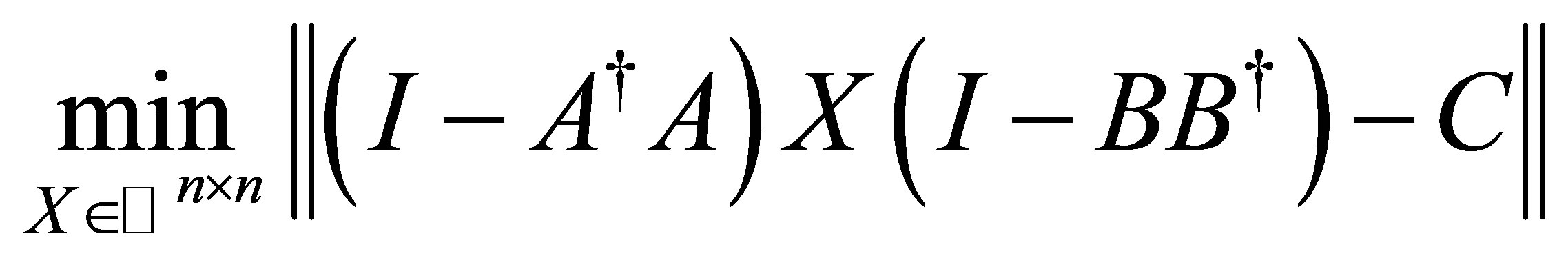
if and only if

It is clear that 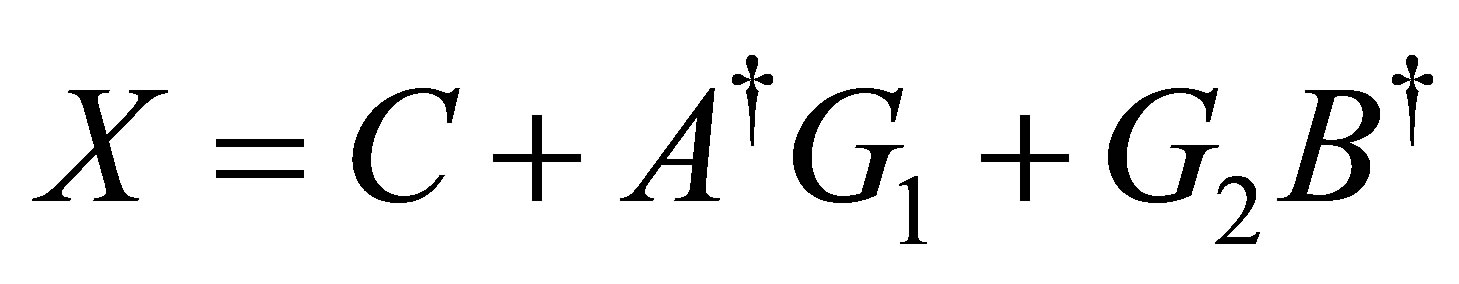 with
with 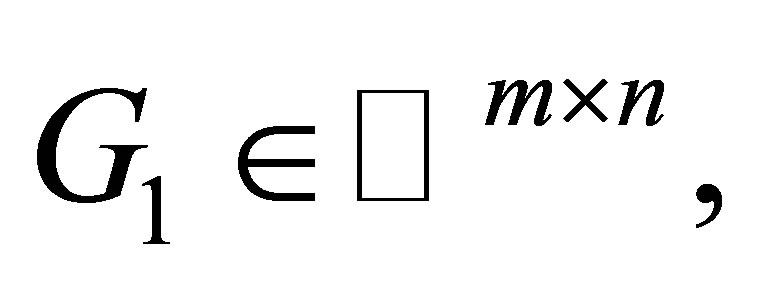
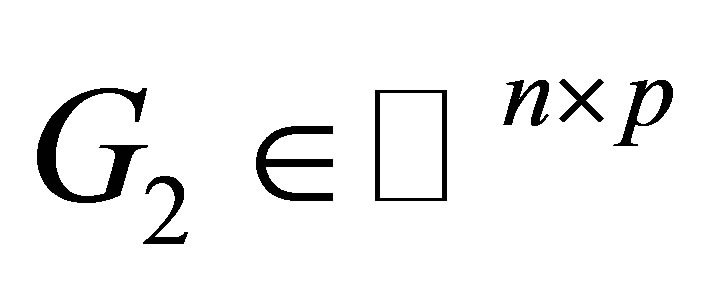 are arbitrary is the solution of the above procrustes problem.
are arbitrary is the solution of the above procrustes problem.
Theorem 3.2. Let 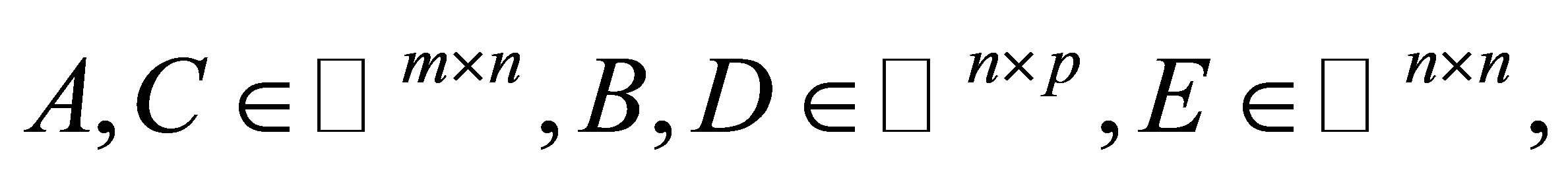 and
and
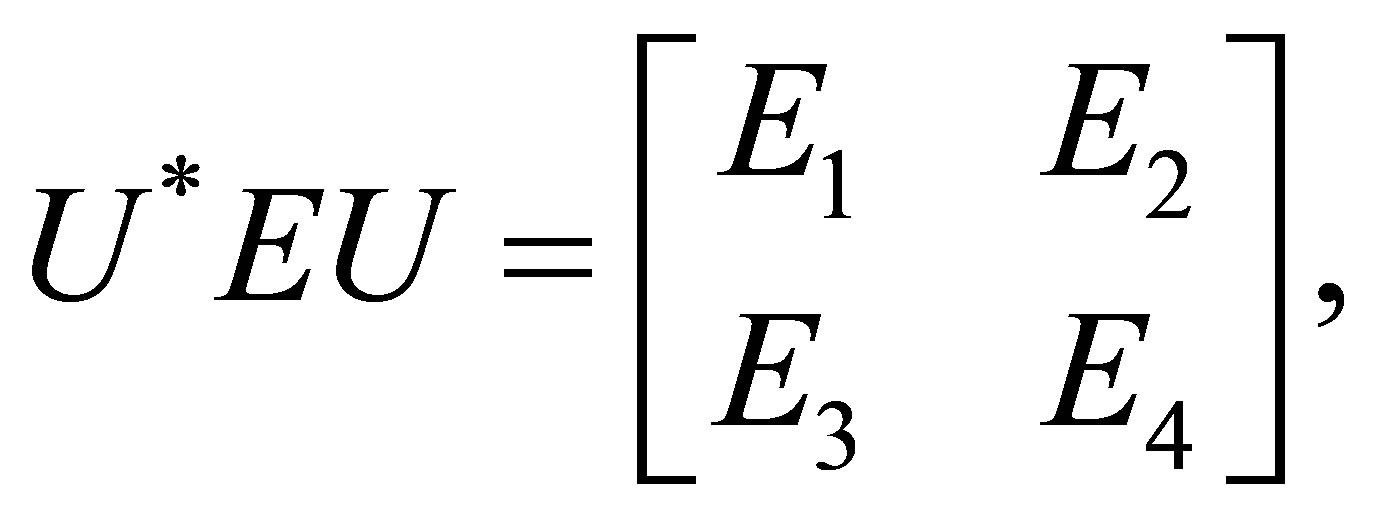 (7)
(7)
where 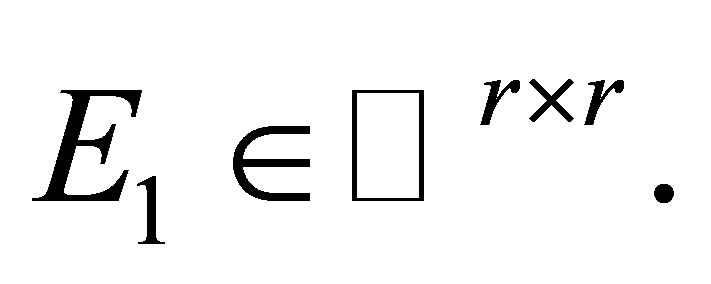 Assume
Assume  is nonempty, then the optimal approximation problem (3) has a unique solution
is nonempty, then the optimal approximation problem (3) has a unique solution  and
and
 (8)
(8)
Proof. Since 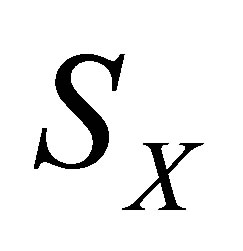 is nonempty,
is nonempty,  has the form of (6). It follows from (7) and the unitary invariance of Frobenius norm that
has the form of (6). It follows from (7) and the unitary invariance of Frobenius norm that

Therefore, there exists 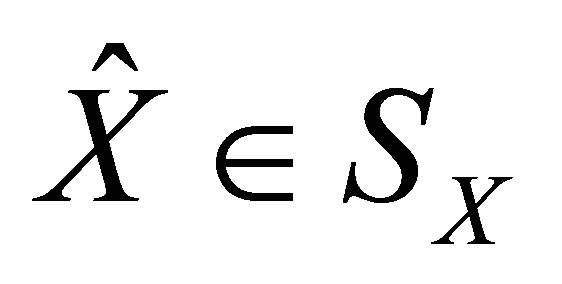 such that the matrix nearness problem (3) holds if and only if exist
such that the matrix nearness problem (3) holds if and only if exist 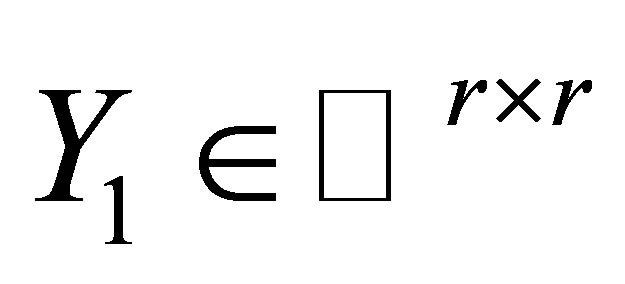 such that
such that
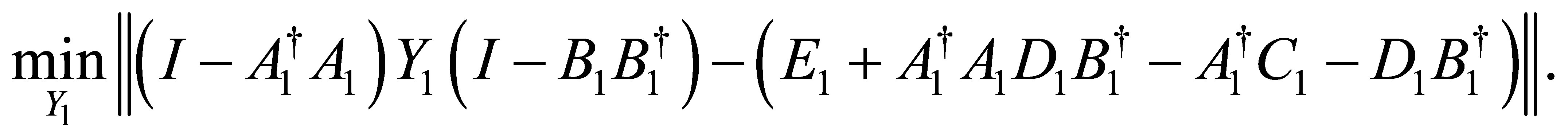
According to Lemma 3.1, we have

where  are arbitrary. Substituting
are arbitrary. Substituting 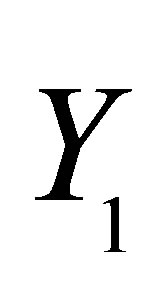 into (6), we obtain that the solution of the matrix nearness problem (3) can be expressed as (8).
into (6), we obtain that the solution of the matrix nearness problem (3) can be expressed as (8).
4. The Least Squares  Solution to (4)
Solution to (4)
In this section, we give the explicit expression of the least squares  solution to (4).
solution to (4).
Lemma 4.1. ([12]) Given 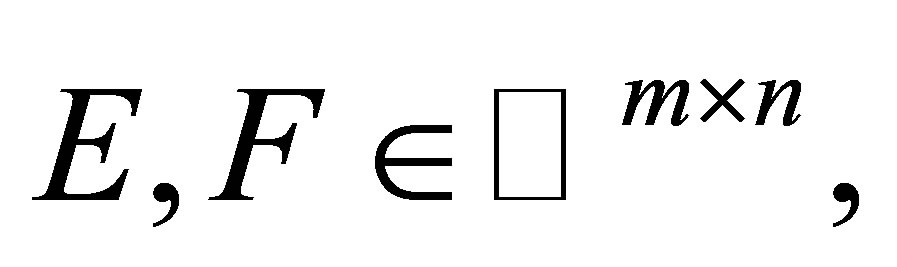

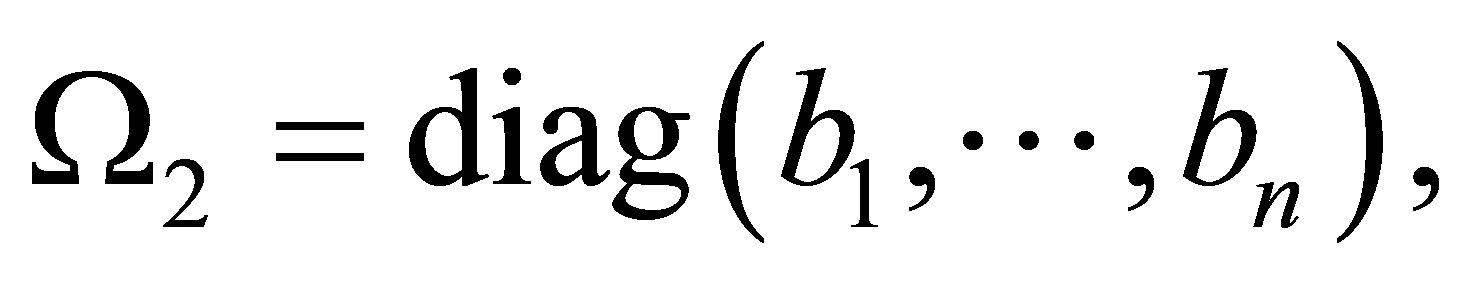
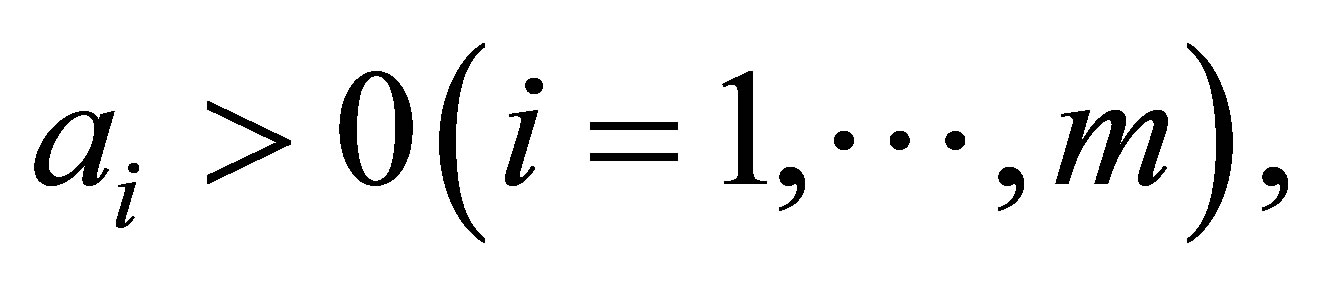
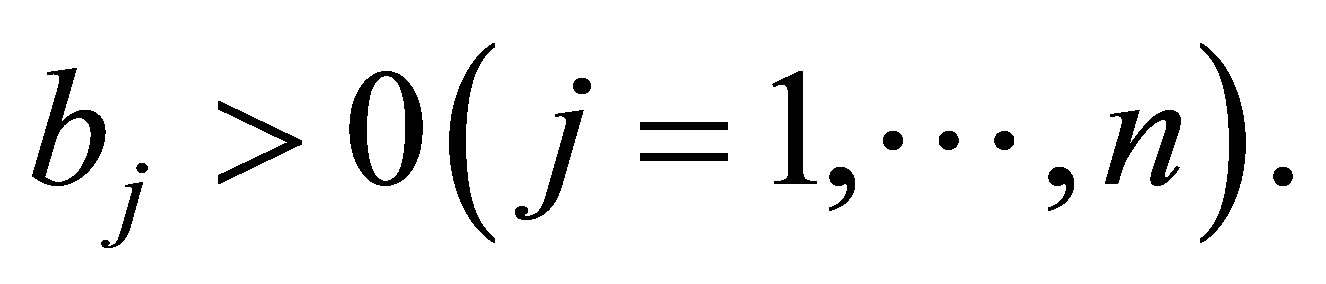 Then there exists a unique matrix
Then there exists a unique matrix  such that
such that
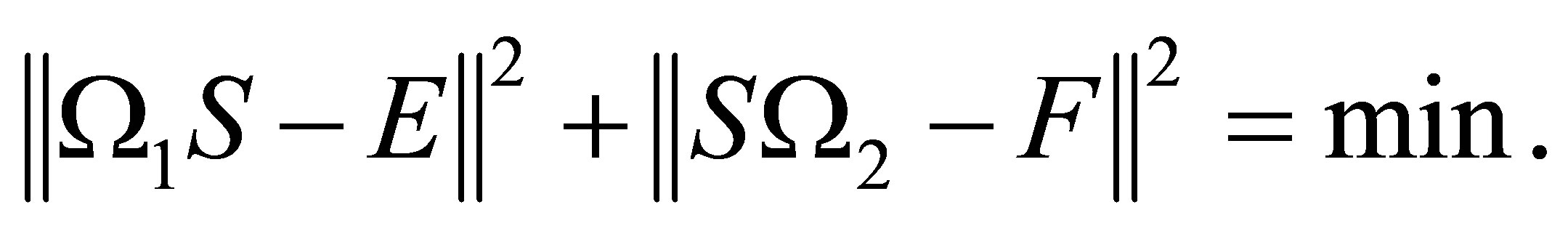
And 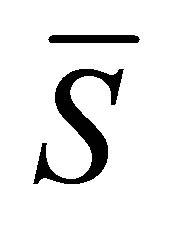 can be expressed as
can be expressed as
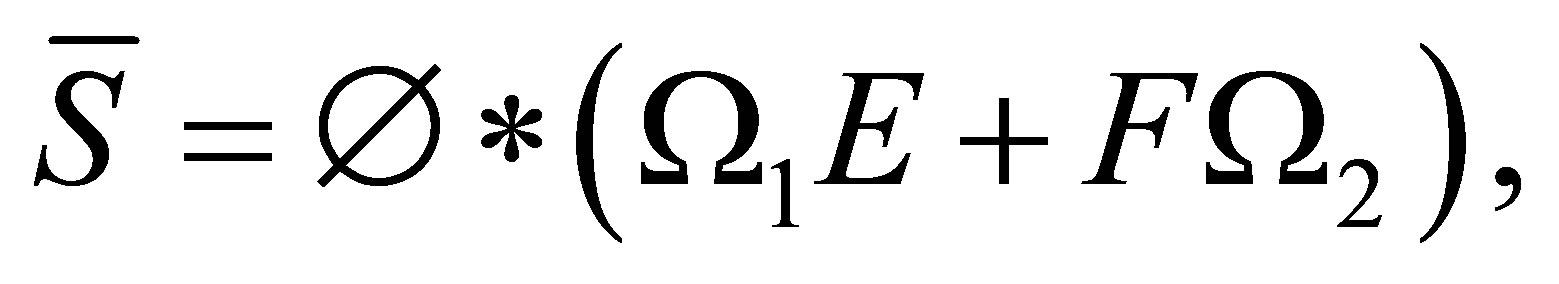
where 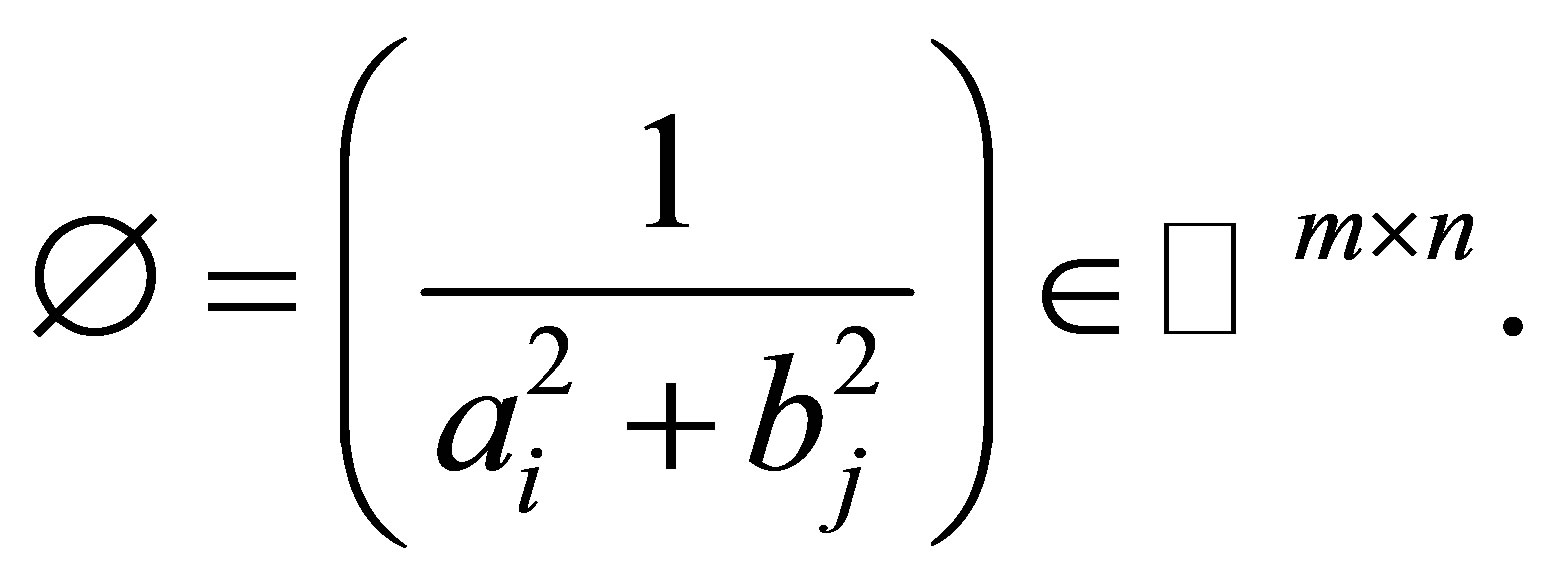
Theorem 4.2. Let 
 and
and
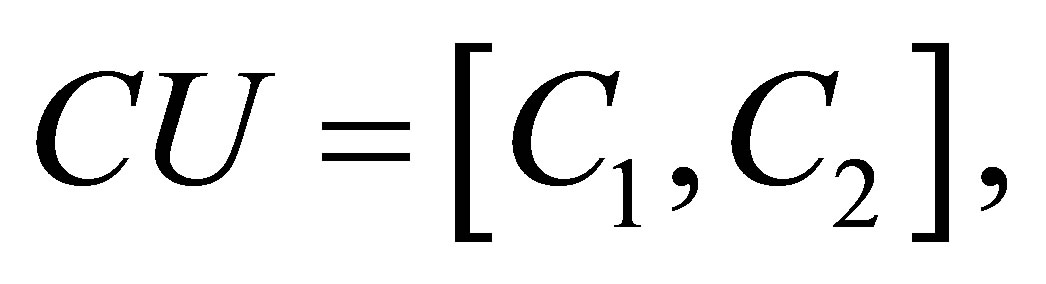
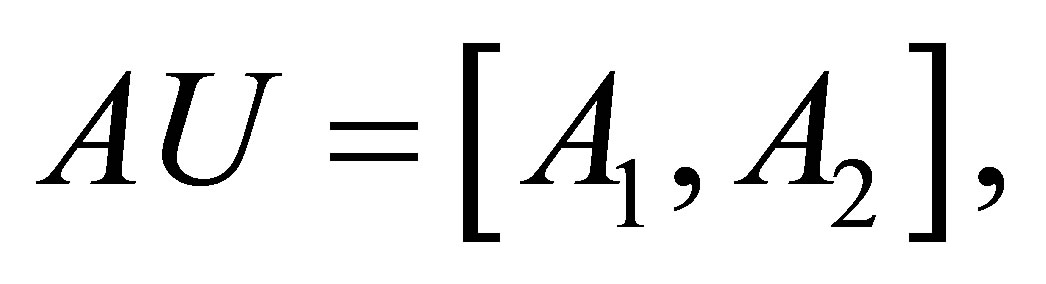

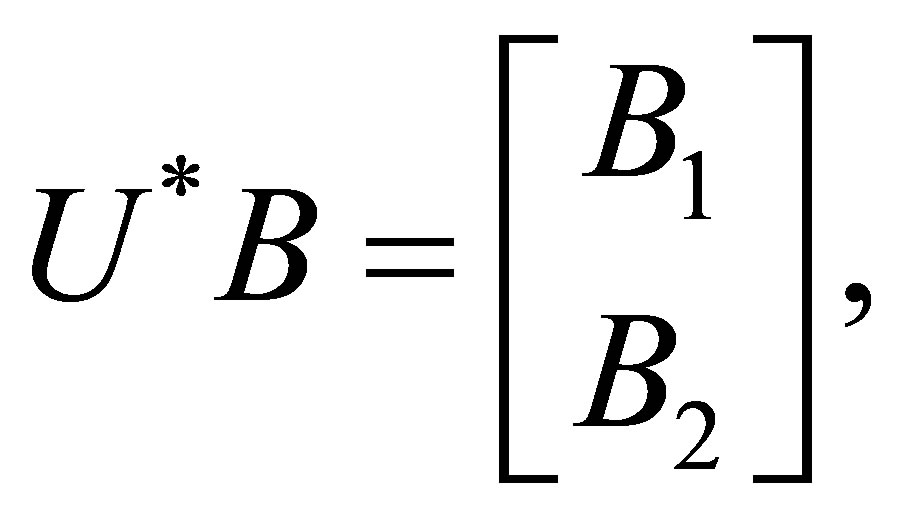
where ,
, 
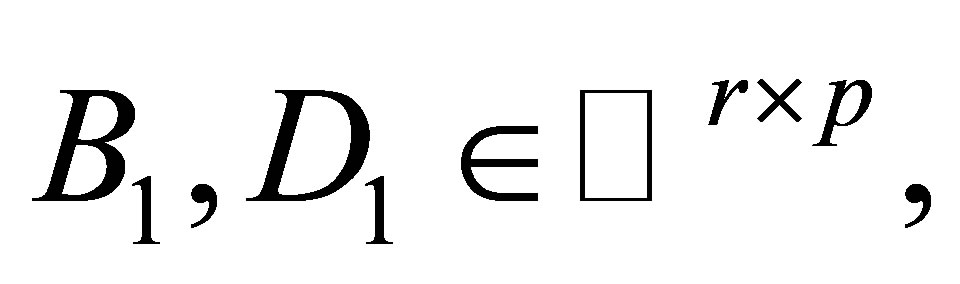
 Assume that the singular value decomposition of
Assume that the singular value decomposition of  are as follows
are as follows
 (9)
(9)
where 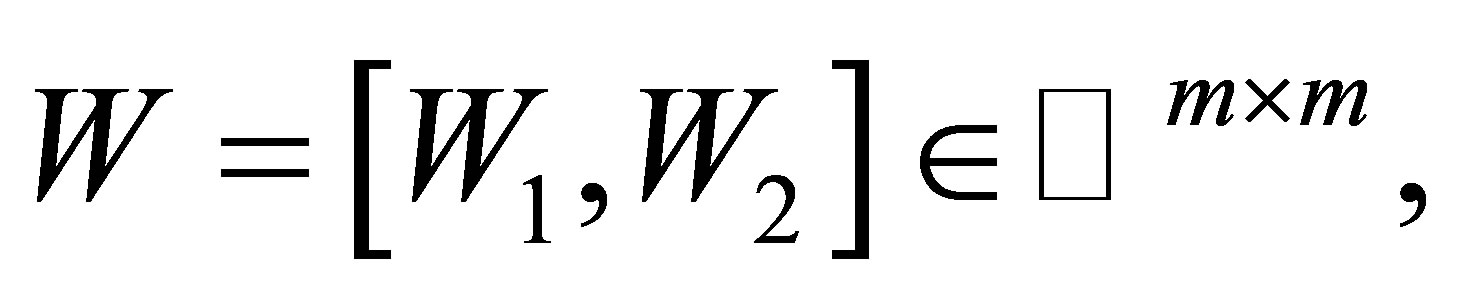

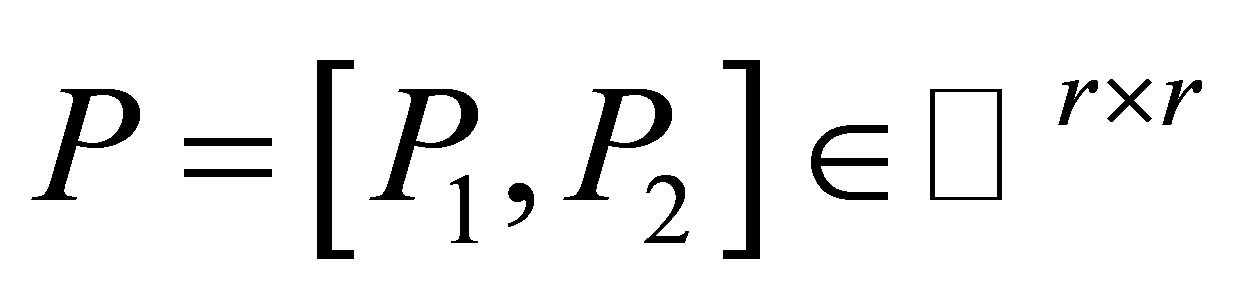 and
and  are unitary matrices,
are unitary matrices, 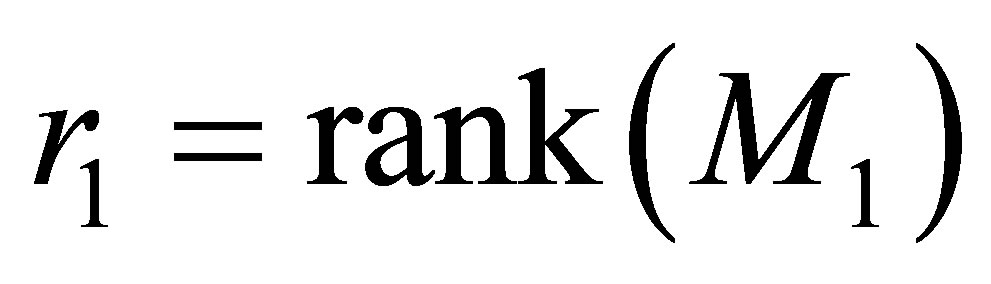

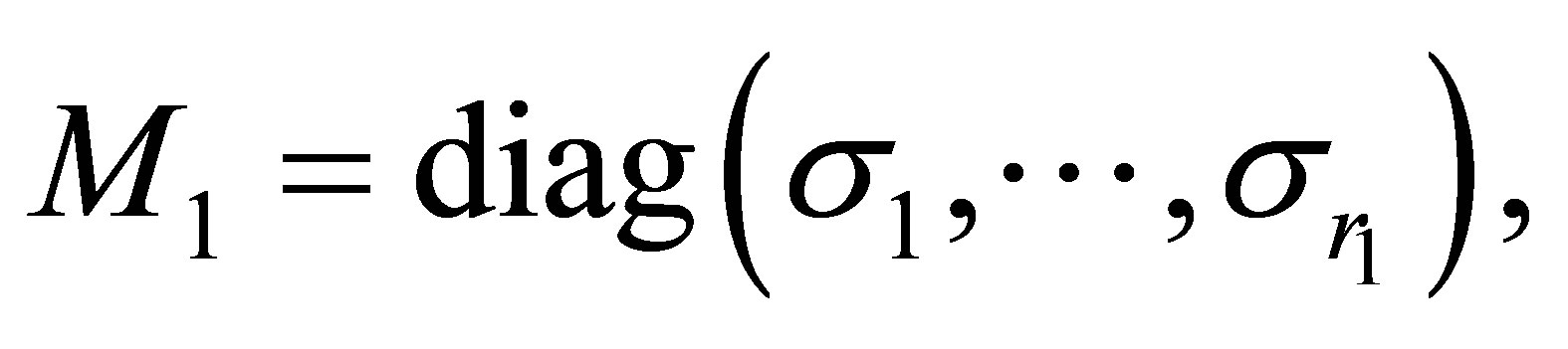 ,
, 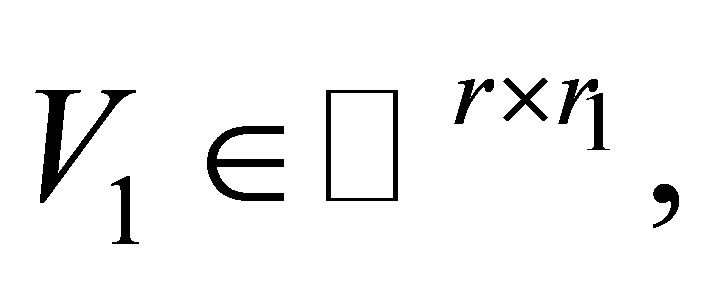





 Then
Then  can be expressed as
can be expressed as
 (10)
(10)
where  and
and 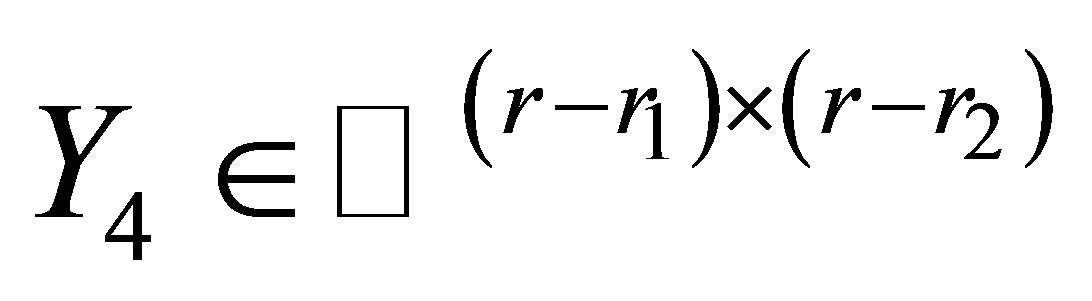 is an arbitrary matrix.
is an arbitrary matrix.
Proof. It yields from (9) that

Assume that
 (11)
(11)
Then we have
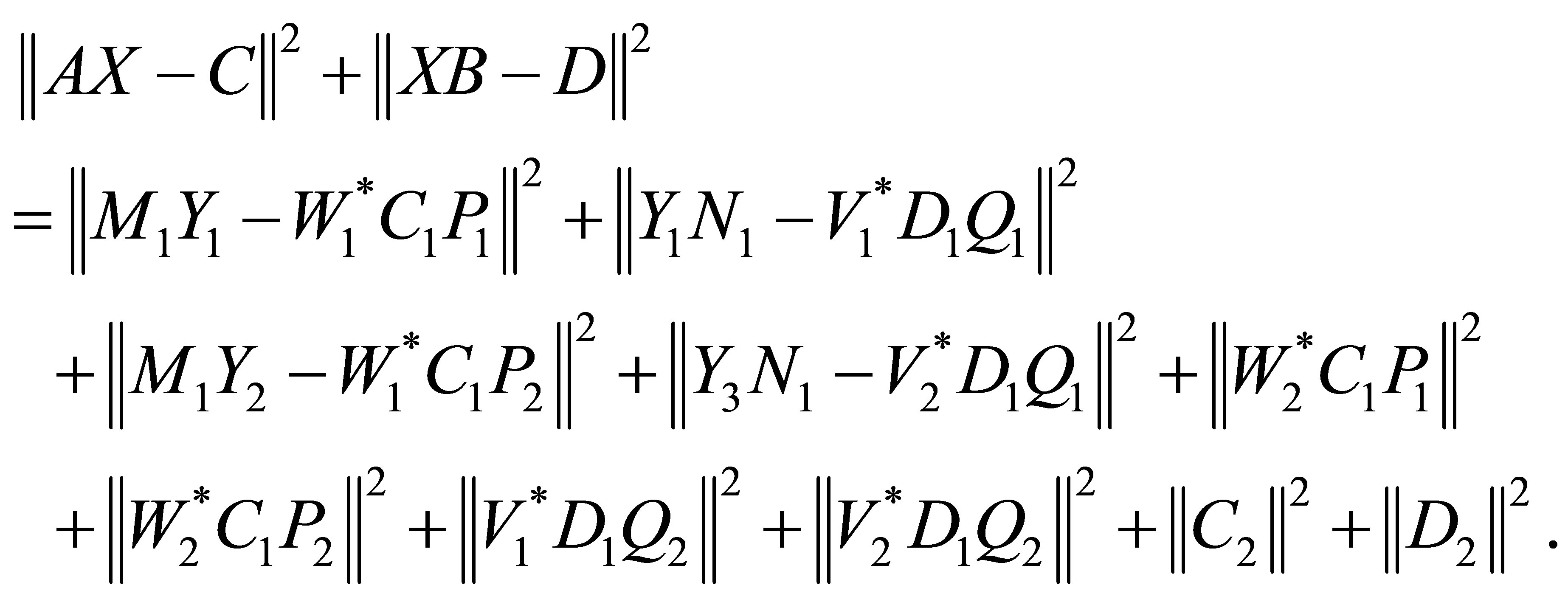
Hence

is solvable if and only if there exist 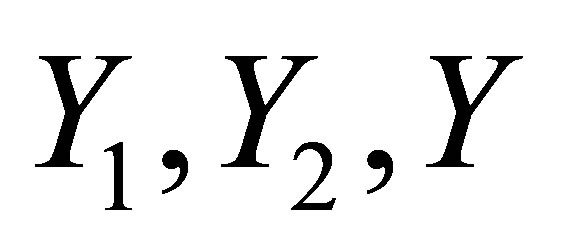 such that
such that
 (12)
(12)
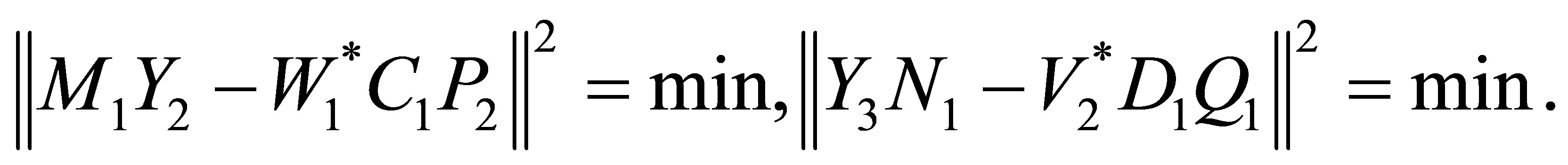 (13)
(13)
It follows from (12) and (13) that
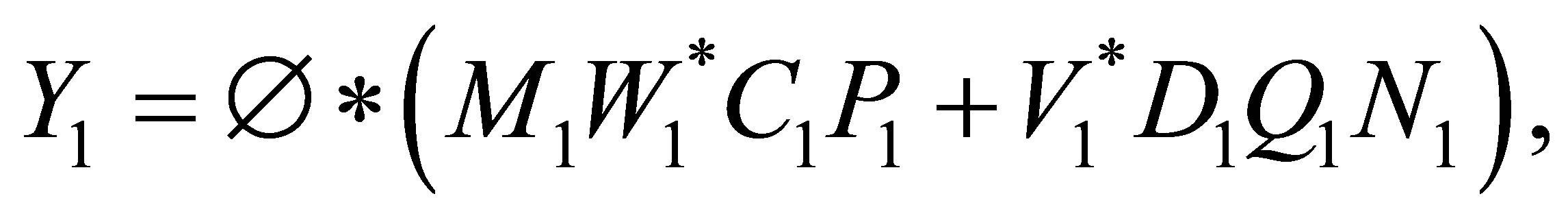 (14)
(14)
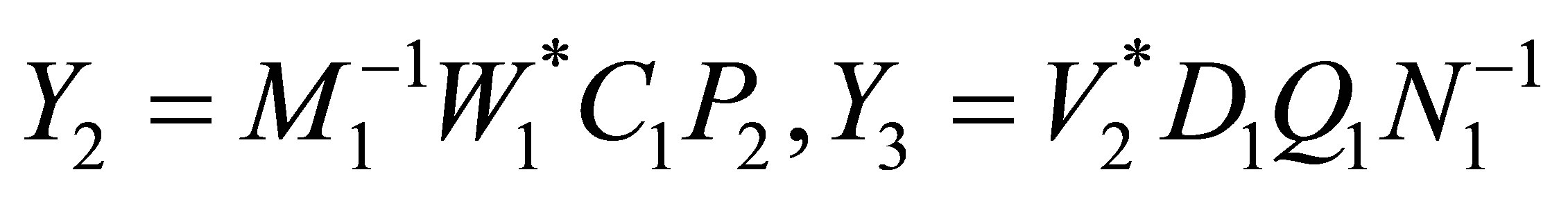 (15)
(15)
where 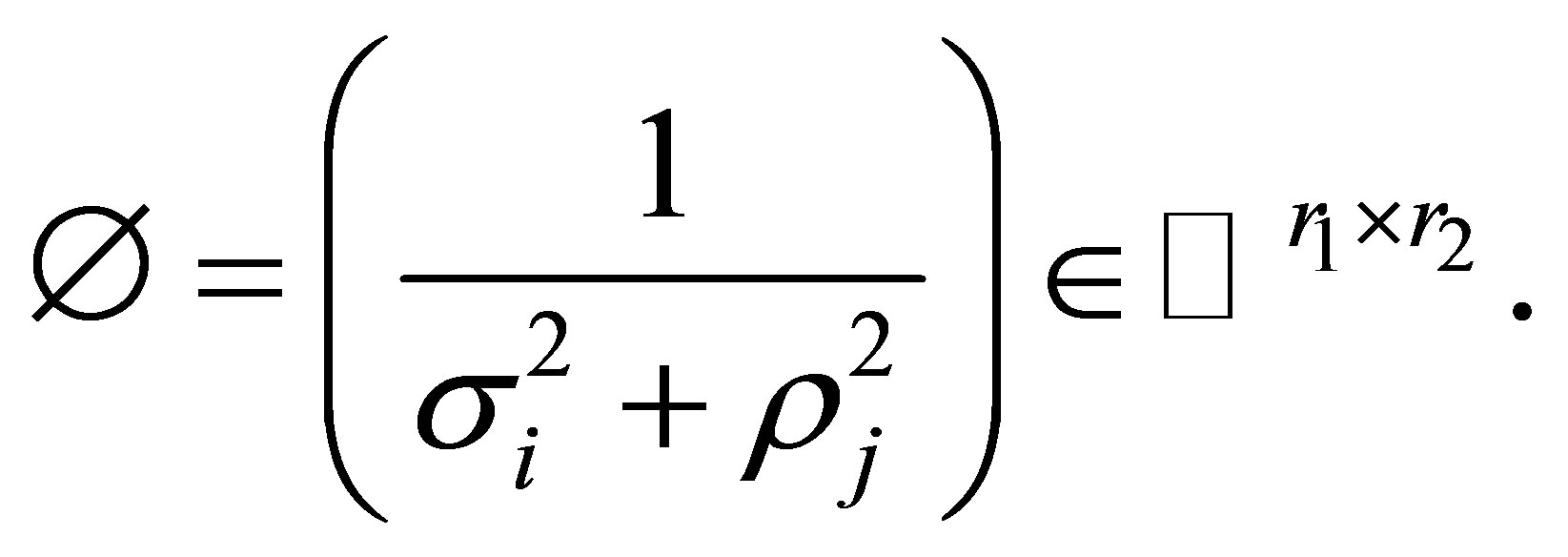 Substituting (14) and (15)
Substituting (14) and (15)
into (11), we can get the form of elements in 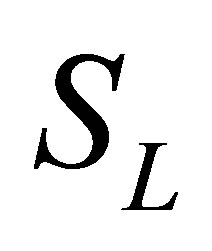 is (10).
is (10).
Theorem 4.3. Assume the notations and conditions are the same as Theorem 4.2. Then

if and only if
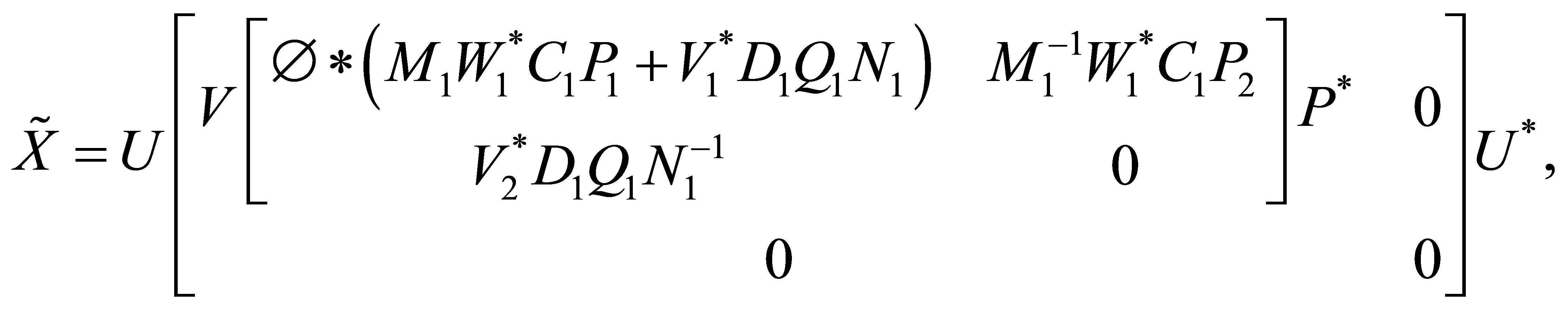 (16)
(16)
where 
Proof. In Theorem 4.2, it implies from (10) that
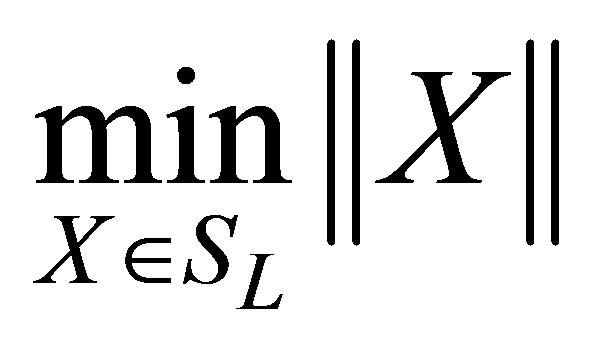 is equivalent to
is equivalent to  has the expression (10)
has the expression (10)
with 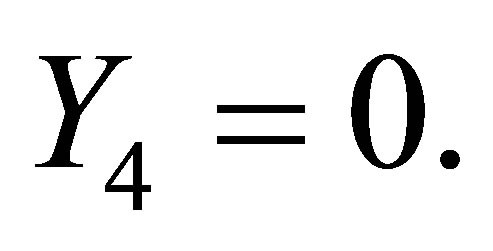 Hence (16) holds.
Hence (16) holds.
5. Acknowledgements
This research was supported by the Natural Science Foundation of Hebei province (A2012403013), the Natural Science Foundation of Hebei province (A2012205028) and the Education Department Foundation of Hebei province (Z2013110).
REFERENCES
- H. Schwerdtfeger, “Introduction to Linear Algebra and the Theory of Matrices,” P. Noordhoff, Groningen, 1950.
- M. H. Pearl, “On normal and
 matrices,” Michigan Mathematical Journal, Vol. 6, No. 1, 1959, pp. 1-5. http://dx.doi.org/10.1307/mmj/1028998132
matrices,” Michigan Mathematical Journal, Vol. 6, No. 1, 1959, pp. 1-5. http://dx.doi.org/10.1307/mmj/1028998132 - C. R. Rao and S. K. Mitra, “Generalized Inverse of Matrices and Its Applications,” Wiley, New York, 1971.
- O. M. Baksalary and G. Trenkler, “Characterizations of EP, normal, and Hermitian matrices,” Linear Multilinear Algebra, Vol. 56, 2008, pp. 299-304. http://dx.doi.org/10.1080/03081080600872616
- Y. Tian and H. X. Wang, “Characterizations of
 Matrices and Weighted-EP Matrices,” Linear Algebra Applications, Vol. 434, No. 5, 2011, pp. 1295-1318. http://dx.doi.org/10.1016/j.laa.2010.11.014
Matrices and Weighted-EP Matrices,” Linear Algebra Applications, Vol. 434, No. 5, 2011, pp. 1295-1318. http://dx.doi.org/10.1016/j.laa.2010.11.014 - K.-W. E. Chu, “Singular Symmetric Solutions of Linear Matrix Equations by Matrix Decompositions,” Linear Algebra Applications, Vol. 119, 1989, pp. 35-50. http://dx.doi.org/10.1016/0024-3795(89)90067-0
- R. D. Hill, R. G. Bates and S. R. Waters, “On Centrohermitian Matrices,” SIAM Journal on Matrix Analysis and Applications, Vol. 11, No. 1, 1990, pp. 128-133. http://dx.doi.org/10.1137/0611009
- Z. Z. Zhang, X. Y. Hu and L. Zhang, “On the HermitianGeneralized Hamiltonian Solutions of Linear Mattrix Equations,” SIAM Journal on Matrix Analysis and Applications, Vol. 27, No. 1, 2005, pp. 294-303. http://dx.doi.org/10.1137/S0895479801396725
- A. Dajić and J. J. Koliha, “Equations
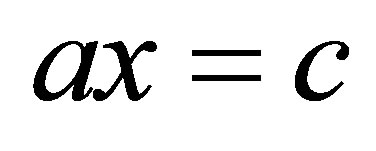 and
and 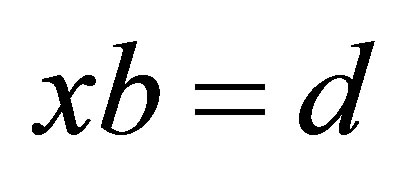 in Rings and Rings with Involution with Applications to Hilbert Space Operators,” Linear Algebra Applications, Vol. 429, No. 7, 2008, pp. 1779-1809. http://dx.doi.org/10.1016/j.laa.2008.05.012
in Rings and Rings with Involution with Applications to Hilbert Space Operators,” Linear Algebra Applications, Vol. 429, No. 7, 2008, pp. 1779-1809. http://dx.doi.org/10.1016/j.laa.2008.05.012 - C. G. Khatri and S. K. Mitra, “Hermitian and Nonnegative Definite Solutions of Linear Matrix Equations,” SIAM Journal on Matrix Analysis and Applications, Vol. 31, No. 4, 1976, pp. 579-585. http://dx.doi.org/10.1137/0131050
- F. J. H. Don, “On the Symmetric Solutions of a Linear Matrix Equation,” Linear Algebra Applications, Vol. 93, 1987, pp. 1-7. http://dx.doi.org/10.1016/S0024-3795(87)90308-9
- H. X. Chang, Q. W. Wang and G. J. Song, “(R,S)-Conjugate Solution to a Pair of Linear Matrix Equations,” Applied Mathematics and Computation, Vol. 217, 2010, pp. 73-82. http://dx.doi.org/10.1016/j.amc.2010.04.053
- E. W. Cheney, “Introduction to Approximation Theory,” McGraw-Hill Book Co., 1966.

