Computational Molecular Bioscience
Vol.2 No.3(2012), Article ID:22495,6 pages DOI:10.4236/cmb.2012.23010
A Mathematical Model for Inter-Cellular Inductive Notch Signaling
The Biocomplexity Institute, Indiana University, Bloomington, USA
Email: sjeyaram@indiana.edu
Received August 14, 2012; revised September 15, 2012; accepted September 23, 2012
Keywords: Delta-Notch Signaling; Apical Ectodermal Ridge; Compucell3D; Boundary Formation; Inductive Signaling
ABSTRACT
In vertebrate limb, a group of specialized epithelial cells called Apical Ectodermal Ridge (AER) form at the boundary of dorsal and ventral limb ectoderm. Recent experiments suggest that AER forms at the boundary of Fringe expressing and Fringe non-expressing cells by a specific type of receptor-ligand interaction called as inductive signaling, involving the transmembrane proteins Notch, Serrate and Delta. Experiments conducted on Drosophila wing disc have shown that Fringe inhibits the binding ability of Serrate ligand to Notch and enhances that of Delta to Notch. Although several of the signaling elements have been identified experimentally, it remains unclear how the inter-cellular interactions can give rise to such a boundary of specialized cells. Here we present an ordinary differential equation (ODE) model involving Delta→Notch and Serrate→Notch interactions between juxtaposed Fringe expressing and Fringe nonexpressing cells. When simulated in a compartmentalized set up, this model gives rise to high Notch levels at the boundary of Fringe expressing and Fringe non-expressing cells.
1. Introduction
Notch signaling is one of the highly conserved signaling pathways in animal kingdom and plays a vital role in determining the fate of developing tissues [1]. Notch receptor and its ligands Delta, Serrate and Lag/Jagged (DSL ligands) are transmembrane proteins that have large extracellular domains with Epidermal Growth Factor (EGF) like repeats. Notch signaling is activated when the Notch receptor of one cell binds with a Notch ligand of the neighboring cell, which is called as trans-activation. Notch activation within the same cell is termed as cisactivation. When Notch receptor accepts a ligand from the neighboring cell, a multi-step cleavage leads to the formation of an active intracellular domain called as Notch intracellular domain (NICD). NICD further activates several other transcription factors required for differentiation and other important transformations [1].
Notch signaling in developing tissues can be categorized into three types: 1) Lateral inhibition: Here equivalent cells in a population acquire different fate due to Notch signaling resulting in one cell with high Notch and the neighboring cell with low Notch forming a checker board pattern; 2) Lineage decisions: An asymmetric cell division occurs where cell progenies acquire different levels of Notch resulting in differentiated cell types, and 3) Induction: Here specialized cells are formed at the boundary of two non-equivalent cell populations that express different genes [2,3]. Inductive signaling of Notch plays a vital role in Drosophila wing disc formation and limb formation in vertebrates [4,5]. In chick embryos, at HH (Hamburger-Hamilton) [6] stage 16, an inductive signaling is believed to occur at the bending of the lateral plate mesoderm across the somites 15 - 18, to give rise to a growing limb bud. This inductive signaling gives rise to a specialized type of cells called Apical Ectodermal Ridge (AER) which secretes the morphogens belonging to the Fibroblast Growth Factor family (Figure 1). The AER runs along the anteroposterior axis of the embryo and forms at the boundary of the dorsal and ventral ectoderm. Several genes are expressed in the dorsoventral domains before the AER formation giving the ectoderm a dorsal and ventral identity. Wnt-7a gene
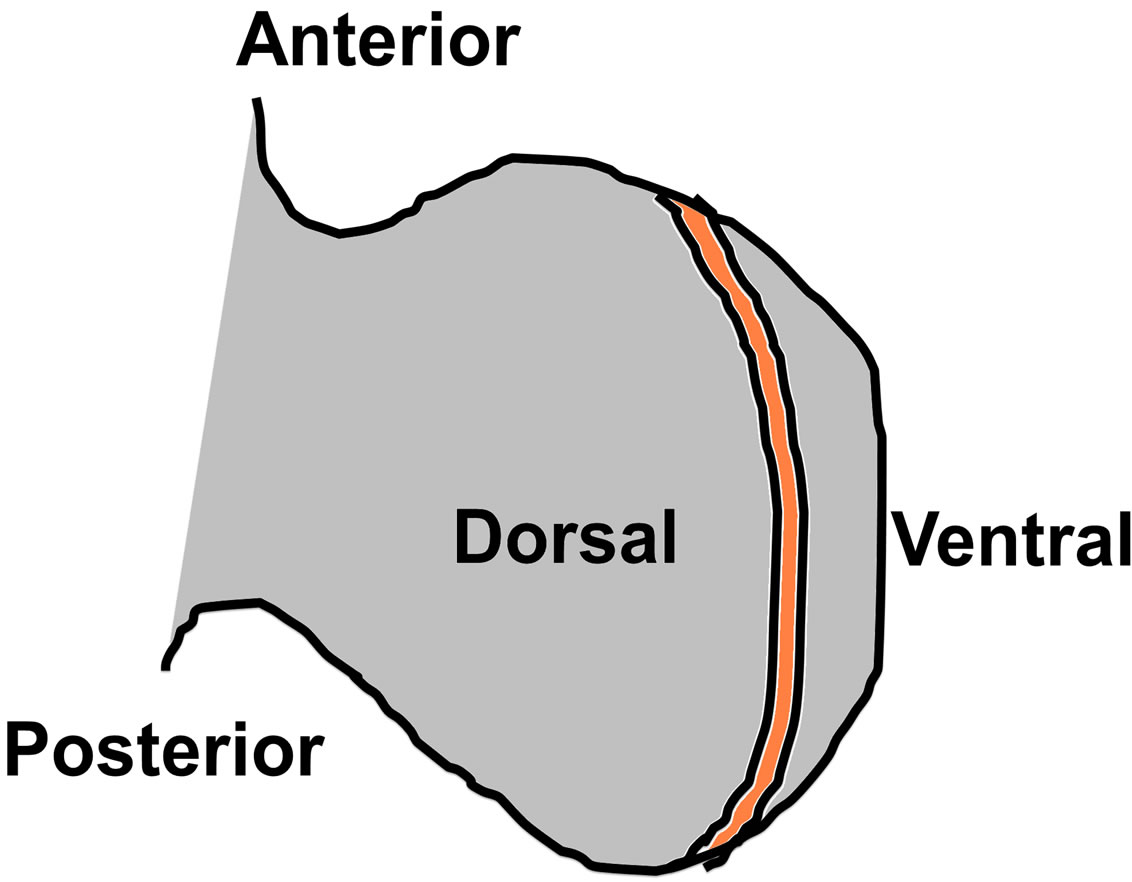
Figure 1. Illustration of limb showing the dorsal and ventral sides with AER (orange).
expressed in the dorsal ectoderm influences the dorsal fate of the ectoderm and the underlying mesenchyme [7,8]. Engrailed En-1 is expressed in the ventral ectoderm and has been shown to influence the ventral cell fate [9]. In Drosophila, the gene fng, which is expressed only in the dorsal ectoderm is believed to be directly involved in the formation of the wing boundary [10,11]. Similarly in chick, an analogous gene has been identified as Radical fng or rfng which is expressed only at the dorsal ectoderm [9,12].
Recent experimental work by Rodriguez-Esteban et al. [9] and Laufer et al. [12] in chick limb, has derived potential parallels between chick AER formation and Drosophila wing disc boundary formation. Laufer et al. [12] suggest the existence of evolutionarily conserved parallels between vertebrate AER and Drosophila wing margin. Although AER forms at the boundary of dorsal and ventral ectoderm, dorsal and ventral identity does not seem to affect its formation. Experiments on Drosophila show that the juxtaposition of Fringe expressing and nonexpressing cells seems to be necessary and sufficient for the boundary formation [13]. Several other genes like Vg (vestigial), Ap (apterous) operate upstream of Fringe in the Fringe-expressing cells [14,15]. In Fringe-nonexpressing cells, expression of Fringe is suppressed or inhibited by the gene Engrailed (En).
Although experiments in Drosophila have shed light on several elements of the signaling mechanism, a complete understanding of this inductive signaling is still unclear. One way of verifying the core signaling is through mathematical modeling involving both interand intra-cellular signaling. In this short report, we propose a mathematical model using ordinary differential equation (ODE) to describe the inductive Notch signaling leading to boundary formation. In order to couple the Notch signaling at the inter-cellular level, we use multiple compartment ODEs. Using our model we show the formation of boundary in 1D dimensional arrangement of cells which qualitatively agrees with the higher Notch levels at the AER in chick limb. We finally discuss the potential application of the model and its future extensions in into 2D and 3D spatial scales.
2. The Model
To build the model we first consider two non-equivalent cell populations of the same cell type juxtaposed in a 1D line: Fringe expressing (dorsal) (2 pink cells in Figure 2) and Fringe non-expressing (ventral) (2 blue cells in Figure 2). Each cell has its own Notch signaling network. We model Notch signaling in each cell using three variables namely, Notch (N), Serrate (S) and Delta (D). Fringe (F) is set as a constant in dorsal cells and absent in ventral cells. Although experiments have shown that the dorsal and ventral identity is not related to the presence of Fringe, in this paper, we will refer Fringe-expressing cells as dorsal and Fringe non-expressing cells as ventral respectively. For the current model, we have not considered the molecular level interaction of Notch and its ligands to form NICD since we believe that biochemistry does not matter greatly for a phenomenological representation. The model is based on the putative core mechanism as follows:
• Dorsal cells express Serrate and Notch.

Figure 2. Illustration of the molecular mechanism for Notch activation at the boundary of Fringe expressing and Fringe non-expressing cells.
• Ventral cells express Notch and Delta.
• In the dorsal cells, activation of Notch through Serrate is prevented by Fringe: Fringe modifies the Notch ligand through glycosylation and decreases Notch’s affinity to Serrate.
• In the ventral cells activation of Notch through Delta is not strong in the absence of Fringe.
• At the boundary, dorsal Serrate is able to activate the Notch in ventral cells without being inhibited by Fringe and ventral Delta is able to activate the Notch in the dorsal cells which is enhanced by Fringe.
• The resulting high Notch activity at the boundary, in turn activates the transcription of the ligands Serrate and Delta possibly forming a positive feedback loop [16].
• The positive feedback loop sustains the high Notch activity as well as the high ligand activity at the boundary.
The above mechanism is illustrated in Figure 2. The mechanism is cast into the following set of differential equations.
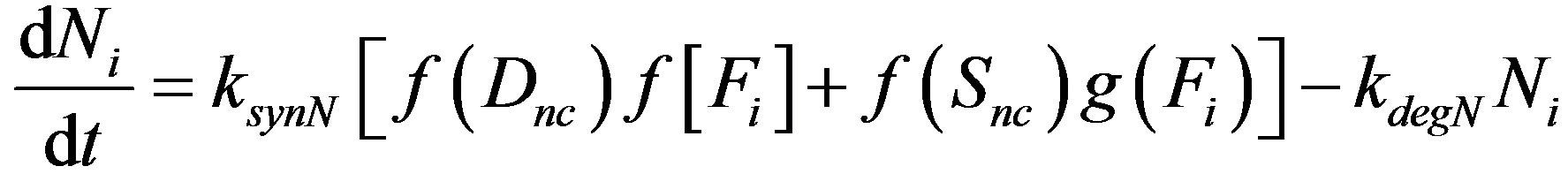 (1)
(1)
 (2)
(2)
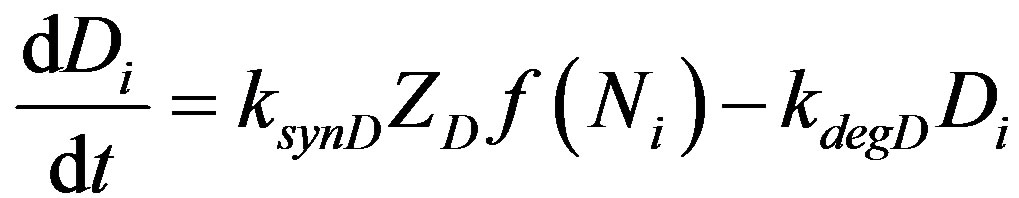 (3)
(3)

Here Ni, Di, Si and Fi represent levels of active Notch, Delta, Serrate and Fringe proteins in cell i, f and g are monotonously increasing and decreasing functions respectively. f and g vary between 0 and 1. ksyn and kdeg are synthesis rate and degradation rate constant of each of the species. Z represents the factor responsible for the differential expression of Serrate and Delta in dorsal and ventral compartments respectively. Z can be considered similar to a cofactor required for the transcription of a specific gene. There is experimental evidence for restriction of Serrate expression in dorsal compartment in drosophila, however, the expression of Delta is unclear [16]. In order to mathematically represent differential expression, we consider Zs = 1 for dorsal cells and Zs = 0 for ventral cells. There is evidence of complimentary expression of Serrate and Delta in chick neural tube [12]. Dnc indicates the activity of Delta in neighboring cells. In a 1D line of cells

and in a 2D arrangement, it is the average taken over the immediate neighbors and given as:
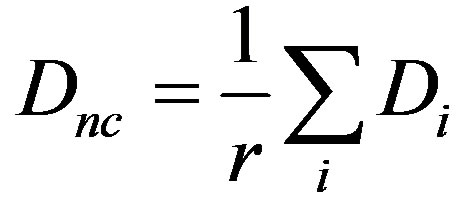
The same principle applies for Serrate also. We do not consider cell division since cell cycle times are much greater than the time scale of the inter-cellular dynamics and hence we assume it does not have an effect.
3. Results
3.1. One-Variable Model
The proposed model can be reduced to a one variable system by making the variables Serrate and Delta constants along with Fringe. We consider n cells arranged in a line in a 1D representation (Figure 3(a)). The initial value of Fringe (F) and Serrate (S) is non-zero for cells from 1 to n/2 and zero from n/2+1 trough n. Similarly the initial value of Delta (D) is zero for cells 1 to n/2 and non-zero for cells n/2+1 to n. The initial value of Notch (N) is low but non-zero throughout the cell arrangement. The boundary condition is non-periodic. The dynamics of Notch inside each cell is reduced as follows:
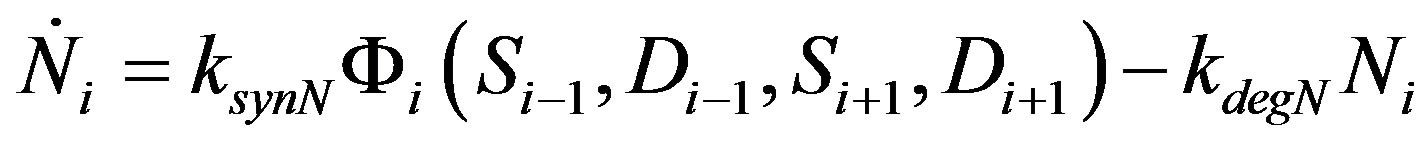 (4)
(4)
where the factor Φi represents all the terms in the parenthesis in Equation (1). Since Serrate (S) and Delta (D) are constants, the factor Φi will also be a constant depending upon the value of S and D in the neighboring cells. This results in a simple stable system with steady states Ni = 0, Ki and solution:
 (5)
(5)
Here
 (a)
(a) (b)
(b)
Figure 3. (a) Open loop of 1D arrangement of cells in a line where 1···n/2, n/2···n are two non-equivalent cell populations of same cell type; (b) Simulation of the one variable model of Notch activation. Note that the steady states depend on the value of Ki.
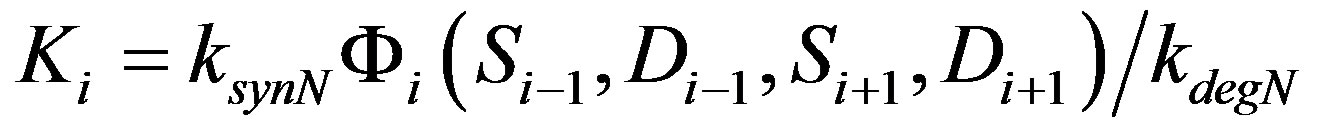
The simulation of various solution curves of N(t) is given in Figure 3(b). The steady state of N is simply Ki, which implies that the steady state level of Notch depends on the ratio of its synthesis and degradation rate. The parameter Ki depends on the Serrate and Delta activities of the neighboring cells. For each cell, the value of Φi is different. This results in a series of coupled system with different Ki s, eventually giving rise to different steady state in each of the cells. Although the dynamics of the single cell is less interesting, when coupled as a four cell system, the two cells at the boundary results in a steady state that has a higher Notch activity when compared to the cells in the either side of the line of cells. We illustrate this in the following section.
3.2. Four-Compartment ODE Model
The three-variable model given in Equations (1)-(3) is more complex as it involves the dynamics of Serrate and Delta. The most important aspect of this model is that a positive feedback is induced by the active Notch over the synthesis of the ligands Serrate and Delta. Unlike the previously known model of lateral inhibition [17] where active Notch has been shown to inhibit Delta in the same cell, in this model active Notch activates Delta and Serrate in the same cell. There is experimental support suggesting a possible positive feedback due to active Notch in Drosophila [16]. The individual dynamics of the system is simple, however when the cell interacts with its neighbors, interesting pattern emerges which is explained in the numerical simulations as follows.
In order to construct a multi-compartment ODE model, we consider the model in Equations (1)-(3) where we have 4 compartments representing four cells i = 1, 2, 3, 4. The initial conditions are set such that compartments 1 and 2 have non-zero levels of Fringe, Serrate and Notch, while compartments 3 and 4 have non-zero levels of Delta and Notch. In each compartment
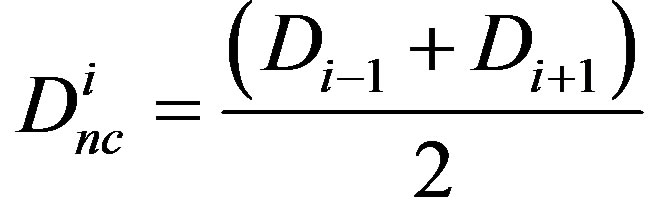
and
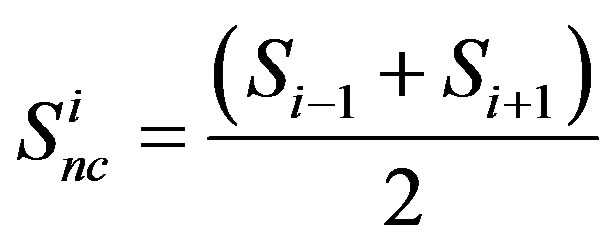
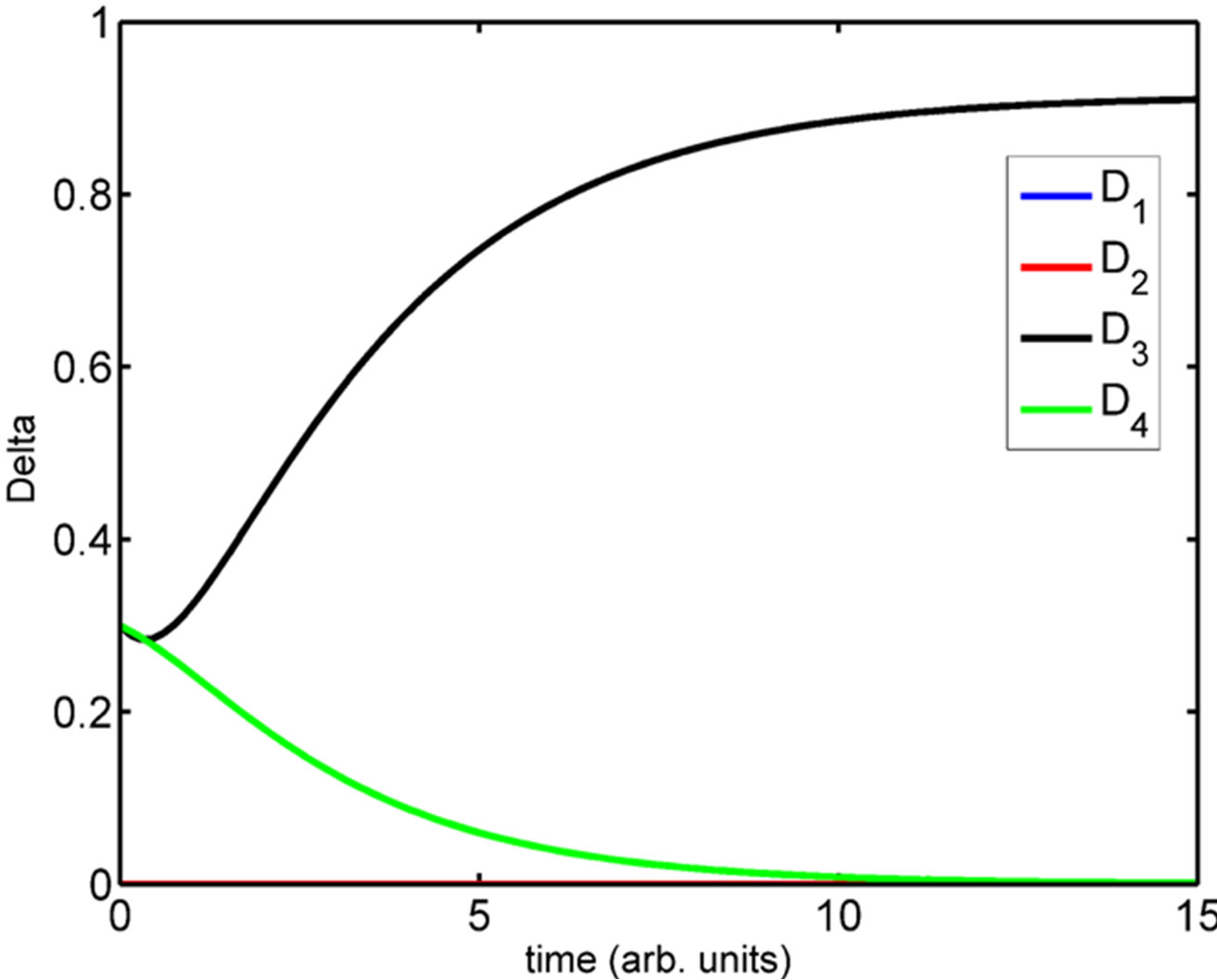
(See Figure 4). We have simulated the four compartment model using Systems Biology Workbench (SBW) [18]. The results of the simulation of the ODE are given in Figure 5. In Figure 5 we show the time evolution of the variables N1 ··· N4, S1 ··· S4, and D1 ··· D4. We can see that in Figure 5(a), the concentrations of N1 and N4 are zero where as N2 and N3 which are at the boundary, are high. Similarly the concentrations of D1, D2 and D4 are zero while D3 is high (Figure 5(c)). The concentrations of S1, S3 and S4 are zero while S2 has a non-zero high value (Figure 5(b)). The parameters of the simulation are given in Supplementary material SBW jarnac code. Since this model involves differentially expressed genes it makes analytical analysis of the large scale model extremely complex. However, as shown above the threevariable model can be reduced to one variable model whose dynamics is described in previous section. Extension of this model into spatial 2D and 3D arrangement of cells is underway.
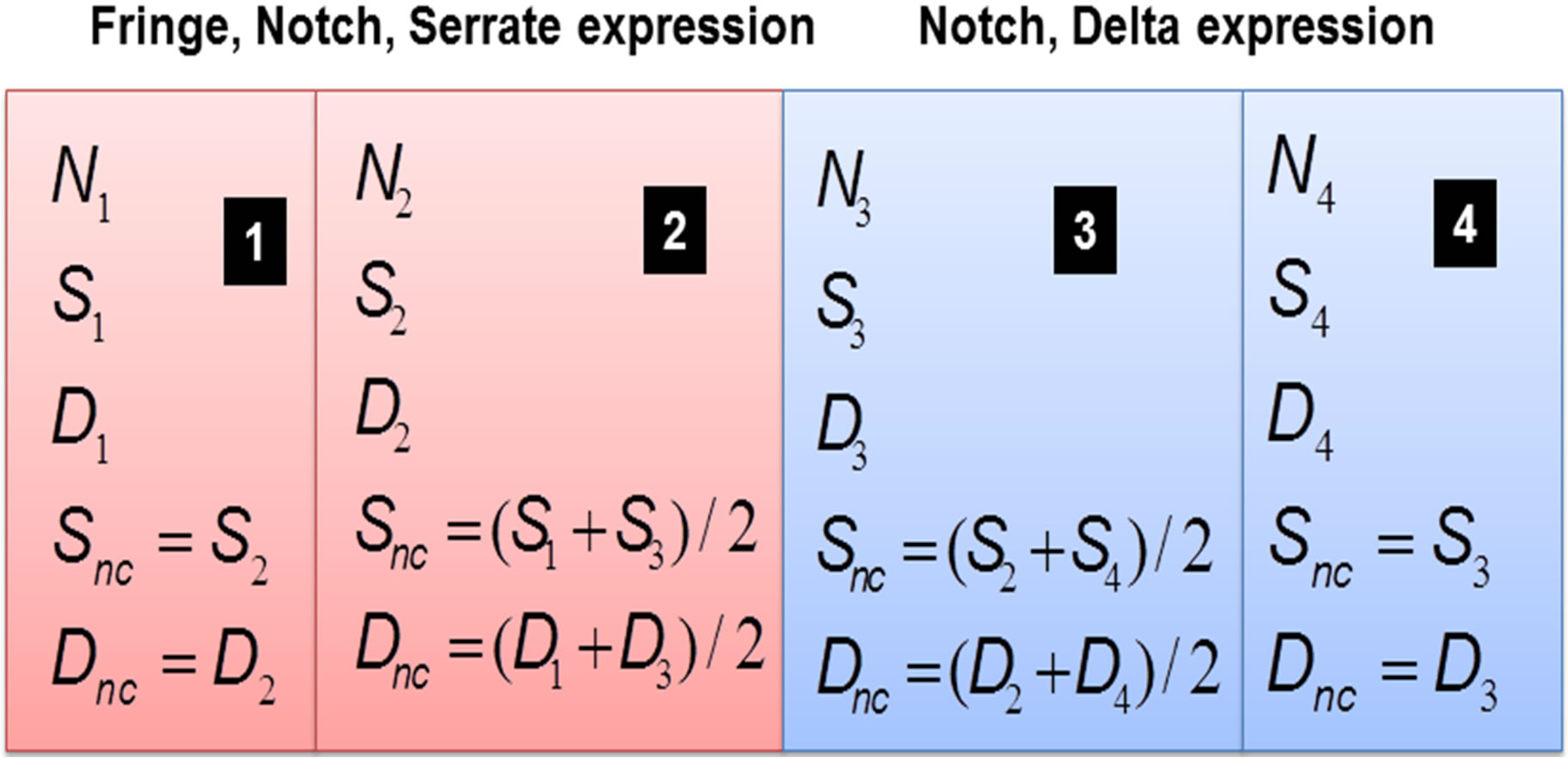
Figure 4. Four compartment ODE model set up with Notch signaling in each compartment. Dnc and Snc indicate the averaged concentrations from neighboring cells as in the ODE simulations.
 (a)
(a) (b)
(b)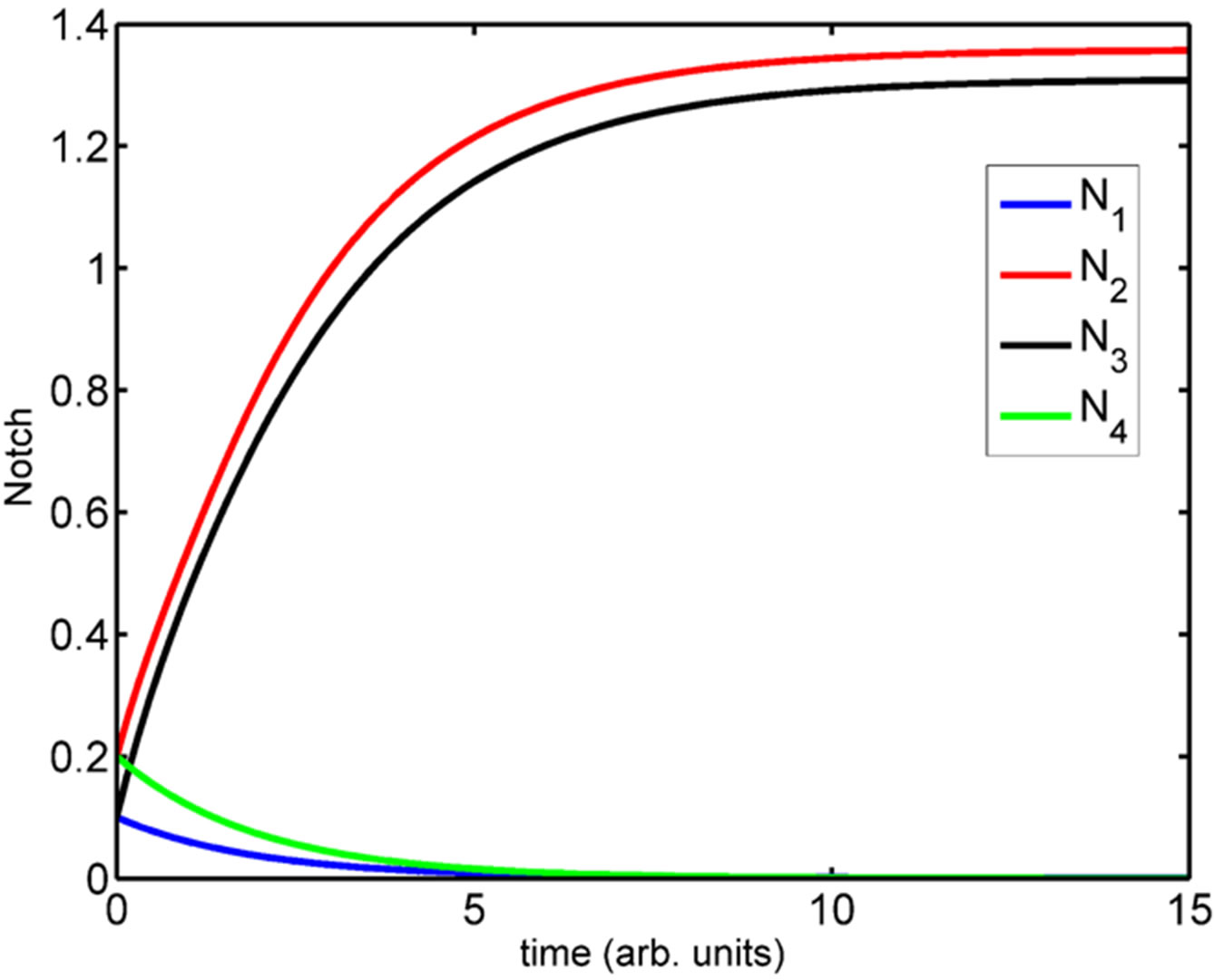 (c)
(c)
Figure 5. Simulation of the four-compartment ODE model depicting the (a) increased Notch levels in compartment 2 and 3; (b) increased Serrate levels in compartment 2 and (c) increased Delta levels in compartment 3.
4. Discussions
In the recent years, significant progress has been made in understanding both the origin and molecular nature of the signals controlling patterning of the dorsoventral limb axis and AER formation. Inductive signaling of Notch has not been well understood despite its critical role in Drosophila wing disc as well as vertebrate limb formation. In addition to this, differential expression of fng and serrate genes has been a hurdle for mathematical modeling efforts. In this short report, we propose an ODE based compartmental mathematical model to describe inductive Notch signaling involved in the boundary formation at the dorsoventral limb axis. Our model is phenomenological and hence does not involve any Notch-related biochemical reactions. This qualitative approach allows us to derive the following conclusions:
• Boundary of specialized high Notch-expressing cells is formed due to the interaction of two cell populations with differential gene expressions: In real biological systems, differential gene expression patterns are programmed in the developmental protocols and hence they need to be considered as such. To interpret this differential gene expression mathematically, we suppressed the dynamics of the relevant variable in the respective compartments. However, this approximation limits the application of global analysis of the model.
• The positive feedback loop at the boundary cells further maintains high Notch levels by activating transcription of more Serrate and Delta: In the experiments on chick limb AER formation, initially Serrate expression is observed throughout the dorsal side and then restricts only to the AER [9,12]. To simulate this observation, the model requires a positive feedback loop from Notch to Serrate and Delta formation, eventually creating a boundary which expresses high Serrate and Delta in addition to Notch. However, this result is left to be shown experimentally.
• This form of model can only account for fine-grained patterns of cell specialization: Our model explains the interactions only between one nearest neighbor. However, there may be long range interactions, which are not accounted in this model.
This is the first attempt to model inductive Notch signaling giving rise to boundary formation in developing tissues. An added advantage of this approach is that this can be extended into 2D arrangement of cells as well as into any agent based modeling approaches potentially leading to a multi-scale model. We are currently making efforts to incorporate this model in a cell-based modeling environment in a 2D and 3D spatial arrangement as well as parameter search that can show this behavior. Our model is the first to represent differential gene expression mathematically and is able to simulate the boundary formation. Our model has some limitations such as 1) absence of dynamics of Fringe and 2) absence of biochemical reactions involving Notch-Delta ligand formation. Nevertheless, this model presents a versatile framework on which further extensive models can be built.
5. Acknowledgements
We would like to acknowledge the EPA grant—The Texas-Indiana Virtual STAR Center; Data-Generating in vitro and in silico Models of Developmental Toxicity in Embryonic Stem Cells and Zebrafish.
REFERENCES
- E. R. Andersson, R. Sandberg and U. Lendahl, “Notch Signaling: Simplicity in Design, Versatility in Function,” Development, Vol. 138, No. 17, 2011, pp. 3593-3612. doi:10.1242/dev.063610
- N. Haines and K. D. Irvine, “Glycosylation Regulates Notch Signalling,” Nature Reviews Molecular Cell Biology, Vol. 4, No. 10, 2003, pp. 786-797.
- S. J. Bray, “Notch Signalling: A Simple Pathway Becomes Complex,” Nature Reviews Molecular Cell Biology, Vol. 7, No. 9, 2006, pp. 678-689. doi:10.1038/nrm2009
- S. S. Blair, “Limb development: Marginal Fringe Benefits,” Current Biology, Vol. 7, No. 11, 1997, pp. R686- R690. doi:10.1016/S0960-9822(06)00356-3
- K. D. Irvine and T. F. Vogt, “Dorsal—Ventral Signaling in Limb Development,” Current Opinion in Cell Biology, Vol. 9, No. 6, 1997, pp. 867-876. doi:10.1016/S0955-0674(97)80090-7
- V. Hamburger and H. L. Hamilton, “A Series of Normal Stages in the Development of the Chick Embryo,” Developmental Dynamics, Vol. 195, No. 4, 1992, pp. 231- 272. doi:10.1002/aja.1001950404
- B. A. Parr and A. P. McMahon, “Dorsalizing Signal Wnt-7a Required for Normal Polarity of D-V and A-P Axes of Mouse Limb,” Nature, Vol. 374, No. 6520, 1995, pp. 350- 353. doi:10.1038/374350a0
- R. D. Riddle, et al., “Induction of the LIM Homeobox Gene Lmx1 by WNT6a Establishes Dorsoventral Pattern in the Vertebrate Limb,” Cell, Vol. 83, No. 4, 1995, pp. 631-640. doi:10.1016/0092-8674(95)90103-5
- C. Rodriguez-Esteban, et al., “Radical Fringe Positions the Apical Ectodermal Ridge at the Dorsoventral Boundary of the Vertebrate Limb,” Nature, Vol. 386, No. 6623, 1997, pp. 360-366. doi:10.1038/386360a0
- T. Klein and A. M. Arias, “Interactions among Delta, Serrate and Fringe Modulate Notch Activity during Drosophila Wing Development,” Development, Vol. 125, No. 15, 1998, pp. 2951-2962.
- C. Rauskolb, T. Correia and K. D. Irvine, “Fringe-Dependent Separation of Dorsal and Ventral Cells in the Drosophila Wing,” Nature, Vol. 401, No. 6752, 1999, pp. 476-480. doi:10.1038/46786
- E. Laufer, et al., “Expression of Radical Fringe in LimbBud Ectoderm Regulates Apical Ectodermal Ridge Formation,” Nature, Vol. 386, No. 6623, 1997, pp. 366-373. doi:10.1038/386366a0
- K. D. Irvine and E. Wieschaus, “Fringe, a BoundarySpecific Signaling Molecule, Mediates Interactions between Dorsal and Ventral Cells during Drosophila Wing Development,” Cell, Vol. 79, No. 4, 1994, pp. 595-606. doi:10.1016/0092-8674(94)90545-2
- M. Milan and S. M. Cohen, “A Re-Evaluation of the Contributions of Apterous and Notch to the Dorsoventral Lineage Restriction Boundary in the Drosophila Wing,” Development, Vol. 130, No. 3, 2003, pp. 553-562. doi:10.1242/dev.00276
- S. Koelzer and T. Klein, “Regulation of Expression of Vg and Establishment of the Dorsoventral Compartment Boundary in the Wing Imaginal Disc by Suppressor of Hairless,” Developmental Biology, Vol. 289, No. 1, 2006, pp. 77-90. doi:10.1016/j.ydbio.2005.10.008
- J. F. de Celis and S. Bray, “Feed-Back Mechanisms Affecting Notch Activation at the Dorsoventral Boundary in the Drosophila Wing,” Development, Vol. 124, No. 17, 1997, pp. 3241-3251.
- J. R. Collier, et al., “Pattern Formation by Lateral Inhibition with Feedback: A Mathematical Model of DeltaNotch Intercellular Signalling,” Journal of Theoretical Biology, Vol. 183, No. 4, 1996, pp. 429-446. doi:10.1006/jtbi.1996.0233
- H. M. Sauro, et al., “Next Generation Simulation Tools: The Systems Biology Workbench and BioSPICE Integration,” OMICS: A Journal of Integrative Biology, Vol. 7, No. 4, 2003, pp. 355-372. doi:10.1089/153623103322637670
Supplementary Material

The above code is in SBW “jarnac” format. SBW can be downloaded from http://sbw.sourceforge.net/. The code is also available upon request.

