American Journal of Analytical Chemistry
Vol.05 No.15(2014), Article ID:51637,10 pages
10.4236/ajac.2014.515111
Disproportionation Reactions of HIO and NaIO in Static and Dynamic Systems
Marcin Toporek1, Anna Maria Michałowska-Kaczmarczyk2, Tadeusz Michałowski1*
1Faculty of Engineering and Chemical Technology, Technical University of Cracow, Cracow, Poland
2Department of Oncology, The University Hospital in Cracow, Cracow, Poland
Email: *michalot@o2.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 September 2014; revised 31 October 2014; accepted 14 November 2014
ABSTRACT
The paper refers to disproportionation of HIO and NaIO in aqueous media, in static and dynamic systems. The results of calculations, realized according to GATES/GEB principles, with use of an iterative computer program, are presented graphically. An example of the computer program with all physicochemical knowledge involved in the related algorithm is attached herewith.
Keywords:
Disproportionation, Generalized Approach to Electrolytic Systems, Generalized Electron Balance, HIO, NaIO

1. Introduction
Quantitative description of electrolytic redox systems is performed by means of electron, charge and concentration balances, and a complete (not contradictory) set of relations for equilibrium constants, related to the system in question. The electron balance, termed as the Generalized Electron Balance (GEB) obtained according to Approach II to GEB, stems from linear combination 2∙f(O)-f(H) of the elemental balances: f(H) for H, and f(O) for O [1] -[11] . This property was extended on non-aqueous and mixed-solvent media [1] [12] [13] , with amphiprotic co-solvents involved. The Approach II is equivalent to the Approach I to GEB, based on the “common pool” of electron-active elements in a system considered. The Approach I, considered as a “short” version of GEB, is applicable in the cases where oxidation numbers for all elements in the redox system are known beforehand [14] - [23] . In the Approach II to GEB, the electron-active and electron-non-active elements are not distinguished, as done in the Approach I. In both Approaches, the roles of oxidants and reductants are not ascribed to particular species , considered as hydrates
, considered as hydrates 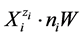 in aqueous (W = H2O) media. The GEB is the immanent part of the Generalized Approach to Electrolytic Systems (GATES); the computer software applied to redox systems is denoted as GATES/GEB [6] .
in aqueous (W = H2O) media. The GEB is the immanent part of the Generalized Approach to Electrolytic Systems (GATES); the computer software applied to redox systems is denoted as GATES/GEB [6] .
Some elements form compounds and species at three or more oxidation degrees. In particular, iodine forms the species on six oxidation degrees 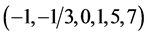 of this element. There are possible transitions between different species, associated with change of the oxidation state of the element; the relationship between concentrations of these species is determined by means of the corresponding standard potential value. The relations of another kind are expressed, inter alia, by the dissociation constants, ionic product of water, stability constants of complexes, solubility products, and other equilibrium constants. The possibility of these transitions is determined by the kinetics of the relevant reactions [3] ; these transitions are defined as the paths of the appropriate chemical reactions [7] . The occurrence of the relevant reaction is possible after crossing the corresponding energy barriers (involved with activation energy), which are associated with the delivery of a sufficient energy to the system, to allow the transition in this system. At shortage of this energy, the system is in a metastable state [6] . When applying the thermodynamic approach, we do not consider the time needed for these reactions to proceed; in this case, the quasi-static course of the process is assumed.
of this element. There are possible transitions between different species, associated with change of the oxidation state of the element; the relationship between concentrations of these species is determined by means of the corresponding standard potential value. The relations of another kind are expressed, inter alia, by the dissociation constants, ionic product of water, stability constants of complexes, solubility products, and other equilibrium constants. The possibility of these transitions is determined by the kinetics of the relevant reactions [3] ; these transitions are defined as the paths of the appropriate chemical reactions [7] . The occurrence of the relevant reaction is possible after crossing the corresponding energy barriers (involved with activation energy), which are associated with the delivery of a sufficient energy to the system, to allow the transition in this system. At shortage of this energy, the system is in a metastable state [6] . When applying the thermodynamic approach, we do not consider the time needed for these reactions to proceed; in this case, the quasi-static course of the process is assumed.
From the preliminary, laconic information [24] - [26] one can state that HIO rapidly decomposes by disproportionation 5HIO = HIO3 + 2I2 + 2H2O (in the original notation applied there) and its salts rapidly disproportionate to form iodides and iodates. This information will be verified on the basis of the results of calculations, presented graphically on the corresponding speciation diagrams.
Information about kinetics of HIO disproportionation was presented in [27] - [30] .
In the present paper, we refer to disproportionation of hypoiodous acid, HIO, and its salt NaIO; oxidation degree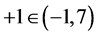 . The calculations are made according to iterative computer program, with the algorithm prepared according to GATES/GEB principles and presented in Appendix. The algorithm contains all the equilibrium constants taken from [31] and referring to forms of iodine and chlorine, used in the calculations related to system, where NaIO is titrated with HCl; in this system, iodine and chlorine are considered as “players” (when perceived from the viewpoint of the Approach I to GEB).
. The calculations are made according to iterative computer program, with the algorithm prepared according to GATES/GEB principles and presented in Appendix. The algorithm contains all the equilibrium constants taken from [31] and referring to forms of iodine and chlorine, used in the calculations related to system, where NaIO is titrated with HCl; in this system, iodine and chlorine are considered as “players” (when perceived from the viewpoint of the Approach I to GEB).
2. Disproportionation in Static Systems
The static systems with C solutions of (1) HIO and (2) NaIO are shown graphically in Figures 1(a)-(c) and Figures 2(a)-(c) with the values pC = −logC on the abscissa. The static system indicate pH, E and 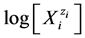 values related to different concentrations C of the corresponding solutes. The relevant graphs can also be applied to the solutions obtained by gradual dilution of 0.1 mol/L (1) HIO, (2) NaIO and (3) equimolar solution of HIO + NaIO with use of pure water.
values related to different concentrations C of the corresponding solutes. The relevant graphs can also be applied to the solutions obtained by gradual dilution of 0.1 mol/L (1) HIO, (2) NaIO and (3) equimolar solution of HIO + NaIO with use of pure water.
2.1. C mol/L HIO
As results from speciation diagram in Figure 1(a), in more concentrated HIO solutions, i.e., at lower pC values, the predominating reactions are as follows:
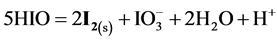 (1)
(1)
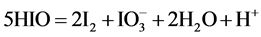 (2)
(2)

with further dilution of HIO solution, reaction (2b) is accompanied, in an increasing degree, by the reaction
 (3)
(3)
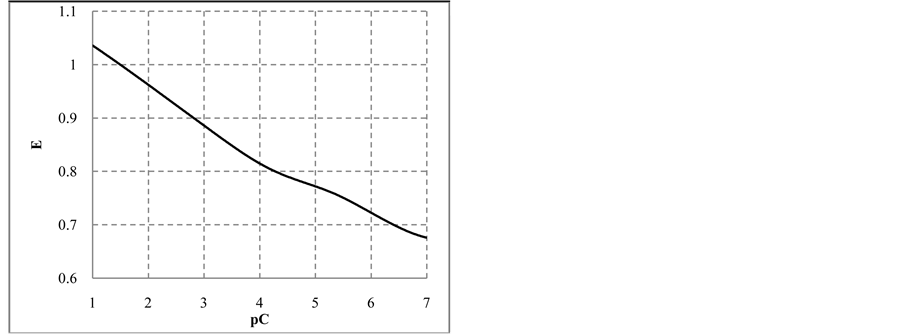
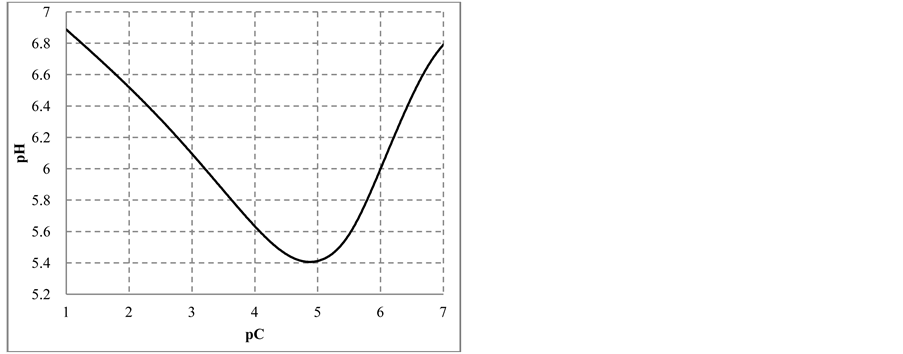
The change in disproportionation scheme, more significant at pC 4 - 5, resulted in a change of the shapes of the plots: E = E(pC) (Figure 1(b)) and pH = pH(pC) (Figure 1(c)).
2.2. C mol/L NaIO
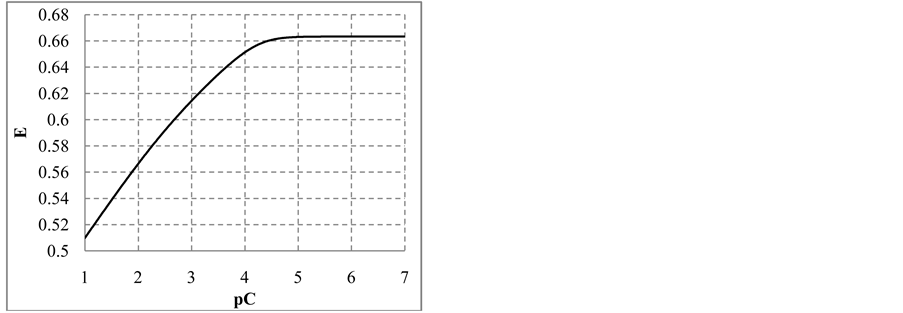
For different pC values, the disproportionation in C mol/L NaIO proceeds there mainly according to the scheme (see Figure 2(a))

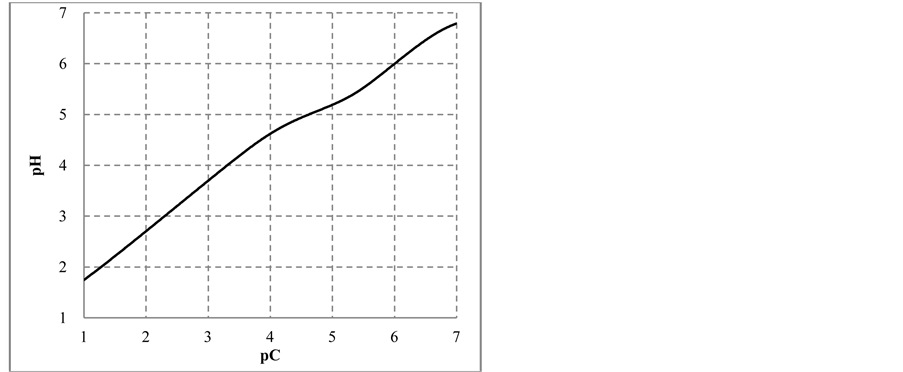
Figure 1. The plots of (a) speciation curves for indicated iodine species 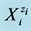 and (b) E vs. pC, (c) pH vs. pC relationships in C mol/L HIO.
and (b) E vs. pC, (c) pH vs. pC relationships in C mol/L HIO.
 (4)
(4)
where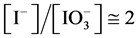 . The plots: E = E(pC) and pH = pH(pC) are presented in Figure 2(b) and Figure 2(c), respectively.
. The plots: E = E(pC) and pH = pH(pC) are presented in Figure 2(b) and Figure 2(c), respectively.
2.3. Mixture HIO (C mol/L) + NaIO (C mol/L)
During the dilution of equimolar mixture of HIO (C = 0.1 mol/L) + NaIO (C = 0.1 mol/L) with water, in the range of higher C (i.e., lower pC) values we have the disproportionation reactions:
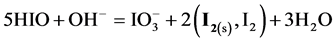 (5)
(5)
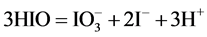
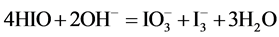
occurring there predominantly, in a comparable degree. Reactions involving IO− occur in a much lesser extent. At pC > 2.40, 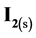
The curve E = E(pC) passes through a maximum (Figure 3(b)), while the curve pH = pH(pC) passes through

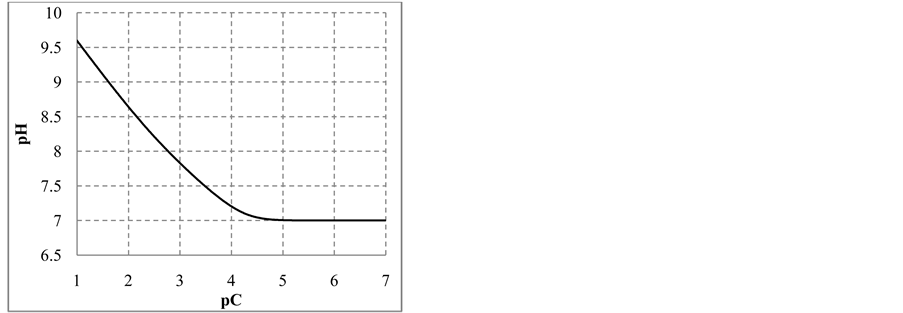
Figure 2. The speciation curves (a) for indicated iodine species 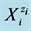
a minimum (Figure 3(c)). This is due to the fact that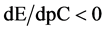
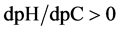

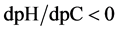
3. Disproportionation in Dynamic Systems
In dynamic systems, the related curves will be plotted on graphs with the fraction titrated
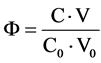
related to addition of V mL of titrant T (C mol/L B) into V0 mL of titrand D (C0 mol/L A); A, B―reagents.
3.1. Titration of HIO (C0, V0) with NaOH (C, V)
The curves plotted at V0 = 10 mL, C0 = 0.01 mol/L and C = 0.1 mol/L, are presented in Figures 4(a)-(c).
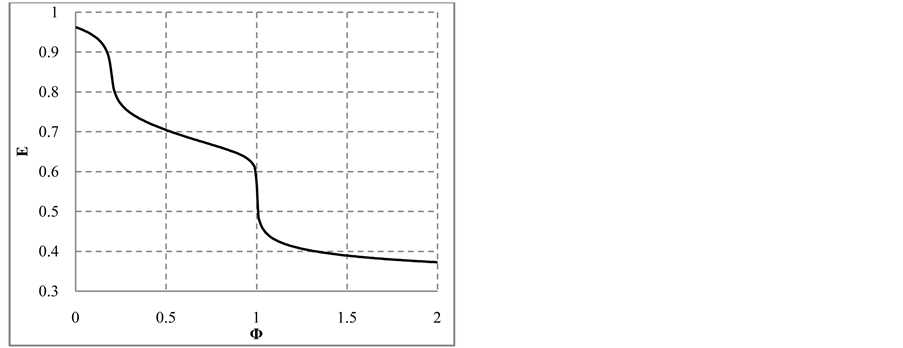
At the initial part of the titration we have the reactions:
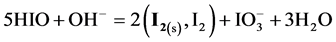
In the following, at Φ ca. 0.20 - 0.22, a pronounced increase in [I−] occurs, as a result of reaction
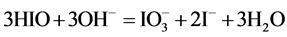
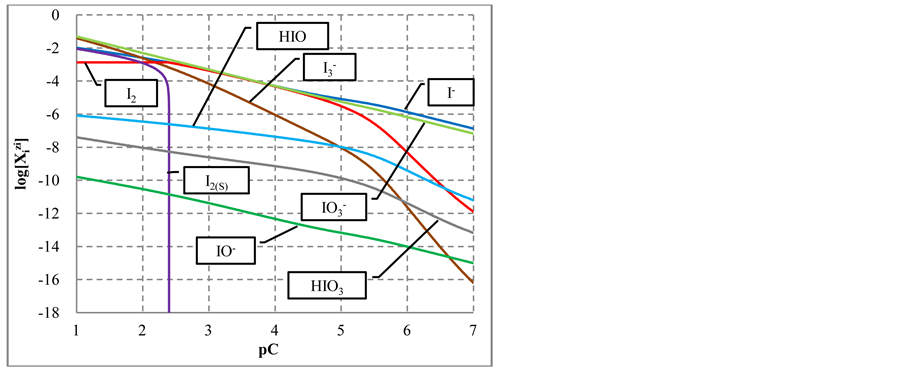
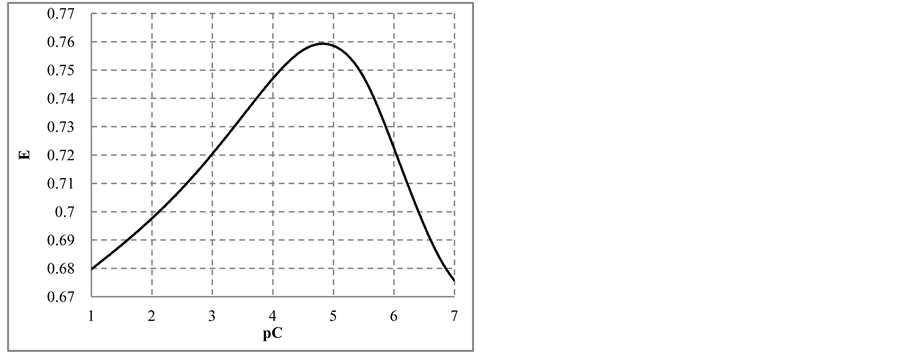
Figure 3. The speciation curves (a) for indicated iodine species 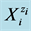
The increase in [I−] is accompanied by an increase in
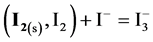
This leads to the gradual disappearance of 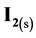

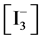
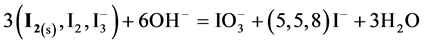
At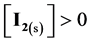
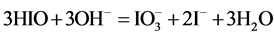
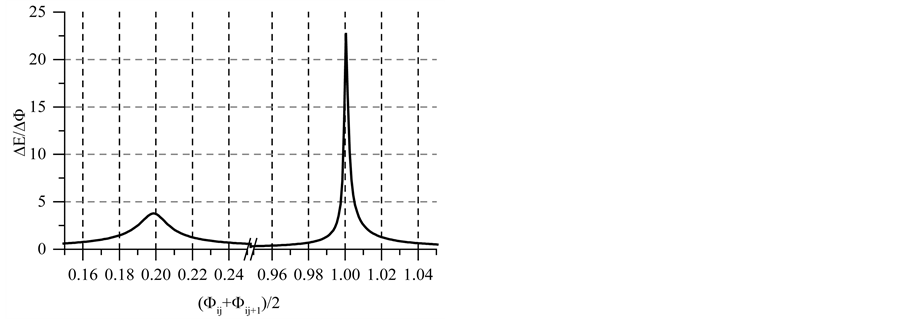
Note that the stoichiometry of the reaction (13) is 3:3 = 1:1, which corresponds to the jump on the curves (4b) and (4c), occuring at Φ = 1. For Φ > 1, we have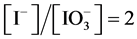
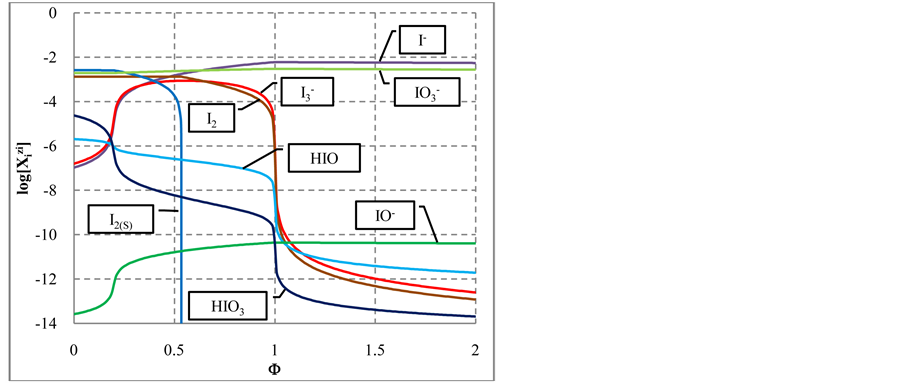
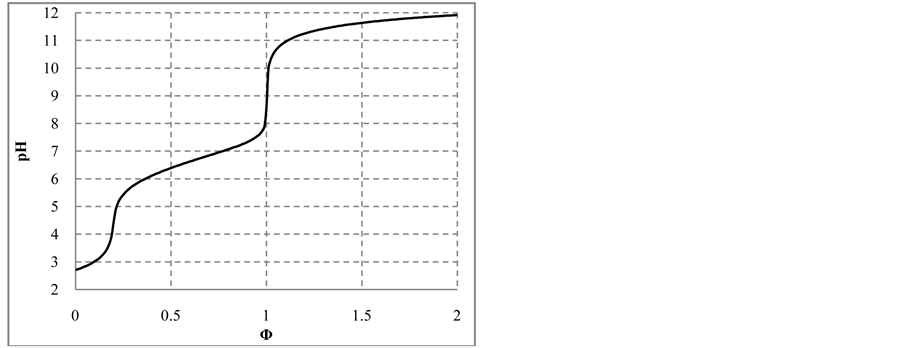
Figure 4. The speciation curves (a) for indicated iodine species 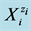

Figure 5. The (a)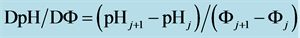
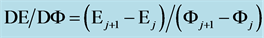

3.2. Titration of NaIO (C0, V0) with HCl (C, V)
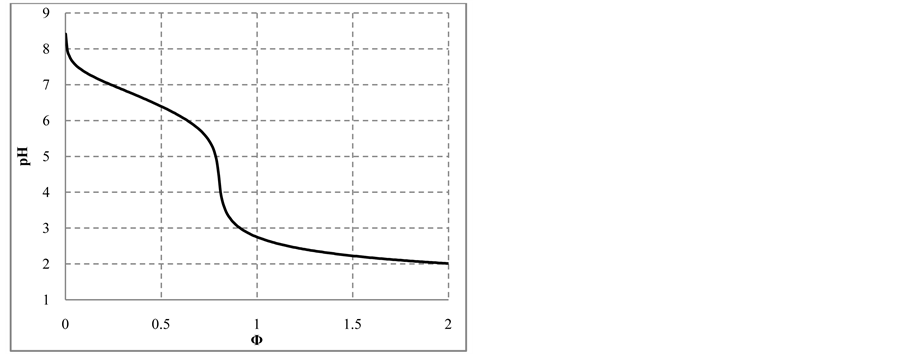
The curves plotted at V0 = 10 mL, C0 = 0.01 mol/L NaIO and C = 0.1 mol/L HCl are presented in Figures 6(a)- (d). Initially, the reaction
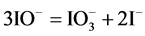
and then the reaction
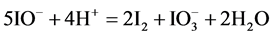
occur. Then I− from (14) and I2 from (15) form 

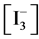
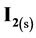
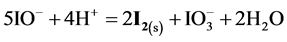
At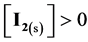
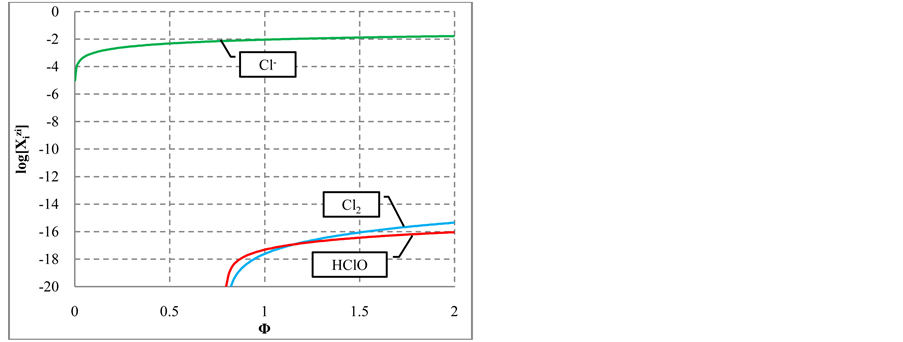
increase in [I2Cl−], and—to a lesser extent—the increases in 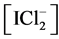
In the algorithm (see Appendix), we have allowed the participation of Cl− ions from HCl solution in the redox reaction. However, the concentration of Cl2 and HClO as the main products of Cl− oxidation (Figure 6(b)) is
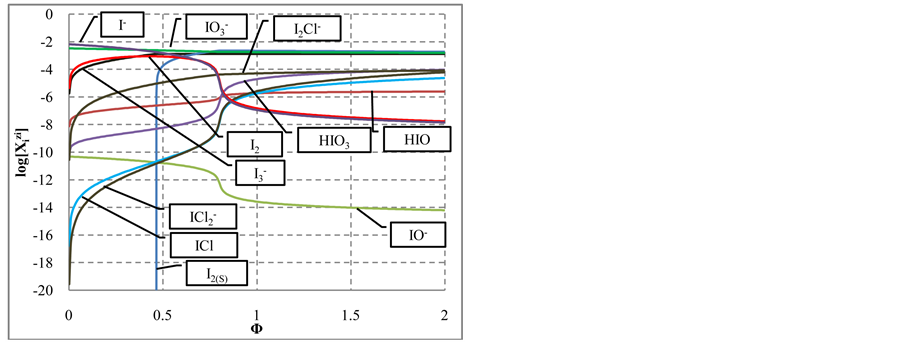
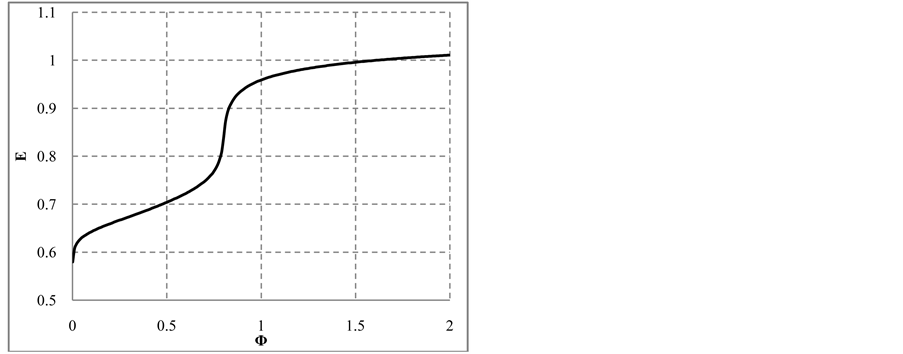
Figure 6. The speciation curves for indicated (a) iodine and (b) chlorine species 
quite negligible. This way, one can state that the Cl− ions practically do not participate the redox reaction as a reducing agent. From linear combination of reactions: (14) and
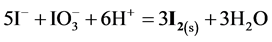
(multiplication by 5 and 2 resp.), cancellations and division by 3, we get the reaction
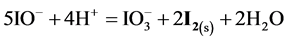
with stoichiometry 4:5 = 0.8, which corresponds to Φ = 4/5 = 0.8, where the inflection point on the curves in Figure 6(c) and Figure 6(d) are observed. The 
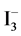
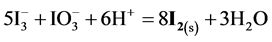
see Figure 6(a).
4. Final Remarks
The disproportionation reactions in the static and dynamic systems with (a) HIO, (b) NaIO, (c) HIO + NaIO were considered. The static systems were equivalent, in principle, with dynamic systems where the related titrand was diluted with pure water. In the dynamic system where NaIO solution was titrated with HCl, chlorine (Cl) was considered as a second “player”, i.e., possibility of oxidation of Cl−-ions was admitted/pre-assumed. However, as stated on the basis of results of calculations, the concentrations of Cl2 and HClO as the main products of Cl oxidation are extremely low. On this basis, it can be considered that the IO− introduced into the system as NaIO, undergoes disproportionation (not a reduction) reaction. All these calculations were made under assumption that the relevant reactions take place in quasi-static manner, under isothermal conditions. The reactions proceeding in the respective systems were formulated under assumption that all equilibrium constants found in the relevant tables (see Appendix) and then used in the calculations are correct.
References
- Michałowska-Kaczmarczyk, A.M. and Michałowski, T. (2014) Compact Formulation of Redox Systems According to GATES/GEB Principles. Journal of Analytical Sciences, Methods and Instrumentation, 4, 39-45.
- Michałowski, T., Toporek, M., Michałowska-Kaczmarczyk, A.M. and Asuero, A.G. (2013) New Trends in Studies on Electrolytic Redox Systems. Electrochimica Acta, 109, 519-531. http://dx.doi.org/10.1016/j.electacta.2013.07.125
- Michałowski, T., Michałowska-Kaczmarczyk, A.M. and Toporek, M. (2013) Formulation of General Criterion Distinguishing between Non-Redox and Redox Systems. Electrochimica Acta, 112, 199-211. http://dx.doi.org/10.1016/j.electacta.2013.08.153
- Michałowska-Kaczmarczyk, A.M. and Michałowski, T. (2013) Comparative Balancing of Non-Redox and Redox Electrolytic Systems and Its Consequences. American Journal of Analytical Chemistry, 4, 46-53. http://dx.doi.org/10.4236/ajac.2013.410A1006
- Michałowski, T., Ponikvar-Svet, M., Asuero, A.G. and Kupiec, K. (2012) Thermodynamic and Kinetic Effects Involved with pH Titration of As(III) with Iodine in a Buffered Malonate System. Journal of Solution Chemistry, 41, 436-446. http://dx.doi.org/10.1007/s10953-012-9815-6
- Michałowski, T. (2011) Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non-Equilibrium Electrolytic Systems, Chapter 1. In: Michałowski, T., Ed., Applications of MATLAB in Science and Engineering, InTech, Rijeka, 1-34. http://www.intechopen.com/books/show/title/applications-of-matlab-in-science-and-engineering.
- Michałowski, T. (2010) The Generalized Approach to Electrolytic Systems: I. Physicochemical and Analytical Implications. Critical Reviews in Analytical Chemistry, 40, 2-16. http://dx.doi.org/10.1080/10408340903001292
- Michałowski, T., Pietrzyk, A., Ponikvar-Svet, M. and Rymanowski, M. (2010) The Generalized Approach to Electrolytic Systems: II. The Generalized Equivalent Mass (GEM) Concept. Critical Reviews in Analytical Chemistry, 40, 17-29. http://dx.doi.org/10.1080/10408340903001342
- Michałowska-Kaczmarczyk, A.M., Asuero, A.G., Michałowski, T. and Toporek, M. “Why Not Stoichiometry” versus “Stoichiometry—Why Not?” Part I. General Context. Critical Reviews in Analytical Chemistry. (In Print)
- Michałowska-Kaczmarczyk, A.M., Asuero, A.G., Toporek, M. and Michałowski, T. “Why Not Stoichiometry” versus “Stoichiometry—Why Not?” Part II. GATES in Context with Redox Systems. Critical Reviews in Analytical Chemistry. (In Print)
- Michałowska-Kaczmarczyk, A.M., Michałowski, T., Toporek, M. and Asuero, A.G. (2014) “Why Not Stoichiometry” versus “Stoichiometry—Why Not?” Part III, Extension of GATES/GEB on Complex Dynamic Redox Systems. Critical Reviews in Analytical Chemistry. (In Print)
- Michałowski, T., Pilarski, B., Asuero, A.G. and Michałowska-Kaczmarczyk, A.M. (2014) Chapter 9.4: Modeling of Acid-Base Properties in Binary-Solvent Systems. In: Wypych, G., Ed., Handbook of Solvents, Volume 1, Chem-Tec Publishing, Toronto, 623-648.
- Michałowska-Kaczmarczyk, A.M. and Michałowski, T. (2014) Generalized Electron Balance for Dynamic Redox Systems in Mixed-Solvent Media. Journal of Analytical Sciences, Methods and Instrumentation. (In Print)
- Michałowski, T., Kupiec, K. and Rymanowski, M. (2008) Numerical Analysis of the Gran Methods: A Comparative Study. Analytica Chimica Acta, 606, 172-183. http://dx.doi.org/10.1016/j.aca.2007.11.020
- Ponikvar, M., Michałowski, T., Kupiec, K., Wybraniec, S. and Rymanowski, M. (2008) Experimental Verification of the Modified Gran Methods Applicable to Redox Systems. Analytica Chimica Acta, 628, 181-189. http://dx.doi.org/10.1016/j.aca.2008.09.012
- Michałowski, T. (2007) Complementarity of Physical and Chemical Laws of Preservation in Aspect of Electrolytic Systems (in Polish). Wiadomości Chemiczne (Chemical News), 61, 625-640.
- Michałowski, T., Rymanowski, M. and Pietrzyk, A. (2005) Non-Typical Brönsted’s Acids and Bases. Journal of Chemical Education, 82, 470-472. http://dx.doi.org/10.1021/ed082p470
- Michałowski, T., Toporek, M. and Rymanowski, M. (2005) Overview on the Gran and Other Linearization Methods Applied in Titrimetric Analyses. Talanta, 65, 1241-1253. http://dx.doi.org/10.1016/j.talanta.2004.08.053
- Michałowski, T., Baterowicz, A., Madej, A. and Kochana, J. (2001) An Extended Gran Method and Its Applicability for Simultaneous Determination of Fe(II) and Fe(III). Analytica Chimica Acta, 442, 287-293. http://dx.doi.org/10.1016/S0003-2670(01)01172-2
- Michałowski, T. (2001) Calculations in Analytical Chemistry with Elements of Computer Programming (in Polish) PK, Cracow. http://suw.biblos.pk.edu.pl/resourceDetails&rId=3974 http://www.chemia.uj.edu.pl/~ictchem/book.html
- Michalowski, T. (1994) Calculation of pH and Potential E for Bromine Aqueous Solutions. Journal of Chemical Education, 71, 560-562. http://dx.doi.org/10.1021/ed071p560
- Michałowski, T. and Lesiak, A. (1994) Acid-Base Titration Curves in Disproportionating Redox Systems. Journal of Chemical Education, 71, 632-636. http://dx.doi.org/10.1021/ed071p632
- Michałowski, T. and Lesiak, A. (1994) Formulation of Generalized Equations for Redox Titration Curves. Chemia Analityczna (Warsaw), 39, 623-637.
- Hypoiodous Acid. http://en.wikipedia.org/wiki/Hypoiodous_acid
- Wiberg, E. and Wiberg, N., Eds. (2001) Holleman-Wiberg’s Inorganic Chemistry. Academic Press, Waltham, 451.
- Glukhovtsev, M.N., Pross, A. and Radom, L. (1996) Acidities, Proton Affinities and Other Thermochemical Properties of Hypohalous Acids HOX (X = F − I): A High-Level Computational Study. Journal of Physical Chemistry, 100, 3498- 3503. http://dx.doi.org/10.1021/jp952561w
- Urbansky, E.T., Cooper, B.T. and Margerum, D.W. (1997) Disproportionation Kinetics of Hypoiodous Acid as Catalyzed and Suppressed by Acetic Acid-Acetate Buffer. Inorganic Chemistry, 36, 1338-1344. http://dx.doi.org/10.1021/ic960745z
- Bichsel, Y. and Von Gunten, U. (2000) Hypoiodous Acid: Kinetics of the Buffer-Catalyzed Disproportionation. Water Research, 34, 3197-3203. http://dx.doi.org/10.1016/S0043-1354(00)00077-4
- Truesdale, V.W., Canosa-Mas, C. and Luther, G.W. (1994) Kinetics of Disproportionation of Hypoiodous Acid. Journal of the Chemical Society, Faraday Transactions, 90, 3639-3643. http://dx.doi.org/10.1039/ft9949003639
- Truesdale, V.W. (1997) Kinetics of Disproportionation of Hypoiodous Acid at High pH, with an Extrapolation to Rainwater. Journal of the Chemical Society, Faraday Transactions, 93, 1909-1914. http://dx.doi.org/10.1039/a700226b
- Lurie, J. (1975) Handbook of Analytical Chemistry. Mir Publishers, Moscow.
Appendix
NOTES
*Corresponding author.