American Journal of Analytical Chemistry
Vol.05 No.07(2014), Article ID:46292,11 pages
10.4236/ajac.2014.57052
An Electrochemical Understanding of Extraction of Silver Picrate by Benzo-3m-Crown-m Ethers (m = 5, 6) into 1,2-Dichloroethane and Dichloromethane
Yoshihiro Kudo, Marina Ogihara, Shoichi Katsuta, Yasuyuki Takeda
Graduate School of Science, Chiba University, Chiba, Japan
Email: iakudo@faculty.chiba-u.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2014; revised 14 May 2014; accepted 22 May 2014
ABSTRACT
Two extraction constants (Kex± and Kex) for extraction of silver picrate (Ag+Pic-) by benzo-15- crown-5 ether (B15C5) and benzo-18-crown-6 one (B18C6) into 1,2-dichloroethane (DCE) and dichloromethane (DCM) were determined at 298 K and given values of ionic strength. Here, Kex± and Kex were expressed as [AgL+]o[Pic-]o/[Ag+][L]o[Pic-] and [AgLPic]o/[Ag+][L]o[Pic-], respectively: L symbolizes B15C5 or B18C6 and the subscript “o” denotes the organic phase composed of DCE or DCM. Individual distribution constants (KD,Pic) of picrate ion, Pic-, into the two diluents were also determined with the determination of Kex. From comparison of these KD,Pic values with those standardized, interfacial potential differences (Dfeq) at extraction equilibria were evaluated. Then, using these Dfeq values, relations of the experimentally-determined logKex± or logKex values with their electrochemically-standardized ones were precisely discussed. Consequently, it was indicated that logKex± should be expressed as a function of Dfeq.
Keywords:
Individual Distribution Constants, Interfacial Potential Differences, Standardized Extraction Constants, Silver Picrate, Benzo Crown Ethers, Dihaloalkanes

1. Introduction
Recently, individual distribution constants (KD,A) of single anions (A-), such as picrate ion (Pic-) and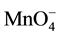 , into various diluents or organic (o) phases have been determined in course of determination of extraction constants (Kex) for the extraction of some salts, MIA and MIIA2, by crown compounds (L) [1] -[4] . Here, KD,A and Kex have been defined as [A-]o/[A-] and [MLAz]o/[Mz+][L]o[A-]z with z = 1 or 2, respectively. For example, the logKD,Pic values were reported to be -2.91 for a benzene (Bz) system, -1.89 for 1,2-dichloroethane (DCE), and -0.94 for nitrobenzene (NB) by PbPic2 extraction experiments with 18-crown-6 ether (18C6) [3] . Also, the values were -6.12 for Bz and -4.35 for DCE from CdPic2 extraction experiments with 18C6 [2] . The logKD,A values were -0.65 for A- = Pic- and -2.137 for
, into various diluents or organic (o) phases have been determined in course of determination of extraction constants (Kex) for the extraction of some salts, MIA and MIIA2, by crown compounds (L) [1] -[4] . Here, KD,A and Kex have been defined as [A-]o/[A-] and [MLAz]o/[Mz+][L]o[A-]z with z = 1 or 2, respectively. For example, the logKD,Pic values were reported to be -2.91 for a benzene (Bz) system, -1.89 for 1,2-dichloroethane (DCE), and -0.94 for nitrobenzene (NB) by PbPic2 extraction experiments with 18-crown-6 ether (18C6) [3] . Also, the values were -6.12 for Bz and -4.35 for DCE from CdPic2 extraction experiments with 18C6 [2] . The logKD,A values were -0.65 for A- = Pic- and -2.137 for 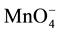 in the CsA extraction by dibenzo-24-crown-8 ether derivatives into DCE [4] . Such differences in logKD,Pic between these extraction experiments may be due to those between experimental conditions, such as kinds of the metal ion, Mz+, and L employed, the values of ionic strength (I) of the aqueous solutions and their pH values. Furthermore, the experimental logKD,Pic values have been different from the values [5] - [8] standardized by electrochemical measurements at the water (w)/DCE and w/NB interfaces. These differences seemed to be beyond the range of experimental errors. The electrochemically standardized values, which should be compared to the above logKD,Pic ones, were
in the CsA extraction by dibenzo-24-crown-8 ether derivatives into DCE [4] . Such differences in logKD,Pic between these extraction experiments may be due to those between experimental conditions, such as kinds of the metal ion, Mz+, and L employed, the values of ionic strength (I) of the aqueous solutions and their pH values. Furthermore, the experimental logKD,Pic values have been different from the values [5] - [8] standardized by electrochemical measurements at the water (w)/DCE and w/NB interfaces. These differences seemed to be beyond the range of experimental errors. The electrochemically standardized values, which should be compared to the above logKD,Pic ones, were  = -1.011 [6] for the distribution into DCE and +0.05 for that into NB [6] . Similar results have been observed in NaMnO4 extraction experiments with Benzo-15-crown-5 ether (B15C5) and benzo-18C6 (B18C6) into DCE and NB [1] ; as examples, the
= -1.011 [6] for the distribution into DCE and +0.05 for that into NB [6] . Similar results have been observed in NaMnO4 extraction experiments with Benzo-15-crown-5 ether (B15C5) and benzo-18C6 (B18C6) into DCE and NB [1] ; as examples, the 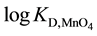 values were -3.3 for the extraction system with B15C5 and -2.5 for that with B18C6 into DCE [1] , while
values were -3.3 for the extraction system with B15C5 and -2.5 for that with B18C6 into DCE [1] , while  was -3.33 [6] . Why are the above logKD,A values much different from the
was -3.33 [6] . Why are the above logKD,A values much different from the  ones? Are the logKex values also different from their standardized ones? Does an extraction constant (Kex±) for the extraction of MLz+ with A- differ from its standardized value? Here, Kex± has been expressed as [ML+]o[A-]o/[M+][L]o[A-] [1] .
ones? Are the logKex values also different from their standardized ones? Does an extraction constant (Kex±) for the extraction of MLz+ with A- differ from its standardized value? Here, Kex± has been expressed as [ML+]o[A-]o/[M+][L]o[A-] [1] .
In the present paper, we determined the KD,Pic and Kex values by the silver picrate (AgPic) extraction-experi- ments with B15C5 and B18C6 into less-polar DCE and dichloromethane (DCM), in order to examine the deviations of the logKD,Pic values from the  ones. In course of this examination, the differences were discussed by introducing interfacial potential differences (Dfeq) at extraction (and distribution) equilibria [9] in an extraction model. Also, it was considered how the extraction constants, Kex and Kex±, were expressed by these Dfeq values. Here, the Kex± values were calculated from the Kex values and other equilibrium constants determined in this study.
ones. In course of this examination, the differences were discussed by introducing interfacial potential differences (Dfeq) at extraction (and distribution) equilibria [9] in an extraction model. Also, it was considered how the extraction constants, Kex and Kex±, were expressed by these Dfeq values. Here, the Kex± values were calculated from the Kex values and other equilibrium constants determined in this study.
2. Theory
2.1. Expression of overall Extraction Processes by Potential differences
The following two overall extraction-processes [1] were considered in this study:
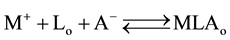 (1)
(1)
and
 . (2)
. (2)
Here, species with and without the subscript “o” denote those in the organic and w phases, respectively.
(A) To the process (1), ideas of electrochemical potentials 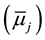 can be applied as follows.
can be applied as follows.
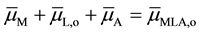 (3)
(3)
This equation was rearranged using the properties [10] of .
.
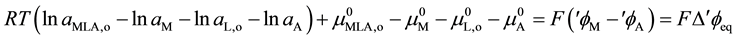 (4)
(4)
Here, aj,a,  and ¢fj (or fj) denote the activity of species j {=M(I), A(-I), L, MLA}, the standard chemical potential of j in a phase a (=o) and the inner potential of j, respectively; D¢feq and
and ¢fj (or fj) denote the activity of species j {=M(I), A(-I), L, MLA}, the standard chemical potential of j in a phase a (=o) and the inner potential of j, respectively; D¢feq and 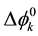 (or
(or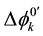 ) refer to the potential difference at an extraction equilibrium in the single phase or between the o and w phases and the potential difference for a process k, such as the overall extraction (k = ex, ex±) and an individual distribution {A(-I), M(I), ML(I)}, respectively. Then, we can obtain from Equation (4) the following equation
) refer to the potential difference at an extraction equilibrium in the single phase or between the o and w phases and the potential difference for a process k, such as the overall extraction (k = ex, ex±) and an individual distribution {A(-I), M(I), ML(I)}, respectively. Then, we can obtain from Equation (4) the following equation

with

and

The symbols, 



with

(B) Similarly, the process (2) was treated with

with


and

From Equation (10), we can easily see that this Dfeq value is an interfacial potential difference at an extraction equilibrium [9] and its form corresponds to a general definition, f(w phase) - f(o phase) [5] [8] , for the ion- transfer potential difference occurred at the w/o interface. So, it was assumed that the Dfeq value in Equation (9) does not become zero, except for an accidental case (see Table 2 for these examples). Thus, the logKex± values determined by extraction experiments were expressed as

This equation clearly shows that logKex± is the function of Dfeq.
2.2. Evaluation of Dfeq
Such Dfeq values can be experimentally obtained as a result of the KD,A determination. In this study, we de-
fined 
meter under the condition of [ML+]o = [A-]o [1] . Regression analysis of the 
According to our previous papers [2] [9] , the logKD,A value has been related to an interfacial potential difference, Df, as

Putting Df = Dfeq into this equation, we can immediately obtain the Dfeq value from a difference between the

(at Dfeq = 0 V) and
uniform on the interface of a given extraction system [9] . The 

DCM systems were available from the references [5] [6] [11] (see Introduction and below). Also, the Kex± values were easily obtained from the relation [1] of

where a combination of 
Kex[M+][L]o[A-] was used for the calculation of KMLA,o (= [MLA]o/[ML+]o[A-]o, see Appendix), namely,


2.3. For expression of Component equilibrium constants by Dfeq
As described in (A) and (B) of the Section 2.1, we can see that the Dfeq (or D¢feq) dependences of logKex± and logKex are different. So, the derivations of standard formal potentials corresponding to the extraction constants from thermodynamic cycles are tried. From the processes (1) and (2), the following cycles can be obtained as examples.


Here, KD,M and KML,o are defined as [M+]o/[M+] and [ML+]o/[M+]o[L]o, respectively; KD,M is called an individual distribution constant of a single M+ into the o phase, KML,o called a complex formation constant for ML+ in the o phase and KMLA,o called an ion-pair formation constant for ML+A- in it.
We will derive the standard formal potentials for the complex formation and then the ion-pair formation in the single phase from the properties [10] of

This equation can be rearranged in the same manner as that described in the Section 2.2.

Similarly, the D¢feq value equals zero [10] , because all species are present in the same phase (see above). Therefore, logKML,o becomes

The same is true of the ion-pair formation for MLA in the o phase: 
the condition [10] of
is transformed into 
2.4. Proofs of 

Introducing Equations (8), (13), (17) and 

and then rearrange it as

Thus, the interfacial potential differences, Dfeq, were canceled out in the cycle (1a). The same is also true of the other cycle [13] of logKex = logKMLKMLAKD,MLA/KD,L because of D¢feq = 0 and accordingly we can obtain

The definition of the component equilibrium constants were KML = [ML+]/[M+][L], KMLA = [MLA]/[ML+][A-], KD,MLA = [MLA]o/[MLA], and KD,L = [L]o/[L]. As a result D¢feq = 0 in Equation (5a) was proved, because all species are either present in the same phase or neutral compounds [10] .
For the cycle (2a), a similar treatment can be performed.

Rearranging this equation, we easily obtain

Consequently, the interfacial potential difference, Dfeq, was not canceled out in the cycle (2a). That is, in this cycle, the experimental potential difference, 

3. Experimental
3.1. Chemicals
Concentrations of aqueous solutions of AgNO3 (>99.8%, Kanto Chemical Co., Inc., Tokyo) were determined by a precipitation titration with NaCl (standard for the volumetric analysis, Wako Pure Chemical Industries, Tokyo); for example, 98.8% was obtained as a purity of AgNO3. Commercially-available B15C5 (>98%, Tokyo Chemical Industry Co. Ltd., Tokyo) and B18C6 (>96%, TCI Co. Ltd.) were dried at room temperature for more than 20 h under reduced pressures. Their purities were checked by measurements of the melting points: as examples, 79.0 - 80.5˚C for B15C5 and 39.0 - 40.0 for B18C6. The concentrations of their solutions were obtained from weighed amounts. Although the melting-point range of B15C5 was a little larger than unity, its purity was calculated as 100%. Concentrations of aqueous solutions of picric acid {HPic, guaranteed pure reagent (GR): > 99.5% after drying, Wako P.C.I.} were determined by 0.1 mol×L-1 NaOH solutions standardized by acid-base titrations with potassium hydrogen phthalate (GR: 99.8% - 100.2%, Wako P.C.I.). Commercially-available DCE (GR: 99.5%, Kanto C.C.) and DCM (GR: 99.5%, Kanto C.C.) were washed three-times with water and kept at water saturated conditions. Other chemicals were of GR grades and used without further purifications. A tap water was distilled once with a still of the stainless steel and then was purified by passing through the Autopure system (type WT101 UV, Yamato/Millipore). This water was employed for preparing all the aqueous solutions.
3.2. Instruments
Mixtures of the w phase with the o phase in stoppered glass tubes were agitated at 298 K for 2 h with an Iwaki shaker system, a water bath (type WTB-24) equipped with a driver unit (SHK driver) and a thermoregulator (type CTR-100). Then, the mixtures were centrifuged by a Kokusan centrifuge (type 7163 - 4.8.20). Total amounts of species with Ag(I) extracted into the o phase were also determined at 328.1 nm by a Hitachi polarized Zeeman atomic absorption spectrophotometer (type Z-6100) equipped with a hollow cathode lamp (type 139-3614, Mito-rika Co. under the license of Hitachi Ltd.) for Ag. The calibration-curve procedure was employed here for the determination of Ag(I) extracted. Besides, some pH values of the w phases centrifuged were measured at 298 K by using a Horiba pH/ion meter (type F-23) with a commercial glass electrode.
3.3. Extraction experiments
Initial concentrations of the aqueous solutions of AgNO3, those of HPic and those of the organic solutions of L employed for the extraction into DCE were (1.5 or 9.8) ´ 10-4 mol×L-1, (3.2 or 3.3) ´ 10-3 and (0.32 - 6.4) ´ 10-4 for L = B18C6; (0.49 or 3.0) ´ 10-3, (2.9 or 3.1) ´ 10-3 and (0.54 - 3.8) ´ 10-4 for B15C5, respectively. Also, the concentrations employed for the extraction into DCM were 1.5 ´ 10-4 mol×L-1 for the aqueous AgNO3 solution, 3.2 ´ 10-3 for HPic and (0.27 - 1.1) ´ 10-4 for the organic solutions of B18C6; (1.8, 4.9 or 5.9) ´ 10-3, (1.8, 4.4 or 5.9) ´ 10-3 and (0.54 - 3.6) ´ 10-4 for those of B15C5, respectively.
The organic solutions containing L were mixed with aqueous ones containing AgNO3 and HPic in the stoppered glass-tubes of about 30 mL, these tubes were vigorously shaken up for 1 minute with hand, and then agitated at 298 ± 0.2 K for 2 h in the water bath (see the Section 3.2). After these operations, the mixtures were centrifuged for 5 minutes. The o phases were separated from the w phases and then the pH values of the latter were measured. The o phases were transferred in part into the glass tubes, aqueous solutions of 0.1 mol×L-1 HNO3 were added in their tubes, and then their mixtures were mechanically agitated for 2 h in the bath. The w phases with HNO3 were separated from the mixtures and then total amounts of Ag(I) in the separated w phases were determined by AAS (see the Section 3.2). The extraction of Ag(I) into the o phases was not detected in blank experiments without L in the both phases.
3.4. Data analysis
Procedures were essentially the same as those reported previously [1] [14] except for an addition of the dissociation of MLA in the o phase: see Appendix. In computations of [Ag+], [L]o and [Pic-] by the successive approximation [1] [14] , KAgLPic, KAgPic [14] and KHPic values [15] were evaluated as the functions of activity coefficients from the I values. Here, KAgPic and KHPic are defines as [AgPic]/[Ag+][Pic-] and [HPic]/[H+][Pic-], respectively. On the other hand, it was assumed that other component equilibrium-constants are independent of I or Io, since experimental ranges of I and Io were narrow in many cases or ratios of activity coefficients for KAgL and KAgL,o (see the Section 4.1 for the definition) were close to unity. The experimental data were I = (3.4 - 5.8) × 10-3 mol×L-1 and IDCE = (1.0 - 1.1) × 10-5 for L = B15C5, (3.2 - 4.0) × 10-3 and IDCE = (6.3 - 6.6) × 10-6 for B18C6; I = (0.35 - 1.2) × 10-2 and IDCM = (2.1 - 6.9) × 10-7 for B15C5 and 3.3 × 10-3 and IDCM = 1.9 × 10-6 for B18C6. The symbols, IDCE and IDCM, denote ionic strength for the DCE phase and that for DCM, respectively. Also, the dissociation of HPic in the DCE or DCM phase was neglected. Namely, this means that a contribution of the distribution of H+ to the Dfeq value is negligible. Besides, the formation of AgLNO3, HLNO3 and HLPic and their distribution into the o phase were neglected.
4. Results and Discussion
4.1. Determination of KD,Pic, Kex and Kex±
The experimental data of [AgLPic]o + [AgL+]o, [Ag+], [L]o and [Pic-] were analyzed using a logarithmic form of
the equation described in the Section 2.2: 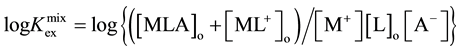
rimental plot analyzed by this equation is shown in Figure 1. Regression lines of the other systems were of a correlation coefficient (R) = 0.196 for the B15C5/DCM system, 0.969 for B18C6/DCM and 0.823 for B15C5/ DCE. From these regression analyses [1] , curve fittings of the plots, we obtained the KD,A and Kex values. The logKex± values were also calculated from the logarithmic form of Equation (14). The thus-obtained values were listed in Table 1.
The experimental logKD,Pic values in Table 1 were much smaller than those standardized on the extra-thermo- dynamic assumption of 
Also, from the logKAg/AgL values in Table 1, we can see that the KAgL,o (= [AgL+]o/[Ag+]o[L]o) values satisfy the relation of B15C5 £ B18C6, because the KD,Ag values are constants for given diluents. Here, KAg/AgL is expressed as the product [16] of KAgL,o and KD,Ag. Moreover, the logKAgLPic,o values which are logarithmic equilibrium constants for the AgLPic formation in the o phases saturated with water were calculated from the relation,

mol×L-1 for L = B15C5, 5.91 ± 0.19 at IDCM,av = 1.9 ´ 10-6 for B18C6, logKAgLPic,DCE = 5.57 ± 0.23 at IDCE,av = 1.0
Figure 1. Plot of 
Table 1. Individual distribution constants of Pic- (=A-) and overall equilibrium constants for the extraction of AgPic by L into DCE and DCM at 298 K.
aAverage values and standard errors. bAverage values of logKD,AgKAgL,o calculated from Equation (2a) and their estimated errors.
´ 10-5 for B15C5, and 6.05 ± 0.67 at IDCE,av = 6.4 ´ 10-6 for B18C6. Here, these IDCM,av and IDCE,av values show those on the average; see the Section 3.4 for their original values. The relation of logKAgLPic,DCM between L is in agreement with that of logKAgLPic at 298 K and I ® 0 in water [14] . Considering this agreement, the dielectric constant of pure DCM < that of pure DCE and a ring size of B15C5 < that of B18C6, these results show that a major interaction of Ag(B15C5)+ with Pic- in the o phases or of AgL+ in DCM saturated with water is coulombic force at least.
4.2. Dfeq Values Evaluated from differences in logKD,Pic between the Electrochemical and Extraction experiments
As can be seen from Table 1, the experimental logKD,Pic values deviate between the B15C5 and B18C6 systems for a fixed diluent. Also their values are different from the 




Also, using Equation (9a) with the experimental logKex± values (Table 1) and the Dfeq ones, we reduced the
experimental potentials 

B15C5/DCE system, 0.13 for B18C6/DCE, 0.43 for B15C5/DCM, and 0.20 for B18C6/DCM. At the same time,
Table 2. Interfacial potentials, Dfeq, at equilibra and standardized formal potentials, 

aV unit. Values were evaluated from the differences between the experimental and standardized logKD,A values and essentially based on the extra-thermodynamic assumption of


their values yielded the standardized logKex± values: 
DCE system; see Table 2 for the other values. The same calculations were also performed for the NaMnO4 or NaPic extraction [1] by B15C5 and B18C6 into DCE and/or NB (see the Section 4.3 for the NaPic-L system).
On the other hand, the experimental logKex values are equal to the 

D¢feq. These results for 
4.3. Evaluation of the Dfeq, 
The Dfeq and logKex± values (listed in Table 2) for the NaPic extraction by L into NB were evaluated from Equations (21) and (9a), using the logKD,Na and logKNaL,NB values: logKD,Na = -5.18 [6] and logKNaL,NB = 6.92 [16] for L = B15C5 and 7.91 [17] for B18C6. The logKex± values evaluated were larger than the 
Similarly, the above procedure was applied for the CsPic and CsMnO4 extraction [4] by 4,5”-bis(tert-ocytl- benzo) dibenzo-24-crown-8 ether (TB24C8) into DCE. From Equation (13), the Dfeq values were evaluated to be -0.021 V for A- = Pic- and +0.067 for

Then, we obtained 

TB24C8. These relations between 
erence.
4.4. For Tendencies of
An order of 

Figure 2. Plot of 

Table 2). This fact indicates that interactions of Pic- with the diluent molecules increase with this order; namely
Pic- is easy to more transfer from water to NB than does to DCE. On the other hand, a relation of
was NB < DCE (<0). These findings suggest that these interfacial formal or ion transfer potentials reflect the interactions of the diluent molecules with A- [8] .
The Dfeq values were in the orders of NaMnO4/DCE (»0 V) £ -/NB and NaPic/NB < AgPic/DCE < -/DCM for L = B15C5 and NaMnO4/DCE < (0 V<) -/NB and NaPic/NB < AgPic/DCE < -/DCM for B18C6. There are
tendencies of DCE £ NB for the NaMnO4 system and NB < DCE < DCM for MPic.
Also, the 
DCE < AgPic/DCM for B15C5 and (NaPic/NB < 0 V <) NaMnO4/NB < NaMnO4/DCE < AgPic/DCE < AgPic/DCM for B18C6. We can easily see from these facts that there is a tendency of NB < DCE < DCM in

tracted with L into NB or DCE than into DCM. In a potential scale, the more the formal (or ion transfer) poten-
tials 
the more anions transfer to the o phase. Probably, the tendency of 
though the process corresponding to 

latter case. There was partially a correlation between the Dfeq and 
4.5. For Tendencies oflogKex± and
Relations, L = B15C5 ³ B18C6 for the AgPic/DCE system and B15C5 < B18C6 for AgPic/DCM, in
are a little difference from those, B15C5 < B18C6 for AgPic/DCE and -/DCM, in logKex± determined experi-
mentally (Table 2). Also, the relations, 
the same as those in the experimentally-determined logKex± values. These results show that properties of the DCE system with AgPic and L are a little different with those of the others. The logKex± values in Table 2 (or Table 1) were in the orders of NaMnO4/NB > AgPic/DCE > NaMnO4/DCE > AgPic/DCM for B15C5 and NaMnO4/NB > AgPic/DCE ³ AgPic/DCM > NaMnO4/DCE for B18C6. This reverse between the AgPic/DCM and NaMnO4/DCE systems for B18C6 suggests that the logKex± value of the NaMnO4/DCE system is so small or that of the AgPic/DCM one so large, although the authors cannot now shows its cause, except for the differences of the Dfeq values related to their systems.
The 
DCM for L = B15C5 and NaPic/NB > NaMnO4/NB > NaMnO4/DCE > AgPic/DCE > AgPic/DCM for B18C6. Except for the NaMnO4/DCE system with B18C6, these orders were in agreement with those (see above) of the experimental logKex± values. This fact indicates that the experimental logKex± values are usually reflected into
the 

together with the data (see the Section 4.3) of the CsPic and CsMnO4 extraction [4] by TB24C8 into DCE. A
plot of 



5. Conclusion
It was demonstrated that the Dfeq values of the MA extraction systems with L are not necessarily zero in some
cases. The logKex± values determined by the solvent-extraction experiments fairly reflected the 
standardized on the electrochemical measure at the w/o interface. The Dfeq (or D¢feq) term disappeared in the extraction constant such as Kex, namely, the constant expressing the system without apparently ion transfer at the w/o interface. The same was true of reactions occurred in the single phase. Also, the above results will be applied to the MIIA2 extraction systems with L. Besides, the introduction of Dfeq in the extraction systems can
solve problems with respect to deviations in logKD,j, 

methods.
References
- Kudo, Y., Harashima, K., Katsuta, S. and Takeda, Y. (2011) Solvent Extraction of Sodium Permanganate by Mono- Benzo 3m-Crown-m Ethers (m = 5, 6) into 1,2-Dichloroethane and Nitrobenzene: A Method Which Analyzes the Extraction System with the Polar Diluents. International Journal of Chemistry, 3, 99-107. http://dx.doi.org/10.5539/ijc.v3n1p99
- Kudo, Y., Horiuchi, N., Katsuta, S. and Takeda, Y. (2013) Extraction of Cadmium Bromide and Picrate by 18-Crown- 6 Ether into Various Less-Polar Diluents: Analysis of Overall Extraction Equilibria Based on Their Component Equilibria with Formation of Their Ion Pairs in Water. Journal of Molecular Liquids, 177, 257-266. http://dx.doi.org/10.1016/j.molliq.2012.10.015
- Kudo, Y., Takahashi, Y., Numako, C. and Katsuta, S. (2014) Extraction of Lead Picrate by 18-Crown-6 Ether into Various Diluents: Examples of Sub-Analysis of Overall Extraction Equilibrium Based on Component Equilibria. Jour- nal of Molecular Liquids, 194, 121-129. http://dx.doi.org/10.1016/j.molliq.2014.01.017
- Levitskaia, T.G., Maya, L., Van Berkel, G.J. and Moyer, B.A. (2007) Anion Partitioning and Ion-Pairing Behavior of Anions in the Extraction of Cesium Salts by 4,5”-Bis(tert-ocytlbenzo)dibenzo-24-Crown-8 in 1,2-Dichloroethane. Inorganic Chemistry, 46, 261-272.
- Markin, V.S. and Volkov, A.G. (1989) The Gibbs Free Energy of Ion Transfer between Two Immiscible Liquids. Elec- trochimica Acta, 34, 93-107. http://dx.doi.org/10.1016/0013-4686(89)87072-0
- Kudo, Y., Harashima, K., Hiyoshi, K., Takagi, J., Katsuta, S. and Takeda, Y. (2011) Extraction of Some Univalent Salts into 1,2-Dichloroethane and Nitrobenzene: Analysis of Overall Extraction Equilibrium Based on Elucidating Ion- Pair Formation and Evaluation of Standard Potentials for Ion Transfers at the Interfaces between Their Diluents and Water. Analytical Sciences, 27, 913-919. http://dx.doi.org/10.2116/analsci.27.913
- Rais, J. (1971) Individual Extraction Constants of Univalent Ions in the System Water-Nitrobenzene. Collection of Czechoslovak Chemical Communications, 36, 3253-3262. http://dx.doi.org/10.1135/cccc19713253
- Kakiuchi, T. (1996) Partition Equilibrium of Ionic Components in Two Immiscible Electrolyte Solutions. In: Volkov, A.G. and Dreamer, D.W., Eds., Liquid-Liquid Interfaces Theory and Methods, CRC Press, Boca Raton, Chapter 1.
- Takeda, Y., Ezaki, T., Kudo, Y. and Matsuda, H. (1995) Distribution Study on Electroneutral and Protonated Amino Acids between Water and Nitrobenzene. Determination of the Standard Ion-Transfer Potentials of Protonated Amino Acids. Bulletin of the Chemical Society of Japan, 68, 787-790. http://dx.doi.org/10.1246/bcsj.68.787
- Bard, A.J. and Faulkner, L.R. (2001) Electrochemical Method: Fundamentals and Applications. 2nd Edition, John Wily & Sons, Inc., New York, 60-62.
- Marcus, Y. (1983) Thermodynamic Functions of Transfer of Single Ions from Water to Nonaqueous and Mixed Solvents: Part 1-Gibbs Free Energies of Transfer to Nonaqueous Solvents. Pure & Applied Chemistry, 55, 977-1021. http://dx.doi.org/10.1351/pac198355060977
- Kudo, Y., Katsuta, S. and Takeda, Y. (2012) Evaluation of Overall Extraction Constants for the Crown Ether-Complex Ions of Alkali and Alkaline-Earth Metal with Counter Picrate Ions from Water into Nitrobenzene Based on Their Com- ponent Equilibrium Constants. Journal of Molecular Liquids, 173, 66-70. http://dx.doi.org/10.1016/j.molliq.2012.06.003
- Takeda, Y. (2002) Extraction of Alkali Metal Picrates with 18-Crown-6, Benzo-18-Crown-6, and Dibenzo-18-Crown-6 into Various Organic Solvents. Elucidation of Fundamental Equilibria Governing the Extraction-Ability and -Selecti- vity. Bunseki Kagaku (Analytical Chemistry), 51, 515-525. http://dx.doi.org/10.2116/bunsekikagaku.51.515
- Kudo, Y., Usami, J., Katsuta, S. and Takeda, Y. (2004) Solvent Extraction Silver Picrate by 3m-Crown-m Ethers (m = 5, 6) and Its Mono-Benzo Derivative from Water into Benzene or Chloroform: Elucidation of an Extraction Equilibrium Using Component Equilibrium Constants. Talanta, 62, 701-706. http://dx.doi.org/10.1016/j.talanta.2003.09.022
- Kudo, Y., Takahashi, Y. and Katsuta, S. (2013) Distribution of Picric Acid into Various Diluents. Journal of Chemistry, 2013, Article ID: 896506.
- Kudo, Y., Takeda, Y. and Matsuda, H. (1991) Ion-Transfer-Polarographic Study of Distribution Equilibrium of Metal Complex Cations with Several Crown Ethers between Nitrobenzene and Water. Bunseki Kagaku (Analytical Chemistry), 40, 779-784. http://dx.doi.org/10.2116/bunsekikagaku.40.11_779
- Kudo, Y., Miyakawa, T., Takeda, Y. and Matsuda, H. (1996) Ion-Transfer Polarographic Study of the Distribution of Alkali and Alkaline-Earth Metal Complexes with 3m-Crown-m Ether Derivatives (m = 6, 8) between Water and Nitrobenzene Phases. Journal of Inclusion Phenomena and Molecular Recognition in Chemistry, 26, 331-341. http://dx.doi.org/10.1007/BF01053550
- Makrlík, E., Va?ura, P. and Da?ková, N. (1999) Contribution of the Thermodynamics of Complexes of Alkali Metal Cation with 18-Crown-6 in the Water-Nitrobenzene System. Journal of Radioanalytical and Nuclear Chemistry, 240, 579-583. http://dx.doi.org/10.1007/BF02349416
Appendix
The extraction model employed here was essentially the same as that reported before [14]. However, the following component equilibrium in the o phase [1] [4] was added:

This introduction in the model is comparable with those of the individual distribution of ML+ and that of A- into the o phase [1] [18]. Therefore, the following equation similar to Equation (13) can be derived.

with



and KD,ML = [ML+]o/[ML+]. As described in the text, this Dfeq value becomes a common value with those of A- and M+, in the extraction system in question.









