American Journal of Analytical Chemistry
Vol.4 No.12(2013), Article ID:40396,7 pages DOI:10.4236/ajac.2013.412087
Calculation of the Voigt Function in the Region of Very Small Values of the Parameter a Where the Calculation Is Notoriously Difficult
1Laboratoire PROTEE-ISO, Université du Sud Toulon-Var, La Garde, France
2Laboratoire d’Electronique Quantique, Faculty of Physique, University of Sciences and Technology Houari Boumediene, Alger, Algérie
Email: amamou@univ-tln.fr
Copyright © 2013 Hssaïne Amamou et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 13, 2013; revised October 25, 2013; accepted November 15, 2013
Keywords: Convolution; Line Profile; Voigt Function; Lorentz Profile; Doppler Profile and Spectral Lines
ABSTRACT
The Voigt function is the convolution of a Lorentzian and a Guaussian density. The computation of these functions is required in several problems arising in a variety of physicochemical subjects; such as nuclear reactors, atmospheric transmittance and spectroscopy. In this work we suggest using a new formula for the calculation of the Voigt function. Our formula is a new integral representation for the Voigt function that gives the perfect results for the Voigt function calculation and is easily calculable. We give also a comparison between our results of calculation of Voigt function for the very small values of the parameter a, where the calculation is notoriously difficult, with those of the various algorithms of other authors.
1. Introduction
The shape of the spectral lines is a subject of great interest in physics and chemistry. Indeed, several important physical and chemical parameters are directly deducted from the spectral lines whose shape is approximated by the Gaussian profile or the Lorentzian profile. Therefore, the parameters obtained do not correspond exactly to the real physical conditions for which the spectral lines have the shape of the distribution of Voigt. For this reason, the study and the calculation of the Voigt function are very interesting in many fields of physics and chemistry. Indeed, for the signal emitted by a plasma, for example, the phenomena that produce the enlargement of the spectral lines are Doppler broadening caused by thermal agitation of the particles, and the enlargement of pressure, which is due to interactions between the transmitters and the neighboring particles, the resulting profile of these physical phenomena is a Voigt profile.
The Voigt function results from the convolution product between a Gaussian profile and a profile Lorentzian and is expressed by the following formula:
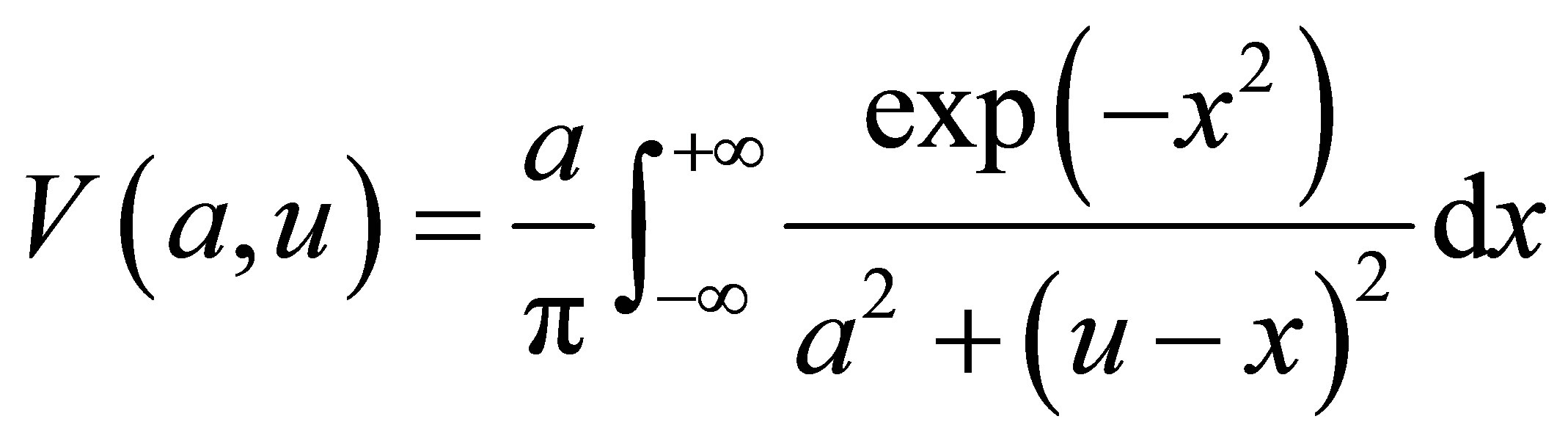 (1)
(1)
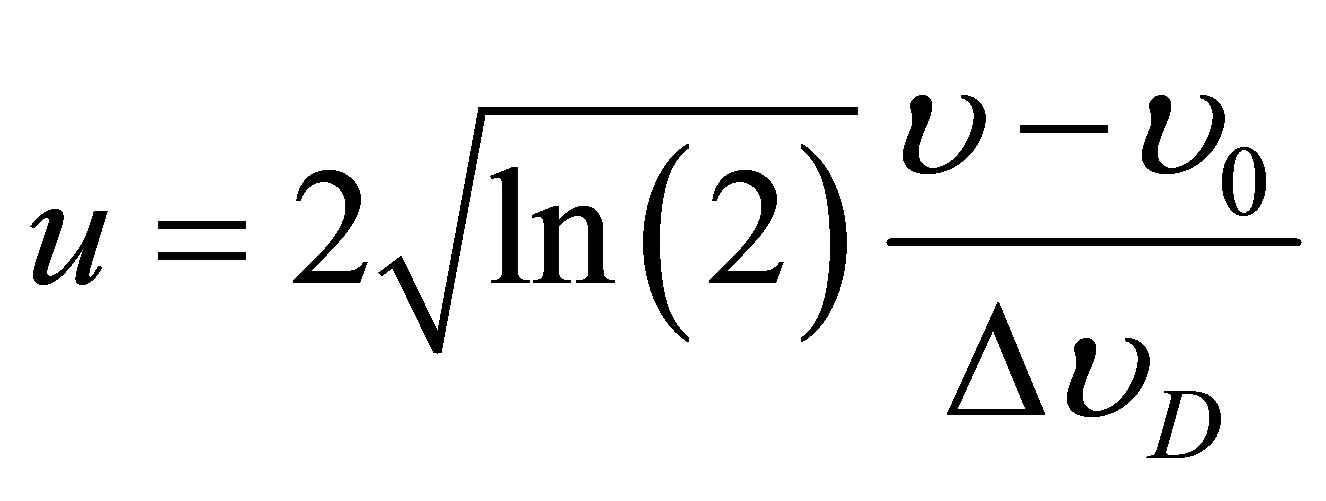 represents the relationship between the distance from the center of the Lorentzian line and the width of the Gaussian line.
represents the relationship between the distance from the center of the Lorentzian line and the width of the Gaussian line.
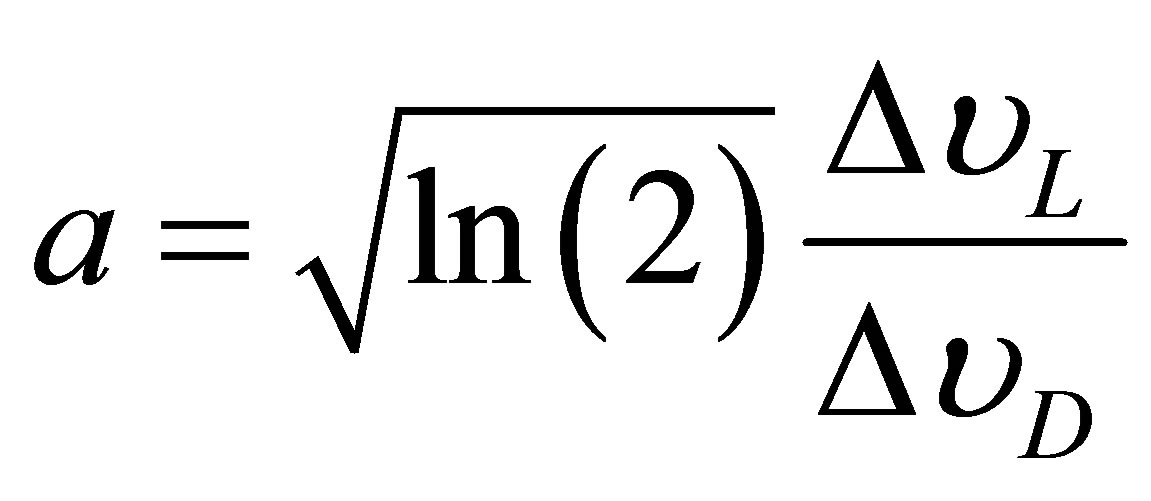 determines the importance of Lorentzian in the profile, thus if this parameter tends towards 0, the Lorentzian is negligible and if it tends towards, the infinite the Lorentzian is dominant.
determines the importance of Lorentzian in the profile, thus if this parameter tends towards 0, the Lorentzian is negligible and if it tends towards, the infinite the Lorentzian is dominant.
 : Frequency.
: Frequency.
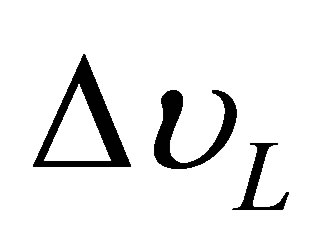 : Lorentz half-width at half maximum in frequency.
: Lorentz half-width at half maximum in frequency.
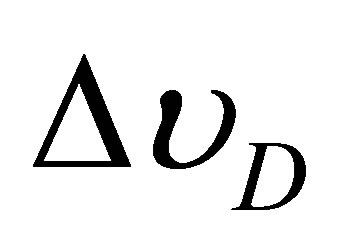 : Doppler half-width at half maximum in frequency.
: Doppler half-width at half maximum in frequency.
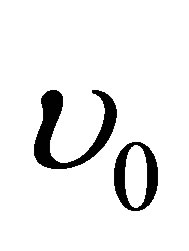 : Frequency in the center of the line.
: Frequency in the center of the line.
This function has been studied recently by several studies [1-8].
2. Calculation of the Voigt Function in the Region near the u Axis
We give our new formula (That we have demonstrated in the article of Amamou et al. [9] (Demonstration given in Appendix 1 of this article)) of Voigt function in the following formula:
 (2)
(2)
This analytical formula of the Voigt function gives a solution to the mathematical problem which is due at the infinite boundaries of the integral which defines the Voigt function. This is a new integral representation for the Voigt function that gives a perfect formula of Voigt function easily calculable and it’s different to the formula given by Roston and Obaid [10] and gives a solution to the problem of exponential growth described by Van Synder [11].
This formula can be used for calculation of the spectral lines whose profile is a convolution of a Lorentzian profile and a Gaussian profile. This type of profile describes the actual physical conditions of several physicochemical phenomena and its use is very interesting to adjust the spectral lines by theoretical models.
In the Figures 1-3, the determination of the Lorentzian profile and the Gaussian profile we have used the following parameters;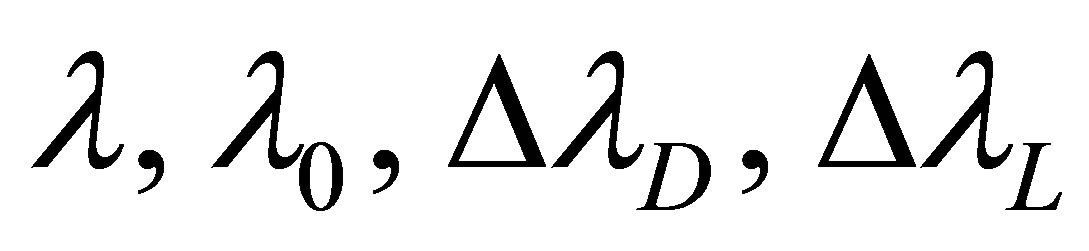 . These figures shows the three profiles; Voigt profile, Gaussian profile and Lorentzian profile for different parameters a and u.
. These figures shows the three profiles; Voigt profile, Gaussian profile and Lorentzian profile for different parameters a and u.
With:
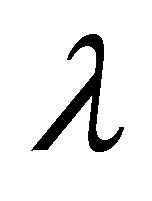 : Wavelength.
: Wavelength.
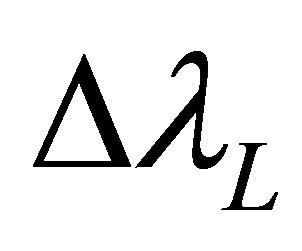 : Lorentz half-width at half maximum in wavelength.
: Lorentz half-width at half maximum in wavelength.
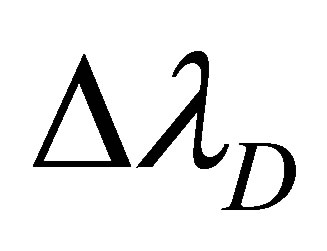 : Doppler half-width at half maximum in wavelength.
: Doppler half-width at half maximum in wavelength.
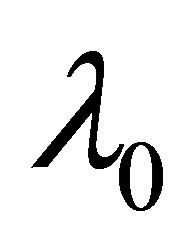 : Wavelength in the center of the line.
: Wavelength in the center of the line.
In the Figure 1 the Lorentzian profile, the Gaussian profile and the Voigt profile are given for the following parameters:

thus the parameter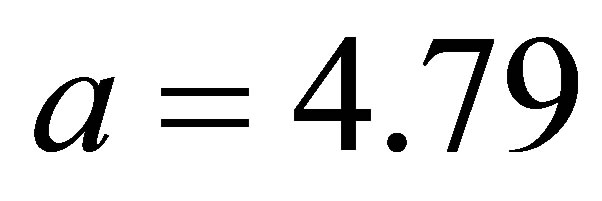 .
.
In the Figure 2 the Lorentzian profile, the Gaussian profile and the Voigt profile are given for the following parameters:
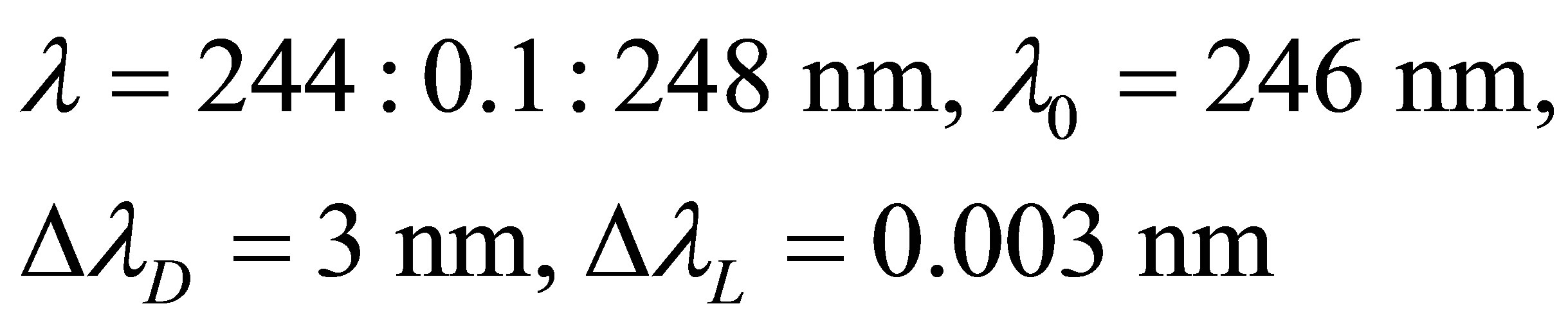
thus the parameter .
.
In the Figure 3 the Lorentzian profile, the Gaussian profile and the Voigt profile are given for the following parameters:

Figure 1. Voigt profile: “black” Voigt, “blue” Gauss and “red” Lorentz.
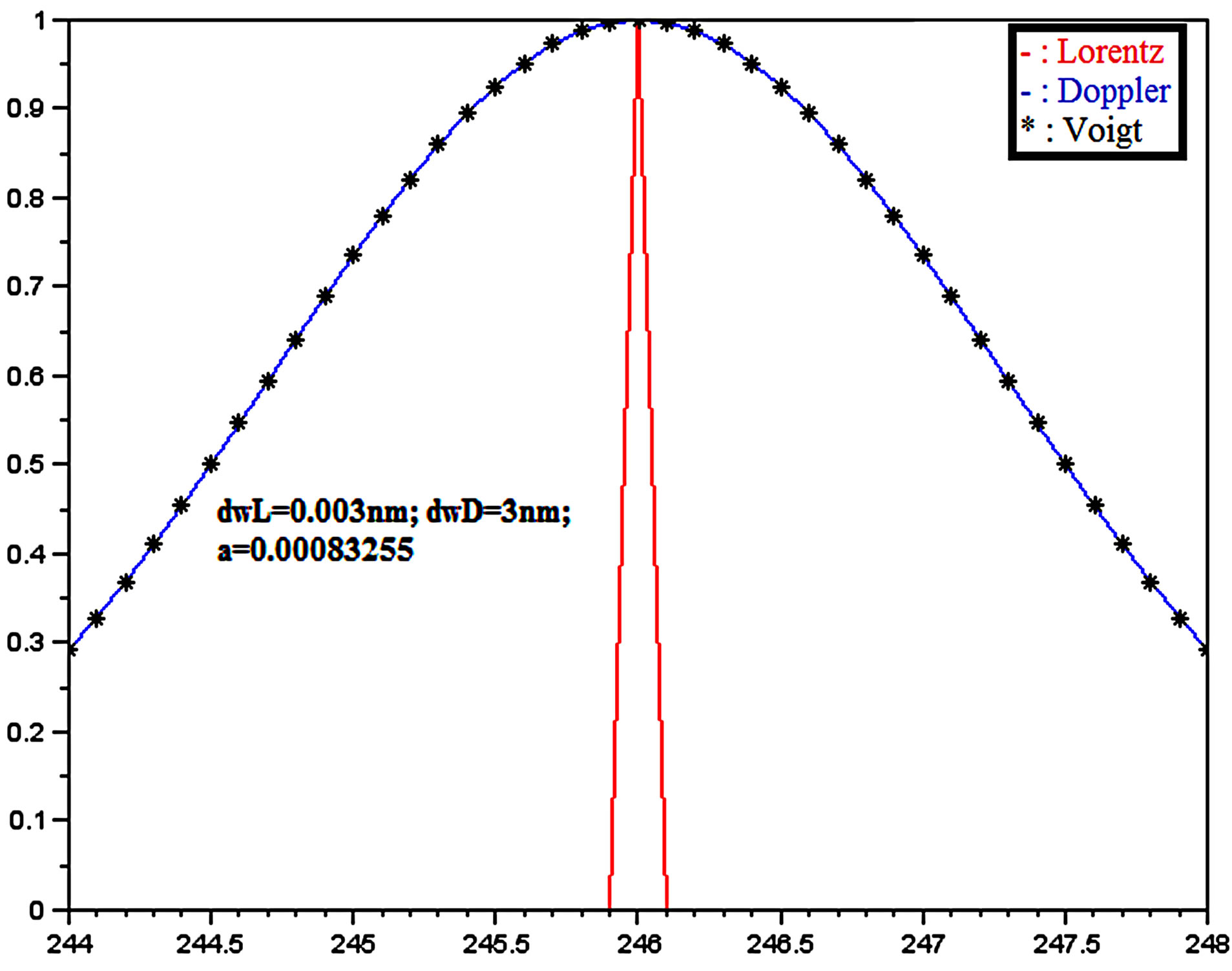
Figure 2. Voigt profile: “black” Voigt, “blue” Gauss and “red” Lorentz.
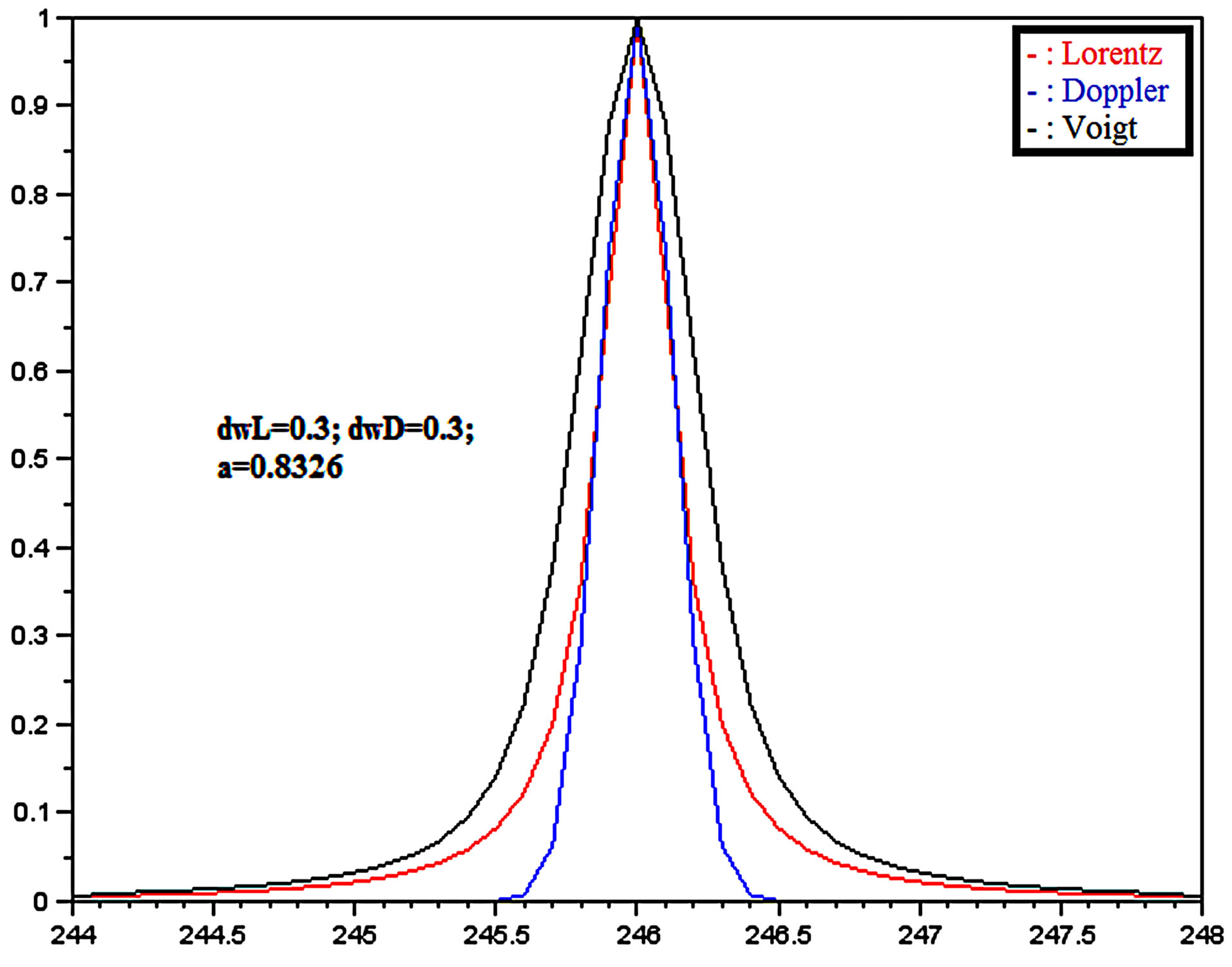
Figure 3. Voigt profile: “black” Voigt, “blue” Gauss and “red” Lorentz.
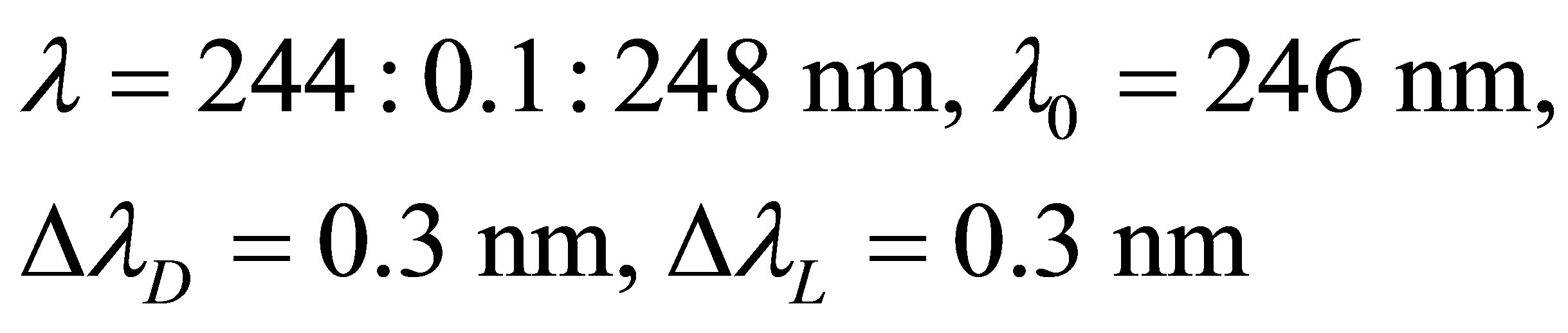
thus the parameter .
.
Our formula is also a very interesting method for easy calculation of the Voigt function. For the calculation of the integrals of Equation (2) the trapezoidal rule method and the adaptive Simpson’s method give very good results.
Table A1 (Appendix 2) gives the values of the Voigt function calculated with the Formula (2) for the very small values of the parameter a where the calculation is notoriously difficult [12]. This table gives also the computation time(s) for the values of each column of the table. This calculation time depends obviously on the performances of the computer. The computer that we have used has a processor Intel pentium 2.3 GHz and a memory (RAM) 4 GHz. This table gives the reference values of the Voigt function calculated from Equation (2).
Table 1 gives a comparison between our results of calculation of Voigt function in the in the region of very small values of the parameter a with those of the various algorithms of other authors.
3. Conclusion
The new representation integral for Voigt function that we have demonstrated and used to adjustment “fitting” of lines spectral in a precedent article is used in this work for calculation of Voigt function. Thus, this function is easily calculable. We also made a comparison between the results obtained by our formula and those obtained by the various algorithms of other authors in the region of

Table 1. Comparison between our results and the results of various algorithms of other authors (D is here for 10).
very small values of the parameter a where the calculation is notoriously difficult.
REFERENCES
- Z. Shippony and W. G. Read, “A Correction to a Highly Accurate Voigt Function Algorithm,” Journal of Quantitative Spectroscopy & Radiative Transfer, Vol. 78, No. 2, 2003, pp. 255-255. http://dx.doi.org/10.1016/S0022-4073(02)00169-3
- M. R. Zaghloul and A. N. Ali, “Algorithm 916: Computing the Faddeyeva and Voigt Functions,” ACM Transactions on Mathematical Software, Vol. 38, No. 2, 2011, pp. 1-22. http://dx.doi.org/10.1145/2049673.2049679
- J. He and Q. G. Zhang, “An Exact Calculation of the Voigt Spectral Line Profile in Spectroscopy,” Journal of Optics A: Pure and Applied Optics, Vol. 9, No. 7, 2007, pp. 565-568. http://dx.doi.org/10.1088/1464-4258/9/7/003
- S. M. Abrarov and B. M. Quine, “Efficient Algorithmic Implementation of the Voigt/Complex Error Function Based on Exponential Series Approximation,” Applied Mathematics and Computation, Vol. 218, No. 5, 2011, pp. 1894-1902. http://dx.doi.org/10.1016/j.amc.2011.06.072
- F. Schreier, “Optimized Implementations of Rational Approximations for the Voigt and Complex Error Function,” Journal of Quantitative Spectroscopy and Radiative Transfer, Vol. 112, No. 6, 2011, pp. 1010-1025. http://dx.doi.org/10.1016/j.jqsrt.2010.12.010
- S. P. Limandri, R. D. Bonetto, H. O. Di Rocco and J. C. Trincavelli, “Fast and Accurate Expression for the Voigt Function. Application to the Determination of Uranium M Linewidths,” Spectrochimica Acta Part B: Atomic Spectroscopy, Vol. 63, No. 9, 2008, pp. 962-967. http://dx.doi.org/10.1016/j.sab.2008.06.001
- S. M. Abrarov, B. M. Quine and R. K. Jagpal, “A Simple Interpolating Algorithm for the Rapid and Accurate Calculation of the Voigt Function,” Journal of Quantitative Spectroscopy and Radiative Transfer, Vol. 110, No. 6-7, 2009, pp. 376-383. http://dx.doi.org/10.1016/j.jqsrt.2009.01.003
- M. R. Zaghloul, “On the Calculation of the Voigt Line Profile: A Single Proper Integral with a Damped Sine Integrand,” Monthly Notices of the Royal Astronomical Society, Vol. 375, No. 3, 2007, pp. 1043-1048. http://dx.doi.org/10.1111/j.1365-2966.2006.11377.x
- H. Amamou, A. Bois, M. Grimaldi and R. Redon, “Exact Analytical Formula for Voigt Function which Results from the Convolution of a Gaussian Profile and a Lorentzian Profile,” Physical Chemical News PCN, Vol. 43, 2008, pp. 1-6.
- G. D. Roston and F. S. Obaid, “Exact Analytical Formula for Voigt Spectral Line Profile,” Journal of Quantitative Spectroscopy & Radiative Transfer, Vol. 94, No. 2, 2005, pp. 255-263. http://dx.doi.org/10.1016/j.jqsrt.2004.09.007
- S. Van, “Comment on ‘Exact Analytical Formula for Voigt Spectral Line Profile’,” Journal of Quantitative Spectroscopy & Radiative Transfer, Vol. 95, No. 4, 2005, pp. 557-558. http://dx.doi.org/10.1016/j.jqsrt.2005.03.001
- R. J. Wells, “Rapid Approximation to the Voigt/Faddeeva Function and Its Derivatives,” Journal of Quantitative Spectroscopy and Radiative Transfer, Vol. 62, No. 1, 1999, pp. 29-48. http://dx.doi.org/10.1016/S0022-4073(97)00231-8
- B. H. Armstrong, “Spectrum Line Profiles: The Voigt Unction,” Journal of Quantitative Spectroscopy and Radiative Transfer, Vol. 7, No. 1, 1967, pp. 61-88. http://dx.doi.org/10.1016/0022-4073(67)90057-X
- J. Humlicek, “Optimized Computation of the Voigt and Complex Probability Functions,” Journal of Quantitative Spectroscopy and Radiative Transfer, Vol. 27, No. 4, 1982, pp. 437-444. http://dx.doi.org/10.1016/0022-4073(82)90078-4
- J. Humlicek, “An Efficient Method for Evaluation of the Complex Probability Function: The Voigt Function and Its Derivatives,” Journal of Quantitative Spectroscopy & Radiative Transfer, Vol. 21, No. 4, 1978, pp. 309-313. http://dx.doi.org/10.1016/0022-4073(79)90062-1
- A. K. Hui, B. H. Armstrong and A. A. Wray, “Rapid Computation of the Voigt and Complex Error Functions,” Journal of Quantitative Spectroscopy & Radiative Transfer, Vol. 19, No. 5, 1978, pp. 509-516. http://dx.doi.org/10.1016/0022-4073(78)90019-5
- F. G. Lether and P. R. Wenston, “The Numerical Computation of the Voigt Function by a Corrected Midpoint Quadrature Rule for (−∞, ∞),” Journal of Computational and Applied Mathematics, Vol. 34, No. 1, 1991, pp. 75- 92. http://dx.doi.org/10.1016/0377-0427(91)90149-E
- A. B. McLean, C. E. J. Mitchell and D. M. Swanston, “Implementation of an Efficient Analytical Approximation to the Voigt Function for Photoemission Lineshape Analysis,” Journal of Electron Spectroscopy and Related Phenomena, Vol. 69, No. 2, 1994, pp. 125-132. http://dx.doi.org/10.1016/0368-2048(94)02189-7
- G. P. M. Poppe and C. M. J. Wijers, “More Efficient Computation of the Complex Error Function,” ACM Transactions on Mathematical Software (TOMS), Vol. 16, No. 1, 1990, pp. 38-46. http://dx.doi.org/10.1145/77626.77629
Appendix 1
The spectral radiant intensity of Voigt profile is given by:
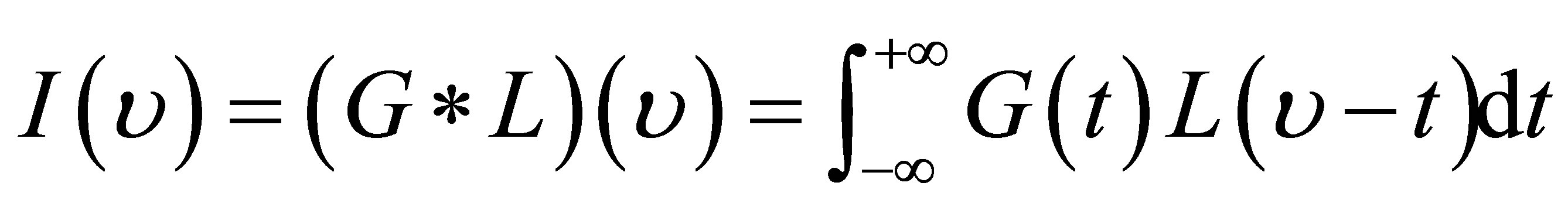 (4)
(4)
With:
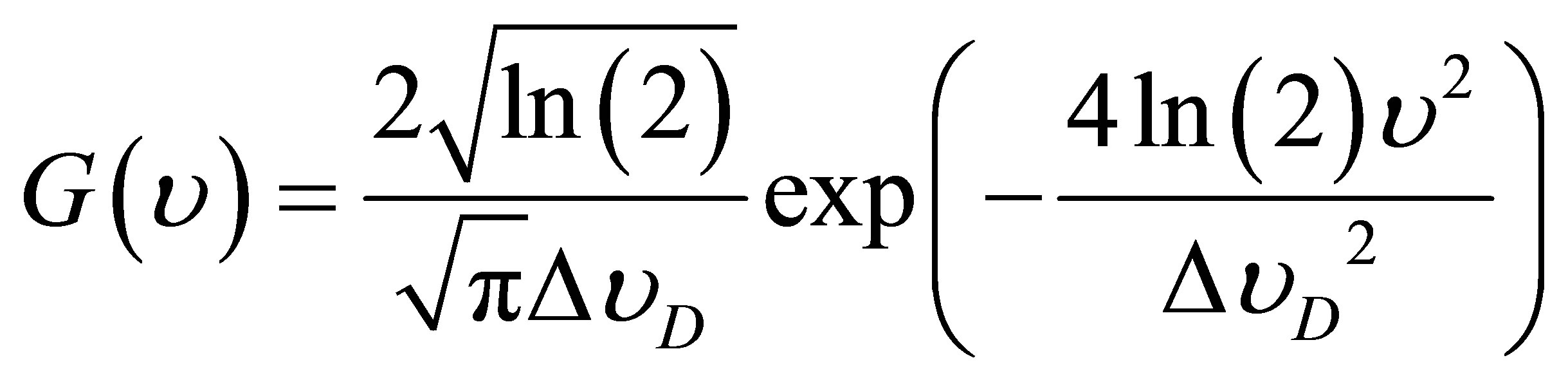 (5)
(5)
is the Gaussian profile whose 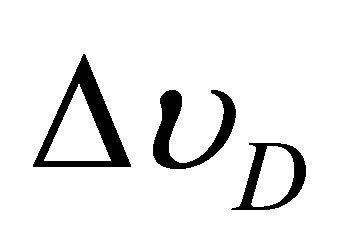 the Doppler halfwidth at half maximum and
the Doppler halfwidth at half maximum and 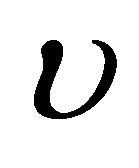 is the frequency.
is the frequency.
And
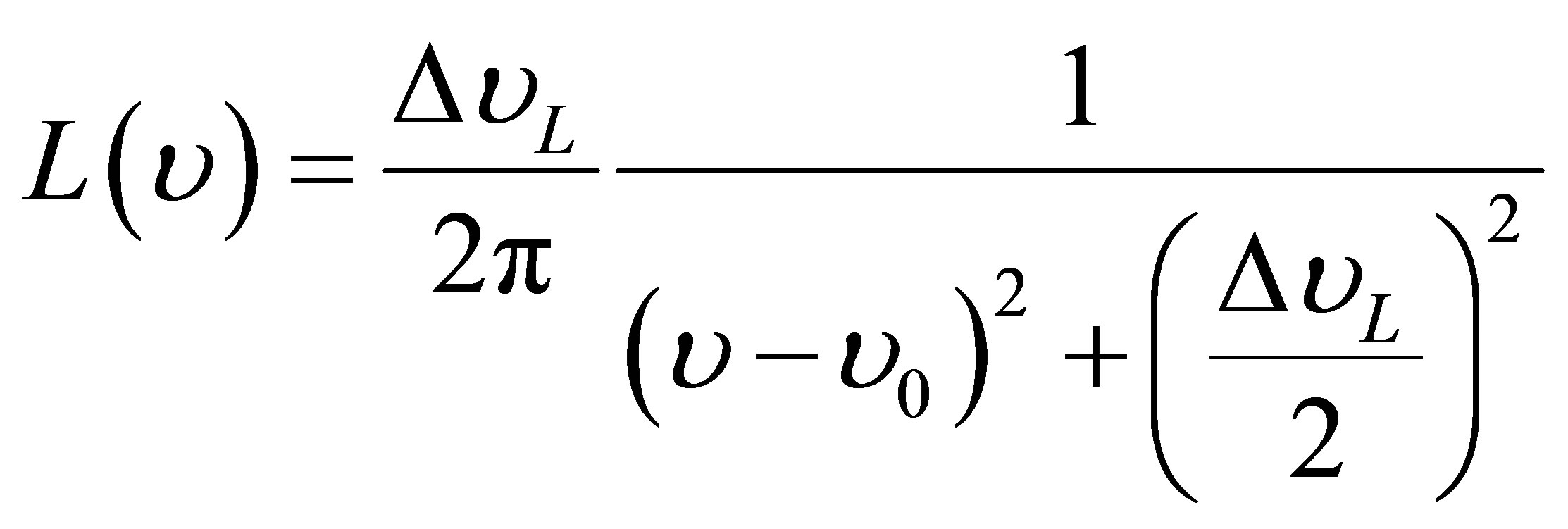 (6)
(6)
is the Lorentzian profile whose 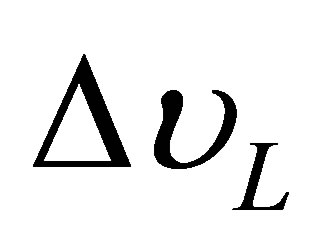 the Lorentz halfwidth at half maximum and
the Lorentz halfwidth at half maximum and  is the frequency in the center of the line.
is the frequency in the center of the line.
By an adequate change of variables, the convolution Equation (4) can be put in the following form:
 (7)
(7)
With
 (8)
(8)
 is the Voigt function whose parameters are:
is the Voigt function whose parameters are:
We can also put the expression (4) in the following form:
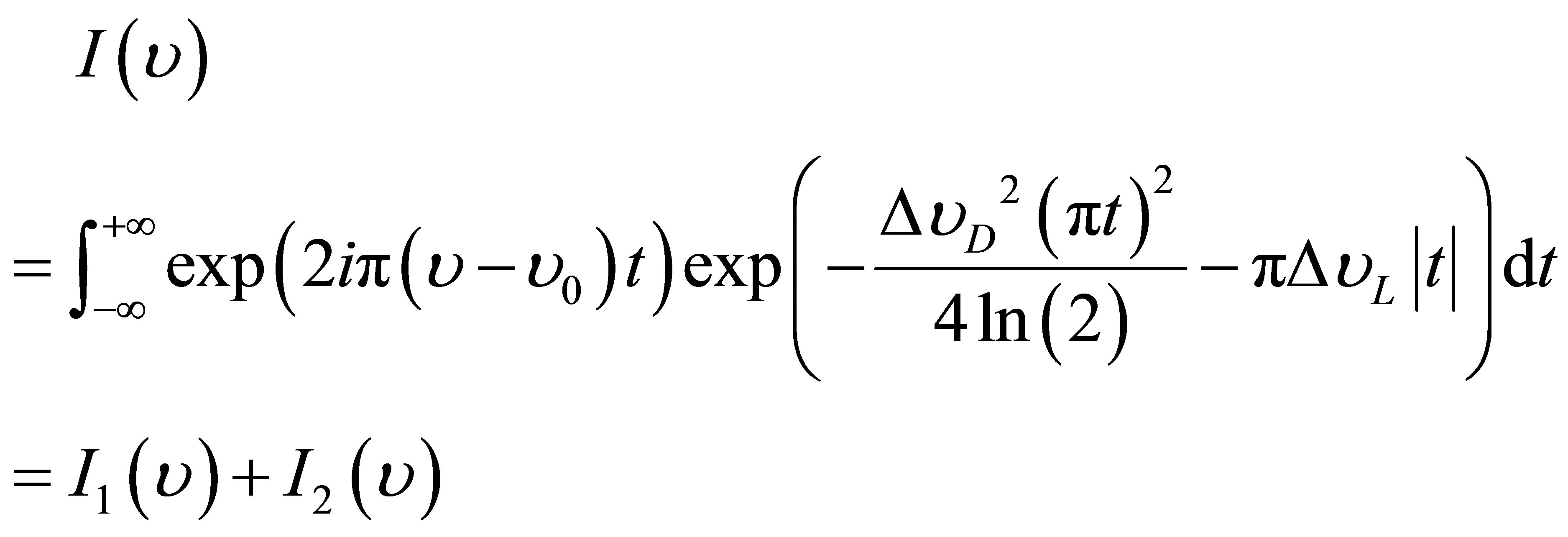 (9)
(9)
The two integrals 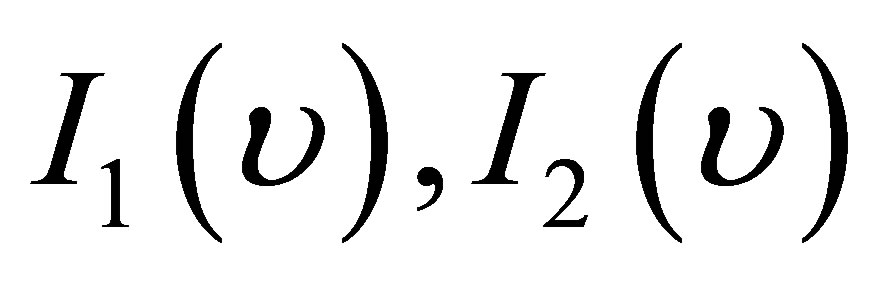 are given by the following relations:
are given by the following relations:
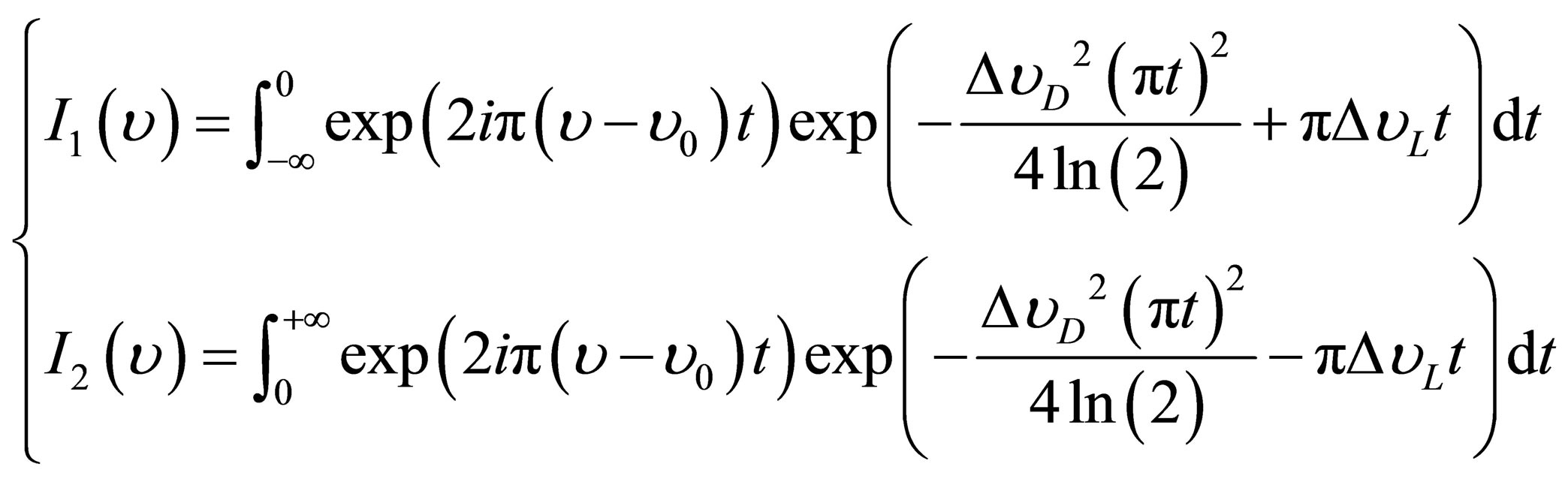 (10)
(10)
which can be also written in the following form:
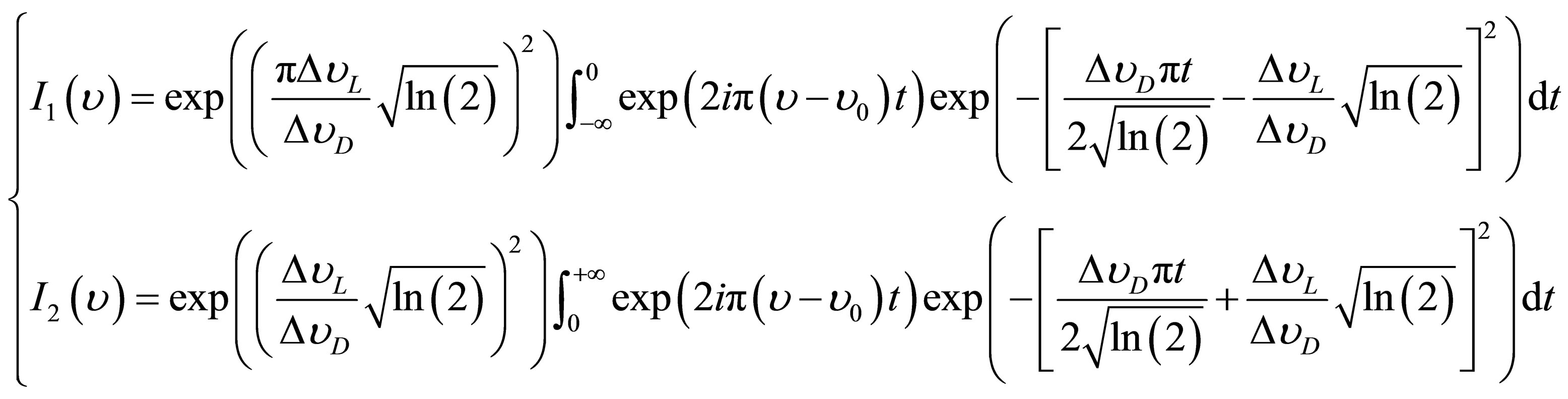 (11)
(11)
By making the change of variable according to:
 (12)
(12)
Thus, the preceding relation could be in the following form:
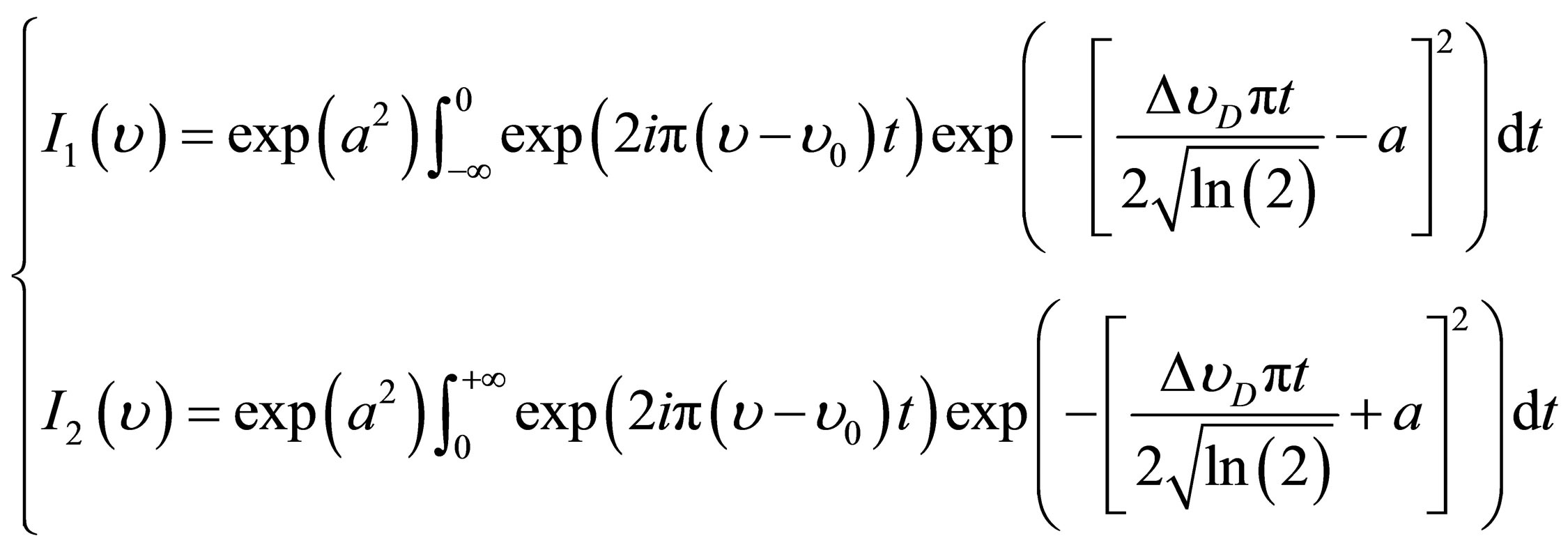 (13)
(13)
By using a suitable change of variable, the expression (13) can be formulated as follows:
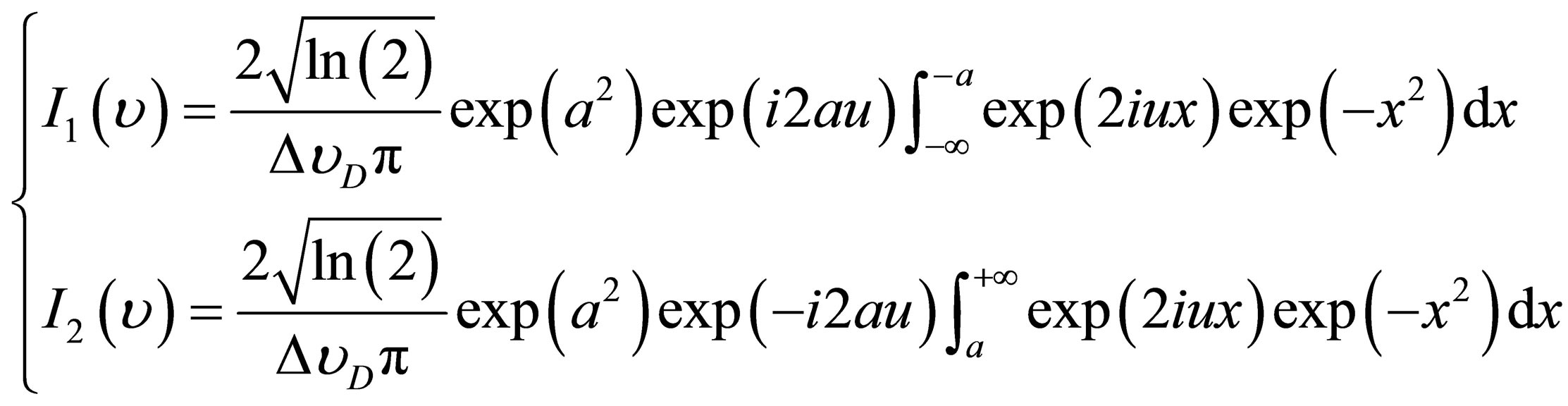 (14)
(14)
Thereafter, we can write the two precedent integrals like:
 (15)
(15)
Thereafter:
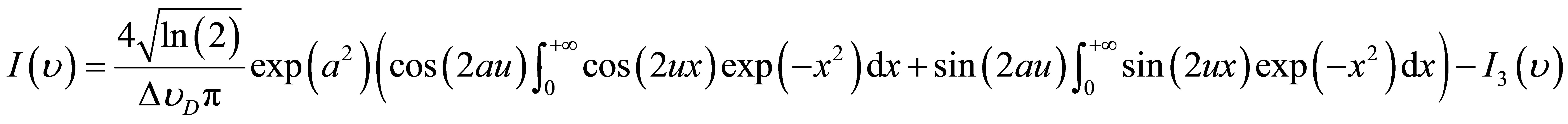 (16)
(16)
with:
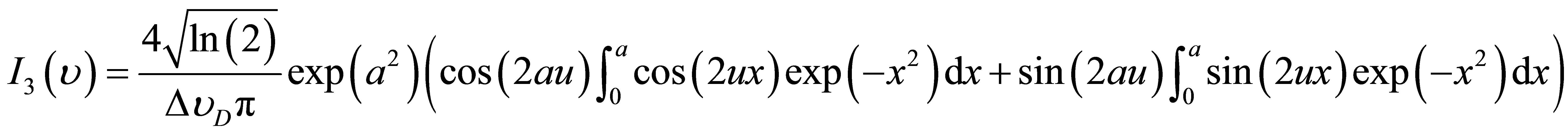 (17)
(17)
By a relatively simple mathematical analysis we can give the following solutions:
 (18)
(18)
Thus, the Voigt profile can be written in the following form:
 (19)
(19)
From this manner and according to the Equation (7) we express the Voigt function in the following way:
 (20)
(20)
Appendix 2

Table A1.Calculation of Voigt function very small values of the parameter a. We give also the calculation times of each 12 values of each column (D is here for 10).

