Modeling and Numerical Simulation of Material Science
Vol.3 No.4(2013), Article ID:37532,5 pages DOI:10.4236/mnsms.2013.34017
One Dimensional Modeling of the Shape Memory Effect
Laboratory of LaSPI2A, Department of Sciences & Technology, University Abbas Laghrour, Khenchela, Algeria
Email: *samsum66@gmail.com
Copyright © 2013 Belkacem Meddour et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 16, 2013; revised March 16, 2013; accepted March 24, 2013
Keywords: Shape; Strain; Detwinned Martensite; Region
ABSTRACT
This paper aims to build a constitutive model intended to describe the thermomechanical behavior of shape memory alloys. This behavior presents many facets, among them we have considered the simple way of shape memory, which is one of most important properties of shape memory alloys. Because of numerous stages of this effect, the subject was divided into three independent parts. For each part, we built the corresponding thermodynamic potential and we deduced the constitutive equations. To make this model workable, we have developed an algorithm. The simulation was performed using the NiTi as shape memory alloy.
1. Introduction
The known behavior of conventional materials has allowed their use in many applications but the discovery of new properties, coming from a singular behavior of materials known as shape memory alloys, opened a way for other applications from medical to aerospace.
This unusual behavior has attracted a significant attention of scientists and researchers. Therefore, various models were proposed.
These models are based on thermodynamics laws and frameworks theories as generalized standard materials. Halphen and Nguyen [1] used by Lexcellent and Licht [2], Edelen’s formalism [3] used by Tanaka and Nagaki [4].
These models can be classified as follows:
1) Macroscopic models: Built of the thermomechanical behavior, they are generally simpler in formulation and geared more towards engineering applications. Thus, the detailed physics of phase transformation are usually not rigorously addressed.
2) Micromechanical models are based on the micromechanics of a single crystal. Chu and James [5]; James et al., [6]; Lexcellent et al., [7]; Govindjee and Hall [8]; Berveiller et al. [9]; Patoor et al. [10]. Generally, this class of model was derived from more fundamental thermodynamic principles and the shape strains of different martensite variants are included.
In this paper, we focus on the effect of simple way shape memory which is the first property discovered. The adopted approach is based on the sharing of the study on three following steps:
1) Orientation of twinned Martensite;
2) Heating for austenite;
3) Cooling for detwinned Martensite.
2. Methods
2.1. Presentation of the Subject (Figure 1)
The thermomechanical cycle to the memory effect of a simple shape is defined the following:
1) Applying a mechanical load under Temperature T1 lower than 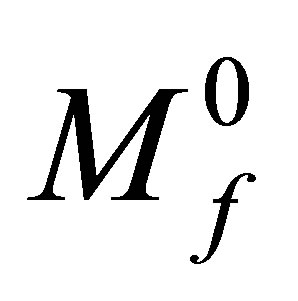 (Temperature of transformation start of Martensite): The material is deformed first elastically, followed by an important deformation due to twinned Martensite orientation. When the load is cancelled the deformation is not fully recovered, only elastic part is recovered.
(Temperature of transformation start of Martensite): The material is deformed first elastically, followed by an important deformation due to twinned Martensite orientation. When the load is cancelled the deformation is not fully recovered, only elastic part is recovered.
2) Heating to a temperature above 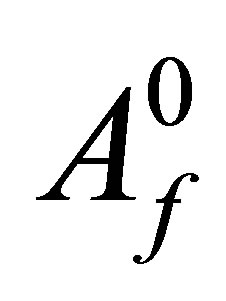 (Temperature of transformation finish of Austenite): When the temperature reaches
(Temperature of transformation finish of Austenite): When the temperature reaches 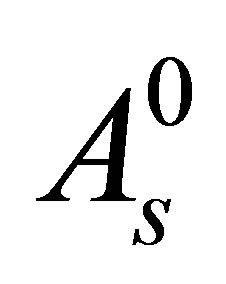 (Temperature of transformation start of Austenite) the deformation begins to recover.
(Temperature of transformation start of Austenite) the deformation begins to recover.
3) Cooling to T1: Austenite begins to transform to Martensite and finally the material is at the origin of the cycle.
2.2. Definition of Regions (Figure 2)
The study will concern three regions which are planes (ε,
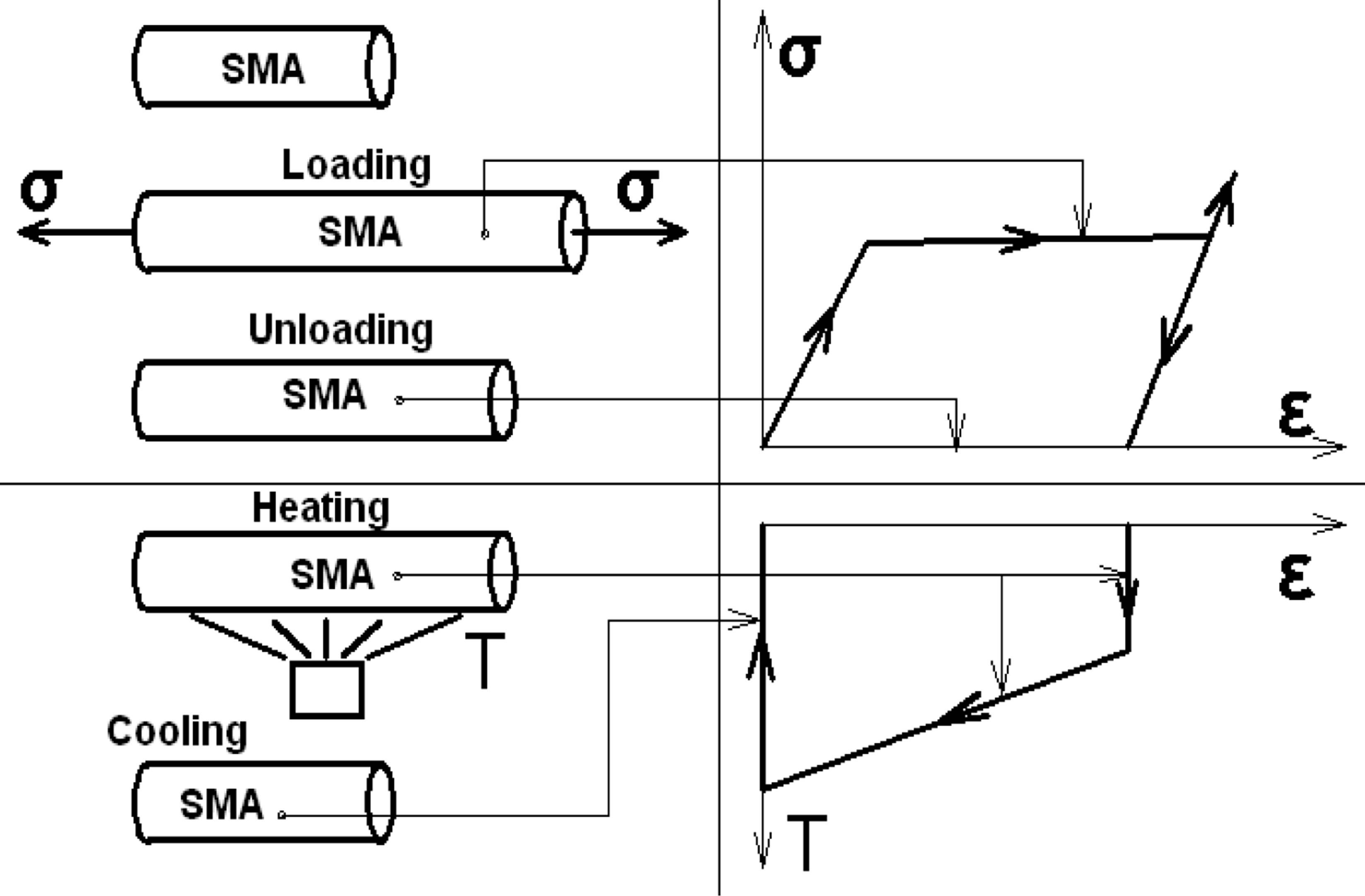
Figure 1. Thermomechanical cycle of way memory effect.
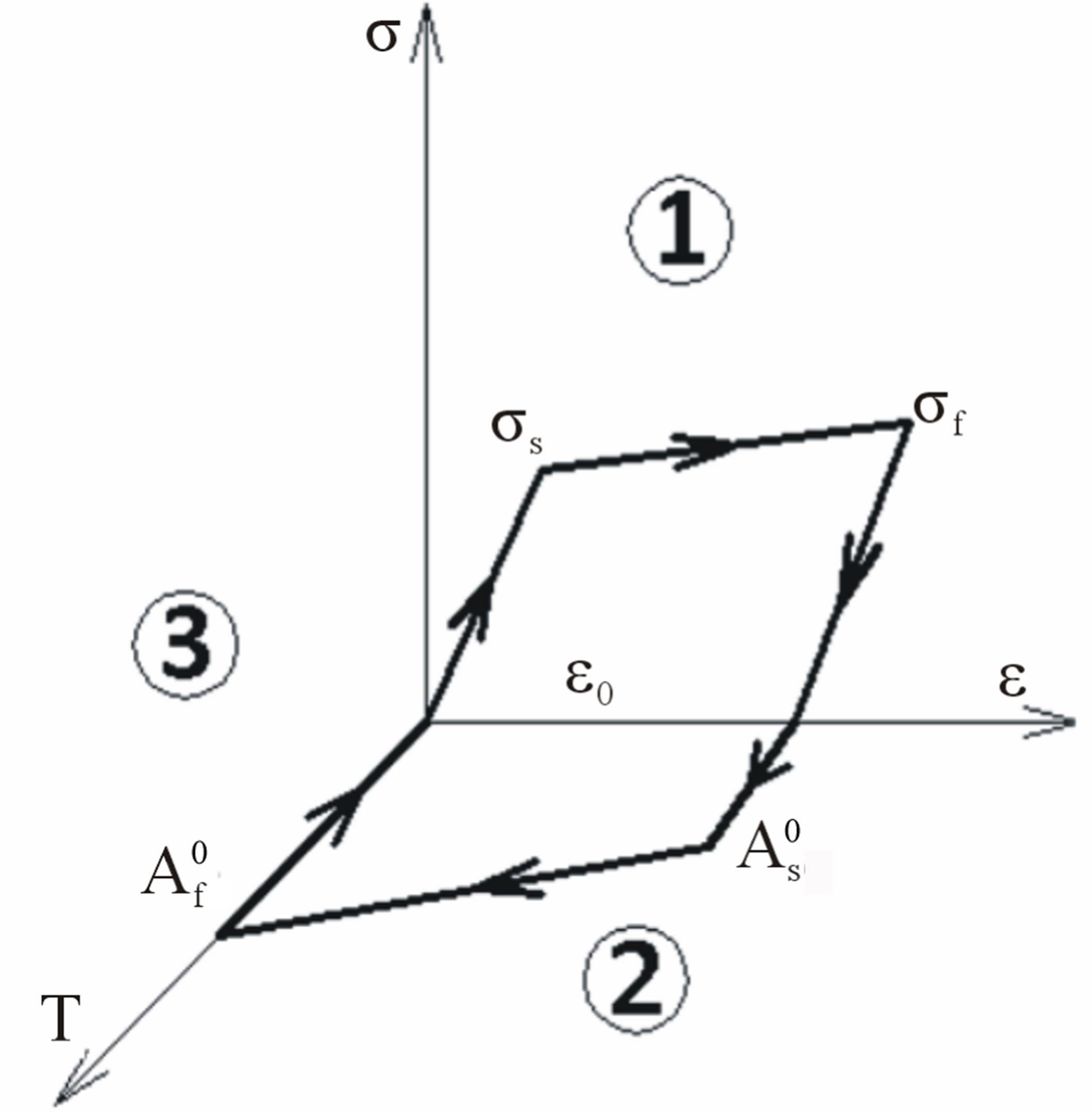
Figure 2. Regions of study.
σ); (ε, T) and axe T:
1) Plane (ε, σ): Region of mechanical loading;
2) Plane (ε, T): Region of thermal loading (heating);
3) Axe T: Region of cooling.
σs: Stress of orientation start of twinned Martensite;
σf: Stress of orientation finish of twinned Martensite;
ε0: Maximum deformation of orientation.
2.3. Constitutive Equations (Figure 3)
In each case, we consider an elementary volume
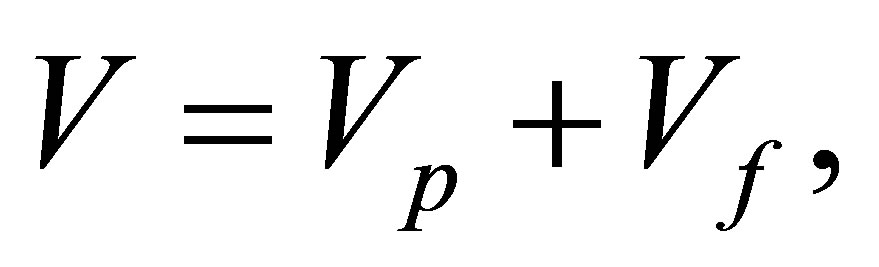
where 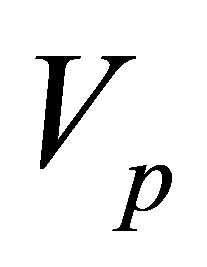 is volume of parent phase and
is volume of parent phase and 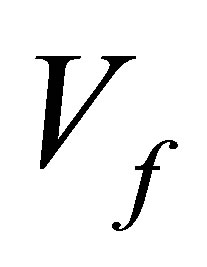 is volume of incipient phase.
is volume of incipient phase.
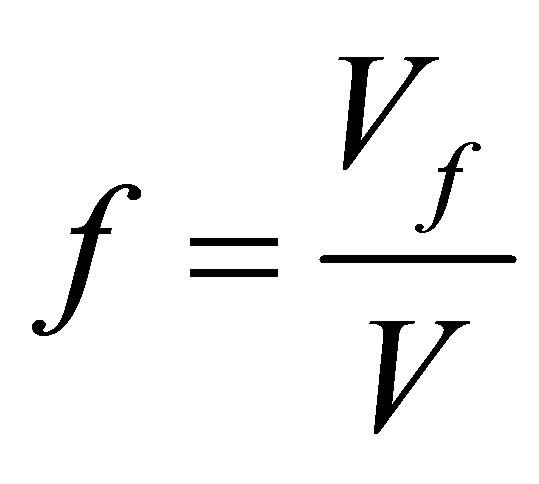
is fraction of incipient phase.
2.3.1. Region 1
Parent phase is twinned Martensite and incipient phase is detwinned Martensite Free energy of Gibbs:
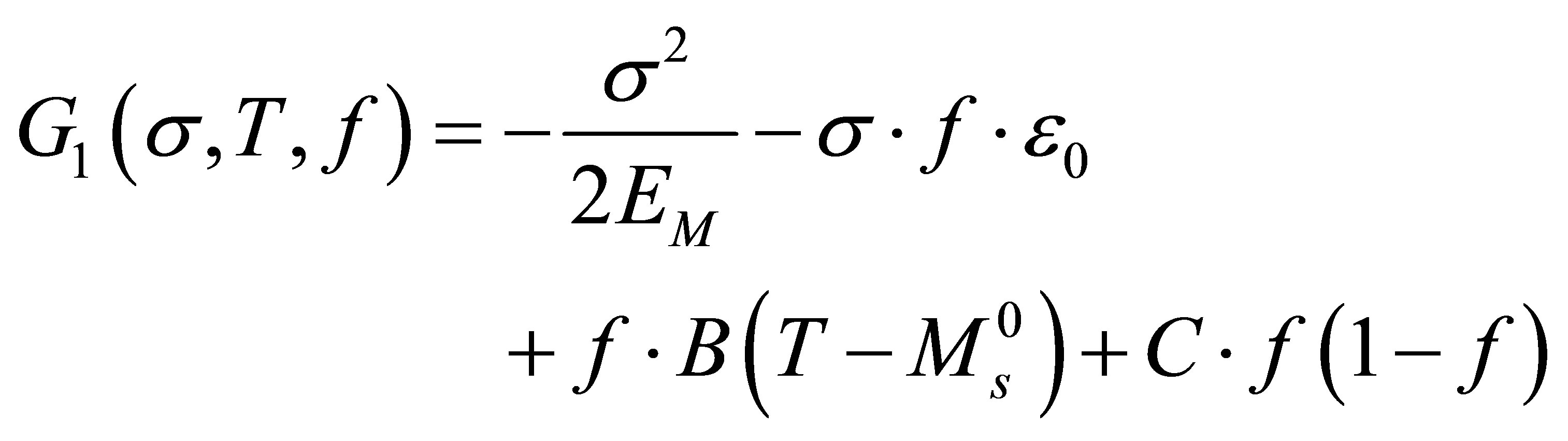 (1)
(1)
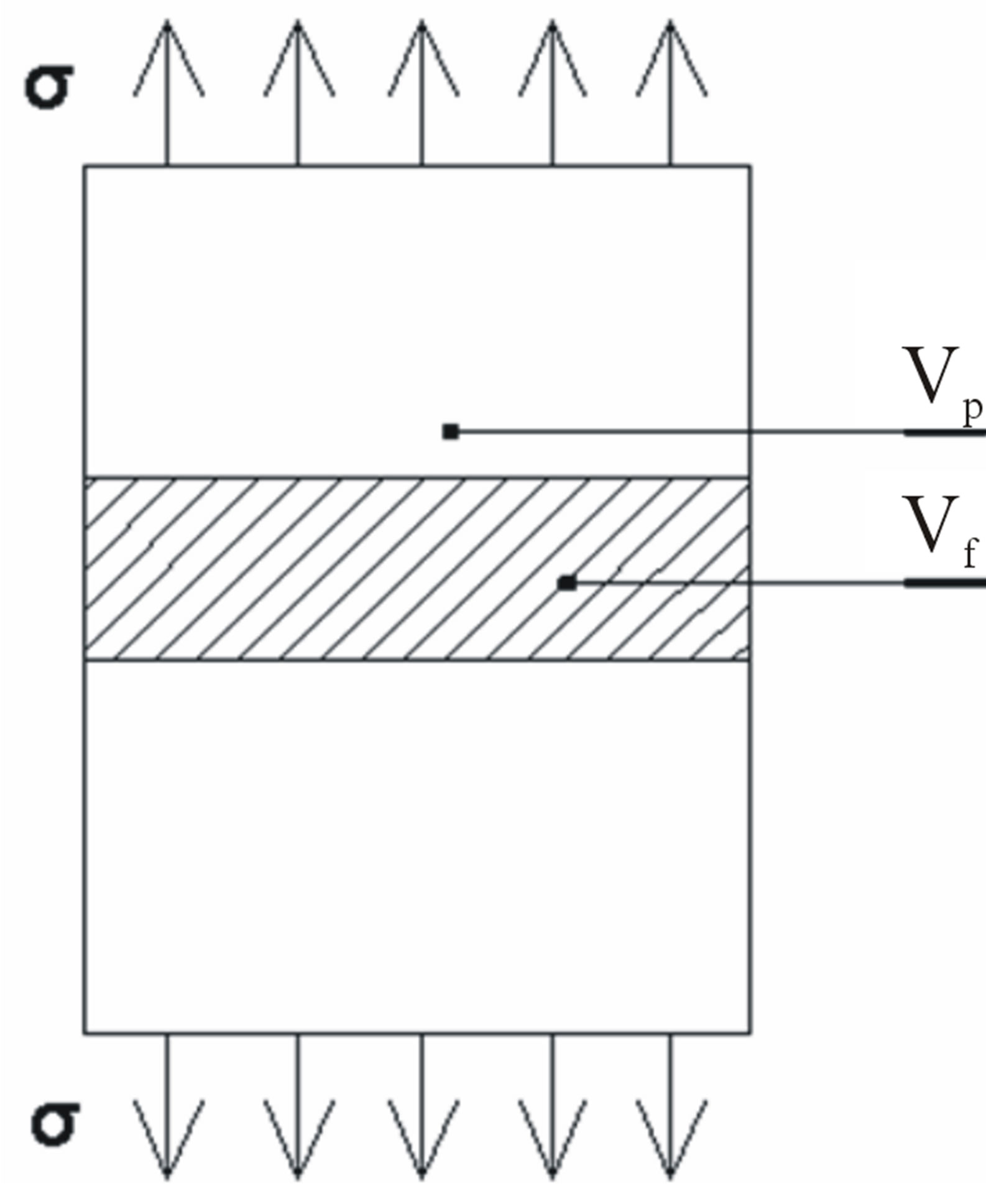
Figure 3. Representative elementary volume.
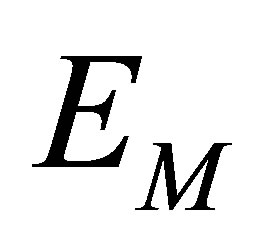 : Young modulus of MartensiteB, C: Coefficients to be determined by tests,
: Young modulus of MartensiteB, C: Coefficients to be determined by tests,
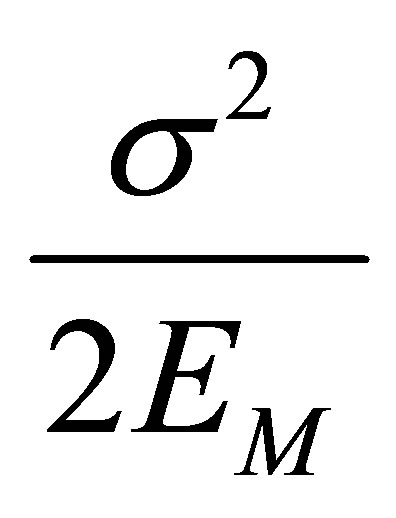 : Elastic energy,
: Elastic energy,
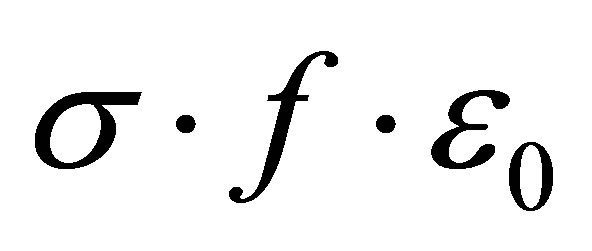 : Energy of deformation due to transformation,
: Energy of deformation due to transformation,
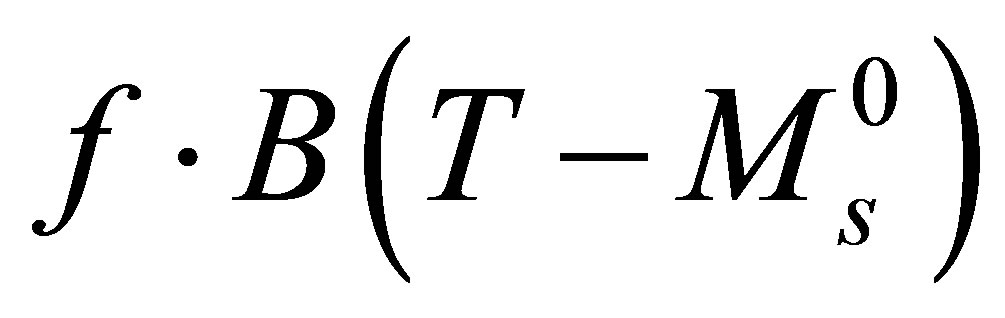 : Free energy of phase change,
: Free energy of phase change,
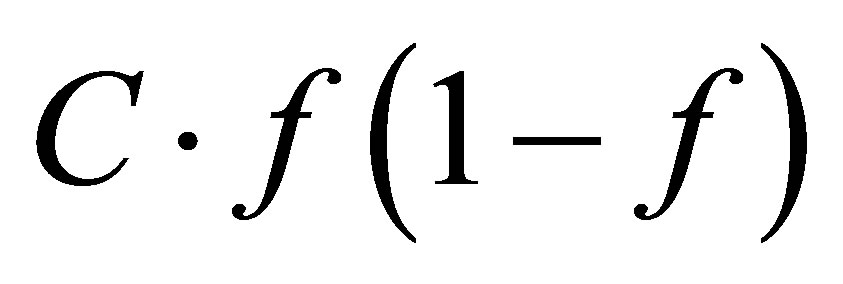 : Energy of interaction between two phases.
: Energy of interaction between two phases.
Assuming that the dissipation occurs during processing Clausius inequality can be written as following:
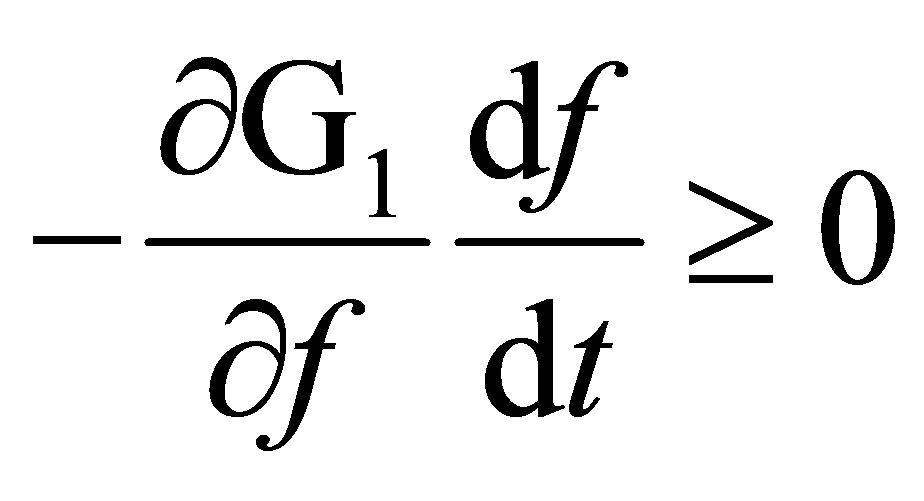 (2)
(2)
Let us write the term:
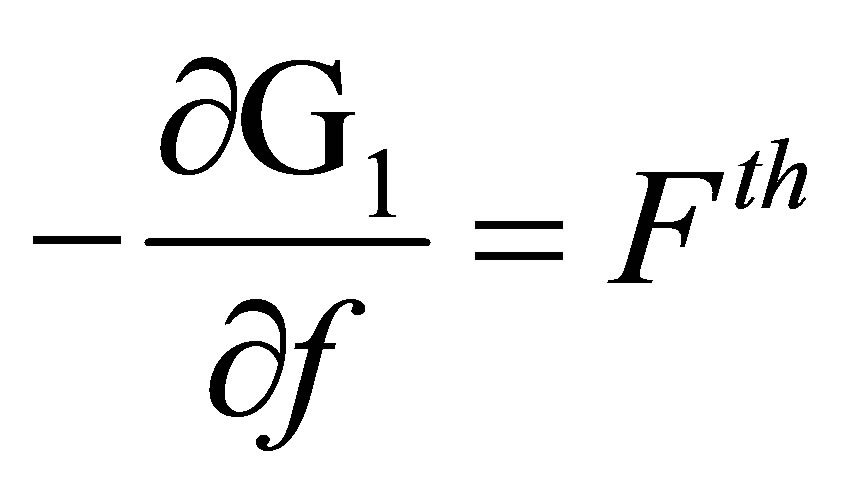
which is the driving force.
The dissipative force can be written:
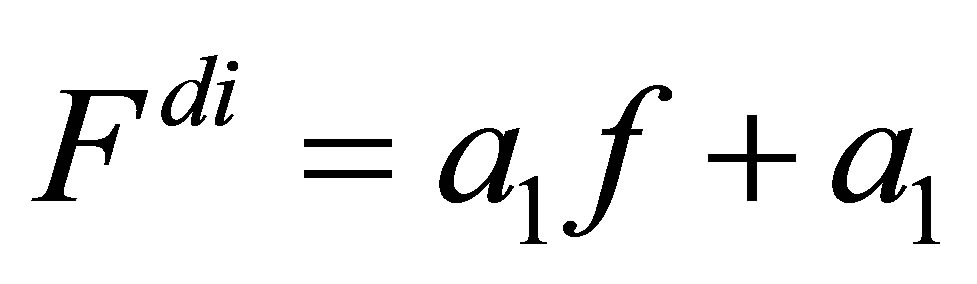 (3)
(3)
The transformation occurs when this condition is satisfied:
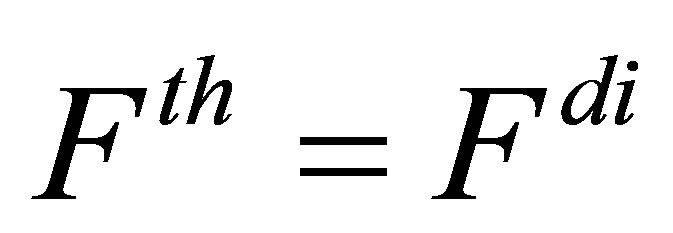 (4)
(4)
It will result:
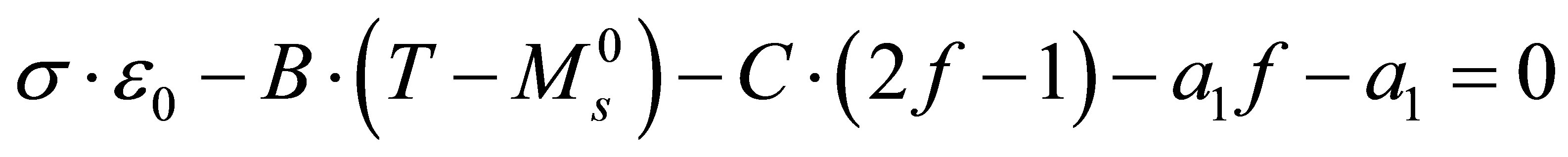 (5)
(5)
Let us use the function:
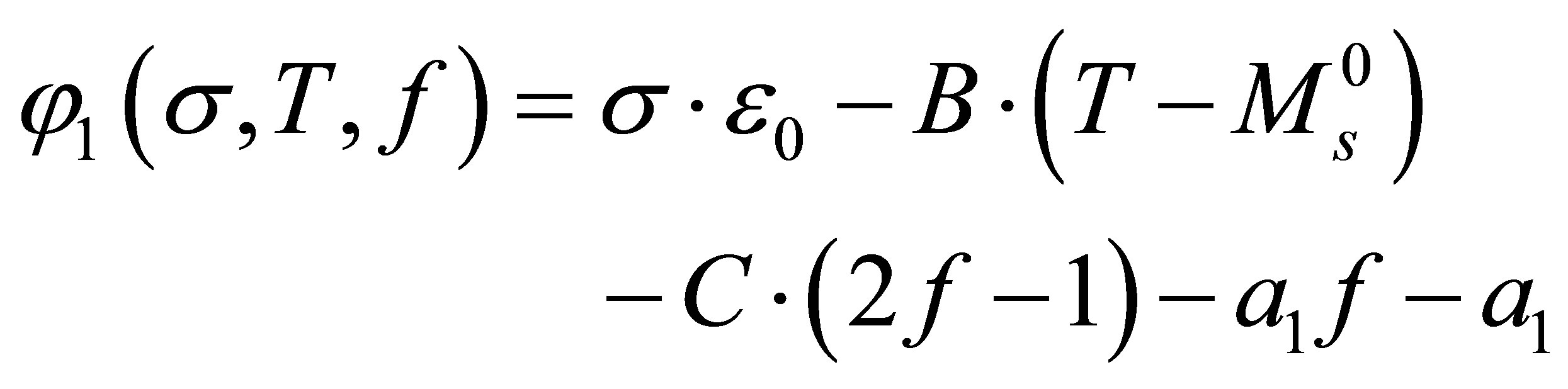 (6)
(6)
To write the evolution of the fraction we use the following expression:
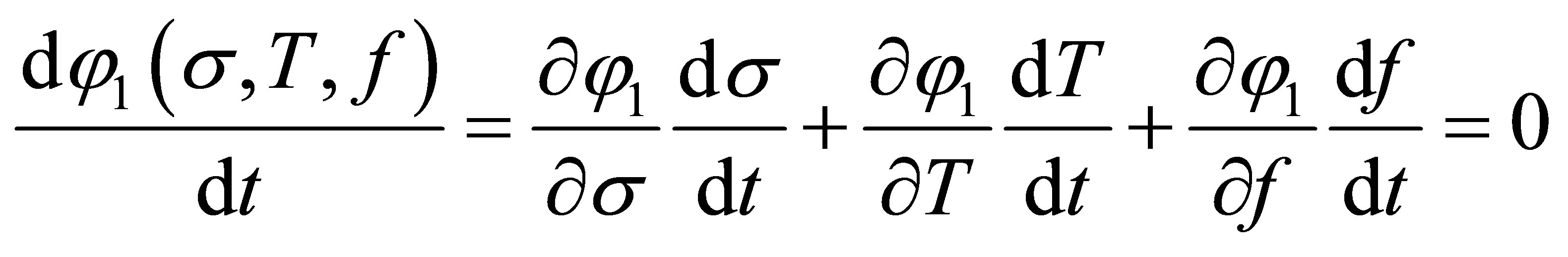 (7)
(7)
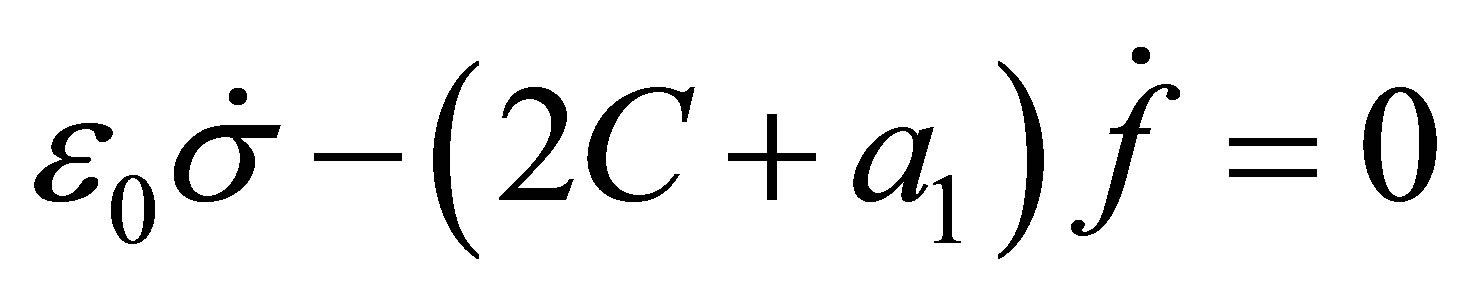 (8)
(8)
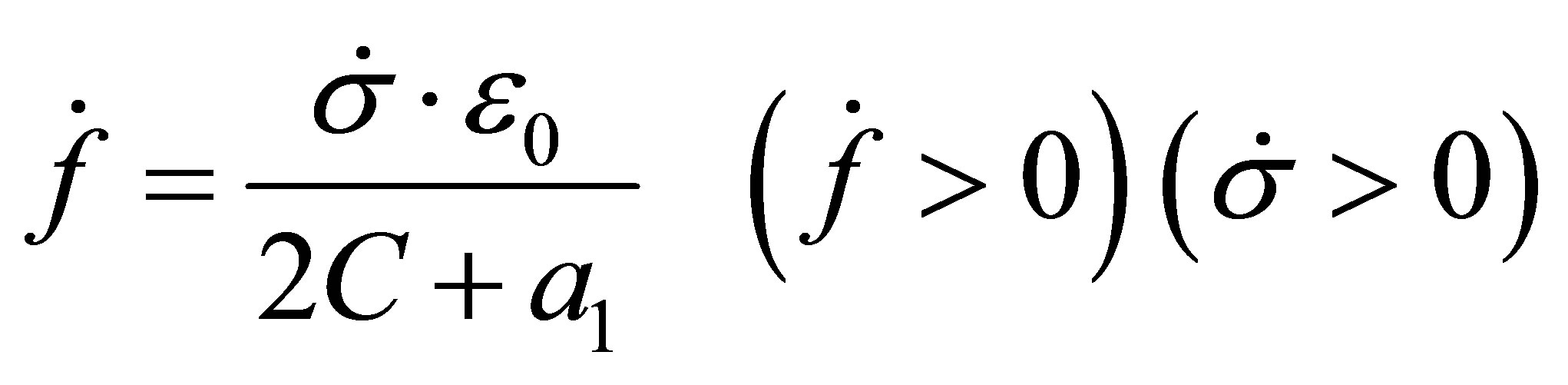 (9)
(9)
The coefficients a1 and C can be determined using limit values of 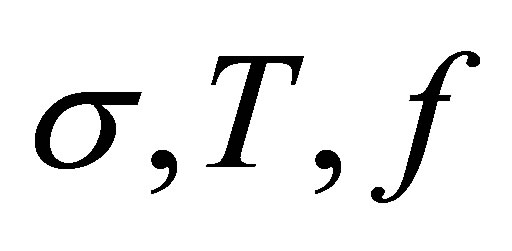 when:
when:
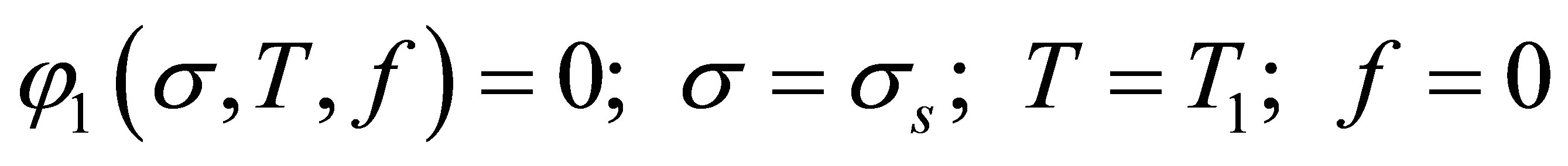 (10)
(10)
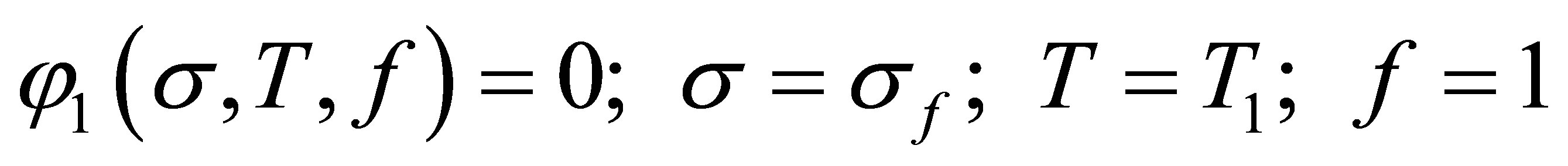 (11)
(11)
It is denoted that parameter B is identified using pseudoelasticity test.
2.3.2. Region 2
Parent phase is detwinned Martensite and incipient phase is Austenite Following the same approach:
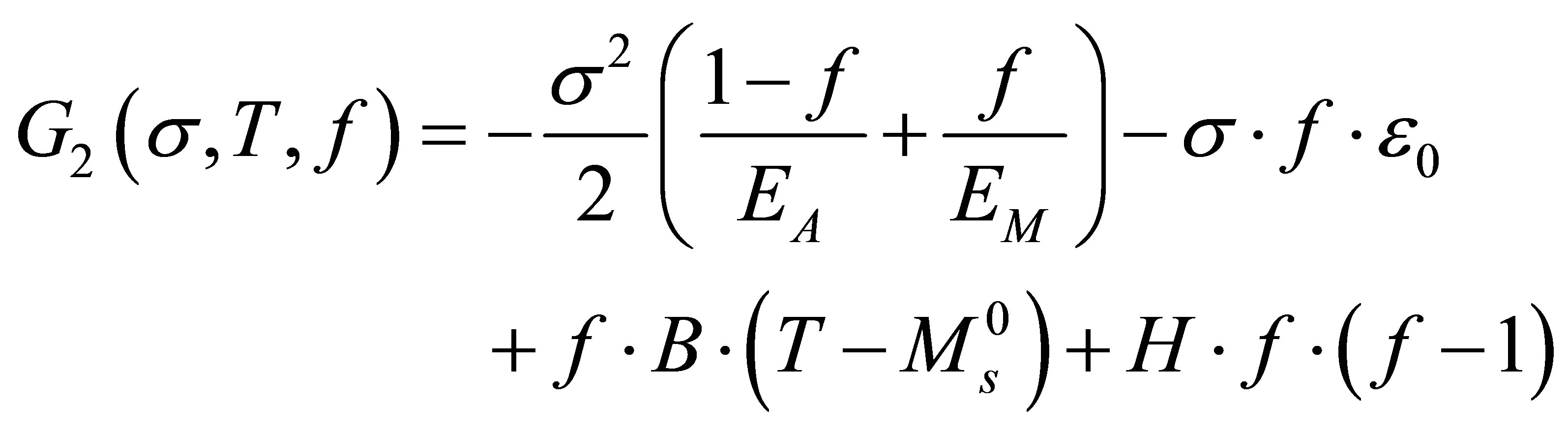 (12)
(12)
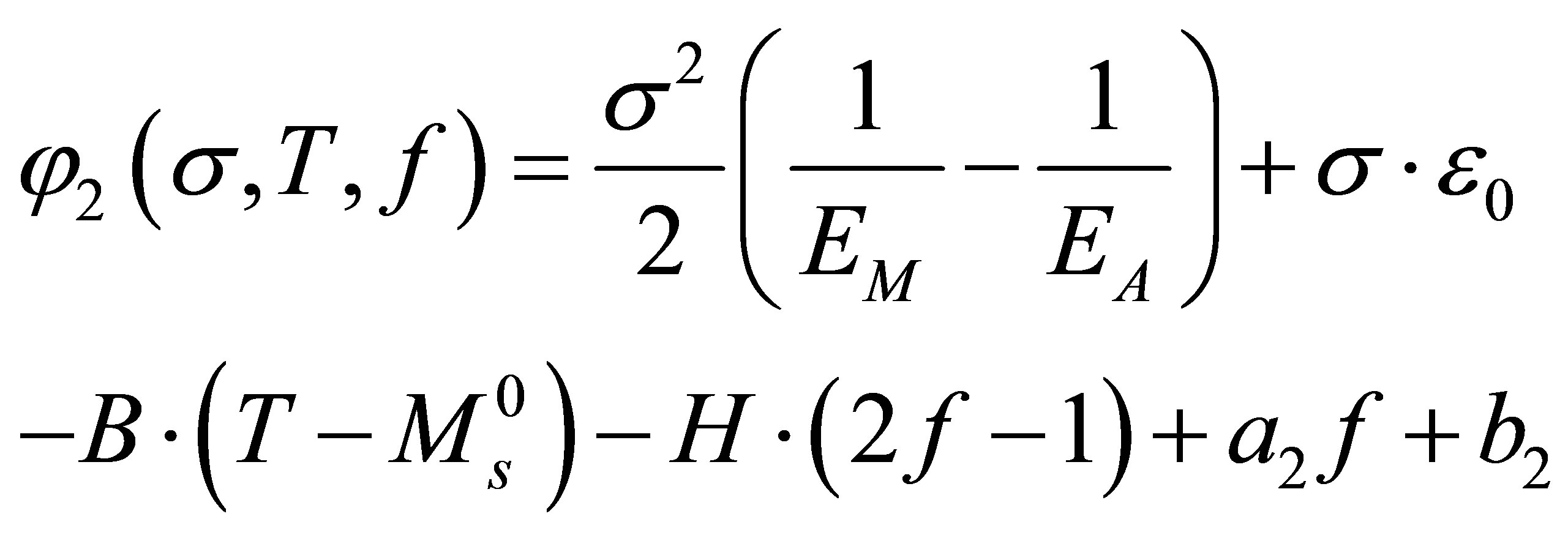 (13)
(13)
Parameter H can also be determined by pseudoelasticity test; the coefficients 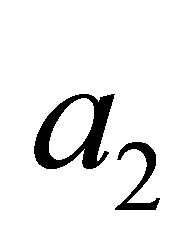 and
and 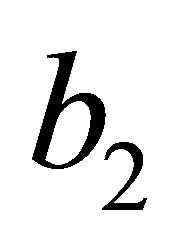 are defined using limit values of
are defined using limit values of 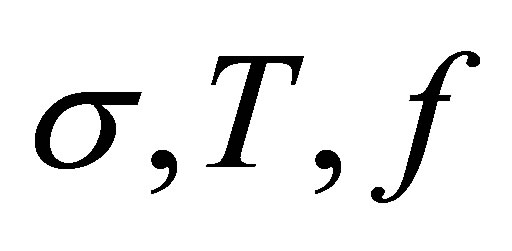 when:
when:
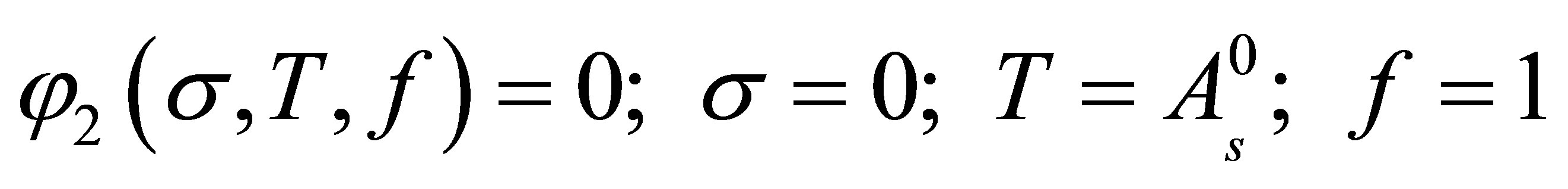 (14)
(14)
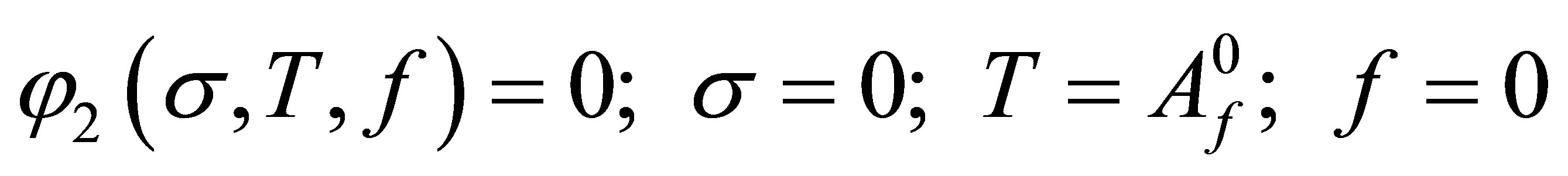 (15)
(15)
The evolution of the fraction of Martensite can be expressed by:
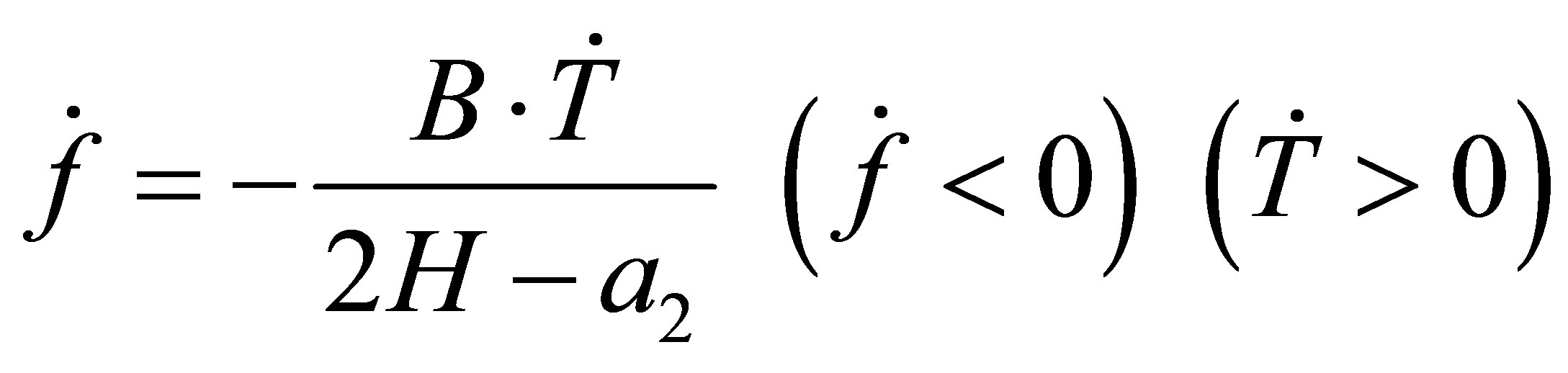 (16)
(16)
2.3.3. Region 3
Parent phase is Austenite and incipient phase is twinned Martensite
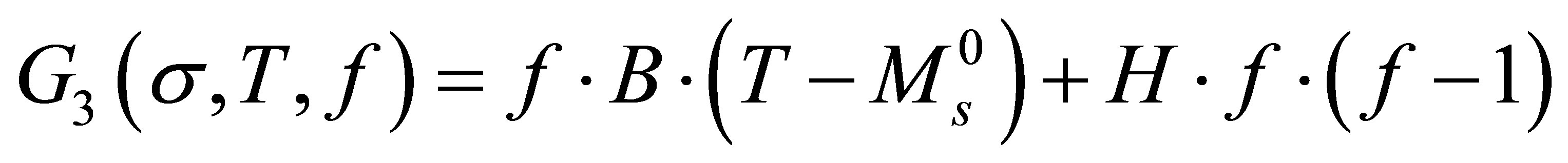 (17)
(17)
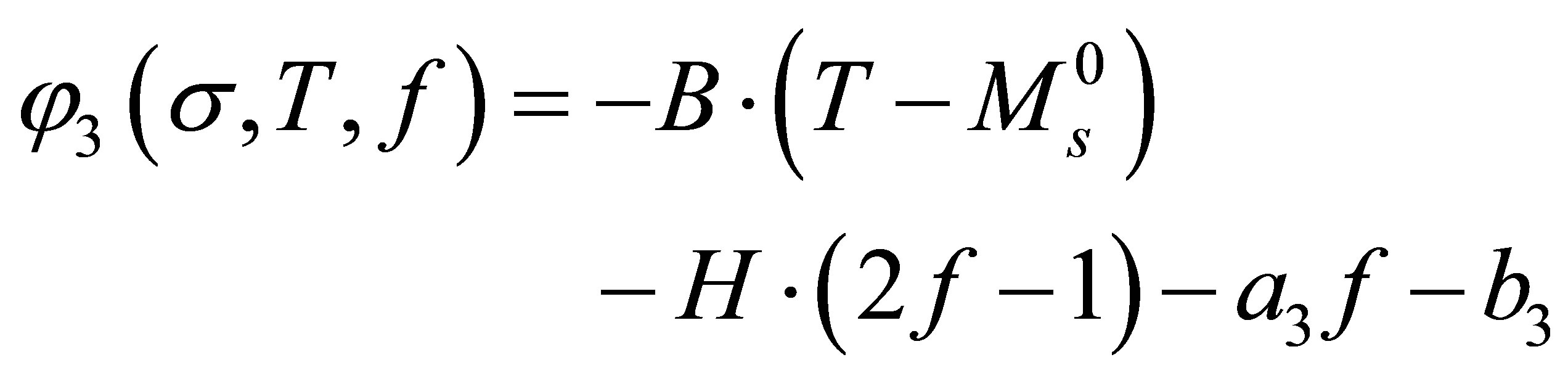 (18)
(18)
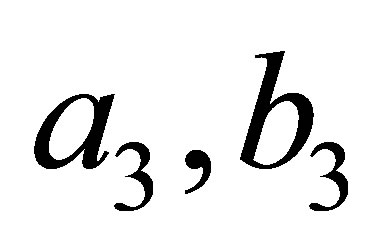 : Parameters to be defined by test using following conditions:
: Parameters to be defined by test using following conditions:
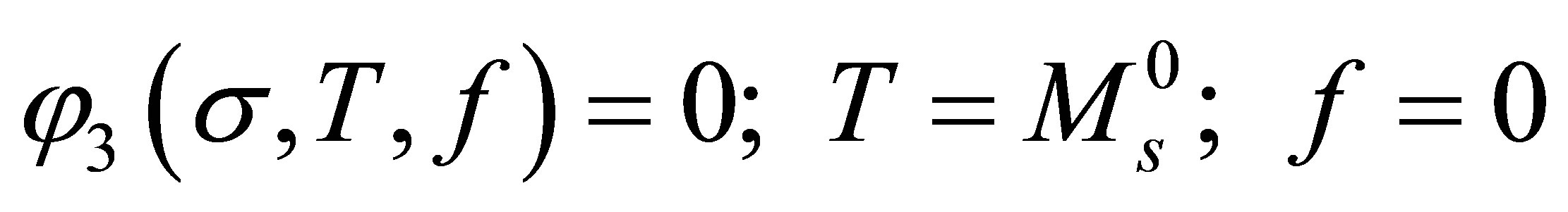 (19)
(19)
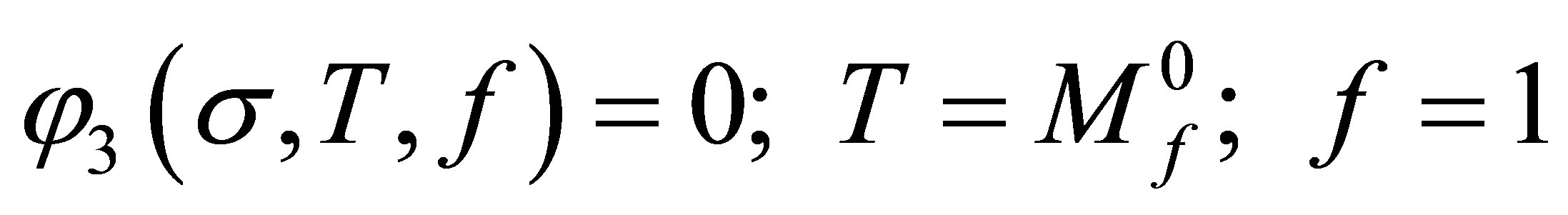 (20)
(20)
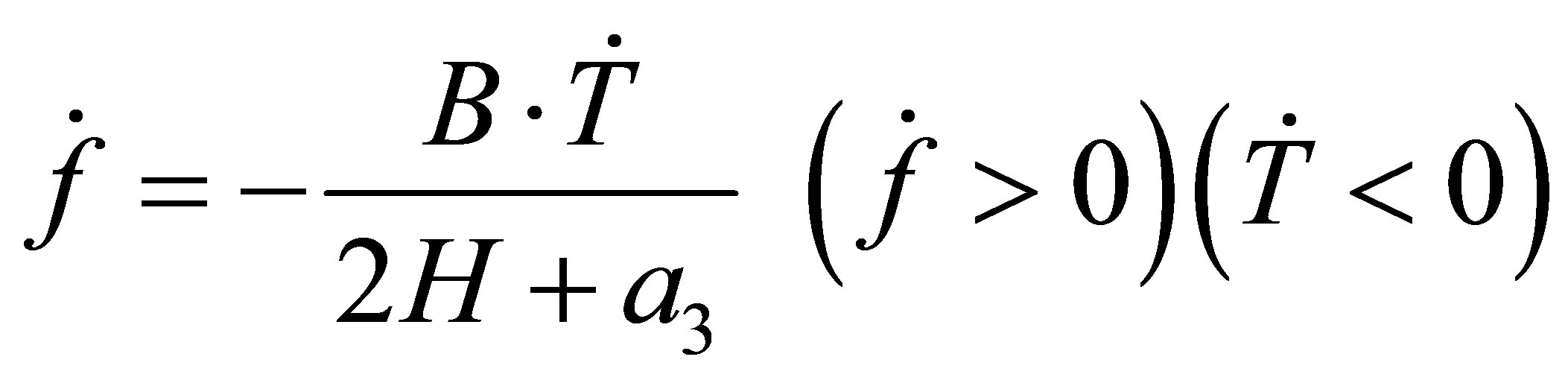 (21)
(21)
2.4. Application of the Model
Using K.L. Ng. and al work [11], where a tensile test was performed on NiTi and the following parameters were determined:

Temperature of orientation loading T1 = 230 K; mechanical load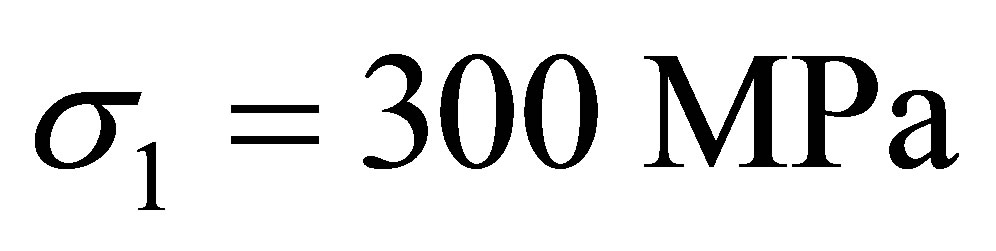 ;
;
3. Results (Figures 4-6)
Discussions
The results obtained coincide well with the experimental
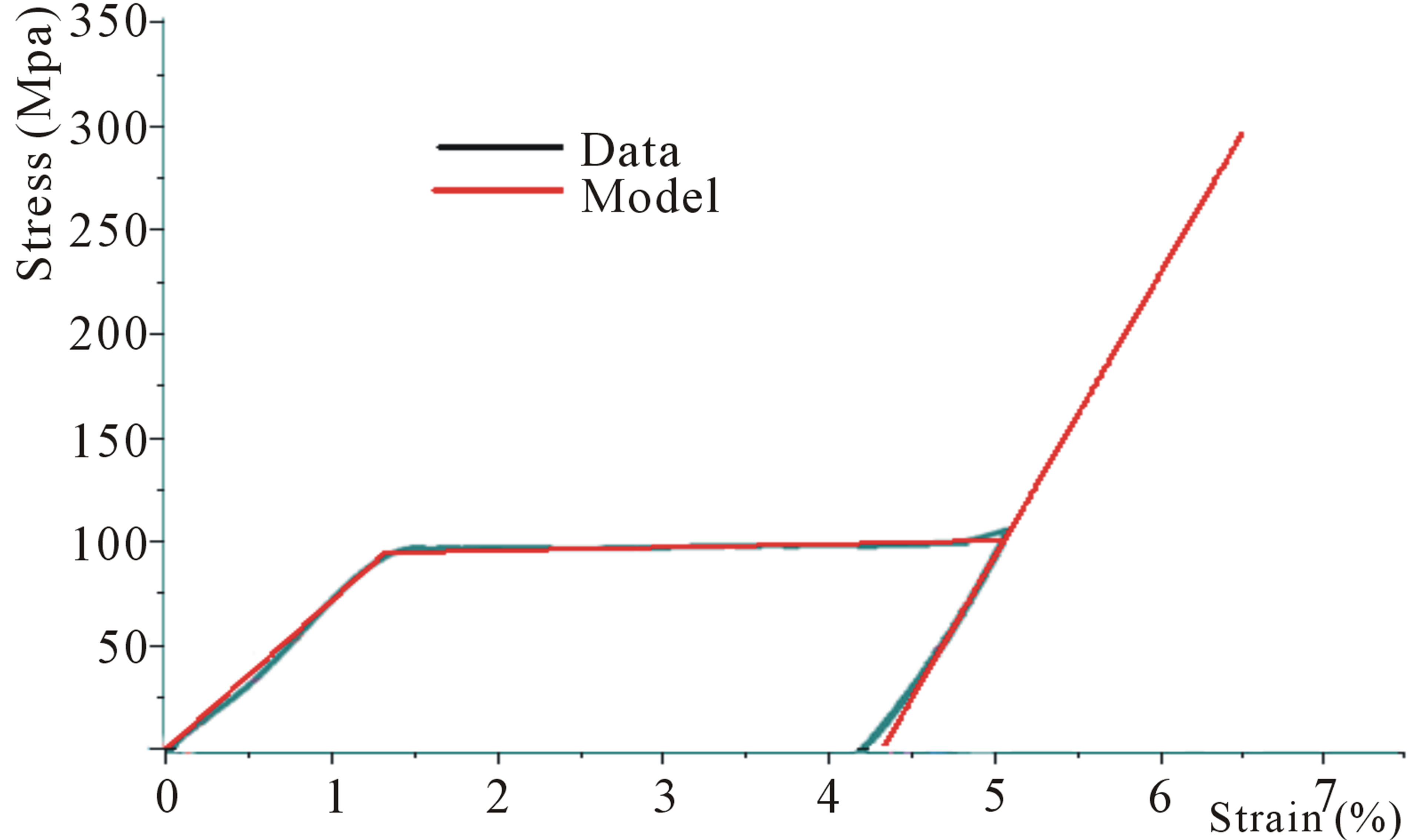
Figure 4. Results of tensile test at T = 23˚C (Test of orientation) performed to validate the model.
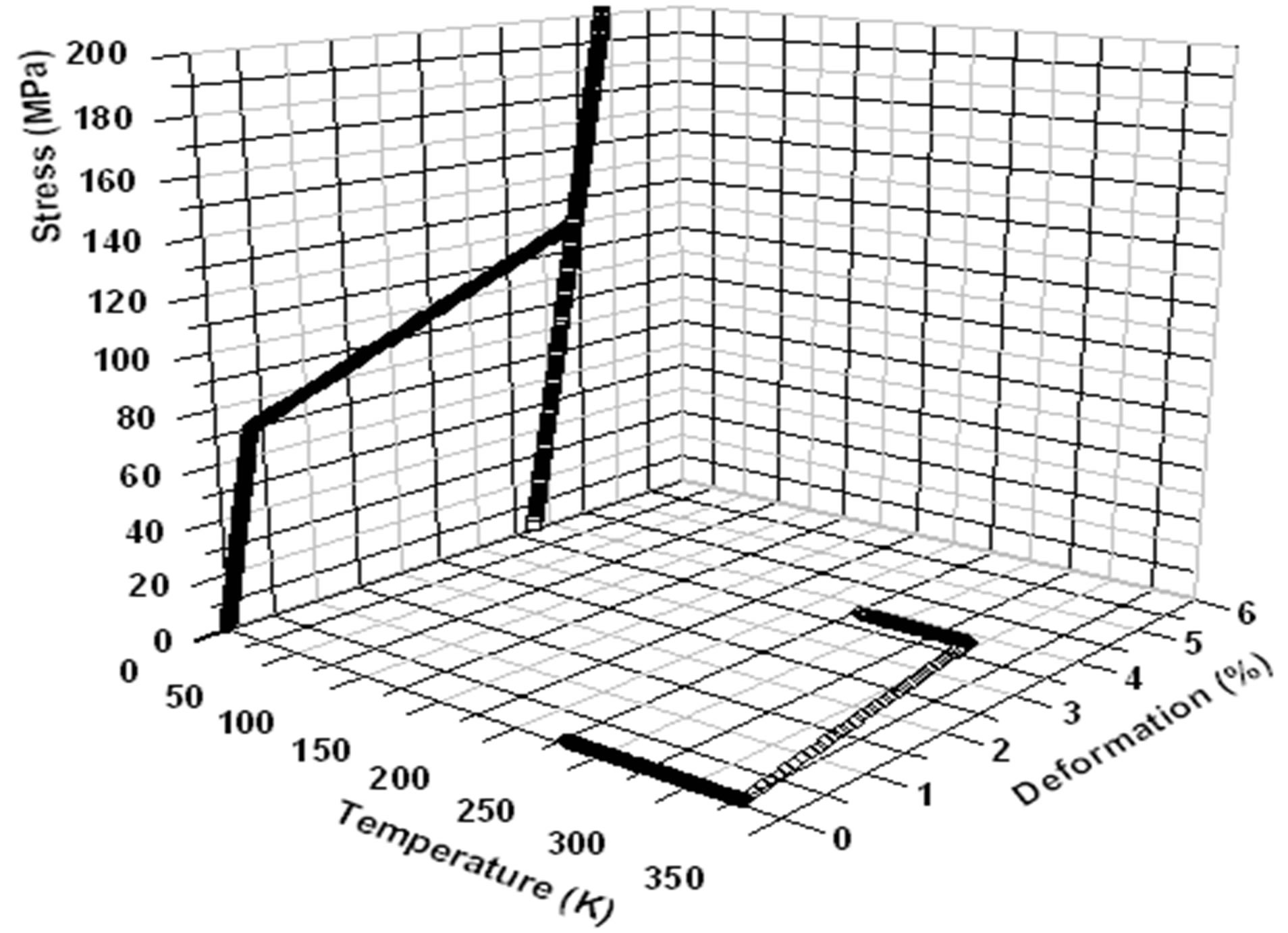
Figure 5. Representation of the shape memory effect in 3D space.
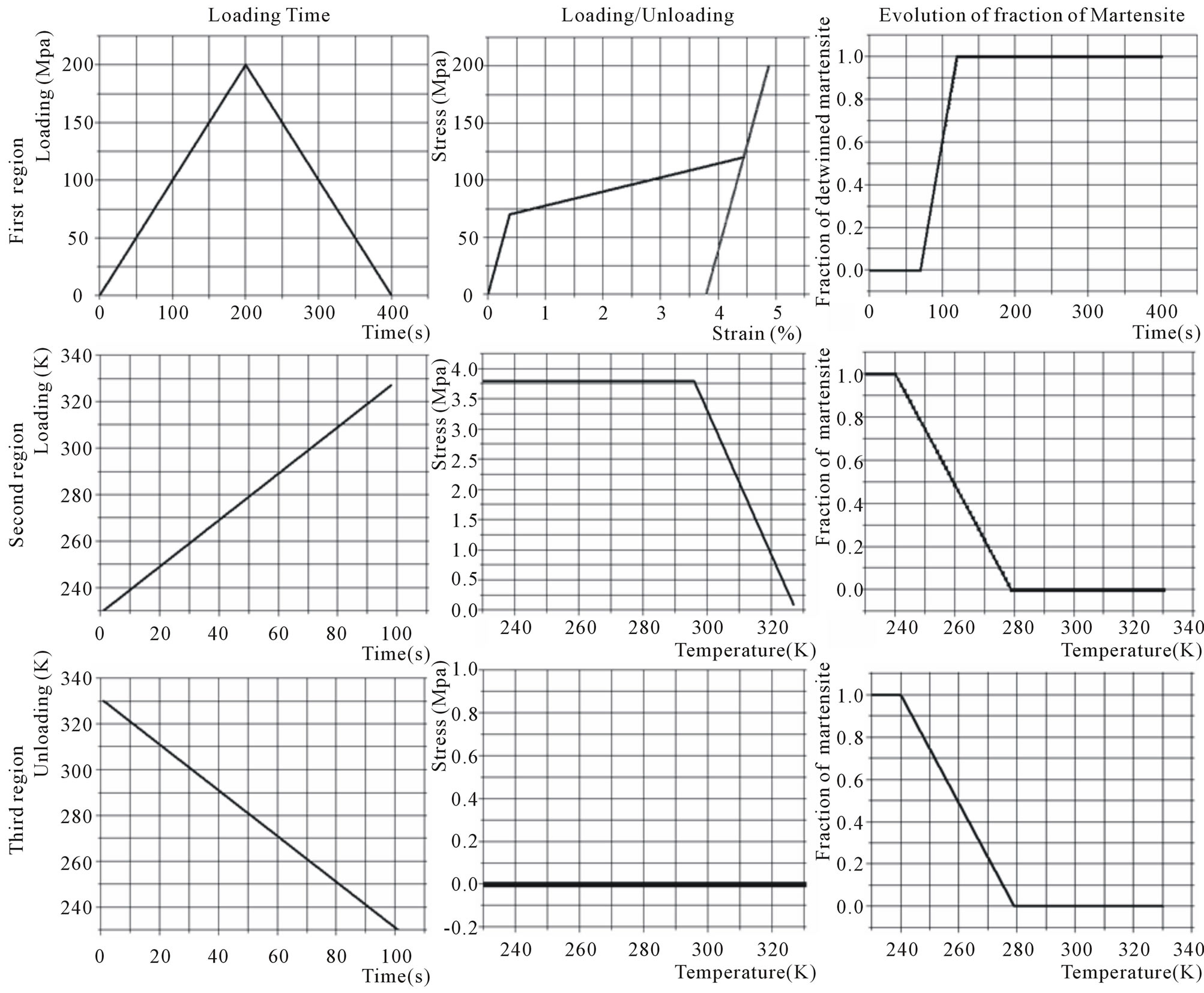
Figure 6. Results of simulation.
data in the case of orientation test, in case of heating to make martensite changing into austenite which occurs with recovering previous deformation and finally changing of martensite into austenite during the cooling. It seems that our results are consistent with practical data of the selected material (NiTi).
In each case we see clearly that deformation is function of transformation of martensite. The cycle beginning from lower temperature reaches the final temperature with recovering the deformation caused by applied mechanical load.
4. Conclusion
This constitutive model presented in this paper was built using a simple formalism. We have divided the work into three parts, and each one has its proper particularities after simulating the model. The results appear in good agreement with experimental data. This model can be used in engineering fields.
REFERENCES
- B. Halphen and Q. S. Nguyen, “Sur les Matériaux Standards Generalisés,” Journal de Mécanique, Vol. 14, 1975, pp. 39-63.
- C. Lexcellent and C. Licht, “Some Remarks on the Modelling of the Thermomechanical Behavior of Shape Memory Alloys,” Journal de Physique IV, Vol.1, No. C4, 1991, pp. C4-35-C4-39.
- D. C. Edelen, “On the Characterization of Fluxes in Nonlinear Irreversible Thermodynamics,” International Journal of Engineering Science, Vol. 12, No. 5, 1974, pp. 397-411. http://dx.doi.org/10.1016/0020-7225(74)90050-0
- K. Tanaka and S. Nagaki, “A Thermomechanical Description of Materials with Internal Variables in the Process of Phase Transformations,” Ingenieur-Archiv, Vol. 51, No. 5, 1982, pp. 287-299. http://dx.doi.org/10.1007/BF00536655
- C. Chu and R. D. James, “Analysis of Microstructures in Cu-14.0%Al-3.9%Ni by Energy Minimization,” Proceedings of the ICOMAT-95, Vol. 5, No. C8, 1995, pp. C8- 143-C8-149.
- R. D. James, R. V. Kohn and T. W. Shield, “Modeling of Branched Needle Microstructures at the Edge of a Martensite Laminate,” Proceedings of the ICOMAT-95, Vol. 5, No. C8, 1995, pp. C8-253-C8-259.
- C. Lexcellent, B. C. Goo, Q. P. Sun and J. Bernardint, “Characterization, Thermomechanical Behaviour and Micromechanical-Based Constitutive Model of Shape-Memory Cu-Zn-Al Single Crystals,” Acta Materialia, Vol. 44, No. 9, 1996, pp. 3773-3780. http://dx.doi.org/10.1016/1359-6454(95)00452-1
- S. Govindjee and G. J. Hall, “A Computational Model for Shape Memory Alloys,” International Journal of Solids and Structures, Vol. 37, No. 5, 2000, pp. 735-760. http://dx.doi.org/10.1016/S0020-7683(99)00048-7
- M. Berveiller, E. Patoor and M. Buisson, “Thermomechanical Constitutive Equations for Shape Memory Alloys,” Journal de Physique IV, Vol. 1, No. C4, 1991, pp. C4-387-C4-396.
- E. Patoor, A. Eberhardt and M. Berveiller, “On Micromechanics of Thermoelastic Phase Transition,” Proceedings of Plasticity 93: The 4th International Symposium on Plasticity and Its Applications, Baltimore, 19-23 July 1993.
- K. L. Ng and Q. P. Sun, “Stress-Induced Phase Transformation and Detwinning in NiTi Polycrystalline Shape Memory Alloy Tubes,” Mechanics of Materials, Vol. 38, No. 1-2, 2006, pp. 41-56. http://dx.doi.org/10.1016/j.mechmat.2005.05.008
NOTES
*Corresponding author.

