Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.03(2016), Article ID:67740,8 pages
10.4236/jhepgc.2016.23028
Cosmological Constant and Energy Density of Random Electromagnetic Field
Ilya A. Obukhov
Research & Development Company “System Recourses”, Moscow, Russia

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 April 2016; accepted 25 June 2016; published 28 June 2016
ABSTRACT
It is shown that the non-equilibrium electrically neutral and relativistically invariant vacuum-like state with the negative energy density and positive pressure may exist at the non-zero temperature in the system of spinor particles, antiparticles, and random electromagnetic field generated by particle-particle, particle-antiparticle, and antiparticle-antiparticle transitions. At the temperature of the order of 10−5 K, the energy density of its state corresponds to the dark energy density in absolute magnitude. The cosmological constant for such material medium turns out to be negative.
Keywords:
Dark Energy, Cosmological Constant, Stochastic Electromagnetic Field, Spinor Particles

1. Introduction
Article [1] shows that the quantum theory allows building up the relativistically invariant state of matter, for which pressure p and energy density 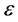 are related as follows
are related as follows
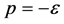 (1)
(1)
Interest in the investigation of such states is related to search for the physical interpretation of the cosmological constant in the Einstein’s equations [1] - [3] and dark energy nature [4] - [6] .
If a material medium exists, whose energy-momentum density tensor is expressible in the following form
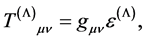 (2)
(2)
then the cosmological constant  in the Einstein’s equations [1] can be related to the energy density of such medium
in the Einstein’s equations [1] can be related to the energy density of such medium 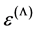
 . (3)
. (3)
Here G is the gravitation constant, c is the velocity of light. In case of the empty flat space, when the Minkovsky’s tensor 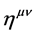 with
with 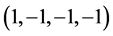 diagonal is the metric tensor
diagonal is the metric tensor , energy density
, energy density  and pressure
and pressure 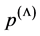 obviously satisfy the relationship (1).
obviously satisfy the relationship (1).
If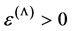 , then negative pressure
, then negative pressure  can be interpreted [4] [6] as the cause of the antigravity. The opposite possibility, where
can be interpreted [4] [6] as the cause of the antigravity. The opposite possibility, where  [1] [2] , is not also excluded. In such a case, the gravitational attraction between massive objects starts increasing at the distances exceeding some threshold one.
[1] [2] , is not also excluded. In such a case, the gravitational attraction between massive objects starts increasing at the distances exceeding some threshold one.
The cosmological constant problem is particularly relevant in the context of the experimental confirmation of the accelerated expansion of the Universe [6] . However, this phenomenon can be explained not only with the help of the General Relativity, but also by the different alternative versions of the Gravity Theory (see [7] and the articles cited there), where dark energy concept isn’t introduced. In paper [7] it is shown that the analysis of the interference of gravitational waves will allow making a choice for that or another Gravity Theory.
Experimental discovery of gravitational waves [8] allows hoping for increasing of our understanding of the nature of gravitation. Data obtained now confirm justice of the General Relativity [8] . But it is only the first experiments and it is not enough for final conclusions.
In any case, up to date, the material medium model-building problem, for which relationship (1) is true and density
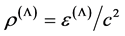 (4)
(4)
is close, at least in the order-of-magnitude, to the value of
resulted from the interpretation of astrophysical data [6] that has not been solved. Solving this problem seems important for the understanding of potential physical phenomena leading to the formation of such material medium.
2. Energy-Momentum Tensor of Random Electromagnetic Field
Let us consider the model where the electromagnetic field tensor

is governed by the Maxwell’s equations

with random source 

We consider that for flow density 

and for potential 

Suppose, devices available enable measuring only some time interval and/or volume mean values, which will be indicated with brackets

but at the same time for decomposition components 


the following relationship is true:

where 
The formal solution of Equations (6) for 

taking into account Decomposition (10), can be written down in the following form

where

Let us determine energy-momentum density tensors of electromagnetic field 


These tensors can be presented using quadratic combinations




Suppose, tensor 







Here indices e and h pertain to particles and antiparticles, respectively; 




indices r and 





the Fermi-Dirac distribution function;



Vectors 

where 



and normalization conditions

It is easy to show that the relations of orthogonality are true

With account of these definitions, Expressions (25), and the formula for the transition from the summation over composite index 

we obtain from Relationships (16.1) and (16.2)





where 
3. Energy Density and Pressure of Interacting Mixture
Assume, the inequations are true

i.e. particle and antiparticle gases are degenerating ones. Let us consider the range of temperature and chemical potential values that satisfy the following conditions:

Here 


In the frame of reference where


related to the components of the energy-momentum tensor by simple relationships

The following formulas are true under Conditions (28) in the same frame of reference for concentrations of particles and antiparticles 




The condition of electroneutrality of the particle and antiparticle gases mixture has the following form

whence it follows that

In such a case, we obtain for the total energy density and pressure


The energy density and pressure of electrically neutral particle and antiparticle gases mixture will be relativistically invariant in two cases [1] where
and where condition (1) is met. In the first case, we obtain from Equations (35.1) and (35.2)

Furthermore, according to Formulas (32.1), concentrations of particles and antiparticles are zero.
In the second case, we obtain the condition of implementing the electrically neutral and relativistically invariant state for the mixture under consideration from Relationships (1), (35.1) and (35.2)

Here the Fermi momentum and temperature, at which conditions (1) is met, are indicated using 


The following expressions are true for the concentrations of particles and antiparticles, energy density and pressure of the mixture


We receive the following from Formulas (3), (4), and (38.2) for the cosmological constant and dark energy density


Here the following is specified

−a dimensionless value representing a gravitational analogue of the fine structure constant in terms of the build-up method, if m is the mass of electron, then
is the analogue of the Compton wave-length
for an object with the energy equal to
If e and m are the charge and mass of electron, and dark energy density


The second of Formulas (39.2) for density 


Note that the contribution of the random electromagnetic field, including the contribution of interaction of this field with particles and antiparticles, to the total energy density in absolute magnitude is thrice as much as the contributions of particles and antiparticles equal to each other

Just due to the random electromagnetic field generated by transitions between particles and antiparticles, the state that satisfies Condition (1) is possible in the system studied.
In the approximation considered, energy density 



Furthermore, the energy dominance [2] is disrupted for 

4. Conclusions
The model of the material medium, for which the electrically neutral relativistically invariant state with non-zero energy density, pressure, concentrations of particles and antiparticles is possible, has been considered. At the same time particles and antiparticles are in the thermal equilibrium, but far from the chemical equilibrium state governed by the equality of their chemical potentials. In the considered case, the expression is true

This non-equilibrium electrically neutral state exists due to the random electromagnetic field generated by spontaneous transitions between particles and antiparticles being in different quantum states. The average vector potential and intensity of this field are zero. But the average components of the energy-momentum density tensor in the random process of transitions between the states of particles and antiparticles are non-zero.
The energy density of the above vacuum-like state can be expressed in terms of its temperature
If the energy density of the system considered is identified with the dark energy density, then temperature 

Cite this paper
Ilya A. Obukhov, (2016) Cosmological Constant and Energy Density of Random Electromagnetic Field. Journal of High Energy Physics, Gravitation and Cosmology,02,312-319. doi: 10.4236/jhepgc.2016.23028
References
- 1. Zel’dovich, Ya.B. (1968) The Cosmological Constant and the Theory of Elementary Particles. Soviet Physics Uspekhi, 11, 381-393. http://ufn.ru/ru/articles/1968/5/m/
- 2. Zel’dovich, Ya.B. (1981) Vacuum Theory: A Possible Solution to the Singularity Problem of Cosmology. Soviet Physics Uspekhi, 24, 216-230. http://ufn.ru/ru/articles/1981/3/c/
- 3. Gliner, E.B. (1966) Algebraic Properties of the Energy-Momentum Tensor and Vacuum-Like States of Matter. Soviet Physics JETP, 22, 378-382. http://www.jetp.ac.ru/cgi-bin/r/index/e/22/2/p378?a=list
- 4. Chernin, A.D. (2008) Dark Energy and Universal Antigravitation. Physics-Uspekhi, 51, 253-282.
http://ufn.ru/ru/articles/2008/3/c/ - 5. Lukash, V.N. and Rubakov, V.A. (2008) Dark Energy: Myths and Reality. Physics-Uspekhi, 51, 283-289. http://ufn.ru/ru/articles/2008/3/d/
- 6. Chernin, A.D. (2013) Dark Energy in Systems of Galaxies. JETP Letters, 98, 394-407.
http://www.jetpletters.ac.ru/ps/2018/article_30426.pdf
http://dx.doi.org/10.1134/S002136401319003X - 7. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282.
http://dx.doi.org/10.1142/S0218271809015904 - 8. Abbott, B.P., et al. (2016) Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters, 116, 061102-01-061102-16.
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.116.061102
http://dx.doi.org/10.1103/physrevlett.116.061102 - 9. de Groot, S.R., van Leeuwen, W.A. and van Weert, Ch.G. (1980) Relativistic Kinetic Theory. Principles and Applications. North-Holland Publishing Company, Amsterdam, New York and Oxford.









