Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.04(2016), Article ID:70013,8 pages
10.4236/jhepgc.2016.24042
Geddanken Experiment for Quark Star Idea, Quantum Wavelength Limit, Minimum Time, and Early Universe Temperature, from First Principles
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 4, 2016; Accepted: August 21, 2016; Published: August 24, 2016
ABSTRACT
We initially look at a non singular universe representation as given by Rovelli and Vidotto, in terms of a quantum bounce, via minimum mass quark stars, as a start of how to estimate of entropy and also of the number of operations of an expanding universe. The bench mark used is, to after considering a quark star, to look at the mass of a universe, estimated, and from there, we can obtain the entropy if we look at the Schwartzshield radii of a universe, and then the radii of the universe about 380,000 years after the big bang. In the latter, we show how to get the number of operations as akin to the reasoning used by Seth Lloyd, in 2001, and also from there close with a few comments as to the “naturalness” of heavy Gravity from this formulation of entropy, which is based upon a start of considering what is a Planck star, as far as minimum quantum effects in Black hole physics, and by extension early universe cosmology.
Keywords:
Quark Star Idea, Quantum Wavelength Limit, Early Universe Temperature

1. Introduction, Setting up for Calculation of Using the Results of Initial Temperature T as a Way to Answer Initial Time Step Value, Initial Energy, and Also Entropy of the Universe, from First Principles
In making the initial assumptions, we will be considering what was brought up by S. Carroll in [1] which reads as follows: If we assume that there is a Schwartzshield radius of the universe, we have to directly qualify it by saying that we are assuming flatness, as a result of inflation, almost from the beginning. We also state that the universe is NOT a black hole, and that we use the Swchwartzschield radii as an approximation only for the purpose of getting initial conditions. Here is what Carroll put in which we quote.
Quote:
You can figure this out by looking at the Friedmann equation, which relates the Hubble parameter to the energy density and the spatial curvature of the universe. The radius of our observable universe is basically the Hubble length, which is the speed of light divided by the Hubble parameter. It’s a straightforward exercise to calculate the amount of mass inside a sphere whose radius is the Hubble length (M = 4πc3H−3/3), and then calculate the corresponding Schwarzschild radius (R = 2GM/c2). You will find that the radius equals the Hubble length, if the universe is spatially flat. Voila!
End of quote.
Our approximation assumes that right after the Pre Planckian regime of space time, that we approach flatness.
In the Pre Planckian space time, we assume that there is a regime of space-time involving a different uncertainty principle than the usual Heisenberg, which we state below.
Start first from [2]
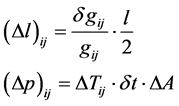 (1)
(1)
If we use the following, from the Roberson-Walker metric [2] [3] .
 (2)
(2)
Following Unruth [4] [5] , write then, an uncertainty of metric tensor as, with the following inputs.
 (3)
(3)
Then, the surviving version of Equation (1) and Equation (2) is, then, if 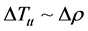 [4] [5]
[4] [5]
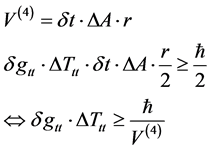 (4)
(4)
This Equation (4) is such that we can extract, up to a point the HUP principle for uncertainty in time and energy, with one very large caveat added, namely if we use the fluid approximation of space-time [6] .
 (5)
(5)
Then by [2]
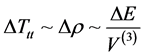 . (6)
. (6)
Then,
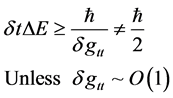 (7)
(7)
This above is what is within the Schwartzshield radius, but also within the Pre- Planckian spacetime regime. In place of a traditional black hole, we have a break from the usual uncertainty relationship. I wish to thank the referee whom pointed out that, of course, that the early universe is not a black hole. However as far as early universe models, the following can be referenced. i.e. look at Valev, as of [7] as to how the Schwarzshield radius of the Universe is commensurate as to the Hubble radius today. i.e. see the work done past Equation (4) of the reference [7] to get: if 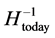 is the inverse of the present Hubble’s law expansion parameter of today, then by [7]
is the inverse of the present Hubble’s law expansion parameter of today, then by [7]
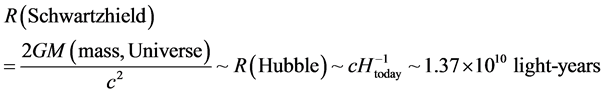 (8)
(8)
Without making too much of it, we will be assuming that in the early universe, the same equivalence shows up, i.e. for the very early universe
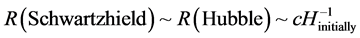 . (9)
. (9)
Within the Hubble radius, as within the presumed Schwartzhield radius, we are assuming that Equation (7) holds, and that right afterwards, the following holds, i.e. Just outside the Hubble “radius” we will be evaluating we assume that instead of Equation (7) that the usual uncertainty principle holds.
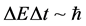 (10)
(10)
This usual treatment of the uncertainty principle holds for space-time just outside the radius as given in Equation (9) whereas Equation (7) would hold for just within the calculated radius as given by Equation (9). Having said that, we will proceed with the thermodynamics of what happens as to the boundary of space-t9me delineated by Equation (9).
We follow what Ha wrote up [1] [8] that there is a way to outline some basic thermodynamic arguments pertinent to quantum gravity. Our first move will be outlining equations of state, thermodynamically speaking as far as entropy, internal energy and a partition function given by Ng [2] [9] as to “infinite quantum statistics” which can be used, then to extract, first an initial temperature, T, which then can be linked to the energy per degree of freedom of the initial cosmological configuration. The temperature T so identified with, is proportional to energy per degree of freedom, and if the degrees of freedom as initially configured, by Kolb and Turner [3] [10] are as high as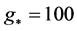 , which is in part confirmed by Standard model. With degrees of freedom contributing to an initial energy configuration as given by
, which is in part confirmed by Standard model. With degrees of freedom contributing to an initial energy configuration as given by
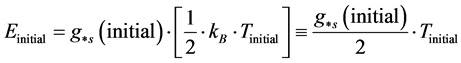 . (11)
. (11)
Then in the spirit of Mukhanov [11] using 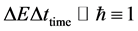 to have, here
to have, here
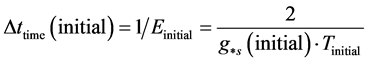 . (12)
. (12)
Then, we go to the Entropy, and state it is due to calculation given by Kolb and Turner [10]
 . (13)
. (13)
Our article will be developed by making sense of the above formalism, and we start by getting the entropy, in its final state, pretty well bench marked, and from there scaling back to determine what entropy should be initially. In doing so, we take some arguments fromBarrau, Rovelli, and Viddotto, [12] [13] , as to quark stars, and minimum quantum effects, as well as some more details given as to [14] - [16] as to the change in degrees of freedom as given in Equation (13) above.
2. Entropy, as Calculated as a Function of Quark Star Arguments, and Quantum Effects. And Number of Operations
The quark star argument comes as to giving the cube of a minimum quantum wavelength for quantum gravitational effects and the linkage to quark stars, etc, as commensurate with [12] [13] .
We are taking a Primoridial black hole mass, in Equation (14) to be such that it would be really small, i.e. if the Earth has a 6 times 1024 kilogram mass, then its Schwartzhield radius would be 8.7 times 10−3 meters. i.e. what we are thinking of is a consortium of mass for tiny black holes of about 3 times 1022 Kilograms, i.e. ~1/10 the mass of the Earth, as a start. So then the following roughly hold.
 (14)
(14)
This is assuming that there would be a continual injection of space-matter energy into the universe, possibly utilizing the cyclical cosmological construction, i.e. a variant of Penrose Cyclic conformal cosmology as given in [14] . i.e. given this the following happens. i.e. we need to look at the phenomenology given in [15] - [17] .
The end result, is if we use Equation (13) and also reference Equation (14) above, as a proportionality factor as far as how to obtain entropy is in having the following set up, i.e.

Furthermore, there is a linkage which can be made to Seth Lloyds number of operations, i.e. [18]

Note the completely different ways of charactering the number of operations, as given by Equation (16) in terms of a linkage to the radii of the universe, at Z ~ 1100, as opposed to the entropy as linked to a radii of the Schwartshield “radii”, as given in Equation (15) and part of the evolution displayed in Equation (14).
3. Conclusion. Calculation of Temperature, and of All That, as Far as Equation (12). Leading to a Graviton Mass?
In order to do this line of reasoning, the temperature can have the following linkage [19]

This would then entail making the following identification. i.e. comparing the wavelength of Equation (17) with the quantum wavelength and linking it to Equation (5) so as to then make the following identification. If so, then if Entropy is identifiable with Equation (5) and then we would use the following identification, namely, if [2] [9]

Also, if a Holographic relationship holds, [20]

And if [13] is true as well, then perhaps if so we have a first principle confirmation of [21]

which in turn may help us understand when the formation of this value occurred, i.e. [20]

We are supposing that Equation (21) holds at the formation of a Schwartzshield mass of the Universe radius. Also, here is our candidate as to the formation of an initial time step. As given.

Then, up to a point, if the above is in terms of seconds, and N sufficiently large, we could be talking about an initial non zero entropy, along the lines of the number of nucleated particles, at the start of the cosmological era. As given by

Initial entropy would be small, but non zero, and would be affected by 
If 

With an initial Graviton formation of mass occurring perhaps as early as

This frequency would be though massively redshifted down due to the onset of inflation. Also, our starting point as to wavelength, is due to the considerations given in [13] and may indeed give confirmation as far as a start to early universe nucleation similar to what is given in the physics written in [23] below. As well as understanding why a graviton mass, as so discussed in Equation (21) as forming at the edge of the Schwartz- shield radii of the universe, may form at a distance 1018 or so meters from the big bang, and is still congruent with [24] in the later universe.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Cite this paper
Beckwith, A.W. (2016) Geddanken Experiment for Quark Star Idea, Quantum Wavelength Limit, Mini- mum Time, and Early Universe Temperature, from First Principles. Journal of High Energy Physics, Gravitation and Cosmology, 2, 478-485. http://dx.doi.org/10.4236/jhepgc.2016.24042
References
- 1. Carroll, S. (2010)
www.preposterousuniverse4.com/blog/2010/04/28/the-universe-is-not-a-black-hole/ - 2. Beckwith, A. (2016) Gedanken Experiment for Refining the Unruh Metric Tensor Uncertainty Principle via Schwartz Shield Geometry and Planckian Space-Time with Initial Nonzero Entropy and Applying the Riemannian-Penrose Inequality and Initial Kinetic Energy for a Lower Bound to Graviton Mass (Massive Gravity). Journal of High Energy Physics, Gravitation and Cosmology, 2, 106-124.
http://dx.doi.org/10.4236/jhepgc.2016.21012 - 3. Gorbunov, D. and Rubakov, V. (2011) Introduction to the Theory of the Early Universe, Cosmological Perturbations and Inflationary Theory. World Scientific Publishing Pte. Ltd, Singapore.
http://dx.doi.org/10.1142/7873 - 4. Unruh, W.G. (1986) Why Study Quantum Theory? Canadian Journal of Physics, 64, 128- 130.
http://dx.doi.org/10.1139/p86-019 - 5. Unruh, W.G. (1986) Erratum: Why Study Quantum Gravity? Canadian Journal of Physics, 64, 128.
http://dx.doi.org/10.1139/p86-019 - 6. Giovannini, M. (2008) A Primer on the Physics of the Cosmic Microwave Background. World Press Scientific, Hackensack. http://dx.doi.org/10.1142/6730
- 7. Valev, D. (2010) http://arxiv.org/pdf/1008.0933.pdf
- 8. Goldhaber, A. and Nieto, M. (2010) Photon and Graviton Mass Limits. Reviews of Modern Physics, 82, 939-979.
http://arxiv.org/abs/0809.1003
http://dx.doi.org/10.1103/revmodphys.82.939 - 9. Haggard, H.M. and Rovelli, C. (2014) Black Hole Fireworks: Quantum-Gravity Effects outside the Horizon Spark Black to White Hole Tunneling. http://arxiv.org/pdf/1407.0989v2.pdf
- 10. Padmanabhan, T. (2002) http://ned.ipac.caltech.edu/level5/Sept02/Padmanabhan/Pad1_2.html
- 11. Ali, A.F. and Das, S. (2015) Cosmology from Quantum Potential. Physics Letters B, 741, 276-279. http://dx.doi.org/10.1016/j.physletb.2014.12.057
- 12. Haranas, I. and Gkigkitzis, I. (2014) The Mass of Graviton and Its Relation to the Number of Information According to the Holographic Principle. International Scholarly Research Notices, 2014, Article ID: 718251. http://www.hindawi.com/journals/isrn/2014/718251/
- 13. Gasiorowitz, S. (1973) Quantum Physics. Wiley Interscience, Boston.
- 14. Lloyd, S. (2002) Computational Capacity of the Universe. Physical Review Letters, 88, 237901.
http://arxiv.org/abs/quant-ph/0110141
http://dx.doi.org/10.1103/physrevlett.88.237901 - 15. http://pdg.lbl.gov/2013/reviews/rpp2012-rev-bbang-cosmology.pdf
- 16. http://www.helsinki.fi/~hkurkisu/cosmology/
- 17. http://www.helsinki.fi/~hkurkisu/cosmology/Cosmo6.pdf
- 18. Beckwith, A.W. (2014) Analyzing Black Hole Super-Radiance Emission of Particles/Energy from a Black Hole as a Gedanken Experiment to Get Bounds on the Mass of a Graviton. Advances in High Energy Physics, 2014, Article ID: 230713. http://dx.doi.org/10.1155/2014/230713
- 19. Barrau, A., Rovelli, C. and Vidotto, F. (2014) Fast Radio Bursts and White Hole Signals.
http://arxiv.org/pdf/1409.4031v3.pdf - 20. Rovelli, C. and Vidotto, F. (2015) Covariant Loop Quantum Gravity, an Elementary Introduction to Quantum Gravity and Spinfoam Theory. Cambridge University Press, Cambridge.
- 21. Mukhanov, Y. (2005) Physical Foundations of Cosmology. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511790553 - 22. Kolb, E. and Turner, M. (1990) The Early Universe. Frontiers in Physics, Vol. 69, Chicago.
- 23. Ng, Y.J. (2008) Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality. Entropy, 10, 441-461. http://dx.doi.org/10.3390/e10040441
- 24. Ha, Y.K. (2014) An Underlying Theory for Gravity. Proceedings of the 7th International Conference on Gravity and Cosmology (ICGC2011), Journal of Physics: Conference Series, 484, Article ID: 012061. http://iopscience.iop.org/1742-6596/484/1/012061/pdf/1742-6596_484_1_012061.pdf http://dx.doi.org/10.1088/1742-6596/484/1/012061

