American Journal of Industrial and Business Management
Vol.4 No.7(2014), Article ID:48065,10 pages
DOI:10.4236/ajibm.2014.47044
A Monte Carlo Based Robustness Optimization Method in New Product Design Process: A Case Study
Jianguo Che, Jing Wang, Kai Li
Department of Industrial Engineering, Nankai University, Tianjin, China
Email: cjg7705@nankai.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 May 2014; revised 19 June 2014; accepted 10 July 2014
ABSTRACT
Monte Carlo method can analyze, solve and optimize many mathematical or physical problems through generating a large number of statistical random samples to simulating stochastic events. It also can be used to remarkably improve design quality of new product. In new product design process, setting distribution characteristics of the design variables is vital to product quality and production robustness. Firstly, response surface model between output characteristics and design variables in new product design is proposed, and the distribution characteristics of design variables and response output are analyzed; then position error model of response output and standard value and allowed error maximum is presented; and then the differences of position error model and allowed error maximum are counted, and reliability ratio is built and calculated, and design robustness of the new product is increased by adjusting the precision value of random design variables in Monte Carlo experiments. Finally, a case is brought forward to verify the validity of the method.
Keywords:Monte Carlo Simulation, Robustness Optimization, New Product Design, Process Improvement

1. Monte Carlo Method
Monte Carlo method is a computer-based simulation or experiment method. It approximately simulates and solves mathematical or physical stochastic problem with statistical random sampling. Compared with traditional algebraic method, due to their reliance on repeated computation of random or pseudo-random numbers, Monte Carlo method can apply Normal distribution, Exponential distribution, Weibull distribution etc. to model phenomena with significant uncertainty in inputs when it is unfeasible or impossible to compute an exact result with a deterministic algorithm, and does not need to know parameter’s distribution type and probability parameter [1] -[5] . In new product design, usually design parameter is a random variable that follows a probability distribution. Design parameter is a key impact factor to design robustness, and distribution of these design parameters determines greatly robustness of output response. It is not reliable to optimize this product design problem using traditional deterministic method. How to find the optimum value of these design parameters is an important problem to improve the design robustness of new product. Here, we propose a robustness optimization method of new product based on Monte Carlo simulation.
Procedures are as followed [6] -[10] :
1) To analyze the problem existing in new product design, and define the relationship
between design variables
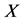 and response output as a response surface model
and response output as a response surface model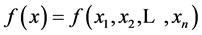 ;
;
2) To analyze design variables’ distribution types and define design variables’ distribution characteristics, such as mean and standard deviation, etc.;
3) To sample from populations of random design variables X, and get the sample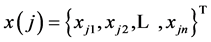 ;
;
4) To bring sample
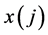 into position error model between response surface model and standard value,
into position error model between response surface model and standard value,
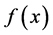 , then get a r position error sample and compose
an experiment
, then get a r position error sample and compose
an experiment
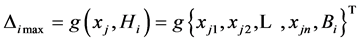 , (
, (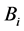 is response output,
is response output,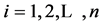 );
);
5) To check if it meets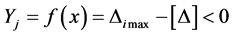 ,
,
 is allowed error maximum.
is allowed error maximum.
6) To repeat step 2) to 5) by k times, and calculate the number of
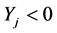 in all independent samples
in all independent samples ,
,
 , here
, here
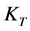 is the number of
is the number of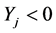 ,
,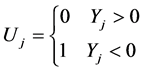 ;
;
7) To calculate reliability ratio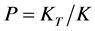 . If
. If
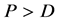 (
(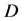 is acceptable reliability), then process or
product is robust, otherwise we need to modify the precision value of random design
variables to enhance reliability ratio and robustness of the manufacture process,
then the manufacture process is optimized.
is acceptable reliability), then process or
product is robust, otherwise we need to modify the precision value of random design
variables to enhance reliability ratio and robustness of the manufacture process,
then the manufacture process is optimized.
2. Case Study
Considering design of a pressure container, according to mechanics of materials,
the pressure container’s axial stress is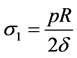 , hoop stress is
, hoop stress is , here
, here
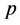 is internal pressure of container;
is internal pressure of container;
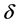 is wall thickness of container;
is wall thickness of container;
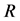 is internal radius of container;
is internal radius of container;
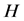 is half height of container. Material of container
is 15 MnV. Through observation of experiment, we defined the design variables and
their distribution characteristics as followed: internal work pressure of container
is half height of container. Material of container
is 15 MnV. Through observation of experiment, we defined the design variables and
their distribution characteristics as followed: internal work pressure of container
 follows lognormal distribution
follows lognormal distribution the tolerance of
the tolerance of
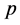 is (10, 20), the material strength limit
is (10, 20), the material strength limit
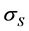 follows lognormal distribution
follows lognormal distribution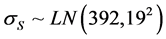 the tolerance of
the tolerance of
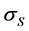 is (340, 420), wall thickness of container
is (340, 420), wall thickness of container
 follows normal distribution
follows normal distribution the tolerance of
the tolerance of
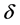 is (1.5, 4.5), internal radius of container R follows normal distribution
is (1.5, 4.5), internal radius of container R follows normal distribution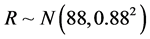 the tolerance of R is (50, 100), half
height of container H follows normal distribution
the tolerance of R is (50, 100), half
height of container H follows normal distribution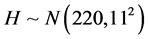 , the tolerance of H is (130, 210). Our objective
is to maximize container’s volume under 95% failure probability (confidence level)
of strength and container size falling Interval
, the tolerance of H is (130, 210). Our objective
is to maximize container’s volume under 95% failure probability (confidence level)
of strength and container size falling Interval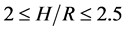 .
.
As known, our objective function is volume maximum of the pressure container, that is
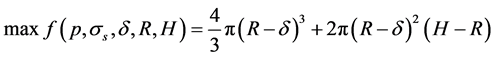
Constraints are
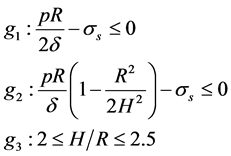
Firstly we established response surface model of response variables
 concerned pressure container and constraints condition, and run Monte Carlo experiment
3000 times using Crystal Ball 7. According to Anderson-Darling testing, Chi-Square
testing and K-S testing [11] -[13]
, we can fit the probability distribution type of all four response variables as
Normal distribution, Gamma distribution, Gamma distribution and Beta distribution,
see Table1
concerned pressure container and constraints condition, and run Monte Carlo experiment
3000 times using Crystal Ball 7. According to Anderson-Darling testing, Chi-Square
testing and K-S testing [11] -[13]
, we can fit the probability distribution type of all four response variables as
Normal distribution, Gamma distribution, Gamma distribution and Beta distribution,
see Table1
Then we get probability distribution and cumulative probability distribution of response variable and constraints as showed in Figure 1.
1) Robust analysis
We can know from Figure 2 that probability which
product design met constraint g1 is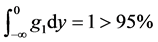 , and probability which
product design met constraint g2 is
, and probability which
product design met constraint g2 is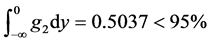 , and probability which
product design met constraint g3 is
, and probability which
product design met constraint g3 is
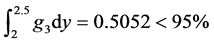 under current design variables value. That iswave range of constraints both g1
and g2 go beyond their allowed range. According to requirements, current
response output value is not robust and need to improve product design level.
under current design variables value. That iswave range of constraints both g1
and g2 go beyond their allowed range. According to requirements, current
response output value is not robust and need to improve product design level.
2) Sensitivity analysis
We can know from Sensitivity Analysis of Response Variables and Constraints in Figure 3 that the significant impact factors of
volume function f of pressure container are
 (positive correlation) and
(positive correlation) and
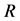 (positive correlation) in order; the significant impact factors of constraint
(positive correlation) in order; the significant impact factors of constraint
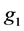 are
are
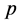 (positive correlation),
(positive correlation),
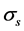 (negative correlation) and
(negative correlation) and
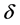 (negative correlation) in order; the significant impact factors of constraint
(negative correlation) in order; the significant impact factors of constraint
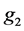 are
are
 (positive correlation),
(positive correlation),
 (negative correlation) and
(negative correlation) and
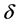 (negative correlation) in order; the significant impact factors of constraint
(negative correlation) in order; the significant impact factors of constraint
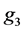 are
are
 (positive correlation) and
(positive correlation) and
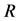 (negative correlation) in order.
(negative correlation) in order.
3) Modification of design variables precision
According to relationships between design variables and response output variable,
and contributions to variance view from Figure 3,
we modified parameter values of the design variables
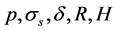 to
to
 ,
,
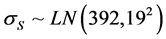 ,
,
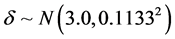 ,
,
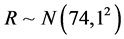 ,
,
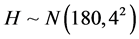 , and get the corresponding probability distribution and cumulative
probability distribution as followed in Figure 4.
, and get the corresponding probability distribution and cumulative
probability distribution as followed in Figure 4.
After Modification of design variables precision, we analyze robustness of response variable and constraints

Figure 1. Pressure container chart.
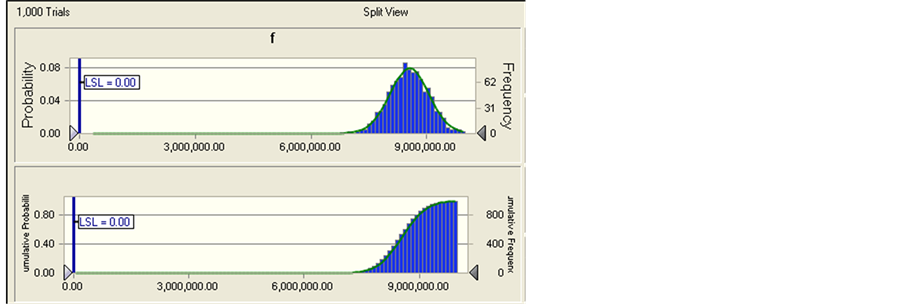
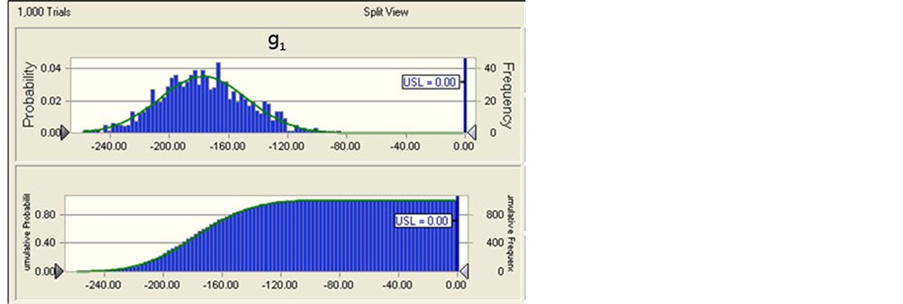


Figure 2. Probability distribution and cumulative probability distribution of response variable and constraints.

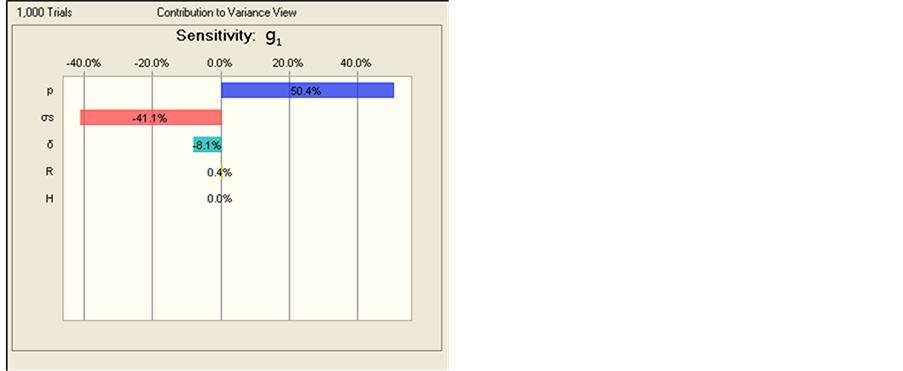
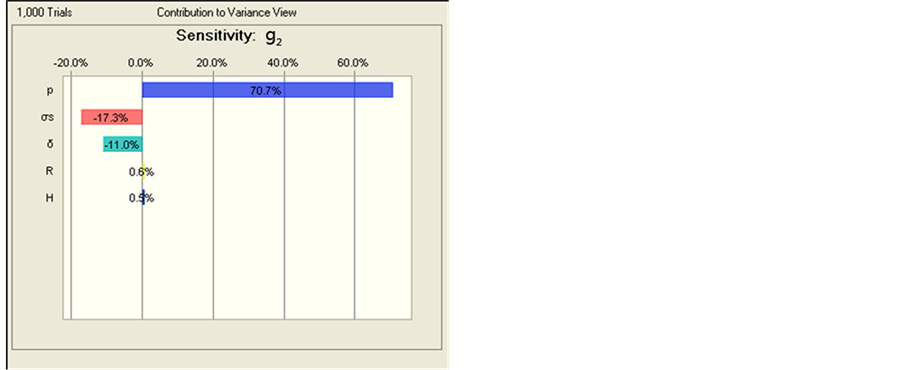
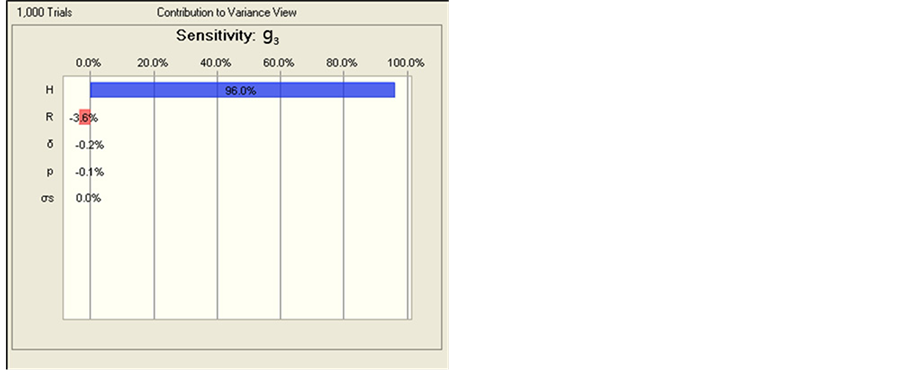
Figure 3. Sensitivity analysis of response variables and constraints.
again, and get the probability that product design met constraints g1
is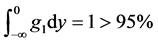 , and the probability that product design met constraints
g2 is
, and the probability that product design met constraints
g2 is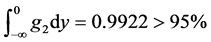 , and the probability that
product design met constraints g3 is
, and the probability that
product design met constraints g3 is , which reached product
design requirements, that is, pressure container is robust enough, and pass percentage
of pressure container has been enhanced greatly. And the maximum volume of container
is
, which reached product
design requirements, that is, pressure container is robust enough, and pass percentage
of pressure container has been enhanced greatly. And the maximum volume of container
is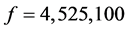 , product robustness has been greatly improved. Meanwhile, we
knew from sensitivity analysis of response variables in
Figure 3 that we should keep monitoring the fluctuation of the significant
impact factors of response variables and constraints to hold robustness of pressure
container.
, product robustness has been greatly improved. Meanwhile, we
knew from sensitivity analysis of response variables in
Figure 3 that we should keep monitoring the fluctuation of the significant
impact factors of response variables and constraints to hold robustness of pressure
container.
4) Design optimization
Now we further optimize the pressure container to enhance the design robustness
using OptQuest optimizer. Here we create the OptQuest model and run simulation experiments
1500 times according to distribution characteristics of design variables and constraints
condition [4] -[6]
, and get the optimum of design variables
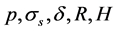 are
are
 in Table 2, then the probability that product design
met constraints g1 are
in Table 2, then the probability that product design
met constraints g1 are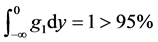 , and the probability that
product design met constraints g2 was
, and the probability that
product design met constraints g2 was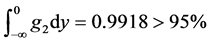 , and the probability that
product design met constraints g3 is
, and the probability that
product design met constraints g3 is
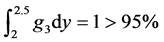 from Figure 5,
and the maximum volume of container is
from Figure 5,
and the maximum volume of container is
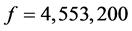 as Figure 6
as Figure 6
showed, so design robustness of pressure container has been further improved than that of last time.
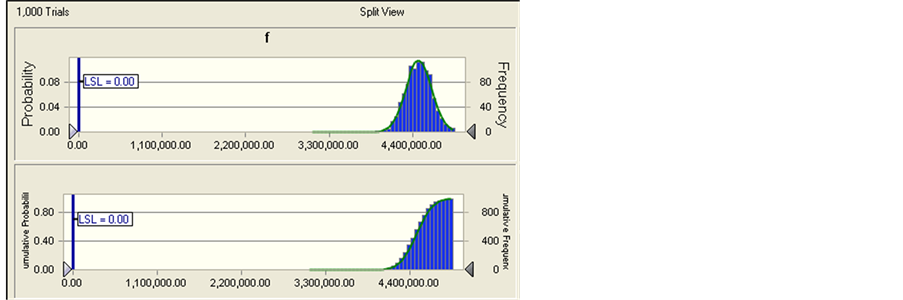
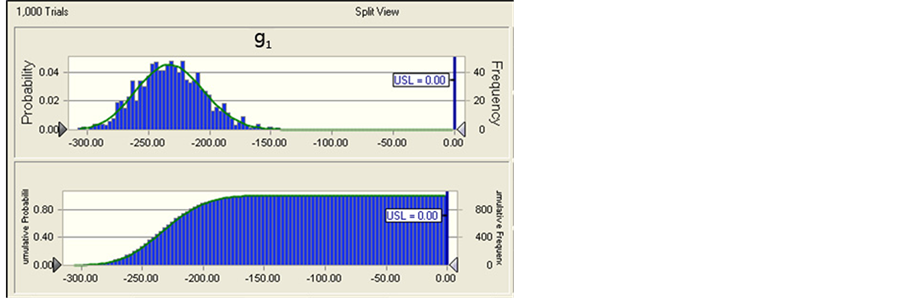
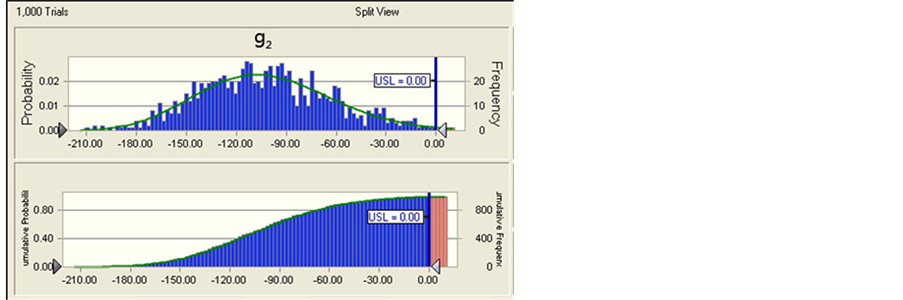
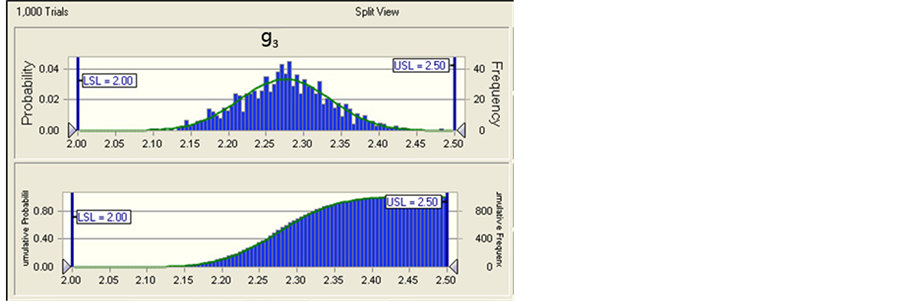
Figure 4. Probability distribution and cumulative probability distribution of response variable and constraints after modification of parameter precision.
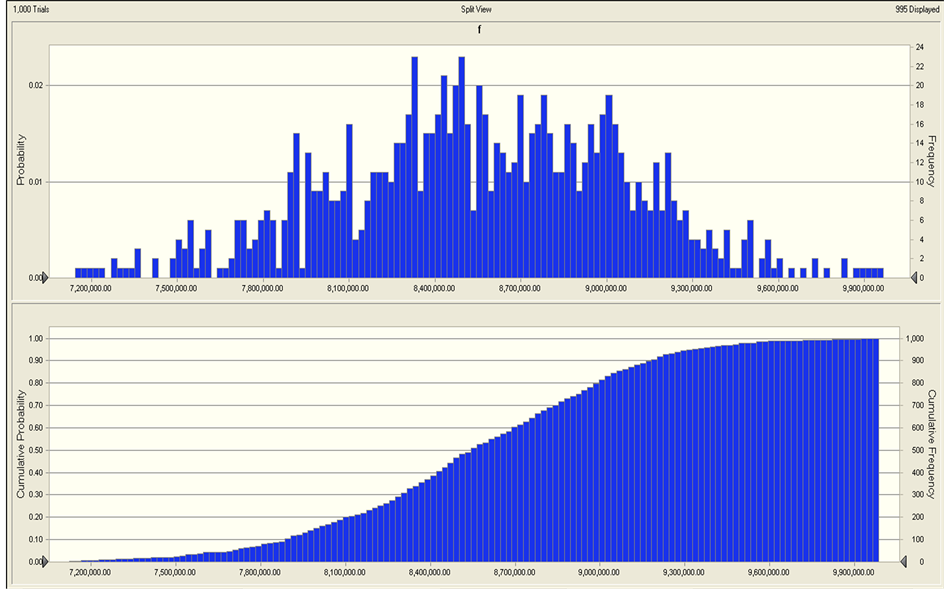
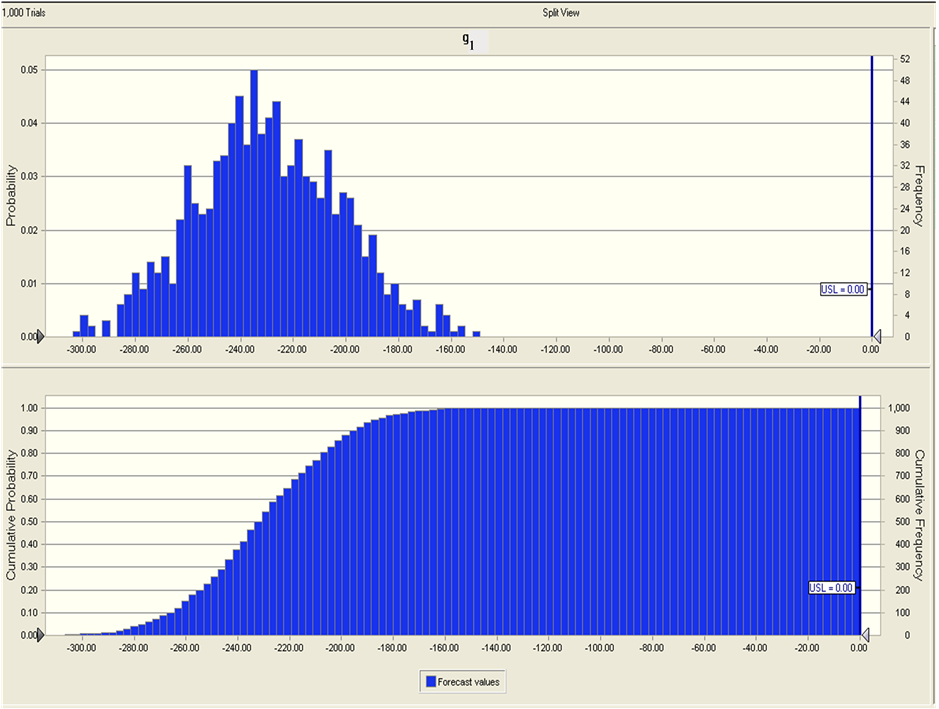
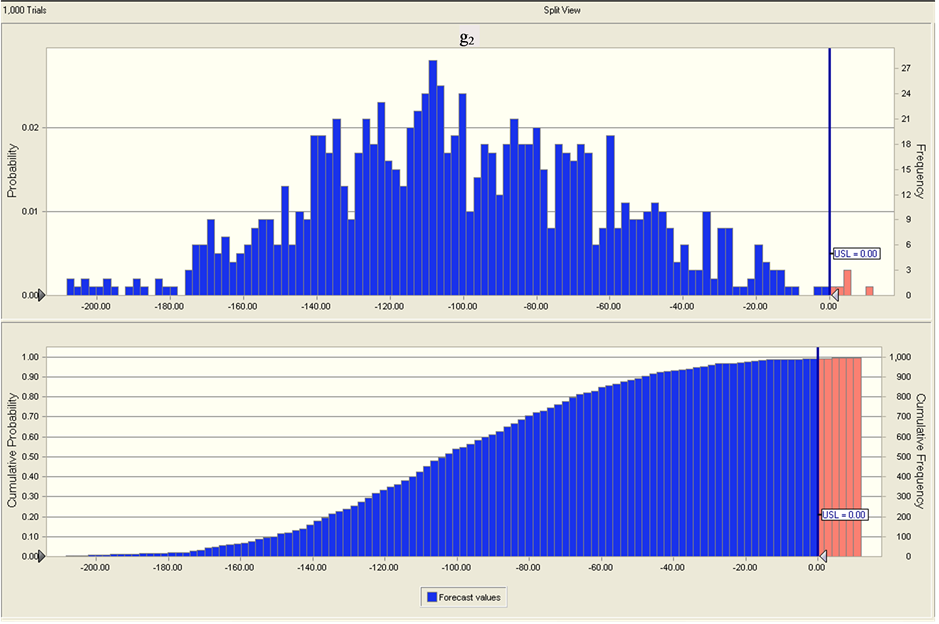
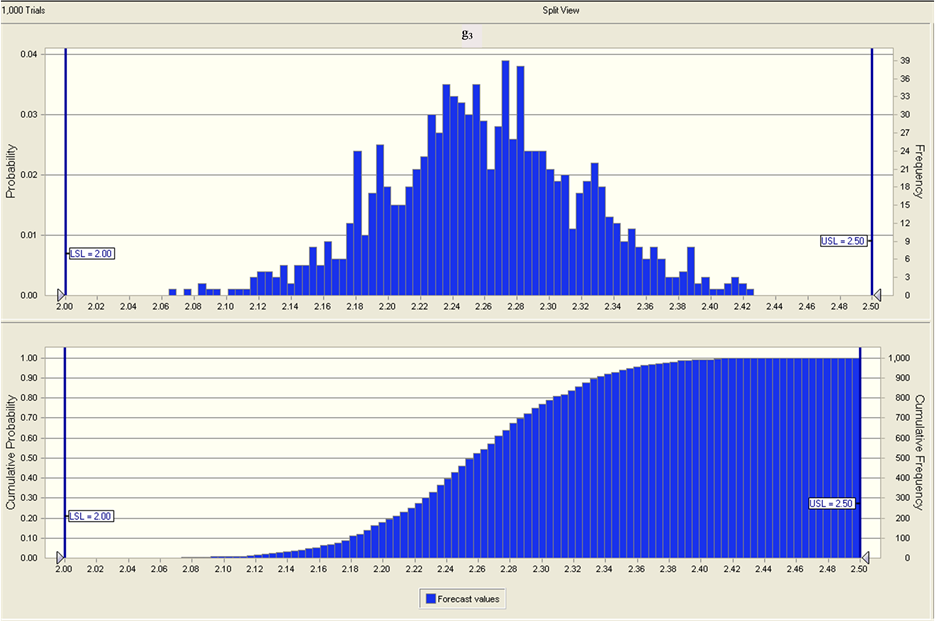
Figure 5. Probability distribution and cumulative probability distribution of response variable and constraints after optimization after OptQuest optimization.
Table 2. Optimum design settings of pressure container with OptQuest.
Figure 6. Optimum design performance gragh of pressure container with OptQuest.
3. Conclusion
When random changes exist in design variables, traditional determined optimization method cannot guarantee robustness of product and process design to the extent. While Monte Carlo method can be used to precision control and optimization in product and process design, which can avoid increasing cost due to duplicate experiments and excessive design precision, as well as low pass percentage due to deficient design precision. In robust analysis and design, Monte Carlo method also can study on change of response model of product and process brought by modification of design variables, get probability distribution and statistical parameters’ values of response variables, further improve design robustness of product and process and realize robustness design and optimization of product and process. It proved that analysis and optimization of response surface model based on Monte Carlo method was a good robustness design method, and can markedly improve robustness, precision and pass percentage of product and process.
Funding
It was supported by National Natural Science Foundation of China (71102047, 71302016, 71302017) and “The Fundamental Research Funds for the Central Universities” (NKZXB1202). Many thanks are also given to anonymous reviewers.
References
- Fonseca, J.R., Friswell, M.I. and Lees, A.W. (2007) Efficient Robust Design via
Monte Carlo Sample Reweighting. International Journal for Numerical Methods in Engineering,
69, 2279-2301.
http://dx.doi.org/10.1002/nme.1850 - Ray, L.R. and Stengel, R.F. (1993)A Monte Carlo Approach to the Analysis of Control System Robustness. Automatica, 29, 229-236. http://dx.doi.org/10.1016/0005-1098(93)90187-X
- Arnér, M. (2014) Monte Carlo Methods for Robust Design. Statistical Robust Design: An Industrial Perspective. Published Online, 177-193. http://dx.doi.org/10.1002/9781118842003.ch10
- Eric, V. (1998) Robust Monte Carlo Methods for Light Transport Simulation. Ph.D. Dissertation of Stanford University, Stanford.
- Conceicao, E.L.T. and Portugal, A.A.T.G. (2011) Finite-Sample Comparison of Robust Estimators for Nonlinear Regression Using Monte Carlo Simulation: Part I. Univariate Response Models. Computers & Chemical Engineering, 35, 530-544. http://dx.doi.org/10.1016/j.compchemeng.2010.04.009
- Todorov, V., Neykov, N. and Neytchev, P. (1994) Robust Two-Group Discrimination by Bounded Influence Regression: A Monte Carlo Simulation. Computational Statistics & Data Analysis, 17, 289-302. http://dx.doi.org/10.1016/0167-9473(94)90122-8
-
Mandur, J. and Budman, H. (2014) Robust Optimization of Chemical Processes Using
Bayesian Description of Parametric Uncertainty. Journal of Process Control, 24,
422-430.
http://dx.doi.org/10.1016/j.jprocont.2013.10.004 -
Wang, Y., Cao, Z.J. and Au, S.-K. (2010) Efficient Monte Carlo Simulation of Parameter
Sensitivity in Probabilistic Slope Stability Analysis. Computers and Geotechnics,
37, 1015-1022.
http://dx.doi.org/10.1016/j.compgeo.2010.08.010 - Meng, X.-J., Zhang, C., Zhan, M.-J. and Shi, Z.-X. (2004) Robustness Analysis of Locus Generating Linkage through Monte-Carlo Method. Journal of Mechanical Science and Technology, 23, 203, 205, 214.
- Zhang, L., Zhang, W.M. and Shen, Y.H. (2006) Robust Design for Locus Generating Steering Mechanism Based on Monte Carlo Method. Journal of University of Science and Technology Beijing, 28, 1174-1177.
- Yan,
Y.D., Meng, Q., Wang, S.A. and Guo, X.C. (2012) Robust Optimization Model of Schedule
Design for a Fixed Bus Route. Transportation Research Part C: Emerging Technologies,
25, 113-121.
http://dx.doi.org/10.1016/j.trc.2012.05.006 - Varas, M., Maturana, S. and Pascual, R. (2014) Ignacio Vargas, Jorge Vera. Scheduling Production for a Sawmill: A Robust Optimization Approach. International Journal of Production Economics, 150, 37-51. http://dx.doi.org/10.1016/j.ijpe.2013.11.028
- Boylan, G.L., Goethals, P.L.
and Cho, B.R. (2013) Robust Parameter Design in Resource-Constrained Environments:
An Investigation of Trade-Offs between Costs and Precision within Variable Processes.
Applied Mathematical Modelling, 37, 2394-2416.
http://dx.doi.org/10.1016/j.apm.2012.05.017


