Open Journal of Medical Imaging
Vol.04 No.04(2014), Article ID:52135,5 pages
10.4236/ojmi.2014.44027
Modelling Magnetization Transfer Considering Spin-Locking Effects
Claus Kiefer
Support Center for Advanced Neuroimaging (SCAN), Institute for Diagnostic and Interventional Neuroradiology, University Hospital Inselspital and University of Bern, Bern, Switzerland
Email: claus.kiefer@insel.ch
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 September 2014; revised 27 October 2014; accepted 26 November 2014
ABSTRACT
Purpose: Recently it was demonstrated that spin-locking (SL) effects can manifest as pseudo magnetization transfer (MT). To our best knowledge the MT models proposed so far cannot distinguish between saturation effects caused by the MT preparation pulses and SL phenomena. Therefore a new MT model is proposed. Materials and Methods: A binary spin-bath model for magnetization transfer was extended in that sense that SL effects are considered. The new modified spin bath model was tested for a phantom with different agar concentrates (2%, 4%, 8%) and a MnCl2 (0.3 mM) solution. Results: The mean fitting error is 3.2 times lower for the modified model compared to the original model. Especially the parameter F for the fractional part of the bounded proton pool describes the situation for the MnCl2 (F = 0) better than the original model (F = 0.004). Conclusion: The proposed mathematical modifications of the binary spin-bath model considering SL seem to be a step in the right direction in that sense that the effects associated with SL are not interpreted as magnetization transfer.
Keywords:
MRI, Magnetization Transfer, Spin-Locking

1. Introduction
The magnetization transfer (MT) contrast [1] -[3] and related model parameters meanwhile deliver an important way to characterize macromolecules resp. diagnostic biomarkers in living tissue as shown in [4] . As already de- monstrated by Stanisz [5] , the MT ratio, which is often clinically used, is prone to T1 and T2 effects and therefore a sophisticated model based approach is more suitable. The binary spin-bath model proposed by Sled [1] -[3] is one of the methodologically most sounded techniques so far. However, as shown by Ulmer [6] , this model should also include spin-locking (SL) effects, because the model used in [1] -[3] cannot distinguish between saturation effects caused by the MT sequences and MT preparation pulses and spin-locking. This is a problem because the model parameter values such as the one for the fraction of the macromolecules maybe wrong.
In this technical note the original spin-bath model proposed by Sled was extended in that sense that SL effects are considered. The new modified spin bath model was tested for a phantom with different agar concentrates (2%, 4%, 8%) and a MnCl2 (0.3 mM) solution.
2. Methods and Materials
The magnetization transfer is described by a system of modified Bloch Equations (1)-(3). As this system is not analytically solvable, Sled proposed a 3-step-strategy divided in a phase of instantaneous saturation of the free pool, the free precession of the free pool and the continuous saturation of the bounded pool. This procedure enables to decouple the transversal magnetization of the free pool from the other components. We follow this approach and start with the description of the longitudinal magnetization assuming that the transversal components are zero at the end of a pulse period
 which can be guaranteed by relaxation or specific spoiling (indices f: free, b: bounded)
which can be guaranteed by relaxation or specific spoiling (indices f: free, b: bounded)
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
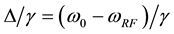 . (5)
. (5)
where
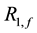 is the T1 relaxation rate (1/sec) of the free pool,
is the T1 relaxation rate (1/sec) of the free pool,
 and
and
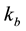 are the exchange rates (1/sec) of the free and bounded pool resp.,
are the exchange rates (1/sec) of the free and bounded pool resp.,
 (3) is the transition rate and
(3) is the transition rate and
 (4) is the absorption lineshape of the bounded pool,
(4) is the absorption lineshape of the bounded pool,
 is the T2 relaxation time (us) of the bounded pool and
is the T2 relaxation time (us) of the bounded pool and
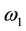 is the “frequency” of the continuous wave. According to Ulmer [6] the spin-locking can be described as
is the “frequency” of the continuous wave. According to Ulmer [6] the spin-locking can be described as
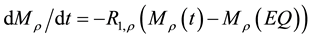 (6)
(6)
 (7)
(7)
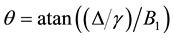 (8)
(8)

Equation (6) has the solution

In the context of the original model (1 - 5) a significant reduction of the signal intensities for off-resonance frequencies greater than 500 Hz (no direct saturation) would be interpreted as magnetization transfer effects. To avoid this, the new model must consider the spin-locking (SL) related changes of the z-component in equation (2):

The coupling parameter

In matrix form the differential equation system (1, 11) can be written as:

(bold type expresses matrices and vectors) where




The effect of both the MT pulse and the excitation pulse on the free pool is modelled as an instantaneous fractional saturation




in which


The general solution of (12) is

From the periodicity property of the sequence


The steady state magnetization




With
Nonlinear fitting was performed with a Levenberg-Marquardt algorithm within a Matlab (R2014a) framework.
The free fitting parameters are





setting 60uT.
The sequence is a 2D-FLASH sequence. The sequence parameters are as follows: flip angle 540 degree (MT preparation pulse), 15 degree (excitation pulse), 30 slices, gap 0, voxel size = 2 mm isotropic, 10 frequency samples, matrix size = 128, TR/TE = 30/4.8 ms, BW = 390 Hz/Px.
Imaging was performed on a 3.0Tesla whole body scanner. The phantom (Figure 1) is a cylinder (13 cm diameter, 10 cm height), filled with water and four integrated tubes filled with agar gel (2%, 4%, 8%) and manganese chloride 0.3 mM respectively. The phantom temperature was kept constant.
3. Results
The mean MT-effects for Agar 8%, 4%, 2%, MnCl2 according to the intensity values listed in Table 1 are

In Figure 2 the fitting results are shown for an exemplary slice using the original model (Figure 2(a)) and the modified model (Figure 2(b)). If we compare the fitting results the mean error is 3.2 times greater using the original Sled model than the modified model. This result does not change if the coupling parameter cSL is not considered as a free adjustable degree of freedom but if it is set to a constant (e.g. 1, assuming the spin locking is generally present).
Numerical post processing according to the original model provides F values 200 ± 2.3, 100 ± 3.3, 45 ± 5.9,

Figure 1. The phantom is a cylinder (13 cm diameter, 10 cm height), filled with water and four integrated tubes filled with agar gel (2%, 4%, 8%) and manganese chloride (MnCl2) 0.3 mM respectively.
MT meas MT fit | meas-fit |

Figure 2. The fitting results are shown for an exemplary slice using the original model (2a) and the modified model (2b).
41 ± 3.5 for Agar 8%, 4%, 2%, MnCl2 (Figure 3(a)) and 201 ± 2.4, 100 ± 4.0, 45 ± 5.1, 0 (Figure 3(b)) using the modified model (scaled with 1e5).
The non-vanishing F values and the significant fitting error within the MnCl2 region in the case of the original spin-bath model are present regardless of the T1 or T2 values (which were set to arbitrary values for test purposes, e.g. 1000 or 10,000 ms) which means that indeed SL effects have to be considered in general (the measured T1/T2 values of MnCl2 are 140/12 ms (literature 144/14 ms)).
The values of the T2,b parameter for the original and modified model are very similar: T2,b (Agar 8%) = 12.95


Figure 3. F maps for the original (3a) and the modified model (3b).
Table 1. Intensity values due to the MT-effects for Agar 8%, 4%, 2%, MnCl2.
± 2.4 μs, T2,b (Agar 4%) = 12.98 ± 0.2 μs, T2,b (Agar 2%) = 12.98 ± 0.5 μs, T2,b (MnCl2) = 1 μs. The T2,b values for distilled water and MnCl2 are arbitrarily set to one because the z-spectrum in the context of the new model is just a constant, except at the resonance (zero).
The kf values using the original model are kf (Agar 8%) = 4.25 ± 0.6, kf (Agar 4%) = 1.66 ± 0.6, kf (Agar 2%) = 0.56 ± 0.1, kf (MnCl2) = 0.42 ± 0.1. The kf values using the modified model are kf (Agar 8%) = 1.98 ± 0.2, kf (Agar 4%) = 1.02 ± 0.1, kf (Agar 2%) = 0.37 ± 0.1, kf (MnCl2) = 0.
4. Conclusion
The proposed mathematical modifications of the binary spin-bath model considering spin-locking seem to be a step in the right direction in that sense that the effects associated with spin-locking are not interpreted as magnetization transfer furthermore. This could be verified by the F parameter which is really zero within the region of MnCl2 using the modified model. The T2,b values of 13 μs for the agar solutions correspond very well with the literature [1] -[3] . The fact, that the good fitting result for the new model is not simply associated with a higher degree of freedom (e.g. using five instead of four free parameters) further supports the proposed approach. The recently proposed extensions on the field of sequence design [7] may further help to transfer this promising technique for the detection of macromolecules resp. biomarkers into clinical routine.
Acknowledgements
This work was supported by the Ruth & Arthur Scherbarth foundation, grant 2249.
References
- Pike, G.B. (1996) Pulsed Magnetization Transfer Contrast in Gradient Echo Imaging: A Two Pool Analytic Description of Signal Response. Magnetic Resonance in Medicine, 36, 95-103. http://dx.doi.org/10.1002/mrm.1910360117
- Sled, J.G. and Pike, G.B. (2000) Quantitative Interpretation of Magnetization Transfer in Spoiled Gradient Echo MRI Sequences. Journal of Magnetic Resonance, 145, 24-36. http://dx.doi.org/10.1006/jmre.2000.2059
- Sled, J.G. and Pike, G.B. (2001) Quantitative Imaging of Magnetization Transfer Exchange and Relaxation Properties in Vivo Using MRI. Magnetic Resonance in Medicine, 46, 923-931.
- Kiefer, C., Brockhaus, L., Cattapan-Ludewig, K., Ballinari, P., Burren, Y., Schroth, G. and Wiest, R. (2009) Multiparametric Classification of Alzheimer’s Disease and Mild Cognitive Impairment: The Impact of Quantitative Magnetization Transfer MR Imaging. NeuroImage, 48, 657-667.
- Stanisz, G.J., Yoon, R.S., Joy, M.L.G. and Henkelman, R.M. (2002) Why Does MTR Change with Neuronal Depolarization? Magnetic Resonance in Medicine, 47, 472-475. http://dx.doi.org/10.1002/mrm.10071
- Ulmer, J.L., Mathews, V.P., Hamilton, C.A., Elster, A.D. and Moran, P.R. (1996) Magnetization Transfer or Spin- Lock? An Investigation of Off-Resonance Saturation Pulse Imaging with Varying Frequency Offsets. AJNR―Ameri- can Journal of Neuroradiology, 17, 805-819.
- Kiefer, C. (2014) Simultaneous Echo Refocused Magnetization Transfer Imaging. Open Journal of Medical Imaging, 4, 154-158. http://dx.doi.org/10.4236/ojmi.2014.43021


