Natural Resources
Vol.5 No.11(2014), Article ID:49161,7 pages
DOI:10.4236/nr.2014.511055
Tidal Prediction in the Sea Scheldt (Belgium) Using a Combination of Harmonic Tidal Prediction and 1D Hydraulic Modeling
Joris Vanlede, Leen Coen, Maarten Deschamps
Flanders Hydraulics Research, Antwerp, Belgium
Email: joris.vanlede@mow.vlaanderen.be
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 May 2014; revised 25 June 2014; accepted 11 July 2014
ABSTRACT
The vertical tide in the Sea Scheldt (Belgium) is predicted using a combination of harmonic tidal prediction and 1D hydraulic modeling. At Prosperpolder (a measurement station close to the Dutch-Belgian border), four years of water level data (2009-2012) are analyzed to obtain the harmonic components at that location. The accuracy of the harmonic prediction is checked with a statistical analysis of an astronomical hindcast for 2009-2012 against measurements. An existing 1D hydraulic model of the tidally influenced part of the Scheldt estuary is cut off at Prosperpolder. The time series of tidally predicted water levels at Prosperpolder is used as a downstream boundary condition for the hydraulic model. In this way, a tidal prediction can be obtained for any location in the Sea Scheldt, also for locations where no harmonic components are available, whilst guaranteeing the consistency between the predicted time series.
Keywords:Harmonic, Tidal Analysis, Tidal Prediction, Modeling, Scheldt

1. Introduction
The Scheldt estuary flows through the Netherlands and Belgium and is connected to the Scheldt River, which originates in the north-west of France. The total length of the Scheldt River including the estuary is about 350 km; the tide penetrates up to the city of Gent in Belgium (about 180 km from the mouth). The Scheldt is considered macro-tidal, with a tidal range exceeding 4 m [1] . The Dutch part of the estuary (the Western Scheldt) is characterized by a system of braided ebb and flood channels and connects to the Sea Scheldt which is the Belgian part of the river from the border to Ghent.
During the past centuries, the tidal regime of the Scheldt estuary has seriously changed. This is due to a complex interaction between naturally occurring processes and human interventions in the estuary, such as land reclamation (polders), enlargement (local widening and/or deepening) of the navigation channel, continuous maintenance dredging works, permanent withdrawal of sand from the estuary for different purposes, changed tidal conditions in the North Sea, changed upstream discharges etc. [2] .
Tidal predictions at locations along the estuary are important for planning purposes in general and for the nautical accessibility in particular. Tidal predictions at Vlissingen, Prosperpolder, Antwerpen and Wintam are published yearly as tidal tables with time and height of predicted high and low waters [3] . The tidal predictions at Vlissingen and Prosperpolder are also published in the Admiralty Tide Tables (ATT), and are listed there as Vlissingen (Flushing) and Antwerp (Prosperpolder) respectively [4] .
The goal of our research is to establish a methodology to obtain a tidal prediction for any location in the Sea Scheldt, also for locations where no harmonic components are available, whilst guaranteeing the consistency between the predicted time series.
2. Methodology
Prosperpolder is the (Belgian) water level measurement station closest to the Dutch-Belgian border, and is chosen as base station for the tidal prediction methodology. Four year of validated water level data at Prosperpolder are analysed to find amplitudes and phase for 94 pre-defined components. The quality of the harmonic analysis is checked with a hindcast for the four years measurements are available. The residual signal is analysed, as is timing and level of high and low water. The available measurements are presented in §3.1. The harmonic analysis is described in §3.2 and the quality check using a hindcast is done in §3.3.
In order to obtain a tidal prediction for any location in the Sea Scheldt, first a harmonic tidal prediction at station Prosperpolder is done using the harmonic components determined in the previous step. This time series is then used as a downstream water level boundary condition for a calibrated 1D hydraulic model. The modeled time series inside the model domain are used as harmonic tidal predictions for these locations. The 1D hydraulic model is introduced in §4. The hybrid technique of harmonic tidal prediction and 1D hydraulic modeling is described in §5. The conclusion section (§6) describes some products that are derived from the tidal predictions in the Sea Scheldt.
3. Harmonic tidal Analysis at Prosperpolder
3.1. Measurements
Four years (2009-2012) of measured water levels at station Prosperpolder in the Sea Scheldt are provided by the Hydrological Information Centre (HIC) of Flanders Hydraulics Research. The location of the measurement station is indicated in Figure 1. The water level at Prosperpolder is measured using two different techniques: paper registration and fully digitally using a radar water level sensor. The digital signal is sent with a one-minute time interval to the HYDRA database servers of Flanders Hydraulics Research. The digital signal is smoothed using a centrally-weighted 9 minute moving average and subsequently validated by linear correlation of the high water (HW) and low water (LW) level between the digital and paper registration [5] . The resulting time series is 89% complete for 2009, and 100% complete for 2010-2012.
The water level measurements are expressed in TAW (Belgian datum). Time is expressed in Middle European Time (MET).
3.2. Harmonic Analysis
The harmonic analysis of the vertical tide at Prosperpolder is done using the algorithms for tidal analysis and prediction from TIDEMAT, a Matlab toolkit for tidal analysis of series of observations of water levels [6] . Those algorithms are based on the theoretical work of Schureman [7] . Nodal or satellite modulations are handled by the code, which makes it possible to derive reliable harmonic components even if less than 18, 6 years of measurement data are analysed.
The harmonic decomposition is done using Equation (1), with
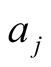 the amplitude and
the amplitude and
 the nodal correction on amplitude of component j with angular frequency
the nodal correction on amplitude of component j with angular frequency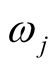 . The phase is decomposed
into the phase in the equilibrium tide
. The phase is decomposed
into the phase in the equilibrium tide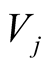 , the phase shift with
respect to the equilibrium tide
, the phase shift with
respect to the equilibrium tide
 and the nodal correction on the phase
and the nodal correction on the phase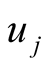 .
.

Figure 1. The scheldt estuary.
 (1)
(1)
The four-year time series is subsampled from a time-interval of 1 minute to a sampling interval of 10 minutes. Theoretically, this means that components up to an angular frequency of 1080˚/hr can be extracted from the data, which is still much higher than the highest identified harmonic component. The Nyquist criterion therefore does not limit the harmonic analysis.
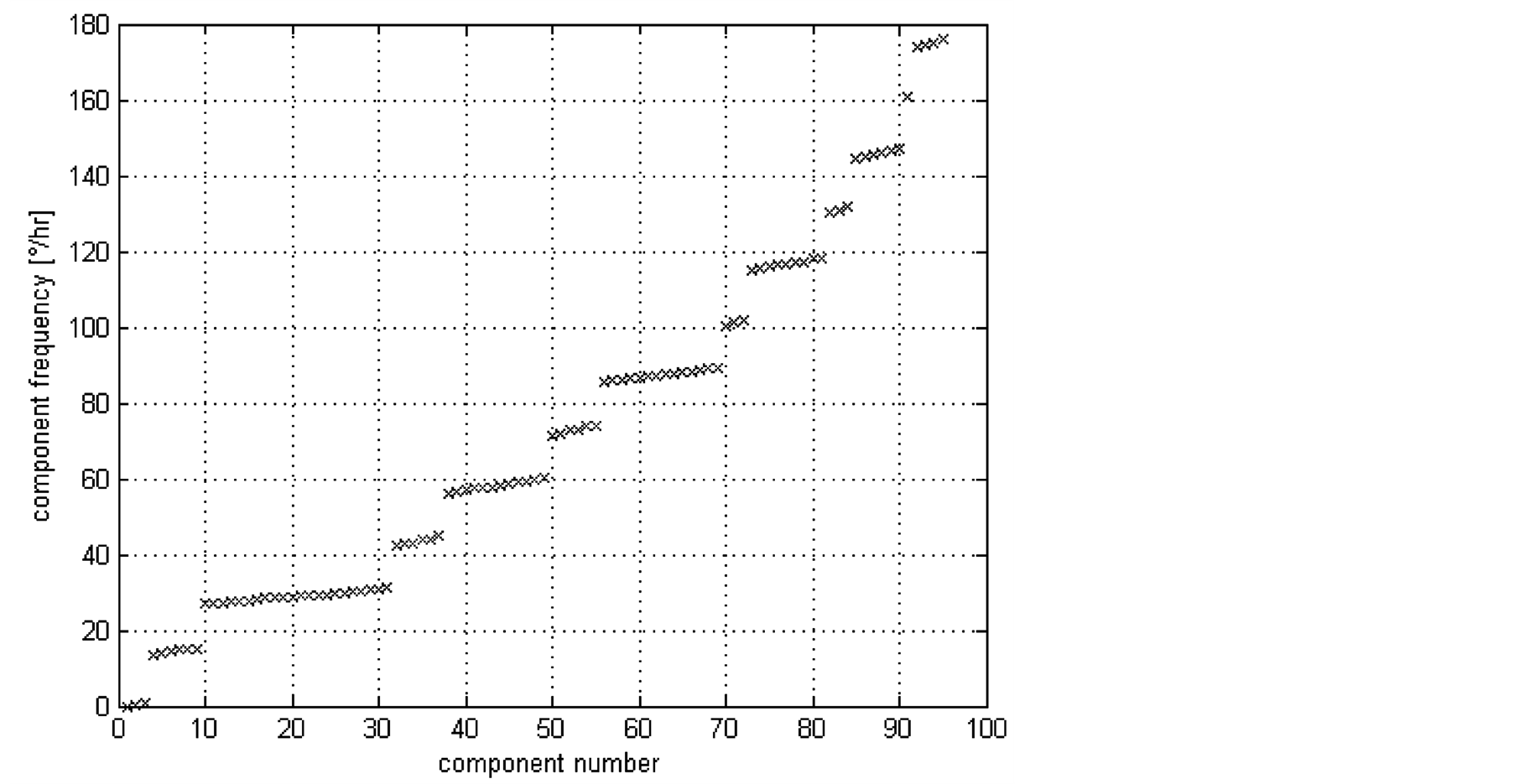
The harmonic analysis of the resulting time series is done in a least-square sense on 94 pre-defined components (angular frequencies) and yields amplitudes aj and phases gj at those 94 frequencies, plus a stationary offset A0. The frequencies of the 94 components are shown in Figure 2.
3.3. Residual Analysis
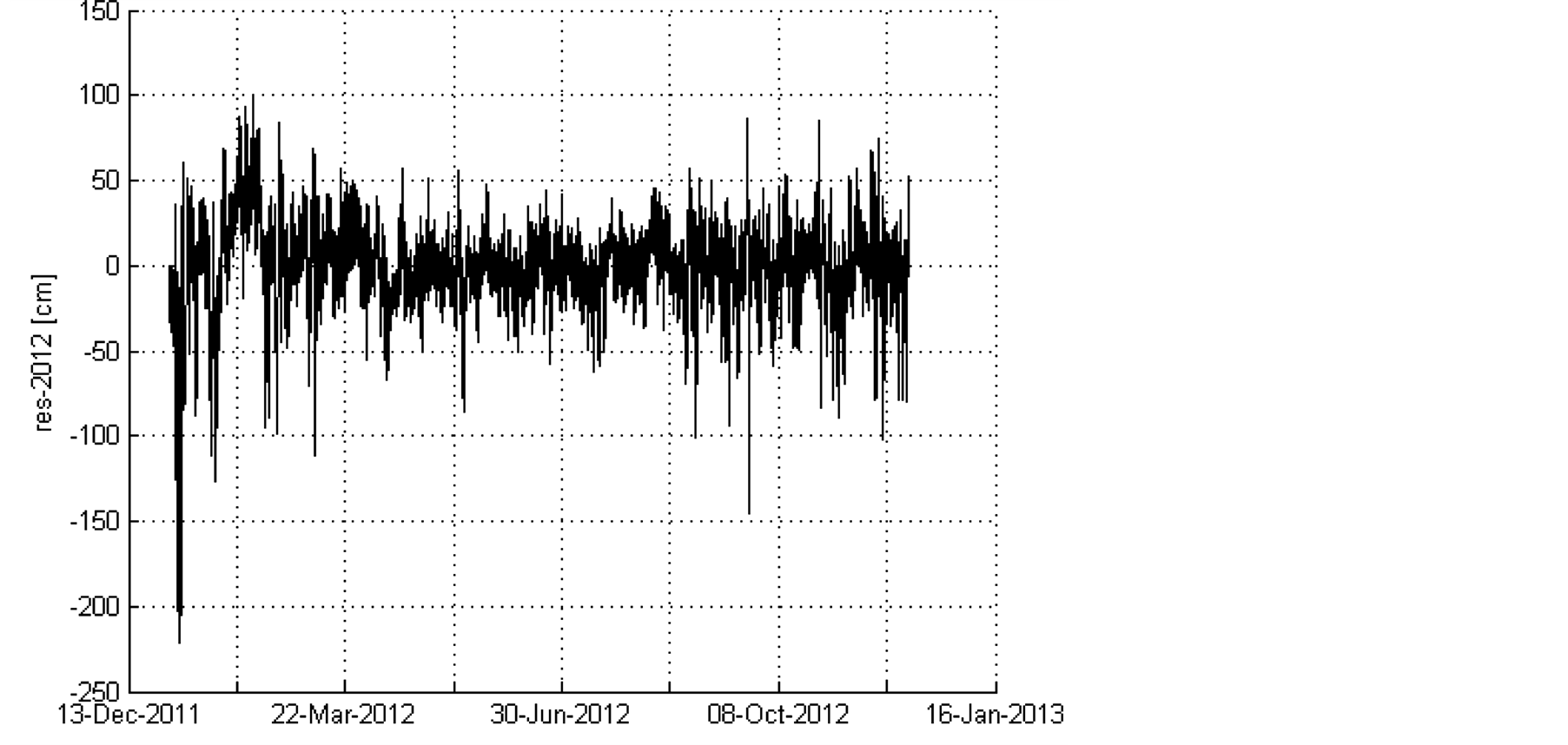
Using the components that are derived from the harmonic analysis, the quality of the analysis is checked by making an astronomical hindcast with a time interval of one minute for the years for which measurement data is available, and comparing the harmonic prediction with the measurements. The residual signal for 2012 is shown in Figure 3. Negative values mean that the astronomical hindcast is lower than the measurements. In the first months of 2012 there is a surge in the North Sea due to prevailing westerly (NW to SW) winds, which raises the water levels in the Scheldt higher than is expected from an astronomical prediction.
A histogram of the difference in level of astronomically predicted high waters is shown in Figure 4. Notice the negative tail in the distribution, which means that the largest devations between harmonically predicted and observed tides occur during periods of positive surge, which is related to the fact that westerly winds (SW to NW) reach relatively higher wind speeds in the Belgian Coastal Zone and have a higher fetch-length over the North Sea.
Table 1 gives a statistical analysis of the astronomical hindcast. Both the residual signal and the difference in timing and level of high and low water are statistically analysed to give an idea of the accuracy of the tidal prediction. The method achieves slightly better results for 2010-2012, but that might be linked by to the fact the time series for 2009 has more gaps, and needed a more elaborate validation of the measurements, which might suggest a lesser quality of the measurements in 2009 compared to 2010-2012. Apart from this, differences between the different analysed years are to be expected due to unique meteorological conditions in every year.
A positive bias means the predicted tide is too low (for level), or too early (for time). The timing of the predicted low waters has the most important bias, with the predicted low waters being 7 to 8 minutes too early. This bias can be found in all analysed years, and is significant when compared to the RMSE (about 50%). Overall, the accuracy of the tidal prediction lies between 21 and 25 cm, both for the extrema and the complete time series. Due to meteorological effects, the harmonically predicted tide can always differ significantly from the real, observed tide.
3.4. Hydraulic Model (1D)
An existing 1D hydraulic model solving the shallow water equations in the tidally influenced part of the Scheldt estuary is cut off at Prosperpolder. Figure 5 shows the channel network of the model. The quality of the thus obtained 1D model is checked with a hindcast run for the year 2012. The model is driven at its downstream boundary with one-minute measurements at Prosperpolder. Measured values of fresh water discharge are imposed at the upstream edges of the model. If those are not available, average values are imposed. The simulated water levels along the Sea Scheldt are compared to observed water levels [8] .
Table 2 shows the statistics for the hindcast for 2012. Most of the error in the RMSE can be explained by the bias, which could be related to the fact that large parts of the bathymetry of the 1D model dates back to 2000. A bathymetric update and recalibration of the 1D model is planned, so in the future a better model quality can be expected.
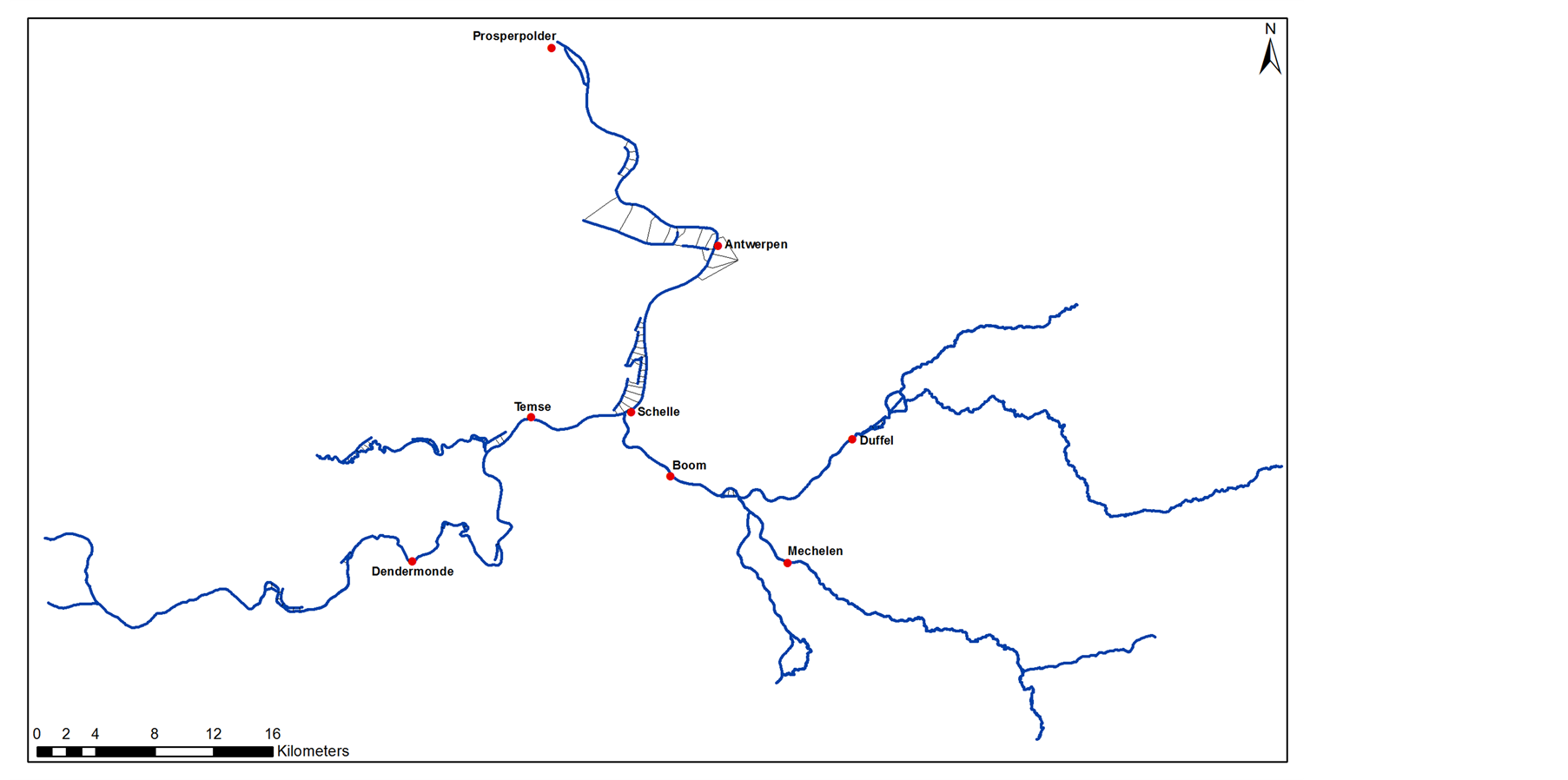
Figure 5. 1D hydraulic model of the tidally influenced part of the Scheldt estuary.
3.5. Tidal Prediction for the Sea Scheldt
With the harmonic components for station Prosperpolder, a harmonic tidal prediction at station Prosperpolder is assembled as a time series with a one-minute time interval. This time series is used as a downstream boundary condition for the 1D hydraulic model. The modeled time series inside the model domain are used as harmonic tidal predictions for these stations. An example set of predicted time series is shown in Figure 6.
Using this hybrid technique, tidal predictions can be made at arbitrary locations along the estuary, provided they are within the model domain. Because a hydraulic model is used to translate the predicted time series at Prosperpolder to time series at other locations in the estuary, the progressive nature of the tidal wave is guaranteed. High water in a station downstream is always later than in a station upstream in this hydraulic model. This internal consistency is not guaranteed when harmonic tidal analysis and subsequent tidal prediction are performed separately on two nearby stations with a distance that is small compared to the tidal wave length, due to the finite accuracy of the tidal components.
Model validation has shown that the hydraulic model accurately captures the deformation of the tidal wave in the estuary due to the combination of channel planimetry, bathymetry and bottom friction [8] . It is therefore believed that using a model to generate tidal predictions at arbitrary locations along the tidally influenced zone of the estuary will have a better accuracy than a simple linear interpolation between two stations where tidal components are available.
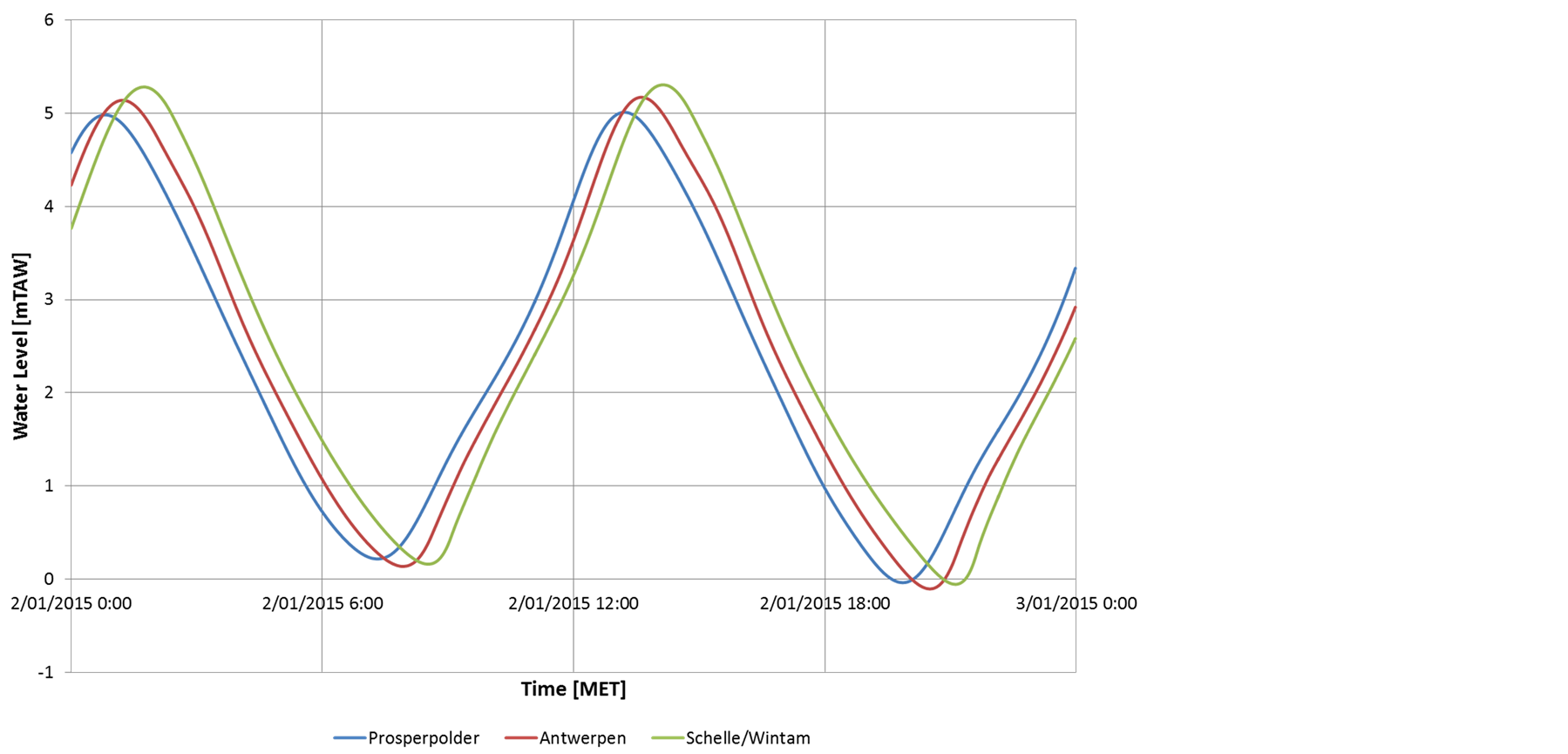
Figure 6. Combined tidal prediction for 3 stations along the Sea Scheldt.
4. Conclusions
The vertical tide in the Sea Scheldt (Belgium) is predicted using a hybrid approach that combines harmonic tidal prediction at a station downstream and 1D hydraulic modeling for the stations further upstream. The accuracy of the tidal prediction at Prosperpolder is naturally limited by the accuracy of the tidal analysis. The accuracy of the tidal prediction at the stations upstream is further limited by the accuracy of the hydraulic model used. The accuracy of the model however (expressed as RMSE) is better than the difference that can be expected between the harmonically predicted tide and the observed tide due to meteorological effects. A planned update of the 1D hydraulic model is expected to increase the accuracy of the model (both in terms of bias and RMSE), and therefore of the tidal predictions upstream.
Different products are derived from the tidal predictions. Predicted time and level of high and low water at Prosperpolder, Antwerpen and Wintam are published annually in tidal tables [3] . The predictions at Prosperpolder are also published annually in the Admiralty Tide Tables. Predicted time series at Kattendijk sluice (close to station Antwerpen) are used to generate a control scheme for the sluice, which only functions between certain water levels. Using the hybrid approach presented here, Flanders Hydraulics can answer ad-hoc questions on expected water levels at arbitrary locations along the estuary, regardless of whether harmonic tidal components are available for those locations.
Acknowledgements
The people at HIC are kindly acknowledged for skillfully preparing the measurement data for analysis. M. Wouters and E. Taverniers assured the quality of the predictions.
References
- Davies, L.J. (1964) A Morphogenic Approach to the Worlds’ Shorelines. Zeitschrift für Geomorphologie, 8, 127-142.
- Plancke, Y., Maximova, T., Ides, S., Peeters, P., Taverniers, E. and Mostaert, F. (2012) Werkgroep O&M—Projectgroep Veiligheid: Sub Project 1: Data Analysis and Hypothesis—Lower Sea Scheldt. Version 4.0. WL Rapporten, 756/05. Flanders Hydraulics Research, Antwerp.
- Afdeling Kust-Vlaamse Hydrografie (2014) Getijtafels voor Nieuwpoort, Oostende, Blankenberge, Zeebrugge, Vlissingen, Prosperpolder, Antwerpen en Wintam. IVA Maritieme Dienstverlening en Kust, Brussel.
- Admiralty Tide Tables (1999) United Kingdom and Ireland (Including European Channel Ports). Vol. 1 NP201-01. The Hydrographer of the Navy, Taunton.
- Vanlede, J., Taverniers, E., Deschamps, M., Verwaest, T. and Mostaert, F. (2013) Harmonische Analyse en Voorspelling: Getij Schelde te Prosperpolder. Versie 2_0. WL Rapporten, 13_055. Waterbouwkundig Laboratorium, Antwerpen.
- Rijkswaterstaat (2004) TIDEMAT Tidal Analysis. User’s Manual, 30 p.
- Schureman, P. (1958) Manual of Harmonic Analysis and Prediction of Tides. Special Publication. US Coast and Geodetic Survey, 98. US Department of Commerce. Coast and Geodetic Survey, Washington DC.
- Coen, L., Deschamps, M. and Mostaert, F. (2012) Berekening Astronomisch getij dmv 1D-Modellering: Validatie Prospermodel. Versie 1.0. WL Rapporten, 12_133. Waterbouwkundig Laboratorium, Antwerpen.