Open Journal of Civil Engineering
Vol.08 No.04(2018), Article ID:88303,21 pages
10.4236/ojce.2018.84030
Dynamic Analysis of Soil Structure Interaction Effect on Multi Story RC Frame
Hailu Getachew Kabtamu1, Gang Peng2, Denghong Chen3*
College of Civil Engineering and Architecture, China Three Gorges University, Yichang, China

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 17, 2018; Accepted: November 2, 2018; Published: November 5, 2018
ABSTRACT
In this study dynamic analysis of Soil Structure Interaction (SSI) effect on multi story reinforced concrete (RC) frame founded on soft soil (flexible base) is made and compared with fixed base. Two model 2D RC frames with 7 and 12 story are selected for analysis. Winkler Spring and half space direct method models are used for flexible base for the frames founded on two types of soft soils with shear velocity Vs < 150 m/s Asper Seismic Codes of Chinese GB50011-2010 Soil IV and Ethiopian ES8-2015 soil D. The frames are subjected to strong ground motion matched to response spectrums of soft soil of Chinese GB50011-2010 and Ethiopian ES8-2015 for linear time history analysis. The dynamic analysis result shows Spring and Fixed base mass participation 90% reaches in 2 or 3 modes but in direct method 11 to 30 modes for story 12 and 7 respectively. However, both flexible base models have bigger fundamental period of vibration and inter story drift but smaller base shear than fixed base. In addition, within the flexible base models the inter-story drift, second order effect (P-Δ) and Story shear distribution are different along the height of frames. The spring model shows larger Story drift and second order effect (P-Δ) at the bottom of Story for both soft soils types. On the other hand, half space direct method model indicates value reverse to spring model; it gives bigger Story drift and P-Δ effect in the top stories than fixed base. Finally, this study concludes that base shear reduction due to SSI may not be always beneficial. Because the gravity load is constant in both fixed and flexible bases that cause bigger P-Δ effect at the bottom stories due to increase, inter story drift and decrease story shear in flexible base.
Keywords:
Soil Structure Interaction, Dynamic Analysis, Fixed Base, Flexible Base, Direct Method, Winkler Spring, Period of Vibration, Story Shear, Story Drift and P-Δ Effect

1. Introduction
In dynamic analysis of a building structure, the base support condition is very essential for calculating its dynamic behavior useful in estimating structural responses and distribution within structural members. The building base condition will be different depending on the type of supporting ground. Fixed base foundation could be assumed on stiff soil and flexible base foundation on soft soil. Flexibility of base causes decrease in structural stiffness and increase period of vibration during earthquake ground motion. Consequently, the building structural responses such as displacement drift, Story shear, and P-∆ effects will be different from fixed base that could beneficial or detrimental. As a result, in the past the dynamic analysis building on soft soil has gained serious attention in seismic active areas.
Wolf 1985 [1] and many other authors noted that for structures built on strong foundation such as rock during earthquake motion, the force generated in the form of overturning moment and transfers shear will not cause deformation to the base in turn; the stiffness of structure remains constant. For a given control of motion, the seismic response of the structure depends only on the properties of the structure, however for soft soils used as base; the base deformation changes the stiffness of structure during earthquake vibration, which in turn affects its response, known as Soil Structure Interaction (SSI) effect. Even if, SSI has both kinematic and inertia effect on structure; in this study only inertia effect is considered.
Figure 1 illustrates SSI effect on structures [2] . For single mass (m), height (H), stiffness (Ks) supported on soft soil foundation lateral stiffness (Ky), and rotational stiffness (Kθ) foundation base radius (r) subjected to ground motion acceleration üg. This causes the base deformation in rotation (θ) and larger translation of at the top of structure that results base flexibility (SSI). Consequently, the dynamic behavior of the structure changes affected structural responses like period of vibration, displacement, base shear, and secondary moment effects P-Δ
Figure 1. Soil Structure Interaction Model Adapted from [2] : (a) Structure supported on soft soil (b) Idealized model for Soil Structure interaction.
(mainly axial load carrying vertical members such as column in multi-story building).
In the past, many studies showed that soil structure interaction (SSI) has both beneficial and detrimental effect on structure. Because SSI increases flexibility of structure, lengthening of structural vibration period and damping. As a result, in building structures, the base shear decreases; however at the same time displacement increases. The decrease in base shear may be advantages, but the increment in displacement induces secondary moments P-∆ effect due to high inter-story drift. Moreover, excessive deflection of building could lead to collision of nearby structures. In addition, P-∆ is highly emphasized structural members supporting big axial load such as tall building, and consequence can be catastrophic which leads to instability of the whole structure. Moreover, there are researches those stating that for some special cases fixed base models can lead to an underestimation of seismic response [3] [4] [5] . According to references [4], the idea of design spectra of the seismic codes along with the increased fundamental period and effective damping due to SSI lead always to reduce forces in the structure is not always true. It is shown that in certain seismic and soil environments, an increase in the fundamental natural period of a moderately flexible structure due to SSI may have detrimental effect on the imposed seismic demand [4] [6] . In contrast [7] study emphasizes the beneficial effect of soil structure interaction for reduction of seismic demand as economic advantage without including the P-∆ effect that may lead to catastrophic failure.
Additionally, the SSI effect has been included in some seismic codes. European regulation for seismic design Eurocode 8 (EC8-2004) [8] of structures from which Ethiopia Seismic Standard Code (ES8-2015) [9] adopted from contains very few information for including Soil-Structure Interaction. Seismic design of foundation regulation EN1998-Part 5 Extension of EC8-2004 [10] states that SSI the fundamental period of vibration of the flexibly-supported structure will be longer than that of the fixed-base structure, the overall damping will increase both due to radiation and the internal damping generated at the soil-foundation interface, in addition to the damping associated with the superstructure. EN1998-Part 5 [10] states for the majority of common building structures, the effects of SSI tend to be beneficial, since it reduce the bending moments and shear forces in the various members of the superstructure. Nevertheless, EN1998-Part 5 [10] noted also the effect of SSI structures supported on soft soils shear velocity Vs < 100 m/s can have detrimental effect on structures where P-∆ (2nd order) effects play a significant role; structures with massive or; slender tall structures, such as towers and chimneys.
On the other hand, the American standard ASCE Standard ASCE/SEI 7 - 10 [11] recognizes the effect of SSI on structures. Yet, ASCE Standard ASCE/SEI 7 - 10 provides more detail information than EN1998-Part 5 by providing equations that considers the effect in the determination of the design earthquake forces and the corresponding displacements of the structure if the model used for structural response analysis does not directly incorporate the effects of foundation flexibility. For equivalent lateral force procedure fulfilling requirement, to account for the effects of soil-structure interaction, the base shear (V) determined from shall be reduced to in Equations (1) and (2)
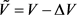 (1)
(1)
The reduction ΔV, shall be computed as follows and shall not exceed 0.3 V
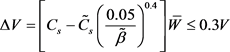 (2)
(2)
where Cs = the seismic design coefficient computed from Equations 12.8-2, 12.8-3 calculated using fixed base fundamental period of vibration (T) and = the value of Cs computed from Equations 12.8-2, 12.8-3 calculated using flexibly supported structure ( ) in ASCE/SEI 7-10 Section 12.8.
= the fraction of critical damping for structure-foundation system.
= the effective seismic weight of structure which shall be taken as 0.7 W, except for structures where effective weight is concentrated at a single level, taken as equal to W.
The effective period shall be determined as follows in Equation (3)
 (3)
(3)
where T = the fundamental period of the structure as determined in 12.8.2 of ASCE7-10.
= the stiffness of the structure where the fixed base, defined by Equation (4)
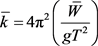 (4)
(4)
where, = the effective height of the structure, which shall be taken as 0.7 times the structural height (hn) except for structures where gravity load is concentrated at a single level, equal to that level.
Ky = the lateral stiffness of the foundation as the horizontal force at level of the foundation necessary to produce a unit deflection at that level, the force and deflection being measured in the direction in which the structure is analyzed.
Kθ = the rocking stiffness of the foundation defined as the moment necessary to produce a unit average rotation of the foundation, the moment and the rotation being measured in the direction in which the structure is analyzed.
g = acceleration due to gravity.
Effective damping factor for structures foundation system shall be computed by Equation (5)
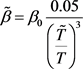 (5)
(5)
β0 = the foundation damping factor as specified in Figure 2 that shows damping factor increase up to 20% for period of vibration lengthening factor of 1.5 to 2.0 compared with fixed base.
Similar to EC8-2004 Part 5 and ASCE/SEI 7-10,Chinese seismic code GB 50011-2010 [12] considers Soil Structure Interaction effect according to Article 5.2.7, horizontal seismic shear force of rigid base may be reduced according to requirements and Story drift may be calculated according to reduced story shear force, however not detailed enough. In conclusion, the three seismic codes do not provide full recommendation, which requires further study.
So far, several SSI study on building report mainly focuses only on period of vibration, displacement, story drift, story shear and geotechnical parameters that affects SSI biased to geotechnical engineering. However, little attention is given to structural responses such as P-∆ effect due to gravity load of building itself affecting vertical structural members for example column, even if many building collapsed as a result of P-∆ secondary moments and instability. In this paper SSI effect (flexible base) on P-∆ effect is additionally studied using two methods: half space direct method of soil structure interaction, and Winkler Spring and then compared with fixed base using SAP2000 structural analysis software [13] for 2D reinforced concrete frame. In addition, soil-structure interaction (SSI) effect responses variation along height of building among fixed and flexible bases is studied.
2. Model Structural System for SSI Analysis
2.1. Structural System and Soil Data
For comparative analysis of fixed base and flexible base structures, two residential buildings frame regular in plan and elevation are considered to avoid secondary
Figure 2. Foundation damping factor adopted from ASCE/SEI 7-10 [11] .
effects due to irregularity. Figure 3 shows the same typical residential buildings plan of 15 m × 32 m for both model frames common Architectural plan in China that can be adopted to Ethiopian construction. The plan is adapted from Chinese Seismic and Concrete Design standards [14] [15] and modified for this study purpose. The 2D model frames here after denoted as, S7 and S12 for 7 and 12-story respectively. Figure 4 shows typical transverse frames S7 and S12 story with first story height 4.50 m and others typical Story height of 3.6 m. The frames are considered in the short transfer direction and carry tributary area of floor load shown in Figure 3 for 2D regular frame analysis. The columns and beams of frames are designed according to Ethiopian Concrete Design Standard ES2-2015 [16] that are subjected to design seismic action of PGA = 0.25 g soil type B design response spectrum [9] . Beam sections for both model frame are the same BM 25 cm × 65 cm, but column sizes are different, CL65 cm × 65 cm
Figure 3. Typical floor plan for model residential building S7 and S12.
Figure 4. Typical model building frames S7 and S12.
for S7 and CL70 cm × 70 cm for S12. Furthermore, the beam and column stiffness in the frame are proportioned to behave in shear mode according to [17] .
In seismic weight calculation, given imposed load on residential building, according to ES1-2015 [18] and GB5009-2012 [19], Uniform Live Load LL = 2.0 kN/m2, Roof live load LL = 1.0 kN/m2 and dead load floor finish and other walls including self-weight is 8.30 kN/m2, and wall load on beam including self-weight of beam is 15.90 kN/m. For seismic weight calculation, GB50011-2010 is used 50% of live load and 100% dead load for dynamic analysis. Total dead load transferred on floor beam using tributary area including self-weight is 55.00 kN/m and roof floor beam is 37.28 kN/m for analysis. Live load transferred on floor beam 8.00 kN/m and 4.00 kN/m on roof beam.
Structural members material strength specifications from [16] [20] : Concrete C-30, Ec = 31 × 106 kN/m2, Concrete Unit Weight = 24 kN/m3 and Steel S-400/HRB400, Es = 200 × 106 kN/m2, Steel Unit Weight = 78.5 kN/m3.
Soil properties supporting the structure: Assumed soft soil category according to GB50011-2010 and ES8-2015 for depth greater than 30 m below the structure Shear Velocity Vs = 150 m/s corresponds to soil D in ES8-2015 [9] and Soil IV in GB50011-2010 [12], Density ρ = 1500.00 kg/m3, Poisson Ratio, ν = 0.40, Shear modulus, G = 33.75 Mpa, and Elastic modulus, E = 94.50 Mpa.
2.2. Soil Structure Interaction Numerical Modelling
To date, many general-purpose structural analysis softwares are available for modelling structural members with well-defined member properties and boundaries of structures in either 3D or 2D analysis. However, Soil Structure Interaction (SSI) analysis model involves both structural member and foundation soil properties, which does not have well defined engineering material properties and boundaries. Because of this many simulation software’s may be suggested for soil structure interaction analysis but may not be suitable in design office for practice [2] . In this study general-purpose structural analysis software SAP2000 [13] is selected that is commonly available in design offices and that has capacity to simulate SSI [21] .
So far, for SSI analysis for both 2D and 3D model has been used using different methods. Using direct half space method, the base soil modelled together structure using 3D solid element [22] and 2D plane strain shell soil element [3] [23] [24] [25] [26] . Also, SSI is modelled using Winkler spring element [27] and Viscous Transmitting boundary method [25] [28] . In addition full 3D direct method for arch bridge analysis is made by [29] . Moreover, authors [25] [28] [30] used direct method in modelling multistory building with equivalent 2D model for the superstructure can be constructed straightforward for the shorter dimension. With this aim, a simple assumption is to take a typical transverse resistant axis loaded by tributary weight/mass over the distance in order to keep nearly the internal forces in structural elements. The stiffness contributions of the transverse elements are ignored. If the foundation is assumed to be infinitely rigid following the longer distance, an equivalent plane-strain foundation-soil model is valid [30] . In the same way in this study, for the regular model building both in plan and in elevation considered above, 2D frame for SSI analysis is used.SSI is modelled using direct half space method and Winkler Spring. Finally, the structural responses of SSI are compared with fixed base.
2.2.1. Direct Half Space Method
Most structural analysis computer programs including SAP2000, chosen for this study, automatically apply the seismic loading to all mass degrees of freedom within the computer model and cannot solve the SSI problem. However, this can be solved using the most common soil-structure interaction (SSI) approach, used three dimensional soil-structure systems, is based on the ‘‘added motion’’ formulation [21] . This formulation is mathematically simple, theoretically correct, and is easy to automate and use within a general linear structural analysis program SAP2000 [21], which is based on modelling SSI with massless foundation. Therefore, in the added mass formulation, the entire structure and soil can be modelled in single system defined as direct method of SSI analysis. The base soil is modelled using half space model with dimensions defined according to [22] . If the soil material can be considered linear, the SAP2000 program, using the Solid element, can calculate either the one-, two- or three-dimensional free-field motions at the base of a structure [21] . In this study Linear time history analysis is made using finite element based structural analysis software SAP2000 [13] . 2D reinforced concrete frame analysis is made without non cracked beam and column stiffness subjected to Matched Loma Prieta earthquake with magnitude-6.9 in 1989 [31] .
For modelling of infinite soil surrounding structure to consider the effect of wave propagation the assumption adopted from [6] sufficiently far from structure as shown in Figure 5. The soil depth D more than 2B is 45 m and with H distance from structure to boundary greater than 3B, the total width of half space more than 7B is 135 m, where B is the width of model of building in short direction. The soil is modelled using 2D plane strain elastic elements as per [30] . The soil elements size meshed by 3 × 3 m and 1 × 3 m larger and smaller elements respectively in Figure 5. The damping is assumed as 5% of the critical damping using Rayleigh damping definition for both structure and soil. The members in the frame structures are modelled using beam elements. The boundary conditions of half space soil for the analytical model a fixed boundary is assumed at the base of the soil model while for vertical soil boundaries artificial viscous spring dashpot is considered according to [32] [33] [34] . The transmitting boundaries are used to represent the effect of the truncated soil by using viscous spring dashpot dampers at the boundaries. These boundaries, which can fully absorb body waves propagating normal and tangential to the boundary, were initially proposed by Lysmer and Kuhlemeyer [32] . Furthermore, after many modification to recent viscous spring equation in artificial boundary with normal and tangential direction adapted from [34] [35] in Equations (6a) to (6f)
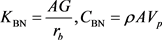 (6a)
(6a)
 (6b)
(6b)
, P-Wave Velocity (6c)
, Shear wave Velocity (S-Wave) (6d)
, Shear Modulus (6e)
, P wave Modulus (6f)
where KBN and KBT are the normal and tangential stiffness coefficients, respectively. CBN and CBT are the normal and tangential damping coefficients, respectively. A is the total area of all elements around the node at the boundary. rb is the distance from the scattering wave source to the artificial boundary point. Vs and Vp are the wave velocities of the S wave and P wave, respectively. G is the medium’s shear modulus, E―Elastic modulus, ν―Poisson ratio and ρ is the medium’s mass density.
Given Soft Soil Properties above;
ρ = 1500.00 kg/m3, ν = 0.40, G = 33.75 Mpa, E = 94.50 Mpa, Vs = 150 m/s, then, Vp = 367.42 m/s, KBN = 2250.0 kN/m, KBT = 1125.0 kN/m, CBN = 1653.0 kN∙s/m and CBT = 675.0 kN∙s/m. This values are used for modelling viscous spring dashpot in SAP2000 [13] using link support element at the half space boundary model of direct method shown in Figure 5.
Figure 5. 2D soil structure model using half space direct method model in SAP2000.
2.2.2. Winkler Spring Method
In addition to the direct method of modelling, for evaluating the seismic response of reinforced concrete multi-story buildings with raft foundation on soft soil, the underneath soil is modeled by Winkler spring approach with equivalent static stiffness based on soil modulus of elasticity [3] [27] . For same soft soil used in direct method with shear velocity of Vs = 150 m/s., equivalent static stiffness for different direction vibration mode, the soil spring stiffness can be calculated using Gazetas 1991 [36] expressions shown in Equations (7a) to (7c).
Vertical direction (Z) (7a)
Horizontal (lateral direction y) (7b)
Horizontal (Longitudinal direction x) (7c)
where G is shear modulus of soil defined in Equation 6(e), E is the modulus of elasticity of soil; ν is the Poisson’s ratio of soil. L and B are the length and width of Raft foundation of the whole building, respectively. For Raft foundation plan Length L = 32 m and Width B = 15 m, Soft soil with shear velocity Vs = 150 m/s, Poisson ratio ν = 0.4, Shear Modulus G = 33.75 Mpa, Modulus of Elasticity E = 94.50 Mpa, Dynamic stiffness in the vertical direction, Kz = 6.00 × 103 (kN/m2)/m, Horizontal in lateral direction Ky = 4.66 × 103 (kN/m2)/m, Horizontal Longitudinal direction Kx = 3.98 × 106 (kN/m2) /m. For 2D frame analysis, the total stiffness of raft is distributed to each column support according to its tributary area.
3. Earthquake Loading
In this study strong ground motion Loma Prieta 1989 from PEER [31] is matched to design response spectrum of soft ground type of Ethiopian Seismic Code and Chinese with shear velocity Vs = 150 m/s, which is used for time history analysis of 2D frame in S7 and S12 model building.
3.1. Design Response Spectrum
Design response spectrum with 10% exceedance in 50 years’ PGA = 0.30 g, M = 8 measured with reference to Chinese Code GB50011-2010 for Soil II is used. This is equivalent to 0.25 g of soil B of Ethiopia ES8-2015 based on Chinese and European seismic code seismic soil equivalency study [37] [38] and can be applied to Ethiopia as it is adopted from EN1998-1 [9] . Figure 6 shows equivalent response spectrum comparison used in this analysis. For flexible base (SSI) analysis, equivalent soft ground types D in ES8-2015 and IV in GB50011-2010, here after denoted as D and IV respectively will be used in the subsequent numerical calculations of structural responses.
3.2. Matched Strong Ground Motion
For dynamic analysis, strong ground motion of Loma Prieta earthquake of USA in 1989 ground motions, PGA = 0.367 g is used [31] . To use ground motion for analysis, matching to the design response spectrum with 5% damping is needed. For matching, procedures outlined in Seismic Code of Ethiopia ES8-2015 [9] are used. The ground motion is matched to equivalent target response spectrum of very soft ground type D of ES8-2015 PGA = 0.25 g and IV of GB50011-2010 PGA = 0.3 g. Seismosmatch 2016 is used for matching [39], a computer program to adjust ground-motion records so that their spectral acceleration response matches a target response spectrum. For matching ES8-2015 recommends 0.2T1 and 2T1 minimum and maximum for specific building structure, where T1 fundamental period of vibration, using modal analysis in SAP2000 with fixed base model the fundamental period of vibration. In this study 12 Story frame with fundamental period of vibration T1 = 2.12 s is used. Accordingly, the matching period for Loma Prieta earthquake is Tmin = 0.424 s and Tmax = 4.0 s. Table 1 and Figures 7(a)-(e) show matched ground motion parameters for the two design response spectrums.
3.3. Time History Analysis
Using the matched strong ground motion linear time history analysis is made for flexible and fixed base support conditions of the frames Story 7 (S7) and Story 12 (S12). For all support conditions, the seismic responses are calculated using SAP2000 structural analysis software [13] .
4. Results and Discussion
This section presents the dynamic analysis results. This includes dynamic properties
Figure 6. Equivalent design response spectrum of GB50011-2010 and ES8-2015.
Table 1. Original and matched ground motion loma prieta earthquake.
Figure 7. (a), (b), (c), (d), and (e) Matching of Loma Prieta Ground Motion. (a) Target Response spectrum soil D ES8-2015 Pseudo acceleration Maximum = 0.70 g; (b) Target Response spectrum Soil IV GB50011-2010 Pseudo acceleration Maximum = 0.68 g; (c) Original Loma Prieta earthquake 1989 M = 6.9; (d) Matched Loma Prieta Ground motion to Response Spectrum of soil D of ES8-2015 PGA = 0.25 g; (e) Matched Loma Prieta Ground motion to Response spectrum of Soil IV of GB50011-2010 PGA = 0.30 g.
and other response of the model structures S7 and S12 shown in table and graph form. All response comparisons are made with reference to fixed base for both types of flexible base models presented in subsequent sections.
4.1. Modal Analysis Result
Modal analysis of the model frames S7 and S12, both fixed and flexible base (SSI), is made using finite element method software, SAP2000 [13] . Flexible base is modelled using the two methods Winkler (SSI WS) and direct method half space method (SSI DM). From the analysis result, mass participation of frames 90% or more reaches with few modes of 2 or 3 in both Spring and Fixed base. On the other hand, in direct method from 11 to 30 modes is required, which corresponds to S12 and S7 frames respectively. This shows higher mode effect is more important in direct method modelling of SSI, which in turn affects the structural responses of frames. Furthermore, the fundamental period of structures with flexible base of SSI-WS and SSI-DM is greater than FB shown in Table 2, for S7 SSI-WS and SSI-DM and greater than FB by 57.50% and 70.00% respectively, in addition, for S12 SSI-WS and SSI-DM greater by 52.00% and 66.50% respectively. The period lengthening shows good agreement with ASCE Standard ASCE/SEI 7 - 10 provisions [11] .
4.2. Story Displacement
Story displacement is very essential parameters for nearby building collision effect in seismic event for making enough separation between nearby structures. The deflection profile is different based on fixity of the base. Figure 8(a) and Figure 8(b) show the displacement difference in fixed and flexible base. The top Story displacement of flexible base is greater than the fixed base by 143% in S7 and 189% in S12 for soil IV in Half space Model. For spring model soil IV, 185% in S7 and 162% in S12.Similar pattern for soil D is shown in Figure 8(a) and Figure 8(b).
4.3. Inter Story Drifts
Story drift is one of the important parameter for lateral load effect on vertical members in stability analysis. Figure 9 shows the Story drift in flexible base compared with fixed base. Figure 9(a) compared to fixed base S7 inter Story drift for Half Space Model SSI-DM, soil D 38% to 295% bottom to top stories and for soil IV 200% to 388%, increasing trend bottom to top. For spring model, however soil D 322% to 134% bottom to top stories and for soil IV 370% to
Table 2. Fundamental period of vibration T1 flexible and fixed base.
Figure 8. Story Displacement of S7 (a) and S12 (b).
179%, decreasing trend. Similarly, Figure 9(b) shows compared to fixed base S12 inter Story drift for Half Space Model SSI-DM, soil D 32% to 304% bottom to top stories and for soil IV 34% to 382%, increasing trend bottom to top. For spring model, however soil D 257% to 143% bottom to top stories and for soil IV 319% to 238%, decreasing trend.
4.4 Story Shear
Figure 10 shows the Story shear flexible base compared with fixed base. In general base shear in flexible base is smaller fixed base in both S7 and S12, which is often taken as advantage of SSI [7] [10] [11] [12] . However, Figure 10(a) for S7 soil D in SSI-DM, direct method the base shear 73%and 104% of fixed base in
Figure 9. Story Drift (a) S7 and (b) S12.
bottom and top stories respectively. Similarly soil IV, 92% and 120% of fixed base in bottom and top stories. On the other hand, spring model for soil D varies 67% to 60% bottom to top and the same trend for soil IV 77% to 70% bottom to top stories of fixed base model decreasing trend.
Furthermore, (Figure 10(b)) S12 soil D in SSI-DM, direct method the base shear 73% and 104% of fixed base in bottom and top stories respectively. Similarly soil IV, 92% and 120% of fixed base in bottom and top stories. However,
Figure 10. Story Shear (a) S7 and (b) S12.
Spring model for soil D varies 53% to 76% bottom to top and the same trend for soil IV 60% to 75% bottom to top stories of fixed base model increasing trend compared to S7. This shows, the decreasing effect is not always true for multi-Story building.
4.5. P Delta Effect
One of the detrimental effect of flexible base is P-Delta effect due to excessive deflection. Because in both fixed base and flexible base the vertical gravity axial load in columns remain constant, but Story shear changes depending on ground motion magnitude, ES8-2015 [9] . Equation (8) shows second-order effects (P-∆ effects) need not be taken into account if the sensitivity coefficient θ is less than 0.10. From Equation (8) and Figure 11, one can understand that second order effect depends on of Story shear (V), gravity axial load (P), inter Story drift (Δ) and Story height. For the same building, the ratio Ptot/h remains the same. The effect of change in base fixity is noted in the ratio of story drift to storey shear (Δ/Vtot). This effect can be shown in Figure 12(a) and Figure 12(b) for S7 and S12.
Figure 11. P-delta effect on column.
Figure 12. Second order effect in S7 (a) and S12 (b).
(8)
where
θ is the inter Story drift sensitivity coefficient;
Ptot is the total gravity load at and above the Story considered in the seismic design situation;
Δ is the design inter story drift, evaluated as the difference of the average lateral displacements ds at the top and bottom of the Story under consideration and calculated in accordance with 4.3.4 of ES8-2015 [9] ;
Vtot is the total seismic Story shear; and
h is the inter story height.
Figure 12(a) and Figure 12(b) show sensitivity coefficient of flexible base and fixed base. (Figure 12(a)) S7 for soil D SSI-DM sensitivity coefficient θ is 52% and 284% of fixed base sensitivity coefficient at the bottom and top Story respectively. On the other hand, for soil IV, 218% and 324% for the corresponding stories in direct method. Furthermore, for soil D spring model the sensitivity coefficient can be 481% and 223% bottom and top stories respectively. On the other hand, for soil IV spring model it is 477% and 256% bottom and top Story.
In addition, Figure 12(b) shows, for S12 the things are somewhat different than S7, for half space model SSI-DM soil D sensitivity coefficient θ is 56% and 148% of fixed base in bottom and top Story respectively, that shows P delta effect smaller bottom Story. Nevertheless, for soil IV it is different case, 143% and 341% greater than fixed base, bottom and top Story respectively. In both soils, P delta effect tends to decrease at bottom Story than top, however soil D is far more small, effect of response spectrum ES8-2015 and while IV, response spectrum GB50011-2010. For SSI-WS, spring model with soil D for S12 sensitivity coefficient θ is 478% and 220% of fixed base in bottom and top Story respectively. On the other hand, soil IV it is 659% and 337% greater than fixed base, bottom and top Story respectively. This shows both spring as well as half space models have their own advantage and disadvantage in SSI modelling.
5. Conclusions
This study shows both flexible base models give bigger fundamental period of vibration and drift with reduced base shear than fixed base, good agreement with seismic codes provisions [10] [11] [12] and previous studies [5] [22] [27] . Furthermore, this study indicates that the drift, P-Δ effect and Story shear vary along the height of building from bottom to top stories differently. Because P-Delta effect shows the combined effect of the story shear, drift, storey height and story axial load. The spring model gives larger Story drift and second order effect at the bottom stories for both soils D and IV, which is detrimental effect maximized at bottom stories. Conversely, half space direct method gives somewhat reverse to spring model, and gives larger Story drift and P-delta effect in the top stories. This may be the direct method due to higher mode effect for mass participation factor of 90% than spring model.
In addition, closer examination of spring model of ground motion effects of D and IV on model frames S7 and S12 is different. The smaller ground motion with soil D gives bigger story drift, P-delta effect and Story shear on S7 than S12 while larger ground motion with Soil IV shows the opposite. This indicates bigger earthquake effect more on taller than short building. Because soil IV ground motion (Chinese GB50011-2010) is greater than soil D (Ethiopian ES8-2015), which is related to the design response spectrum of the corresponding seismic codes magnitude.
To sum up, SSI effect may not be always beneficial in multi-story RC frame compared to fixed base. Because the beneficial effect reduction in base shear may be smaller than detrimental effect of P-delta increment on vertical load carrying members. The results obtained in this study is limited to linear time history analysis regular 2D RC frame; however it is good indicator of SSI effect; further study can be made in future to take non linearity effect both in structure and soil.
Acknowledgements
The first Author thanks China Scholarship Council (CSC) for sponsoring this study in China Three Gorges University. In addition, all references and softwares used from different sources are duly acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Kabtamu, H.G., Peng, G. and Chen, D.H. (2018) Dynamic Analysis of Soil Structure Interaction Effect on Multi Story RC Frame. Open Journal of Civil Engineering, 8, 426-446. https://doi.org/10.4236/ojce.2018.84030
References
- 1. Wolf, J.P. (1985) Dynamic Soil Structure Interaction.
- 2. Livaoglua, R. and Dogangun, A. (2006) Simplified Seismic Analysis Procedures for Elevated Tanks Considering Fluid-Structure-Soil Interaction. Journal of Fluids and Structures, 22, 421-439. https://doi.org/10.1016/j.jfluidstructs.2005.12.004
- 3. Kraus, I. and Džakić, D. (2013) Soil-Structure Interaction Effects on Seismic Behaviour of Reinforced Concrete Frames. SE-50EEE, International Conference on Earthquake Engineering, Skopje, 29-31 May 2013, Paper Number: 645073. https://bib.irb.hr/prikazi-rad?&lang=EN
- 4. Mylonakis, G. and Gazetas, G. (2000) Seismic Soil Structure Interaction: Beneficial or Deterimental? Journal of Earthquake Engineering, 4, 277-301. https://doi.org/10.1080/13632460009350372
- 5. Behzad, F., Reza, T.S.H. and Bijan, S. (2014) Soil-Structure Interaction vs Site Effect for Seismic Design of Tall Buildings on Soft Soil. Geomechanics and Engineering, 6, 293-320. https://doi.org/10.12989/gae.2014.6.3.293
- 6. Tabatabaiefar, H.R. and Clifton, T. (2016) Significance of Considering Soil-Structure Interaction Effects on Seismic Design of Unbraced Building Frames Resting on Soft Soils. Australian Geomechanics, 51, 55-64.
- 7. Asrat, W. (2014) Soil-Structure Interaction Provisions; a Potential Tool to Consider for Economical Seismic Design of Buildings? Journal of the South African Institution of Civil Engineering, 56, 54-62.
- 8. Eurocode 8 EN1998-1 (2004) Design of Structures for Earthquake Resistance, Part 1: General Rules, Seismic Actions and Rules for Buildings. Brussels.
- 9. ES8-2015 (2015) Ethiopian Standard 8 Based European Norms; Design of Earthquake Structures for Earthquake Resistance, Part 1: General Rules, Seismic Actions and Rules for Buildings. Ethiopia Ministry of Construction, Addis Ababa.
- 10. Eurocode 8 EN1998-5 (2004) Design of Structures for Earthquake Resistance, Part 5: Foundations, Retaining Structures and Geotechnical Aspects. EN1998-5, Brussels.
- 11. ASCE/SEI 7-10 American Society of Civil Engineers (2010) Minimum Design Loads for Buildings and Other Structures.
- 12. GB50011-2010 (2010) China Code for Seismic Design of Buildings. China Architecture & Building Press, Beijing.
- 13. CSI (2009) Structural Analysis Program SAP2000 Advanced 14.0.0. Computers and Structures, Inc., Berkley.
- 14. Zhao, W.X.L., Sheng, C.L., Hui, Q. and Le, L. (2015) Reinforced Concrete Fundamentals according to Chinese Building Code GB50010-2010. China building Industry Press, Beijing.
- 15. Ling, L.X., Yuan, Z.D., Ming, L.S. and Liang, L.H. (2011) Seismic Design Theory and Example of Building Structure. Tongji University Press, Shanghai.
- 16. ES2-2015 (2015) Ethiopian Standard 2 Based on European Norme: Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings. Ethiopia Ministry of Construction, Addis Ababa.
- 17. Sinan Akkar, U.Y. and Gülkan, P. (2005) Drift Estimates in Frame Buildings Subjected to Near-Fault Ground Motions. Journal of Structural Engineering, 131, 1014-1024. https://doi.org/10.1061/(ASCE)0733-9445(2005)131:7(1014)
- 18. ES1-2015 (2015) Ethiopian Standard 1 Based on European Norms: Actions on Structures—Part 1-1: General Actions-Densities, Selfweight, Imposed Loads for Buildings. Ethiopia Ministry of Construction, Addis Ababa.
- 19. GB50009-2012 (2012) Load Code for the Design of Building Structures. China Building Industry Press.
- 20. GB50010-2010 (2010) China Code for Concrete Design of Structures. China Architecture & Building Press, Beijing.
- 21. Wilson, E.L. (2002) Three-Dimensional Static and Dynamic Analysis of Structures a Physical Approach with Emphasis on Earthquake Engineering. Computers and Structures, Berkeley.
- 22. Tabatabaiefar, H.R. and Massumi, A. (2010) A Simplified Method to Determine Seismic Responses of Reinforced Concrete Moment Resisting Building Frames under Influence of Soil-Structure Interaction. Soil Dynamics and Earthquake Engineering, 30, 1259-1269. https://doi.org/10.1016/j.soildyn.2010.05.008
- 23. Sáez, E., Lopez-Caballero, F. and Modaressi-Farahmand-Razavi, A. (2013) Inelastic Dynamic Soil-Structure Interaction Effects on Moment-Resisting Frame Buildings. Engineering Structures, 51, 166-177. https://doi.org/10.1016/j.engstruct.2013.01.020
- 24. Lu, X.-Z., Ye, L.-P., Ma, Y.-H. and Tang, D.-Y. (2011) Lessons from the Collapse of Typical RC Frames in Xuankou School during the Great Wenchuan Earthquake. Advances in Structural Engineering, 15, 139-153.
- 25. Manafpour, A. R. and Moradi, V. (2012) Investigating Conventional FE Modelling for Dynamic Soil-Structure Interaction under Horizontal and Vertical Ground Motions. Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, 24-28 September 2012, 20147-20157.
- 26. Petronijevic, P., Zdravkovic, S., Mdladnovic, B., Zlatkov, D. and Petronijevic, A.M. (2014) Analysis of a Potential Collision of Building Earthquake Based Computer Simulation. Tehnicki Vjesnik, 21, 1125-1133.
- 27. Raheem, S.E.A., Ahmed, M.M. and Alazrak, T.M.A. (2015) Evaluation of Soil-Foundation-Structure Interaction Effects on Seismic Response Demands of Multi-Story MRF Buildings on Raft Foundations. International Journal Advanced Structural Engineering, 7, 11-30. https://doi.org/10.1007/s40091-014-0078-x
- 28. Karabork, T. and Bilgehan, R.P. (2014) A Comparison of the Effect of SSI on Base Isolation Systems and Fixed-Base Structures for Soft Soil. Geomechanics and Engineering, 7, 87-103. https://doi.org/10.12989/gae.2014.7.1.087
- 29. Güllü, H. and Pala, M. (2014) On the Resonance Effect by Dynamic Soil-Structure Interaction: A Revelation Study. Natural Hazards, 72, 827-847. https://doi.org/10.1007/s11069-014-1039-1
- 30. Saez, E., Lopez-Caballero, F. and Modaressi-Farahmand-Razavi, A. (2008) Influence of 2D and 3D Soil Modeling on Dynamic Nonlinear SSI Response. The 14th World Conference on Earthquake Engineering, Beijing, 12-17 October 2008, Paper ID: 14-0057. http://www.14wcee.org/Proceedings/isv7/main.htm
- 31. PEER. PEER Strong Motion Database. https://peer.berkeley.edu/peer-strong-ground-motion-database
- 32. Lysmer, J. and Kuhlemeyer, R.L. (1969) Finite Dynamic Model for Infinite Media. Journal of Engineering Mechanics Division, 95, 859-878.
- 33. Song, C. and Wolf, J.P. (1994) Dynamic Stiffness of Unbounded Medium Based on Damping-Solvent Extraction. Earthquake Engineering and Structural Dynamics, 23, 169-181. https://doi.org/10.1002/eqe.4290230205
- 34. Chen, D.-H., Du, C.-B., Yuan, J.-W. and Hong, Y.-W. (2012) An Investigation to Influence of Damping on the Earthquake Response Analysis of High Arch Dam. Journal of Earthquake Engineering, 16, 329-349. https://doi.org/10.1080/13632469.2011.638697
- 35. Liu, J., Du, Y., Du, X., Wang, Z. and Wu, J. (2006) 3D Viscous-Spring Artificial Boundary in Time Domain. Earthquake Engineering and Engineering Vibration, 5, 93-102. https://doi.org/10.1007/s11803-006-0585-2
- 36. Gazetas, G. (1991) Formulas and Charts for Impedances of Surface and Embeded Foundations. Journal of Geotechnical Engineering, 117, 1363-1381. https://doi.org/10.1061/(ASCE)0733-9410(1991)117:9(1363)
- 37. Kaihai, L. and Yayong, W. (2012) Researches about the Conversion Relationships among the Parameters of Ground Motions in the Seismic Design Codes of China, America and Europe. World Conference on Earthquake Engineering, Lisbon, 24-28 September 2012, 10882-10892.
- 38. Shi, G., Hu, F. and Shi, Y. (2016) Comparison of Seismic Design for Steel Moment Frames in Europe, the United States, Japan and China. Journal of Constructional Steel Research, 127, 41-53. https://doi.org/10.1016/j.jcsr.2016.07.009
- 39. Seismosoft (2016) SeismoMatch 2016—A Computer Program for Spectrum Matching of Earthquake Records.














