Open Journal of Civil Engineering
Vol.06 No.03(2016), Article ID:66893,11 pages
10.4236/ojce.2016.63031
Experimental and Numerical Investigation of Stress Condition in Unstable Soil
Marx Ferdinand Ahlinhan1*, Emmanuel Kokou Wouya2, Yvette Kiki Tankpinou2, Marius Bocco Koube1, Codjo Edmond Adjovi1
1School of Sciences and Technologies for Building and Road (ESTBR), Polytechnic University of Abomey (UPA), Abomey, Benin
2Institute University of Technology Lokossa (IUT), University of Lokossa, Lokossa, Benin

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 March 2016; accepted 24 May 2016; published 27 May 2016
ABSTRACT
In unstable soils, a special erosion process termed suffusion can occur under the effect of rela- tively low hydraulic gradient. The critical hydraulic gradient of an unstable soil is smaller than in stable soils, which is described by a reduction factor α. According to a theory of Skempton and Brogan (1994) [1] , this reduction factor is related to the stress conditions in the soil. In an unsta- ble soil, the average stresses acting in the fine portion are believed to be smaller than the average stresses in the coarse portion. It is assumed that the stress ratio and the reduction factor for the hydraulic gradient are almost equal. In order to prove this theory, laboratory tests and discrete element modelings are carried out. Models of stable and unstable soils are established, and the stresses inside the sample are analysed. It is found that indeed in unstable soils the coarse grains are subject to larger stresses. The stress ratios in stable soils are almost unity, whereas in unstable soils smaller stress ratios, which are dependent on the soil composition and on the relative density of the soil, are obtained. A comparison between the results of erosion tests and numerical modeling shows that the stress ratios and the reduction factors are strongly related, as assumed by Skempton and Brogan (1994) [1] .
Keywords:
Unstable Soil, Suffusion, Hydraulic Gradient, Stress Reduction Factor, Laboratory Tests, Discrete Element Modeling

1. Introduction
For the subsoil below pavements, dams or dikes, the stability against erosion with regard to seepage forces induced by under-seepage flow has to be proved. In that respect, it is of particular importance to identify and assess unstable soils, because here at relatively small hydraulic gradients, a special erosion process termed “suffusion” can occur. In general, gap-graded or well-graded soils are sensitive to suffusion. As result of the process, the fine fraction of the soil is washed out through the pores between the coarse-grained soil fraction. This increases the soil permeability and can lead to large civil works settlements or to the failure.
To assess whether suffusion is possible, in general the composition of the soil and the geometry of the pore channels have to be considered. Suffusion is only possible if the grains of the fine soil can pass through the pores of the coarse soil matrix. Since the pore channel geometry cannot be exactly measured, the assessment is based on the curve of the grain size distribution, which is related to the pore channel geometry. According to the Kenney and Lau (1986) criterion [2] , a value (H/F)min derived from the grain size distribution shall be less than 1.0. Here, H is the masse percent of soil between the grain diameter d and 4d. F is the mass percent of grain with diameter smaller than d. The authors of the paper in hand proposed to derive a parameter (dc,15/df,85)mod from the grain size distribution and to use (dc,15/df,85)mod < 4 as a stability criterion, Ahlinhan (2011) [3] [4] .
If the “geometric” criterion yields the result that suffusion is possible, i.e. the soil is potentially unstable the minimum hydraulic gradient necessary to cause erosion and to transport the fine soil grains has to be assessed by
a “hydraulic” criterion. In stable soils, the critical hydraulic gradient for vertical upwards seepage flow 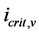 as per Terzaghi and Peck (1967), [5] is
as per Terzaghi and Peck (1967), [5] is
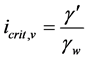 (1)
(1)
with:
 = effective unit weight of soil.
= effective unit weight of soil.
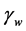 = unit weight of water.
= unit weight of water.
In unstable soils, the respective hydraulic gradient is generally smaller. This fact can be described by a stress reduction factor α. Skemptonand Brogan (1994) [1] supposes that the reason for the reduction of the critical vertical gradient is that the average effective stresses acting in the fine portion are smaller than the average effective stresses in the coarse portion of the soil. Furthermore, they assume that the stress ratio is the same as the reduction coefficient α, which is related to the critical hydraulic gradient  as follows:
as follows:
 (2)
(2)
and
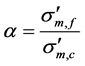 (3)
(3)
with:
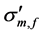 = mean effective stresses acting on particles of fine fraction.
= mean effective stresses acting on particles of fine fraction.
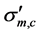 = mean effective stresses acting on particles of coarse fraction.
= mean effective stresses acting on particles of coarse fraction.
In this paper, the results of experimental tests regarding critical hydraulic gradients for upwards seepage in different soils with varying relative densities are presented. Also discrete element models are performed to determine the stress ratios in these soils. By comparison of the results, the validity of the Skempton and Brogan [1] approach stated in Equations (2) and (3) is assessed. Based on the discrete element models, it is shown that the stress reduction factor α depends on the soil type, the grain size distribution curve and the relative density of the soil.
2. Experiments
Five different non-cohesive soils were tested in a specially developed test device under vertical upward seepage flow. The hydraulic gradient was increased slowly and gradually in order to identify the critical gradient at which erosion begins. The initial relative density of the soils was varied in the laboratory tests. The used relative
density is defined as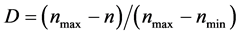 . Here, nmax is the maximum porosity, nmin is the minimum porosity and n is the actual porosity of the soil.
. Here, nmax is the maximum porosity, nmin is the minimum porosity and n is the actual porosity of the soil.
The grain size distributions of the five soils are shown in Figure 1 and the relevant soil parameters are given in Table 1. The soils A1 and A2 are fine to medium and medium to coarse sands, respectively, which are poorly graded and stable with respect to all geometric criteria (Kenney and Lau (1986) [2] parameter (H/F)min = 4.4 and 5.93). The soils E1, E2 and E3 are gap-graded soils, which were produced artificially. E2 and E3 are clearly unstable soils, whereas E1 has an (H/F)min value of 1.1 and so lies on the border between the stable and unstable region with regard to the Kenney and Lau (1986) [2] criterion. Applying the criterion with (dc,15/df,85)mod < 4 also leads to a close decision regarding internal stability.
A photographic view and a schematic drawing of the test device for vertical upward flow are shown in Figure 2. The soil sample with a diameter of 28.5 cm and a height of 30 cm was subjected to a gradually increased vertical hydraulic gradient. During the test, the water discharge and the water pressures along the sample’s height were recorded almost continuously.
Details regarding sample preparation, execution and evaluation of the tests can be found in Ahlinhan and Achmus (2011) [3] . The experimentally determined hydraulic gradients for vertical upward flow are given in Figure 3, depending on the initial relative density of the soil samples.
For the stable soils A1 and A2 the obtained critical gradients agree quite well with the theoretical values according to Terzaghi [5] . In fact, slightly lower values were found with a maximum deviation of about10%, which might be a result of unavoidable heterogeneities of the samples.
For the clearly unstable soils E2 and E3 very small critical gradients between 0.18 and 0.23 were measured. There is only a small dependence on the relative density of the sample. On the contrary, for soil E1, which is on
Figure 1. Grain size distributions of the soils used in the experiments.
Table 1. Properties of the soils used in the experiments.
Figure 2. Test device for vertical upward seepage flow.
Figure 3. Critical gradients determined for vertical upward seepage flow.
the border between stable and unstable, a stronger dependence of the critical hydraulic gradient on the relative densities was found. For a very dense state the critical hydraulic gradient is about double the value determined for a medium dense state. However, the value for very dense state is also significantly smaller than the theoretical critical hydraulic gradient as per Terzaghi [5] (i.e. Equation (1)). Thus, soil E1 has to be classified as potentially unstable soil.
Figure 4 shows the critical hydraulic gradients determined for the unstable soils dependent once on (H/F)min and once on (dc,15/df,85)mod. The values obtained by Skempton and Brogan (1994) [1] for dense sand are also depicted. The dependence on (H/F)min suggested by Skempton and Brogan (1994) [1] is confirmed, with the exception of the potentially unstable soil E1, where the critical gradient is very much dependent on the initial relative density. There is also a correlation between the critical hydraulic gradients and the index of instability (dc,15/df,85)mod, but the scatter here is slightly larger. The trend lines in Figure 4 right are suggested curves regarding the effect of relative density. Evidently, the “more stable” a soil is, the more important is the relative density.
3. DEM Modeling of the Stress Conditions in Non-Cohesive Soil
The determination of effective stresses acting in the fine and coarse portions of the soils A1, E1, E2 and E3 given in Figure 1 have been determined by means of the discrete element method (DEM). The Particle Flow Code software PFC, Itasca 2003 [6] has been used. Here, the soil grains are idealized as perfect spheres and its behavior is idealized by a linear contact stiffness constitutive law (normal stiffness kn, tangential stiffness ks) and the Coulomb friction law (friction coefficient μs). The maximum shear force Fsmax is related to the normal force Fn by Fsmax = μs∙Fn. (Figure 5) The values of these parameters are determined by calibration with the results of triaxial tests on real soils.
Figure 4. Critical gradients dependent on index of instability.
Figure 5. Model of the normal stiffness and tangential stiffness in PFC.
3.1. Numerical Simulation of Triaxial Test
For the numerical simulation of the triaxial test the particles were generated using the “fill and expand” method (Itasca 2003 [6] ) inside a cylinder with diameter b and height h. The diameter has been chosen so that it was at least 10 times the maximum particle diameter of the sample and the height was chosen to be at least 2 times the diameter (Figure 6).
During the calibration process first the model parameters kn (normal stiffness) and ks (tangential stiffness) were varied in order to match the stress-strain curve of real soil for strains lower than 1%, i.e. the deformation modulus, while the other parameters were kept constant. Then the inter-particle friction µs was varied to adjust the peak failure stress. The mobilized interne friction angle according to Equation (4) and the volumetric strain development of soil A1 are shown in Figure 7.

As can be seen in Figure 7, there is a fair agreement between experimental mobilized friction angle φmob and the simulated triaxial tests by using kn = ks = 105 N/m, µs = 2 for soil A1. The volumetric strain results show that the discrete element assembly exhibits more initial compression and more subsequent dilation than the real soil. This result corresponds to those observed in similar numerical simulations by tom Woerden et al. (2004) [7] . In order to match approximately the experimental and numerical volumetric strain Belheine et al. (2008) [8] introduced in their DEM-model other parameters such as rolling stiffness coefficient and non-dimensional plastic coefficient of the contacts. However, since here only stress conditions in the soils under vertical loading without shear shall be determined, the agreement of numerical and experimental results is considered sufficient.
In a similar way, the parameters for the soil E2 have been calibrated on triaxial tests carried out with this soil. Here, the parameters kn = ks = 105 N/m, µs = 3.2 have been found to give optimum agreement of experimental and numerical results. The same set of parameters has been used for the other unstable soils E1 and E3.
Figure 6. Numerical triaxial test specimen for soil.
Figure 7. Mobilized friction angle and volumetric strain versus axial strain for soil A1.
3.2. Numerical Model for Calculation of the Stress Reduction Factor α
In order to keep the calculation effort in reasonable limits, the assessment of the reduction factor α was carried out with a two-dimensional model, i.e. using the PFC2Dsoftware. A numerical model of 2.50 cm × 3.75 cm was developed in PFC2D (Figure 8). First, the particles were generated randomly with respect to the grain size distribution. After activation of the acceleration of gravity the particle fall down into the defined container and move in mutual interaction in free positions. The calculation of the process was carried on until an equilibrium state was reached. Then the vertical and horizontal stress states in the samples were checked. To achieve a “k0-state” (σh = k0∙σv with k0 = 1 − sinφ’), a small reduction of particle sizes was carried out and the redistribution of particles was again calculated until equilibrium was found. In all cases, the required particle size reduction was less than 0.1%.
To achieve different relative densities of the resultant sample, a method described in detail in tom Woerden et al. (2004) [7] was used. To achieve a “densest” (D = 1.0) sample, an inter-particle friction value μs = 0 was used during sample generation, and to achieve a “loosest” (D = 0.0) sample, the value was set to μs = 15. Intermediate μs-values were then used to achieve relative densities of 0.25, 0.50, 0.75 and 0.95.
The final step was the calculation of the reduction factor α. To do this, the intersected particles at a cross section through a defined depth of the sample were identified. The effective stresses in each particle were determined with a special calculation routine using the “Fish” macro language in PFC Itasca 2003 [6] . Coarse and fine particles were distinguished by consideration of the grain diameter at which (H/F)min according to the Kenney and Lau (1986) [2] criterion is obtained. With that, the mean effective stresses in the coarse and fine particle fractions could be determined separately and the reduction factor α was calculated according to Equation (3).
It was found that the α-values are dependent on the considered depth of the cross section. This is shown by the results for the soils A1 and E2 given in Table 2. In the following evaluation, the values derived from the intermediate depth of 1.80 cm below sample surface were taken. However, it has to be noted that a certain variation with respect to the position of the considered position must be taken into account.
Regarding the random generation of particles, only minor effects on the determined α-value were found. Table 3 shows results from repeated numerical simulations with the soils A1 and E2. The maximum deviations of the results are small. Thus, the numerical model is regarded as robust as far as the random generation is concerned.
Figure 8. PFC2D model of soil E3.
Table 2. Reduction factor depending on depth position of cross section.
Table 3. Reduction factor depending on random generation of particles.
Figure 9 shows the evaluation of the results for the sample E2. In the graphs the effective stresses acting on particles which were identified to be intersected by the cross section line are depicted. From the mean values of the effective stresses in the particles of the fine and the coarse fraction, respectively, the α-values were calculated. Evidently, for the unstable soil E2 the mean values of effective stresses acting in the fine particle fraction are considerably smaller than the stresses acting in the coarse particles, i.e. the α-values are considerably smaller than unity.
3.3. Results
In Figure 10, the reduction factors determined for the numerical simulations are given dependent on the considered relative densities. There is a slight influence of relative density on the reduction factor. However, the influence of the soil type, i.e. the grain size distribution, is clearly decisive. For the stable soil type A1 reduction factors only slightly less than unity are obtained, as to be expected from Equation (1). For the clearly unstable soils E2 and E5, reduction factors between 0.01 and 0.20 were found, whereas the reduction factors for the potentially unstable soil E1 lie between 0.30 and 0.38.
As mentioned in Section 2, an instability index (dc,15/df,85)mod can be used to formulate an instability criterion. In Figure 10, the numerically obtained α-values are depicted dependent on this parameter. Evidently, the stress reduction factor decreases with the index of instability in a similar manner as the critical vertical gradient does (cf. Figure 11).
4. Comparison between Experimental and Numerical Results
From the experiments, reduction factors were determined as follows:

These experimental results, which are related to hydraulic gradients, are compared to the numerical simulation results related to stress ratios. Figure 12 shows the comparison between the experimental and the numerical stress reduction factor. In general, good agreement of the values both qualitatively and to a slightly lower extent also quantitatively can be stated. Significant differences occur for the soil E1 at very dense state and for the soil E2 at medium dense states. This might partially be due to the inhomogeneous stress state in the test sample for unstable soil due to soil compaction in laboratory. However, perfect agreement of the results could not be expected due to uncertainties both in experimental and numerical modeling. The overall agreement of the experimental and numerical results can be stated as remarkably good.
5. Conclusions
Experimental tests presented in the paper in hand show that the critical hydraulic gradient for upward seepage flow is dependent on the instability index of the soil and to a minor extent also on its relative density. According to a hypothesis formulated by Skempton and Brogan (1994) [1] , the reduction of the critical gradients of unstable soil compared to stable soils is connected to non-homogeneous stress conditions in the fine and coarse grain portions of an unstable soil.
This hypothesis is checked by means of numerical simulations with the discrete element method and laboratory tests. Different soils are considered, and the model parameters are calibrated by comparison with the results of triaxial tests. It is found that the non-linear behavior of non-cohesion soil can be simulated fairly well by means of discrete element method. With the numerical model, stress ratios describing the non-homogeneity of stress conditions can be derived.
Figure 9. Simulation results for soil E2 with different relative densities: particle positions and force chains (left); effective stress values for particles intersected by a cross section in a depth of 1.8 cm (right).
Figure 10. Dependence of reduction factor on soil type and relative density.
Figure 11. Dependence of reduction factor on index of instability.
Figure 12. Comparison of experimental and numerical results.
Good agreement is obtained between reduction factors regarding hydraulic gradients stemming from experimental tests and the stress reduction factors obtained in the numerical simulations. These results indicate that there is indeed a strong relation of these factors and thus strongly support the hypothesis of Skempton and Brogan (1994) [1] . Furthermore, it is found that the reduction factor depends on the soil type, the grain size distribution and the relative density of the soil.
Acknowledgements
This research was partially supported by the Germany Ministry of Education and Research through IPSWaT (International Postgraduate Studies in Water Technologies). This support is gratefully acknowledged.
Cite this paper
Marx Ferdinand Ahlinhan,Emmanuel Kokou Wouya,Yvette Kiki Tankpinou,Marius Bocco Koube,Codjo Edmond Adjovi, (2016) Experimental and Numerical Investigation of Stress Condition in Unstable Soil. Open Journal of Civil Engineering,06,370-380. doi: 10.4236/ojce.2016.63031
References
- 1. Skempton, W. and Brogan, J.M. (1994) Experiments on Piping in Sandy Gravels. Géotechnique, No. 3, 449-460.
http://dx.doi.org/10.1680/geot.1994.44.3.449 - 2. Kenney, T.C. and Lau, D. (1986) Internal Stability of Granular Filters: Reply. Canadian Geotechnical Journal, 23, 420-423.
http://dx.doi.org/10.1139/t86-068 - 3. Ahlinhan, M.F. (2011) Stability of Non-Cohesive Soils Due to Internal Erosion. PhD Thesis, Leibniz University Hannover, Hannover.
- 4. Ahlinhan, M.F. and Achmus, M. (2010) Experimental Investigation of Critical Hydraulic Gradients of Unstable Soils. Scour and Erosion, San Francisco, 7-10 November 2010, 599-608.
http://dx.doi.org/10.1061/41147(392)58 - 5. Terzaghi, K. and Peck, R.B. (1967) Soil Mechanics in Engineering Practice. John Wiley & Sons, New York.
- 6. Itasca (2003) PFC3D PFC2D User′s Manual. Itasca Consulting Group Inc., Minneapolis.
- 7. tom Woerden, F., et al. (2004) Finite Element and Discrete Element Modeling for the Solution of Spatial Active Earth Pressure Problems. Proceedings of the 2nd Int. PFC-Symposium on Numerical Modeling in Micromechanics via Particle Methods, Kyoto, 28-29 October 2004, 45-50.
http://dx.doi.org/10.1201/b17007-8 - 8. Belheine, N., Plassiard, J.-P., et al. (2009) Numerical Simulation of Drained Triaxial Testing Using 3D Discrete Element Modeling. Computers and Geotechnics, 36, 320-331.
http://dx.doi.org/10.1016/j.compgeo.2008.02.003
NOTES
*Corresponding author.
















