Received 1 July 2015; accepted 11 September 2015; published 14 September 2015

ABSTRACT

Currently, Global Positioning System (GPS) techniques are becoming a much larger part of the surveying industry. Many companies are now using GPS in their everyday work activities. The Real Time Kinematic (RTK) positioning is an integral part of topographic surveys, road surveying, constructions and most civil engineering applications. Normally, RTK can be used to collect the positioning data successfully and quickly. The civil and construction projects are designed in ground distances while RTK measurements are done in grid coordinate system, in which the distances between points are different from ground. The RTK measurements should be converted to ground for compatibility with the designed. In this paper, the accuracy of three alternatives for converting RTK measurements to ground was studied. These alternatives are, using scale factor, using two ground reference points and using Low Distortion Projection (LDP) surface. For the accuracy investigation purpose, a traverse of 14 points elongated for a distance of about 1400 m was constructed. Its coordinates were measured using total station, then the misclosure error was computed and the coordinates were adjusted. The traverse points coordinates were measured again using RTK_GPS considering one of them as base point. The three studied alternatives were applied and the results were compared. The results show that the accuracy of the three alternatives is ranging from 2.1 to 2.9 cm in the relative position of points to the base point. For absolute position accuracy, the two ground reference points alternative is the most accurate alternative with an average error of 3.8 cm while the other two alternatives are almost the same with an average error of 12.3 cm.

Keywords:

RTK, Grid, Ground, Conversion, Accuracy

1. Introduction

The Real Time Kinematic (RTK) approach is a differential positioning technique that uses known coordinates of a reference station occupied by one receiver to determine coordinates of unknown points visited by a rover receiver [1] . Similar to static GPS the reference station is set on a point of known coordinates but the use of a data link, to transfer measurements acquired at the reference receiver to the roving receiver, permits the calculation of the rover coordinates at the time of measurement [2] . Details on RTK ambiguity resolution, data transmission and operational considerations can be found in [1] . Reference [3] stated that studies on RTK techniques estimated cost savings of 25% - 50% compared with ground survey methods. The reduction in field expenses results from reducing the number of surveying crew members, frequent setups of the surveying instruments are no longer required, and eliminating the need for accurate local traverses or multiple control stations within the site. RTK system is the best compromise between usability and accuracy [4] .

The accuracy of RTK compared to the static GPS and total stations was investigated by many authors. According to the work by [5] , a horizontal coordinate accuracy of 1 cm has been achieved. Reference [6] concluded that the comparison of two techniques including RTK-GPS and TS revealed that RTK-GPS based surveys not only are practical and fast but also yield more accurate topographic maps for design purposes. Reference [7] compares between total station and GPS tools from different points of view including range, accuracy, flexibility and price. He mentioned that the accuracy of total station is 3 to 10 times better than the GPS. Reference [8] investigated the vertical accuracy of RTK and his results indicated that the RTK-GPS has a vertical error of about 2 cm. Reference [9] stated that when using RTK method, 9 mm in horizontal and 1.5 cm accuracy in vertical coordinates has been achieved. Reference [10] concluded that RTK provides high-resolution control on topographical surveying within limits on the order of 1 cm level accuracy in the horizontal and 2 cm in vertical dimension. Reference [11] compared RTK to static GPS and to total station and concluded that they reached an achievable and repeatable accuracy of approximately 2.5 cm. Reference [12] studied the average time needed for high accuracy RTK measurements and concluded that observations should be averaged over a window of 1 minute. Averaging over 2 minutes should be applied at longer ranges and/or when better height results are sought. The maximum difference from the mean according to [12] was found to be 50 mm in horizontal and 200 mm in vertical coordinates. The high accuracy of RTK makes it a common positioning tool for most of civil engineering applications like precise mapping, setting out of utilities, bridge movement measuring, road alignment and construction.

None of the previous authors mentioned how the RTK and Total Station (TS) coordinates were compared although RTK produces projected (Grid) coordinates while total station produces ground coordinates. The distances between the same points are different in the two coordinate systems. On the other hand, most of the accuracy comparisons were derived according to measurements performed on small sites.

In this paper, alternative solutions of converting RTK coordinates to total station coordinates will be presented. The accuracy of RTK measurements compared to that of total station will be calculated from measurements cover an area of 296,000 m². The measured points extend 1400 m away from the reference point.

2. Data and Field Observations

To check the accuracy of RTK measured coordinates, a traverse of 14 points in the King Abdulaziz University (KAU) campus was constructed as shown in Figure 1. The traverse was surveyed first using Topcon total station GPT-7501 with angle accuracy of 1 sec and distance accuracy of 2 mm + 2 ppm. The misclosure error was adjusted and the corrected coordinates of the traverse points were calculated. Point (S177) was used as base point and the coordinates of the rest points were measured using RTK technique with two Topcon GR3 geodetic receivers. The duration of observation was 3 minutes for each point as recommended by [12] .

3. Grid to Ground Solutions

In this paper, the accuracy of three alternatives for converting RTK (Grid) measurements to equivalent total station (TS) (Ground) coordinates was compared. These alternatives are: using scale factor, using two ground reference points and using Low Distortion Projection (LDP). Details on these alternatives are in the following sections.

3.1. First Alternative: Scale Factor

For each project area, there are three different surfaces representing the earth as shown in Figure 2; the Ground (TS distances), the Ellipsoid, and the Grid (RTK distances) Plane. As can be visually seen in Figure 2, whenever points are transformed from one surface to another, the distance between them change, i.e. the scale changes. When transform points from the grid plane to the ground, one must first pass through the ellipsoid. Therefore, transforming points from grid to ground involves first a transform to the ellipsoid and then a transform to the ground. Each step includes its own scale change.

The scale value that defines the difference in distance between two points on the grid plane (grid distance d_grid) and those same two points on the ellipsoid (ellipsoid or geodetic distance d_ellip) is called the Scale Factor (SF). The scale difference is caused by transforming from a flat surface (Grid Plane) to a curved surface (Ellipsoid). The scale factor at each point can be calculated using Equation (1).

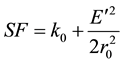(1)

where:

k₀ = Grid scale factor at central meridian (0.999600)

r₀ = Geometric mean radius of curvature scaled to the grid

E' = Easting of the point-false easting at central meridian

The approximate ellipsoidal distance between two points can be calculated by taking the grid distance between the two points, then dividing that value by the effective scale factor, SF_eff. The effective scale factor, SF_eff, can be determined from the Equation 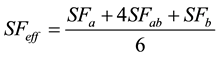(2).

(2)

where:

SF_a is the scale factor for one of the points,

SF_b is the scale factor for the other point, and

SF_ab is grid scale factor for the point midway between the two points.

The grid distance d_grid can be transformed to an ellipsoidal distance d_ellip using Equation (3).

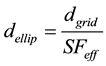(3)

The scale value that defines the difference in distance between two points on the ellipsoid (geodetic distance d_ellip) and those same two points on the ground (ground distance d_ground) is called the Elevation Factor (EF). Scale changes between these two surfaces because the two surfaces are different distances from the center of the earth. The elevation Factor can be calculated using Equation (4).

(4)

where:

R = Mean earth radius

N = Geoid height

H = mean orthometric height

Using the Elevation Factor, one can determine the ground distance d_ground from the geodetic distance d_ellip, by using Equation 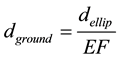(5).

(5)

The most common transformation is between points on the grid plane and points on the ground. The scale value that will allow a direct transformation from grid to ground is called the Combination Factor (CF). The Combination Factor is the product of the Scale Factor and the Elevation Factor:

(6)

Using the Combination Factor, one can determine the ground distance d_ground from the grid distance d_grid, by using Equation 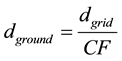(7).

(7)

Beside the correction of distances using scale factor, the azimuth of lines connected the points to the base point can be computed using equations presented in [13] . The last step is to compute the convergence angles. The convergence angle γ can be approximated using Equation (8). The units of γ are the same as the units of ∆λ. This equation is accurate to better than ±0.2 arc-second if the computation point is within about ±1˚ of the central meridian.

(8)

To use this alternative to convert RTK coordinates to equivalent total station coordinate, the following steps should be followed:

- Compute the length and the corrected azimuth of lines connecting the base point to the all measured points

- Compute the Combination Factor (CF) for each line

- Compute the ground distance from the grid one

- Use the ground distance and the former computed azimuth to calculate the departure and latitude of each line

- Compute the ground coordinates of the points using the base point coordinate and the calculated the departure and latitude

3.2. Second Alternative: Using Two Ground Reference Points

For this alternative solution, at least two points with both grid and ground coordinates to transform all grid coordinates to ground coordinates are needed. Therefore, at least two of the existing points with ground coordinates must have been observed with GPS. Once processed, these points can be used to compute the transformation parameters relating the grid coordinate to the ground coordinates. These transformation parameters will then be applied to all points in the project to produce ground coordinates.

Another option, the RTK grid coordinates are aligned and scaled using the two ground reference points. This can be done in an easy way in CAD environment.

3.3. Third Alternative: Using Low Distortion Projection (LDP)

The issue of grid/ground distance differences came to the fore in the 1980s as the use of GPS by the surveying community became more commonplace. Although the LDP name was adopted later, the grid/ground distance difference was often handled by what was called “project datum” or “surface” coordinates [14] .

Reference [15] explained the six steps of designing LDP which can be summarized as follows:

- Define project area and choose representative ellipsoid height, h_o (not elevation)

- Choose projection type and place projection axis near centroid of project area

- Scale central meridian of projection to representative ground height, h_o

- Check distortion at points distributed throughout project area

- Keep the definition SIMPLE and CLEAN

- Explicitly define linear unit and geometric reference system (i.e., geodetic datum)

According to [16] [17] a Low Distortion Projection (LDP) for the study area was constructed as follows:

- Use WGS84 as a reference datum

Create a projection surface that is tangent with the average ellipsoidal height of the project area as shown in Figure 3. The ellipsoidal distance is scaled up using Equation 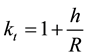(9).

(9)

where

k_t = scale factor for tangent projection (1.00000611 for the study area)

h = ellipsoidal height (39 m for the study area)

R = ellipsoidal radius (6,378,137 for WGS84)

- Lowering the Projection surface slightly to increase the extents of the usable zone as shown in Figure 4. The scale factor is multiplied by an additional factor k_r. the reduction factor k_r depends on the project width and can be computed using Equation (9). The secant scale factor is computed using Equation 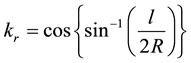(10).

(10)

where

k_r = scale reduction factor

l = project width

R = ellipsoidal radius (6,378,137 for WGS84)

(11)

where

k_s = scale factor for secant projection (1.00000511 for the study area)

k_t = scale factor for tangent projection (1.00000611 for the study area)

k_r = scale reduction factor (0.99999 for 20 km project width)

- Check the distortion δ and if it exceeds the limits, the datum scale factor should be adjusted. The distortion can be computed using Equation (12)

(12)

where

δ = the distortion (1 ppm for 20 km project width)

k_s, R and h are as defined before

- Define the latitude and central meridian of the origin

- Define False Northings and Eastings in such a way that the coordinates cannot be confused with other standard coordinate systems for the area

The LDP parameters are as follows

The last step is to compute the convergence angles. The convergence angle γ can be approximated using Equation (8). For the study area γ = 5.49'.

This LDP can be defined on the GPS data logger to get the new coordinate directly from the receiver or define the LDP surface in ArcGIS software and project the RTK data to it.

4. Results and Discussion

The three alternatives were applied on the RTK measurements. The distance from the base point to the rest of the traverse points were computed and the residual of each distance was calculated and shown in Table 1 and represents graphically in Figure 5. From Table 1 it’s clear that the error in the distances calculated from RTK measurements is directly proportional to the distance to the base point. Applying the Combination Factor to convert the grid distances to the ground ones, the errors were reduced to an average of 2.6 cm while the maximum error was 4.2 cm. Using two ground reference points to convert RTK distances to ground distances reduce the error to an average of 2.1 cm with a maximum error of 3.8 cm. Applying LDP surface to get ground distances reduced the error to 2.9 cm with a maximum error of 4.5 cm.

Although converting grid distances to ground reduce the error in distances to about 2 cm and the relative position of points are very close to the correct one, the error in absolute position of the points depends on the azimuth of the line connecting the particular point to the base point as shown in Table 2 which shows the error in easting and northing of each point. Refer to Figure 1 and Table 2 it can be noticed that for points close to the

north-south direction (e.g. points A and B), the errors in northing is minimum and maximum in easting while for points close to the east-west direction (e.g. points I and G), the errors in easting is minimum and maximum in northing. The average error in easting direction was about 4 cm for both of using combination scale factor and LDP while it was 2.6 cm for using two ground reference points. The average error in northing direction was 10.8 cm for both of using combination scale factor and LDP while it was 1.0 cm for using two ground reference points. The maximum error in easting direction was about 7 cm for both of using combination scale factor and LDP while it was 4.2 cm for using two ground reference points. The maximum error in northing direction was 20.0 cm for both of using combination scale factor and LDP while it was 2.3 cm for using two ground reference points.

The displacement at each point was shown in Table 3 and represented graphically in Figure 6. The average displacement was 12.3 cm for both of using combination scale factor and LDP while it was 3.8 cm for using two ground reference points. The maximum displacement was about 20.2 cm for both of using combination scale factor and LDP while it was 5.1 cm for using two ground reference points. The displacement in absolute position increases with increase the distance to the base point when using scale factor and LDP and with increase the distance to the reference points when using two ground reference points.

5. Conclusions

In this paper, three alternative techniques for converting RTK coordinates to ground coordinates are discussed. These techniques are 1) using combination scale factor to scale the grid distances to the ground, 2) using two ground reference points and 3) using Low Distortion Projection LDP surface. The accuracy of these techniques was compared to the total station coordinates as most of civil engineering projects were designed on ground coordinates. From the results of converting grid coordinates to ground using the three studied techniques, the followings could be concluded:

1) The three alternative techniques are very close to each other for converting grid distances to ground, i.e. when comparing the relative position of points to the base point.

2) The average differences in relative position between the converted RTK system and the precise traditional surveying were 2.1 cm when using two ground reference points, and 2.6 cm and 2.9 cm when using scale factor and Low Distortion Projection respectively.

3) The error in absolute coordinates affected by the orientation of line connected the particular point to the base point. Lines in north south direction have a maximum error in easting coordinates while lines in east west direction have the maximum error in northing coordinates.

4) The average differences in absolute position between the converted RTK system and the precise traditional surveying were 3.8 cm when using two ground reference points, and 12.3 cm and 12.4 cm when using scale factor and Low Distortion Projection respectively.

5) The most appropriate alternative for minimum errors in relative and absolute position is using two ground reference points.

6) To keep the error within 2 cm, the distance between the two ground reference points should be within 500 m.

7) Scale factor alternative and LDP almost gave the same results.

8) Using LDP is easier in computation comparing to combination scale factor as LDP converts all project data in one step while scale factor converts distances separately.

Acknowledgements

Thanks are due to Mr. Talal Al-Thebety for assistance in performing the field measurements.

Cite this paper

RagabKhalil,11, (2015) Alternative Solutions for RTK-GPS Applications in Building and Road Constructions. Open Journal of Civil Engineering,05,312-321. doi: 10.4236/ojce.2015.53031

References