Open Journal of Civil Engineering
Vol.04 No.04(2014), Article ID:52263,14 pages
10.4236/ojce.2014.44029
Sensitivity Analysis of Key Parameters in Decision Making of Two-Stage Evolutionary Optimization Maintenance Strategies
Elia A. Tantele*, Renos A. Votsis, Toula Onoufriou
Department of Civil Engineering and Geomatics, Cyprus University of Technology, Lemesos, Cyprus
Email: *elia.tantele@cut.ac.cy
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 October 2014; revised 2 November 2014; accepted 18 November 2014
ABSTRACT
Preventative maintenance (PM) measures for bridges are proactive maintenance actions which aim to prevent or delay a deterioration process that may lead to failure. This type of maintenance can be justified on economic grounds since it can extend the life of the bridge and avoid the need for unplanned essential/corrective maintenance. Due to the high importance of the effective inte- gration of PM measures in the maintenance strategies of bridges, the authors have developed a two-stage evolutionary optimization methodology based on genetic algorithm (GA) principles which links the probabilistic effectiveness of various PM measures with their costs in order to de- velop optimum PM strategies. In this paper, the sensitivity of the methodology to various key input parameters of the optimization methodology is examined in order to quantify their effects and identify possible trends in the optimum PM intervention profiles. The results of the sensitivity studies highlight the combined use of both proactive and reactive PM measures in deriving optimum strategy solutions. The precise mix and sequence of PM measures is clearly a function of the relative effectiveness and cost of the different available PM options as well as the various key parameters such as discount rate, target probability of failure, initial probability of failure and service life period examined. While the results highlight the need for more reliable data they also demonstrate the robustness and usefulness of the methodology; in the case where data is limited it can be used as a comparative tool to improve understanding of the effects of various strategies and enhance the decision making process.
Keywords:
Preventative Maintenance, Corrosion, Genetic Algorithm, Optimization, Reinforced Concrete Bridges, Sensitivity Analysis

1. Introduction
Maintenance measures can be applied to ensure that the bridge reliability remains below an acceptable probabil- ity of failure, i.e. the probability that the bridge will reach a specific limit state during its service life.
The constantly growing demand for reliable bridges, with low maintenance cost has highlighted the need to investigate the use of PM measures, as part of a proactive approach since “prevention is better than cure”. This proactive management approach may not be essential now but it can be justified on economic grounds since it can enable the postponement of essential rehabilitation work, extend the service life and reduce the whole life cost of bridge structures [1] .
However, there are significant uncertainties associated with the effectiveness of various PM measures which calls for a probabilistic approach. To this end a probabilistic methodology is developed by the authors, to ad- dress the effectiveness of PM measures. This is combined with an optimization methodology based on GA principles to create a tool which is capable of identifying optimum PM strategies against the specific forms of deterioration encountered in structures.
For the current study deterioration due to chloride induced corrosion is considered and the PM measures are actions designated to alleviate the corrosion process.
In this development a proactive approach is adopted in which PM measures are considered for maintaining the probability of corrosion initiation within an acceptable target level. The effectiveness of PM is modelled probabilistically. The various PMs fall in three categories depending on their effect on the probability of corrosion initiation through their ability to: 1) keep the reinforcing bar (rebar) free from chlorides ions (Cl−); 2) reduce the total diffusion coefficient; 3) prevent further chloride ingress by removing the chloride ions from the rebar.
A probabilistic methodology developed in [2] incorporate the uncertainties that influence the PM degree of effectiveness (such as the amount of diffusivity of chloride when concrete is treated with PM), and predict the effectiveness of different PM actions.
By applying PM measures at different time intervals, corrosion initiation can be postponed and/or inhibited. As a result, the probability of failure (pf) can be maintained within an acceptable target level. In the context of this study, the initiation of corrosion is adopted as the critical failure incident. In particular, failure (i.e. initiation of corrosion) occurs when the concentration of chlorides at the surface of the steel rebar exceeds a predefined threshold value. Mathematically, this can be expressed through the following limit state:
 (1)
(1)
where
 is the threshold chloride concentration (kg/m3);
is the threshold chloride concentration (kg/m3);
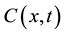 is the chloride concentration at steel rebar (kg/m3) calculated using Fick’s second law of diffusion and
is the chloride concentration at steel rebar (kg/m3) calculated using Fick’s second law of diffusion and
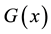 is the limit state.
is the limit state.
The pf is estimated using the Monte Carlo simulation method [2] [3] . Different PM measures will clearly result in different pf profiles depending on their ability to reduce the diffusivity of chloride ions or to remove them from the reinforcement surface.
In the following sections, the probabilistic methodology is outlined and its sensitivity to key parameters is examined. Furthermore various trends in the optimum PM intervention profiles and whole life costs emerging from the results are presented.
2. GA Based Methodology for Optimum PM Strategies
The GA principles are adopted for optimization of the PM strategies. The GA method was invented by John Holland [4] while Goldberg was the first to solve engineering optimization problems using GA [5] . Miyamoto et al., [6] described the GA as a power tool for obtaining optimal maintenance plans. Other work using this approach for maintenance optimization is carried out by Liu and Frangopol [7] , Furuta et al. [8] and Morcous and Lounis [9] . In the present application the developed GA based optimization methodology combines probabilistic effectiveness modelling of PM with the cost of different PM measures to identify optimum strategies that will combat the corrosion deterioration of RC structures. The GA methodology which is developed for this applica- tion [2] [3] is briefly outlined in this section and is depicted in Figure 1.
2.1. Objective of the Methodology
The aim of this study is to identify a PM strategy that will maintain the pf of an examined bridge element under
Figure 1. Proposed two stage GA methodology.
the actions of different PM measures, with the minimum possible cost (Equation (2)) lower than a target lifetime pf (Equation (3)). Within the context of this study, the pf represents the probability of corrosion initiation on the top level of the steel rebar.
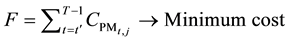 (2)
(2)
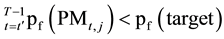 (3)
(3)
where
 is the total cost of PM measures;
is the total cost of PM measures;
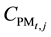 is the cost of PM measure
is the cost of PM measure
 carried out in year
carried out in year ;
;
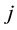 is
is
the type of PM measure chosen for year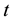 ; pf
; pf
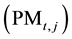 is the probability of failure for PM measure
is the probability of failure for PM measure
 carried out in year
carried out in year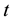 ; pf (target) is the maximum acceptable value of pf;
; pf (target) is the maximum acceptable value of pf;


2.2. Development and Implementation of GA Based Methodology
The key elements of the developed GA based methodology are outlined in this section (Figure 1) while a more detailed description can be found in [2] . The interpretation of Figure 1 shows that initially GA produces a popu- lation of chromosomes; all are representing a possible solution to a given problem (Step 1). During each successive generation every member is tested according to a fitness function (Step 2). Highly “fit” chromosomes are ranked at the top of the pool and can be selected to mate with other highly fit members (form the parents) to produce new chromosomes (offsprings) [10] (Step 3). The offsprings contain characteristics from both of the parent chromosomes. Furthermore, in a few randomly selected individuals some arbitrary changes are made in their characteristics through mutation to add some diversity to the population (Step 4). However, it does provide ac- countable improvement to perform mutation to already good solutions. For this reason elitism selection is often embedded [6] [8] to enforce the preservation of the best individual chromosomes of the current generation to the next. With elitism, a number of good solutions are designated as elite solutions and are destined to propagate unchanged. At this point a new population is formed with chromosomes closer to the optimum solution (Step 5). Therefore, although GA is randomized, it efficiently incorporates information from previous generations to create new search points and explores the most promising areas.
The entire process is repeated for a number of generations until the chromosomes will evolve and ultimately converge to an optimum solution. The convergence in this study is reached when in the parent population the chromosomes are the same. Hence, in this case even after crossover, there is no change in the genes and therefore one optimum solution is proposed (Step 6 in GA Part A, Figure 1). The entire “GA Part A” process shown in Figure 1 is repeated to obtain a number of optimum solutions and to select the solution that fits best the objec- tive/fitness functions.
Unfortunately, the “GA Part A” may fail because of a convergence to an unacceptable local optimum. To overcome this limitation, an improved two-stage GA methodology (Part A + Part B), outlined in Figure 1, is proposed. The purpose of the “GA Part B” is twofold: firstly, to aid the finding of the optimum solution and secondly, to ascertain whether there are flaws in the selection of key parameters of the GA process in order to revise them and achieve convergence more efficiently.
As Figure 1 illustrates, “GA Part A” is executed and the collected optimum solutions form the genome which is treated as the initial population in “GA Part B” (Step 1 in GA Part B). The simulations in “GA Part B” stop when all the chromosomes of the genome are the same, thus one optimum solution (optimum PM strategy) is proposed. The termination of the simulations is based on the logic that “optimum” parents (optimum solutions) cannot produce “more optimum” offspring (optimum solutions). For the implementation of the proposed methodology a computer program was developed using Visual Basic environment.
3. Sensitivity Study
In total, 19 case studies are reported here. In each case a number of PM actions are defined as options and the methodology is used to identify the most optimum whole life strategy. The PM actions include proactive measures such as surface treatment measures (silane, sealer, and coating) and reactive measures such as cathodic protection (CP), electrochemical chloride extraction (ECE) and concrete replacement (CR). The interval for PM maintenance action is assumed to be 5 years.
The parameters examined within the sensitivity study are summarized in Table 1. The case studies examined a bridge beam with average quality Portland cement (PC) and a 40 mm cover (Cases 1-19 in Table 1) while Case 19 investigates a bridge deck with similar quality concrete, and depth of cover. An initial pilot case (i.e. Case 1) is presented first in the following section, which forms the basis of comparison with all the other cases to identify trends and to study the sensitivity of different input data of the GA methodology.
The encoding representation and the genetic operators used for the GA based optimization methodology are presented in Table 2 and Table 3 respectively. A more detailed discussion of the basis of these parameters is given in [2] . For the parameter representation real value encoding is used so the actions are represented as integers. The parameters of the generic operators of the GA methodology were taken from literature while the population size and the mutation rate are based on sensitivity studies carried out by the authors. The service life and cost of PM measures are summarized in Table 4. These values are based on reports from Weyers et al. [11] , HA [12] , Pearson and Cuninghame [13] , Kepler et al. [14] and Krauss et al. [15] . Whole life costing (WLC) is used to ena- ble the economical appraisal of different PM strategies where expenditure is discounted over time and normalized to a common base year. The cost is discounted to the present value (PV) according to [16] :

where



The effectiveness of PM actions is based on the probabilistic models developed by the authors and presented elsewhere [17] .
3.1. Pilot Case: Effectiveness of Different Proactive and Reactive Measures
A Pilot case is examined first in which all the proactive and reactive measures shown in Table 2 are included as options. In this application it is assumed that the discount rate is 3% [18] , the target pf is 0.1 [19] -[21] , the initial pf is 0 (representing either a new element or one where chloride ingress has not commenced) and the service life of the element is 120 years.
A WLC of ∈00.7/m2 is obtained for the optimum strategy. Table 5 presents the different actions selected at 5-year intervals as established by the GA methodology. A combination of surface treatments and “do nothing” option are selected initially until pf reaches the target value at which point a reactive measure is used. Based on
Table 1. Parameters examined in sensitivity study.
Table 2. Parameter representation.
Table 3. Parameters of the genetic operator.
Table 4. Service life and cost of PM measures [11] -[15] .
*The maintenance cost includes maintenance of the anodes, application of sealer and inspection costs for every 5 years.
Table 5. Optimum PM plan of pilot case.
Decoded Actions: 1: Do nothing; 2: Silane; 3: Sealer; 4: P-m Coating; 6: ECE; -: P-m coating still effective due to its service life (10 years).
the input data for this case ECE is identified as the best reactive PM measure to use as opposed to CP or CR when critical concentration of chloride is predicted on the rebar. This makes sense since the use of ECE has a dramatic impact on the pf profile at little cost compared to the other reactive options. The cycle of proactive PM followed by a reactive PM is repeated throughout the lifetime. The combination of proactive measures is not the same throughout the lifetime of the element since the costs are discounted and cheaper solutions are sought at the beginning of the strategy (0 - 20 years)
The element performance when this recommended optimum PM plan is applied can be seen in Figure 2 which shows the pf profile with time. At no time frame the pf exceeds the target pf failure.
3.2. Effect of Different Discount Rates
The use of appropriate discount rate is important as this affects the sequence of application of PM and therefore the WLC profoundly (Equation (4)). The discount rates are quite variable between different agencies and are normally within the range of 2% - 8% [22] . Here, in addition to the Pilot case in which the discount rate is taken as 3%, other cases with 0%, 3.5%, 6% and 8% are investigated.
Cases 2-5 examine the sensitivity of the optimum strategy outcome to changes in the discount rate. As shown in Figure 3 the highest WLC is obtained when the discount rate is 0% while the lowest cost is obtained when the rate is 8%. It is also clear that the sensitivity of the WLC results to the discount rate is significantly higher within the lower range of values.
The optimum maintenance plans proposed for different discount rates can be seen in Table 6, which shows that when the discount rate is 0% P-m coating is utilized for most PM intervals. However, Table 5 and Table 6 show that when the discount rate is higher than 0% (e.g. 3%, 3.5%, 6%, 8%) the optimization method selects less costly actions for the first 20 years, such as “do nothing”, followed by the use of ECE and surface treatment at different PM intervals for the remaining life of the element. Where the higher discount rates are used (6% and 8%) there is a bigger reduction in costs with time (through discounting) compared to the lower discount rates (Equation (4)). This result in the increased use of ECE which is employed almost twice as many times compared to the lower discount rate cases (0%, 3%, 3.5%). The same optimum strategy is obtained for the two higher discount rates (6%, 8%) as shown in Table 6 and Figure 5. While there is some difference in the discounting between these two cases this is not sufficiently high to change the optimum strategy solution. This is due to the number of available PM options investigated. A wider range of PM measures may result in different PM strategies between the higher discount rates. Figure 4 and Figure 5 illustrate the pf profile under the action of the proposed PM plans. At no point in time does the pf exceed the target pf.
Figure 2. Probability of failure profile after the application of proposed strategy.
Figure 3. Effect of discount rate on the WLC.
Figure 4. Probability of failure profile: Case studies (2-3) & pilot case.
Figure 5. Probability of failure profile: Case studies (4-5).
Table 6. Optimum PM plan with different discount rate: Case studies (2-5).
Decoded Actions: 1: Do nothing; 2: Silane; 3: Sealer; 4: P-m Coating; 6: ECE; -: P-m coating still effective due to its service life (10 years).
3.3. Effect of Different Target pf
The target probability of failure is an important parameter in any probabilistic approach, within the context of in- tegrity management of structures. Acceptable levels of probability of failure are not easy to define and depend on complex issues such as acceptable levels of risk and social impact. Some guidelines are provided in this area within Eurocode BS EN 1990 (2002) Annex B [20] .
While a value of 0.1 was assumed for the Pilot study based on recommendations from codes of practice BS EN 1990 [20] and JCSS [21] a range of pf values are examined within the sensitivity study to quantify the effect of this parameter. Case studies 6-13 adopt values within ±5%, ±10%, ±15% and ±20% of the assumed target pf used in the pilot case. From the results of these cases it is clear that the target pf influences highly the outcome of the WLC. Figure 6 shows that when the target pf increases the cost decreases. This is to be expected since increased reliability (lower pf) would require more frequent use of PM measures and hence higher overall cost.
It is interesting to note that while on the whole the WLC decreases with increased target pf the reduction in WLC is not continuous. This is due to the availability of the options to fit a strategy to ensure that the pf remains below a target pf. As more options are available the difference in WLC between the cases is expected to be more uniform. While the WLC is sensitive to changes in pf the percentage change in WLC is lower than the corres- ponding change in pf. A ±20% change in pf results in only +8.1% and −8.3% change in WLC.
The optimum plans obtained from the GA methodology for a selection of case studies which their target pf value provides minimum, maximum and average WLC are given in Table 7.
The pf profiles of these cases are shown in Figure 7. Despite some differences in the choice of PM actions, a similar general pattern can be identified from these figures. The element is left to deteriorate with no action tak- en, approximately for the first 20 years. Then some surface treatments are selected for a period of 20 - 30 years
Figure 6. Effect of target pf on the WLC.
Figure 7. Probability of failure profile: Case studies 6; pilot case 13.
Table 7. Optimum PM plan with different target pf: Case studies 6; pilot case 13.
Decoded Actions: 1: Do nothing; 2: Silane; 3: Sealer; 4: P-m Coating; 6: ECE; -: P-m coating still effective due to its service life (10 years).
followed by the use of ECE. The latter pattern is repeated throughout the lifetime of the bridge element.
3.4. Effect of Initial pf
Another important parameter is the initial pf of the examined element. This parameter represents the probability of corrosion initiation on the reinforcement of the element at the time examined. For example, if the initial pf is zero then it means that the element is either new or chloride propagation has not commenced. The sequence of application of PM will be influenced by the initial pf value.
Therefore the following case studies are examining the effect of initial pf on the WLC. As expected with higher initial pf the WLC also increases (Figure 8). This is due to the fact that more money is needed to restore the initial condition of the bridge element to safe levels (concerning its probability of failure) at an early stage. It can be seen that there is a significant increase in cost (85%) with an increase of the pf from 0% to 10%. This relatively large increase in the WLC is due the cost of the PM actions required to restore the initial condition of the element. As these actions are applied at the beginning of its life they are not discounted, hence they have a marked effect on the overall cost of the strategy.
As shown in Table 8 the first use of a reactive PM measure within each strategy is brought forward as the initial pf increases. This is then followed by various cycles which combine either “do nothing” with sealer and ECE or “do nothing” with P-m coating and ECE. The use of P-m coating generally seems to increase in later years due to the discounting.
The optimum plans for different initial pf are given in Table 8.
3.5. Effect of Different Service Life
The service life of an element is defined as the period of time during which it meets the standards and/or the target specified [23] . In the Pilot case the time period is set to 120 years to comply with the service life span of
Figure 8. Effect of initial pf on the WLC.
Table 8. Optimum PM plan with different initial pf: Case studies (14-16) & pilot case.
Decoded Actions: 1: Do nothing; 2: Silane; 3: Sealer; 4: P-m Coating; 6: ECE; -: P-m coating still effective due to its service life (10 years).
bridges designed before Eurocode requirements [24] . Additional analyses are performed to examine the effect of the service life on the optimum strategy selection. The service life values examined in Cases 17-18 are 60 years and 100 years [19] .
Figure 9 illustrates the corresponding pf profiles of these cases. The outcome of the analyses, which are the optimum strategies, the WLC and the corresponding pf profile are presented in Table 9 and Figure 10. The PM strategy is the same for all three cases for the first 30 years and combines the use of surface treatments and “do nothing” until the target pf is reached when the reactive measure ECE is applied. In the subsequent cycles the P-m coating which is the most effective and expensive proactive measure becomes more beneficial and is se- lected more often. This is justified due to the combination of the longer life considered and the effect of the dis- counted cost. For the cases considering 60 and 100 years service life, two applications of ECE are required while in the case of 120 years, four applications are scheduled. When considering the WLCs for the three cases (Figure 11) it can be seen that as expected the WLC increases as the service life period increases although the rate of increase reduces with larger service life periods. The average cost per year reduces approximately linearly with increasing service life. The latter is partly due to the effect of discounting and also due to the fact that a longer service life plan provides more flexibility with the combination of options which can result in reduced overall cost.
3.6. Application of GA Methodology to Different Bridge Elements
So far the optimization methodology and its sensitivity were demonstrated with respect to a bridge beam. The methodology, however, is generic and can be applied to different bridge elements or even different deteriorating structures. In this example the methodology is demonstrated for a bridge deck instead of a beam. In the case of bridge decks the use of waterproofing system (WS) is mandatory in the UK since 1965 [13] therefore the WS is applied at year zero (0). Other actions that can be applied to bridge decks are the cathodic protection (CP) and concrete replacement (CR) hence these are also included as PM options in the analysis. Surface treatments with inadequate depth of penetration are not recommended since they can quickly wear when exposed to traffic abrasion [11] therefore they are excluded from this example.
Figure 9. Probability of failure profile: Case studies (14-16) & pilot case.

Figure 10. Effect of service life on (a) WLC; (b) Average cost per year.
Figure 11. Probability of failure profile: Case studies (17-18) & pilot case.
Table 9. Optimum PM Plan with different service life: Case studies (17-18) & pilot case.
Decoded Actions: 1: Do nothing; 2: Silane; 3: Sealer; 4: P-m Coating; 6: ECE; -: P-m coating still effective due to its service life (10 years).
The WS is assumed to have a service life of 25 years [13] and the cost is taken as ∈1/m2 [12] . Following the initial application of WS which is effective for 25 years the methodology is free to select any of the PM options included to maintain the pf profile within acceptable limits and minimize the WLC.
In this case the use of WS is selected throughout the 120 years instead of CP or CR (Table 10). The WS is applied every 25 years (service life of WS) with the exception of a 5-year gap (at the 25th year) during which the deck can be left to deteriorate with no action taken (Figure 12). The repeated application of WS is sufficient to ensure that pf remains below the critical pf of 0.1 for the entire 120 years period without the need for any of the reactive PM measures CP and CR. The WLC is equal to ∈5.5/m2 which is significantly less than the beam element WLC of ∈00.7/m2. This suggests that the WS applied on bridge decks is a very effective PM measure.
Figure 12. Probability of failure profile―Case study 19.
Table 10. Optimum PM plan of case study 19.
Decoded Actions: 1: Do nothing; 8: waterproofing system; -: waterproofing system still effective during its service life (25 years).
4. Conclusions
A methodology is developed which combines probabilistic modelling of PM effectiveness with a GA based optimization methodology for identifying optimum PM strategies for reinforced concrete bridges. The PM strategies target one of the dominant deterioration problems in reinforced concrete bridges. The aim of the PM strategies is to delay/prevent the reinforcement corrosion of RC elements through contamination from chloride ions present in de-icing salts. The sensitivity of the methodology to various key input parameters is examined in order to quantify their effects and identify possible trends in the optimum PM intervention profiles. The results of the sensitivity studies highlight the combined use of both proactive and reactive PM measures in deriving optimum strategy solutions. When changes are introduced in the various parameters the methodology is capable of identifying optimum strategies which satisfy the pf constraints and deliver minimum WLC. The precise mix and sequence of PM measures is clearly a function of the relative effectiveness and cost of the different available PM options as well as the various key parameters such as discount rate, target probability of failure, initial probability of failure and service life period examined.
As the discount rate increases the WLC reduces and becomes less sensitive towards the higher and of the range of 6% - 8%. In this range there is no change in the intervention sequence although the WLC is reduced due to increased discounting. Higher discount rate cases make increasingly more use of expensive options towards the end of life.
As expected the methodology is sensitive to the target pf, with WLC increasing as the target pf increases. There appears to be approximately a linear dependence with some small step changes observed between different strategy combinations. Within the range examined the percentage rate of change in WLC of the optimum strategy is about half that of the change in target pf.
The initial condition of the element (pf value) has a large effect on the WLC of the optimum strategy. This is due to the PM actions required to restore the initial condition of the element. As these initial actions are applied at the beginning of the life, when the discounting effect is small, they have a marked effect on the overall strategy cost.
As the service life increases the WLC increases, however the sensitivity reduces with higher service life periods. This is mainly due the discounting but also due to the possibility of identifying more optimum PM combinations with a longer service life. This trend is also observed in the average cost per year which reduces linearly with the service life period.
Overall, the various case studies presented demonstrate the applicability of the methodology and highlight the efficiency and consistency in the results while showing some interesting trends. While the results highlight the need for more reliable data they also demonstrate the robustness and usefulness of the methodology. Where data is limited it can be used as a comparative tool to improve understanding of the effects of various strategies and enhance the decision making process. The methodology presented here although demonstrated for reinforced concrete bridge elements is generic and can be adapted to other type of deteriorating structures, systems or networks.
Acknowledgements
The support of this research by the UK Highways Agency (HA) and Transport Research Laboratory (TRL) is gratefully acknowledged. The opinions and conclusion presented in this paper are those of the authors and do not necessarily reflect the view of the sponsoring organizations.
References
- FHWA (2011) Bridge Preservation Guide, Maintaining a State of Good Repair Using Cost Effective Investment Strategies. Federal Highway Administration, US Department of Transportation, FHWA Publication Number, FHWA-HIF- 11042.
- Tantele, E.A. and Onoufriou, T. (2010) Optimization of Life-Cycle Preventative Maintenance Strategies Using Genetic Algorithm and Bayesian Updating. Proceedings of the 5th International Conference on Bridge Maintenance, Safety and Management, IABMAS’10, Smart EN ITN Mini-Symposium, Philadelphia, 11-15 July, 2010.
- Tantele, E.A. and Onoufriou, T. (2009) Optimum Preventative Maintenance Strategies Using Genetic Algorithm and Bayesian Updating. Ships and Offshore Journal, 4, 299-306. http://dx.doi.org/10.1080/17445300903247162
- Holland, J.H. (1975) Adaptation in Natural and Artificial Systems. University of Michigan Press, Ann Arbor.
- Goldberg, D.E. (1983) Computer-Aided Gas Pipeline Operation Using Genetic Algorithms and Rule Learning. Ph.D. Thesis, University of Michigan, Ann Arbor.
- Miyamoto, A., Kawamura, K. and Nakamura, H. (2000) Bridge Management System and Maintenance Optimization for Existing Bridges. Computer Aided Civil and Infrastructure Engineering, 15, 45-55. http://dx.doi.org/10.1111/0885-9507.00170
- Liu, M. and Frangopol, D.M. (2004) Optimal Bridge Maintenance Planning Based on Probabilistic Performance Pre- diction. Engineering Structures, 26, 991-1002. http://dx.doi.org/10.1016/j.engstruct.2004.03.003
- Furuta, H., Nakatsu, K., Ishibashi, K. and Miyoshi, N. (2014) Optimal Bridge Maintenance of Large Number of Bridges Using Robust Genetic Algorithm. Structures Congress, Boston, 3-5 April 2014, 2282-2291.
- Morcous, G. and Lounis, Z. (2005) Maintenance Optimization of Infrastructure Networks Using Genetic Algorithms. Automation in Construction, 14, 129-142. http://dx.doi.org/10.1016/j.autcon.2004.08.014
- Haupt, R. and Haupt, S. (2004) Practical Genetic Algorithms. 2nd Edition, John Wiley and Sons, Inc., New York.
- Weyers, R.E., Prowell, B.D., Sprinkel, M.M. and Vorster, M. (1993) Concrete Bridge Protection, Repair, and Rehabilitation Relative to Reinforcement Corrosion: A Methods Application Manual. SHRP-S-360, Strategic Highway Research Program, Washington DC.
- Highways Agency (1999) Serviceable Life of Highway Structures and Their Components. Final Report, Project Number 970530.
- Pearson, S. and Cuninghame, J.R. (1997) Water Management for Durable Bridges. Project Report PR/CE/91/97, Trans- port Research Laboratory, Berkshire.
- Kepler, J.L., Darwin, D. and Locke, C.E. (2000) Evaluation of Corrosion Protection Methods for Reinforced Concrete Highway Structure. Structural Engineering and Engineering Materials SM Report No. 58, University of Kansas Center for Research, Inc., Lawrence.
- Krauss, P.D., Lawler, J.S. and Steiner, K.A. (2009) Guidelines for Selection of Bridge Deck Overlays, Sealers and Treatments. Wiss, Janney, Elstner Associates, Inc., Northbrook.
- Tilly, G.P. (1996) Principles of Whole Life Costing. Proceedings of Conference on Safety of Bridges, ICE, Thomas Tel- ford, London, 138-144.
- Tantele, E.A., Onoufriou, T. and Mulheron, M. (2005) Effectiveness of Preventative Maintenance for Reinforced Concrete Bridges―A Stochastic Approach. Proceedings of the 5th International Conference on Bridge Management, Surrey, 11-13 April 2005, 443-451.
- Treasury, H.M. (2003) The Green Book: Appraisal and Evaluation in Central Government: Treasury Guidance. TSO, London.
- Li, C.Q. (2003) Life-Cycle Modelling of Corrosion―Affected Concrete Structures: Propagation. Journal of Structural Engineering, 129, 753-761. http://dx.doi.org/10.1061/(ASCE)0733-9445(2003)129:6(753)
- BS EN 1990 (2002) Eurocode: Basis of Structural Design. British Standards Institution, London.
- JCSS (2000) Probabilistic Model Code, Part 1―Basis of Design. Joint Committee on Structural Safety, JCSS-OSTL/ DIA/VROU-10-11-2000.
- Val, D.V. and Stewart, M.G. (2003) Life-Cycle Cost Analysis of Reinforced Concrete Structures in Marine Environments. Structural Safety, 25, 343-362. http://dx.doi.org/10.1016/S0167-4730(03)00014-6
- OECD (1992) Bridge Management, Road Transport Research. Paris.
- BS 5400 (1998) Steel, Concrete and Composite Bridges―Part 1: General Statement. British Standards Institution, London.
NOTES
*Corresponding author.















