Modern Mechanical Engineering
Vol.2 No.3(2012), Article ID:22198,14 pages DOI:10.4236/mme.2012.23012
Quasi-Relaxation Transforms, Meromorphic Curves and Hereditary Integrals of the Stress-Deformation Tensor to Metallic Specimens
1Department of Research in Mathematics and Engineering, Tecnológico de Estudios Superiores de Chalco, Mexico, Russia
2Baikov Institute of Research in Metallurgy and Material Sciences, Mexico, Russia
Email: francisco.bulnes@tesch.edu.mx, stropoy@baikov.institute.ru, yermishkinv@baikov.institute.ru
Received April 23, 2012; revised May 31, 2012; accepted June 11, 2012
Keywords: Hereditary Integrals; Meromorphic Curves; Meta-Stability State, Plastic Energy; Quasi-Relaxation Transforms
ABSTRACT
Into the study of quasi-relaxation, in the past researches it has been concluded that the condition of meta-stability in the metallic specimen is given by the plasticity explained by the plastic energy in the process of the quasi-relaxation. It is calculated through quasi-relaxation functional of this energy to obtain a spectra in the space D(σ – ε; t), that induces the existence of functions φ(t), and Ψ(t), related with the fundamental curves of quasi-relaxation given by σ(t), with their poles in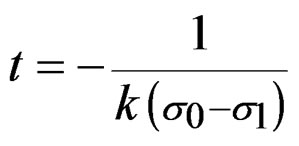 , which is got in the maximum of stress given by σ0 = σ1. Also the tensor of plastic deformation that represents the plastic load during the application of specimen machine, cannot be obtained without poles in the space D(σ; t), corresponding the curves calculated into the space D(σ – ε; t), by curves that in the kinetic process of quasi-relaxation are represented by experimental curves in coordinates log σ – t. This situation cannot be eluded, since in this phenomena exist dislocations that go conform fatigue in the nano-crystalline structure of metals. From this point of view, is necessary to obtain a spectral study related to the energy using functions that permits the modeling and compute the states of quasi-relaxation included in the poles in the deformation problem to complete the solutions in the space D(σ – ε; t), and try a new method of solution of the differential equations of the quasi-relaxation analysis. In a nearly future development, the information obtained by this spectral study (by our integral transforms), will be able to give place to the programming through the spectral encoding of the materials in the meta-stability state, which is propitious to a nano-technological transformation of materials, concrete case, some metals.
, which is got in the maximum of stress given by σ0 = σ1. Also the tensor of plastic deformation that represents the plastic load during the application of specimen machine, cannot be obtained without poles in the space D(σ; t), corresponding the curves calculated into the space D(σ – ε; t), by curves that in the kinetic process of quasi-relaxation are represented by experimental curves in coordinates log σ – t. This situation cannot be eluded, since in this phenomena exist dislocations that go conform fatigue in the nano-crystalline structure of metals. From this point of view, is necessary to obtain a spectral study related to the energy using functions that permits the modeling and compute the states of quasi-relaxation included in the poles in the deformation problem to complete the solutions in the space D(σ – ε; t), and try a new method of solution of the differential equations of the quasi-relaxation analysis. In a nearly future development, the information obtained by this spectral study (by our integral transforms), will be able to give place to the programming through the spectral encoding of the materials in the meta-stability state, which is propitious to a nano-technological transformation of materials, concrete case, some metals.
1. Introduction
In the last 30 years, the experimental technique to the characterization of materials with the use of testing machines has experimented a big heyday. In the conventional machines of essays, where the specimen previously is loaded up to an initial level of the stress, after that which the motorize system of the machine is disconnected, it is a observed a spontaneous fall of stress. The kinetic of the fall of the stress is registered during all the process of the essays [1]. Similar experiment must be executed in a programmed specially machine, in which during the essay of automatic manage stays constant the longitude of the specimen that; is to say, the condition of the essay in regime of quasi-relaxation can be expressed in the following form
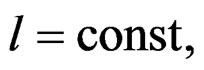 (1)
(1)
or well,
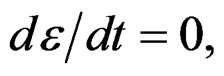 (2)
(2)
This condition define the meta-stability as a state of constant deformation only in their plastic characteristics in the initial process of dislocations [2,3], where the energy of the nano-crystals accumulate the enough energy to maintain the specimen in a stable range of recovering to original state, in a very short time interval [2,4]. In this respect, it is necessary to realise a deep study of traces of deformation tensor in function of the stress tensor corresponding plastic deformation and use a functional of energy [5], that measures this recover energy due the nanocrystals [6].
2. Constitutive Equations to Stress-Deformation Tensor
Considering a material M, like the defined space by the limit surface specimen-machine; (the surface or zone of work of the machine on specimen [5]):
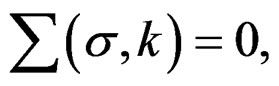 (3)
(3)
where 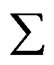 is the differentiable surface in
is the differentiable surface in 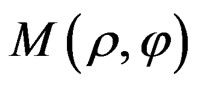 ×
×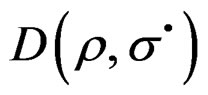 [7]. Here
[7]. Here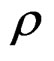 , is the density of the dislocations, is the relaxation function, and
, is the density of the dislocations, is the relaxation function, and , is the velocity of applied stress to specimen.
, is the velocity of applied stress to specimen.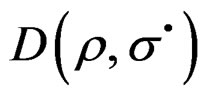 , is the stress space [3,7,8]
, is the stress space [3,7,8]
 (4)
(4)
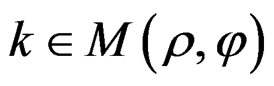
 , with k, the state tensor of media. By stress-deformation theory [3], the rate of the stress tensor
, with k, the state tensor of media. By stress-deformation theory [3], the rate of the stress tensor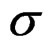 , comes give by the expression in all region all space of the material M,
, comes give by the expression in all region all space of the material M,
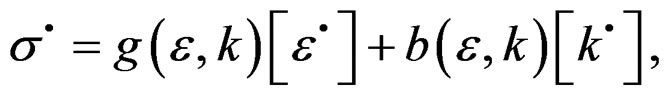 (5)
(5)
to all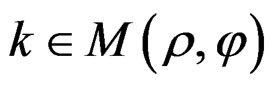 , with k, the state tensor of media and
, with k, the state tensor of media and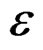 , the deformation tensor. Then [9]:
, the deformation tensor. Then [9]:
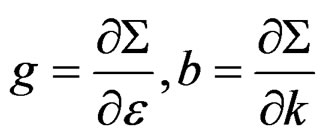 (6)
(6)
where , is the conformal elastic tensor of
, is the conformal elastic tensor of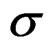 , and
, and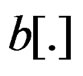 , is conformal inelastic tensor of the tensor
, is conformal inelastic tensor of the tensor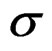 . Note that b, is an element belonging to tensor space
. Note that b, is an element belonging to tensor space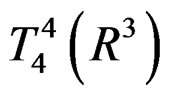 , (tensor of range 4, in the ordinary space) [6,10,11], which participates in the symmetrization of the elastic module tensor of the deformation tensor
, (tensor of range 4, in the ordinary space) [6,10,11], which participates in the symmetrization of the elastic module tensor of the deformation tensor , and analogously
, and analogously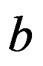 , to the elastic part of
, to the elastic part of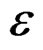 . This helps us to understand that the realised transforms on the material subject to the stresses
. This helps us to understand that the realised transforms on the material subject to the stresses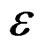 , are plastic transformations and produces only dislocations or laminar displacements in the material [4,7,12], (staying invariant the structure), thus the actions of the contributions of the inelastic and elastic conformal components of the rate of stress
, are plastic transformations and produces only dislocations or laminar displacements in the material [4,7,12], (staying invariant the structure), thus the actions of the contributions of the inelastic and elastic conformal components of the rate of stress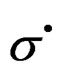 , and
, and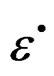 , are linear and these are superposes [8]. Then the stress space
, are linear and these are superposes [8]. Then the stress space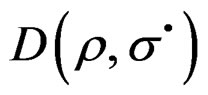 , satisfies the orthogonal relations to
, satisfies the orthogonal relations to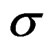 , and
, and , respectively [9]:
, respectively [9]:
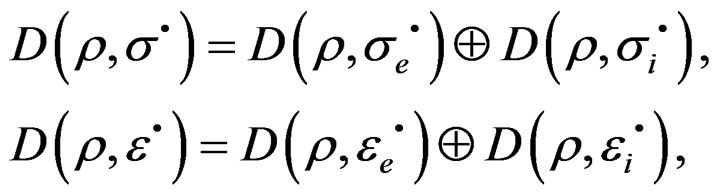
As consequence of it, the set of solutions or integrals that we obtain to method of quasi-relaxation is included in this orthogonal decomposition to their more general integral, which is determined through the corresponding hereditary integrals in solid deformations [2,7], and whose quasi-relaxation can be study in the space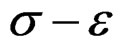 , like the sum of two components of the tensor
, like the sum of two components of the tensor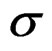 , as the produced by the external stresses, and other by the inner stresses due to the dislocation. The similar thing to the deformations. Now we precise the necessary roll of the analysis of the deformations.
, as the produced by the external stresses, and other by the inner stresses due to the dislocation. The similar thing to the deformations. Now we precise the necessary roll of the analysis of the deformations.
Consider the deformation tensor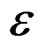 , which is given by the function [1]
, which is given by the function [1]
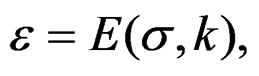
to all E-differentiable surface in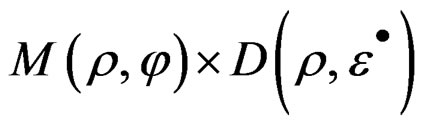 , [3,7]. Deriving with respect to t, result the rate of analogous deformation like given to the tensor
, [3,7]. Deriving with respect to t, result the rate of analogous deformation like given to the tensor , to know
, to know
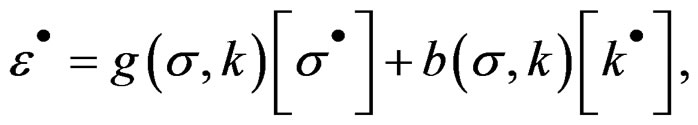 (7)
(7)
where
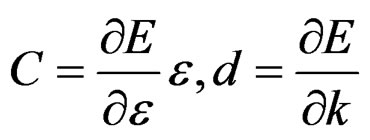 (8)
(8)
where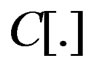 , is the elastic modulus tensor defined by the map [6,8,11]
, is the elastic modulus tensor defined by the map [6,8,11]
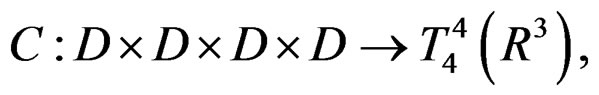 (9)
(9)
with correspondence rule
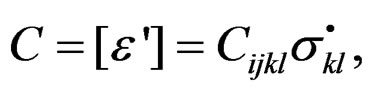 (10)
(10)
and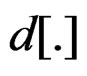 , is the inelastic modulus tensor of the tensor ε, which is a map of k(depends only on the specific properties of k).
, is the inelastic modulus tensor of the tensor ε, which is a map of k(depends only on the specific properties of k).
In general, in the deformation analysis the tensors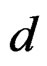 , and
, and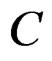 , is a dependence on
, is a dependence on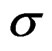 , and k. Then through their components to a transformation system of coordinates in the space
, and k. Then through their components to a transformation system of coordinates in the space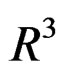 , belonging to a group of orthogonal transformations of range 2 [6], takes the form
, belonging to a group of orthogonal transformations of range 2 [6], takes the form
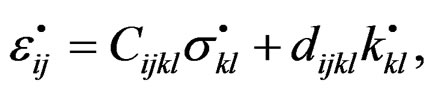 (11)
(11)
Since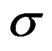 , and
, and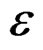 , are symmetrical, the tensor
, are symmetrical, the tensor . Then the differentiable function
. Then the differentiable function , must be invertible in
, must be invertible in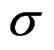 , the tensor
, the tensor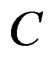 , must be non singular and the differentiable equivalence of the limit surfaces of the material M, submitted to stress-deformation of the tensors
, must be non singular and the differentiable equivalence of the limit surfaces of the material M, submitted to stress-deformation of the tensors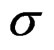 , and
, and , come given by the differentiable equivalence between the deformations space
, come given by the differentiable equivalence between the deformations space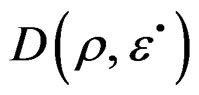 , [5], and the stresses space
, [5], and the stresses space , under the differentiable maps
, under the differentiable maps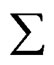 , and E [5,7,11].
, and E [5,7,11].
Given that the elastic energy that is got in a specimen under stress-deformation comes measured for the elastics fields of the dynamical dislocations [4], the contribution of the inelastic modulus tensor to the given deformations for the inner stresses, that is to say, due to the dislocations, contribute to the velocity of total deformation in the quasi-relaxation equation, thus
 (12)
(12)
Note: k, represent the state tensor (consider variables like density, mass, temperature, pressure, etc),
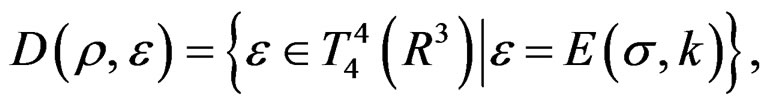
Then the total deformation by the tensor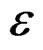 , comes given by
, comes given by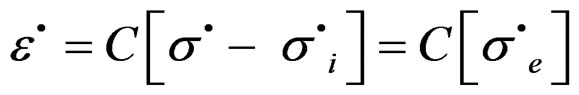 , which clearly contributes to value of the external stresses to material
, which clearly contributes to value of the external stresses to material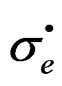 , which results of relevance to the deformation in quasi-relaxation (stress of the machine on the specimen).
, which results of relevance to the deformation in quasi-relaxation (stress of the machine on the specimen).
Lemma 2.1. The velocity of total deformation given by the tensor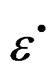 , in the quasi-relaxation equation come given by
, in the quasi-relaxation equation come given by
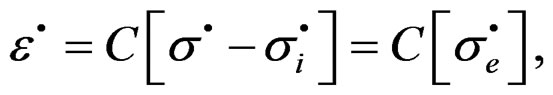 (13)
(13)
Proof. If we write the tensor of deformation ε, like the composition of functions [5,13,14]
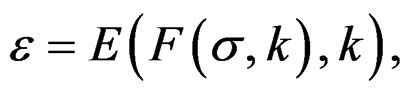 (14)
(14)
and using the rule of the chain of derivation we have the tensors
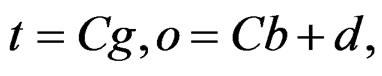 (15)
(15)
Since C, is not singular then
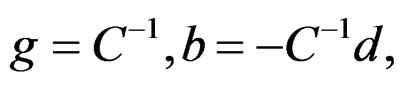 (16)
(16)
Using the elements of inelastic transformation of the second component of the space of the Equations (5), to the tensor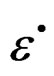 , descript in the form
, descript in the form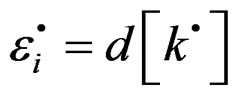 , by a correspondence between
, by a correspondence between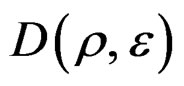 , and
, and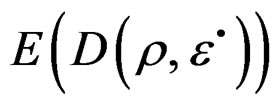 , and the elements of the second component of the space of the Equations (5), to the tensor
, and the elements of the second component of the space of the Equations (5), to the tensor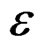 , descript by
, descript by
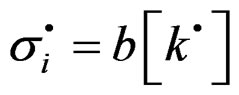 , the inelastic contribution of the rate of deformation
, the inelastic contribution of the rate of deformation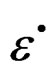 , and the inelastic contribution of the rate of the stress
, and the inelastic contribution of the rate of the stress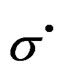 , are related by the Equation (12). Then fitting
, are related by the Equation (12). Then fitting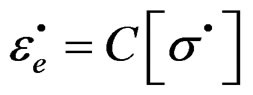 , and the Equations (5), in the orthogonal decomposition of
, and the Equations (5), in the orthogonal decomposition of , result the required relation. Now it is necessary to demonstrate whose relation satisfies the equation of quasi-relaxation, that is to say, the velocity of total deformation is the given by the Equation (13).
, result the required relation. Now it is necessary to demonstrate whose relation satisfies the equation of quasi-relaxation, that is to say, the velocity of total deformation is the given by the Equation (13).
In effect, considering the reasons of deformation of the fundamental equation of quasi-relaxation and the Equations (6)-(8) and (12), we have that

and given that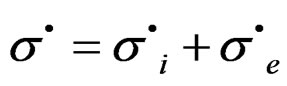 , then [13]
, then [13]

and
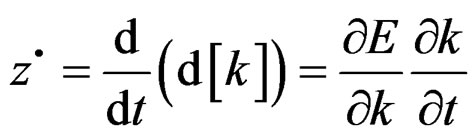
Integrating we obtain an expression of the deformation tensor in function of the integrals of the stress tensor or stress with some constants that depends on the used parameters in the machine-specimen to along of the quasi-relaxation process of the material [7].
Lemma 2.2. The tensor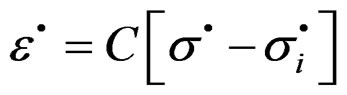 , is a rate of plastic deformation [14,15] and represents the plastic load during the application of machine-specimen.
, is a rate of plastic deformation [14,15] and represents the plastic load during the application of machine-specimen.
Proof. By the lemma 2.1,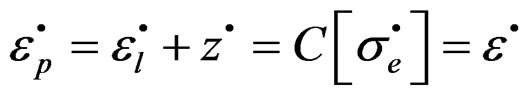 . But given that is had considered a surface of load of the specimen given by the function given by Equation (14), then applying the load machine-specimen is had that
. But given that is had considered a surface of load of the specimen given by the function given by Equation (14), then applying the load machine-specimen is had that
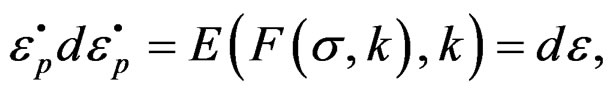 (17)
(17)
of where . Integrating both members we have that
. Integrating both members we have that
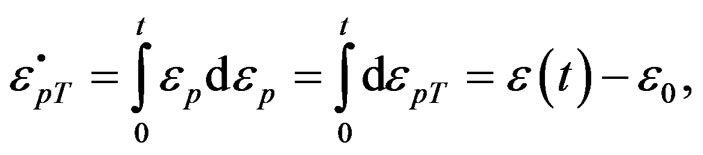 (18)
(18)
But the total deformation obtained in this quasi-relaxation process satisfies the entire load
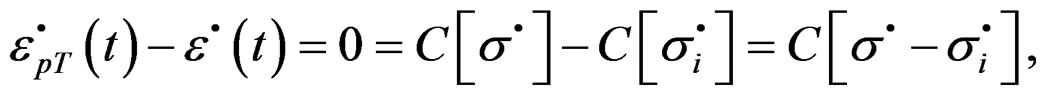 (19)
(19)
The lemma 2.2. tells us that the plastic deformation during the application of the machine-specimen is the required to the quasi-relaxation and the lemma 2. 1, warns us that the quasi-relaxation process can be measure it through that plastic deformation obtained in the machine-specimen. But whose plastic deformation is a reflex of the work that realizes the machine to obtain the meta-stability conditions that defines the quasi-relaxation in the circuit machine-specimen [14,16,17]. Thus, the form to measure and determine the quasi-relaxation is through the work of plastic deformation during the application of the system machine-specimen. Of this manage we can to define to functional 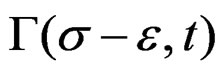 [17-20], like the density of power of the stress on the surface of work in the process of quasi-relaxation to apply the stress-deformation in the system machine-specimen at the time t. Then as was had descript in before studies [7,21].
[17-20], like the density of power of the stress on the surface of work in the process of quasi-relaxation to apply the stress-deformation in the system machine-specimen at the time t. Then as was had descript in before studies [7,21].
Theorem 2. 1. (Bulnes-Yermishkin) [21]. The quantity of accumulated energy , during the quasi-relaxation is determined by the work of plastic deformation during the application of the system machine-specimen and
, during the quasi-relaxation is determined by the work of plastic deformation during the application of the system machine-specimen and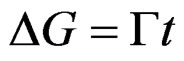 .
.
Proof. Is uses the Lagrangian action the energy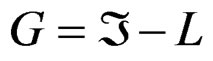 , of the mono-crystals under the plastic deformation tensor
, of the mono-crystals under the plastic deformation tensor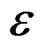 , to along of
, to along of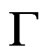 , establishing the action [13,19].
, establishing the action [13,19].
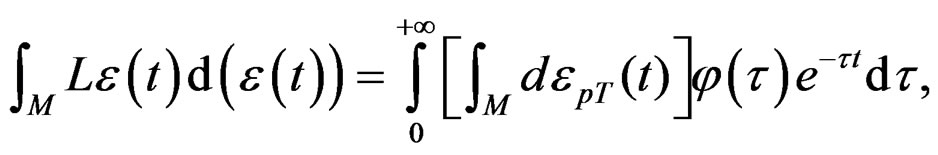 (20)
(20)
To see details of the demonstration of this result consult [4,11].
3. Functional of Plastic Energy that Promote the Dislocations
The study of the resultant energy due to the meta-stables conditions that is obtained in the quasi-relaxation phenomena established clearly their plastic nature for the suffered deformations on the specimen. Nevertheless their study can require the evaluation of the field of plastic deformation on determined sections to a detailed study on the liberated energy in the produced dislocations when the field of plastic deformation acts. Thus, it is doing necessary the introduction of certain evaluations of the actions of the field to along the dislocation trajectories in mono-crystals of the metals with properties of asymptotic relaxation. Thus we consider like specimens, mono-crystals of Molybdenum (Mo), subject to stress tensor that produces the plastic deformation given by the action Equation (20). By the theorem of Bulnes-Yermishkin [20], all functional of stress-deformation to along the time must satisfy for hereditary integrals in the quasi-relaxation phenomena that
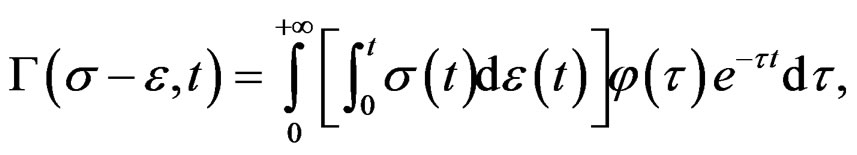 (21)
(21)
Studies in mathematics [9-11], can demonstrate that the integral from Equation (21), is an integral transform, if the expression between the brackets is a function with analytic properties that joins with  [10,13], determine the kernel of the integral transform and characterize like a quasi-relaxation transform. Our functional of energy are the evaluations of the field of plastic deformation considering the quantity of energy of liberated plastic deformation by the specimen for unit of time
[10,13], determine the kernel of the integral transform and characterize like a quasi-relaxation transform. Our functional of energy are the evaluations of the field of plastic deformation considering the quantity of energy of liberated plastic deformation by the specimen for unit of time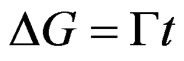 , in the generated dislocations in the specimen under the regimens of quasi-relaxation. If we consider the average energy of the longitude unit for line of dislocation, the integral form Equation (21), takes the form for the Burgers vector b, and the initial reserve of elastic energy in the specimen [21]
, in the generated dislocations in the specimen under the regimens of quasi-relaxation. If we consider the average energy of the longitude unit for line of dislocation, the integral form Equation (21), takes the form for the Burgers vector b, and the initial reserve of elastic energy in the specimen [21]
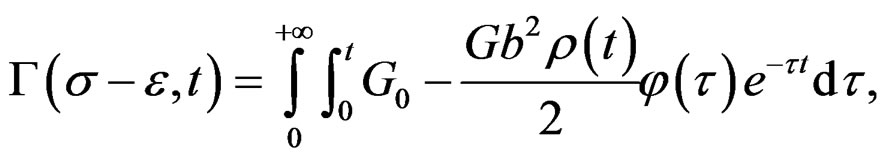 (22)
(22)
During the unloaded of the specimen, stressed in the elastic field, these dislocations transform in a density of initial dislocations. The realised videos on the evolution of the dislocational structure in mono-crystals of Molybdenum (Mo), (images of the transitory given by the Laplace transform involucrate in the functional of Equation (21), (see Figure 1, of mono-crystal evolution), during the load and unload, demonstrates the reversibility of the sliding character of the dislocations, and of variation of the density of these, in the field where the metal behaviors elastically. The dislocations that could already exist in the stressed crystal, and that is annihilated during the unload, we call dynamical dislocations. Like is had demonstrate [21], practically all the elastic energy of the specimen it arises during the load and it is accumulates in form of the elastic fields of the dislocations, in base to
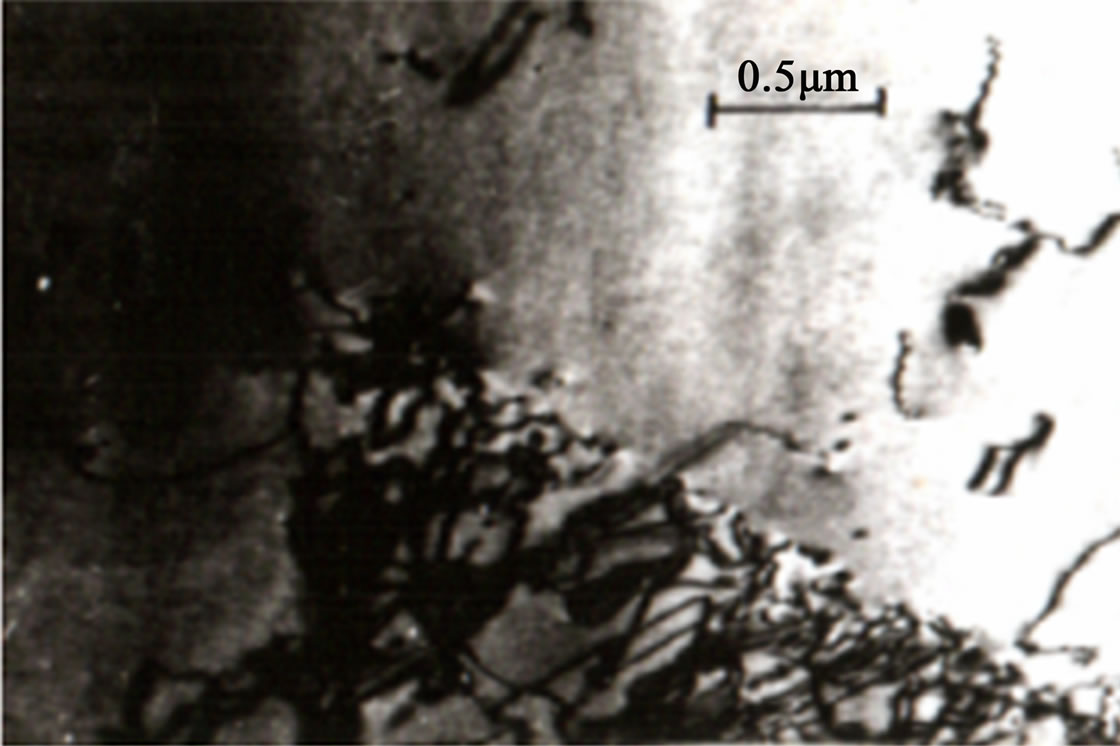
Figure 1. Image of the electronic microscope of high voltage, HVTEM of Moybdenum single crystal in regime of quasirelaxation [2].
the conservation law, in the volume unit of the deformed material during the load, it is describes through the following equation:
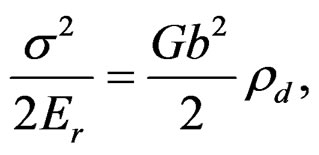 (23)
(23)
Do not use hard tabs, and limit use of hard returns to only one return at the end of a paragraph. Do not add any kind of pagination anywhere in the paper. Do not number text heads—the template will do that for you.
where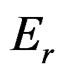 , is the value of modulus of normal elastic relaxation, that is to say, the valued energy considering the elasticity of the essay machine
, is the value of modulus of normal elastic relaxation, that is to say, the valued energy considering the elasticity of the essay machine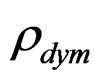 , the density of the dynamical dislocations, expressed in the right part of the Equation (23). Here is necessary observe that the property of the integral transforms to the obtaining of the spectral state of the quasi-relaxation phenomena, bounded by constants or coefficients that is computes in the corresponding energy space of signals
, the density of the dynamical dislocations, expressed in the right part of the Equation (23). Here is necessary observe that the property of the integral transforms to the obtaining of the spectral state of the quasi-relaxation phenomena, bounded by constants or coefficients that is computes in the corresponding energy space of signals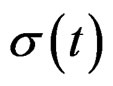 , or
, or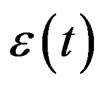 , that is to say, in the space
, that is to say, in the space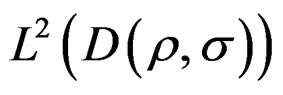 , it reflexes in the norm of technology (given to nano-components like can be nano-crystal [15,16]), given by [20], and bounding the Lagrangian action given by the Equation (20), to know:
, it reflexes in the norm of technology (given to nano-components like can be nano-crystal [15,16]), given by [20], and bounding the Lagrangian action given by the Equation (20), to know:
 (24)
(24)
where , is the foreseen action in the Theorem 2.1, and
, is the foreseen action in the Theorem 2.1, and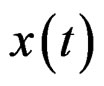 , is a particle of the material specimen
, is a particle of the material specimen 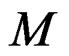 [10,20], with values in
[10,20], with values in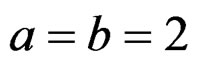 . The controls to
. The controls to , are given for
, are given for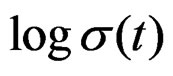 , and
, and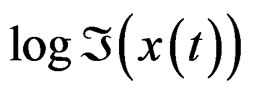 , [3, 8]. But the one that are isometrics in the context of
, [3, 8]. But the one that are isometrics in the context of , (space of measures obtained in the panel of control of the specimen-machine (See Figure 2 and also the Figure 3 to their spectra).
, (space of measures obtained in the panel of control of the specimen-machine (See Figure 2 and also the Figure 3 to their spectra).
Example 3. 1. [20]. Consider the following example. Be the signal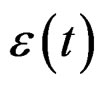 , emitted by a system anyone of deformation (for example our system machine-specimen). Let us consider a machine of deformation controlled with
, emitted by a system anyone of deformation (for example our system machine-specimen). Let us consider a machine of deformation controlled with

Figure 2. Specimen-machine to obtain the quasi-relaxation state of a material [5].
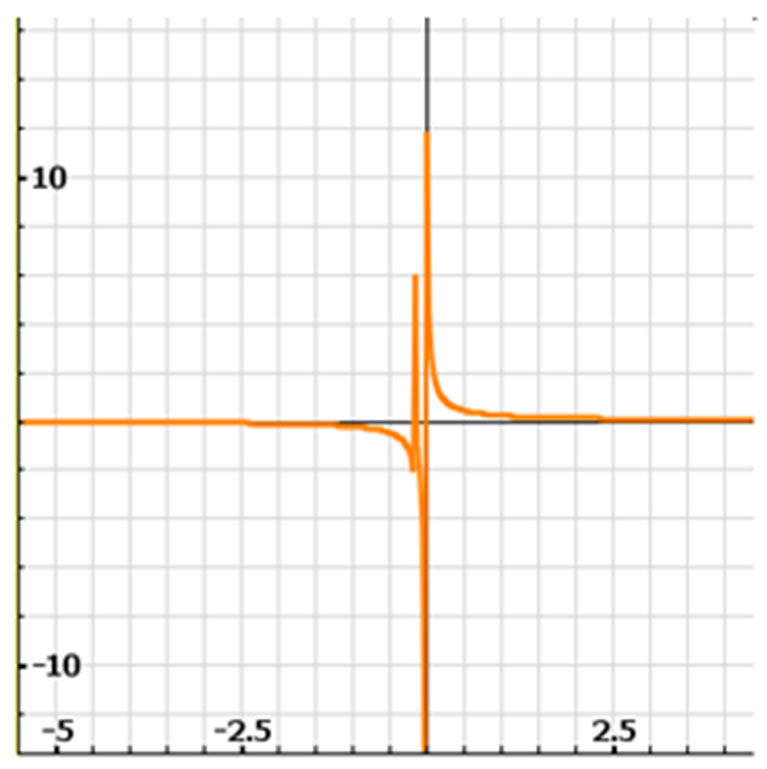
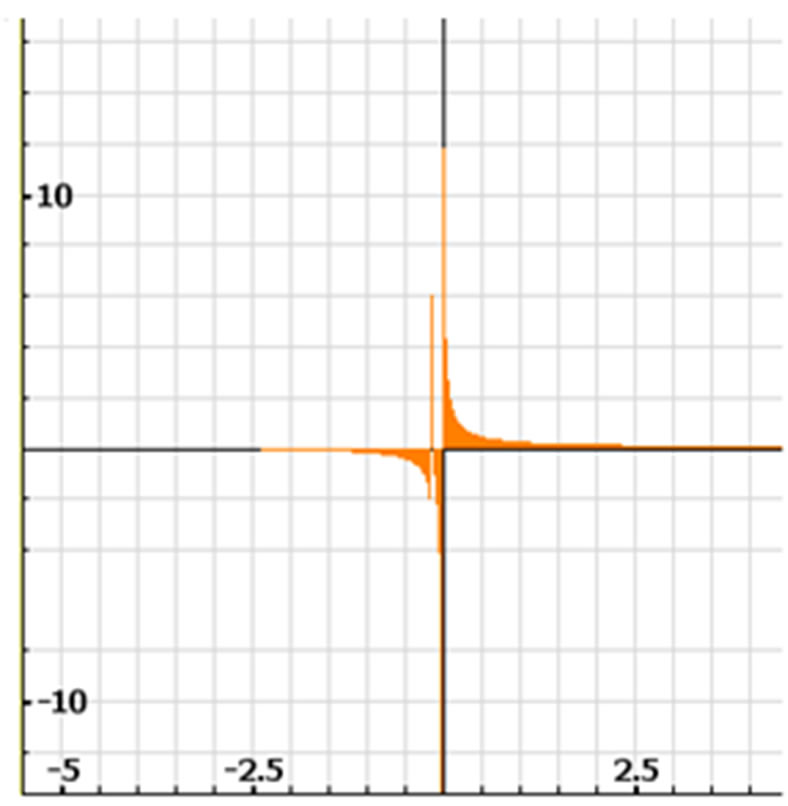
Figure 3. Spectral densities measured in space 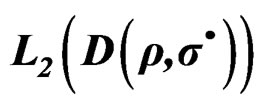
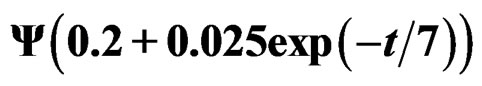 , is the spectral density of quasirelaxation function of
, is the spectral density of quasirelaxation function of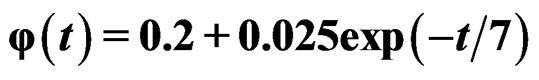 . It is had used the simulation program space-time 4.0.
. It is had used the simulation program space-time 4.0.
deformations given by the signals:
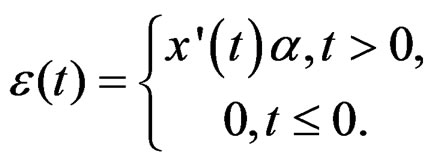 (25)
(25)
It is wanted to evaluate the quasi-relaxation obtained by this machine through their answer, for what we can define the space of these new states are given by the quasi-relaxation on a test specimen is necessary to define the space
 (26)
(26)
where the application of stress are those pre-designed by the functional coefficients , of the matrix of the tensor of enforce of Cauchy, the one which in turn depends on the gradient of deformation
, of the matrix of the tensor of enforce of Cauchy, the one which in turn depends on the gradient of deformation
 (27)
(27)
Then the new states that are the deformations required according to the rule of correspondence dictated previously come given by
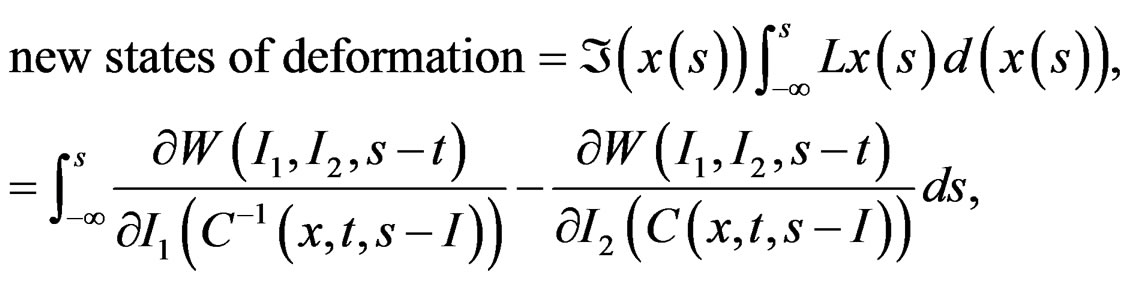 (28)
(28)
that is to say,
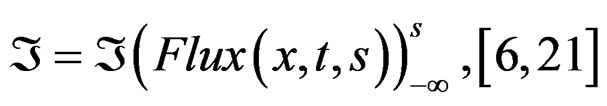 (29)
(29)
The flux obtained in the Equation (29) is the plastic flux of the particles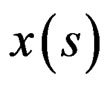 , before to risk dislocations [12]. The limit before dislocations in the system described comes given by
, before to risk dislocations [12]. The limit before dislocations in the system described comes given by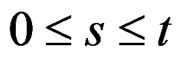 :
:

The function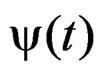 , is the fluency function that appears into the hereditary integral to deformation phenomena.
, is the fluency function that appears into the hereditary integral to deformation phenomena.
Taking the traces of the matrices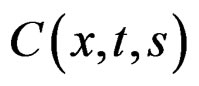 , and
, and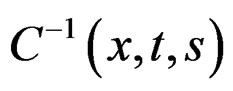 , of the Equation (28) [5], and considering the initial conditions of the action given by the Equation (20) with the longitude
, of the Equation (28) [5], and considering the initial conditions of the action given by the Equation (20) with the longitude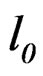 , of circuit of force of the machine remaining constant (Lagrangian action of the operator L) (Figure 2), we have an expression to the deformation in one general forms obtained experimentally [21]:
, of circuit of force of the machine remaining constant (Lagrangian action of the operator L) (Figure 2), we have an expression to the deformation in one general forms obtained experimentally [21]:
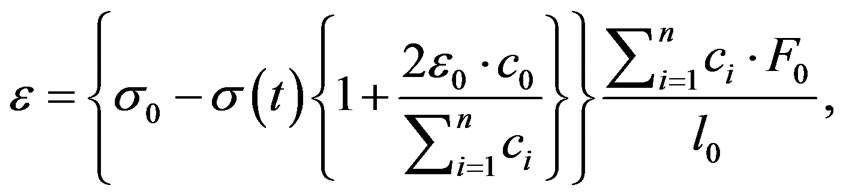 (30)
(30)
The enters of the matrices are elastic tensors components such that each one of them are bounded by the coefficients ci, for which with more precision we have 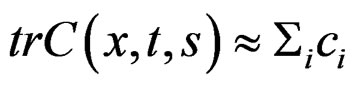 [3].
[3].
Now well, is necessary, that the energy of the elastic field of the dislocations have a logarithmic member. More yet, in the nucleus of the dislocations is concentrates to until the 10% of the total energy of the dislocations, and the energy of the elastic field so much of helical dislocation as rim is distinct, even to an approximate isotropic evaluation. This logarithm behavior, that is asymptotic to certain limit of dependent velocity of the time of thoroughness of the dislocation for the contention barrier in the machine-specimen, it is reflexes in the hyperbolic component of the curves of quasi-relaxation , to know (see Figure 4):
, to know (see Figure 4):
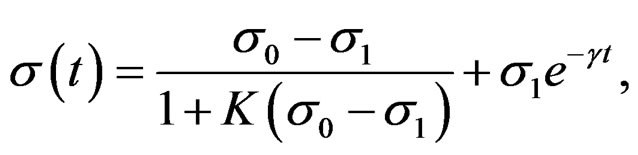 (31)
(31)
This hyperbolic component is responsible in their totality for the helical dislocations, being able to demonstrate through the quasi-relaxation transform [22], and for the help of the Hilbert transform, certain periodicity of the field of plastic deformation [2,5,14,17], in the elastic component of the field. In the selected crystal of Molybdenum the prevalence of the helically dislocations to manage thanks there is a mechanism of double transversal sliding during the process when the dislocation it is multiplies. This effect can be very notorious realizing a study on mono-crystals of Fe (see Figure 5).
Then the energy of inner-relation of dislocations W, is equal to work of the slide of a second dislocation into the field of stress of the first, until to risk a determined distance between them [12]. Then the integral of energy of the expression between the square brackets of the Equation (21), takes the form using the Equation (23),
 (32)
(32)
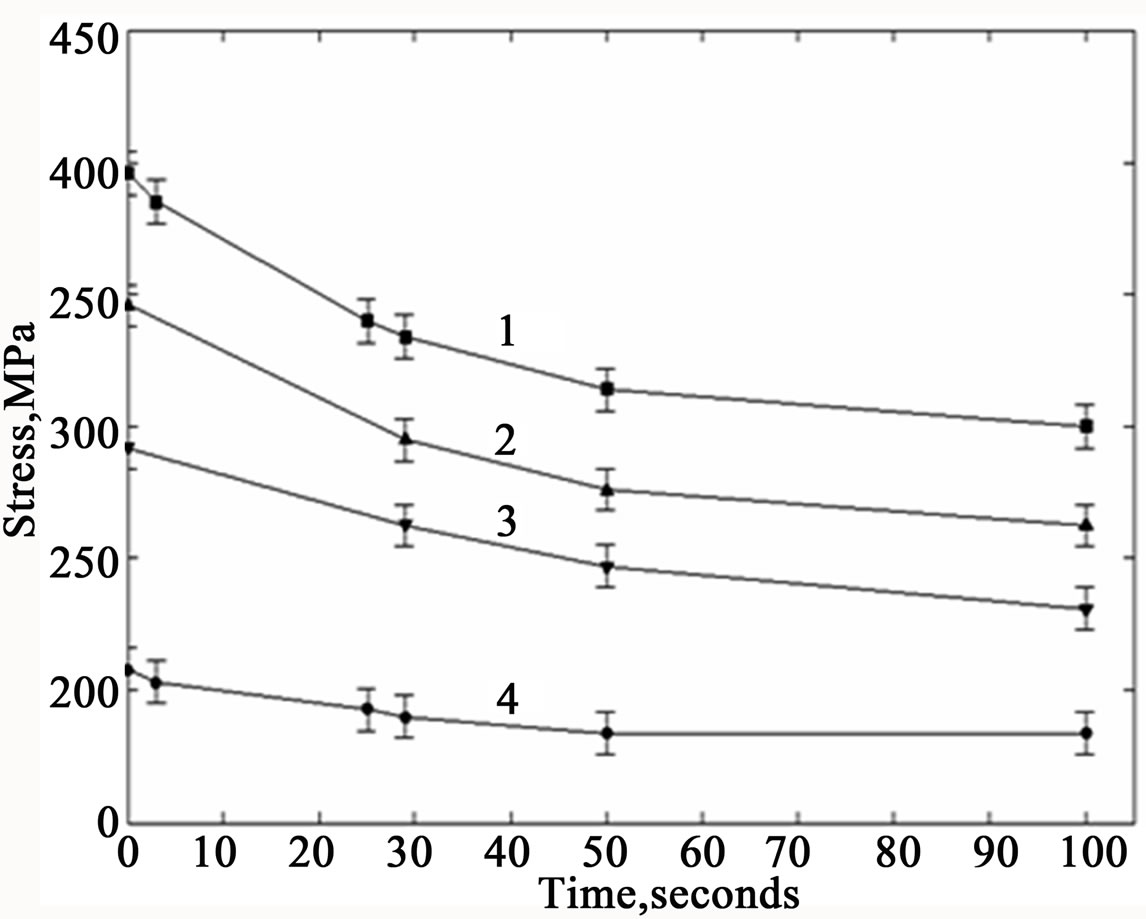
Figure 4. Quasi-relaxation curves for Molybdenum single crystal: 1.— s0 = 396 MPa, 2.—s0 = 346 MPa, 3.—s0 = 292 MPa, 4.—s0 = 208 MPa, Mo<100>{100}, at T = 293˚C.

Figure 5. Sub-boundaries in one mono-crystal of Fe. The effect of dislocations is consumed with the pass of time. The limit of meta-stability is when . Here we have considered a relaxation time
. Here we have considered a relaxation time , for single crystals of Fe, as measured from the quasi-relaxation data [22].
, for single crystals of Fe, as measured from the quasi-relaxation data [22].
which characterize the hyperbolic part of all quasi-relaxation function in the analytic function given by Equation (31). Then the generalized functional of stress-deformation to the quasi-relaxation functions given in the Equation (21), takes the form
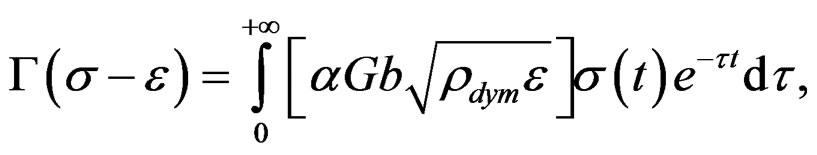 (33)
(33)
where , comes given by the Orowan Equation (22). The results obtained before, we use to the analysis of the curves of stress in steel of low Carbon of type 08KP, in normalised state [1,14]. In the Figure 6, it is shown the curves of stress to two structural states of the steel. Observe that the curves of the corresponding signal to each specimen
, comes given by the Orowan Equation (22). The results obtained before, we use to the analysis of the curves of stress in steel of low Carbon of type 08KP, in normalised state [1,14]. In the Figure 6, it is shown the curves of stress to two structural states of the steel. Observe that the curves of the corresponding signal to each specimen , have the foreseen behavior and bounded by the logarithmic curves of the Equation (24), in a short interval of deformation.
, have the foreseen behavior and bounded by the logarithmic curves of the Equation (24), in a short interval of deformation.
The Figure 7, in the I + II, of the deformation field correspond to the elastic zone of the helical dislocations, in relation with the steel 08KP, showed in the Figure 6, with a surplus of 1350 Mpa. In the stage III, of the deformation field is observes an accumulation of constant type due to sliding of the dislocations like such. This behavior is observed with a constant and soft sliding to the other sample of steel (Figure 6, curve in green). In the curve in blue of the Figure 6, the constant and soft sliding is almost null due to the accumulation of elastic sliding of the stage I, and II. That takes to the stage V, of form very early. Our functional of energy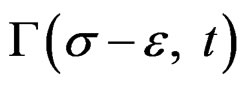 , to the curve in blue of the Figure 6, shows that the interval of duration of elastic dislocations is very short and invest little energy although accumulative that, is to say, exist the superposition phenomena of dislocations of the two types.
, to the curve in blue of the Figure 6, shows that the interval of duration of elastic dislocations is very short and invest little energy although accumulative that, is to say, exist the superposition phenomena of dislocations of the two types.
The increase of velocity of the accumulating could

Figure 6. The curves of the before samples in regime of temperature of T = 20˚C, obtains an image of the space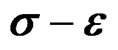 , in their stages III and V, (see Figure 7), of the corresponding levels of scales of the loss of stability of the slide in poly-crystal metals under stress.
, in their stages III and V, (see Figure 7), of the corresponding levels of scales of the loss of stability of the slide in poly-crystal metals under stress.
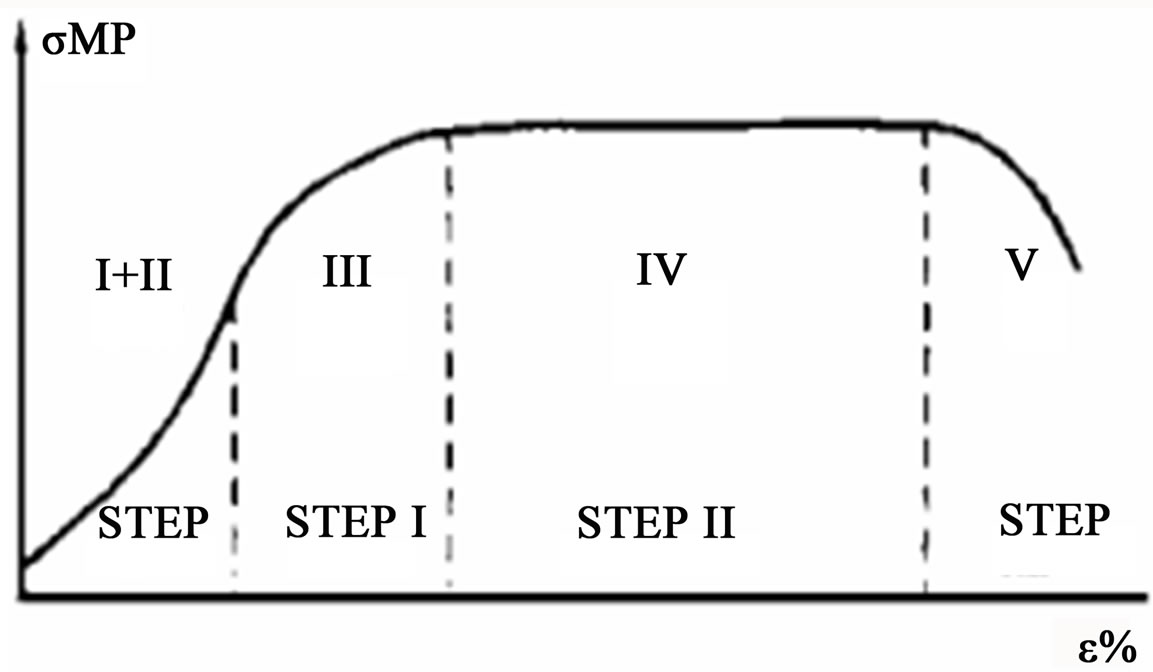
Figure 7. Scheme of the stages of the curve “stress-deformation”, and the corresponding levels of scales of the loss of stability of the slide in poly-crystal metal under stress [14].
have an energy consumption of the 2.5%, having a logarithmic growth in the stress. Now well, in the Figure 5, it is shows a mono-crystal of Fe, after of the quasi-relaxation in which is observes fine segregations belonging to the phase II, established in the Figure 7, in an amount of defect of agglomeration. Their corresponding spectral curves characterize their coefficient of behavior of segregation, by the theory explained through of the integral transforms with the specialized use in each case. It is can to note that the multiplication of dislocation in a monocrystal of Fe, occurs at least to a stress of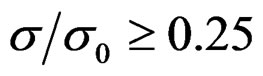 .
.
These results throws interesting properties of the materials in regime of quasi-relaxation that cans be used in devices submitted to continuous stresses and that not produces an alteration of the crystalline structure major to the apparent dislocation sliding in quasi-relaxation. The energy in such case can be used to a metal transform that be technologically useful, such and like it is had foreseen by the bounds given in the Equation (24), [20]. The reader cans re-emitters to the lecture of [20], and study the integral operator to this study.
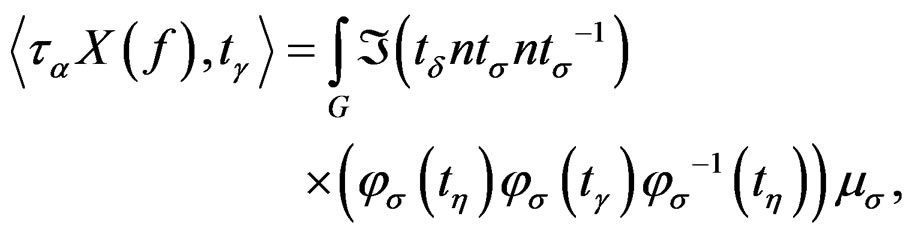 (34)
(34)
In where it is gives the classification of the technologies using these operators and the integral operators explains in this work.
Here we consider to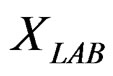 , like the space of rehearsals or tests of the technological process (in our porpoises experiments of quasi-relaxation and implications in metal processing). We endow
, like the space of rehearsals or tests of the technological process (in our porpoises experiments of quasi-relaxation and implications in metal processing). We endow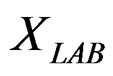 , of a structure of Hilbert space also of the Hamiltonian structure that have due at their ergodicity (see ergodic theory of dynamical systems, [3]), then the space of true propositions verified in
, of a structure of Hilbert space also of the Hamiltonian structure that have due at their ergodicity (see ergodic theory of dynamical systems, [3]), then the space of true propositions verified in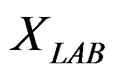 , satisfies
, satisfies
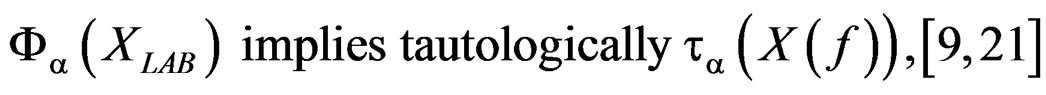 (35)
(35)

 ,
,  , the transfer technologies operator (technologies transferred from country to country (for example, the composites, or alloys)), and where belonging to a class (that is to say, applicable to a certain class of technologies), they are isometrics from
, the transfer technologies operator (technologies transferred from country to country (for example, the composites, or alloys)), and where belonging to a class (that is to say, applicable to a certain class of technologies), they are isometrics from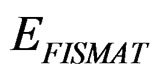 , (space of knowledge in physic and mathematics of the matter [9], of engineering study(in our case material physics)), to
, (space of knowledge in physic and mathematics of the matter [9], of engineering study(in our case material physics)), to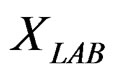 , having that for a variety of technological applications and with the relevancy of considering widespread measures of the technological applications is complies the Equation (34).
, having that for a variety of technological applications and with the relevancy of considering widespread measures of the technological applications is complies the Equation (34).
4. Pair of Quasi-Relaxation Transforms
In our study is evident a bi-univocally correspondence between the quasi-relaxation function and their spectra through of the corresponding transformation that is establishes into the space of the material. By functional analysis it is can prove the uniquely of this transformation, and using the characteristic of energy given by our generalized functional given by the Equation (20), that involves the Laplace transform [9,17], that expresses the action of the viscous-elasticity phenomena into the quasirelaxation process, we can obtain un pair of integral transforms to this study.
Considering that in the research realised on quasi-relaxation in metallic specimens [1,17,20,22], it has been achieved identify to the condition of meta-stability that define univocally a state of quasi-relaxation [21], through of plastic deformation expressed by the plastic work (theorem 2.1), that invert the system of machine-specimen to the deformation of the nano-crystalline structure of the metals (to see Figure 8) risking the state of the curves (the history of deformation under stress , to along of time t), like the given by the Equation (21), then
, to along of time t), like the given by the Equation (21), then

Figure 8. Dislocation structure of a mono-crystal of Molybdenum during the plastic deformation. The functional measures of the plastic energy of the deformation in regime of quasi-relaxation of a monocrystal with tensor C[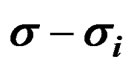 ], are the maclas. The mono-crystal was deformed into the column of the HV ´25,000.
], are the maclas. The mono-crystal was deformed into the column of the HV ´25,000.
the quasi-relaxation function given by the distribution (distribution in the functional context), is
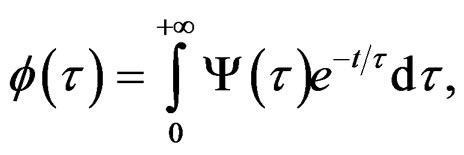 (36)
(36)
where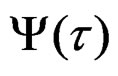 , is the density of distribution of the times of relaxation or spectra of relaxation [2,3,13]. Given that these applications conforms a class of functions
, is the density of distribution of the times of relaxation or spectra of relaxation [2,3,13]. Given that these applications conforms a class of functions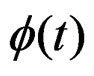 , such that [9,13]
, such that [9,13]
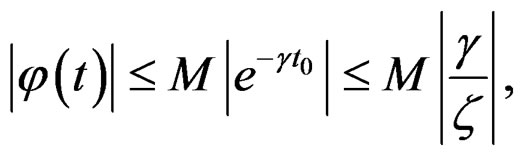 (37)
(37)
To the integral operator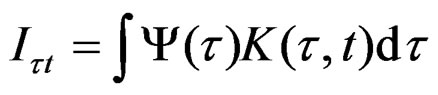 , whose nucleus is
, whose nucleus is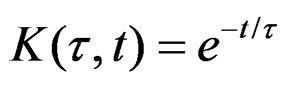 , and due to that
, and due to that
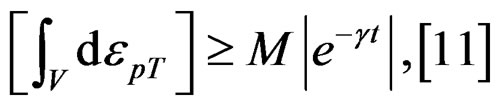 (38)
(38)
then exists two integral transforms of quasi-relaxation of the curves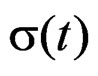 , under the regime of plastic deformation given by the Equation (10), and with the following result:
, under the regime of plastic deformation given by the Equation (10), and with the following result:
Theorem 4. 1. (Bulnes F., Stropovsvky Y., and Yermishkin V.) [17]. The nucleus K(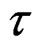 , t), defined to operator Iτt, verify
, t), defined to operator Iτt, verify 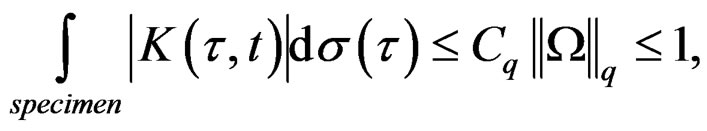
with . Then "
. Then " 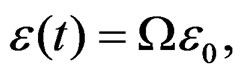 the pair of transforms are:
the pair of transforms are:
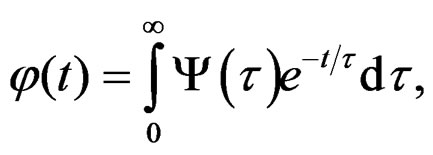 (39)
(39)
 (40)
(40)
Proof. By [9,10,12].
Corollary 4. 1. (Bulnes F. and Stropovsvky Y.). All quasi-relaxation in the stress-deformation process is a response of relaxation type with singularities in the limit after of obtains the meta-stability conditions in Mt.
Proof. First we must demonstrate that a quasi-relaxation function is a response of relaxation type. After, are necessary to show that this function have singularities in

the limit after of enter to the meta-stability conditions yet with the residual relaxation effects given by the term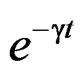 . Using the quasi-relaxation transform given by the Equation (39), and the hereditary integrals to a load given by
. Using the quasi-relaxation transform given by the Equation (39), and the hereditary integrals to a load given by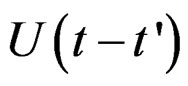 , it is has that:
, it is has that:
 (41)
(41)
Thus is a function of relaxation type, and only is relaxation into a finite interval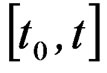 . When is carries the conditions of stress outside of this interval, we pass to the quasi-relaxation (we keep the load of deformation
. When is carries the conditions of stress outside of this interval, we pass to the quasi-relaxation (we keep the load of deformation ). Here is had used the identity
). Here is had used the identity

and also the fact of that 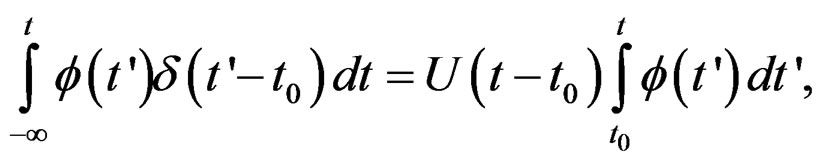
into the functional analysis [10,13].
Now well, we use an interval more wide that the given by the interval [t0, t], to involucrate the conditions to infinite given to establish the meta-stability conditions. For it, we consider a more wide domain through of consider the complex spectra of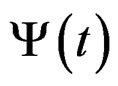 , is to say, the function
, is to say, the function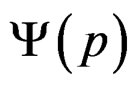 , with
, with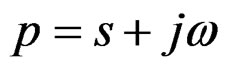 , like their analytic extension of
, like their analytic extension of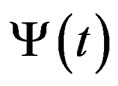 , [18], from their field of definition [9]. By the arguments of L2-sumability [10], we can be demonstrate that the singularities of
, [18], from their field of definition [9]. By the arguments of L2-sumability [10], we can be demonstrate that the singularities of , are confined to the negative part of the real axis included the origin. For other side we know that
, are confined to the negative part of the real axis included the origin. For other side we know that , is defined
, is defined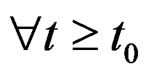 , and have been assumed to take character of a response of type of quasi-relaxation. But the singularities are poles of the meromorphic function given by
, and have been assumed to take character of a response of type of quasi-relaxation. But the singularities are poles of the meromorphic function given by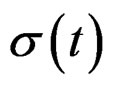 , given by the Equation (31) [18]. This poles are of first order, since any pole of superior order could elevate of term of
, given by the Equation (31) [18]. This poles are of first order, since any pole of superior order could elevate of term of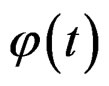 , of the form
, of the form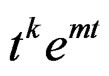 , which inconsistent with a behavior of relaxation type, like have been demonstrated to the beginning of the demonstration of this result. Then the singularities are confined in the negative part of real axis. This want to say in terms of quasi-relaxation, that in the meta-stable conditions only these singularities is sees reflected in the imaginary part of
, which inconsistent with a behavior of relaxation type, like have been demonstrated to the beginning of the demonstration of this result. Then the singularities are confined in the negative part of real axis. This want to say in terms of quasi-relaxation, that in the meta-stable conditions only these singularities is sees reflected in the imaginary part of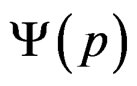 . Relating the two quasi-relaxation spectra (is to say the
. Relating the two quasi-relaxation spectra (is to say the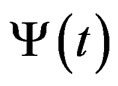 , and their complex extension), we have by the Carson transform [2,11], that:
, and their complex extension), we have by the Carson transform [2,11], that:
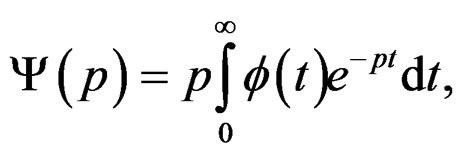 (42)
(42)
and their inverse:
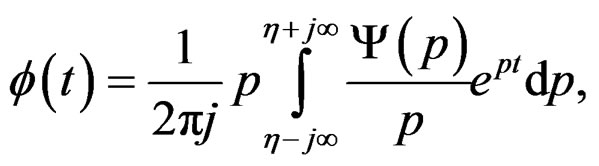 (43)
(43)
The singularities of , must be considered like simple poles (due to that the
, must be considered like simple poles (due to that the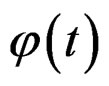 , must be character like response of type quasi-relaxation yet in the conditions to infinite). Then could be given by the sum of terms of the form
, must be character like response of type quasi-relaxation yet in the conditions to infinite). Then could be given by the sum of terms of the form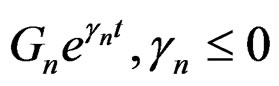 , where the sum could be finite or infinite. This can be writing in terms by the quasi-relaxation spectra like:
, where the sum could be finite or infinite. This can be writing in terms by the quasi-relaxation spectra like:
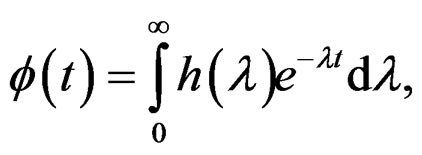 (44)
(44)
with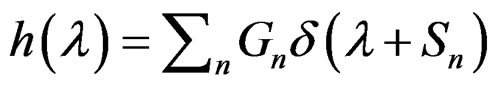 , (that is an of the solutions proposed in the Table 1), and given that by the hereditary integrals a quasi-relaxation function is precisely the function of relaxation type obtained by
, (that is an of the solutions proposed in the Table 1), and given that by the hereditary integrals a quasi-relaxation function is precisely the function of relaxation type obtained by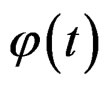 .
.
An important characteristic of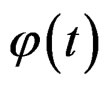 , is that is a monotonic non-decreasing function and have not oscillatory terms. This goes agree to the observations of the curves of stress-deformation schematized in the Figure 7.
, is that is a monotonic non-decreasing function and have not oscillatory terms. This goes agree to the observations of the curves of stress-deformation schematized in the Figure 7.
Then in the meta-stability conditions (after the simple relaxation), that is to say with quasi-relaxation, the function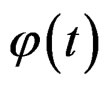 , takes the form, consider the complex extension of their spectra by the Equation (40):
, takes the form, consider the complex extension of their spectra by the Equation (40):
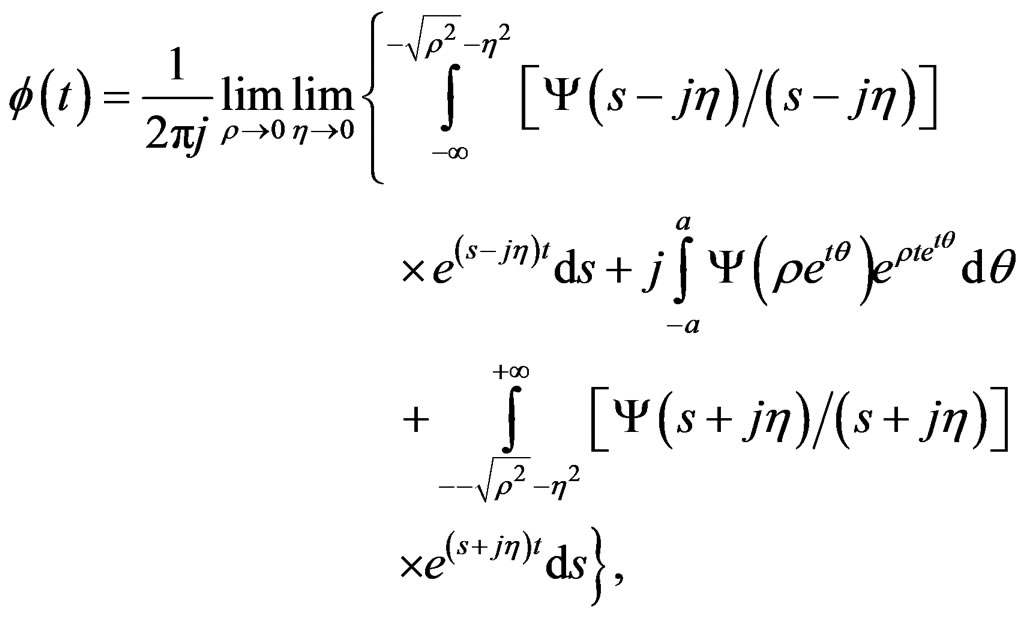 (45)
(45)
Always with .
.
The second term of the Equation (45) yields
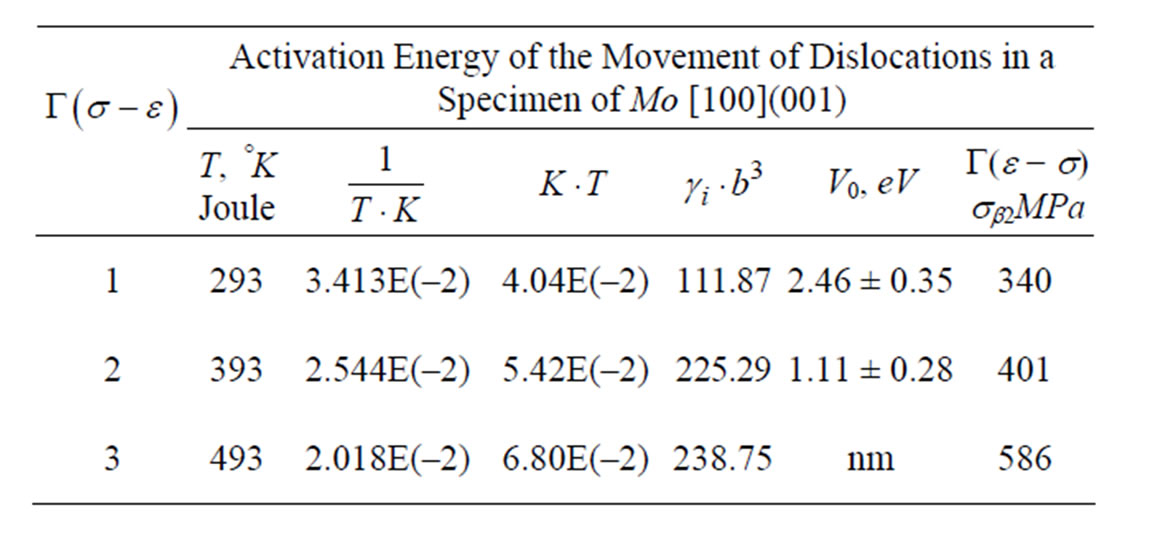
Table 1.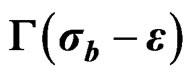 , with.
, with. , in x = 0, to an interval [0, 100], seconds using the method of the integral functional [17],
, in x = 0, to an interval [0, 100], seconds using the method of the integral functional [17], .
.
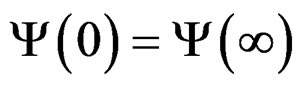 . The first and third terms can be combined, using the fact that
. The first and third terms can be combined, using the fact that , of p-conjugate equals the conjugate of
, of p-conjugate equals the conjugate of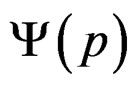 , to give:
, to give:
 (46)
(46)
That is:
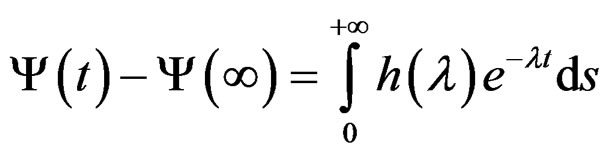 (47)
(47)
Is to say, it is conserves the relaxation characteristic to our quasi-relaxation function, yet after the simple relaxation and with their singularities. This has proved the result.
Of the Equation (44), it is had calculated [10,11,13], that
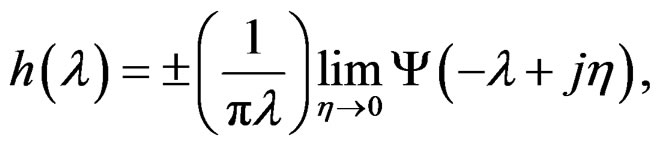 (48)
(48)
This last spectrum appears in the study of the relaxation in polymeric materials like hard rubbers. But this is equivalent to spectra due to the plastic energy that is accumulated in metals in the quasi-relaxation process before of the dislocations, save the multiplicative coefficient of dislocations 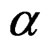 [21].
[21].
Our quasi-relaxation spectrum for a re-scaling with the coefficient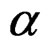 , given by
, given by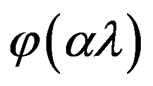 , [9], is continuous on
, [9], is continuous on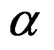 , over the region of the dislocations. If it is applies to a function characterized by simple poles it will yield zero for
, over the region of the dislocations. If it is applies to a function characterized by simple poles it will yield zero for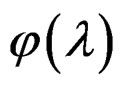 , except at the poles where
, except at the poles where , goes to infinity. It is recovers the relaxation remains in the singularities by the quasi-relaxation function (to see Figure 9).
, goes to infinity. It is recovers the relaxation remains in the singularities by the quasi-relaxation function (to see Figure 9).
The same procedure can be used to define the retardation spectrum from the relation between
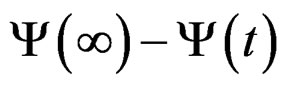
and its transform, where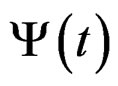 , is the recoverable part of the creep function
, is the recoverable part of the creep function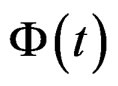 , [2, 11].
, [2, 11].
Using the Radon transform in their version like transform of dimensions, [19], we can compute distinct values
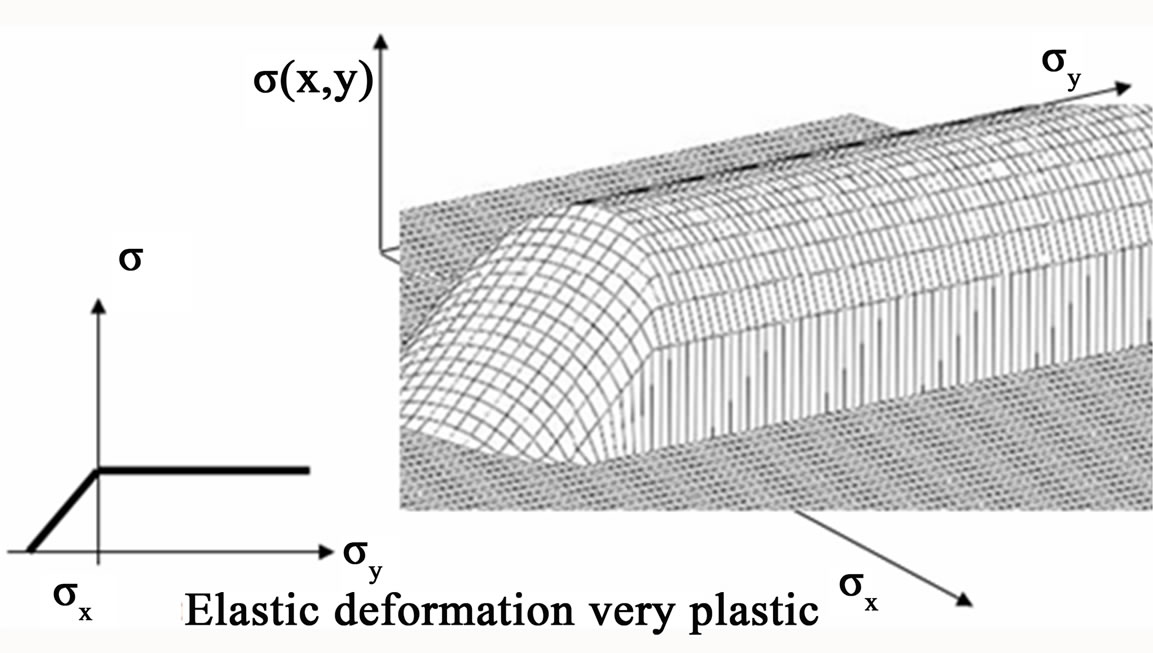
Figure 9. Half-infinite surface of localized plastic deformation (for example the mono-crystal of Fe of Figure 5).
of some metals series (see Table 2), using an appropriate percolation [23]. The process to compute consist in rewrites the transform of dimensions for this case like:
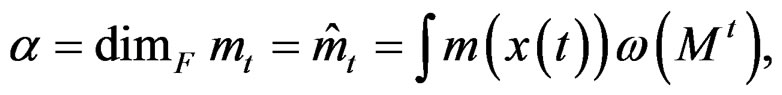 (49)
(49)
considering to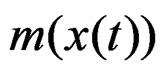 , a function that depends of the geometrical action of the curves graphed by the experiments under quasi-relaxation conditions of the specimen
, a function that depends of the geometrical action of the curves graphed by the experiments under quasi-relaxation conditions of the specimen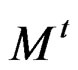 , in the fractal form applied to a particle
, in the fractal form applied to a particle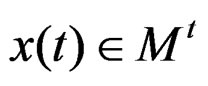 , [23], and
, [23], and
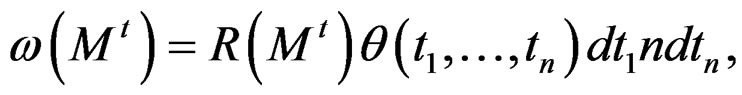 (50)
(50)
is the fractal volume of specimen, and R(Mt), is the fractal density of the space Mt. In our case the transform of dimension takes the fractal dimension defined by values:
 = {evaluation in quasi-relaxation times of analytic curves of maximum increasing of segregation by dislocations in quasi-relaxation regime to each metal}
= {evaluation in quasi-relaxation times of analytic curves of maximum increasing of segregation by dislocations in quasi-relaxation regime to each metal}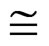 {maximum increasing of plastic energy to each metal} =
{maximum increasing of plastic energy to each metal} =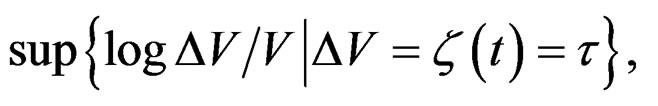 (51)
(51)
Example 4.1. Consider a specimen the Ag, of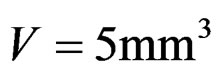 , which have an area of exposition under quasi-relaxation of 4mm2, where it is has applied a stress of 0.5 Kgs/mm2. Considering their fractal dimension using the space of analytic curves given by
, which have an area of exposition under quasi-relaxation of 4mm2, where it is has applied a stress of 0.5 Kgs/mm2. Considering their fractal dimension using the space of analytic curves given by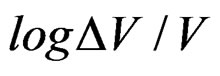 , with fractal measure
, with fractal measure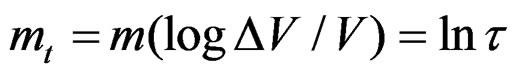 , where
, where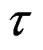 , is the relaxation time. The
, is the relaxation time. The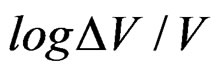 , can be write in terms of distribution of times of relaxation like
, can be write in terms of distribution of times of relaxation like
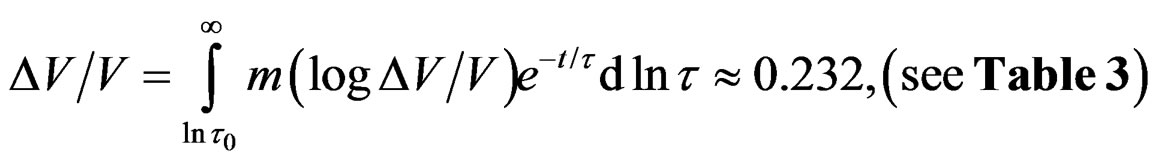 (52)
(52)
where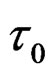 , is a microscopic time, due of the microscopic effects of activation energy to dislocations [12]. Observe that the Equation (48), is of the class of one of these the calculated by transforms in the Table 2. Now well,
, is a microscopic time, due of the microscopic effects of activation energy to dislocations [12]. Observe that the Equation (48), is of the class of one of these the calculated by transforms in the Table 2. Now well, 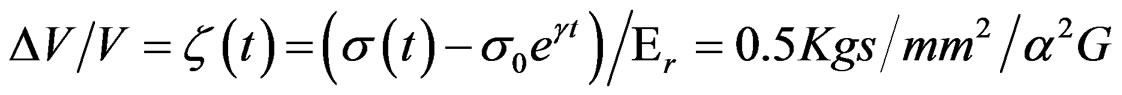 , [5]. G, is the elastic constant that to this case takes the value 85.6 (Cizalle Modulus to Ag), [2]. The functional integral given by the Equation (48), have the value 0.232, like a quasi-relaxation (see Table 3).
, [5]. G, is the elastic constant that to this case takes the value 85.6 (Cizalle Modulus to Ag), [2]. The functional integral given by the Equation (48), have the value 0.232, like a quasi-relaxation (see Table 3).
Finally
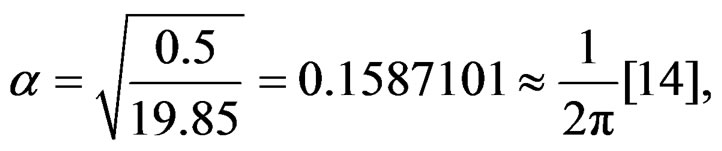 (53)
(53)
where the value 19.85, correspond to the equivalent , to Ag, used to study of curves of flux due to deformation field [14,15], to the group of metals of curves with coordinates “
, to Ag, used to study of curves of flux due to deformation field [14,15], to the group of metals of curves with coordinates “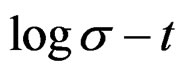 ”. These curves characterize the fractals in the fractal measure
”. These curves characterize the fractals in the fractal measure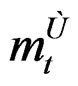 , obtained by the Equation (48).
, obtained by the Equation (48).
Using the energy bounds foreseen in the Equation (24), and the 2-norm of our spectra energy, we have that the Equation (49), can to take the form:

Table 2. Example of quasi-relaxation integral transforms table considering the factor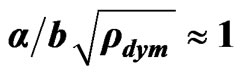 , and using the substitution
, and using the substitution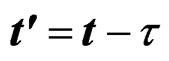 .
.
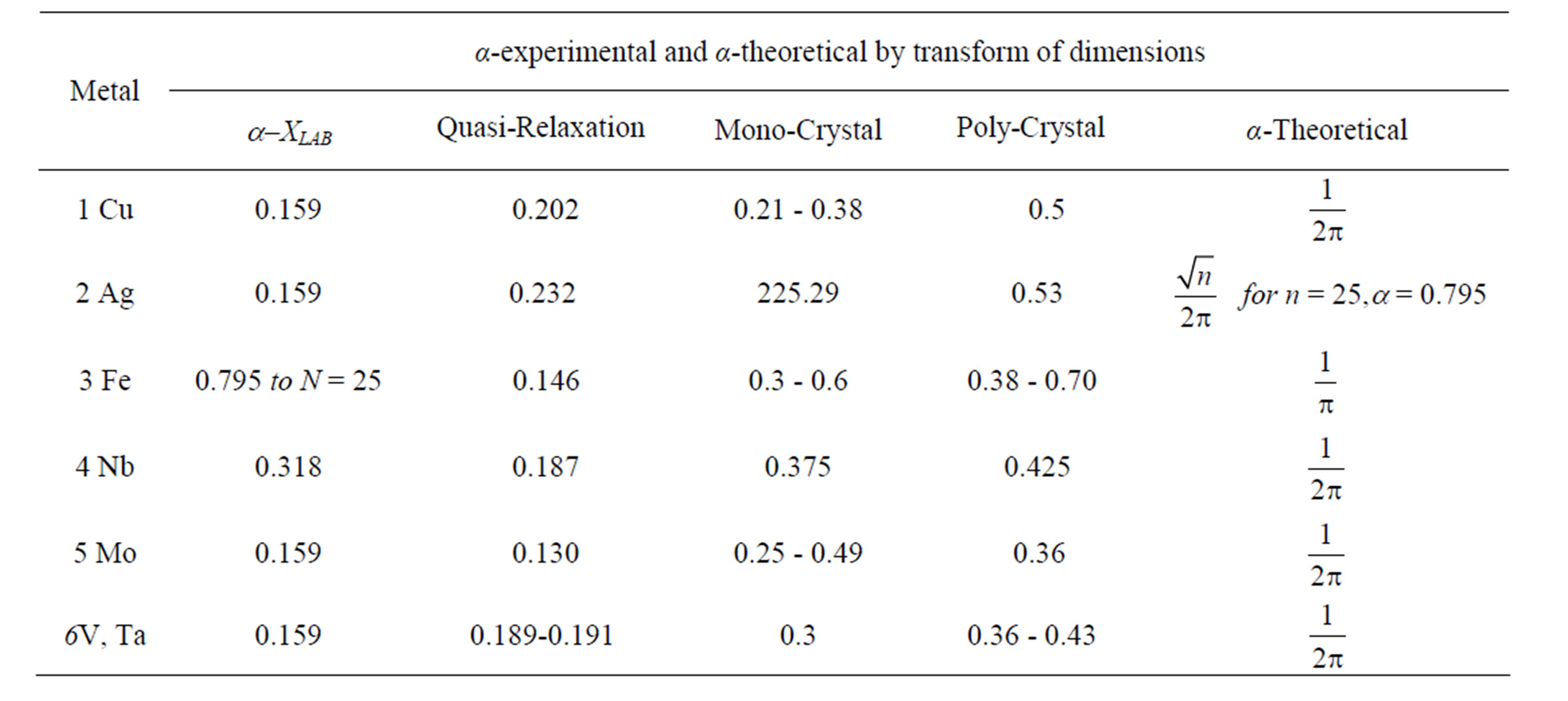
Table 3. Multiplicative dislocations coefficient [21].
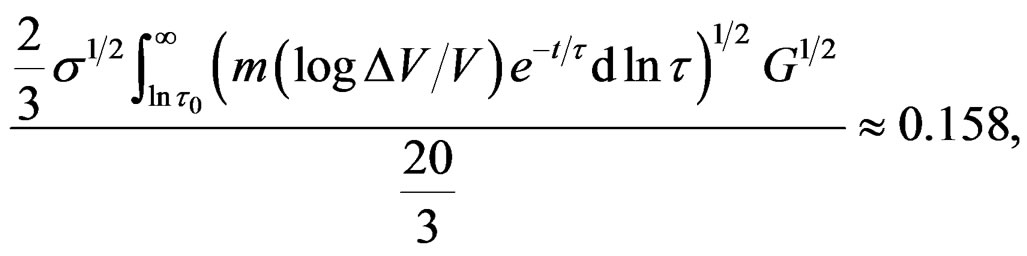
which is not a simple coincidence, since 2/3, is a the factor into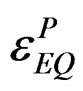 , always present due to that the maximum value of plastic deformation that is gives in
, always present due to that the maximum value of plastic deformation that is gives in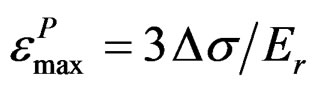 , with
, with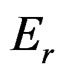 , the value of the modulus of normal elastic relaxation.
, the value of the modulus of normal elastic relaxation.
Then the bounds given by the Equation (24), to the property of the coefficient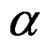 , they can be estimated under the integral inequality (under 2-norm to the plastic energy always present in quasi-relaxation process):
, they can be estimated under the integral inequality (under 2-norm to the plastic energy always present in quasi-relaxation process):

with the values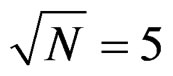 , and
, and
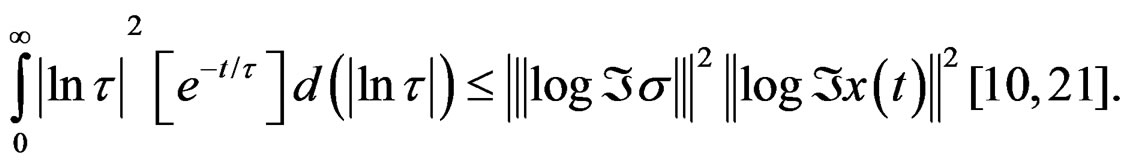
5. Meromorphic Curves in the Quasi-Relaxation Spectra
The spectral function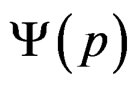 , have cuts in the quasirelaxation curves due to enters of dislocations phase due increasing of plastic energy in all crystals of the metal (macla of energy). These curves are analytic in all domain except in singular points
, have cuts in the quasirelaxation curves due to enters of dislocations phase due increasing of plastic energy in all crystals of the metal (macla of energy). These curves are analytic in all domain except in singular points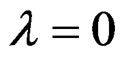 , or
, or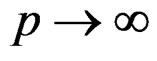 , when the quasi-relaxation spectra satisfies with help of the Laplace transform that
, when the quasi-relaxation spectra satisfies with help of the Laplace transform that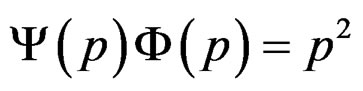 , where the function
, where the function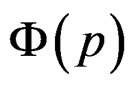 , Figures 10 and 11, are the fluency spectra corresponding to the fluency function that appear after of increasing too much to the sliding dislocations (see example 3.2 of this work), being possible detect the plastic deformation to macroscopic level. The factor
, Figures 10 and 11, are the fluency spectra corresponding to the fluency function that appear after of increasing too much to the sliding dislocations (see example 3.2 of this work), being possible detect the plastic deformation to macroscopic level. The factor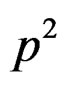 , define the duplicity of these actions through of relation between both functions [2], (see the corresponding Carson transform to the two functions
, define the duplicity of these actions through of relation between both functions [2], (see the corresponding Carson transform to the two functions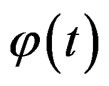 , and
, and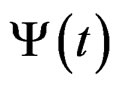 , and their functional relation, [11]).
, and their functional relation, [11]).
6. Conclusions
The introduction of the integral transforms in the quasi-relaxation study helps to establish with major precision the limits of the existence of the quasi-relaxation of a material summated to a constant load in an interval to along of the time, before off to risk arrive to the accumulation plastic energy necessary to the crystalline dislocations in metals and after of this stage. The quasi-relaxation spectra also of support analytic information on the meromorphic behavior of the quasi-relaxation curves use to obtain information that can be codified in the field of the complex frequencies to their possible material decoding and with it open the possibility of manipulate in this meta-stable state to the material, being able to fill codes that can facilitate the transformation of the metals and their alloys [17,22].
The quasi-relaxation conditions help to obtain special properties of the metals, likewise some alloys. For example, an of the alloys obtained to the program of spatial research in Russia, with the object of obtain metals with anti-corrosive memory and lightness (and the same time to support major temperatures to 650˚C, for example, in the turbines of the reaction airplanes), [15], are the experiments on an alloy of Zr + 2.5% Nb, after of the quasi-relaxation in the which is observes fine segregations of the phase II, in a considerable count of effects of agglomeration.
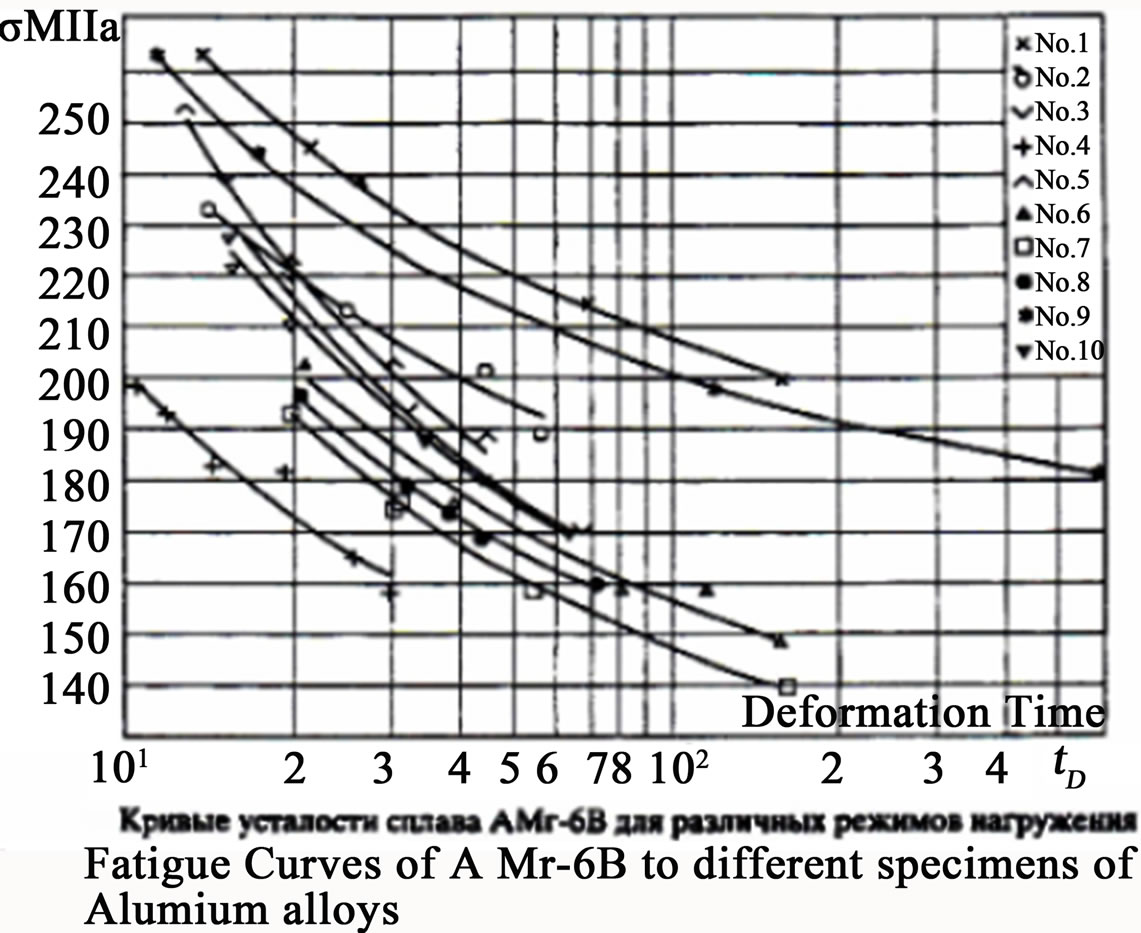
Figure 10. Meromorphic curves of quasi-relaxation. These are obtained by experiments of metal specimens under big stress obtaining [21]. These experimental results proved that our quasi-relaxation functions have ideal behavior very similar to the obtained one earlier (compare these curve with the curves of the Figure 4), except in the singularities due to the entered of the hyperbolic part contemplated of the functions from Equation (31). These curves measure fatigue for big stress after of the quasi-relaxation (appear the singularities).
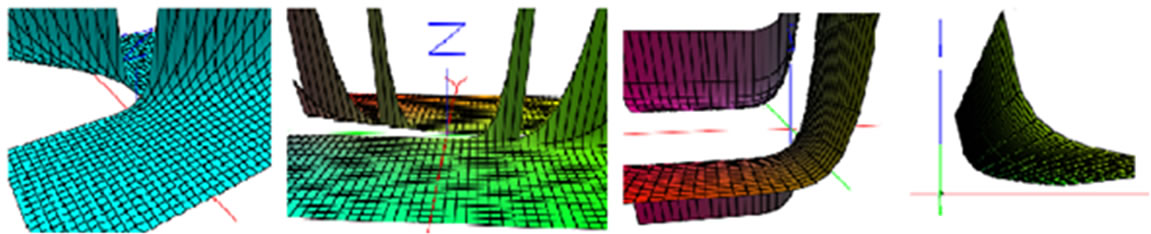 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 11. (a)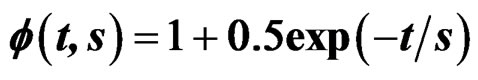 , with stress tensor
, with stress tensor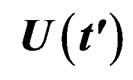 , with
, with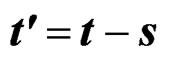 . (b) Surface of quasi-relaxation function
. (b) Surface of quasi-relaxation function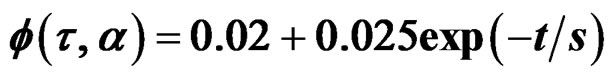 . Observes the curves of quasi-relaxation in the plane XZ, accord of the curves predict in Figure 4, after of a fatigue to Aluminum with Magnesium (Yermishkin). (c) Quasi-relaxation surface with quasi-relaxation curves in black such like the predicted in Figure 2, with stress
. Observes the curves of quasi-relaxation in the plane XZ, accord of the curves predict in Figure 4, after of a fatigue to Aluminum with Magnesium (Yermishkin). (c) Quasi-relaxation surface with quasi-relaxation curves in black such like the predicted in Figure 2, with stress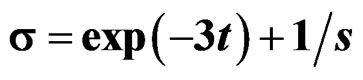 , in the plane YZ, with the fatigue time t = 50 seconds to AMg—6B. (d)
, in the plane YZ, with the fatigue time t = 50 seconds to AMg—6B. (d)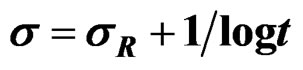 , with
, with , Observes the curves of quasi-relaxation in the plane YZ, accord of the curves predict in Figure 4, after of the fatigue to t = 50 seconds.
, Observes the curves of quasi-relaxation in the plane YZ, accord of the curves predict in Figure 4, after of the fatigue to t = 50 seconds.
In the Russian aerospace industry they are studying diverse metallic alloys to establish ranges of meta-stability in the deformation fields produced by the materials proposed [15,16]. It is wants to obtain lightness materials and more resistant to the corrosion and deformations. Go of remains to mention that in the last researches, considering the analytic characterization proposed by Bulnes and Yerminshkin [20,21], it is wants like priority the development of precise methods on the multiple manipulations that we can realize of the metals in the meta-stable regime using the pre-disposition that these presents in accumulate energy to can realize actions like re-programming their nano-crystal structure and think in the possibility of obtain nano-technological transformations of the materials [20,22], using their spectral encoding. Finally we believe that the use of inverse methods of the functional analysis in material physics can to help to development and obtaining of a complete theory of quasi-relaxation to characterization and transformation of materials of any nature [20,22].
7. Acknowledgements
One We are grateful with the research data bank from Baikov Institute of Research in Material Sciences and Metallurgy, and the Department of Research in Mathematics and Engineering of TESCHA, for the for the support offered during the achievement of the work.
REFERENCES
- V. S. Ivanova and V. Yermishkin, “Prochnost i Plastichnost Tugoplavkij Metallov i Monokristallov,” Metallurgiya, Vol. 1, Moscow, 1976, pp. 80-101.
- B. Gross, “Mathematical Structure of the Theories of Viscoelasticity,” Hermann and Cie, Paris, 1953.
- J. Casey and P. M. Naghdi, “Constitutive Results for Finitely Deforming Elastic-Plastic Materials,” In: K. J. Willam, Ed., Constitutive Equations: Macro and Computational Aspects, Cap I and II ASME, New Orleans, 1984.
- T. Imura, “Dynamic Study of the Dislocation Progress of the Plastic Deformation and Fracture by High Voltage Electron Microscopy,” Academic Press, London-New York, 1974.
- C. Truesdell, “Rational Mechanics,” Academic Press, New York, 1983.
- J. E. Marsden and R. Abraham, “Manifolds, Tensor Analysis and Applications,” Addison-Wesley, Massachusetts, 1983.
- L. Landau and E. M. Lifshitz, “Mechanics, Theoretical Physics Vol. I,” Addison-Wesley, New York, 1960.
- C. Truesdell and R. A. Toupin, “The Classical Field Theories,” In: R. G. Lerner, Ed., Encyclopedia of Physics, Chapter 1, Springer-Verlag, Berlin, 1960.
- F. Bulnes, “Treatise of Advanced Mathematics: Analysis of Systems and Sign,” Monograph Vol. 1, 1st Edition, Faculty of Sciences, Universidad Nacional Autónoma de México, Mexico, 1998.
- B. Simon and M. Reed, “Mathematical Methods for Physics: Functional Analysis,” Vol. 1, Academic Press, New York, 1972.
- J. Dieudonnè, “Tratise on Analyse,” Vol. 4, Academic Press, New York, 1978.
- J. P. Hirth and J. Lothe, “Theory of Dislocations,” McGraw-Hill Book Company, Institute of Physics, Oslo University, New York, 1972.
- W. Rudin, “Real and Complex Analysis,” Academic Press, New York, 1969.
- R. Jonikomb, “Plasticheskaya Deformaciya,” Mir Metallov, Moscu, 1972.
- V. Yermishkin and V. Polin, “Monokristally Tugoplavkij i Redkij Metallov, Splavov i Soyedininii,” Nauka, Moscow, 1977, pp. 157-159.
- E. M. Savitsky and V. S. Ivanova, “Struktura i Svoystva Monokristallov Tugoplavkij Metallov,” Nauka Academy of Sciences Publisher, Moscow, 1973, pp. 139-143.
- F. Bulnes, V. Yermishkin and E. Toledano, “Constitutive Equations of the Stress-Strain Tensor for a Metal Specimen Rehearsal in Quasi-Relaxation Regime and Their Generalized Functional of Energy,” Proceedings of the 2nd CIMM, Vol. III, Department of Mechanical Engineering, Universidad Nacional de Colombia, Bogota, 8-9 October 2009, pp. 12-0001-1-0010.
- A. I. Markusevich, “Theory of Analytic Functions. Vol. I, and II,” Mir, Moscu, 1980.
- F. Bulnes and M. Shapiro, “On General Theory of Integral Operators to Analysis and Geometry,” IM/UNAM, SEPI/IPN Monograph in Mathematics, 1st Edition, P. Cladwell, Mexico, 2007.
- F. Bulnes, “Analysis of Prospective and Development of Effective Technologies through Integral Synergic Operators of the Mechanics,” Proceedings in Mechanical Engineering of 14a. CCIA-CIM ISPJAE, Vol. 3, Habana, 1-5 December 2008, pp. 1021-1029.
- F. Bulnes, V. Yermishkin and P. Tamayo, “New Method of the Characterization of Materials of Engineering: Quasi-Relaxation, Science of Materials,” Proceedings of Appliedmath I, Mexico, 22-24 September 2005, pp. 240- 254.
- V. N. Geminov and V. Yermishkin, “Quasirelaxation as a Powerful Method of a Steady-State Creep Characteristics Prediction,” Proceeding of II International Conference on Mechanical Behavior of Materials, Vol. 1, Boston, 16-20 August 1976, pp. 138-154.
- B. West, M. Bologna and P. Grigolini, “Physics of Fractal Operators,” Institute for Non-Linear Science, Springer, New York, 2003.
Technical Notation
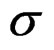 —Stress tensor applied in the quasi-relaxation process in the machine-specimen.
—Stress tensor applied in the quasi-relaxation process in the machine-specimen.
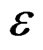 —Deformation tensor applied in the quasi-relaxation process in the machine-specimen.
—Deformation tensor applied in the quasi-relaxation process in the machine-specimen.
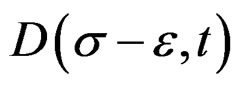 —Topological vector space of stress-deformation curves. In this characteristic of space of continuum media we can have two cases of study: In the limit to dislocations and when it gives the dislocations.
—Topological vector space of stress-deformation curves. In this characteristic of space of continuum media we can have two cases of study: In the limit to dislocations and when it gives the dislocations.
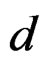 —Inelastic module tensor of the tensor.
—Inelastic module tensor of the tensor.
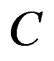 —Elastic module tensor of the tensor.
—Elastic module tensor of the tensor.
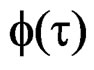 —Function of quasi-relaxation spectra.
—Function of quasi-relaxation spectra.
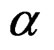 —Dislocation multiplicative coefficient, dependent on a number of physical conditions.
—Dislocation multiplicative coefficient, dependent on a number of physical conditions.
M—Specimen.
t —Time of relaxation.
L—Lagrangian operator.
b—Burgers number, which represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice.
Mt—Specimen under some temporal mechanical transformation.
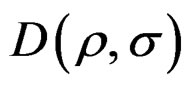 —Topological tensor space of stress or stress space. Into this space succeeds the deformations by the deformation tensor.
—Topological tensor space of stress or stress space. Into this space succeeds the deformations by the deformation tensor.
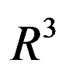 —Real ordinary space or 3-dimensional real space.
—Real ordinary space or 3-dimensional real space.
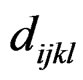 —Indicial form of inelastic module tensor d. It use to realize the orthogonal transforms by orthogonal group of Euclidean space
—Indicial form of inelastic module tensor d. It use to realize the orthogonal transforms by orthogonal group of Euclidean space .
.
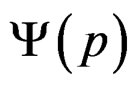 —Complex extension of quasi-relaxation spectra of
—Complex extension of quasi-relaxation spectra of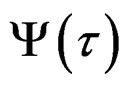 . Is the complex spectra of the quasi-relaxation function
. Is the complex spectra of the quasi-relaxation function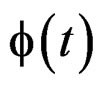 .
.
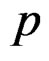 —Complex frequency given by
—Complex frequency given by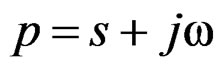 . This is the variable of all the class of Laplace transforms, in the dynamical of the physical systems in our analysis of quasi-relaxation.
. This is the variable of all the class of Laplace transforms, in the dynamical of the physical systems in our analysis of quasi-relaxation.
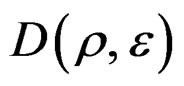 —Topological tensor space of deformation or deformation space. Into this space occurs the deformations by the stress tensor.
—Topological tensor space of deformation or deformation space. Into this space occurs the deformations by the stress tensor.
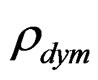 —Density of the specimen on the dislocating dynamics.
—Density of the specimen on the dislocating dynamics.
 —Direct sum of functional spaces or vector topological spaces. In this case, our spaces are the of tensors and continuum media of the material of the specimen used.
—Direct sum of functional spaces or vector topological spaces. In this case, our spaces are the of tensors and continuum media of the material of the specimen used.
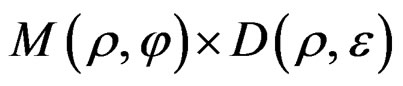 —Space of test of specimen-machine. Correspond to the surface on which it applies the stress and where occurs the deformation in the quasirelaxation process.
—Space of test of specimen-machine. Correspond to the surface on which it applies the stress and where occurs the deformation in the quasirelaxation process.
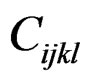 —Indicial form of elastic module tensor
—Indicial form of elastic module tensor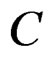 . It uses to realize the orthogonal transforms by the orthogonal group of Euclidean space
. It uses to realize the orthogonal transforms by the orthogonal group of Euclidean space .
.
L 2(G)—Space of measures obtained by the signals space 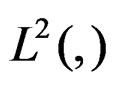 in the instrumental of measurements.
in the instrumental of measurements.
G—Quasi-relaxation curve.
 —Group of actions on crystal structure of the specimen.
—Group of actions on crystal structure of the specimen.
 —Constants of elastic module.
—Constants of elastic module.
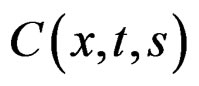 —Matrix of Cauchy tensor to 1-dimensional behavior of deformation tensor.
—Matrix of Cauchy tensor to 1-dimensional behavior of deformation tensor.
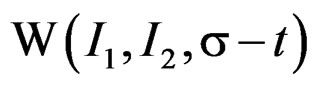 —Matrix of relaxation deformations.
—Matrix of relaxation deformations.
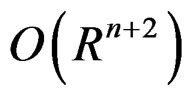 —Group of orthogonal transforms due to Lagrangian actions on tensor components of the deformation tensor. Is on
—Group of orthogonal transforms due to Lagrangian actions on tensor components of the deformation tensor. Is on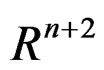 , since each tensor is in function of two tensors, for example:
, since each tensor is in function of two tensors, for example: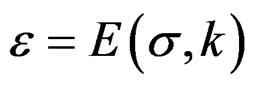 , which is a differentiable function on space
, which is a differentiable function on space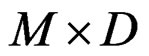 .
.
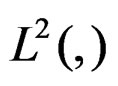 —Space of signals detected by instruments of measure in the panel of machine-specimen in the quasirelaxation system [19].
—Space of signals detected by instruments of measure in the panel of machine-specimen in the quasirelaxation system [19].
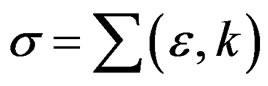 —Surface subject to the stress applied by a system of specimen-machine. This surface is defined like a function of their deformation suffered by the stress and by the state conditions (thermal and media conditions), to which is subject.
—Surface subject to the stress applied by a system of specimen-machine. This surface is defined like a function of their deformation suffered by the stress and by the state conditions (thermal and media conditions), to which is subject.
ci —Coefficients of bound of the components of elastic modulus tensor.
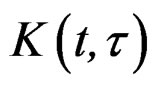 —Kernel of integral transform of quasi-relaxation.
—Kernel of integral transform of quasi-relaxation.
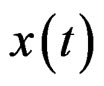 —Particle of the specimen M.
—Particle of the specimen M.
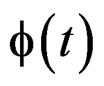 —Function of response of type relaxation.
—Function of response of type relaxation.
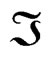 —Lagrangian action of the meta-stability in the quasi-relaxation process. The meta-stability state is risks when with the longitude lo of circuit of force of the machine remaining constant and the analytic curves have a hyperbolic component of decreasing of fall of stress due to plastic energy in nano-crystal level.
—Lagrangian action of the meta-stability in the quasi-relaxation process. The meta-stability state is risks when with the longitude lo of circuit of force of the machine remaining constant and the analytic curves have a hyperbolic component of decreasing of fall of stress due to plastic energy in nano-crystal level.
 —Signal of stress tensor registered by the panel of machine-specimen and with measure on a square integrable space
—Signal of stress tensor registered by the panel of machine-specimen and with measure on a square integrable space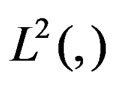 , to measures responses of the stress tensor through of their characteristic energy.
, to measures responses of the stress tensor through of their characteristic energy.
 —Signal of deformation tensor registered by the panel of machine-specimen and with measure on a square integrable space
—Signal of deformation tensor registered by the panel of machine-specimen and with measure on a square integrable space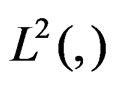 , to measurable responses of the deformation tensor through of their characteristic energy.
, to measurable responses of the deformation tensor through of their characteristic energy.
 —Is the conformal elastic tensor of
—Is the conformal elastic tensor of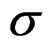 .
.
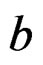 —Is the conformal inelastic tensor of
—Is the conformal inelastic tensor of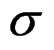 .
.
Abbreviations
MPa—Mega-Pascal.
HVTEM—High Voltage Transmission Electron Microscopic (this is a microscopic belonging to the generation of microscopic to research in nanotechnology).
ev—Electron volts.
08KP—Steel is used to make bimetallic cold-rolled strip with an Aluminum. The optimum Oxygen content of low-Carbon steels (such as grade 08KP).
˚K—Temperature Kelvin Degrees.

