Open Journal of Biophysics
Vol.4 No.1(2014), Article ID:42410,10 pages DOI:10.4236/ojbiphy.2014.41005
Does Life Need Water or Can It Be Generated by Other Fluids?
National Council of Research of Italy, Area of Pisa, Pisa, Italy
Email: pchiare@ifc.cnr.it
Copyright © 2014 Piero Chiarelli. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Piero Chiarelli. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 4, 2013; revised January 6, 2014; accepted January 13, 2014
Keywords:Order Generation; Far from Equilibrium Kinetics; Matter Self-Assembling; Maximum Free Energy Dissipation; Minimum Entropy Production
ABSTRACT
In the present work the Stochastic generalization of the quantum hydrodynamic analogy (SQHA) is used to obtain the far-from-equilibrium kinetics for a real gas and its fluid phase. In gases and their liquids, interacting by Lennard-Jones potentials whose mean distance is bigger than the quantum correlation distance and the molecular interaction distance r0, it is possible to define a Fokker-Plank type equation of motion as a function of the mean phase space molecular volume that far-from-equilibrium shows maximizing the dissipation of a part of the generalized SQHA-free energy. In the case of a real gas with no chemical reactions with small temperature gradients, the principle disembogues into the maximum free energy dissipation confirming the experimental outputs of electro-convective instability. In this case, the model shows that the transition to stationary states with higher free energy can happen and that in incompressible fluids, the increase of free energy is almost given by a decrease of entropy leading to the appearance of self-ordered structures. The output of the theory showing that the generation of order via energy dissipation, is more efficient in fluids than in gases, because of their incompressibility, which leads to the reconciliation between physics and biology furnishing the explanation why the life was born in water. The theoretical output also suggests that the search for life out of the earth must consider the possibility to find it in presence of liquid phases different from water.
1. Introduction
The missing bridge between the physics and life disciplines constitutes one of the greatest problems of science nowadays. The situation is similar to that exists between physics and chemistry at the beginning of the past century. Every scientist was intimately convinced that once the physical laws of particles belonging to the atoms were established, the chemical properties of elements should possibly be derived and explained.
With the advent of quantum mechanics, this view came to realization and the quantum physics is at the base of modern chemistry.
A similar state of fact exists between the physics and biology. The unavailability of a physical theory capable of explaining the order generation at the base of the evolution of biological system is the major obstacle to give the physical basis to biology.
One of the most known and experimentally verified laws of the physics is the second law of thermodynamics that expresses the tendency of any physical system toward the maximum possible disorder. Even verified only near the thermodynamic equilibrium, this law has lead many thinkers to a “pessimistic” view of the world and to the so-called “obscurantism” in many fields of human science.
Starting by the thirties of the last century, mainly due to the work of Prigogine, it was born in the physicists and chemists the idea that the tendency to the entropy production was a bounded process and that generation of order was possible out of the neighborhoods of thermodynamic equilibrium [1-8]. Various principles have been proposed for the self-organized regimes governed by classical linear and non-linear non-equilibrium thermodynamic laws, with stable stationary configurations being particularly investigated.
Nevertheless, an organic understanding for a long time has been unavailable. In 1945, Prigogine [1,2] proposed the “Theorem of Minimum Entropy Production” which applies only to near-equilibrium stationary state. The proof offered by Prigogine is open to serious criticism [3]. Šilhavý [4] offered the opinion that this variational principle of near-equilibrium thermodynamics does not have any counterpart in far-from-equilibrium steady states despite many claims in the literature.
Sawada postulated the principle of largest amount of entropy production [5]. He started by the work given by Malkus and Veronis [6] about the earth’s atmospheric turbulence where the principle of maximum heat current, holding in fluid mechanics, has been proven to drive the energy transport process. Sawada showed that for a given boundary condition this law corresponds to the maximum entropy production, but this inference is not ever valid.
Sawada and Suzuki showed that the maximum entropy production leads electro-convective phenomena to the maximum rate of energy dissipation. This principle was confirmed, both by numerical simulations and by experiments [8], in electro-convective instabilities. Moreover, they showed that ordered metastable states were visited by the system with a living time proportional to the rate of energy dissipation.
The rate of dissipation of energy appeared for the first time in Onsager’s work [7] on this subject. An extensive discussion of the possible principles of maximum entropy production and/or of dissipation of energy was given by Grandy [9]. He found difficulty in defining the rate of internal entropy production in the general case, showing that sometimes, for the prediction of the course of a process, the maximum rate of dissipation of energy may be more useful than that of the rate of entropy production.
Nowadays, the debate about the principle of maximum free energy dissipation (MFED) and the Prigogine’s one comes to a possible solution. The author has shown that in the frame of the quantum stochastic approach of hydrodynamic analogy [10-13], it is possible to define a phase space Wigner-type distribution functions. In (classical) phases, the mean of inter-particle distance is bigger than the distance over which the quantum correlations take place. It can lead to the definition of an energy function (named stochastic free energy) whose dissipation is at maximum during the out of equilibrium relaxation process.
Following the tendency to reach the highest rate stochastic free energy dissipation (SFED), a system relaxing to equilibrium goes through states with higher order so that the matter self-organization becomes possible.
Moreover, near equilibrium the maximum of SFED is shown to lead to the Prigogine’s principle of minimum entropy production, while far-from-equilibrium, in quasi-isothermal states and in the case of elastic molecular collisions and in absence of chemical reactions, the maximum SFED reduces to the maximum free energy dissipation.
The Prigogine’s principle of minimum entropy production near-equilibrium and the far-from-equilibrium Sawada’s principle of maximum energy dissipation consists of two complementary principia of a more general theory that do not contradict each other. The availability of a clear general model applying to the irreversible processes far from equilibrium is a great tool to investigate the generation of order and matter self-assembling in presence of large gradients of thermodynamic forces.
In the present paper the author shows that in quasiisothermal far from equilibrium states with no chemical reactions, the principle of maximum SFED, that can generally lead to transition to a state with an increase of free energy, in the case of incompressible phase (e.g., fluid one) this increase of free energy is basically almost given by an increase of order since the energy variation of the system associated to the external work is quite null.
For the first time it comes out from a physical theory the information about how and why a fluid phase is necessary to the development of matter self-assembling process that is at the base of the emerging of life.
The physical model is not devoid of new information signaling that ordering processes (and life) can also happen in fluids different from water, an interesting chance in searching for life in the universe out of the earth.
2. The SQHA Equation of Motion
The quantum hydrodynamic analogy (QHA) equations are based on the fact that the Schrödinger equation, applied to a wave function , is equivalent to the motion of a fluid owing the particle density
, is equivalent to the motion of a fluid owing the particle density  with a velocity
with a velocity governed by the equations [10-14]
governed by the equations [10-14]
 , (1)
, (1)
 , (2)
, (2)
 , (3)
, (3)
where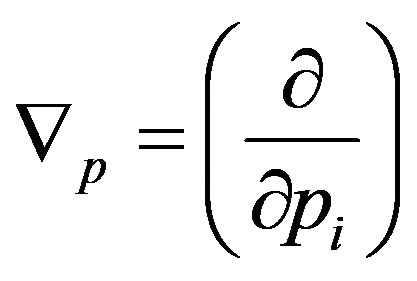 ,
, ,
,  is the Hamiltonian of the system and
is the Hamiltonian of the system and 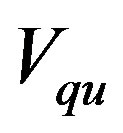 is the quantum pseudo-potential that reads
is the quantum pseudo-potential that reads
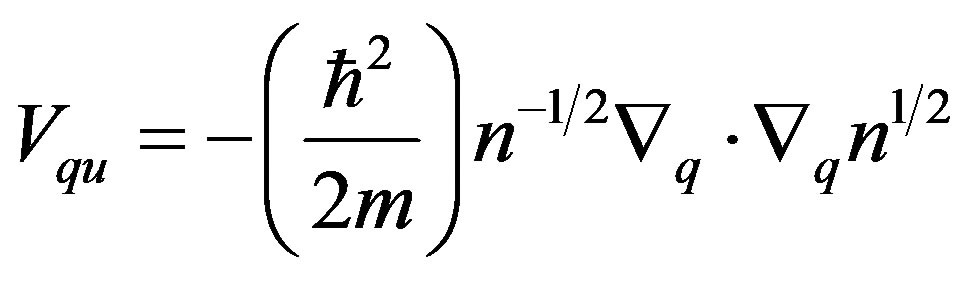 . (4)
. (4)
For the phase space analysis, it is useful to observe that Equations (1)-(3) can be derived by the following phase-space equations [13]
 (5)
(5)
where 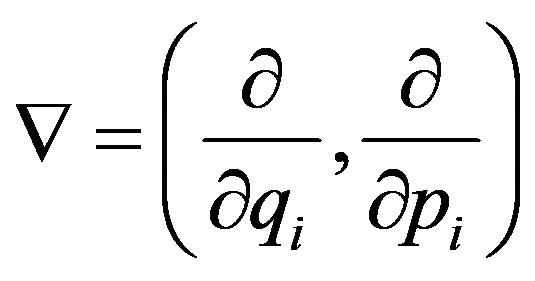 and where
and where
 . (6)
. (6)
 (7)
(7)
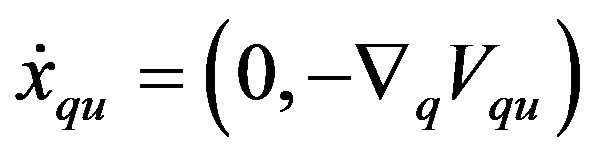 (8)
(8)
where
 , (9)
, (9)
and where
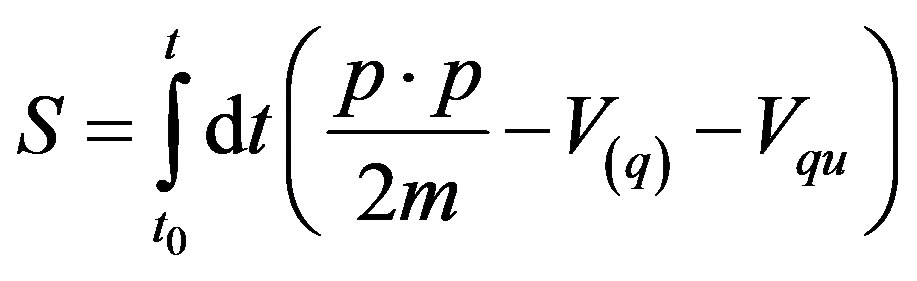 , (10)
, (10)
The Madelung approach, as well as the Schrödinger one, are non-local and are not able to give rise to local limit.
When fluctuations are added to the QHA equation of motion, the resulting stochastic-QHA (SQHA) dynamics shows that is possible to obtain local dynamics on large scale, preserving the quantum behavior on a microscopic one. In a preceding paper [13] the author has shown that in presence of vanishing small stochastic Gaussian noise, the QHA motion equation (at first order of approximation in the noise amplitude ) reads
) reads
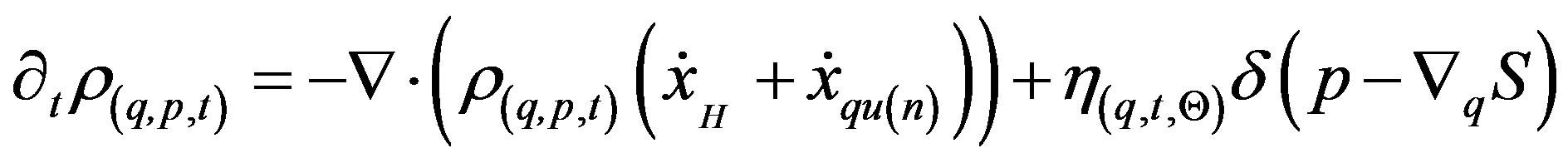 (11)
(11)
where the phase space distribution
 (12)
(12)
is a Wigner-like distribution obeying, in the limit of null noise, to the property
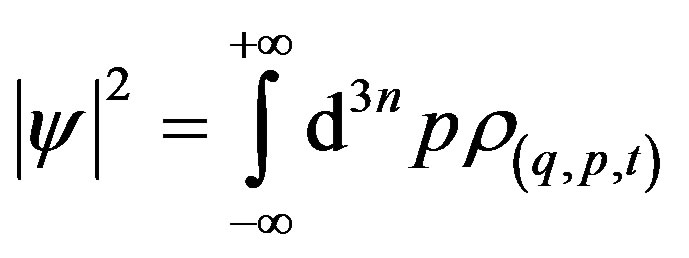 , (13)
, (13)
where  is a measure of the vacuum noise amplitude (VNA) and
is a measure of the vacuum noise amplitude (VNA) and
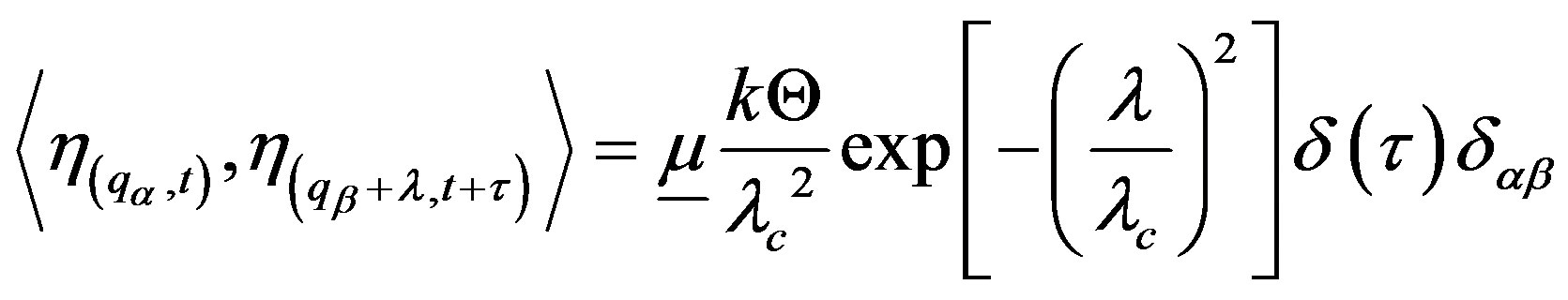 (14)
(14)
is the VNA variance, where the quantum correlation length 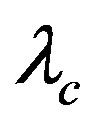 reads [13]
reads [13]
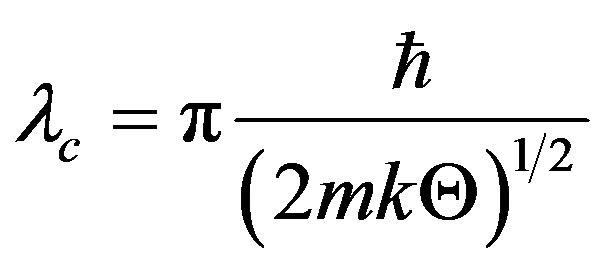 (15)
(15)
 (16)
(16)
 (17)
(17)
where
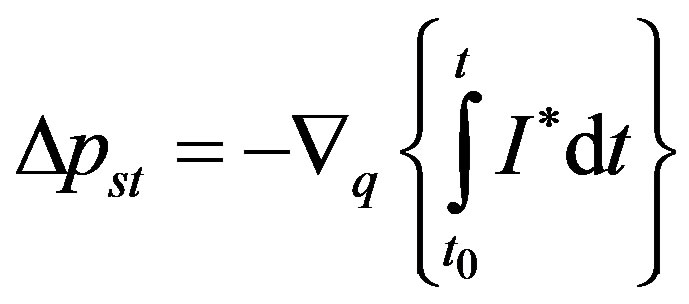 (18)
(18)
where
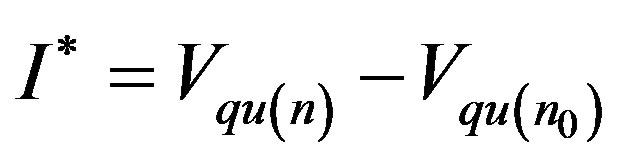 (19)
(19)
where  is obtained from the zero order of approximation Equation (1).
is obtained from the zero order of approximation Equation (1).
3. Macroscopic Local Dynamics
Given 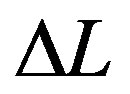 the physical length of the system, the macroscopic local dynamics is achieved for those problems that satisfy the condition
the physical length of the system, the macroscopic local dynamics is achieved for those problems that satisfy the condition
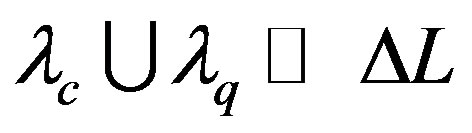 .
.
From the condition 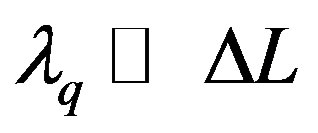 it follows that [13]
it follows that [13]
 (20)
(20)
and the SPDE of motion acquires the form [13]
 (21)
(21)
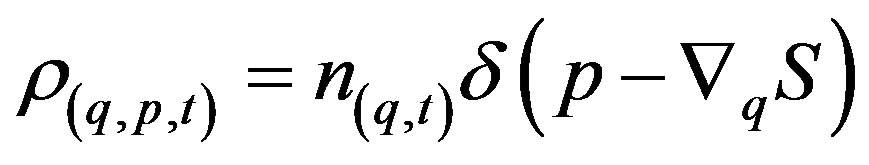 , (22)
, (22)
 (23)
(23)
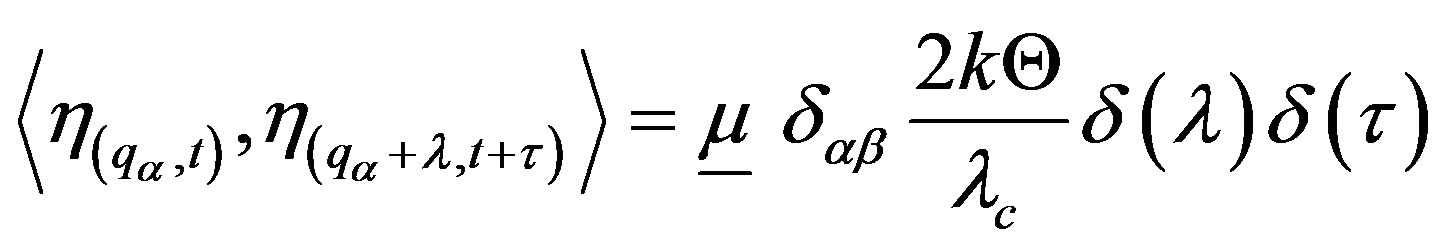 (24)
(24)
 (25)
(25)
where dp is a small fluctuation of momentum and
 , (26)
, (26)
Being also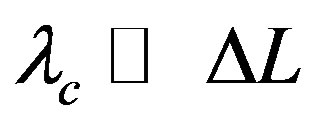 ,
, 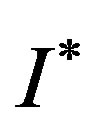 represents a small energy fluctuation due to the quantum potential [13].
represents a small energy fluctuation due to the quantum potential [13].
4. The Kinetic Equation for Classical Real Gas and Fluid Phase
As derived in reference [14], for a gas or mean-field fluid phases, we can describe our system by a single particle SQHA distribution function (DF)  from which we can extract the statistical single particle distribution
from which we can extract the statistical single particle distribution 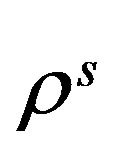 that obeys to the equation.
that obeys to the equation.
 (27)
(27)
With , where
, where 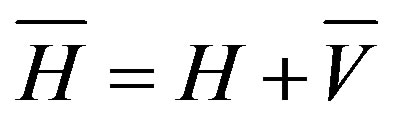 is the mean-field Hamiltonian, and where
is the mean-field Hamiltonian, and where 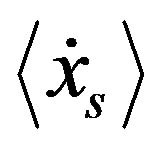 obeys to the equation [14]
obeys to the equation [14]
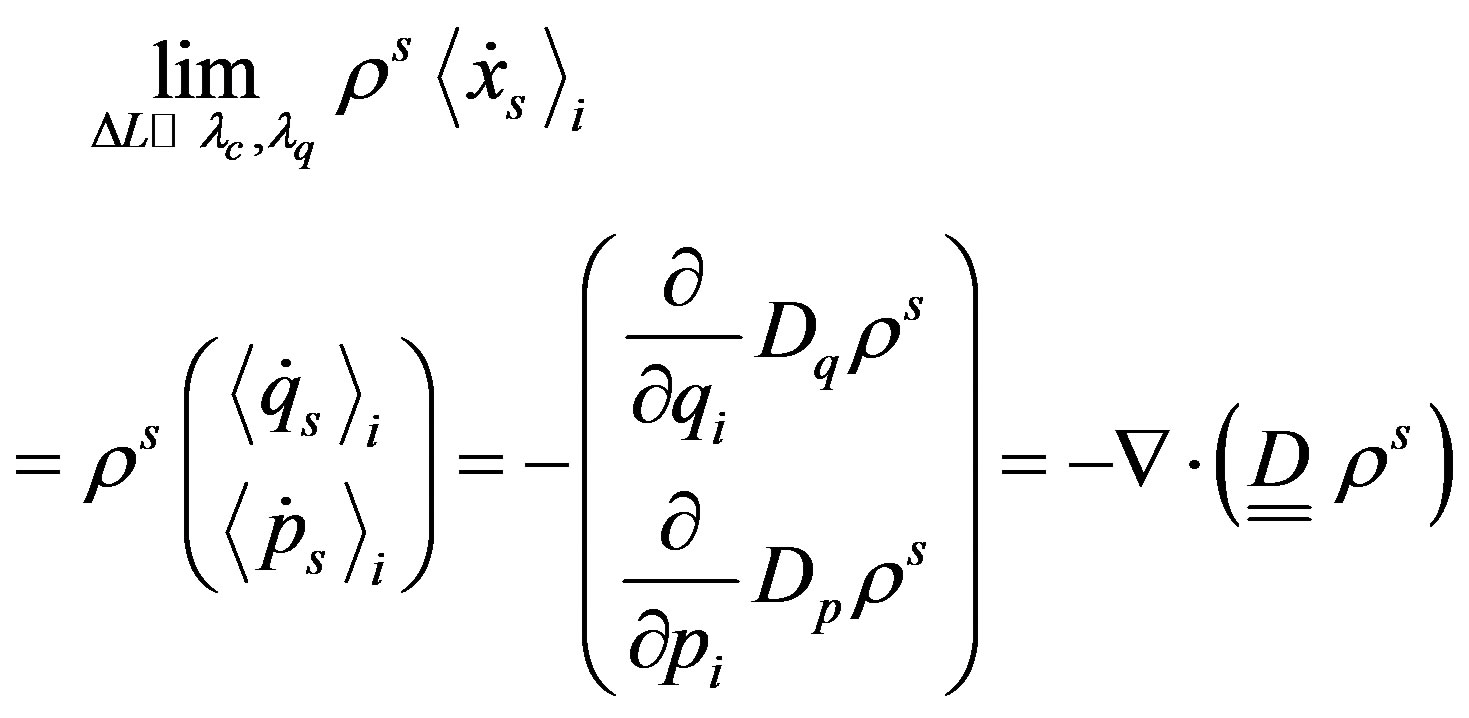 (28)
(28)
For a (classical) gas phase made up of structureless point-like particles interacting by central symmetric potential that do not undergo to chemical reactions (particles do not have bounded states (e.g., Lennard-Jones potential with small well, compared to the mean energy of particles) so that molecules with internal structure are not created) can be further simplified by excluding the cross-correlations concerning different co-ordinates components, namely
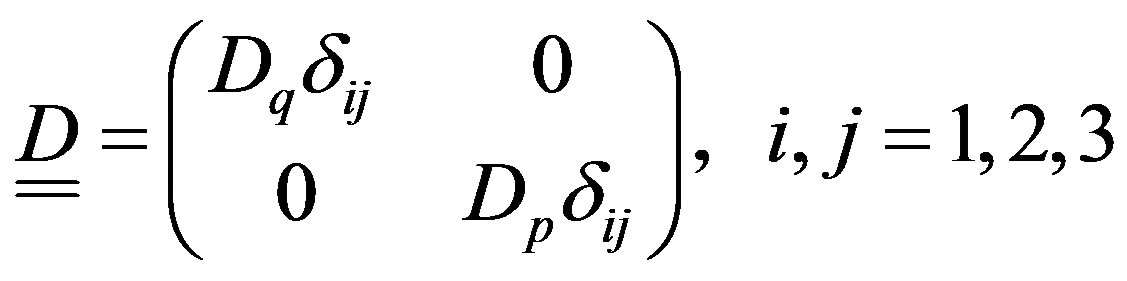 (29)
(29)
Equation (28) is basically the Fokker-Plank form of the Maxwell equation.
In order to obtain from (28) a closed kinetic equation, the standard approach is to introduce additional information about the diffusion coefficient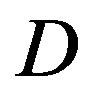 . Under the local equilibrium condition this is usually achieved by the semiempirical assumption of linear relation between flows and fluxes.
. Under the local equilibrium condition this is usually achieved by the semiempirical assumption of linear relation between flows and fluxes.
In order to obtain an evolutionary principle far from equilibrium, here we use (28) without the assumption of linear relation between flows and thermodynamic forces.
4.1. The Mean Phase Space Molecular Volume of Wave function Modulus
In order to grasp information from (28) we observe that (for gasses and mean-field fluids) the SQHA approach shows two competitive dynamics: 1) the enlargements of the molecular DF [14] between two consecutive collisions, 2) the diffusion of the molecules, in term of their mean position, as a consequence of the molecular collisions (that cause the WFM collapse [15]).
As consequence of free expansions and collapses, the pseudo-Gaussian molecular DF in the phase space cell  will occupy the mean volume
will occupy the mean volume 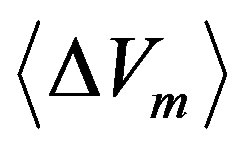 that we pose
that we pose
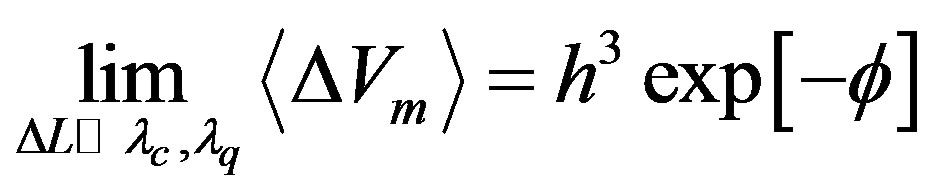 (30)
(30)
where 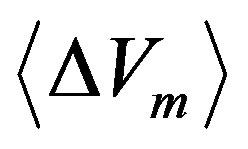 reads:
reads:
 (31)
(31)
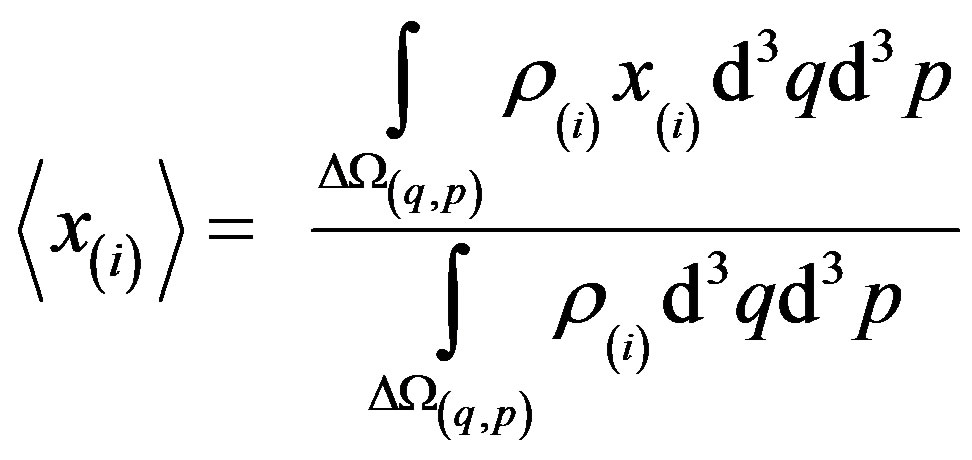 (32)
(32)
where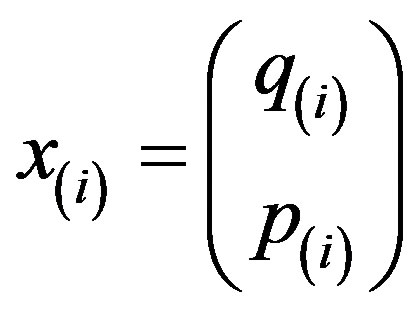 .
.
In the case of sufficiently weak radiative coupling between vacuum fluctuations and thermal ones [14], (28) simplifies as
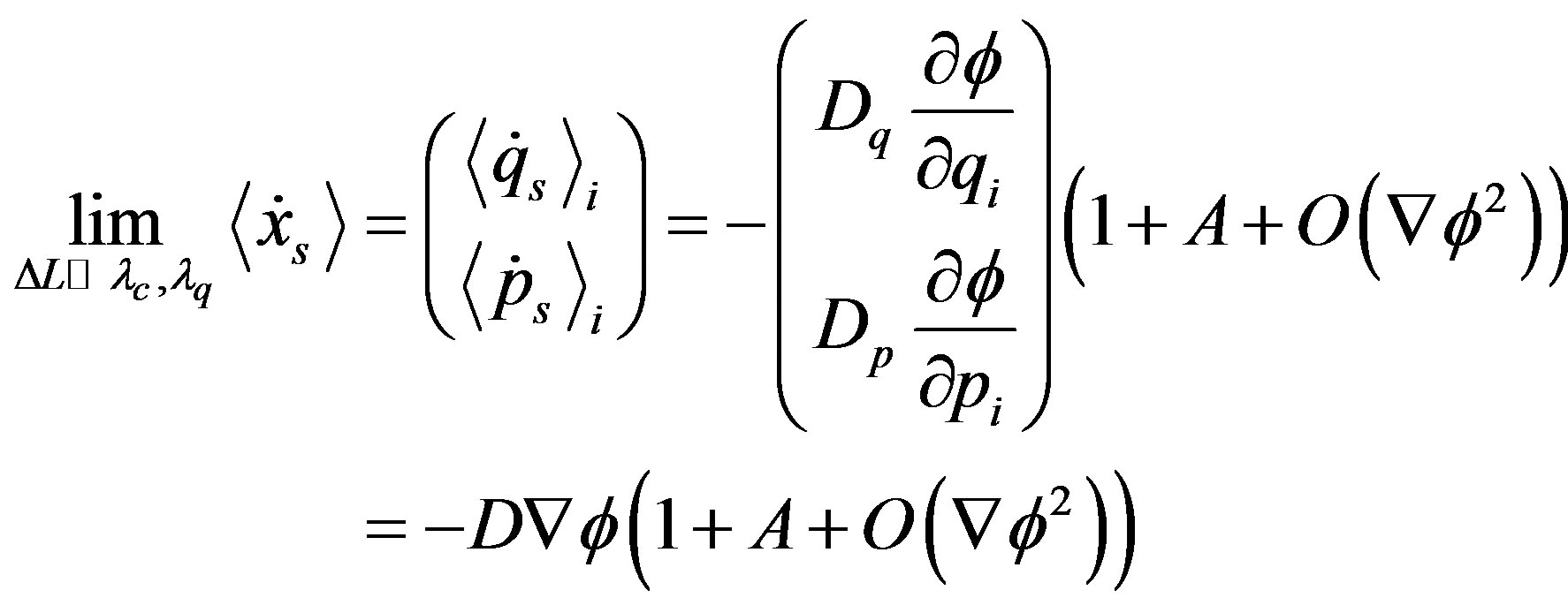 (33)
(33)
where in the synthetic notation of the right side
 is a 2 × 2 matrix that applies to the 2-element vector representing phase space gradient
is a 2 × 2 matrix that applies to the 2-element vector representing phase space gradient
 that introduced into the FPE (27)
that introduced into the FPE (27)
leads to the kinetic equation for stationary states [14]
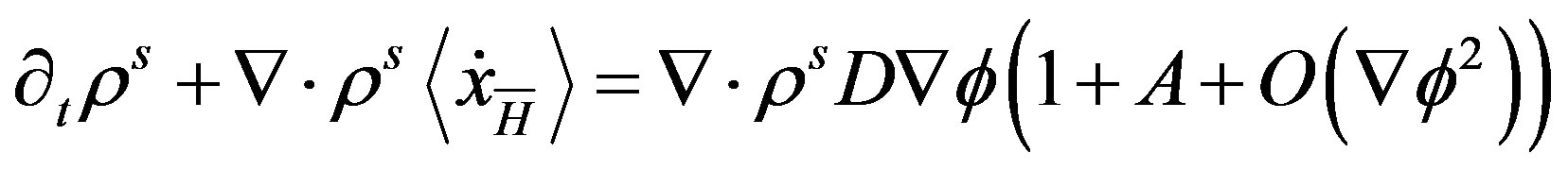 (34)
(34)
4.2. Far from Equilibrium Relaxation and Maximum Stochastic Free Energy Dissipation in Stationary States
Even if the 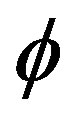 -function is well defined far from equilibrium, without the explicit form of the diffusion coefficient
-function is well defined far from equilibrium, without the explicit form of the diffusion coefficient 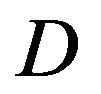 and the initial and boundary conditions of an assigned problem, the kinetic Equations (27) and (28) are just symbolic equations.
and the initial and boundary conditions of an assigned problem, the kinetic Equations (27) and (28) are just symbolic equations.
Nevertheless, the existence of the 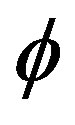 -function far from equilibrium allows the definition of a formal criterion of evolution.
-function far from equilibrium allows the definition of a formal criterion of evolution.
In fact from Equation (33) it is possible to derive an evolutionary principle along the relaxation pathway that can be formulated in terms of dissipation of the 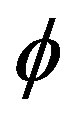 -function (named here normalized hydrodynamic free energy (NHFE) since at equilibrium it converges to the free energy normalized to kT [14].
-function (named here normalized hydrodynamic free energy (NHFE) since at equilibrium it converges to the free energy normalized to kT [14].
Given that, the total differential of the normalized hydrodynamic free-energy  can be written as a sum of two terms, such as:
can be written as a sum of two terms, such as:
 (35)
(35)
where we name
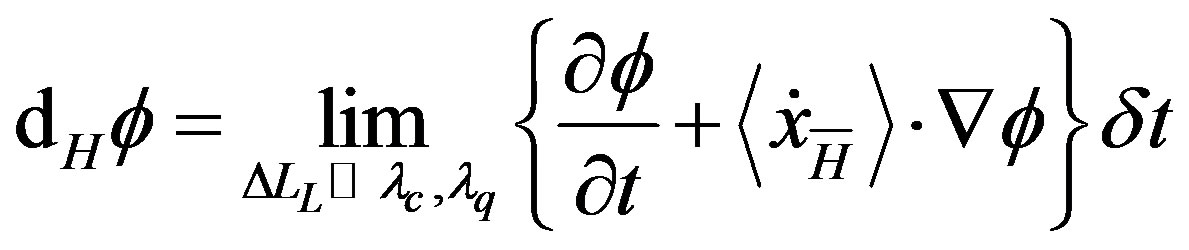 (36)
(36)
as “dynamic differential” and
 (37)
(37)
as “stochastic differential”.
Under the range of validity of Equation (35) (i.e., structureless punt-like particles, interacting by L-J central symmetric potential that do not undergo to chemical reactions) the stochastic velocity vector evolves through a pathway that follows the  -function negative gradient so that
-function negative gradient so that
 is minimum with respect the choice of
is minimum with respect the choice of  (38)
(38)
With 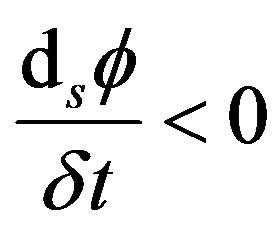 since
since  and
and 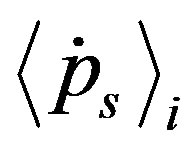 are anti-parallel to
are anti-parallel to  and
and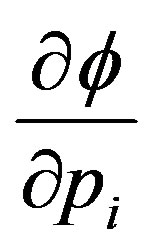 , respectively.
, respectively.
Sometime, some authors speak in term of energy dissipation, so that in this case the criterion (38) reads
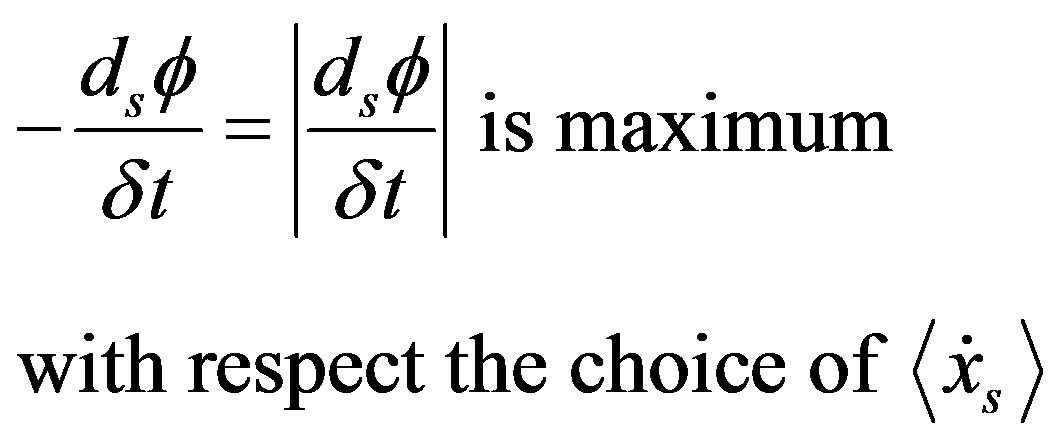 (39)
(39)
5. Maximum Stochastic Free Energy Dissipation in Quasi-Isothermal Stationary States
In order to elucidate the significance of the criterion given by (39), we analyze the spatial kinetics far from equilibrium.
5.1. Spatial Kinetic Equations
By using a well known method [16] we transform the motion Equation (34) into a spatial one over a finite volume V.
Given a quantity per particle
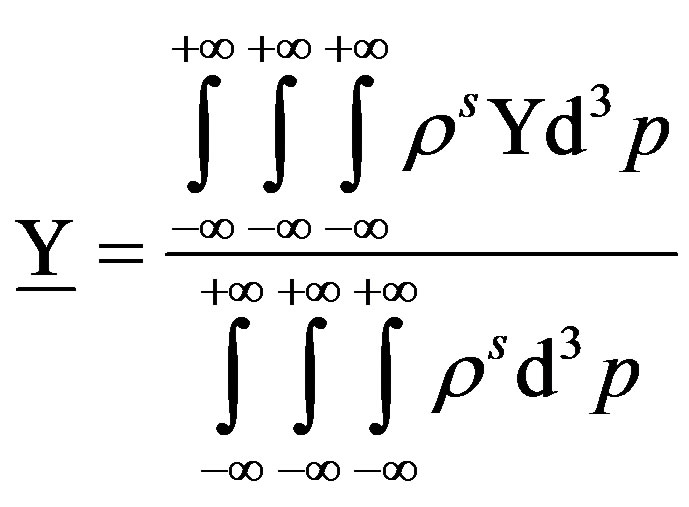 (40)
(40)
its spatial density:
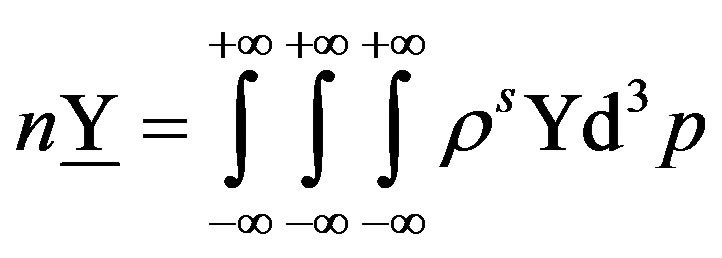 (41)
(41)
and its first moment
 (42)
(42)
by using the motion Equation (34) it is possible to obtain the spatial differential equation:
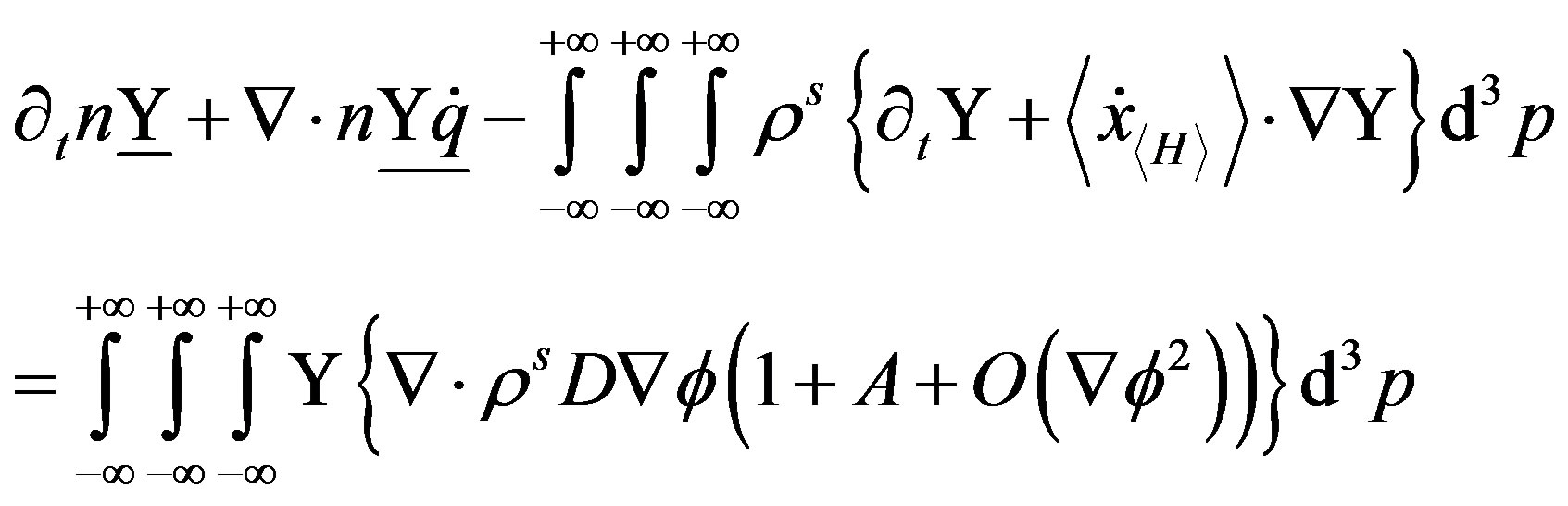 (43)
(43)
that by choosing
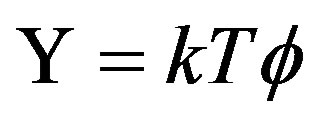 , (44)
, (44)
where T is the “mechanical” temperature defined as
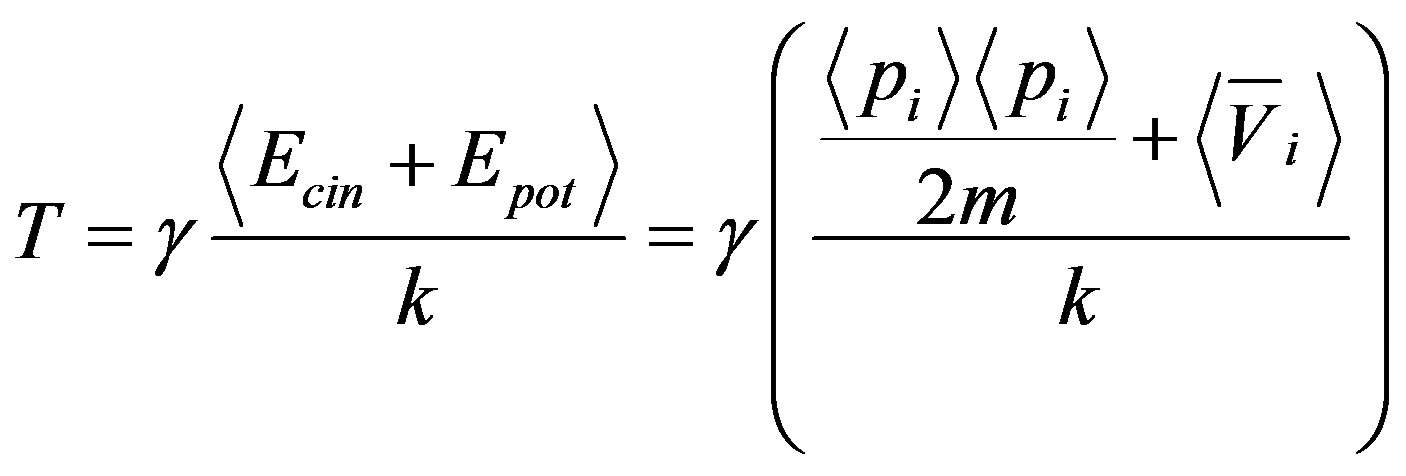 , (45)
, (45)
where 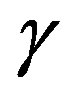 is defined at thermodynamic equilibrium, in quasi-isothermal condition and elastic molecular collisions (i.e., absence of chemical reactions) leads to the maximal condition respect to
is defined at thermodynamic equilibrium, in quasi-isothermal condition and elastic molecular collisions (i.e., absence of chemical reactions) leads to the maximal condition respect to  [14] that reads
[14] that reads
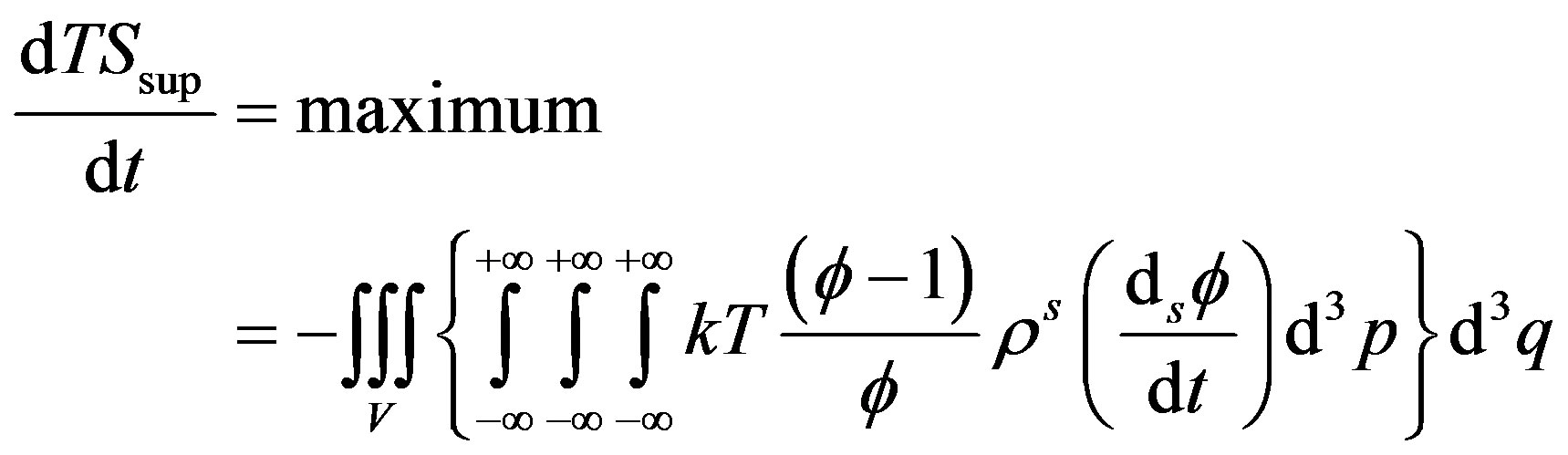 (46)
(46)
Equation (46) has been proven to be experimentally verified by Sawada in the electro-convective instability [8,17].
5.2. Spontaneous Free Energy Increase in Far from Equilibrium Steady-State Transition
From general point of view the SQHA system of differential equations is unmanageable as well as the far-from equilibrium kinetics.
In order to gain information about (46) let’s analyze it in the simple case of quasi-isothermal stationary states far from equilibrium (chemically and mechanically speaking). This case is still sufficiently general to be interesting since the matter self-assembling phenomena concerning the life generation happen in quasi-isothermal condition.
As a figurative example we take in mind the case of the electro-convective instabilities [17].
In the case of quasi-isothermal system with no chemical reaction taking place, it has been assumed that each infinitesimal volume of fluid is at quasi-thermal equilibrium. On this base, in Equation (46)  equals the free energy F, as well as Ss the thermodynamic entropy S.
equals the free energy F, as well as Ss the thermodynamic entropy S.
In the following we are going to show that the transitions to states with a higher amount of free energy are possible in far from equilibrium kinetics.
To this end, let’s consider the overall system with the energetic reservoirs that works reversibly onto the system so that we have
 (47)
(47)
where  is the energy of reservoir that for our purpose can be assumed to work in reversible manner onto the system, and the heat generated into the system is exchanged with the environment reversibly so that
is the energy of reservoir that for our purpose can be assumed to work in reversible manner onto the system, and the heat generated into the system is exchanged with the environment reversibly so that
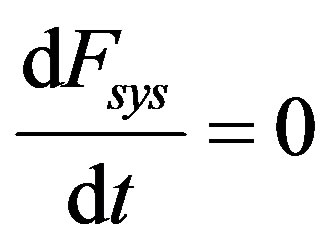 (48)
(48)
and
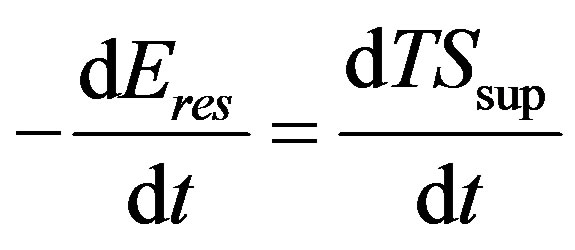 (49)
(49)
then, for the overall system it follows that
 (50)
(50)
This has been proven in electro-convective instability very far from equilibrium and confirmed by numerical simulation by Sawada et al. [17]. The experimental counterproof of posing a diode to the electric power in order to prevent that electric energy would flow back into the reservoir also showed to not modify the electro-convective kinetics.
Let’s consider the case that, far from equilibrium in subcritical conditions, the system makes a transition (at time t = 0) from a metastable state 1) to another metastable one 2) so that for t < 0- and t > 0+ we have the sub-system in a stationary state for which it holds
 (51)
(51)
so that by (50) for (t ¹ 0) we have
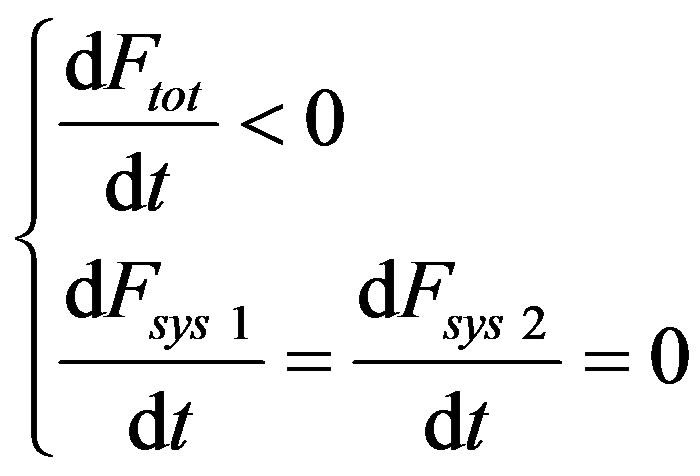 (52)
(52)
Given (50), in principle, the following cases are possible when the system makes the transition between states 1 and 2. Case “a”:
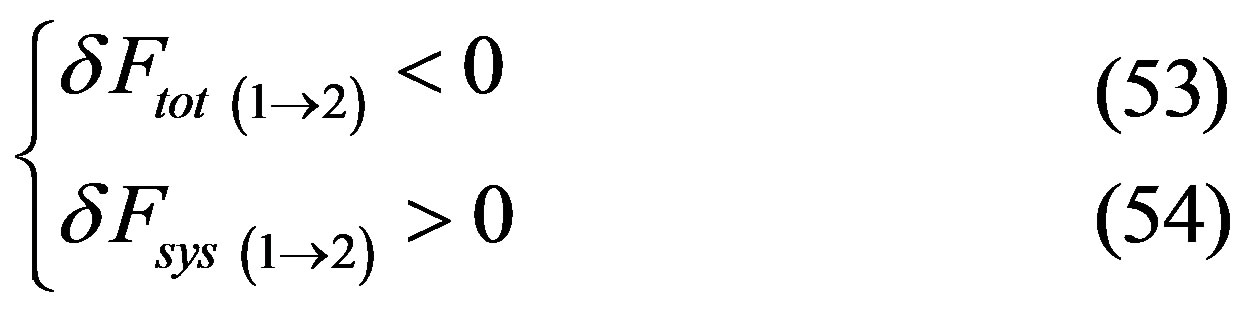
Case “b”:

Hence, given that for the inverse transition 2®1 it would result Case “a”
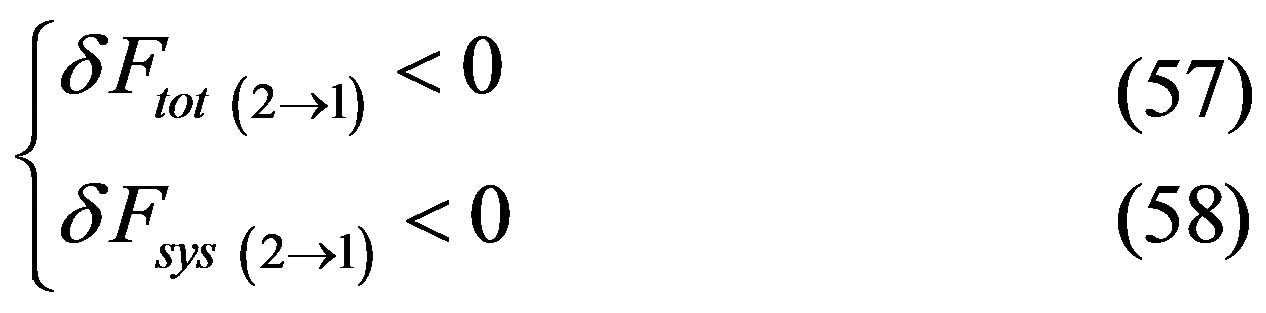
Case “b”:
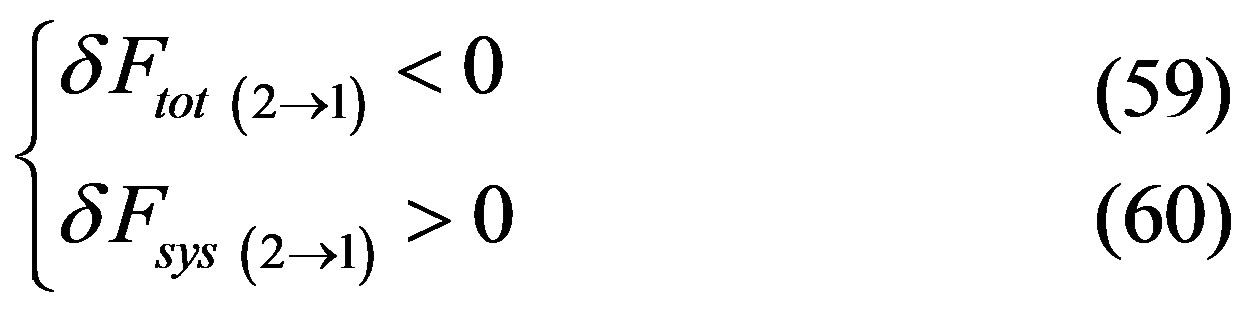
since transition between metastable happens in both directions, it follows that one of the two following cases must happen
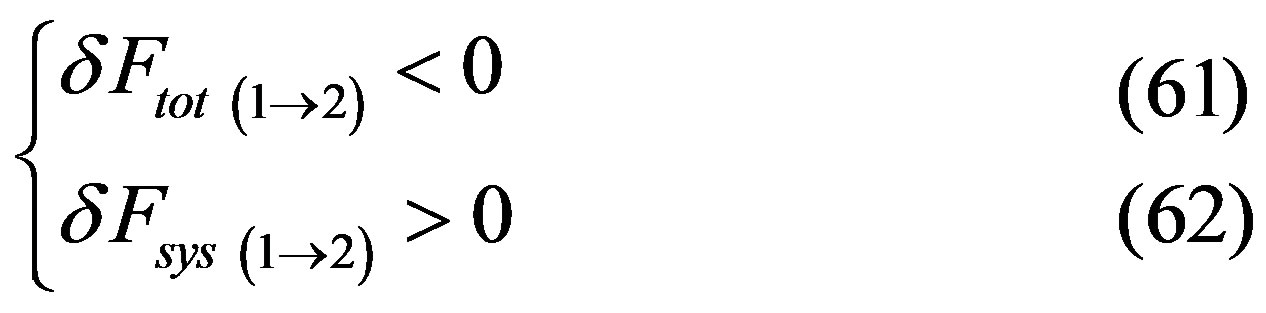
or

and since , considering the whole back and forth transition cycle, at least in one of the two directions, we have that
, considering the whole back and forth transition cycle, at least in one of the two directions, we have that
 (65)
(65)
5.3. Entropy Decrease in Incompressible Phases
Generally speaking, the increase of free energy does not also mean that the entropy of the system decreases. This depends by how much is the energy change in the transition.
Nevertheless due to the incompressibility of the fluid phase that makes null energy variations due to the volume change, from the general point of view, in isothermal transitions in fluids (as the electro-convective ones) the free energy increase is almost due by the entropy decrease.
In fact given that

Since in isothermal transitions in fluids the temperature as well as the fluid density is practically constant, for van der Waals type fluids where the internal energy 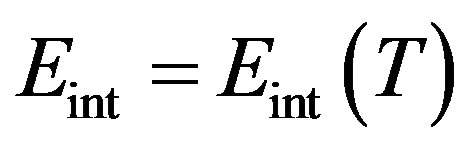 depends only by the temperature, it follows that
depends only by the temperature, it follows that 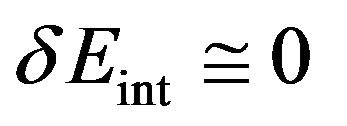 and hence that
and hence that
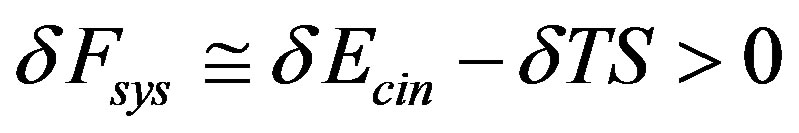
Moreover, given that in transition between metastable state the macroscopic kinetic energy  of the molecules may not appreciably increases (as showed by Sawada and Suzuki [17] in electro-convective instability) we have
of the molecules may not appreciably increases (as showed by Sawada and Suzuki [17] in electro-convective instability) we have  and hence that
and hence that

From (62) we can see that the ability of a system to make back and forth transitions between metastable states as the consequence both of the presence of fluctuations and the tendency to the maximum stochastic free energy dissipation, allows the spontaneous increase of order in far from equilibrium stationary states in incompressible fluid phase.
Finally it is worth mentioning that the possibility of having matter self-assembling in fluids different from water, in principle, allows the possibility to find organized structures and even living ones in presence of liquid phase such the methane ocean of the Saturn’s moon Titan as hypothesized by the NASA [18,19].
6. Discussion
Actually, Equation (37) has not been directly used to obtain (65). Nevertheless, it enters in the mechanism that allows the system to make transitions between metastable states.
Even if a large fluctuation would displace the system from a metastable stationary state, this fact will not be enough to bring the system toward a different stationary state.
It is the tendency to the (local) maximum stochastic free energy dissipation that makes it possible.
As shown by Sawada and Suzuki in electro-convective instabilities [8,17], the tendency to maximize the free energy is the real force that attracts the system toward the new stationary condition. In fact, they showed that: 1) The stationary state with the higher free energy dissipation is the most stable (i.e., it owns a longer living time before the transition to another metastable state takes place); 2) Approaching the fully stationary condition, the free energy dissipation of the system increases and reaches the top at the establishing of final stationary configuration.
Therefore, we can depict the following mechanism: the maximum free energy dissipation generates a basin of attraction (see the appendix) (possibly larger, higher is the dissipation rate of the metastable state) for each metastable state and the fluctuations make the system to jump between them.
This process allows having transition to a state with higher free energy, but this still does not warrant the generation of order.
It is the incompressibility of fluids that transforms the free energy increase into an increase of system order.
This step is just the first step toward the generation of life since many subsequent steps are needed.
It is matter of evidence that living systems own four common elements: 1) The matter substrate, 2) Energy, 3) Organization, and 4) Water (fluid). Even this is well accepted, the relationship between these characteristics has to be fully disclosed.
As shown by Katchalsky and Perelson [20-22] the physical approach to biological systems puts its foundations on the postulate that it is possible to have spontaneous order generation and that the physical law of entropy increase can break itself down far from equilibrium. Although the Prigogine’s principle brought new perspectives, it is limited to the existence of local equilibrium and a coherent general understanding is not available.
On the other hand, it is possible to model the generation of organic molecules at the base of living structures [23,24] and in some cases the far from equilibrium evolution can be described by reaction-kinetics equations, but a general criterion is not available.
The present paper shows that organization is promoted by energy dissipation and that the fluid is the phase that allows the generation of order. This picture satisfactorily explains why the four basic characteristics of living system appear always together.
Given this mechanism, the development of life follows a well-defined pathway.
The need of (fluid) water-type chemical process and reactions with the advantages of owing a rheological organized structure has brought to development of the biphasic structure in living system.
The wide spread bi-phasic structure of living systems (a solid matrix whose interstitial pores are filled by a fluid [25]) is the nature solution to the problem of maintaining the matter-energy flows of chemical processes and reactions in a fluid environment (diffusivity in solids is typically one thousandth of that one in water and makes not possible the living dynamics) and obtain a rheological structure able to maintain topological complexity, the premise of performing complexes functions.
Energy is necessary for both macroscopic movements and microscopic ones (such as: tissue plasticity, selfrepairing, brain plasticity, fluxes of matter and energy at the base of information storing and thinking) and it is at the base of the development, transformation and functioning of any “living” system.
The matter is just the substrate. Thence being the energy the fundamental element of life, the evolution of living systems follows the way of finding better and better synergies.
The system that is more efficient has higher probability of adaptation (to develop functionalities that improve its existence) and surviving, so that life is not only complexity of structure but also (and mainly) complexity of functions.
The present work aims to bring to the light the general criterion able to get insight into life expression and evolution eliminating the non-communicability between the physics and the life science.
7. Conclusions
In the present work the SQHA is used as a model to obtain the non-equilibrium kinetics of a real gas of L-J interacting particles and its fluid phase.
In the case of particles whose mean distance is bigger than the quantum potential range of interaction. For L-J interaction potential is of order of the molecular interaction distance (so that particles can be described by the classic rigid sphere approximation), it is possible to describe the SQHA evolution by means of a Fokker-Plank equation holding even far from the local thermodynamic equilibrium.
In gasses and Marcovian liquids, close to stationary states, it is possible to define the kinetic equation of motion as a function of the mean phase space molecular volume that shows maximizing the dissipation of the stochastic part of the SQHA-free energy.
In the case of a real gas with no chemical reactions and at quasi-isothermal conditions, the principle disembogues into the maximum free energy dissipation confirming the experimental outputs of electro-convective instability.
In this case, the model shows that the transition to states with higher free energy can happen and that the increase of free energy in incompressible fluids is almost given by a decrease of entropy leading to order increase and hence to matter self-organization.
The output of the theory showing that the generation of order, via energy dissipation, is more efficient in fluids than in gases, because of their incompressibility, which leads to the re-conciliation between physics and biology furnishing the explanation why the life was born in water.
The theoretical output also suggests that the life searching, out of the earth, must consider the possibility to find organized structures in presence of liquid phases different from water.
REFERENCES
- I. Prigogine, “Moderation et Transformations Irreversibles des Systemes Ouverts,” Bulletin de la Classe des Sciences, Academie Royale de Belgique, Vol. 31, 1945, pp. 600-606.
- I. Prigogine, “Étude Thermodynamique des Phenomènes Irreversibles,” Desoer, Liege, 1947.
- B. H. Lavenda, “Thermodynamics of Irreversible Processes,” Macmillan, London, 1978.
- M. Šilhavý, “The Mechanics and Thermodynamics of Continuous Media,” Springer, Berlin, 1997, p. 209. http://dx.doi.org/10.1007/978-3-662-03389-0_14
- Y. Sawada, “A Thermodynamic Variational Principle in Nonlinear Non-Equilibrium Phenomena,” Progress of Theoretical Physics, Vol. 66, No. 1, 1981, pp. 68-76. http://dx.doi.org/10.1143/PTP.66.68
- W. V. R. Malkus and G. Veronis, “Finite Amplitude Cellular Convection,” Journal of Fluid Mechanics, Vol. 4, No. 3, 1958, pp. 225-260. http://dx.doi.org/10.1017/S0022112058000410
- L. Onsager, “Reciprocal Relations in Irreversible Processes. I,” Physical Review, Vol. 37, No. 4, 1931, pp. 405- 426. http://dx.doi.org/10.1103/PhysRev.37.405
- M. Suzuky and Y. Sawada, “Relative Stabilities of Metastable States of Convecting Charged-Fluid Systems by Computer Simulation,” Physical Review A, Vol. 27, No. 1, 1983, pp. 478-489.
- W. T. Grandy, “Entropy and the Time Evolution of Macroscopic Systems,” Oxford University Press, New York, 2008. http://dx.doi.org/10.1093/acprof:oso/9780199546176.001.0001
- E. Madelung, “Quantentheorie in Hydrodynamischer Form,” Zeitschrift für Physik, Vol. 40, No. 3-4, 1926, pp. 322-326. http://dx.doi.org/10.1007/BF01400372
- I. Bialynicki-Birula, M. Cieplak and J. Kaminski, “Theory of Quanta,” Oxford University Press, New York, 1992.
- J. H. Weiner, “Statistical Mechanics of Elasticity,” John Wiley & Sons, New York, 1983, pp. 316-317.
- P. Chiarelli, “Can Fluctuating Quantum States Acquire the Classical Behavior on Large Scale?” Journal of Advanced Research in Physics, Vol. 2, 2013, pp. 139-163.
- P. Chiarelli, “Far from Equilibrium Maximal Principle Leading to Matter Self-Organization” Journal of Advances in Chemistry, Vol. 5, No. 3, 2013, pp. 753-783. http://www.researchgate.net/publication/235794865_Far_from_equilibrium_maximal_principle_leading_to_matter_self-organization?ev=prf_pub
- P. Chiarelli, “Quantum to Classical Transition in the Stochastic Hydrodynamic Analogy: The Explanation of the Lindemann Relation and the Analogies between the Maximum of Density at He Lambda Point and that One at Water-Ice Phase Transition,” Physical Review & Research International, Vol. 3, No. 4, 2013, pp. 348-366.
- Y. B. Rumer and M. S. Ryvkin, “Thermodynamics, Statistical Physics, and Kinetics,” Mir Publishers, Moscow, 1980.
- M. Suzuki and Y. Sawada, “Propagation Transitions of Electroconvection,” Physical Review A, Vol. 31, No. 14, 1985, pp. 2548-2555.
- C. P. McKay and H. D. Smith, “Possibilities for Methanogenic Life in Liquid Methane on the Surface of Titan,” Icarus, Vol. 178 No. 1, 2005, pp. 274-276. http://dx.doi.org/10.1016/j.icarus.2005.05.018
- Committee on the Limits of Organic Life in Planetary Systems, Committee on the Origins and Evolution of Life and National Research Council, “The Limits of Organic Life in Planetary Systems,” The National Academies Press, Washington DC, 2007, p. 74.
- M. Paecht-Horowitz, J. Berger and A. Katchalsky, “Prebiotic Synthesis of Polypeptides by Heterogeneous Polycondensation of Amino-Acid Adenylates,” Nature, Vol. 228, No. 5272, 1970, pp.636-639.
- A. Katchalsky and P. F. Curran, “Nonequilibrium Thermodynamics in Biophysics,” Harvard University Press Cambridge, 1965.
- A. S. Perelson, “Network Thermodynamics,” Biophysical Journal, Vol. 15, No. 7, 1975, pp. 667-685. http://dx.doi.org/10.1016/S0006-3495(75)85847-4
- R. Shapiro, “Origins: A Skeptic’s Guide to the Creation of Life on Earth,” Bantam Books, 1987, p. 110.
- C. Menor-Salván, D. M. Ruiz-Bermejo, M. I. Guzmán, S. Osuna-Esteban and S. Veintemillas-Verdaguer, “Synthesis of Pyrimidines and Triazines in Ice: Implications for the Prebiotic Chemistry of Nucleobases,” Chemistry, Vol. 15, No. 17, 2007, pp. 4411-4418. http://dx.doi.org/10.1002/chem.200802656
- P. Chiarelli and D. De Rossi, “Polyelectrolyte Intelligent Gels: Design and Application,” In A. Ciferri and A. Perico, Eds., Ionic interactions in Natural and Synthetic Molecules, John Wiley and Sons Ltd., Chichester, 2012, pp. 602-604.
Appendix
If we instantaneously perturb the stationary state at time t = 0 (i.e., by generating a force input
 ) so that the total
) so that the total  -derivative
-derivative
(37) reads
 (A.1)
(A.1)
for t > 0, it follows that the system begins a transient maximizing the stochastic free energy dissipation by aligning  and
and  along each other. If the process ends in a stationary state, the final kinetic equation reads
along each other. If the process ends in a stationary state, the final kinetic equation reads
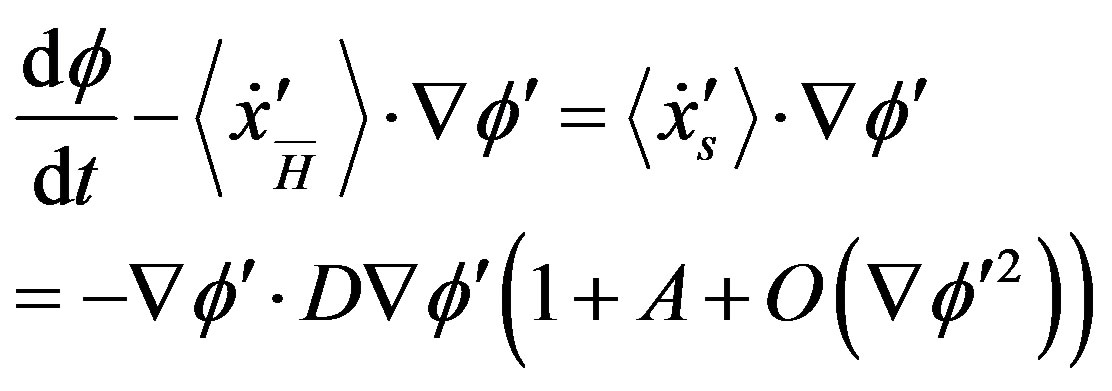 (A.2)
(A.2)
Depending by the boundary conditions and by the physical constants of the system, assigned a perturbation  (or a fluctuation) leading to a response
(or a fluctuation) leading to a response
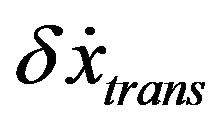 , the final stationary value
, the final stationary value  is assigned.
is assigned.
During the relaxation process 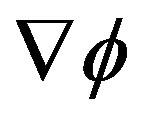 and
and  are coupled each other. Approaching the stationary state, the vector
are coupled each other. Approaching the stationary state, the vector 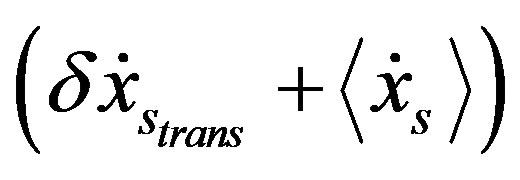 draws closer to the vector
draws closer to the vector 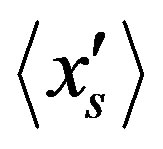 with
with 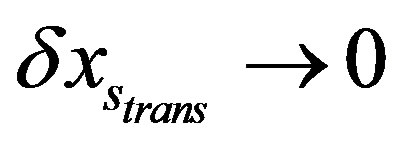 complying with the maximum SFED given by the right side of (A.2).
complying with the maximum SFED given by the right side of (A.2).
The maximal condition of right side of (A.2) is just a local property holding for sufficiently small variation. The basin of attraction of such maximum is the complex core of the problem once the system is assigned. It depends by the specific kinetic behavior of the system that defines the coupling between 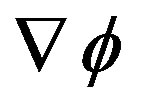 and
and .
.
If we apply a large perturbation  the final stationary state (configuration) may differ from the initial one.
the final stationary state (configuration) may differ from the initial one.
If the fluctuation or perturbation is large enough to generate a response  able to sensibly modify the free energy gradient field
able to sensibly modify the free energy gradient field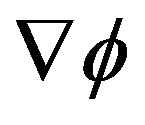 , the system falls into the basin of convergence of a different local maximum so that the maximum SFED brings the system to a new stationary state [17].
, the system falls into the basin of convergence of a different local maximum so that the maximum SFED brings the system to a new stationary state [17].

