Open Journal of Biophysics
Vol.3 No.4(2013), Article ID:38152,13 pages DOI:10.4236/ojbiphy.2013.34029
Fractal Networks of Real Worlds of Fluorescing DNA in Complete Set of Chromosomes inside Blood Cells for Medical Diagnostics
Department of Experimental Physics, Saint-Petersburg State Polytechnic University, Saint-Petersburg, Russia
Email: n.galich@mail.ru
Copyright © 2013 Nikolay E. Galich. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 10, 2013; revised August 15, 2013; accepted September 18, 2013
Keywords: Abnormal Fractals in DNA Activity; Complex Networks of 3D-DNA; Diagnostics and Hysteresis in Fractal Networks of DNA; DNA Packing; Networks of “Exponentially Small Worlds”; Shannon-Weaver Biodiversity of DNA Activity inside Cells
ABSTRACT
We analyze fluorescence due to oxidizing activity of DNA in neutrophils of peripheral blood in the large populations ~104 - 105 of cells. Fluorescence is registered by flow cytometry method. Spatial resolution is about a few nanometers for varied complex three-dimensional (3D) DNA nanostructures of all non-coding and coding parts of DNA. It’s shown that oxidative activity of all 3D DNA in the full set of chromosomes inside cells is defined by new standards for complex networks of “exponentially small worlds”, with more dense packing than in the well known networks of “small worlds”. Analysis of various blood samples in vivo and during medical treatment had shown that only two classes of Good and Bad Networks of DNA for a good and a bad health existed. This division is defined by any network to one from two classes of “n” or “s” shaped curves for typical deviations and from straight line in perfect networks of “exponentially small worlds”, as for two types of hysteresis curves at phase transitions or at switching of bistability. These deviations coincide with two types of positive and negative trends of changing fractal dimension by changing the scales of multi-scale networks of fluorescing DNA. These trends give the overall assessments of human immunity, including hidden and unidentified diseases, and as a sum of all kinds of health and illness of given person, from the point of view the inner life of neutrophils, living in different parts of human body in given time. Characteristics of deviations associated with type, level and complexity of illness in the dependence on the scale of networks and Shannon-Weaver biodiversity of neutrophils, i.e. information entropy for DNA activity in cells. These results were used for analysis of fluorescing DNA inside chicken erythrocytes, in assessing the health status of young hens and roosters, and may be helpful in veterinary medicine.
1. Introduction
We present results of a novel nonlinear analysis of flow cytometry experiments on immunofluorescence with nanometer spatial resolution in the flow direction [1] for large populations ~104 - 105 of neutrophils in the peripheral blood of human. These results are used also for populations of chicken erythrocytes in the blood of young hens. Fluorescence of DNA inside cells is initiated by oxidative burst reaction at using ethidium bromid as a dye [2]. In each experiment, we observe fluorescence of three-dimensional (3D) DNA nanostructures of all noncoding and coding parts of DNA. Each cell has the chaotic Brownian motions and rotations in the jet of bloodflowing through the laser beam during flow cytometry measurements. Therefore, each histogram presented a rich statistics for a rich set of various two dimensional (2D) projections on the photomultiplier, which includes all possible detailed spatial images of fluorescing DNA inside neutrophils, i.e. for real 3D-distributions of chromosomal DNA in large populations of cells. Detailed analysis of statistical data on 3D DNA fluorescence inside neutrophils [1-4] shows that the actual topology of complex networks for full set chromosomes in living cells is much more complicated than traditional schematic description mesh, ring and other computer nets. Typical approaches of structural biology here are also inadequate for correct description of fractal structures and switches in large-scale correlations for oxidative activity of 3D DNA in cellular nuclei. However, there are some common patterns, versatile features and switching in fluorescence networks which allow us to classify different types of correlations at oxidative activity of DNA inside cells for any donor [1-4]. New features of biophysical and mathematical characteristics of 3D DNA activity inside cells, living inside a given person at a given time, provide new opportunities in medical diagnostics and classification of all basic types of health and immunity.
Let us consider mainly quantitative peculiarities of immunofluorescence. Some applications of oxidative burst reaction in diagnostics, standard biochemical procedures for preparing samples and basic experiments of flow cytometry for blood samples volume ~1 ml are described in [1-4]. The volume of blood is V = 1 - 2 ml. Blood with heparin additives is diluted by physiological solution in a ratio of 1/3. Hydroethidine addition with concentration of 150 μg/ml is used for initiation of DNA fluorescence. At the beginning, hydroethidine is transformed into ethidium bromide as a result of chemical oxidative reactions in the blood cells. Small concentration 100 ng/ml additives of phorbol myristate acetate (PMA) to blood samples ensure the intensive staining of the cell nuclei of polymorph nuclear leukocytes. The staining reflects differences in the ability of cells to produce oxygen radicals, i.e. the respiratory burst activity. The fluorescence is proportional to the ability of neutrophils to produce the active forms of oxygen. Hydroethidine binds with fragments of nuclear DNA and has strong, red fluorescence excited by TEM00 mode radiation from Argon laser light at 488 nm wavelengths. Fluorescence is registered by flow cytometry technique. The rate of measurements is about (1 - 2) × 104 cells per/min. The flow velocity is about 1 m/s. The mean time of measurements of one model is about 2 minutes. This empirically selected regime is selfconsistent with noises of various nature and gives statistically stable and reproducible results. The inaccuracy and reproducibility for preparations and measurement procedures usually compose of not more than a few percent or more correctly of ≈2%. Spatial resolution of the instruments in flow cytometry may be very high [4]. This fact is little known and poorly used. Resolution and sensibility in flow cytometry measurement allows registering very small heterogeneities of neutrophils, with dimensions of the order of nanometers and smaller sizes, inaccessible of optical microscopy. Registration of fluorescence with flash duration ~10−9 s in the jet of blood flowing through the laser beam with the velocity ~1 m/s provides measurement with spatial scales ~10−9 m in the flow direction [4]. Synchronization and registration of short fronts ~10−12 s of fluorescence pulses give an increasing of sensitivity and decreasing the lower limit of spatial measurements in the flow direction.
Each experiment reflects a considerable statistics for frequency distribution of flashes for approximately 104 and more than 104 fluorescing neutrophils in the blood of any donor. Corresponding examples for frequency distributions of fluorescence are presented below in Figures 1, 3 and 4. These experiments form various experimental data for 3D-correlations of all chromosomal DNA in large populations ~104 - 105 of cells. We have many new unknown details for inner life of genome and chromosomes inside cells for oxidizing activity of real 3D DNA in nanometer scales. These details cannot be seen in the optical microscope. These details are reflected in histograms of fluorescence, but we don’t know how to extract and decrypt corresponding information. At present, we have no adequate knowledge in mathematics, physics, information theory, medicine and biology for absolutely
 (a)
(a)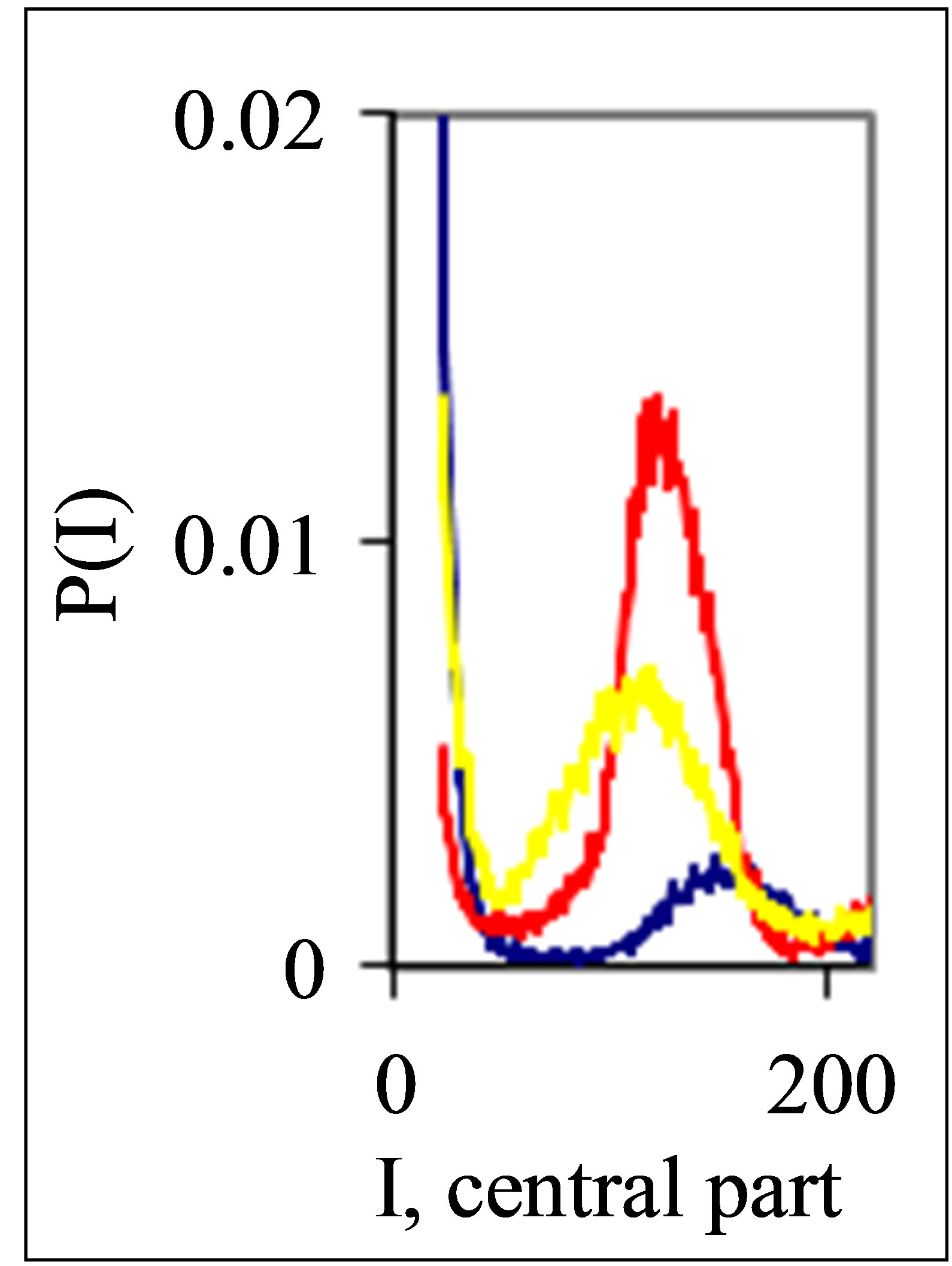 (b)
(b)
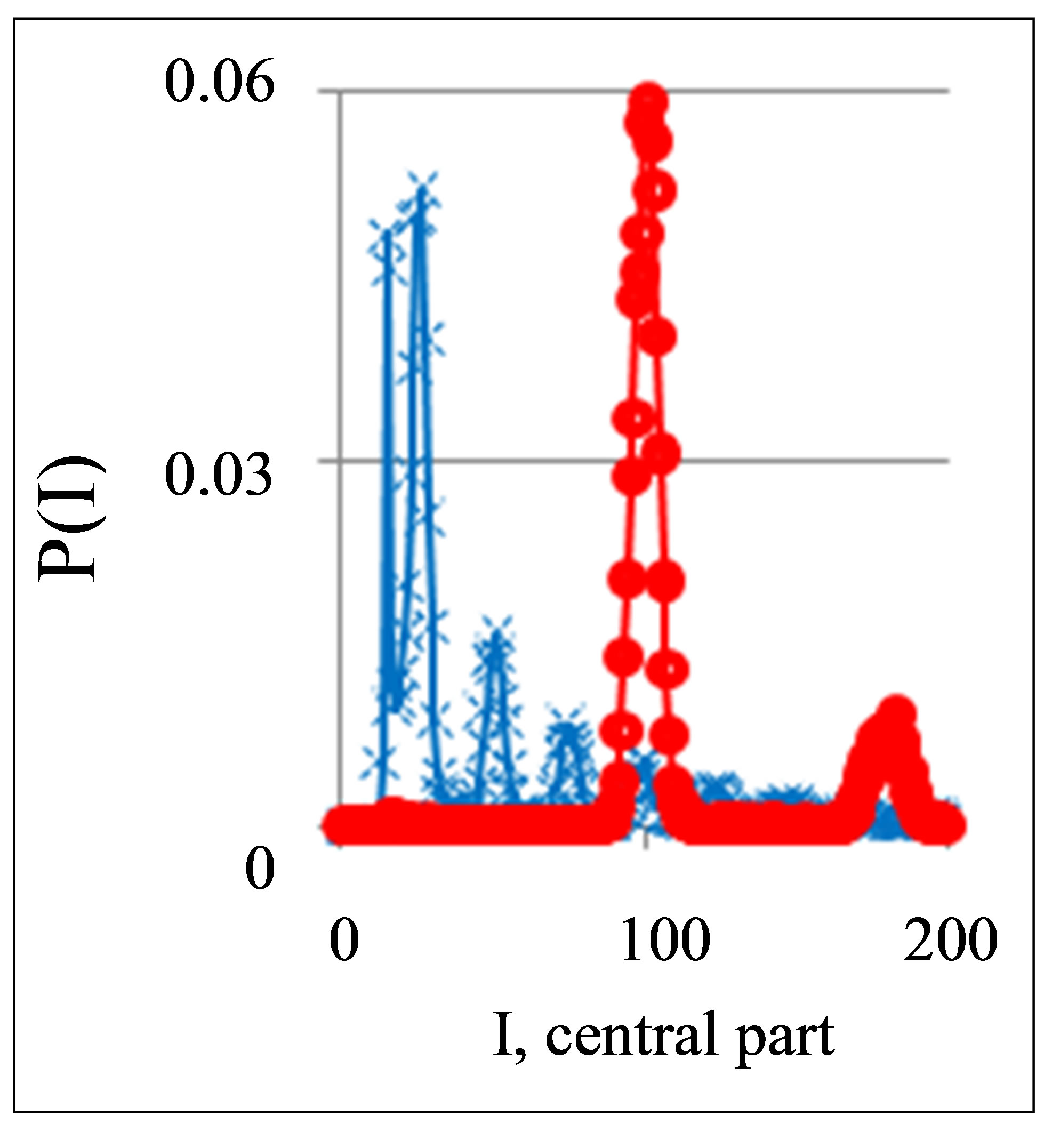
Figure 1. Dependence of normalized frequency distribution of flashes P(I) on their intensity I (a) and for clearest only central part of histogram (b). The area under the final histograms of P(I) normalized to unit; rhombus points correspond to bronchial asthma. Total number of flashes is N0 = 76,623; quadrate points correspond to the healthy donor. Common number of flashes is N0 = 40,109; triangle points correspond to the oncology disease. Common number of flashes is N0 = 40,752.
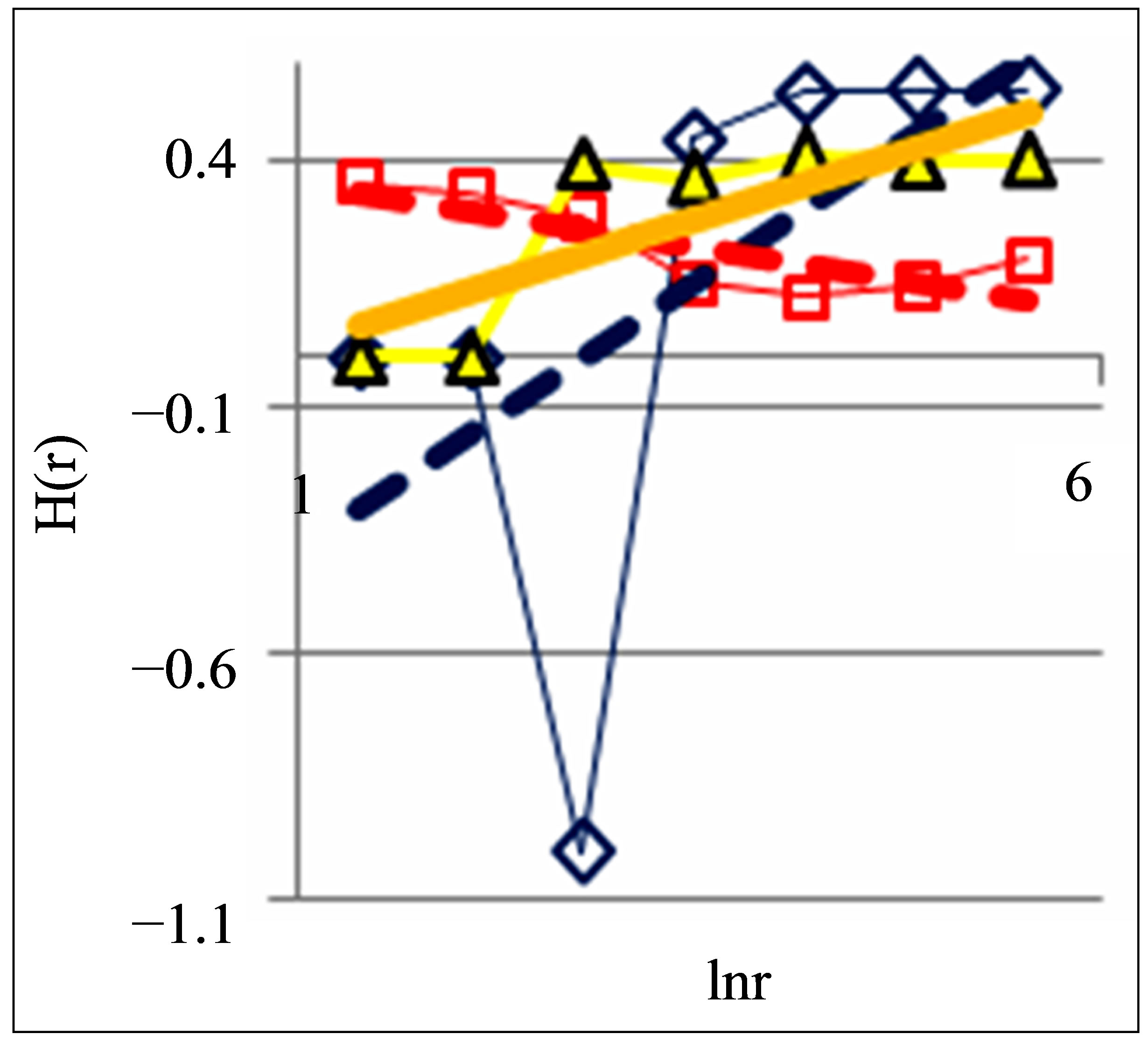
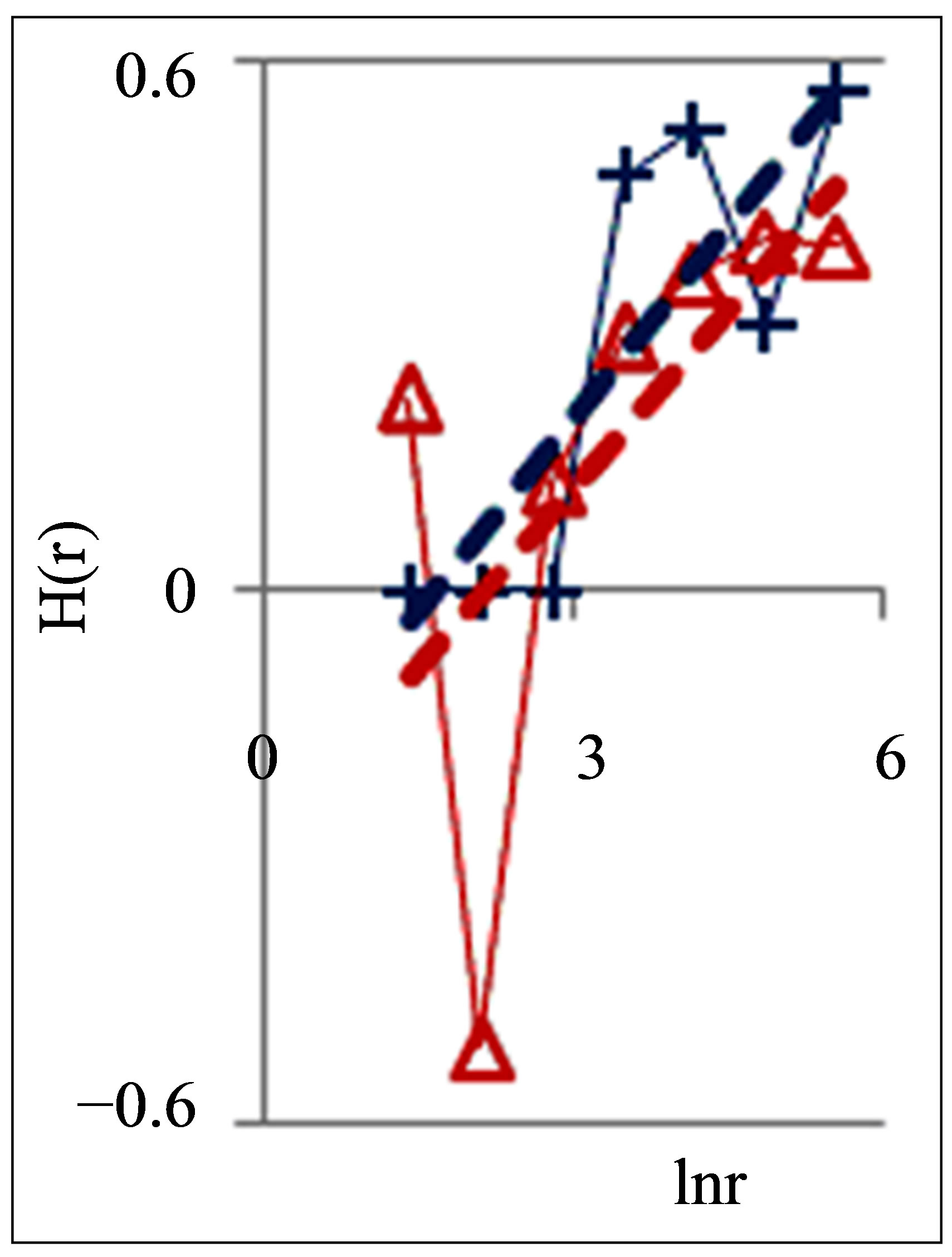
Figure 2. Dependence of Hurst index H(r) on logarithm of range r in networks of DNA fluorescence with different scales for three different states of health connected with asthma, with good health and at oncology; dash-and-dot lines correspond to the main overall trends; initial histograms see in Figure 1.
 (a)
(a) (b)
(b)
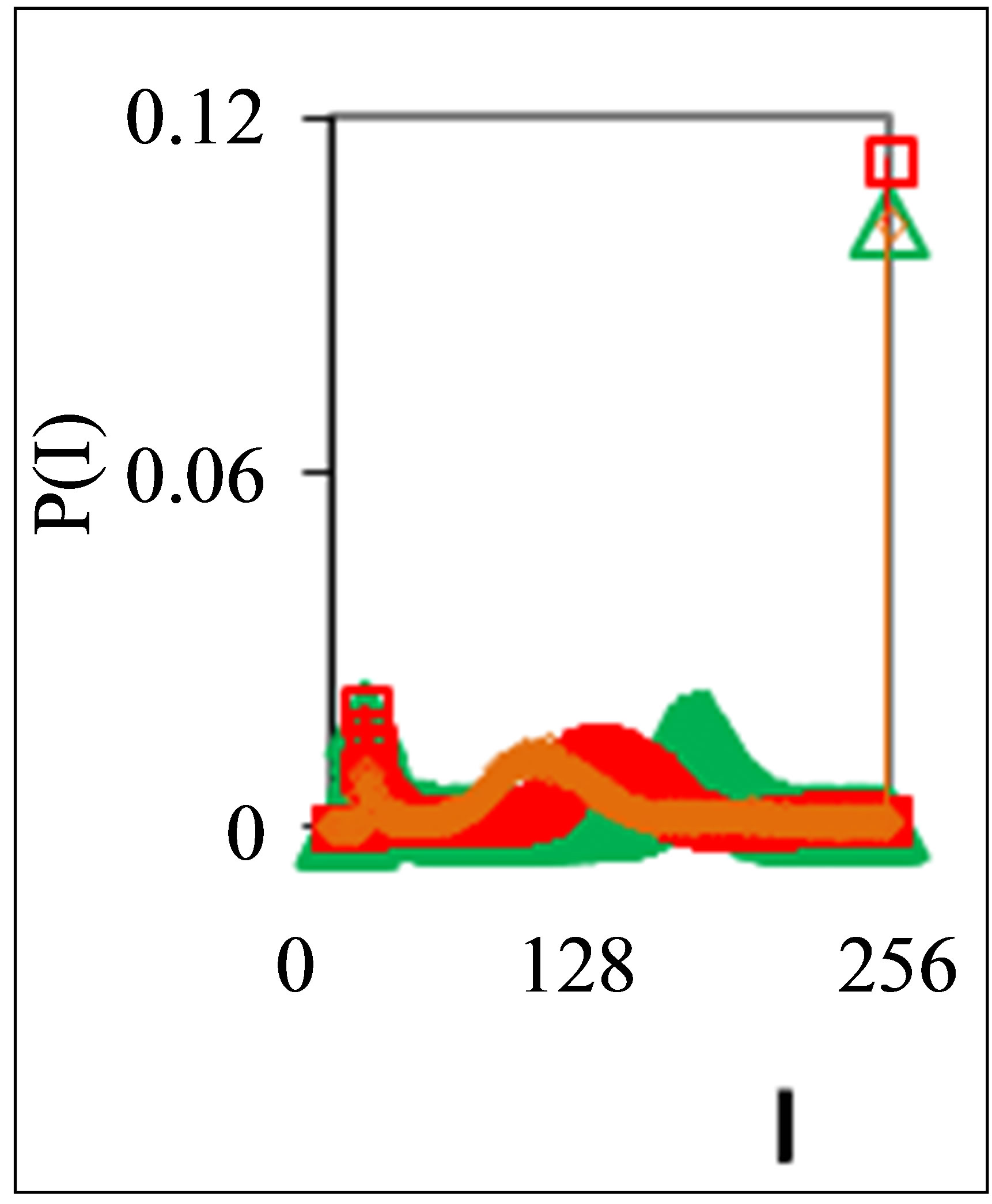
Figure 3. Dependence of normalized frequency distribution of flashes P(I) on their intensity I (a) and for clearest only central part of histogram (b), for one and the same invariably healthy, donor in different times. Triangle green Rhombus points correspond to the total flashes number N0 = 30 832, analysis time is 19 July (first year); rhombus yellow points correspond to the total flashes number N0 = 38,758, analysis time is 11 July (next year); square red points correspond to the total flashes number N0 = 40,109, analysis time is 03 June, before 11 July, histogram range r = 256.
 (a)
(a)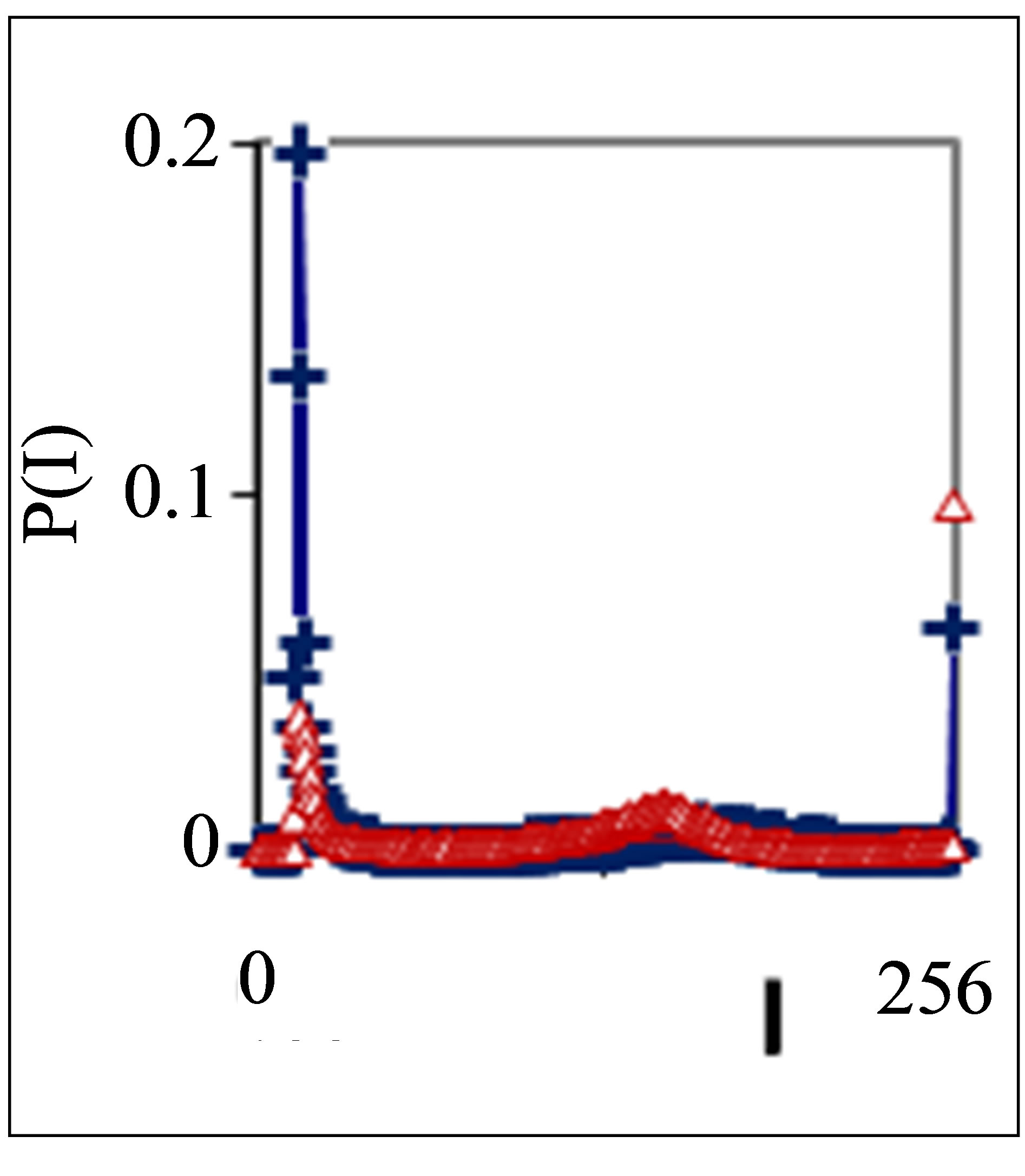 (b)
(b)
Figure 4. Dependence of normalized frequency distribution of flashes P(I) on their intensity I (a) and for clearest only central part of histogram (b) for one and the same patient with oncology and hepatitis B; symbol blue cross relates to analysis date 05 November, one year N0 = 43,752; symbol red triangle corresponds to 15 December, this year, after treatment of hepatitis B, N0 = 26,265; patient was infected hepatitis B during treatment of main oncology disease.
correct, coherent, consistent and complete interpretation of this new and significant information about 3D DNA activity inside cells. Some of these unsolved problems may be associated with abnormal fractals; complex networks of 3D-DNA activity; fractals in networks of “exponentially small worlds”; information entropy or Shannon-Weaver index of biodiversity for activity of DNA inside cells; etc.
In the parts 2 and 3 of this article we define fractal property of multi-scale networks of fluorescence and Shannon-Weaver biodiversity of neutrophils. In the parts 4 and 5 we define packing of DNA activity in multi-scale fractal networks in order to classify a good and bad DNA networks, and a good/bad health status, as for two various types of packing and deviations from perfected ideal. In the part 6, we show that large-scale networks for fluorescing DNA in neutrophils of healthy and unhealthy humans are similar to fractal networks for fluorescing DNA of chicken erythrocytes in the blood of healthy and unhealthy young hens and roosters. This similarity caused by the proximity of networks of “real worlds” for oxidative activity of chromosomal DNA in the living cells to standards of “exponentially small worlds”. This new class of complex networks has much denser packaging than well-known [5] networks of “small worlds”. We observed the similar deviations from ideal networks of “exponentially small worlds” for a good and bad health of humans and birds. Therefore, oxidizing activity of DNA in a full set of chromosomes inside cells has some universality in behavior of large-scale correlations and networks for all healthy and unhealthy human beings.
Here we present some approaches, semi-empirical results and first steps in the direction of practical needs for medical diagnosis and treatment monitoring complex analysis of immunofluorescence. We continue to develop various new methods and approaches [1,3,4,6] to the contemporary nonlinear analysis of modern experiments on oxidative activity and inner life of DNA inside cells.
2. Fractals and Trends in Oxidative Activity of Fluorescing DNA inside Neutrophils
Three examples of typical cytometry histograms are shown in Figure 1. Detailed accurate statistical analysis of these histograms currently is absent. Standard smoothing eliminates, destroys natural peculiarities of fractal networks and correlations in DNA activity, changes the real statistics, blurs and distorts many aspects of reality. Large-scale correlations for fluorescence of DNA inside living cells differ from those that we would like to see by abnormal fractal dimensions and non-trivial noises at substantially non-Gaussian statistics [1,3,4,6].
These natural peculiarities of immunofluorescence often are accompanied by statistical instabilities of local intensity distributions [1,3,4,6]. Statistical instabilities ensure insolvency and inapplicability of standard methods of data analysis, when there isn’t lawful basis for their applicability. Here statistical instabilities of local intensity distributions mean that the average value of intensity is smaller than dispersion, dispersion is smaller than asymmetry and other higher statistical moments of intensity fluctuations [3,4,6]. The exponential growth of central moments of fluorescence intensity reflects the clear sign of turbulence [3]. Therefore, here not meaningless to compare average or local values of intensity for different distributions in various histograms, even for one and the same patient in different time; one may to compare Figures 1(b), 4(b) and 3(b) for different healthy and unhealthy people and for one and the same healthy man in Figure 3(b). Here absence any systematic displacements for any local and average value of intensity in the dependence on the states of health.
In the case of Gaussian statistics corresponding statistical moments of fluctuations have an opposite trend to rapid exponential increasing. Therefore here domain lower statistical moments, i.e. average and standard deviation.
Thus, statistical instability of immunofluorescence prevents an application of traditional data analysis. Fast exponential growth of higher statistical moments means that even a low level small noise of fluorescence for higher orders of correlation and autocorrelation of noise provides the intermittency of DNA fluorescence, i.e. rare irregular bright flashes in time [7]. It also means that any forced smoothing of experimental statistical data radically alters the nature and structure of DNA fluorescence. Intermittency in random media and an exponentially rapid growth of high-order statistical moments of fluctuation are discussed in [7].
We need to develop a sequence of new nonlinear statistical methods to data analysis of immunofluorescence.
Let us consider some fractal peculiarities of immunofluorescence. Different analogies of various fractal networks such as bronchial tree, structure of oncology tumor, arterials tree, etc. with networks and distributions of immunofluorescence are described in [3]. Many histograms of different origin are similar to various histograms for fluorescence of neutrophils in Figure 1 [3]. Range of histogram r interconnected with the selection of multistage clusters in networks with structure of bronchial tree; here range r coincides with the number of columns in a histogram or with the number of channels for measurements of fluorescence intensity at given maximal value of dimensionless intensity, i.e. r = Imax. In our experiments maximal number of channels is 256. Variations of range r, i.e. rank of histogram r, or variations the scale r, when r = Imax, provide the changes in irregularity and brokenness of frequency distribution of fluorescence for histograms of various ranks [3]. The quantitative measure of irregularity and brokenness for frequency distribution of flash in histograms may serve a Hurst index H.
Hurst exponent H [8] is determined by means of regression equation
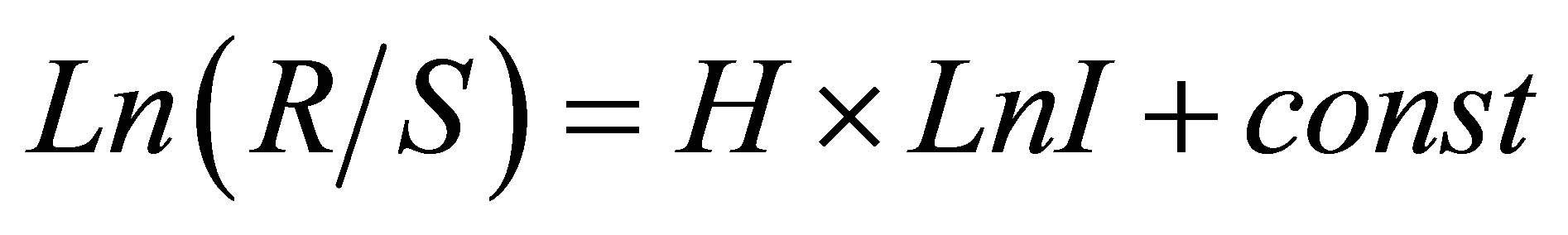 (1)
(1)
where R/S is rescaled range (R = S), R is range or maximal deviation of P(I) from local mean level, S is standard deviation of P(I). Illustration of definition Hurst index was presented in [1,4]. Hurst index H for frequency of flashes P(I) connected with fractal (Hausdorff) dimension D [8]
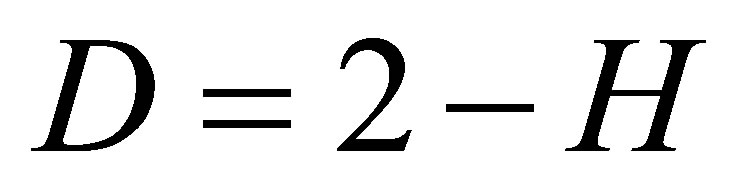 (2)
(2)
Examples for three distributions of Hurst index in the hierarchy of fractal clusters with various scales, corresponding to data in Figure 1, are shown in Figure 2.
According to Figure 2 a good health corresponds to the negative trend in the dependence of H on lnr, i.e. dH/dlnr < 0. The positive trends for dependencies of H on lnr, when dH/dlnr > 0, correspond to a bad health at various diseases.
The values of dH/dlnr depend on different states of health or illness and may be use in monitoring the states of health over time in vivo and in medical treatment [1]. In [1] presented different variations of fractal topology networks of DNA activity for healthy donor and donor with oncology in real time and during treatment. Some examples changing networks of DNA activity in real time, for initial histograms in Figures 3 and 4, presented in Figure 5 to illustrate changeability of fractal topology (Hurst index) at oxidative activity of DNA inside neutrophils, living in the healthy and unhealthy men.
According to Figures 2 and 5, a good and a bad health various people differ a positive and negative overall trends in changes of fractal dimension D(r) or a positive and negative derivatives dD/dr > 0 and dD/dr < 0. The values of (dD/dr) depend on the health status, type of disease and vary in time for one and the same human and for different people.
Thus, we got the empirical rule for classifying the General State of Health in the form of answer Yes/No or healthy/sick, i.e. dD/dr > 0 or dD/dr < 0, for all donors [1,4] from the point of view diverse populations of neutrophils, living in different parts of the human body in different conditions. This response includes the presence
 (a)
(a)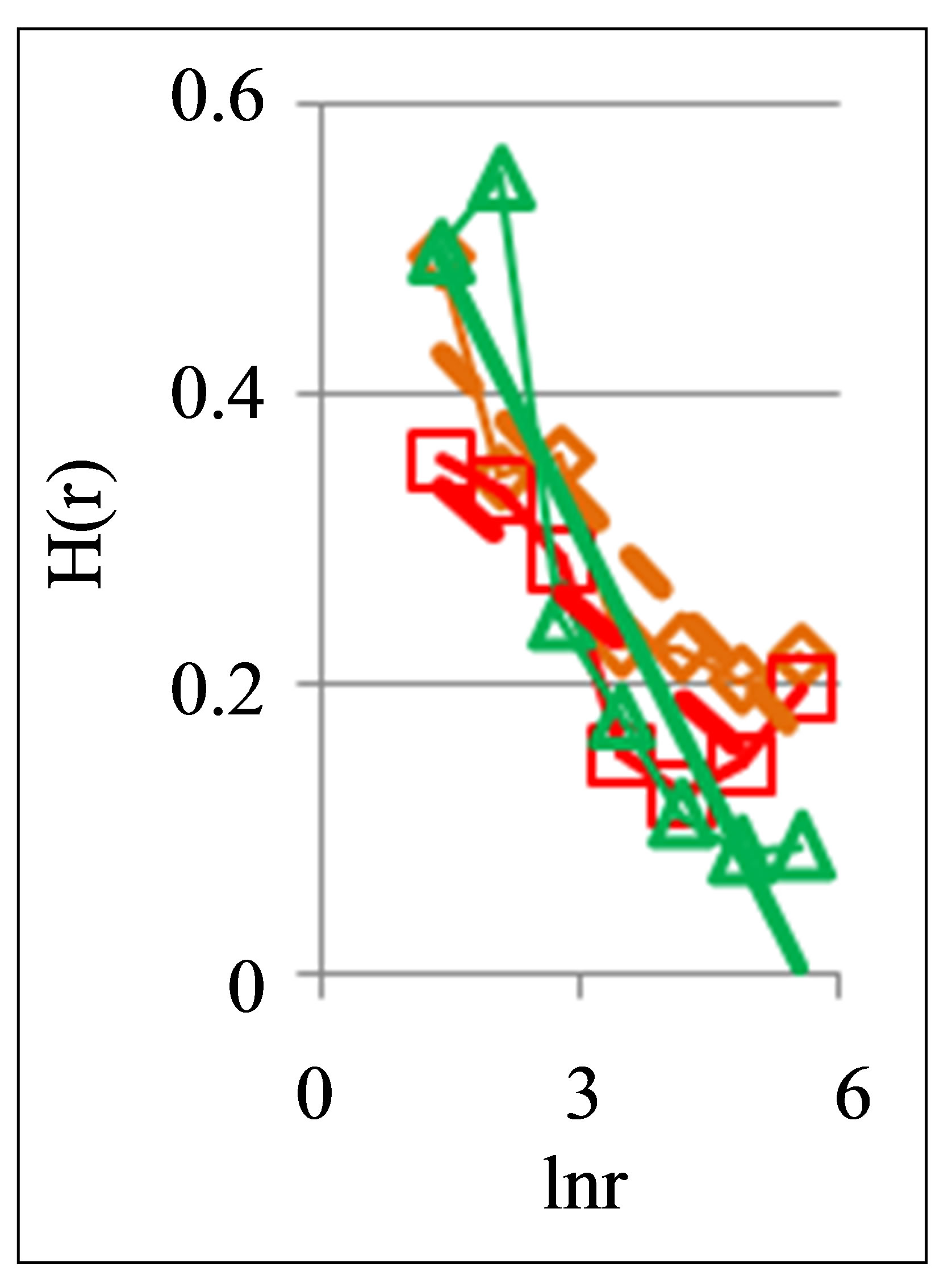 (b)
(b)
Figure 5. Dependence of Hurst index H(r) on logarithm of range r: (a) One and the same invariably healthy, donor in different times, initial histograms see in Figure 3; (b) One and the same unhealthy donor with oncology and hepatitis B, before and after hepatitis treatment; initial histograms see in Figure 4; dash-and-dot lines correspond to the main overall trends.
of all kinds of health and illness, including hidden and unidentified diseases. This classification is defined by the change of signs of plus/minus in the overall trends of fractal topology, i.e. in the dynamics and direction of changes of fractal dimension or Hurst index, with a monotonic decrease of scales r of networks or sizes r of clusters in fractal correlations for oxidative activity of DNA inside cells. Sequential analysis of features and causes in systematic changes of fractal topology in networks for oxidative activity of DNA in neutrophils for different samples of blood presented below in this article.
Next comments describe the typicality of normal and abnormal fractals for networks of DNA fluorescence. Normal fractal dimension D corresponds to the interval 1 < D < 2 for positive Hurst index H > 0. Negative Hurst index H < 0 gives the anomalous fractal dimensions D = (2 − H) > 2. Absolute majority of the authors ignore any anomaly fractal dimensions. Nevertheless, negative Hurst index H < 0 does not contradict the main definitions of the power-law correlations for fractal distributions [9], subject to rejection from the hypothesis of self-affinity. It is possible that in the case when H < 0 anomalous fractal dimension D > 2 gives a measure of fragmentation [10] correlations in complex networks. Anomalous fractal dimension D > 2, if H < 0, we observe during strong inflammations at asthma for range r = 64 in Figure 2 and at hepatitis B for r = 8 in Figure 5. Thus, the abnormal fractal dimensions D > 2 in oxidative activity of DNA inside cells closely connected with fragmentation of correlations during the serious inflammations. In this case we have a mix of normal D < 2 and abnormal D > 2 fractals for various scales of clusters, at various range r.
Other comments connected with differentiation and classification varied distributions of Hurst index in Figure 2. In particular Hurst exponent H indicates persistent or correlated (H > 1/2) and anti-persistent or uncorrelated (H < 1/2) behavior of trend of irregularity in the frequency distributions of flashes. Persistent behavior is observed in Figure 2 for asthma, when H (r = 256) = 0.5435. Anti-persistent behaviors are observed for healthy person with H (r = 256) = 0.1971 and for oncology with H (r = 256) = 0.4018. In the last cases fractal dimensions belong to the interval 1, 4 < D < 1, 8. We observe different behavior of Hurst exponent for varied groups the states of health in Figure 5. Good health corresponds to anti-persistent behavior of H < 1/2 for any range r. Unhealthy people corresponds to persistent behavior of H > 1/2 for range r > 64. Absolute dominants of anti-persistent behavior of immunity for healthy people give more rich spectra responses of immunity than persistent and predictable behavior for rather poor immune reactions of unhealthy people. The ratio of richness/poorness for immunity here often connected with more rich biodiversity of neutrophils in the blood of healthy people than for poor biodiversities of neutrophils in the blood of unhealthy people [1,4], as it is shown in Figure 6. Here we use Shannon-Weaver biodiversity of neutrophils [1,4].
3. Biodiversity and Trends in Oxidative Activity of DNA inside Neutrophils
Let us define Shannon-Weaver biodiversity of fluorescing neutrophils. The function of P(I) = Pi can be considered as density of probability for frequency of flashes Pi. We can enter the information for the frequency distribution of flashes 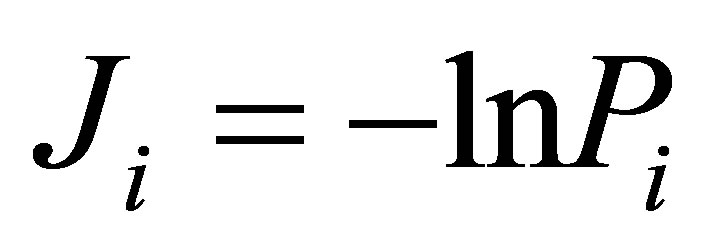 and Shannon information entropy
and Shannon information entropy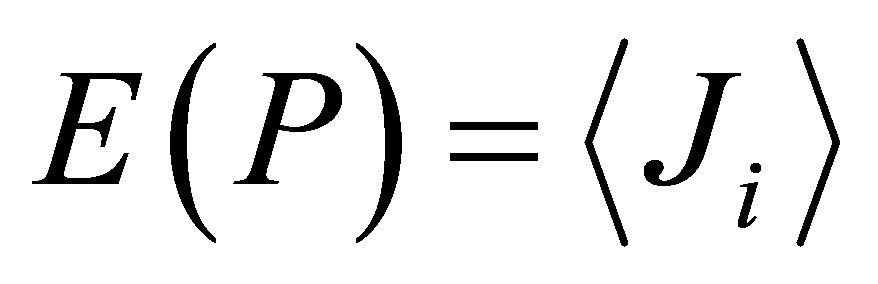 , where
, where
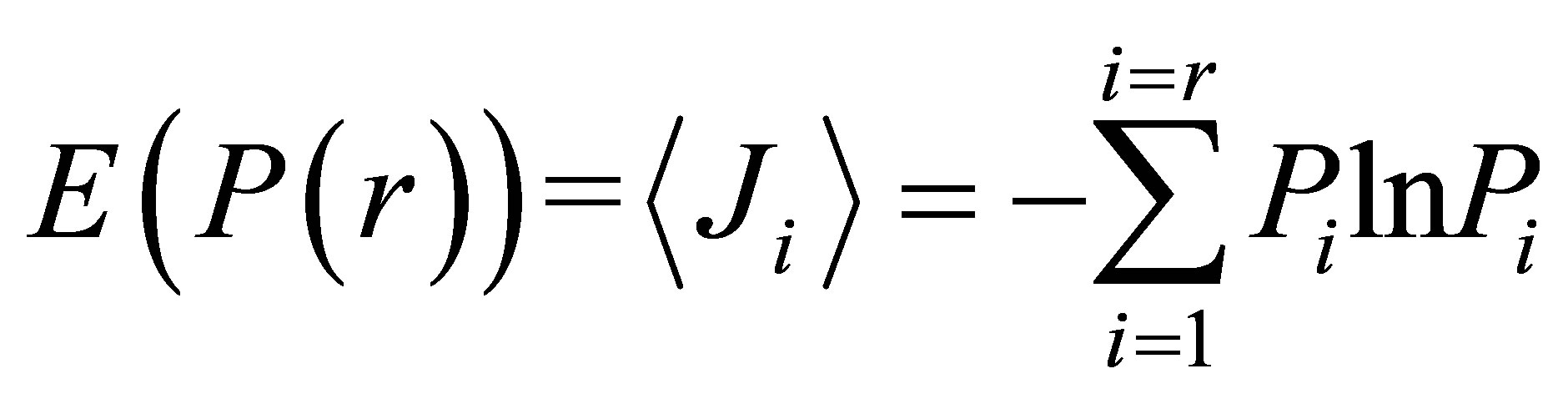 (3)
(3)
 (a)
(a) (b)
(b)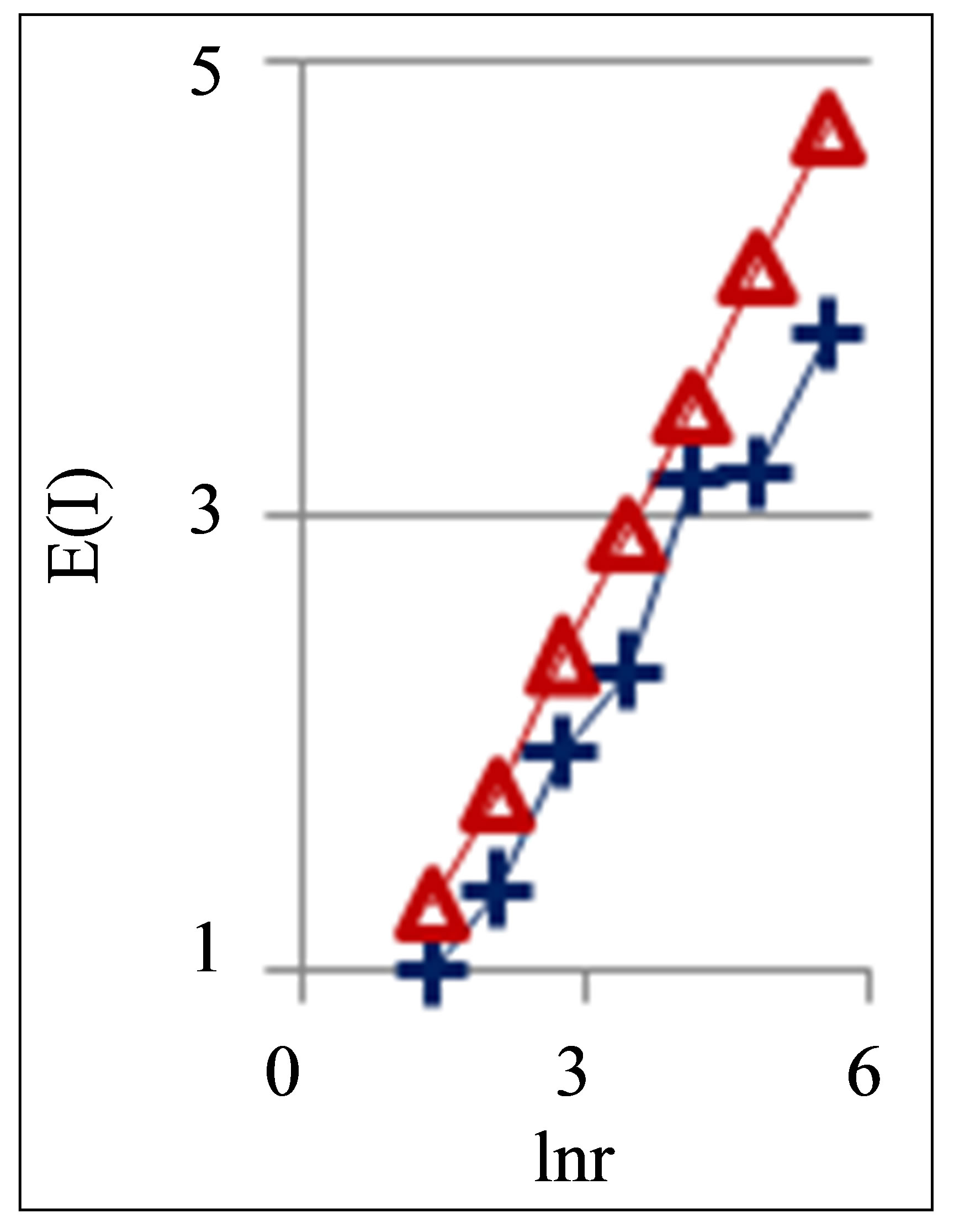 (c)
(c)
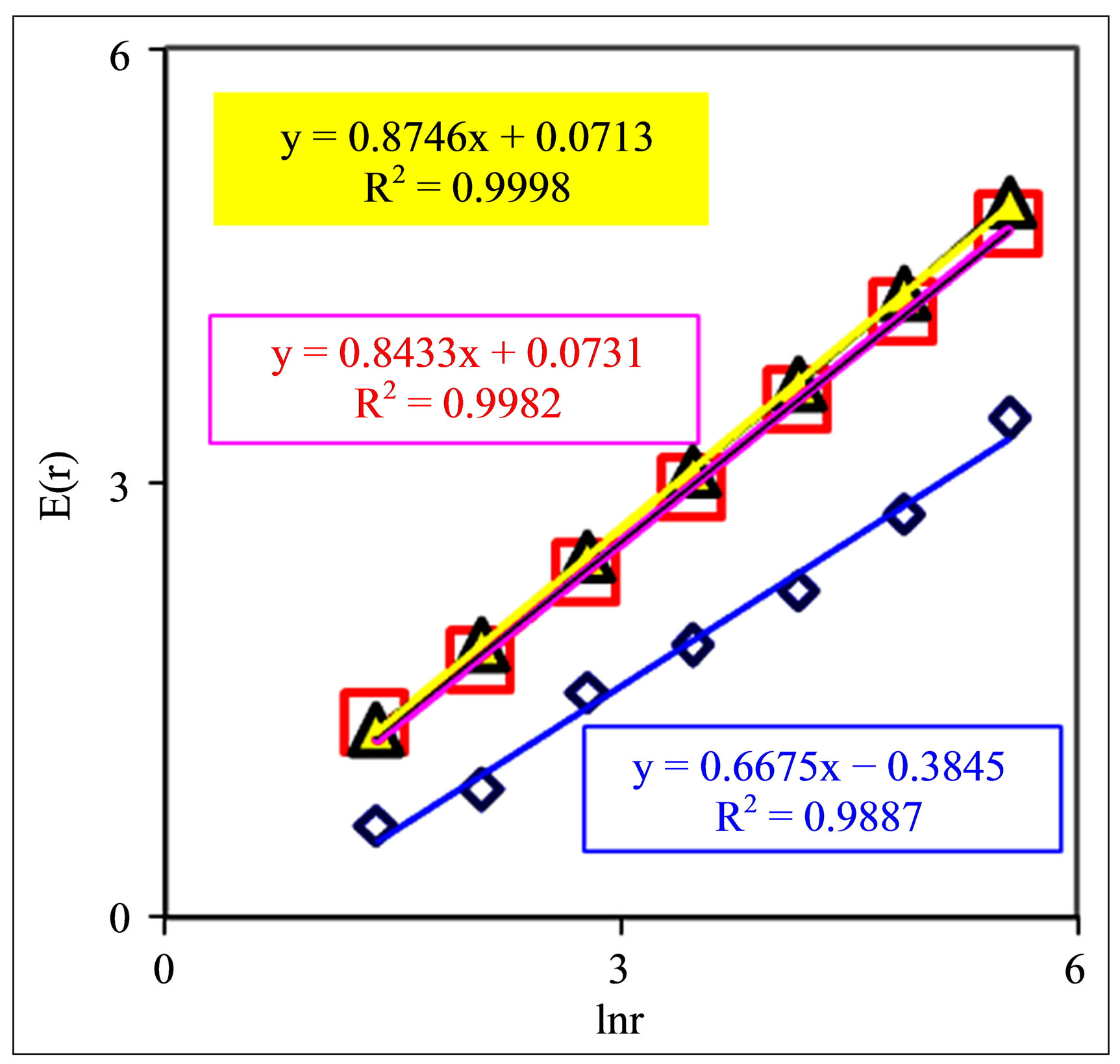
Figure 6. Dependences of Shannon-Weaver biodiversity E(r) of neutrophils on logarithm of range r: (a) Three different donor with oncology, asthma and good health; initial histograms see in Figure 1; (b) One and the same healthy man in different time; initial histograms see in Figure 3; (c) One and the same patient with combined disease of oncology and hepatitis B before (lower line) and after medical treatment; initial histograms see in Figure 4.
Shannon entropy E(r) for frequency distribution of flashes depends on histogram’s range r, which coincides with the maximal number of channels of intensity measurements at given range r. Information 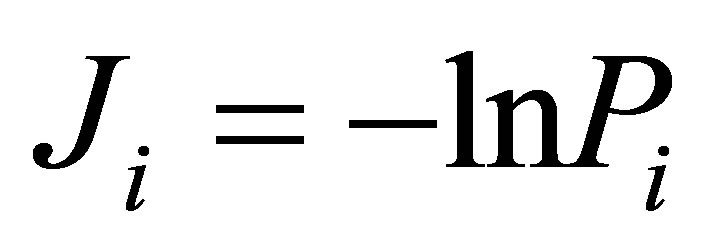 is defined by the flash probability P(I) of fluorescing neutrophils with specified intensity in the specified channel. Thus, fluorescence’ histogram visualizes the probability of existence of neutrophils with a specific oxidizing activity of chromosomes in the given sample of blood. Therefore, Shannon entropy E(r) also characterizes the Shannon-Weaver index E(P) [5,6] for the biological diversity of neutrophils. Distinctive features of neutrophils here are determined by different oxidizing activities of various DNA, which are reflected in fluorescence. Distinctions in neutrophil activity for oxygen metabolism and fluorescence interconnected with peculiarities of chromosomes structure and large-scale chromosomal correlations in the nucleus of neutrophils. These correlations reflect the distribution networks of ethidium bromide in chromosomes, coinciding with networks of oxidizing activity of fluorescing DNA. The same approach may be used for definition biodiversity of any other cells.
is defined by the flash probability P(I) of fluorescing neutrophils with specified intensity in the specified channel. Thus, fluorescence’ histogram visualizes the probability of existence of neutrophils with a specific oxidizing activity of chromosomes in the given sample of blood. Therefore, Shannon entropy E(r) also characterizes the Shannon-Weaver index E(P) [5,6] for the biological diversity of neutrophils. Distinctive features of neutrophils here are determined by different oxidizing activities of various DNA, which are reflected in fluorescence. Distinctions in neutrophil activity for oxygen metabolism and fluorescence interconnected with peculiarities of chromosomes structure and large-scale chromosomal correlations in the nucleus of neutrophils. These correlations reflect the distribution networks of ethidium bromide in chromosomes, coinciding with networks of oxidizing activity of fluorescing DNA. The same approach may be used for definition biodiversity of any other cells.
Biodiversity of Shannon-Weaver E(r) of neutrophils in the blood of various people with different states of health, associated with Figure 1, presented in Figure 6.
These illustrations show that Shannon-Weaver biodiversity for populations of neutrophils E(r) depend on the states of health. These illustrations show also that biodiversity E(r) for neutrophils living inside given person depend on range r, which determined by the scale r of clusters in DNA network, by the resolution of the device with maximal number of channels is equal to r or by parameter r as the governing by the scale of averaging.
Figures 6 show a clear logarithmic growth of Shannon-Weaver biodiversity of neutrophils E(r) with increasing of range r or of maximal number r of measuring channels; dE/dlnr > 0 for any kinds the states of health.
We observe richer biodiversity of neutrophils for oncology and poorer biodiversity for inflammatory disease (bronchial asthma) in Figure 6(a). Difference in the Shannon-Weaver index for oncology and for asthma here reaches ≈40% when r = 256 and ≈100% when r = 4.
According to Figure 6(b) Shannon-Weaver biodiversity of neutrophils in the blood of healthy human remains stable over time for any and different scales of fluorescence networks. It means stability of immunity and good health status for given healthy donor during one year. This is general integrated picture of biodiversity conservation of neutrophils, living inside healthy human. According to Figure 5(a) fractal distributions of fluorescence in the localized networks of neutrophil’ populations here are changing in time. Thus, in Figure 5(a) we observe in real time serial individual changes of inner life in various populations of neutrophils, living inside one and the same healthy human in different time, at very high degree of conservation of their overall biodiversity.
Biodiversity of neutrophils in the blood of patient with complex diseases of cancer and hepatitis B, depends on medical interventions, as can be seen in Figure 6(c) in real time. Here treatment of inflammation, associated with the treatment of hepatitis B, leads to the stratification in the dependence of Shannon entropy E on lnr. Hepatitis ensures a marked decrease of neutrophils’ biodiversity (see lower line in Figure 6(c)). The fractal dimension of largest scale networks (r = 4) in this case is D = 2, as and for deterministic functions (see the bottom point in Figure 5(b)). Thus, here observed deterministic network without fractal structure (D = 2), for large-scale network at r = 4. i.e. for intercellular correlations [1], of unknown origin in the populations of peripheral blood neutrophils for given combined disease of hepatitis B and cancer.
The clear decreasing of biodiversity of neutrophils we observe for any inflammations in Figures 6(a) and (c). Thus, a bad health corresponds to decreasing of biodiversity of neutrophils in human body, i.e. leads to a weakness of immune response, just as the sad trend of species extinction successfully ensured by means of a bad ecology.
Let us consider the mean values for overall trends of fractal dimension D = 2 − H for all ranges of r in networks of fluorescing neutrophils with different biodiversity E(r). The negative dependence of fractal dimension D on range r in Figures 2 and 5 for negative sign of derivative dD/dlnr < 0 give very clear criteria of a bad health. The positive sign of derivative dD/dlnr > 0 give very clear criteria of a good health. Shannon-Weaver biodiversity E(r) of neutrophils always defined by the positive logarithmic dependence of E ~ lnr; dE/dlnr > 0 [1]; see also Figures 6. Therefore, the positive trends of dD/ dE > 0 or increase fractal dimension D with increase the biodiversity E(r) of neutrophils correspond to a good health. In this case increasing of biodiversity E or information
According to Figures 2 and 5(b) most notable contribution to the persistent behavior of fractal distributions for unhealthy people brings the value of H(r) < 1/2 at low values of r, corresponding to intercellular correlations [1]. Thus, persistent behavior of intercellular correlations corresponds to more stable and predictable populations of cells, with relatively lower biodiversity E(r) of populations in Figure 6. Restriction and decrease of biodiversity E(r) of neutrophils for manifold autoimmune diseases, inflammations and infections often observed for different diseases [1,4]. In this case, a bad ecology for neutrophils are determined by the disease of human and unhealthy environment provides a robust degradation of each succeeding generation of neutrophils. This is main reason of predictability and persistent Hurst index H < 1/2 for distributions of immunofluorescence. We always prefer the predictable behavior or more simple, rough and predictable responses in more primitive situations with poor choice. Various communities of neutrophils living in the body of unhealthy people have a tendency to conformism correlated behavior and to predictability of correlations due to forced restriction of biodiversity, as in the isolated human communities, living under pressure. All of this, no doubt, weakens the immunity.
Shannon-Weaver index for biodiversity of neutrophils E(r), i.e. Shannon information entropy, presents clear parameter reflecting overall immunity condition at monitoring of health.
Networks of DNA activity in cells interconnected with networks of biodiversity in cells’ communities.
Rich biodiversity of neutrophils E(r) prolongs human life for people with a good and bad health status by increasing the diversity of immune reactions. Good immunity is ensured by a care about a high biodiversity of own neutrophils and good conditions of their environment in the human body.
4. Networks of “Small Worlds” in the Clusters of Fluorescing DNA inside Neutrophils
Consider an undirected network, and let us define d as the mean geodesic (i.e., shortest) distance between pairs of vertex or nodes in a network of flashes of fluorescence. The certain number N of synchronized nodes-flashes in networks of DNA fluorescence inside cells are characterized by the intensity I ~ N, where N defines a common number of correlated nodes in network, if every node in fluorescence network has the approximately identical fragment of oxidative activity of DNA with approximately identical quantity of fluorescing dye. More detailed determination of correlated nodes N in the clusters of fluorescence networks of DNA inside cells now is unknown. The correlation length d depends on the network topology. Random networks with a given degree distribution may be the networks of “small worlds” [5]. Small world behavior is typically characterized by logarithmic scaling for path length tends d ~ lnN [5]. On the other hand the expression of d ~ N1/D defines a linear size of D-dimensional lattice or the size of a fractal cluster d ~ N1/D. Therefore estimation of fractal dimension D of fluorescence in the networks of “small worlds” is D(N) ~ lnN/lnlnN. Standard definition of fractal dimension D [8,10].
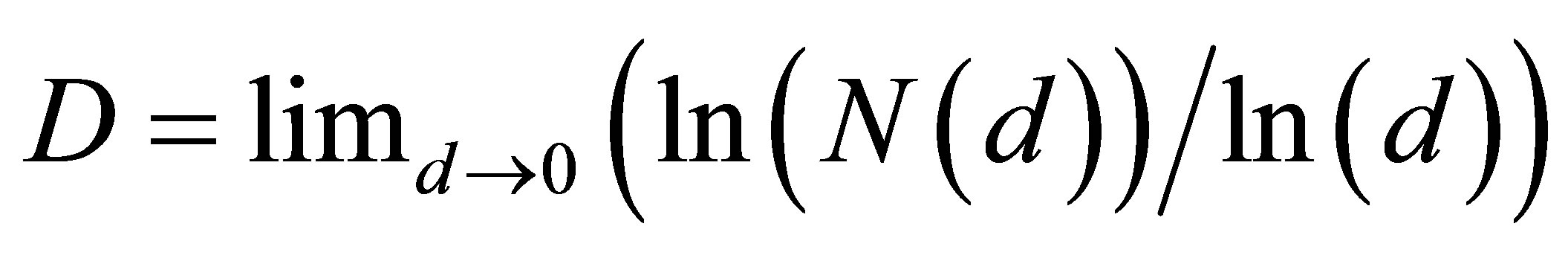 (4)
(4)
also gives D(N) ~ lnN/lnlnN in “small worlds” network. We use the experimental data in immunofluorescence histograms to define Hurst index H and fractal dimension D according to Equations (1)-(3). The transformation of “small worlds” due to reduction of range r = I ~ N leads to expression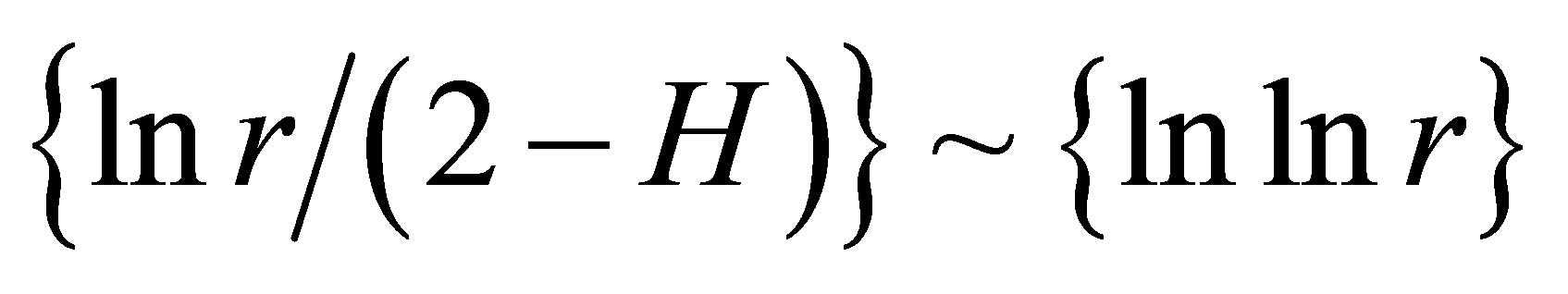 . We used this correlation in the linear approximations of experimental data in Figure 2 in [1] and in Figure 7(a) in this paper. Much more detail picture, at more detailed small scales and without linear approximation presented in Figure 7(b).
. We used this correlation in the linear approximations of experimental data in Figure 2 in [1] and in Figure 7(a) in this paper. Much more detail picture, at more detailed small scales and without linear approximation presented in Figure 7(b).
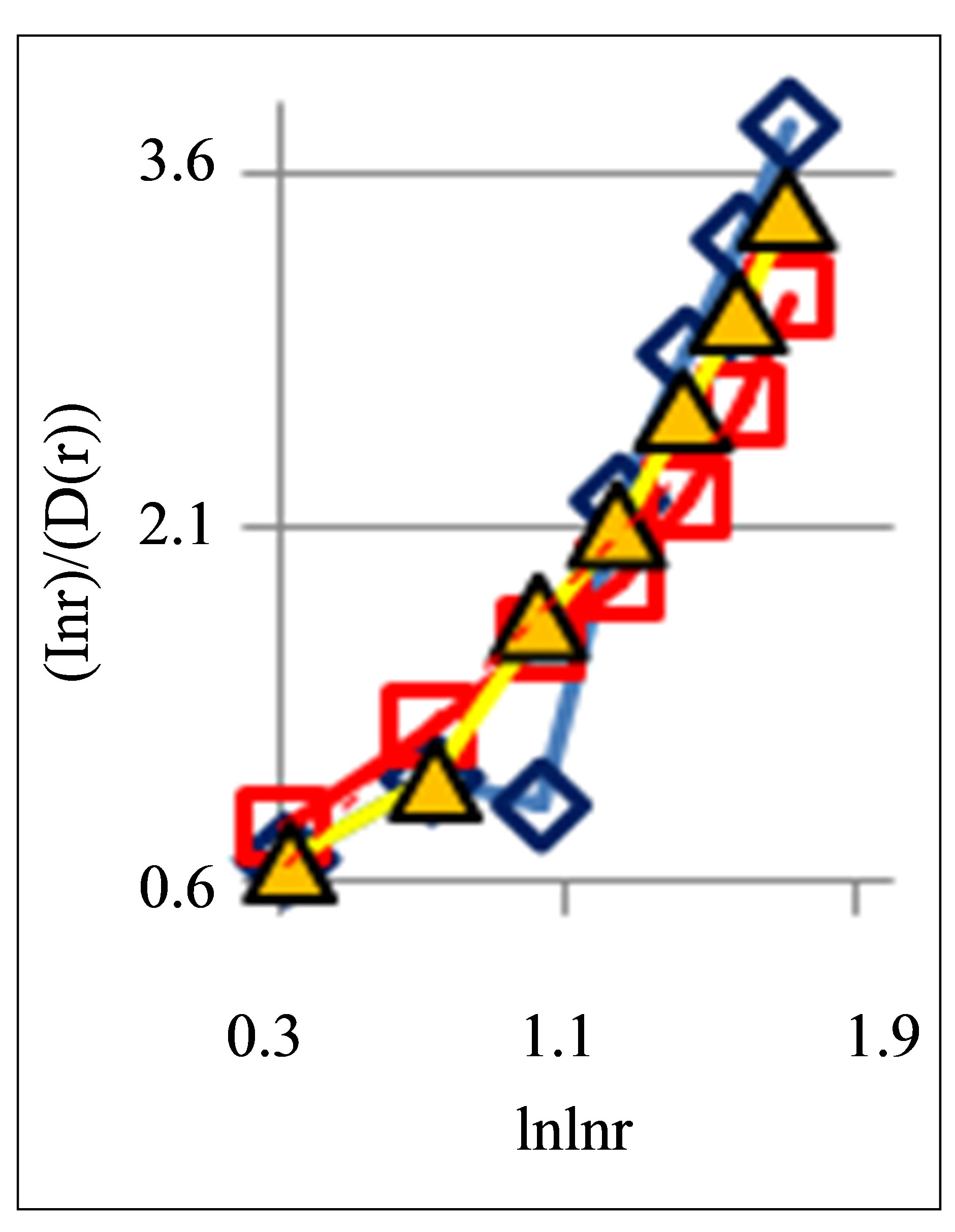
The increasing of the small details in Figure 7(b) form a clear vision that linear growth rate of the functions  in Figure 7(a) gives not very good approximation for more fast than linear growth in the dependence of ln(r/D) on lnlnr for one and the same distributions in Figures 7(a) and (b). Therefore real networks of DNA activity inside cells differ from the ideal net-works of “small worlds” and have more dense packing at decrease of scale or at increase of range r.
in Figure 7(a) gives not very good approximation for more fast than linear growth in the dependence of ln(r/D) on lnlnr for one and the same distributions in Figures 7(a) and (b). Therefore real networks of DNA activity inside cells differ from the ideal net-works of “small worlds” and have more dense packing at decrease of scale or at increase of range r.
 (a)
(a)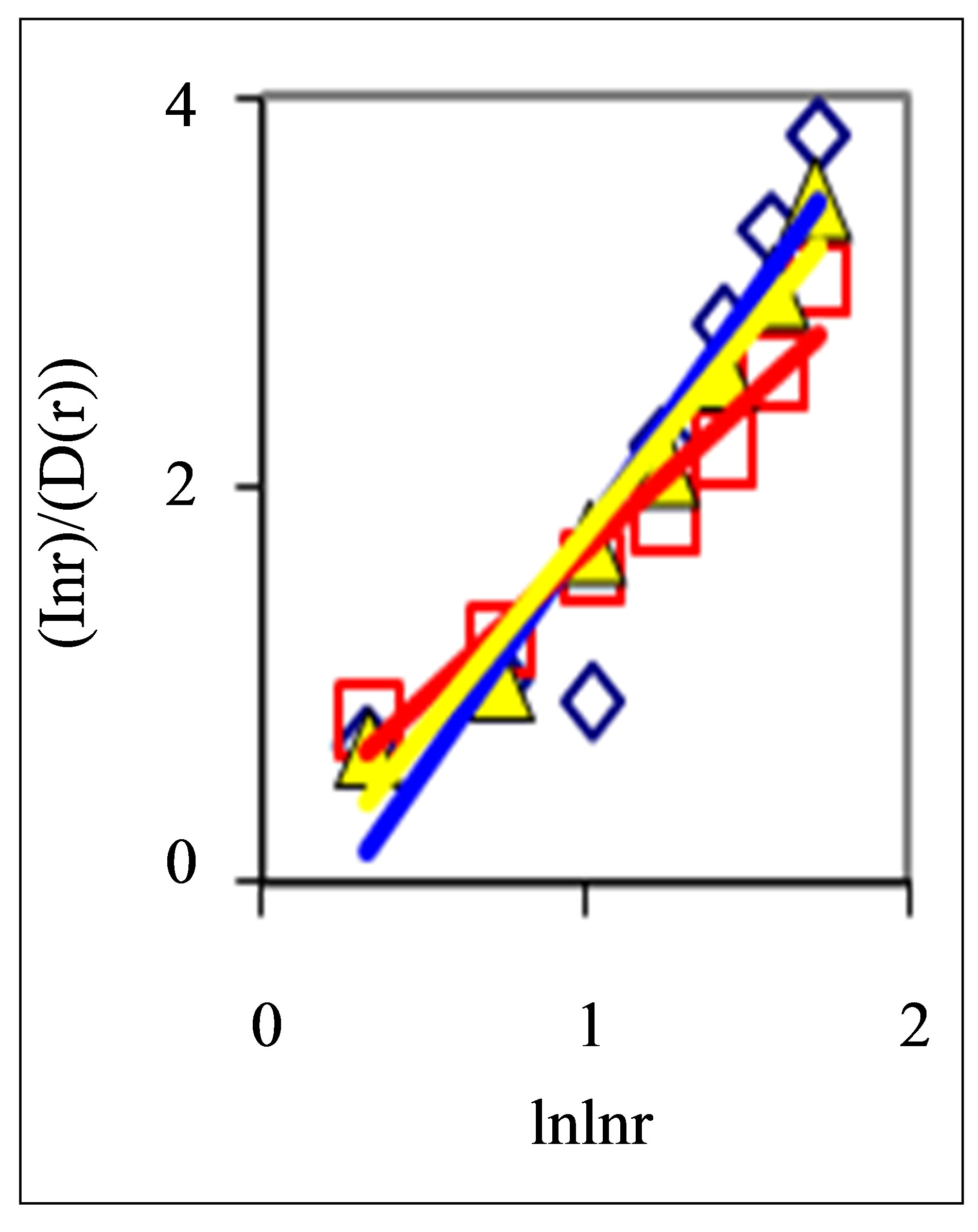 (b)
(b)
Figure 7. Large-scale distributions of : (a) Linear approximations; (b) Detailed non-linear smallscale distributions of
: (a) Linear approximations; (b) Detailed non-linear smallscale distributions of ; initial histograms see in Figure 1.
; initial histograms see in Figure 1.
5. Networks of “Exponentially Small Worlds” of Fluorescing DNA inside Neutrophils
Let us consider the linear dependencies of 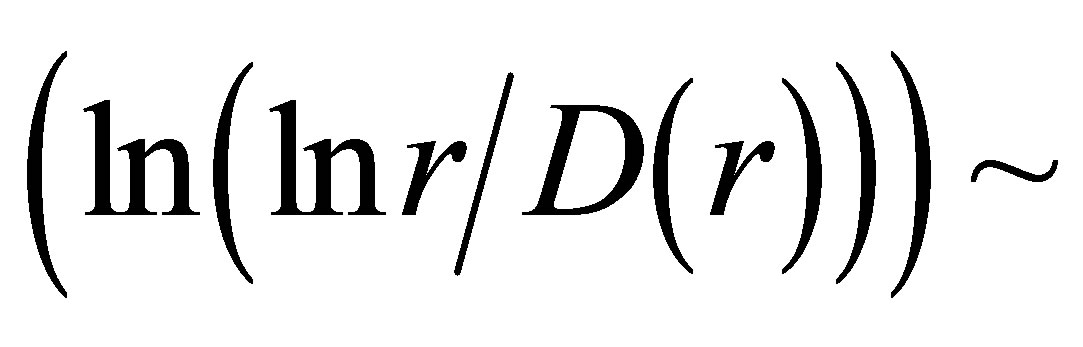
 as the basic approximations of real correlations of DNA activity. In this case we have networks of “exponentially small worlds” with more dense parking than networks of “small worlds”, where
as the basic approximations of real correlations of DNA activity. In this case we have networks of “exponentially small worlds” with more dense parking than networks of “small worlds”, where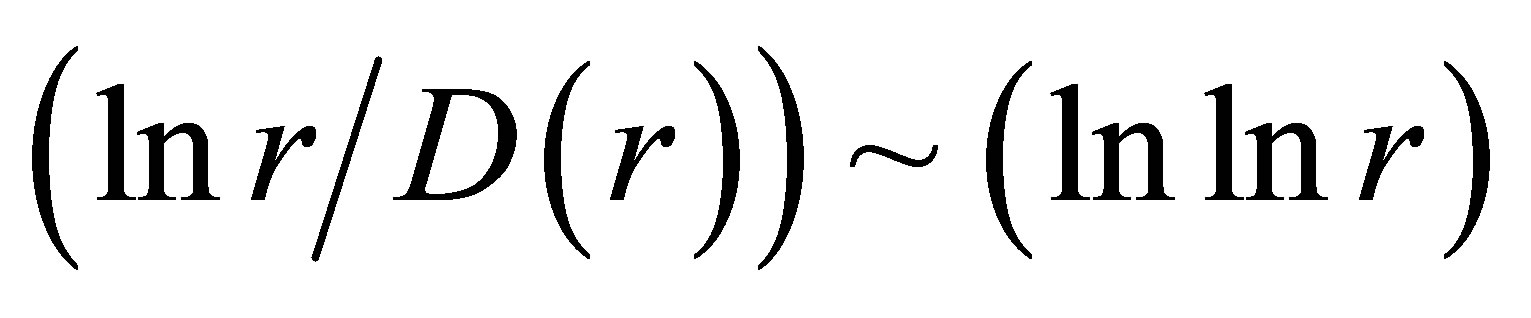 . In our case networks of “exponentially small worlds” are more sensitive for registration of dynamical changes in “real world” networks and deviations from ideal of a good health than networks of “small worlds” presented in [1]. The ideal networks of “exponentially small worlds” without fractals corresponds to D = 2 when
. In our case networks of “exponentially small worlds” are more sensitive for registration of dynamical changes in “real world” networks and deviations from ideal of a good health than networks of “small worlds” presented in [1]. The ideal networks of “exponentially small worlds” without fractals corresponds to D = 2 when 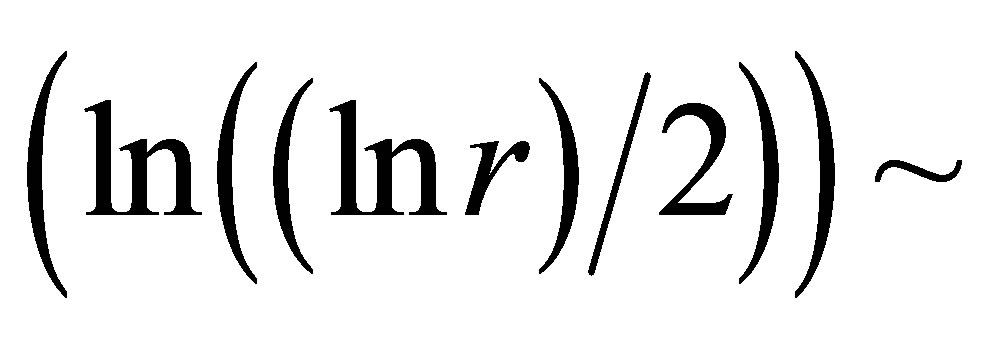
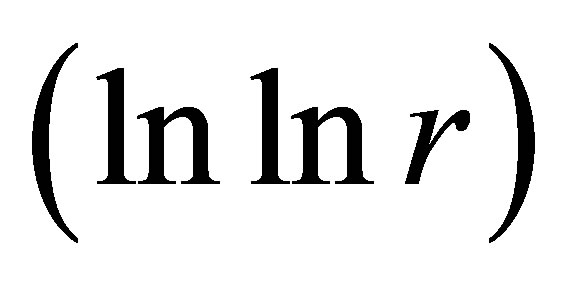 . Ideal and real distributions of
. Ideal and real distributions of  for various states of health for different people in vivo and at medical treatment presented in Figure 8.
for various states of health for different people in vivo and at medical treatment presented in Figure 8.
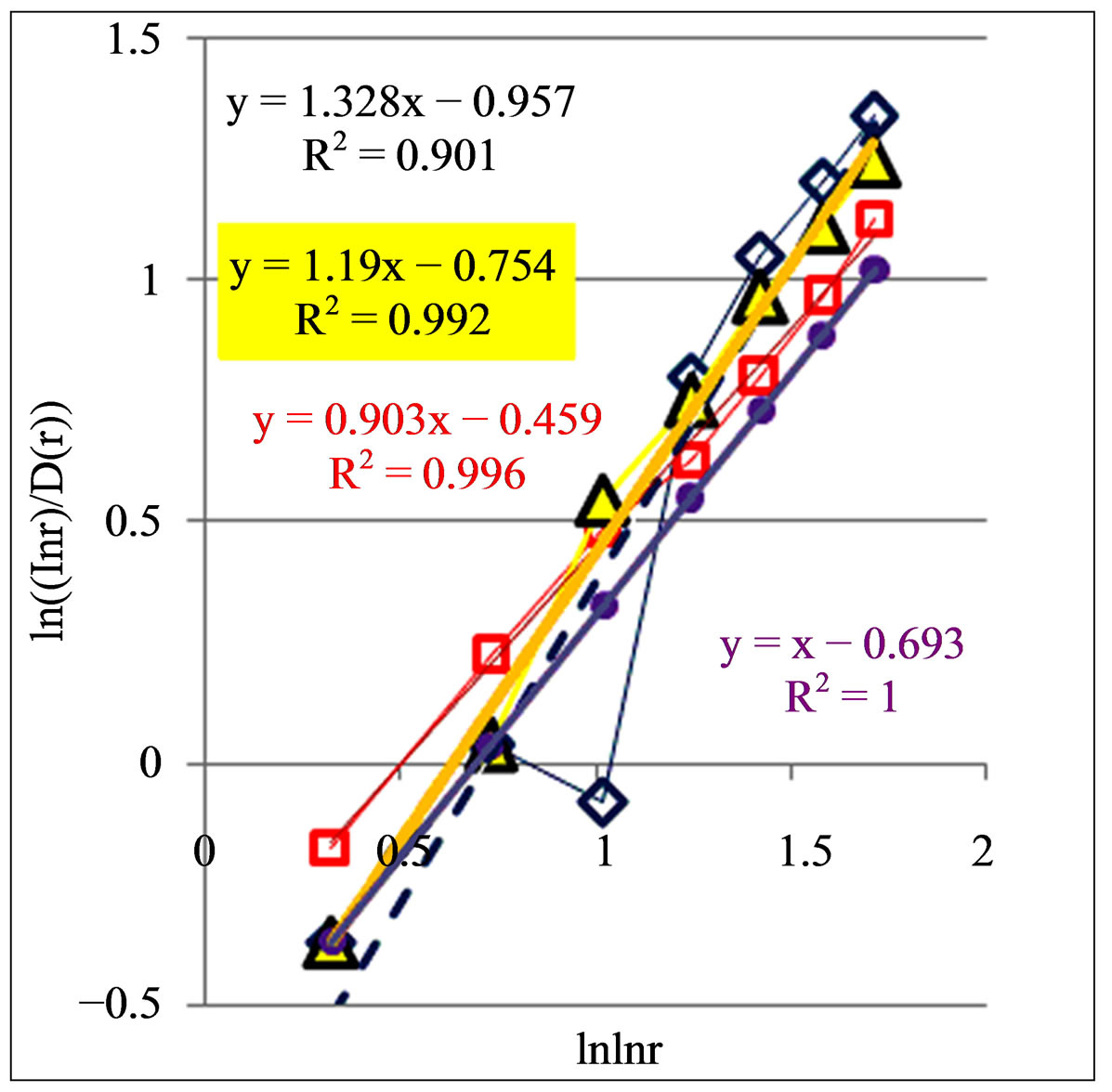
In Figure 8 are observed only two types of deflections, such as “n” and “s” shaped curves, from the linear approximations of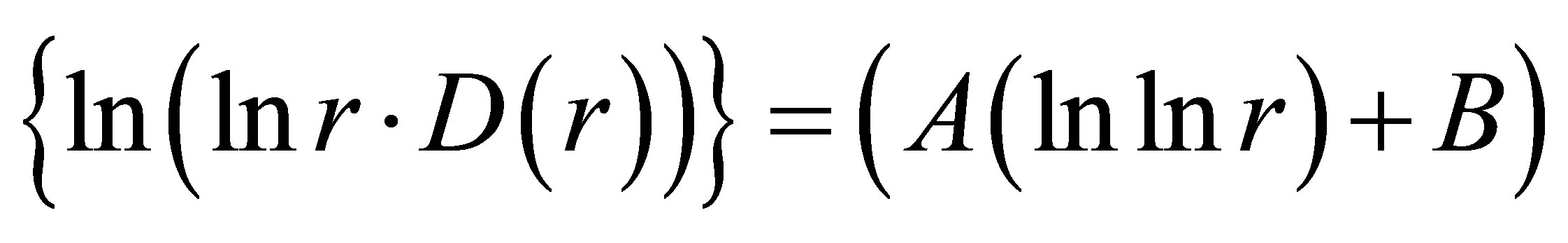 , where constants of A and B are defined and presented in Figure 8 for each given distribution of
, where constants of A and B are defined and presented in Figure 8 for each given distribution of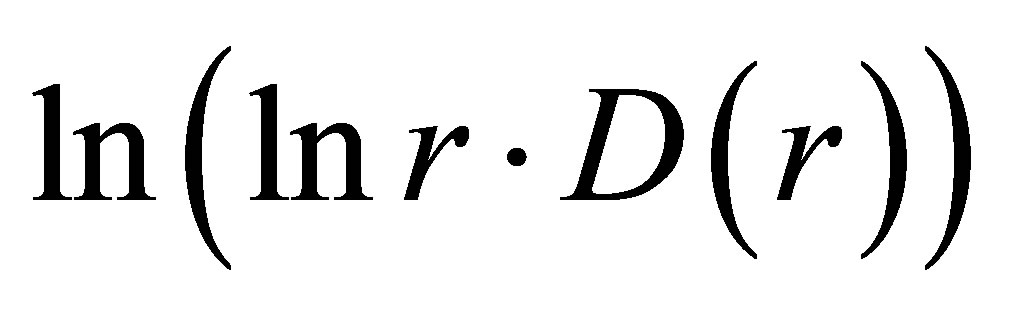 , as an individual line of linear regression in networks of “exponentially small worlds”. Let us introduce the ideal standard for not existing ideal of a perfect good health, at full absent of fractals (D = 2). Then any arbitrary distribution of
, as an individual line of linear regression in networks of “exponentially small worlds”. Let us introduce the ideal standard for not existing ideal of a perfect good health, at full absent of fractals (D = 2). Then any arbitrary distribution of 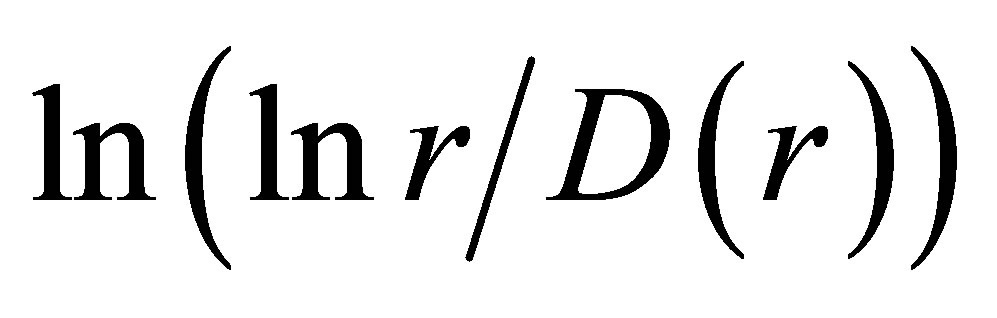 in networks of “exponentially small worlds” may to compare with ideal of
in networks of “exponentially small worlds” may to compare with ideal of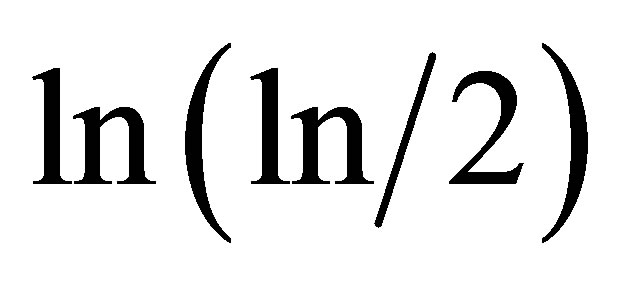 , presented as violet line with round dots in Figure 8.
, presented as violet line with round dots in Figure 8.
Actual behavior of any functions of  in Figure 8 is similar to “n” or “s” shaped curves, as for two types of hysteresis curves at phase transitions and for switching of bistability. These pictures reflect corresponding distributions of “n” and “s” shaped curves for various Hurst indices in Figures 2 and 5. The positive linear trends of dH/dlnr > 0 in Figures 2 and 5 correspond to “s” shaped curves in Figure 8. The negative linear trends of dH/dlnr < 0 in Figures 2 and 5 correspond to “n” shaped curves in Figures 8. Here “n” types of deflections reflect a good health, i.e. good networks of DNA inside cell. Here “s” types of deflections reflect a bad health for bad DNA networks inside cell. This is a very clear assessment of the quality of DNA network for general large-scale communications within of one DNA and between different DNA in the chromosomes inside cells.
in Figure 8 is similar to “n” or “s” shaped curves, as for two types of hysteresis curves at phase transitions and for switching of bistability. These pictures reflect corresponding distributions of “n” and “s” shaped curves for various Hurst indices in Figures 2 and 5. The positive linear trends of dH/dlnr > 0 in Figures 2 and 5 correspond to “s” shaped curves in Figure 8. The negative linear trends of dH/dlnr < 0 in Figures 2 and 5 correspond to “n” shaped curves in Figures 8. Here “n” types of deflections reflect a good health, i.e. good networks of DNA inside cell. Here “s” types of deflections reflect a bad health for bad DNA networks inside cell. This is a very clear assessment of the quality of DNA network for general large-scale communications within of one DNA and between different DNA in the chromosomes inside cells.
Moreover, the values of parameter A, for linear regression of y = Ax + B in Figure 8, give the quantitative signs of a health condition. A bad health is characterized by the values of A more than 1, A > 1. At a good health all values of A less than 1, A < 1. Perfected networks of ideal health, without fractal correlations in DNA activity, when D = const = 2, corresponds to A = 1. In the actual, fractal networks, with different values of D(r), unstable borderline between health and disease also corresponds
 (a)
(a)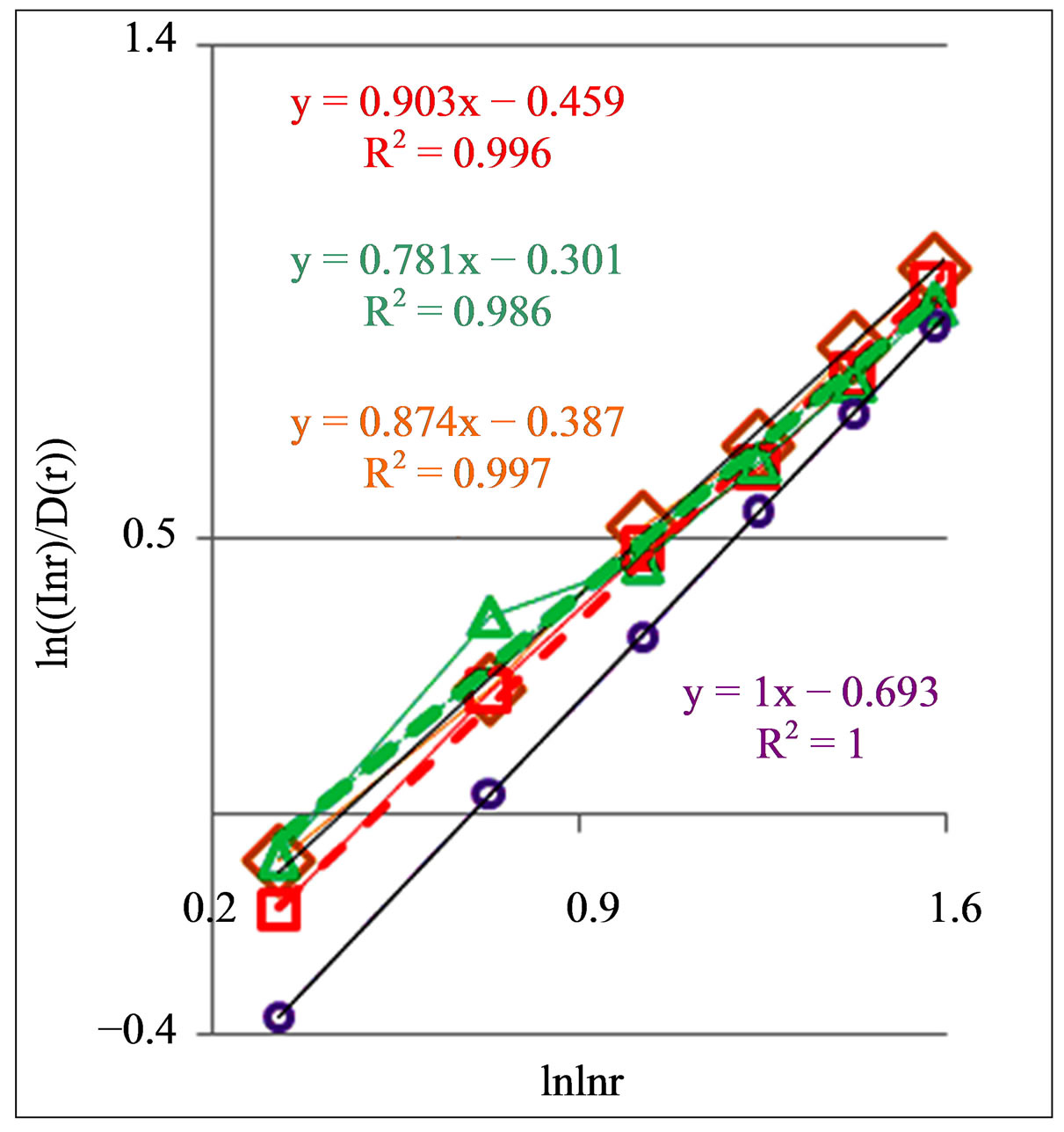 (b)
(b)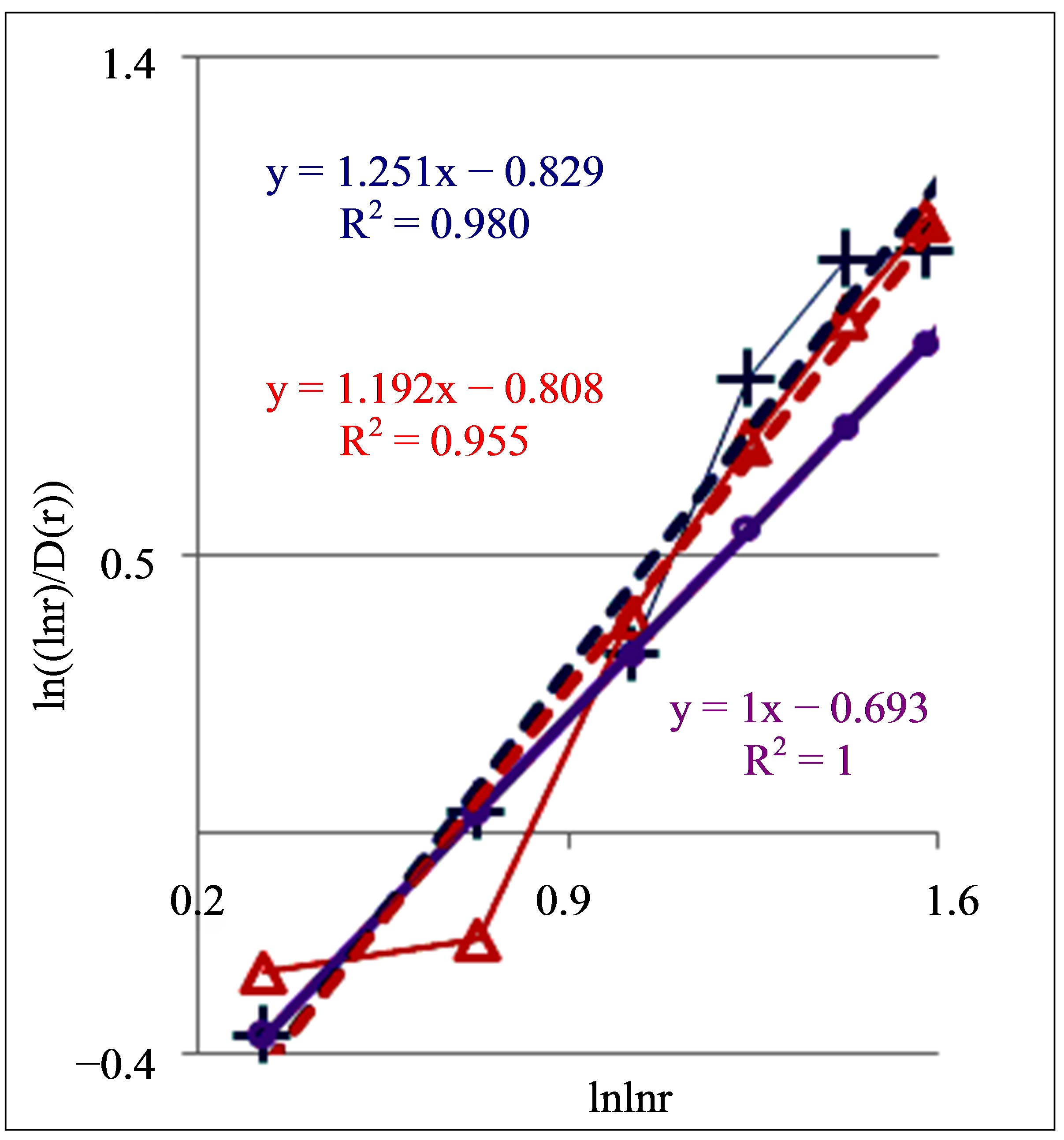 (c)
(c)
Figure 8. Dependence of (ln(lnr/D(r))) on double logarithm of range r in multi-scale networks of “real worlds” and in networks of “exponentially small worlds” for fluorescing DNA inside neutrophils; ideal network of “exponentially small worlds”, without fractals (D = 2), corresponds to violet line with round dots; overall trends as the linear approximations of ln(lnr·D(r)) = A(lnlnr) + B presented here as the equations for dash-and-dot lines in networks of “exponentially small worlds”; (a) Initial histograms for a healthy man and patients with diseases of oncology and asthma see in Figure 1; (b) Initial histograms for one and the same healthy man in different time see in Figure 3; (c) Initial histograms for patient with complex diseases of oncology and hepatitis B before and after medical treatment see in Figure 4.
to A = 1. This value of A = 1 corresponds to unstable not existing situation. Changeability and variations the values of A are varied in time and depend on the states of health in vivo and in medical treatment, as it is shown in Figure 8. Moreover, linear regression of 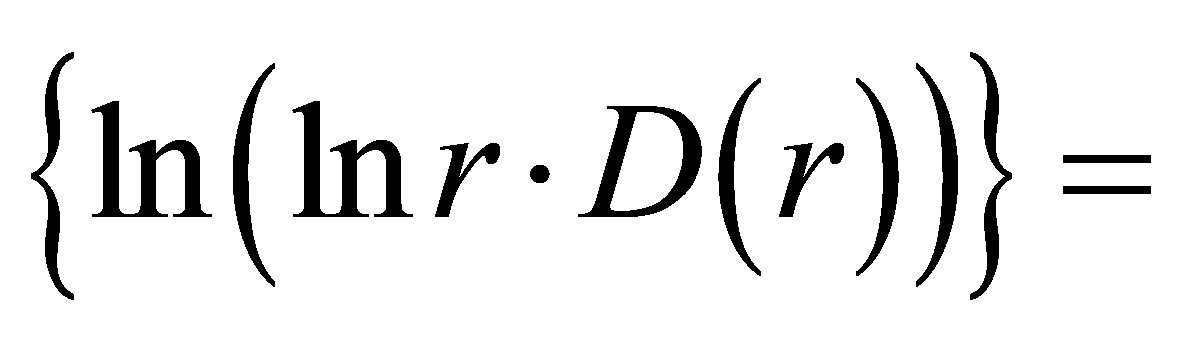
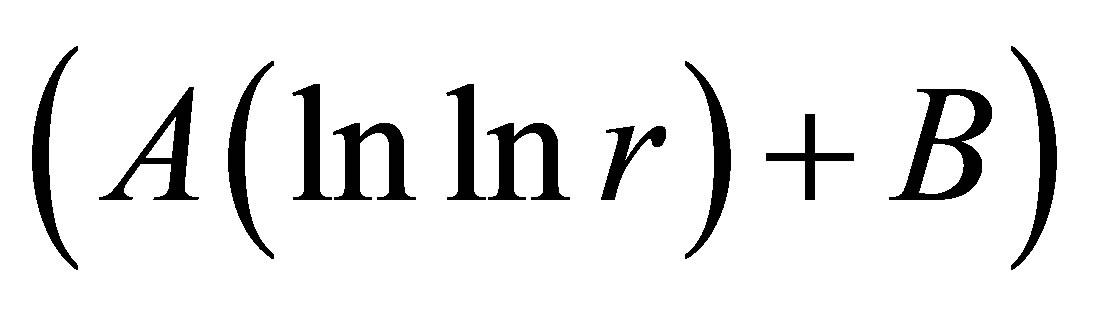 in Figure 8 have a very clear tendency to the increase of inclination angle or value of A at the increase of inflammations. Therefore monitoring for distributions of “n” or “s” shaped curves and values of A for trends in fractal networks of “exponentially small worlds” give very clear and rather simple qualitative and quantitative estimations of health status and common immunity condition for given person at given time from the point of view the inner life of neutrophils in the blood of given human. In this case we define very clear quantitative signs for diagnostics of health at registration chromosomal networks of DNA activity inside neutrophils.
in Figure 8 have a very clear tendency to the increase of inclination angle or value of A at the increase of inflammations. Therefore monitoring for distributions of “n” or “s” shaped curves and values of A for trends in fractal networks of “exponentially small worlds” give very clear and rather simple qualitative and quantitative estimations of health status and common immunity condition for given person at given time from the point of view the inner life of neutrophils in the blood of given human. In this case we define very clear quantitative signs for diagnostics of health at registration chromosomal networks of DNA activity inside neutrophils.
In Figure 8(b) are observed a notable changeability in real time for values of A < 1 for one and the same healthy man in vivo. It means stability of immunity and good health status for given healthy donor during one year.
Systematic changes of biodiversity for neutrophils living inside sick man in Figure 6(c) and changes in fractal networks in Figures 5(b) and 8(c) in real time are showing that medical treatment here reduces the inflammation at decreasing a value of parameter A. This is a sign of successful and good treatment. Medical treatment increases the immunity, i.e. increases the biodiversity of neutrophils E(r) in Figure 6(b), but do not change the positive trends in Figure 5(b) and the types of “s” shaped curves in Figure 8(c) for given patient with incurable diseases of cancer and hepatitis B.
Figure 8 illustrate also notable differences between patients with different states of health in different types of deflections, such as “n” and “s” deflection from ideal linear correlation  in “exponentially small worlds”. Now we don’t know what types of correlations in DNA activity may to produce these ordered consistency from two classes of distributions of fractal structures for “n” and “s” shaped curves. Usually “n” and “s” shaped curves as two types of hysteresis curves are observed at phase transitions and at bifurcations due to switching of bistability. Currently are unknown the origin and detailed correlations between largescale fragments of DNA activity inside cells which provide two types of hysteresis in networks of “exponentially small worlds” of DNA. In networks of “small worlds” two types and examples of hysteresis were described in [11]. If to use compression and transformation for networks of “small worlds” to networks of “exponentially small worlds” then it is possible to conserve hysteresis induced in network of “small worlds”.
in “exponentially small worlds”. Now we don’t know what types of correlations in DNA activity may to produce these ordered consistency from two classes of distributions of fractal structures for “n” and “s” shaped curves. Usually “n” and “s” shaped curves as two types of hysteresis curves are observed at phase transitions and at bifurcations due to switching of bistability. Currently are unknown the origin and detailed correlations between largescale fragments of DNA activity inside cells which provide two types of hysteresis in networks of “exponentially small worlds” of DNA. In networks of “small worlds” two types and examples of hysteresis were described in [11]. If to use compression and transformation for networks of “small worlds” to networks of “exponentially small worlds” then it is possible to conserve hysteresis induced in network of “small worlds”.
Here hysteresis may be connected also with different types of synchronizations in cell cycles for populations of neutrophils living inside healthy and unhealthy body. This is also only hypothetic possibility. Here exist many unstudied and unsolved problems also in information processes and synchronization between coalitions of chromosomal DNA for inter and inner correlations of (in) cells, inside cells and between different cells, such as different neutrophils, lymphocytes and other cells of blood and body, in addition to or instead of epigenetics.
Let us note, also, some fragments of deterministic communications of unknown origin in networks of DNA activity. We often observe mix of fractal and non-fractal correlations for different scales (rank) of r in different samples of blood for unhealthy people. According to Figures 2 and 5(b) most notable contribution to the persistent behavior of fractal distributions for unhealthy people brings the value of H(r) < 1/2 at low range number of r, corresponding to intercellular correlations [1]. Thus, persistent behavior of intercellular correlations corresponds to more stable and predictable populations of cells, with relatively lower biodiversity E(r) of populations in Figures 6. Fractal dimension of largest scale networks (r = 4) in this case is D = 2, as for smooth deterministic functions (see the bottom points in Figures 2, 5(b), and 8(a), (c)). Thus, here observed the deterministic networks without fractal structure (D = 2) at rank r = 4. This case corresponds to intercellular correlations [1] of unknown origin in the populations of neutrophils for combined disease of hepatitis and cancer, for bronchial asthma and for oncology.
Thus, now we haven’t clear understanding many details of DNA life and activity inside living cells. In this regard let us note some modern approaches, based on new results in the last few years, which no reflected in textbooks, but give important new accents for researchers and for discussions of two classes of features in Figures 2, 5 and 8. At first, in nano-scale range in 3D chaotic coil of nuclear DNA various intra-chromosomal and interchromosomal correlations in the coalitions of DNA may to play the effective role of varied networks consisting from self-organized nanopores for segments of DNA. Nanopores produce various modifications and different switching of multistability in the behavior of various fragments of DNA [12]. At rather dense packing of chromosomes in the cells very small local changes in networks of “exponentially small worlds” may have serious the effects of. Moreover, topological constraints in DNA activity inside cells interconnected with varied diseases [1]. For instance, cancer cells carry numerous genomic rearrangements. Networks of DNA correlations inside cells as the chromatin structure could play a role in molecular mechanisms involved in formation of genomic rearrangements and influence the distribution of rearrangements observed in cancer [13]. It’s not epigenetics.
More exotic and hypothetic possibilities of a new regulation in DNA activity connected with building a chromosome segregation machine [14]. It’s not epigenetics.
Rather prosaic reasons for existence of two classes the ordering of results in Figures 2, 5 and 8 connected with two dominant types of statistical stability for nonlinear distributions of DNA activity inside cells. Two dominant classes for negative and positive trends in Figures 2 and 5 and for “n” and “s” shaped curves in Figure 8 reflect the sum of effects oxidative activity of DNA inside cells. This dual or bistable behavior interconnected with two dominant types of positive and negative statistical stability for large-scale activity of fluorescing DNA [3]. Here a good health reflected in the stable and attractive distributions of DNA fluorescence, inflammation is reflected in the unstable distributions and autoimmune diseases are reflected in the neutral stability for large-scale distributions of immunofluorescence [3]. These changes of stability correspond to transcritical bifurcation of averaged large-scale distributions of immunofluorescence [3]. Last comments belong to the stability of large-scale distributions with range = 4. More detailed connections of “n” and “s” shaped curves in networks of “exponentially small worlds” and bifurcations for the averaged largescale distributions of fluorescing DNA are unknown. It’s not epigenetics.
6. Diversity and “Exponentially Small Worlds” for Nets of DNA inside Chicken Erythrocytes
Proposed criteria a good and bad health can to use for definition a diagnosis and estimation of health not only a human. Let us consider fractals and diversity in the oxidative activity of DNA inside chicken erythrocytes in the blood of young hens and roosters. Preparation and measurements fluorescence of chicken erythrocytes is the same than fluorescence of human neutrophils. Two examples of typical cytometry histograms for young birds are shown in Figure 9.
Initially we offered that in our experiments participate only healthy chickens. We were sure that we are dealing only with healthy birds. Analysis results which presented in Figures 9(c) and (d), where observed two types of positive and negative trends in topology of DNA networks, as for good and bad health of human in Figures 2, 5 and 8 shows that it is not so.
In Figures 9(a) and (b) multiple peaks (maxima) correspond to different cell adhesion complexes of several cells. Adhesion complexes of several cells are reflected in the structure of networks of DNA fluorescence and in the structure of biodiversity E(r) of cells in Figure 10.
Here more diverse adhesions of cells lead to increasing of Shannon-Weaver biodiversity E(r). Actual biodiversity for lonely erythrocytes of chickens is less than in Figure 10. Nevertheless, the main features of classifica-
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 9. Characteristics fluorescing chicken erythrocytes in the blood of two chickens: dependence of normalized frequency distribution of flashes P(I) on their intensity I (a) and for clearest only central part of histogram (b) for two chickens; first chicken has symbol cross. Common number of flashes is N0 = 20,363; second chicken has symbol red ring. Common number of flashes is N0 = 25,306; (c) Dependence of Hurst index H(r) on logarithm of range r in networks of DNA fluorescence with different scales; (d) Dependence of 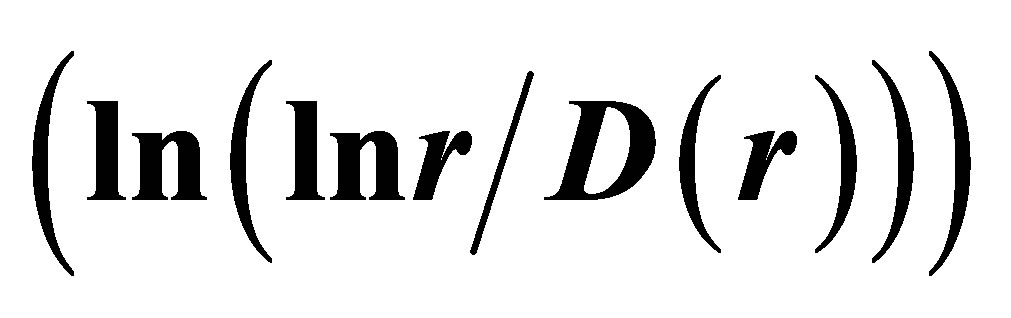 on double logarithm of range r in multi-scale networks of “real worlds” and in networks of “exponentially small worlds”; ideal network of “exponentially small worlds”, without fractals (D = 2), corresponds to violet line with round dots; overall trends as the linear approximations of
on double logarithm of range r in multi-scale networks of “real worlds” and in networks of “exponentially small worlds”; ideal network of “exponentially small worlds”, without fractals (D = 2), corresponds to violet line with round dots; overall trends as the linear approximations of  presented here as the equations for dash-and-dot lines in networks of “exponentially small worlds”.
presented here as the equations for dash-and-dot lines in networks of “exponentially small worlds”.
tion of health of young birds based on fluorescing DNA inside chicken erythrocytes in Figures 9(c), (d) and 10 similar to those of the classification of human health for fluorescing DNA inside human neutrophils in Figures 2, 5 and 8. Positive and negative trends in topology, Good and Bad DNA Network in chicken erythrocytes are defined as for human neutrophils. These responses reflect the common estimations of chicken immunity, including hidden and unidentified diseases, as for common sum of all kinds of health and illness.
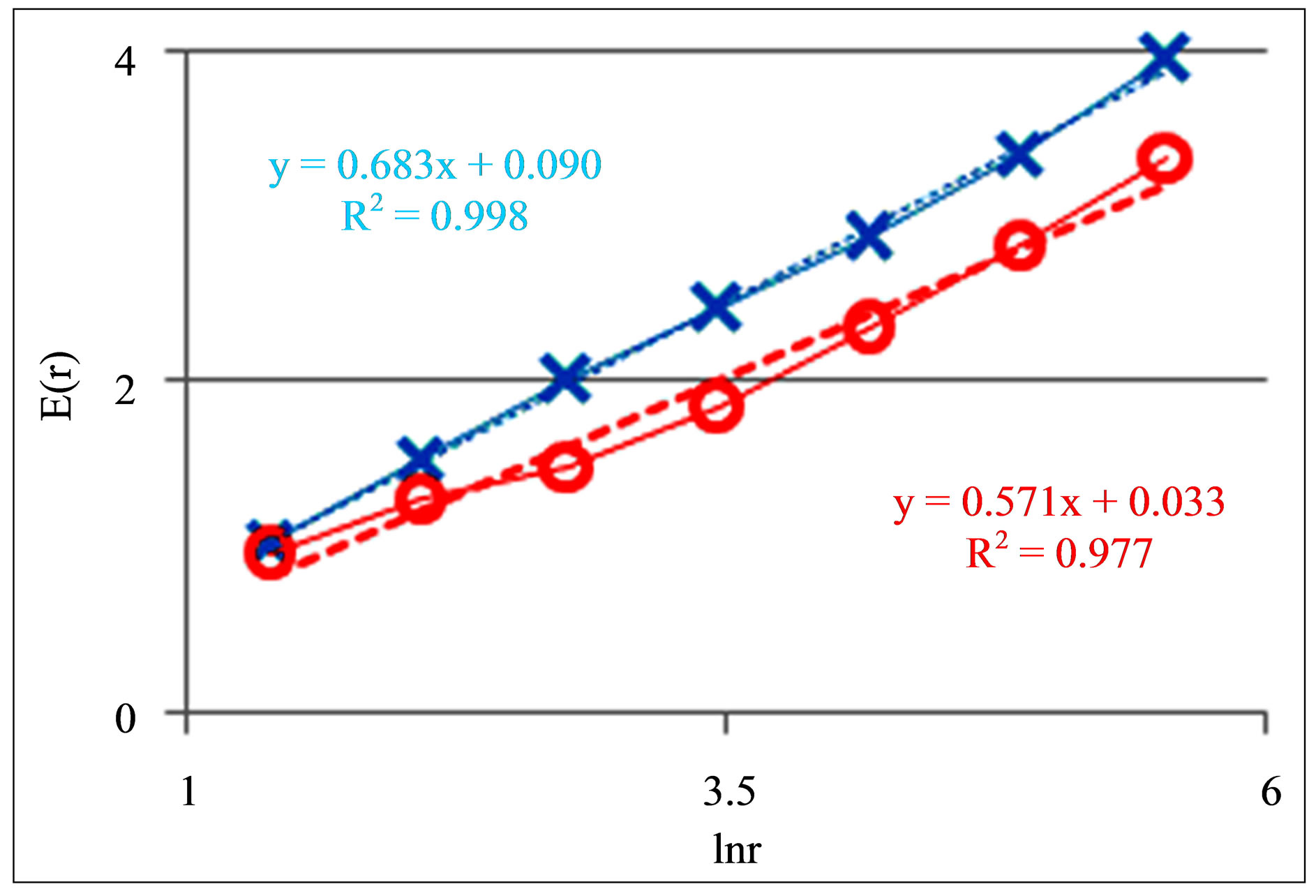
Figure 10. Dependences of Shannon-Weaver biodiversity E(r) of chicken erythrocytes on logarithm of range r; cross and ring points corresponds to unhealthy and healthy chickens; initial histograms see in Figures 9(a) and (b).
According to Figure 10 dependences of biodiversity E(r) on scale r are monotonic and E(r) ~ lnr. Therefore, Figures 9(c) and (d) also define networks of DNA activity in the dependence on biodiversity E(r) of erythrocytes inside chicken body. Main results for fluorescing DNA in human neutrophils may to apply to assess the health status of chicken at analysis of fractal networks of fluorescing DNA inside chicken erythrocytes. Therefore, these approaches are useful for veterinary medicine.
Thus, large-scale fractal networks for fluorescing DNA in neutrophils and erythrocytes of healthy and unhealthy humans and birds are similar. This universality is connected with the proximity of networks of “real worlds” for oxidative activity of chromosomal DNA in the living cells to standards of “exponentially small worlds”. Here observed also similarity in the character of topology trends and deviations from ideal networks of “exponentially small worlds” for a good and bad health of different humans and different birds. Thus, we may to propose that 3D oxidizing activity of real nuclear DNA for complete set of chromosomes inside cells has some universality in the structure and behavior of large-scale correlations for all healthy and unhealthy humans and beings.
7. Conclusions
In other words, neutrophils are familiar and are meeting with all, without exception, local inflammations, viruses and bacteria, many results of their activities and other inhabitants of human body, biography, heredity, daily life, traditions and structures of master’s biology, architecture and geography for flora and fauna entire ecology and physiology of inner life of human and all its agencies and organs. These knowledge and communications are reflected in changeable structures of large-scale networks for DNA activity inside neutrophils, in various local and individual deformations of correlations in densely packing fractal networks of “exponentially small worlds”, as it is shown in Figures 5, 8 and 9. This response includes the presence of all kinds of health and illnesses, including hidden and unidentified diseases. This response reflects overall estimation of immunity, like for a common sum dominating of influences of positive (good health) or negative (illness) reactions of a given person, from the point of view the inner life of neutrophils’ community, living in different parts of the human body in different conditions.
Main peculiarities of typical distributions for a good and bad health are described like “n” and “s” shaped curves in Figures 2, 5 and 8, as two typical classes of deviations of real situation in health status from violet straight line in networks of “exponentially small worlds” in Figure 8, which play the role not existing, perfected ideal of absolutely good health. The values of inclination angles in these trends, i.e. values of A > 1 and A < 1 for lines of linear regression y = Ax + B in Figure 8, give very clear and rather simple qualitative and detailed quantitative estimations of health, immunity and types of illness.
Networks of DNA activity for a man with a good health in real life are personal and changeable in time, according to Figures 5(a) and 8(b). Here occurs serial changes in the inner life; various populations of neutrophils, living inside one and the same healthy human during one year, are shown in Figures 4, 5(a) and 8(b), at conservation of a good immunity of human. The conservation of a good immunity of humanity is reflected in the stable behavior of the negative trends and values of A < 1 for linear regressions in Figures 5(a) and 8(b). Here exists also conservation of a rather high level of biodiversity of Shannon-Weaver in all populations of neutrophils, as it is shown in Figure 6(b).
Shannon-Weaver index for biodiversity of neutrophils E(r), i.e. Shannon information entropy based on distribution of oxidative activity of DNA inside cells, presents clear parameter reflecting overall immunity condition at monitoring of health. Shannon information entropy E(r) for DNA activity in the full set of chromosomes is very important in the cell life. Networks of DNA activity inside cell interconnected with ecological networks for cells’ communities, i.e. with networks of Shannon entropy. Higher values of information entropy or biodiversity E(r) are preferable for a good immunity. A poorness of information, communications or Shannon entropy restricts a life and development of human.
There is an extremely dense packing of information on DNA activity inside cells. Currently, any other information networks, in nature or in computer and information systems, have much less dense packaging of information than new classes of densely packed “exponentially small worlds” for oxidative activity of DNA inside cells, which are introduced here as experimental facts. These empirical facts are illustrated here by the results of experimental data analysis in Figures 8 and 9. These empirical facts define a very high density packaging of DNA activity in the chromosomal networks, existing for ensuring life activity of cells. A level of complexity of these correlations in Figures 8 and 9 is very high; generalization of all fractal correlations exists only in the double-double (quadruple) logarithmic scale. One may say that these are ugly, bad pictures. Forming pictures in Figures 2, 5, 8 and 9 associated with high compression of manifolds of diverse images and fractal correlations, with their fragmentation and intermittency. Real traffic in complex networks never is smooth [15,16].
Here is the sign of a good health associated with the “s” shaped curves, in the chromosomal networks of “exponentially small worlds” and with high ShannonWeaver biodiversity of neutrophils, i.e. with rather high level for Shannon entropy in the information activity of DNA inside cells. More simple criteria for classifying the General State of Health in the form of answer Yes/No or healthy/sick are based on positive or negative trends in fractal topology, i.e. positive dD/dr > 0 or negative dD/dr < 0 trends in multi-scale fractal networks at increasing of scale r in Figures 2 and 5, giving much less details. Good health of human also is reflected in the increasing of fractal dimensions D(r) with increasing of Shannon Weaver biodiversity E(r) ~ lnr of neutrophils. Bad health reflects the opposite trends.
These topological and informational features of fractal patterns in large-scale packing of DNA activity inside cells reflect the experimental facts about two universal classes of Good and Bad DNA networks, which are not needed in the existence of epigenetics or other hypotheses.
Thus, complex networks, information entropy (Shannon Weaver biodiversity) and fractals in large-scale information structures of DNA activity inside cells belong to the basic target of identification and to the main objects of study and analysis in diagnosing the life of cells, human health and human immunity. Here presented only the first steps to understanding of informational laws, patterns and functions of large-scale correlations for oxidative activity of DNA inside cells.
To be continued.
8. Acknowledgments
The author thanks M. Filatov, for kindly providing the experimental data. I also would be grateful researchers in physics, medicine and immunology for kindly providing the serial systematic experimental data from clinical studies of cells in oncology, cardiology, inflammations, infections, autoimmune, and neurodegenerative diseases with multichannel recording (more than 1000, 10,000 and more channels) of the DNA activity inside different cells by flow cytometry, scanning electron microscopy, their combinations and other methods of high-resolution of spatial dimensions, for reproducible physical measurements of DNA activity inside any cells.
REFERENCES
- N. E. Galich, “Complex Networks, Fractals and Topology Trends for Oxidative Activity of DNA in Cells for Populations of Fluorescing Neutrophils in Medical Diagnostics,” Physics Procedia, Vol. 22, 2011, pp. 177-185. http://dx.doi.org/10.1016/j.phpro.2011.11.028
- M. V. Filatov, E. Y. Varfolomeeva and E. A. Ivanov, “Flow Cytofluorometric Detection of Inflammatory Processes by Measuring Respiratory Burst Reaction of Peripheral Blood Neutrophils,” Biochemistry & Molecular Medicine, Vol. 55, No. 2, 1995, pp. 116-121. http://dx.doi.org/10.1006/bmme.1995.1041
- N. E. Galich, “Bifurcations of Averaged Immunofluorescence Distributions Due to Oxidative Activity of DNA in Medical Diagnostics,” Biophysical Reviews and Letters, Vol. 5, No. 4, 2010, pp. 227-240. http://dx.doi.org/10.1142/S1793048010001196
- N. E. Galich, “Shannon-Weaver Biodiversity of Neutrophils in Fractal Networks of Immunofluorescence for Medical Diagnostics,” Journal of WASET, Vol. 70, 2010, pp. 504-515. http://www.waset.org/journals/waset/v45/v45-92.pdf
- M. E. J. Newman, “The Structure and Function of Complex Networks,” SIAM Review, Vol. 45, No. 2, 2003, pp. 167-256. http://dx.doi.org/10.1137/S003614450342480
- N. E. Galich, “Cytometric Distributions and Wavelet Spectra of Immunofluorescence Noise in Medical Diagnostics,” O. Dossel and W. Schlegel, Eds., WC 2009 IFMBE Proceedings, Vol. 25/IV, 2009, pp. 1936-1939.
- Ya. B. Zel’dovich, et al., “Intermittency in Random Media,” Soviet Physics Uspekhi, Vol. 30, No. 5, 1987, pp. 353-385. http://dx.doi.org/10.1070/PU1987v030n05ABEH002867
- J. Feder, “Fractals,” Plenum Press, New York, 1988. http://dx.doi.org/10.1007/978-1-4899-2124-6
- T. Gneiting and M. Schlather, “Stochastic Models That Separate Fractal Dimension and the Hurst Effect,” SIAM Review, Vol. 46, No. 2, 2004, pp. 269-282. http://dx.doi.org/10.1137/S0036144501394387
- B. Mandelbrot, “The Fractal Geometry of Nature,” W.H. Freeman, San Francisco, 1977.
- M.-B. Hu, et al., “Dynamical Hysteresis Phenomena in Complex Network Traffic,” Physical Review E, Vol. 79, No, 4, 2009, Article ID: 047101.
- M. Wanunu, “Nanopores: A Journey towards DNA Sequenching,” Physics of Life Reviews, Vol. 9, No. 2, 2012, pp. 125-158. http://dx.doi.org/10.1016/j.plrev.2012.05.010
- L. A. Mirny, “The Fractal Globule as a Model of Chromatin Architecture in the Cell,” Chromosome Research, Vol. 19, No. 1, 2012, pp. 37-51. http://dx.doi.org/10.1007/s10577-010-9177-0
- K. Bloom1 and A. Joglekar, “Towards Building a Chromo Some Segregation Machine,” Nature, Vol. 463, No. 7280, 2010, pp. 448-456.
- A. C. Gilbert, W. Willinger and A. Feldmann, “Scaling Analysis of Conservative Cascades, with Applications to Network Traffic,” IEEE Transaction on Information Theory, Vol. 45, No. 3, 1999, pp. 971-981. http://dx.doi.org/10.1109/18.761336
- B. Tadi, G. J. Rodgers and S. Thurner, “Transport on Complex Networks: Flow, Jamming and Optimization,” International Journal of Bifurcation and Chaos, Vol. 17, No. 7, 2007, pp. 2363-2385. http://dx.doi.org/10.1142/S0218127407018452

