Open Journal of Biophysics
Vol.3 No.3(2013), Article ID:34505,5 pages DOI:10.4236/ojbiphy.2013.33024
Stochastic Modelling of Relative Light Sensitivity of Hair Follicles*
Wellcomet GmbH, Karlsruhe, Germany
Email: i.kruglikov@wellcomet.de
Copyright © 2013 Ilja L. Kruglikov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 25, 2013; revised April 27, 2013; accepted May 3, 2013
Keywords: Light Sensitivity; Hair Follicle; Mathematical Model
ABSTRACT
Relative light sensitivity (RLS) of HFs was mathematically described as the ratio of two stochastic variables presenting the durations of light sensitive and light insensitive sub-phases of the cycle according to a new theory of HF light sensitivity formulated in our previous article (Kruglikov, Am J Cosm Surg, 2012, 29:266 - 272). RLS gives possibility to rank the HFs from different body regions according to their light sensitivities. Application of proposed method for estimation of the light sensitivity of scalp hairs predicts remarkable difference in light sensitivities of HFs in alopecic and non-alopecic patients.
1. Introduction
Photoepilation (hair removal through light irradiation) is one of the most important applications of light therapy. According to widely accepted hypothesis of selective photothermolysis, local light absorption and respectively the local temperature increase in a hair follicle (HF) are primarily dependent on its melanin content. This content dynamically changed during HF cycle being the highest during the anagen phase. Correspondingly, the HF light sensitivity must be also periodically changed during the cycle. This idea led to a natural classification of HF light sensitivities in different body areas according to relative duration of their anagen phases in a whole HF cycle, making the facial hairs having this ratio of 0.65 - 0.75 much more light sensitive as in other body areas. Additionally, this idea significantly influenced the optimal treatment strategy since the interval between consequent irradiations in a photoepilation must be long enough to allow the HFs to reach the anagen phase in the next cycle of their development.
However this theory faces different contradictions [1]. Most important of them is the remarkable discrepancy between the theoretical ratio of light sensitive HFs and the number of light irradiations needed for significant reduction of the number of cycling HFs. Another one is the lower light sensitivity of HFs with prolonged anagen phase, which can be observed for example in hirsutism. To resolve these contradictions, we have recently proposed a new theory of HF light sensitivity [1,2]. According to this theory, a HF’s light sensitivity is not simply dependent on its melanin content, but varies significantly in different sub-phases of anagen (A); sub-phases A-III/V are much more light-sensitive than the longest anagen sub-phase connected with growth of hair shaft, A-VI. The light sensitivity of a given HF can be consequently defined as the ratio of its A-III/V duration to the total duration of the HF cycle. This revised theory consequently demands modification in description of HF light sensitivity as well as in irradiation schedule. For this, formalistic description of the light sensitivity of HF population is needed.
Although several authors presented the models of HF cycling [3-5], their results cannot be directly applied for description of HF light sensitivity. These models concerned the deterministic [3] or stochastic [4,5] aspects of HF cycling trying to describe the distribution of durations of different cycle phases in terms of their moments. However, HF light sensitivity must be defined as a ratio of two variables which are the duration of the light sensitive part and the total duration of HF cycle. Since HF cycling is a stochastic process, this parameter is generally not a simple ratio of two average values and needs a stochastic description.
2. Stochastic Description of Relative Light Sensitivity
Let us consider an ensemble of independent HFs with no spatial or temporal correlation in their development. At any moment of time, each HF can be either in a growth phase (anagen, A), undergo the involution (catagen, C), or cease to grow (telogen, T). Further, we will neglect the duration of C compared to other phases of HF cycle and consider it to be apart of T-phase.
Relative HF light sensitivity, RS, is dimensionless and for a given HF it can be written as a ratio
 (1)
(1)
Here 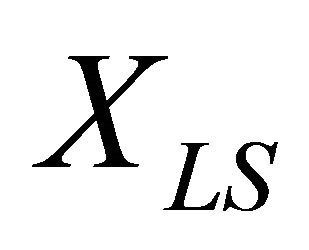 and
and 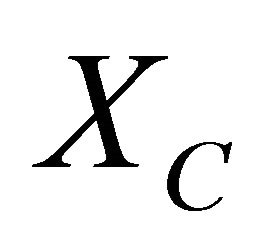 are the random variables (r.v.s) describing the durations of light sensitive periods of HF cycle and of total HF cycle, respectively. As we show later in this article,
are the random variables (r.v.s) describing the durations of light sensitive periods of HF cycle and of total HF cycle, respectively. As we show later in this article, 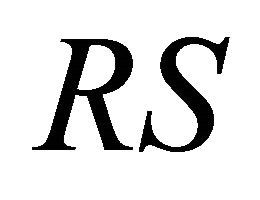 can significantly vary from one HF to another as well as in progressive cycles of the same HF. This significantly deviates from the assumption made in [3] that durations of different HF-phases have the coefficients of variation of approximately 10% and thus the evolution of HFs can be described with deterministic and not with stochastic equations.
can significantly vary from one HF to another as well as in progressive cycles of the same HF. This significantly deviates from the assumption made in [3] that durations of different HF-phases have the coefficients of variation of approximately 10% and thus the evolution of HFs can be described with deterministic and not with stochastic equations.
The average relative light sensitivity,  , of HF population in a given body area can be calculated as
, of HF population in a given body area can be calculated as
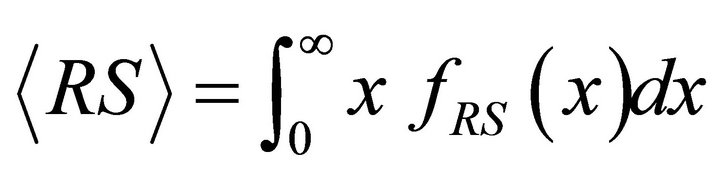 (2)
(2)
where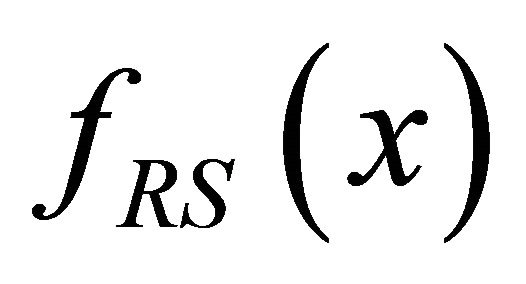 is a probability density function (pdf) of
is a probability density function (pdf) of . Consequently, to receive information about the relative light sensitivity of HFs in a given body region, the data must be collected in pairs
. Consequently, to receive information about the relative light sensitivity of HFs in a given body region, the data must be collected in pairs 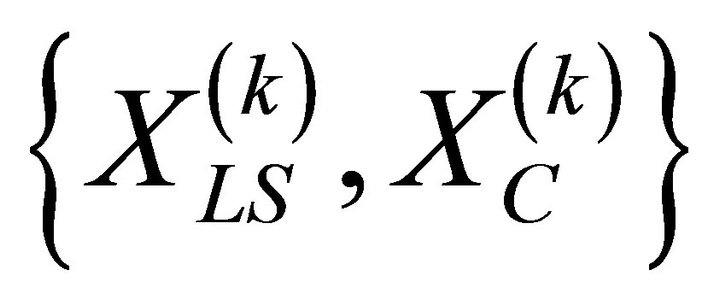 for each HF number k. Only when both
for each HF number k. Only when both  and
and 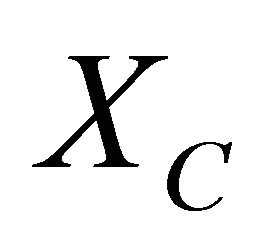 have very small dispersions, will
have very small dispersions, will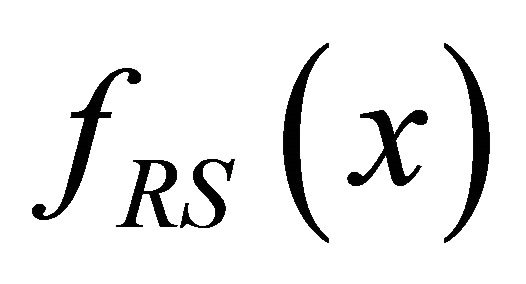 be close to delta-function
be close to delta-function
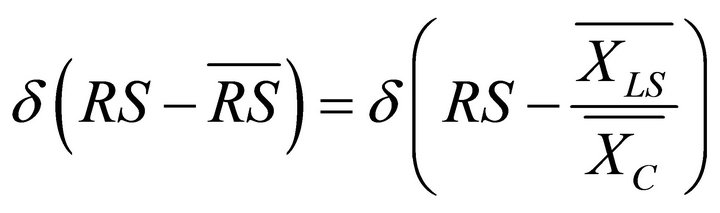
and the stochastic properties of 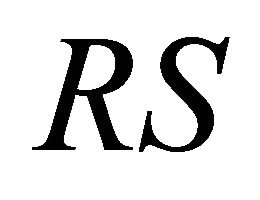 can be neglected.
can be neglected.
We will further consider a stationary population of HFs with the total number of follicles remaining constant during observation time. For this, we assume the HFs can neither miniaturize or dye, and thus cannot leave the cycle. This could be, for example, the case for the intact HF population before light irradiation. Every phase, i, of this multi-phase stationary system can be described by its own distribution of phase durations and can be written in the form which is well known from failure analysis
 (3)
(3)
Here, 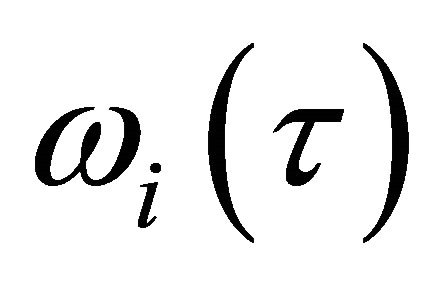 is the conditional probability, a HF of the “age” τ in a phase i will move into the next phase of its cycle.
is the conditional probability, a HF of the “age” τ in a phase i will move into the next phase of its cycle.
Further, to receive the analytical description we consider  to be a gamma distribution with parameters (α, λ):
to be a gamma distribution with parameters (α, λ):
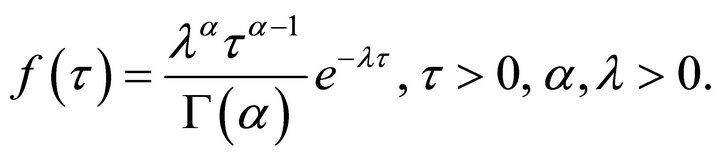 (4)
(4)
Here, we omitted for simplicity the indexing of HF phases. This distribution has the following mean value,  , dispersion,
, dispersion, 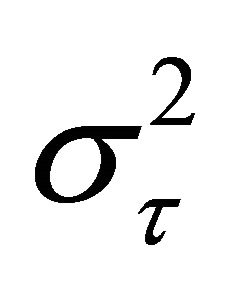 , and coefficient of variation,
, and coefficient of variation, :
:
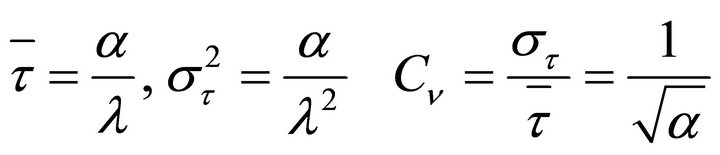 (5)
(5)
To describe the relative light sensitivity of HFs, let us now consider two independent r.v.s, X1 and X2, which are the durations of two different phases of HF cycle. Both X1 and X2 are described by gamma distribution (4), with parameters  and
and  respectively. We are interested in a distribution function of the ratio
respectively. We are interested in a distribution function of the ratio
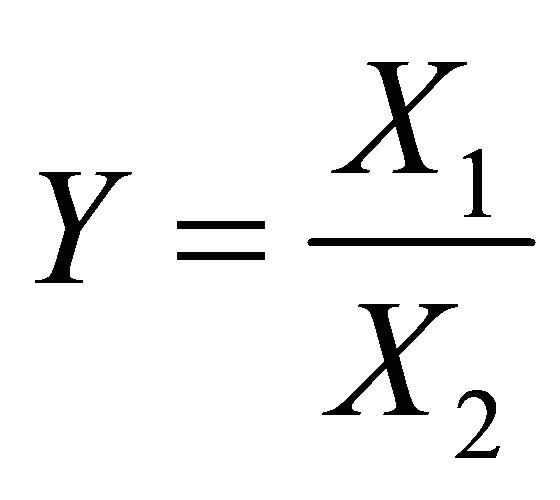 (6)
(6)
It can be shown with application of conventional methods that pdf of Y has the form
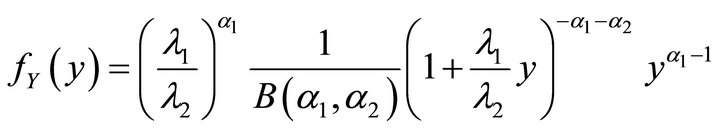 (7)
(7)
where is a beta function with arguments
is a beta function with arguments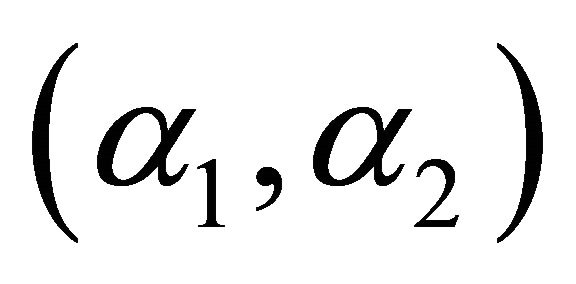 .
.
Let XLS and XLI be the r.v.s describing the durations of light sensitive and light insensitive parts of HF cycle respectively. According to [1], XLS is the sum of durations of A sub-phases III, IV and V, and XLI consists of A sub-phases I, II and VI, as well as of Tand C-phases of HF cycle.
Durations of A-I and A-II as well as of C-phase are generally much smaller than that of A-VI; thus we can further neglect these sub-phases, considering that XLI = XA-VI + XT. Additionally, we will not differentiate between the consequent sub-phases of A-III/V, considering them to be one and the same sub-phase which can be described with one set of parameters. To calculate the relative light sensitivity of anagen we must analyse the ratio
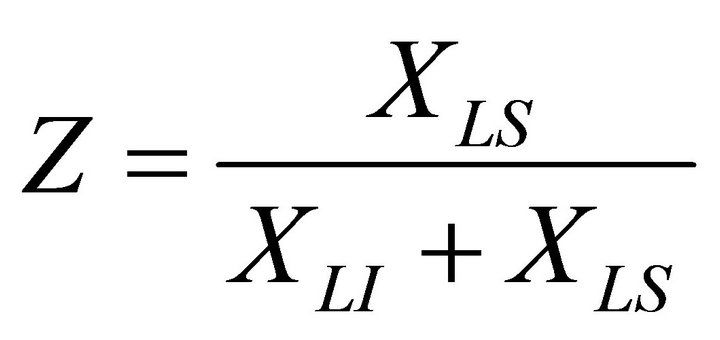 (8)
(8)
Ratio (8) can be transformed into
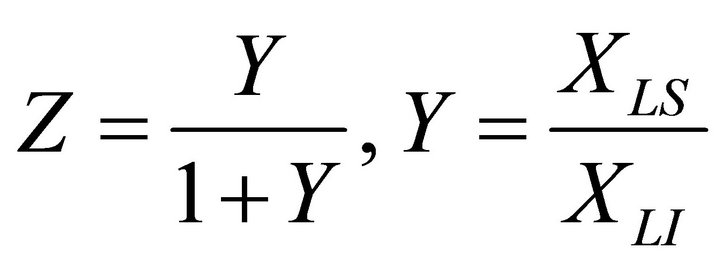 (9)
(9)
Using (7), the pdf of Z can be now presented in a form (0 < z < 1)
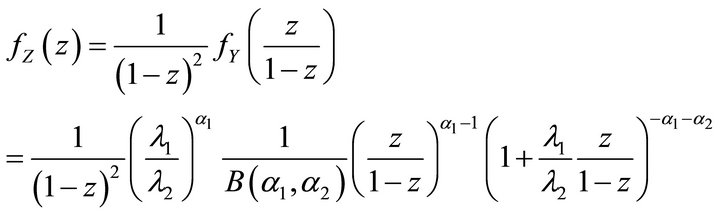 (10)
(10)
Expression (10) gives the formal stochastic description of HF relative light sensitivity. The average value of the ratio (8),  , can be calculated from Equation (2). It takes a simple form for the case of low relative light sensitivity,
, can be calculated from Equation (2). It takes a simple form for the case of low relative light sensitivity,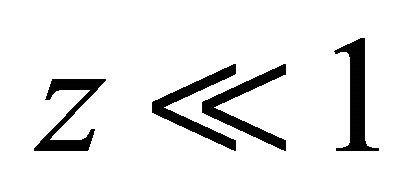 .
.
The statistics of Z can be presented analytically for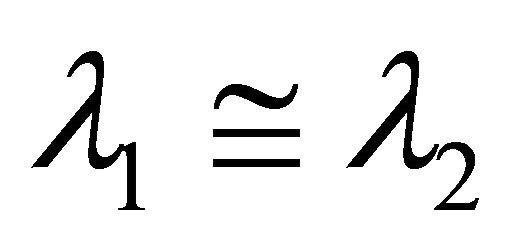 . In this case, (10) takes the form
. In this case, (10) takes the form
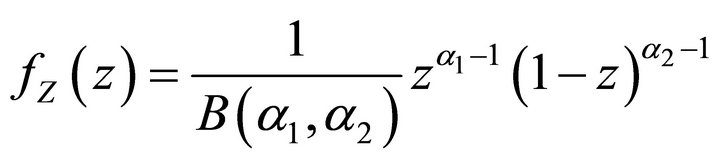 (11)
(11)
and
 (12)
(12)
Taking (5) into account, one can easily show that a simple approximation
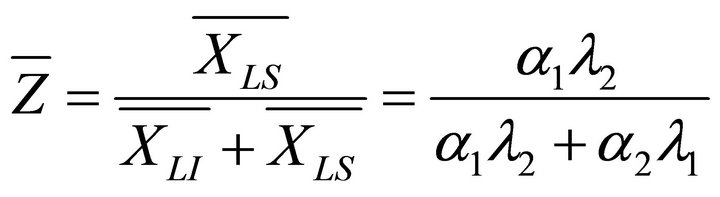 (13)
(13)
gives for 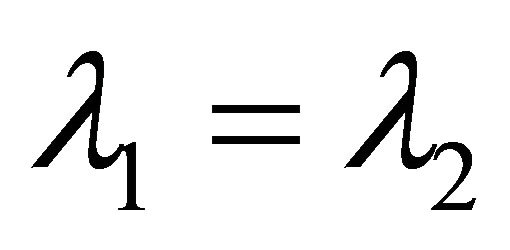 the same result as (12). That means, only for
the same result as (12). That means, only for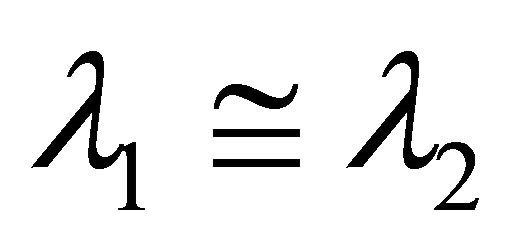 the simple approximation (13), which uses solely the information about the mean values of phase durations and don’t need any other characteristics of their distribution, can be applied.
the simple approximation (13), which uses solely the information about the mean values of phase durations and don’t need any other characteristics of their distribution, can be applied.
3. Relative Light Sensitivity of HFs from Different Body Regions
There is no reliable information about HF phase distributions in different body regions. The best known classification was presented in [6] (see Table 1).
According to classical photoepilation theory, the body regions with higher relative content of anagen hairs must have higher relative light sensitivity. This would make HFs from the cheeks, upper lip and chin much more sensitive to the light irradiation than HFs from other body regions. Theoretically these “light sensitive” HFs could be hit after just 2 light irradiations. As discussed in [1], this picture confronts different experimental and clinical results and must be revised.
To make the approximate classification of relative HF light sensitivities, let us now calculate 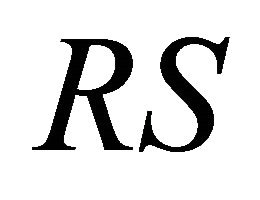 as
as
 (14)
(14)
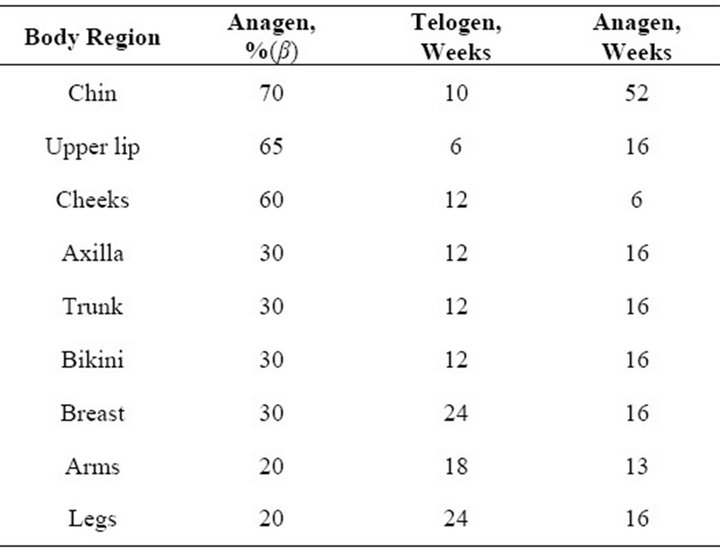
Table 1. Parameters of HFs in different body regions. Data from [6].
Here, β is the proportion of anagen hairs in the whole population of HFs in a given body region. The data in Table 1 give no possibility of calculating the absolute HF light sensitivities, but it does allow the ranking of HF sensitivities. This ranking is possible based on the assumption that the duration of A-I/V is similar in different body regions, which could be a good approximation [7].
Ratio of light sensitivity of HFs from two body regions can be calculated as
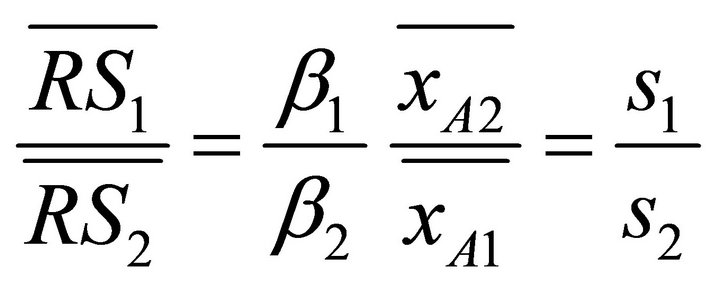 (15)
(15)
Here, we introduced the parameter, ![]() , describing the relative light sensitivity of HFs in a body region, i:
, describing the relative light sensitivity of HFs in a body region, i:
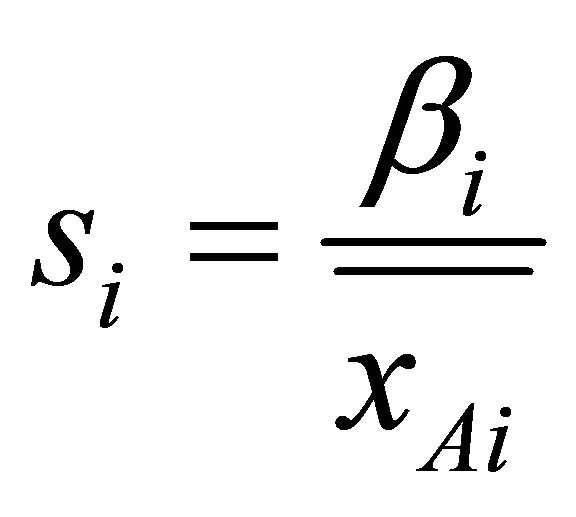 (16)
(16)
Parameters ![]() (%/week) which can be used for ranking the HF light sensitivities in different body regions according to data from Table 1 are presented in Table 2.
(%/week) which can be used for ranking the HF light sensitivities in different body regions according to data from Table 1 are presented in Table 2.
It is well known that cheek and upper lip hairs have higher light sensitivity and can be reduced with photoepilation more effectively than HFs in other body regions. Similarity of light sensitivities of axilla and bikini HFs also does not contradict the known experimental and clinical results. However, the situation with chin HFs is very different. While the majority of chin HFs are indeed in the A phase, the duration of A for these hairs is very long, which evidently points to their strong anagenization. According to [1], this phenomenon must effectively reduce the relative light sensitivity of HFs.
Whereas this ranking correlates well with clinical experience, the accuracy of the data in Table 1 is poor. To use this estimation for practical purposes, we must assess possible deviation between the exact, 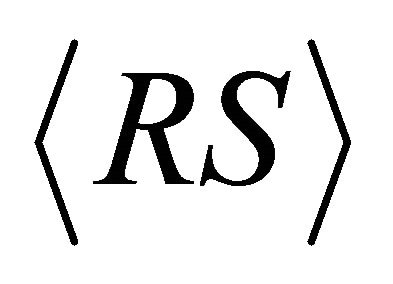 , and approximate,
, and approximate,  , estimations of light sensitivity.
, estimations of light sensitivity.

Table 2. Relative light sensitivities and ranking of HFs from different body regions.
4. Estimations on the Basis of Phototrichogram Analysis
The most common practical method for experimental assessment of HF phases is the phototrichogram technique. This method can differentiate between growing hairs that change their length between two subsequent trichograms and ceased hairs that fail to grow. Consequently, trichograms cannot differentiate between the sub-phases of A and thus interpret the sub-phase A-VI (during which the hair shaft visibly grows) as the whole anagen phase. To describe the experimental results obtained with trichograms, the fictive latency phase, L, was implemented, which is the period of HF cycle following the hair shedding and preceding the onset of the next A-phase. While this phase does not exist in a classical description of HF cycle, it is useful for the interpretation of trichograms, since the spatial fixation of single hairs allows its identification. The L-phase mainly corresponds to the phases A-IV/V of HF cycle in its classical description [8]. At the same time, the “T”-period of trichograms must, according to the classical interpretation of HF cycle, represent the sum of real Cand T-phases, eventual eclipse time, which is the delay of transition T→A, and the duration of sub-phases A-I/III during which the hair shaft is still reserved in HF, but it does not demonstrate any visible growth.
According to the theory described in [1], relative HF light sensitivity can be described as the ratio of duration of light-sensitive (A-III/V) sub-phases of anagen and the whole duration of the HF cycle. Since the sub-phases A-I/III belong to the total measured “T”-phase in phototrichograms, we cannot separate them from true T phase. To make a rough estimation, we assume the A-I/III duration is negligible compared to A-IV/V, which underestimates the light sensitivity. The measured values of the “T”-phase for the scalp hairs were indeed much less than durations of the “L”-period [9]. While this relation can not be directly transferred to other body regions, it allows us to make an estimation of the light sensitivity.
The only known well-documented investigation of a big HF population during long observation time was done in [9-11]. These authors traced the evolution of about 9.000 hair cycles of about 930 scalp HFs during 144 successive months. The measured parameters for 3 alopecic (#2, #3, #5) and non-alopecic (#1, #4) patients from this study are shown in Table 3. Table 4 presents the corresponding coefficients of variation, 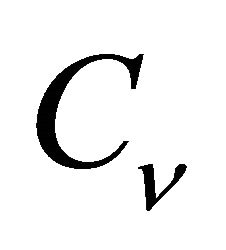 (ratio of standard deviation to the mean value), calculated from Table 3.
(ratio of standard deviation to the mean value), calculated from Table 3.
It is seen that 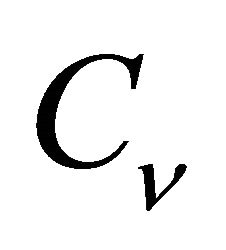 demonstrates significant inter-phase and inter-subject variation and can reach more than 200%, whereas the lowest variability was registered in the “T”-phase and the highest in the “L”-phase of a scalp HF cycle.
demonstrates significant inter-phase and inter-subject variation and can reach more than 200%, whereas the lowest variability was registered in the “T”-phase and the highest in the “L”-phase of a scalp HF cycle.
Since in a phototrichogram analysis “A” mainly corresponds to A-VI and “L” mainly corresponds to A-IV/V, one can see the striking variability of both photoepilation relevant (A-IV/V) and irrelevant (A-VI) anagen sub-ph-

Table 3. Experimental values of mean durations and their standard deviations, SD, for different phases of scalp HFs measured with phototrichograms [9-11].

Table 5. Relative light sensitivity, .
.
ases. Although the investigation [9] was provided for the scalp hairs, one can assume the phenomenon of HF cycling dispersion is of common nature and will take place also for the hairs in other body areas. This can have a severe impact on the interpretation of photoepilation results, which must be strongly dependent on the heterogeneity of A-phase in HF population, and makes a simple deterministic description proposed in [3] and based on approximate 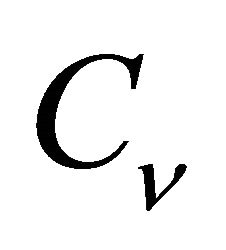 values of 10% inapplicable.
values of 10% inapplicable.
Since the “T”-phase for the scalp hairs is much shorter than the “A”-phase, we can calculate the mean relative light sensitivity of these HFs,  , from (9), where we take now
, from (9), where we take now 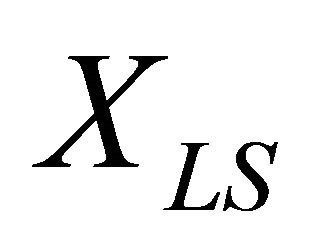 and
and 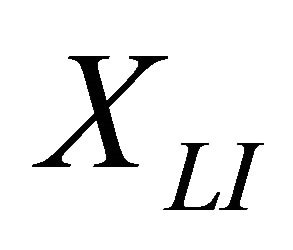 to be the durations of the “L”-period and “A”-period, respectively. The results calculated from Table 3 using Equation (13) are presented in Table 5.
to be the durations of the “L”-period and “A”-period, respectively. The results calculated from Table 3 using Equation (13) are presented in Table 5.
Estimations of  for three alopecic patients #2, #3 and #5 give much higher relative light sensitivities than corresponding values for non-alopecic patients, #1 and #4. While there are no reliable clinical studies concerning laser hair removal on scalp, there have been some anecdotal reports that the hairs in alopecia can be more easily removed by photoepilation and that the front scalp hairs in alopecia need less laser treatments than the back scalp ones, which indirectly supports our calculations.
for three alopecic patients #2, #3 and #5 give much higher relative light sensitivities than corresponding values for non-alopecic patients, #1 and #4. While there are no reliable clinical studies concerning laser hair removal on scalp, there have been some anecdotal reports that the hairs in alopecia can be more easily removed by photoepilation and that the front scalp hairs in alopecia need less laser treatments than the back scalp ones, which indirectly supports our calculations.
5. Conclusions
In this paper we have proposed a stochastic model of HF light sensitivity based on the ideas of the new photoepilation theory presented in [1,2]. According to this model, the ranking of HF light sensitivities cannot be done simply on the basis of relative duration of the anagen phase in the whole HF cycle and must take into account the durations of light sensitive and light insensitive anagen sub-phases. It was shown that stochastic nature of single phases’ duration plays an important role in inter-regional or inter-individual ranking of light sensitivity of HFs. Distribution of sensitivities of a single HF in a given body area can be described by Equation (10) and its average value can be found from Equation (2). Approximate ranking of HFs’ light sensitivities in different body regions can be done with a simple parameter (16). Application of this method for estimation of the light sensitivity of the scalp hairs predicts a remarkable difference in light sensitivities of HFs in alopecic and non-alopecic patients.
This model may be further applied for calculation of optimal intervals between the single irradiations for development of an optimal treatment strategy in a photoepilation.
REFERENCES
- I. L. Kruglikov, “Melanin Light Absorption is the Necessary but Not the Sufficient Condition for the Photoepilation: Heterogeneous Light Sensitivity of Anagen SubPhases,” The American Journal of Cosmetic Surgery, Vol. 29, No. 4, 2012, pp. 266-272.
- I. L. Kruglikov, “Melanin Light Absorption is the Necessary but Not the Sufficient Condition for the Photoepilation: Miniaturisation and Eclipse Phenomena,” The American Journal of Cosmetic Surgery, Vol. 30, No. 1, 2013, pp. 21-27.
- V. Kolinko and C. M. Littler, “Mathematical Modelling for the Prediction and Optimization of Laser Hair Removal,” Lasers in Surgery and Medicine, Vol. 26, No. 2, 2000, pp. 164-176. doi:10.1002/(SICI)1096-9101(2000)26:2<164::AID-LSM7>3.0.CO;2-W
- J. Halloy, B. A. Bernard, G. Loussouarn and A. Goldbeter, “Modelling the Dynamics of Human Hair Cycles by a Follicular Automation,” Proceedings of the National Academy of Sciences, Vol. 97, No. 15, 2000, pp. 8328-8333. doi:10.1073/pnas.97.15.8328
- J. Halloy, B. A. Bernard, G. Loussouarn and A. Goldbeter, “The Follicular Automation Model: Effect of Stochasticity and Synchronization of Hair Cycles,” Journal of Theoretical Biology, Vol. 214, No. 3, 2002, pp. 469-479. doi:10.1006/jtbi.2001.2474
- R. N. Richards, M. Uy and G. Meharg, “Temporary Hair Removal in Patients with Hirsutism: A Clinical Study,” Cutis, Vol. 45, No. 3, 1990, pp. 199-202.
- M. Saitoh, M. Uzuka and M. Sakamoto, “Human Hair Cycle,” Journal of Investigative Dermatology, Vol. 54, No. 1, 1970, pp. 65-81. doi:10.1111/1523-1747.ep12551679
- K. S. Stenn and R. Paus, “Controls of Hair Follicle Cycling,” Physiological Reviews, Vol. 81, 2001, pp. 449- 494.
- M. Courtois, G. Loussouarn, C. Hourseau and J. F. Grollier, “Hair Cycle and Alopecia,” Skin Pharmacology, Vol. 7, No. 1, 1994, pp. 84-89. doi:10.1159/000211279
- M. Courtois, G. Loussouarn, C. Hourseau and J. F. Grollier, “Ageing and Hair Cycles,” British Journal of Dermatology, Vol. 132, No. 1, 1995, pp. 86-93. doi:10.1111/j.1365-2133.1995.tb08630.x
- M. Courtois, G. Loussouarn, C. Hourseau and J. F. Grollier, “Periodicity in the Growth and Shedding of Hair,” British Journal of Dermatology, Vol. 134, No. 1, 1995, pp. 47-54. doi:10.1111/j.1365-2133.1996.tb07839.x
NOTES
*Conflict of Interests: Dr. I. Kruglikov is the managing partner of Wellcomet GmbH.


