Open Journal of Biophysics
Vol.2 No.3(2012), Article ID:21421,7 pages DOI:10.4236/ojbiphy.2012.23012
Dynamic and Configurational Approach to the Glass Transition by Nanoscale Cooperativity
Physics Department and INFM, Messina University, Messina, Italy
Email: gio.romeo@tiscali.it
Received August 25, 2011; revised September 27, 2011; accepted October 9, 2011
Keywords: Glass-Forming; Neutron Scattering; Einstein-Debye’s Breakdown; Cooperative Rearranging Region
ABSTRACT
Here we examine the findings obtained for disaccharide/water mixtures near glass transition that involves cooperative relaxation features on kinetic by viscosity and on thermodynamic behaviour by neutron scattering. Then to address cooperative phenomena that mitigate the Debye-Waller behaviour we invoke Adam-Gibbs’ idea of a cooperative rearranging region. Neutron results suggest that the excess mean square displacement behaves as free volume and is closely connected to an elementary step of the structural relaxation. Then viscosity data evidence a breakdown of the Einstein-Debye relation, decoupling attributed to the intermolecular cooperativity.
1. Introduction
The microscopic origin of the protective action of treha-lose on cells and tissues from stress conditions such as freezing or dehydration, is at present matter of extensive discussion [1]. Trehalose is a non reducing disaccharide having high glass transition temperature, is well known for effective stabilization of macromolecules like pro-teins [2], small molecules [3], and it also acts as a cryo- preservative of cellular membranes [4]. The name treha-lose was introduced in 1858 to describe a main constitu-ent of shells that are secreted by various insects on tree leaves in the Middle East [5]. Then α,α-trehalose is a dis- accharide of glucose constituted by two pyranose rings in the same β configuration, linked by a glycosidic bond be- tween the chiral carbon atoms C1 of the two rings. Tre-halose is present in several organisms and common foodstuffs such as bread, wine, beer, vinegar, and honey [6]. In addition to being non-reducing, trehalose pos-sesses several unique properties, including high hydro-philicity, chemical stability, non-hygroscopic glass for-mation and no internal hydrogen bond formation. The combination of these features does not explain the role of trehalose as a stress metabolite. While sucrose belongs to the small set of compounds that were selected by organisms, ranging from single cells to amphibians and higher plants, to resist dehydration, osmotic shock, and freezing at subzero temperatures [7-10]. More precisely, sucrose is constituted by a glucose ring in the β configuration and a fructose ring in the β configuration; the α and β structures of the same monosaccharide differ only in the orientation of the OH groups at some carbon atom in the ring itself.
Experimentalists, to get some insight into the molecu-lar mechanisms of cryo-preservation, and to clarify the reasons that make these molecules effective bio-protector, have examined aqueous solutions of disaccharide in a wide range of concentration and temperature [11,12]. While various neutron diffraction results [13-20] show for all disaccharides, and for trehalose to a large extent, a strong distortion of the peaks linked to the hydrogen- bonded network in the partial radial distribution functions that can be attributed to the destroying of the tetrahedral coordination of pure water. Viscosity measurements on sugar aqueous solutions [15] demonstrate that trehalose has, in respect to the other disaccharides, a stronger kinetic character in the Angell’s classification scheme [21-23].
Here we report a study on the molecular kinetics of sucrose and trehalose aqueous mixtures by viscosity measurements, and by neutron scattering in thermody-namics manner. We highlight glass-forming liquids in which the Debye-Waller factor [24] slope change with temperature can be connected to the Adam-Gibbs’ idea of cooperative rearranging regions, CRR [25]. Micro-scopically, a glass still has liquid-like structure; no struc- tural change has been found which would explain the glass transition.
The size of CRR for disaccharide-water mixtures was calculated using neutron scattering data by “bond-lattice” model. In this sense, about the dynamics properties, the cooperatively rearranging region, CRR, is the smallest freely fluctuating representative subsystem functional to the α process [26]. The term “fluctuating” refers to a thermal fluctuation of CRR in glass transition range. Mean thermal fluctuation could be considered as an intrinsic parameter of glass transition that is responsible for changes in CRR volume due to the changes of conformational entropy. These changes generate the rearranging of short part bead in the molecule [27] o the monomer unit in the polymer independently of their neighboring regions. CRR can be described as the volume of material with autonomy of relaxation process induced by thermal fluctuations. Then, the study of CRR could improve the understanding of the relaxation processes in amorphous materials at temperatures close to the glass transition temperature value, where, glass transition process could be evaluated in terms of coopertively rearranging regions. We test the validity of the Adam Gibbs theory [25] for our glassformers in order to describe this microscopic dynamical mechanism. The flow in a supercooled fluid involves cooperative motion of molecules and the struc-tural arrest at the glass transition is due to a divergence of the size of cooperating regions.
Donth [28] proposed an interpretation of CRR in terms of thermodynamic fluctuation model of small volume in material based on configurational entropy fluctuations. Such small volume that is named as sub-system is assigned to a local cubic nanometer size volume in amorphous materials. Later, Sillescu [29] connect the CRR term to dynamic heterogeneity of such sub-system. According to his conclusions more available conformational states are possible only if CRR is large enough.
A fundamental difference between a glass and a su-percooled liquid is the presence in the latter of both con-formational and vibrational motion. Motion in the liquid can be represented by an atom vibrating about an equi-librium position which is itself changing with time as a result of diffusion. Conformational motion, also know as relaxation, and vibrational motion are distinguished by time scale of typically one nano-second and one pico- second, respectively. While, what is not understood is the way in which conformational motion freezes out at the glass transition temperature and the way in which it in-fluences thermodynamic properties. The fast process with characteristic times of the order of a picosecond [30,31] that set in at around the Vogel-Fulcher temperature [32] is directly related to the glass transition. While it was found [30,31] that the slow process with temperature character-istic times of several hundred picoseconds setting in near glass transition temperature is an elementary process connecting to the conformational transition. In accordance with the onset of the fast processes, the mean-square displacement shows an excess value [33], suggesting that the excess volume is required for these motions.
On the other hand, as a glassforming liquid is cooled, we observe a macroscopic viscosity divergence that is related to the divergence of the microscopic structural relaxation time. In the free volume theory [34] viscosity is related to free volume. These observations remind us of the model proposed by Buchenau and Zorn [35-38]. These authors suggest a close connection between viscosity and the relaxational mean square displacements of atoms. Theoretical models predicted that a given atom group performs back-and-forth motions in a cage, the fast process, where the probability distribution in the cage motion is a Gaussian with the mean-square displacement. If the amplitude of the fast process exceeds a critical displacement, u0, the slow process takes place. Assuming that the characteristic time of the fast process is inde-pendent of temperature [39], the waiting time for the occurrence of the slow process, at a given atom is pro-portional to the probability of finding an atom outside the sphere with radius u0 .The slope of the linear relation in provides u0, which may be considered to be a critical value of the excess mean square displacement required for the structural relaxation. Therefore, Johari-Goldstein process β [40,41] is considered to reflect a localized motion in a “island of mobility”: in the inner less dens and more mo-bile part of a CRR [42].
2. Experimental Details
Ultrapure powdered trehalose and sucrose purchased by Aldrich-Chemie were used for the experiments. Care was taken in order to obtain stable, clear and dust-free samples stored in the dark to minimize biological and photochemical degradation. Elastic incoherent neutron scattering experiments were performed by using the IN13 spectrometer at the Institute Laue Langevin in Grenoble, France. The relatively high energy of the incident neutrons (16 meV) makes it possible to span a wide range of momentum transfer, Q ≤ 5.5 Å 21, with a very good energy resolution about 8 meV. In the used IN13 configuration the incident wavelength was 2.23 Å and the Qrange was 0.28 - 4.27 Å–1. Raw data were corrected for cell scattering and detector response and normalized to unity at Q = 0 Å–1. Measurements were performed in a temperature range of 18 - 310 K on hydrogenated trehalose and sucrose in H2O at weight-fraction values corresponding to 19 water molecules for each disaccharide molecule. Measurements were performed on sucrose/ H2O and α,α-trehalose/H2O solutions at a molar fraction φ = nd/(nd + nw) = 0.05, where nd and nw denote the disaccharide and water mole numbers, respectively.
3. Results and Discussion
The elastic data concerning the atomic motions in glassforming samples have been analyzed [43] by considering a two-state model [44] that fits the data reasonably well: the hydrogens can fluctuate between two sites of different free energy ΔG and separated by a distance d.
In this picture, the elastic scattering intensity is given by:
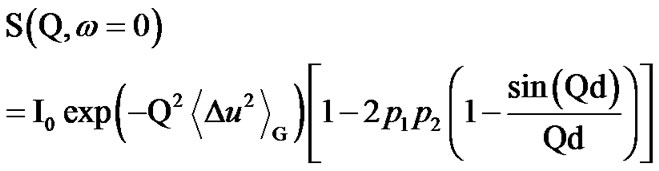 (1)
(1)
in which the first term gives the Gaussian contribution to the proton mean square displacement (MSD) (Figure 1):
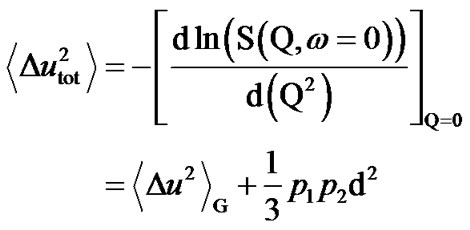 (2)
(2)
where p1 and p2 are the probabilities of finding a hydrogen in the ground or excited state.
At below dynamical transition temperature ![]() is dominated by the vibrational contribution
is dominated by the vibrational contribution
![]() (3)
(3)
and the second term,
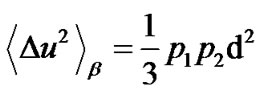 (4)
(4)
takes into account the emerging contribution related to jumps between the two wells, i.e. relaxations faster than experimental energy resolution. As shown in Figure 2, the trend of 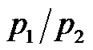 for the samples can be well described with an Arrhenius function:
for the samples can be well described with an Arrhenius function:
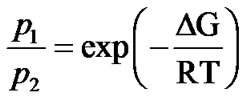 (5)
(5)
where ΔG = ΔH – TΔS is the free energy change due to the jump of mobile protons from the ground to the excited state with ΔH and ΔS the corresponding enthalpy and entropy change respectively. The 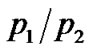 ratio of hydrated samples shows the existence of two different Arrhenius-like trends. The first one describes the
ratio of hydrated samples shows the existence of two different Arrhenius-like trends. The first one describes the 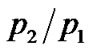 low-temperature region and at a certain temperature
low-temperature region and at a certain temperature 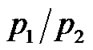 begins to deviate from this low-T curve, then a second Arrhenius trend is needed to represent the ratio. This behaviour seems to indicate the onset of a second anharmonic process corresponding to the dynamical transition where the excited state of the double well begins to be occupied. When
begins to deviate from this low-T curve, then a second Arrhenius trend is needed to represent the ratio. This behaviour seems to indicate the onset of a second anharmonic process corresponding to the dynamical transition where the excited state of the double well begins to be occupied. When 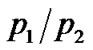 begins to deviate from this low-T curve, then the enthalpy and the entropy change are consistent with the activation of a dynamical process and the onset of new anharmonic degrees of freedom.
begins to deviate from this low-T curve, then the enthalpy and the entropy change are consistent with the activation of a dynamical process and the onset of new anharmonic degrees of freedom.
In this picture Sc(T) (Figure 2 inset), the macroscopic configurational entropy per mol of particles, is given by contributions from both the excitation entropy and the entropy of mixing of the unexcited and excited states [43]. Sc (Figure 2 inset) quantifies the excess of configurations accessible to H atoms via jumps from the ground to the excited state, within the double-well model schematization. From the increase of Sc we can infer that the solution makes accessible to the proton a higher number of substates.
From Adam-Gibbs model, as the temperature decreases, Sc(T), decreases towards zero at the so called Kauzmann [45] temperature. Kauzmann pointed out a peculiar thermodynamic circumstance presented by glass-forming
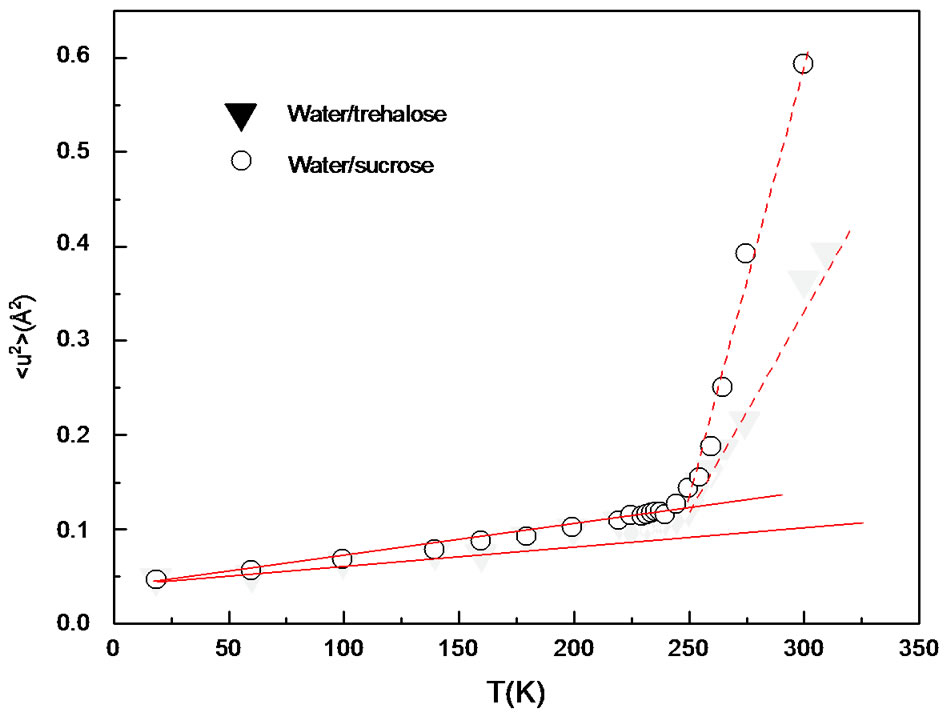
Figure 1. Average mean-square hydrogen displacement obtained from the analysis Iel(Q) [44] are displayed for comparison.

Figure 2. Arrhenius plot of occupation probabilities of finding a hydrogen in the ground or excited state for hydrated samples, obtained from the analysis of S(Q) function [44]. Inset: Sc as a function of the temperature.
liquids, that achives its most vivid form for the fragile liquids [15]. About the concept of fragility [22,23], one might say that the concept is based upon the observation that strong liquid that tend to form strong direct intermolecular bonds, exhibit Arrhenius behaviour with rather large activation energies over the entire accessible temperature range, whereas fragile liquids that tend to form rather weak, undirected intermolecular bonds, exhibit super-Arrhenius behaviour over the lower part of the accessible temperature range and Arrhenius behaviour with rather low activation energy in the upper part of the accessible temperature range. We now enquire whether or no the observed non-Arrhenius molecular kinetics of our “fragile” samples (Figure 3) is consistent with the cooperative rearrangement of molecules which dominate the relaxation kinetics of a viscous liquid. This may be done in terms of the Adam and Gibbs formalism which relates viscosity and relaxation time to the configurational entropy.
Assuming the relaxation time for cooperative rearrangements is driven by decrease in entropy Sc(T) [46, 47], we obtain
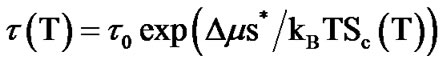 (6)
(6)
where, s* is the “critical” entropy of the rearranging region, Δμ is the potential energy barrier per molecule, τ0 has units of time and is weakly temperature dependent, and kB is the Boltzmann constant.
The premise is that the non-Arrhenius molecular cinetics arises from the fraction of CRRs, the independent distinguishable subsystems into which the total system is subdivided. CRR area [25] is in weak contact with the system and is capable of independent rearrangement because of enthalpy fluctuations [41]. The size of the CRR
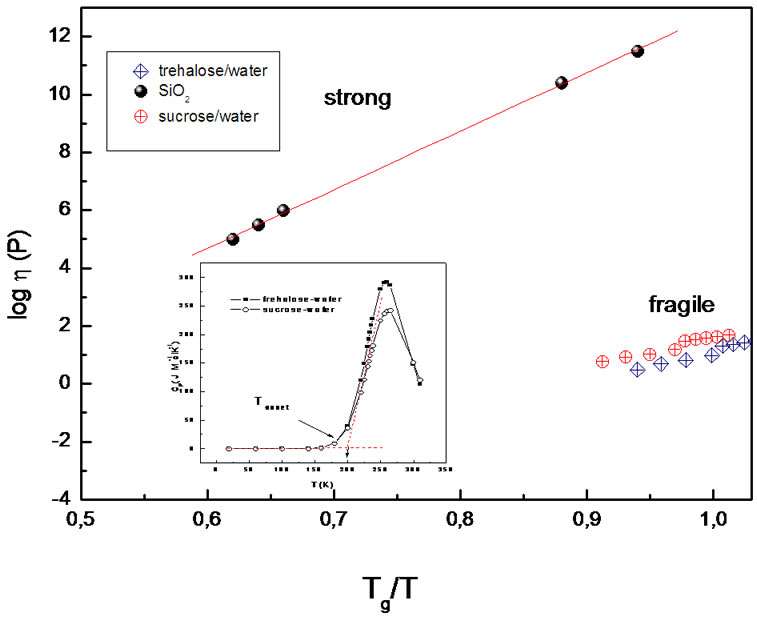
Figure 3. Logarithm of viscosity as a function of Tg/T. Inset: Heat capacity [44] evaluated for trehaloseand sucrosewater samples through the glass transition. Schematic representation indicating the onset temperature value. “Glass transition temperature” is usually defined by reference to the rather sharp decrease in heat capacity which occurs when the system falls out of equilibrium during cooling and the even sharper increase in heat capacity which occurs when equilibrium is regained on warming.
increases on cooling and the configurational entropy decreases. This means that viscosity (or relaxation time) increases on cooling for the thermal energy decreases (specifically for thermally activated process) and for configurational entropy decreases. Because molecules individually do not contribute to the Sc(T) of a liquid, but they do so as a group.
The probability of cooperative rearrangement is obtained by introducing a term, z*(T), the minimum size of a region that can rearrange into another configuration. An average transition rate with a non-Arrhenius T dependence is observed experimentally in dielectric or mechanical relaxation. By assuming that the transition rate is proportional to the fraction of subsystems permitting cooperative transitions, an Arrhenius type expression for the average rate is
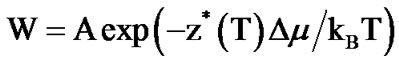 (7)
(7)
where 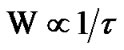 and Δμ is of the order of the free energy barrier per molecule necessary for cooperative rearrangement of the z*(T) molecules per CRR. The point of the AG model is that there is no distinction between the correlated region, cluster, and the unit of molecules for the correlated motion.
and Δμ is of the order of the free energy barrier per molecule necessary for cooperative rearrangement of the z*(T) molecules per CRR. The point of the AG model is that there is no distinction between the correlated region, cluster, and the unit of molecules for the correlated motion.
According to the potential energy landscape theory [48], when a liquid is cooled and maintained at a thermodynamic equilibrium, the probability of finding its structure in the lower energy-configurations or in deeper minima of the energy landscape increases. This means that the number of configurations, Ω, available to its structure decreases and, according to the Boltzmann equation, Sc = kBlnΩ, Sc decreases too. The ratio of the total number of particles N to z*(T) becomes equal to the ratio of the total configurational entropy Sc(T) to the minimum entropy of a CRR, 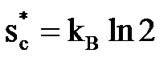 , allowing for a transition between two states:
, allowing for a transition between two states: 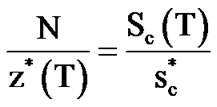 . We evaluate z*(T), called “cooperativity”, by
. We evaluate z*(T), called “cooperativity”, by
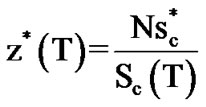 (8).
(8).
Thus, substituting Equation (8) in Equation (6) the final equation obtained is
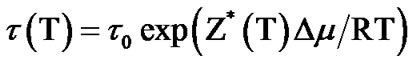 (9)
(9)
with R gas constant.
At equilibrium, as the temperature decreases, Sc(T) decreases towards zero resulting in an increase in z* to infinity at TK. While, at a given temperature namely crossover temperature, Tc, the system would be entirely filled by such elementary CRRs. A common interpretation of Tc is that it signals a crossover to strongly activated dynamics. From Ngai’s coupling model point of view [49], the degree of intermolecular cooperativity increases enormously below Tc. In other words, molecules at lower temperatures (T < Tc) move by crossing substantial potential energy barriers. However, at higher temperatures (T > Tc), thermal energies are comparable to the barrier heights and translational motion have a fundamentally different character [50,51].
CRR average size is the characteristic length, l, describing a characteristic volume, (l)3, with z*(T), particles within. We evaluate l, using the fluctuation formula [26]:
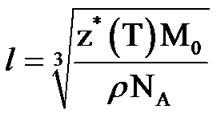 (10)
(10)
where ρ is the mass density, NA the Avogrado number and M0 the molar weight.
We evaluate the temperature dependence of the CRR size, z*, for our disaccharide-water solutions that increases on cooling and for the configurational entropy decreases. In fact, Figure 4 and Table 1 show the temperature dependence of the size and characteristic length of CRR calculated by using Equation (8) and Equation (10), respectively. For the molecules examined, the CRR size increases with decreasing temperature and trehalose molecules tend to form a larger CRR than sucrose molecules. This implied that the probability of cooperative transitions which determine the relevant relaxation rates increases and, by assuming that the transition rate is proportional to the fraction of subsystems permitting cooperative transitions, this difference corresponds in a decrease in the rate of relaxation processes.
In other words, Tc, the temperature for onset of significant intermolecular cooperativity, could be considered as the temperature below which the system packs completely by multiple CRRs. Kahle et al. [52] reported a correlation between fragility index and length scales of cooperativity (cube root of the mean volume of the CRR). Also a linear correlation between fragility and the size of cooperative units has been found by Solunov [53]. As a result, the larger cooperative domain size could be correlated to trehalose-water fragility enhancement and so
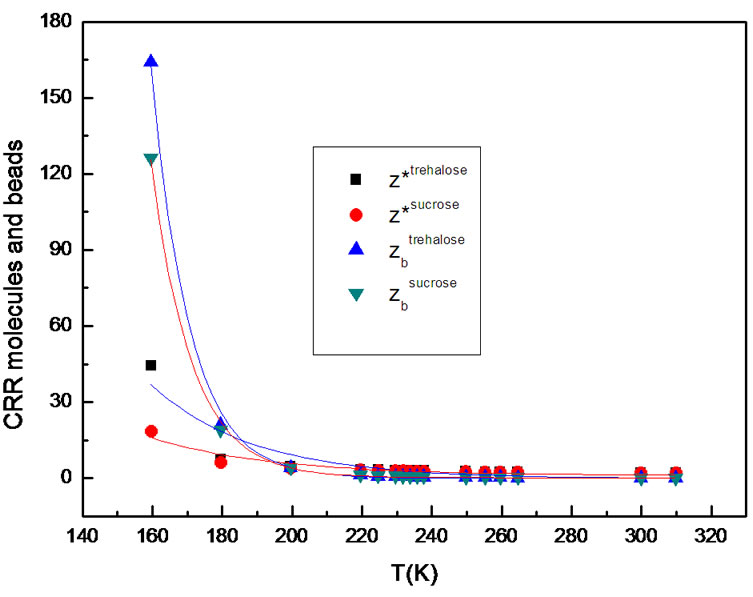
Figure 4. Comparison between z*(T), number of the particles which are rearranging cooperatively and zb(T) number of thermodynamics “beads” in the CRR.
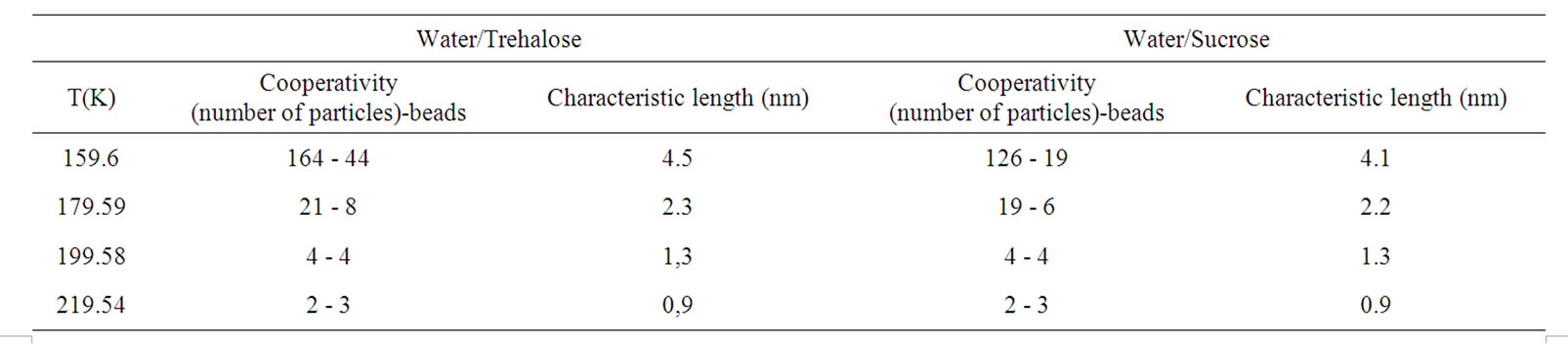
Table 1. The table illustrate the number of molecules (z*and zb) in CRR and Characteristic length (nm) of CRR, l, for trehaloseand sucrose-water solutions as defined in the text.
confirming previous results obtained by Differential Scanning Calorimetry and viscosity measurements [15,54].
We evaluate z*(T) for our samples (Figure 4) by Equation (8) and the minimum entropy of a CRR by using the Boltzman relation for the configurational entropy of the CRR: 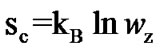 where
where 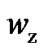 is the number of configurations in CRR. Various evidence that the basic molecular units in the CRR are not molecules but fragments of them, known in thermodynamic as “beads” [55-57] As suggested by Solunov, the measured number of configurations of CRR in polymers and optical glass [55,57] has been found to be of the order of the beads in the same range. This is in contrast to the Adam-Gibbs assumption that their number is two, independent of the substances: one configuration before the rearrangement and the second one during the rearrangement.
is the number of configurations in CRR. Various evidence that the basic molecular units in the CRR are not molecules but fragments of them, known in thermodynamic as “beads” [55-57] As suggested by Solunov, the measured number of configurations of CRR in polymers and optical glass [55,57] has been found to be of the order of the beads in the same range. This is in contrast to the Adam-Gibbs assumption that their number is two, independent of the substances: one configuration before the rearrangement and the second one during the rearrangement.
The number of molecules in the CRR, z*, and the number of beads in the molecule, zb, which allows the number of configuration in the CRR, 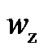 , and the number of configurations per bead,
, and the number of configurations per bead, 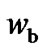 , to be estimated, respectively.
, to be estimated, respectively.
We could compare Sc (Figure 2) and 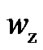 (Figure 5), it may be realized that the reduction of the vibration component in the Sc slightly reduces the values of the configurations. The plot of the number of configuration,
(Figure 5), it may be realized that the reduction of the vibration component in the Sc slightly reduces the values of the configurations. The plot of the number of configuration, 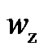 and
and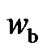 , as a function of temperature evidence a larger increase of
, as a function of temperature evidence a larger increase of  than
than 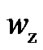 with increasing temperature, so the rearranging molecular units still participate in activating hopping transport. Attention will be drawn to the obtained values of
with increasing temperature, so the rearranging molecular units still participate in activating hopping transport. Attention will be drawn to the obtained values of 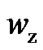 that are larger than 2. This supports the statement that CRR is not a rigid system (as accepted by Adam and Gibbs) and the Solunov interpretation [55-57]: CRR is a liquid unit with its own internal rearrangement. Regarding beads as basic molecular units, the intramolecular degree of freedom participate in the cooperative molecular dynamics and are a substanzial factor in avoiding crystallization.
that are larger than 2. This supports the statement that CRR is not a rigid system (as accepted by Adam and Gibbs) and the Solunov interpretation [55-57]: CRR is a liquid unit with its own internal rearrangement. Regarding beads as basic molecular units, the intramolecular degree of freedom participate in the cooperative molecular dynamics and are a substanzial factor in avoiding crystallization.
Some facts are evident from the Table 1. The cooperativity increase continuosly starting with small values and CRR size, z*(220 K) ≈ 2 and l = 1 nm, near the onset and reaches large cooperativities at low temperature, z*(179.5 K) ≈ 21 and l = 2 nm, so confirming previous results obtained for model fragile [58-60] glassformer, like o-terphenyl [61], by Donth [62] (2 nm), by Sillescu [63] (2.8 nm) and by Ediger [64] (2.5 nm).
While the configurational contribution to heat capacity (Figure 3) in the temperature range T > Tc is very small. Each particle is only weakly affected by other particles and diffuses and relaxes in a non cooperative way. The motions are expected to be a small scale cage escaping, and material to be homogeneus (no dynamic heterogeneity) [65,66].
Then we could characterize the glass transition region with kinetics data. We compare the solution viscosity data
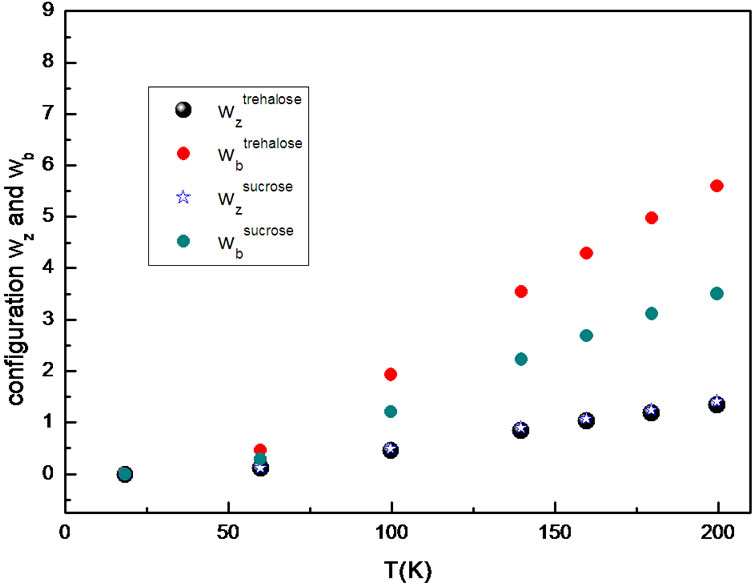
Figure 5. Comparison between wz(T), number of configuration in CRR and wb(T) number of configuration per thermodynamic “bead” (a basic molecular unit) in the CRR.
with the inverse of the double-well relaxational contribution to the atomic mean square displacements related to picosecond-time-scale fluctuations, the so-called fast process. Where, the slow process is an elementary process connecting to the conformational transition or structural relaxation. In accordance with the onset of the fast processes, the mean-square displacement shows an excess value, suggesting that the excess volume is required for these motions. In the conventional theories, the free volume per molecule is phenomenologically defined on the total free volume evaluated from the macroscopic measurements of thermal expansion of specific volume. Microscopic interpretation of the free volume per molecule is still open to question. In this picture, we re-examine the free-volume theory from a microscopic point of view. As microscopic quantities, we employ mean square displacement measured by neutron scattering and discuss the microscopic basis of the free-volume theory and the critical value of the mean square displacement for structural relaxation on the basis of the relation between the < U 2> and the viscosity.
If logarithm of the viscosity is plotted against the inverse of the excess mean-square displacement in the temperature range 170 K and 250 K, a linear relation is obtained as shown in Figure 6. So, we used a relationship developed by Buchenau and Zorn [35-38]. This relation between the viscosity and the relative relaxational MSD is described by
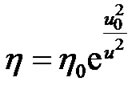 (11)
(11)
where 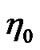 and
and  are constants. It has been verified over a wide range of temperatures above the glass transition temperature and is close to the equation derived from the free-volume concept [66] in which the random distribution of an average free volume per atom is assumed. An
are constants. It has been verified over a wide range of temperatures above the glass transition temperature and is close to the equation derived from the free-volume concept [66] in which the random distribution of an average free volume per atom is assumed. An
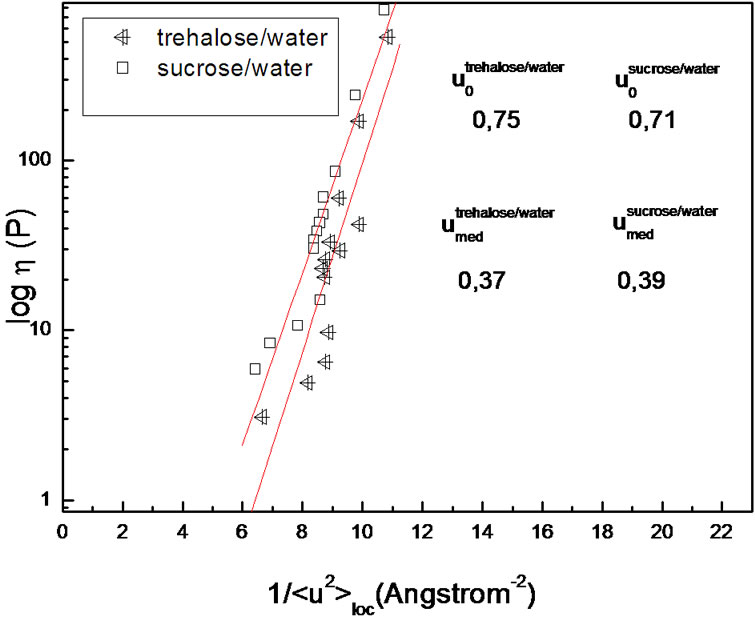
Figure 6. Logarithm of viscosity as a function of the inverse of the local contribution to total< U 2> at weight fraction: 0.05, where dotted lines are fit of Buchenau equation [35].
atom performs the fast motion having a characteristic time of an order of a picosecond in a cage, but it makes a jump to escape from the cage if the mean-square displacement exceeds a critical value, u0, which is larger than the average value of < U 2>. This large difference implies that cooperative motions of surrounding molecules are required for the structural relaxation. CRR is also defined as the part of subsystem which is in weak contact with the remaining part of the system, and which is capable of independent rearrangements because of fluctuation of enthalpy [24,46].
The critical values for the excess mean-square displacement u0 for the trehaloseand sucrose-water samples are larger than the corresponding average values (Figure 6). This could be explained by a small jump probability for conformational transition or structural relaxation, the slow process, occurring during the cage motion, the fast process, implying that cooperative motions are necessary for structural relaxation. For molecules to make such a large jump, they must move cooperatively, giving a very small jump probability. This probability is approximately given by the ratio of the characteristic time of the fast process to that of the slow process. The small probability of the jump may explain the large difference between the average value and the critical value of msd, and vice versa.
We found that the effective critical value, u0, is comparable to the size, z*(T), of the cooperatively rearranging region [67] for the slow process in glassforming solutions. This may be done in terms of the Adam and Gibbs formalism which relates the relaxation time or viscosity to z*(T) by Equation (9). For that we use the viscosity data plotted in Figure 6, and Equation (11): the slope value, (u0/u)2, at T = 199 K is 56.25 for trehalose/water and 50.41 for sucrose/water. According to Equation (9) we consider (u0/u)2 is equal to z*(T)Δμ/RT. We take z*(199K) as ≈4.2 for disaccharide solutions and calculate:
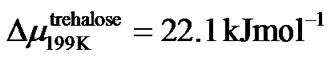 and
and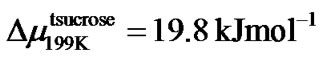 which is about the energy needed to break H bond. Evidently, these are physically reasonable values of energy term Δμ and we could confirm the validity of the Adam and Gibbs theory for our fragile glassformer.
which is about the energy needed to break H bond. Evidently, these are physically reasonable values of energy term Δμ and we could confirm the validity of the Adam and Gibbs theory for our fragile glassformer.
We see from the above Figure 6 that a striking linear relationship is observed in the whole investigated temperature range and neither does the viscosity follow a simple Arrhenius like behaviour nor is the u2 trend linear, then the result we found is rather surprising.
The relation between the viscosity and the relaxation times of liquid is determined by the Einstein-Debye relation [68,69]:
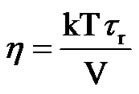 (12)
(12)
where τr is the rotational relaxation time and V denotes the molecular volume. Equation (12) derived for Brownian particles that have dimensions larger than molecules, but it is utilized to characterize molecular motions [70-72]. As suggested by Cornicchi [73], if we describe the picosecond time scale motions of a particle in terms of Brownian diffusion, then the Stokes Einstein law leads to an inverse relationship between u2 and viscosity (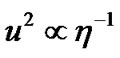 ) for a fixed experimental temporal window. While the Equation (11) implies a weaker dependence between u2 and viscosity (
) for a fixed experimental temporal window. While the Equation (11) implies a weaker dependence between u2 and viscosity (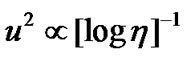 ). When temperature is lowered, continuous diffusion is replaced by single particle hopping processes and an estimate of the characteristic length of such jump like diffusive dynamics is provided by u0 value reported in Figure 6. Chang and Sillescu [74] found that the relationship (4) was constant at high temperatures, for which low molecular weight glass forming fluids that have low viscosities, and upon approach to the glass transition this ratio rise as much as one order of magnitude with a breakdown of ED relation. Then Fisher [75] suggested the decoupling between viscosity and reorientational times in the glassformer o-terphenyl [61] by temperature dependence of the characteristic length for the dynamic glass transition. While onset of the deviation occurred between the translational diffusion constant and reorentational correlation times in the vicinity of the critical temperature, predicted by mode coupling theory, was reported for 1,3,5-tri-α- naphthyl benzene by Rössler [76].
). When temperature is lowered, continuous diffusion is replaced by single particle hopping processes and an estimate of the characteristic length of such jump like diffusive dynamics is provided by u0 value reported in Figure 6. Chang and Sillescu [74] found that the relationship (4) was constant at high temperatures, for which low molecular weight glass forming fluids that have low viscosities, and upon approach to the glass transition this ratio rise as much as one order of magnitude with a breakdown of ED relation. Then Fisher [75] suggested the decoupling between viscosity and reorientational times in the glassformer o-terphenyl [61] by temperature dependence of the characteristic length for the dynamic glass transition. While onset of the deviation occurred between the translational diffusion constant and reorentational correlation times in the vicinity of the critical temperature, predicted by mode coupling theory, was reported for 1,3,5-tri-α- naphthyl benzene by Rössler [76].
Our approach is as follows. Phenomenological AdamGibbs theory postulates that the CRRs grow upon cooling, and relaxation slows down because a concerted motion of larger and larger groups of particles is required. Therefore solutions approaching the glass transition should relax in dynamically correlated regions (this type of dynamics is commonly referred to as spatially heterogeneous dynamics [76-82]). Thus quantification of the size of these dynamically active regions clearly demonstrates that their size increases as a glass transition is approached. CRRs were found to be relevant to the process of cage rearrangement and relaxation. As suggested by Fisher [83] if we plot CRR volume (Figure 7) of trehalose and sucrose water solutions as a function of logarithm of viscosity: the cooperativity dimension is constant at high temperatures, for which the mixtures have low viscosities, while upon approach to the glass transition, this dimension systematically increased, with its value rising as much as 1 order of magnitude at the glass transition temperature. Therefore the breakdown of the Stokes Einstein relation near Tg, referred to as a decoupling (Chang and Sillescu [84]) phenomenon, is due to the spatial heterogeneity [74-80] inherent to supercooled liquids: at a given time, different regions relax with different rate.
Figures 8 and 9 show the viscosity temperature dependence, plotted logarithmically as a function of (1000/T)2 in the low temperature range and of 1000/T in the high temperature range, respectively.
In Figure 8 we see the best fit of the Ferry law [85] to the viscosity data. This plot implies that the relation introduced by Ferry (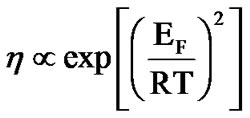 ), originally introduced empirically, and not the usual Arrhenius relation, is appropriate for describing the temperature activation (
), originally introduced empirically, and not the usual Arrhenius relation, is appropriate for describing the temperature activation ( = 48 k JK–1·mol–1,
= 48 k JK–1·mol–1, 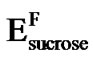 = 47 k JK–1·mol–1) of these samples. It is also obtained in Figure 9 an Arrhenius fit with
= 47 k JK–1·mol–1) of these samples. It is also obtained in Figure 9 an Arrhenius fit with 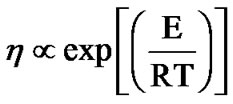 of viscosity data that yields an activation enthalpy for the two solutions (Etrehalose = 16 k JK–1·mol–1, Esucrose = 13 k JK–1·mol–1).
of viscosity data that yields an activation enthalpy for the two solutions (Etrehalose = 16 k JK–1·mol–1, Esucrose = 13 k JK–1·mol–1).
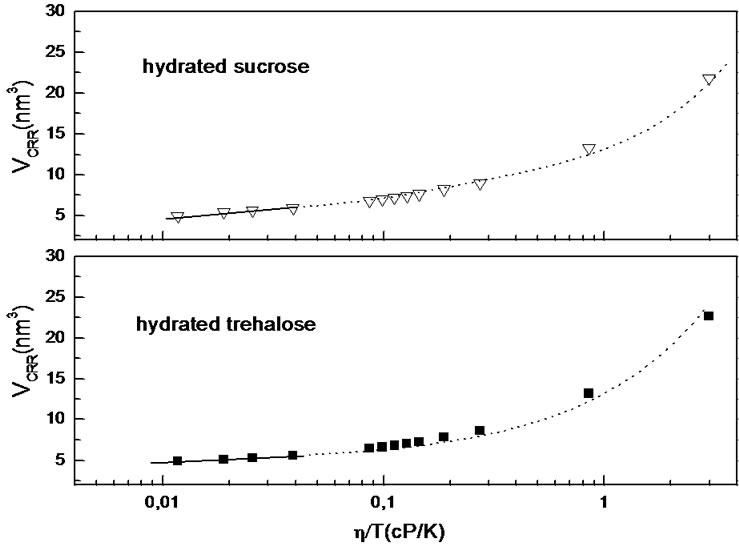
Figure 7. CRR volume of trehalose and sucrose water solutions (at weight fraction: 0.05) as a function of logarithm of viscosity, where dotted lines are lines for eyes.
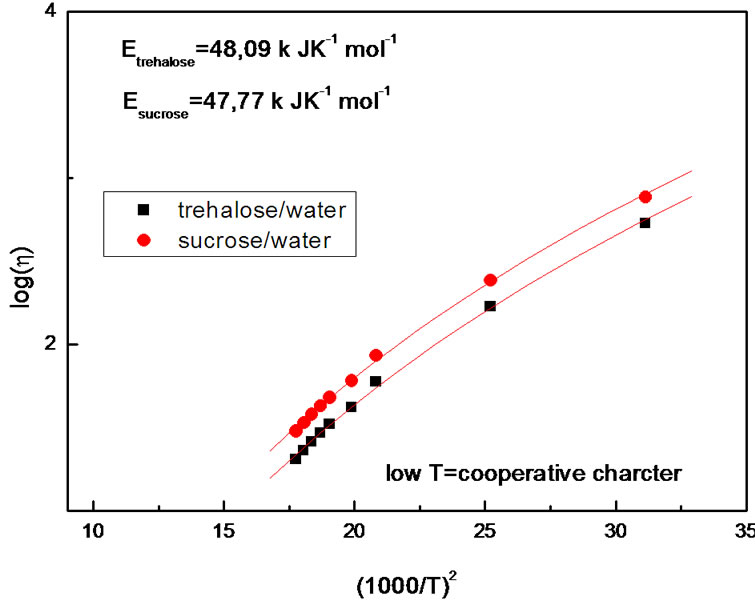
Figure 8. Logarithm of viscosity as a function of the inverse of (1000/T)2.
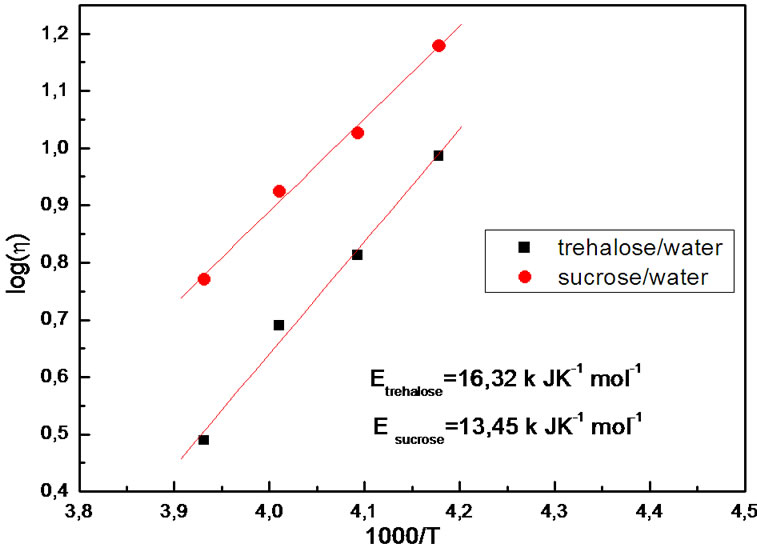
Figure 9. Logarithm of viscosity as a function of the inverse of 1000/T.
Where the high enthalpies and pre-exponentials clearly evidence a complex phenomena indicating a cooperative character and not single barrier crossings of the Arrhenius type. This behaviour is supported by the necessity of breaking, passing over the energy barrier, a certain amount of hydrogen bonds. A thermally activated process, namely making and breaking of the intermolecular H-bond, can drive both the processes and allow to frame the investigated samples in the Angell’s classification of strong and fragile liquids [58-60]. Liquids in the strong class change their viscosity with temperature exhibiting only a single relaxation time (Arrhenius character).In fragile liquids viscosity changes in more complex way, exhibiting temperature regions of non-Arrhenius character. This classification is strictly connected with the number of configurations (thermodynamically-based) that the liquid can assume when the temperature is changed and with the energy barriers (kinetically-based) between them. Hydrogen bonded liquids in this frame show an exceptional fragility and, so we can speak of a high density of configurational states, large energy barriers between adjacent configurational states. In this framework, clearly we note the direct correlation of the thermodynamic related fragility with kinetic fragility in accord with the prediction of simulation studies of Sastry [86].
Relaxation phenomena near and below the glass transition temperature range are non-exponential and nonlinear. Non-exponentially is very common in condensed media, but non-linearity in the glass transition is unusual because it is observed under normal experimental conditions using small temperature perturbations from equilibrium. Most methods used in describe non-linearity are based on pioneering work of Tool [87], who expressed the relaxation time of an exponentially decaying process as a function of both temperature and departure from equilibrium. It is convenient to express the structural state of a relaxing system in terms of the fictive temperature introduced by Tool and Eichlin as the equilibrium temperature [87,88], and defined by them as the temperature at which the observed value of an intensive property would be the equilibrium one. In the equilibrium state above Tg (jn the linear region) the Arrhenius form is only accurate for small temperature ranges (a better fit being provided over wider temperature ranges by the empirical Vogel equation). If the enthalpy relaxation is considered here: EF is the activation energy in the glassy state at fictive temperature and E the activation energy in the equilibrium state above Tg. Then the large value of EF has been rationalized in terms of the cooperative motions of many molecules so that the activation energy is shared by a large number of relaxing species.
From the linear form of AG equation, the effective activation energy for the relaxation time has a temperature dependence determined by the temperature dependence of the number of cooperatively rearranging molecules: E = zΔμ, where Δμ is the elementary excitation energy and z the number of rearranging particles. It is assumed that only the minimum value of z, z*, contributes to the relaxation time, because processes associated with larger z values produce exponentially longer average relaxation times that are short circuited by the fastest relaxations, since the groups of z particles must rearrange independently for the definition of z. As indicated above, larger values of E correspond to larger values of z*, minimum number of particles able to rearrange, so more cooperativity.
4. Conclusion
The viscosity of supercooled liquids undergoes substantial increase on temperature reduction that is accompanied by a large increase in the timescale of molecular rotational and translational motions. The rate of change of viscosity on liquid super-cooling often deviates from the Arrhenius relationship.
The magnitude of such deviation can be described using the fragility concept. Non-Arrhenius behaviour in the super-cooled region can be accounted for by the presence of cooperative molecular motions. This notion has often been invoked in situation where simple explanation of dynamical properties (viscosity) failed. In a much quoted paper Adam and Gibbs postulated the existence of cooperative rearranging region, CRR. The central idea of the AG theory is that the number of particles that cooperatively rearrange increases with decreasing temperature, and that the observed activation energy is the product of this number and an elementary energy corresponding to the activation energy per particle.
A striking feature of our results is the strong correlation between ED breakdown and cooperativity. The bond lattice model that we have described above shows good promise of ability to account for the thermodynamic properties of glasslike transitions. For the equilibrium liquid the number of molecules z* in a region of the liquid of sufficient size to posses a critical configuration entropy 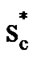 ≈ kBln2, increases with decreasing temperature. Alternatively, one may simply interpret Sc as a good metric of the liquid structure and its effect on the rate of structural relaxation. Although the Adam-Gibbs theory by itself cannot explain dynamic properties it is useful to examine how the thermodynamic quantity z* changes with temperature. We have shown for the two glassformers that the CRR size increases with decreasing temperature. Then decoupling between solution viscosity with the inverse with the double-well relaxational contribution to total atomic mean square displacements is described. Where the breakdown of the Einstein-Debye relation is attributed to the intermolecular cooperativity.
≈ kBln2, increases with decreasing temperature. Alternatively, one may simply interpret Sc as a good metric of the liquid structure and its effect on the rate of structural relaxation. Although the Adam-Gibbs theory by itself cannot explain dynamic properties it is useful to examine how the thermodynamic quantity z* changes with temperature. We have shown for the two glassformers that the CRR size increases with decreasing temperature. Then decoupling between solution viscosity with the inverse with the double-well relaxational contribution to total atomic mean square displacements is described. Where the breakdown of the Einstein-Debye relation is attributed to the intermolecular cooperativity.
Therefore viscosity data taken show an Arrhenius behaviour over a range temperature above the glass transition temperature and a departure of this type of temperature dependence at low T. While the apparent activation enthalpy has a physically meaningful: a constant value in the Arrhenius regime that increase as temperature is lowered. Remarkably, z* exhibits crossover properties similar to kinetic parameters: specifically, z*, close to unit at high temperature, on decreasing temperature increases monotonically. Therefore we could conclude that a similar temperature dependence reveal a synergy between thermodynamics and intermolecular coupling in governing the dynamic properties of our glassformers.
REFERENCES
- F. J. Chavarri, M. De Paz and M. Nueez, “Cryoprotective Agents for Frozen Concentrated Starters from Non-Bitter Streptococcus Lactis Strains,” Biotechnology Letters, Vol. 10, No. 1, 1988, pp. 11-16. doi:10.1007/BF01030016
- J. K. Kaushik and R. Bhat, “Why Is Trehalose an Exceptional Protein Stabilizer? An Analysis of the Thermal Stability of Proteins in the Presence of the Compatible Osmolyte Trehalose,” Journal of Biological Chemistry, Vol. 278, No. 29, 2003, pp. 26458-26465. doi:10.1074/jbc.M300815200
- A. Morana, P. Stiuso, G. Colonna, M. Lamberti, M. Carten and M. De Rosa, “Stabilization of S-Adenosyl-L-Methionine Promoted by Trehalose,” Biochimica et Bio-physica Acta, Vol. 1573, No. 2, 2002, pp. 105-108.
- L. S. Limaye and V. P. Kale, “Cryopreservation of Human Hematopoietic Cells with Membrane Stabilizers and Bioantioxidants as Additives in the Conventional Freezing Medium,” Journal of Hematotherapy and Stem Cell Research, Vol. 10, No. 5, 2001, pp. 709-718. doi:10.1089/152581601753193931
- A. B. Richards, S. Krakowka, L. B. Dexter, H. Schmid, A. P. M. Wolterbeek, D. H. Waalkens Berendsen, et al., “Trehalose: A Review of Properties, History of Use and Human Tolerance, and Results of Multiple Safety Studies,” Food and Chemical Toxicology, Vol. 40, No. 7, 2002, pp. 871-898. doi:10.1016/S0278-6915(02)00011-X
- A. D. Elbein, Y. T. Pan, I. Pastuszak and D. Carroll, “New Insights on Trehalose: A Multifunctional Molecule,” Glycobiology, Vol. 13, No. 4, 2003, pp. 17R-27R. doi:10.1093/glycob/cwg047
- P. H. Yancey, M. E. Clark, S. Hand, R. Bowlus and G. N. Somero, “Living with Water Stress: Evolution of Osmolyte Systems,” Science, Vol. 217, No. 4566, 1982, pp. 1214-1222. doi:10.1126/science.7112124
- J. F. Carpenter and J. H. Crowe, “Modes of Stabilization of a Protein by Organic Solutes during Desiccation,” Cryobiology, Vol. 25, No. 5, 1988, pp. 244-255. doi:10.1016/0011-2240(88)90032-6
- J. H. Crowe, L. M. Crowe and S. A. Jackson, “Preservation of Structural and Functional Activity in Lyophilized Sarcoplasmic Reticulum,” Archives of Biochemistry and Biophysics, Vol. 220, No. 2, 1983, pp. 477-484. doi:10.1016/0003-9861(83)90438-1
- L. M. Crowe, D. S. Reid and J. H. Crowe, “Is Trehalose Special for Preserving Dry Biomaterials?” Biophysical Journal, Vol. 71, No. 4, 1996, pp. 2087-2093. doi:10.1016/S0006-3495(96)79407-9
- S. Magazù, G. Maisano, H. D. Middendorf, P. Migliardo and V. Villari, “Hydration and Transport Properties of Aqueous Solutions of α-α-Trehalose,” Journal of Chemical Physics, Vol. 109, No. 3, 1998, pp. 1170-1174. doi:10.1063/1.476662
- C. Branca, S. Magazù, G. Malsano, F. Migliardo, P. Migliardo, G. Romeo and E. Vorobieva, “Hydration Properties of Disaccharide Aqueous Solutions,” Molecular Crystals and Liquid Crystals, Vol. 372, No. 1, 2002, pp. 25-35. doi:10.1080/10587250127596
- C. Branca, S. Magazu and F. Migliardo, “New Perspectives on Bioprotectant Complex Molecules: Spectroscopic Findings,” Recent Research Development in Physical Chemistry, Vol. 6, 2002, pp. 35-73.
- C. Branca, S. Magazu, G. Maisano, F. Migliardo and G. Romeo, “Vibrational Versus Relaxational Contribution for Disaccharide-Water Glass Formers: Neutron Scattering Evidence,” Philosophical Magazine Part B, Vol. 82, No. 3, 2002, pp. 347-355. doi:10.1080/13642810208221314
- C. Branca, S. Magazu, G. Maisano, F. Migliardo and G. Romeo, “α,α-Trehalose/Water Solutions. 5. Hydration and Viscosity in Dilute and Semidilute Disaccharide Solutions,” Journal of Physical Chemistry B, Vol. 105, No. 41, 2001, pp. 10140-10145. doi:10.1021/jp010179f
- C. Branca, S. Magazu, G. Maisano and F. Migliardo, “Vibrational and Relaxational Contributions in Disaccharide/ H2O Glass Formers,” Physical Review B, Vol. 64, No. 22, 2001, Article ID: 2242041. doi:10.1103/PhysRevB.64.224204
- S. Magazu, P. Migliardo, A. M. Musolino and M. T. Sciortino, “α,α-Trehalose-Water Solutions. 1. Hydration Phenomena and Anomalies in the Acoustic Properties,” Journal of Physical Chemistry B, Vol. 101, No. 13, 1997, pp. 2348-2351. doi:10.1021/jp961139s
- S. Magazu, V. Villari, P. Migliardo, G. Maisano and M. T. F. Telling, “Diffusive Dynamics of Water in the Presence of Homologous Disaccharides: A Comparative Study by Quasi Elastic Neutron Scattering. IV,” Journal of Physical Chemistry B, Vol. 105, No. 9, 2001, pp. 1851-1855. doi:10.1021/jp002155z
- C. Branca, A. Faraone, S. Magazu, G. Maisano, F. Migliardo, P. Migliardo and V. Villari, “Structural and Dynamical Properties of Trehalose-Water Solutions: Anomalous Behaviour and Molecular Models,” Recent Research Developments in Physical Chemistry, Vol. 3, 1999, pp. 361-403.
- C. Branca, S. Magazu, G. Malsano and P. Migliardo, “Anomalous Cryoprotective Effectiveness of Trehalose: Raman Scattering Evidences,” Journal of Chemical Physics, Vol. 111, No. 1, 1999, pp. 281-287. doi:10.1063/1.479288
- M. C. Donnamaria, E. I. Howard and J. R. Grigera, “Interaction of Water with α,α-Trehalose in Solution: Molecular Dynamics Simulation Approach,” Journal of Chemical Society, Faraday Transactions, Vol. 90, No. 18, 1994, pp. 2731-2735. doi:10.1039/ft9949002731
- C. A. Angell, P. H. Poole and J. Shao, “Glass-Forming Liquids, Anomalous Liquids, and Polyamorphism in Liquids and Biopolymers,” Il Nuovo Cimento D, Vol. 16, No. 8, 1999, pp. 993-1025. doi:10.1007/BF02458784
- C. A. Angell, “Glassforming Liquids with Microscopic to Macroscopic Two-State Complexity,” Progress of Theoretical Physics, Suppl. 126, pp. 1-8. doi:10.1143/PTPS.126.1
- M. Bée, “Quasielastic Neutron Scattering: Principles and Applications in Solid State Chemistry, Biology and Material Science,” Adam Hilger, Bristol, 1988.
- G. Adam and J. H. Gibbs, “On the Temperature Dependence of Cooperative Relaxation Properties in GlassForming Liquids,” Journal of Chemical Physics, Vol. 43, No. 1, 1965, pp. 139-146. doi:10.1063/1.1696442
- E. Donth, “Can Dynamic Neutron Scattering Help to Understand a Thermodynamic Variant of an Internal Quantum-Mechanical Experiment in the Angstrom Range?” European Physical Journal E, Vol. 12, No. 1, 2003, pp. 11-18. doi:10.1140/epje/i2003-10051-5
- H. Solunov, “Significance of the Intramolecular Degrees of Freedom on the Glass-Forming Process,” Journal of Optoelectronics and Advanced Materials, Vol. 7, No. 1, 2005, p. 365.
- E. Donth, “The Glass Transition. Relaxation Dynamics in Liquids and Disordered Materials,” Springer, Berlin, 2001.
- H. Sillescu, “Heterogeneity at the Glass Transition: A Review,” Journal of Non-Crystalline Solids, Vol. 243, No. 2-3, 1999, pp. 81-108. doi:10.1016/S0022-3093(98)00831-X
- T. Kanaya, T. Kawaguchi and K. Kaji, “Local Dynamics of Cis-1,4-Polybutadiene near the Glass Transition Temperature Tg,” Physica B: Condensed Matter, Vol. 182, No. 4, 1992, pp. 403-408. doi:10.1016/0921-4526(92)90043-R
- T. Kanaya, T. Kawaguchi and K. Kaji, “Low-Energy Excitation and Fast Motion near Tg in Amorphous Cis-1, 4-Polybutadiene,” Journal of Chemical Physics, Vol. 98, 1993, pp. 8262-8270. doi:10.1063/1.464531
- J. Ferry, “Viscoelastic Properties of Polymers,” Wiley, New York, 1980.
- S. Magazù, G. Romeo and M. T. F. Telling, “Temperature Dependence of Protein Dynamics as Affected by Sugars: A Neutron Scattering Study,” European Biophysics Journal, Vol. 36, No. 7, 2007, pp. 685-691. doi:10.1007/s00249-007-0190-y
- M. H. Cohen and D. Turnbull, “Molecular Transport in Liquids and Glasses,” Journal of Chemical Physics, Vol. 31, No. 5, 1959, pp. 1164-1169. doi:10.1063/1.1730566
- U. Buchenau and R. Zorn, “A Relation between Fast and Slow Motions in Glassy and Liquid Selenium,” Europhysics Letters, Vol. 18, No. 6, 1992, p. 523. doi:10.1209/0295-5075/18/6/009
- A. P. Sokolov, et al., “Dynamics of Strong and Fragile glass Formers: Differences and Correlation with LowTemperature Properties,” Physics Review Letters, Vol. 71, No. 13, 1993, pp. 2062-2065. doi:10.1103/PhysRevLett.71.2062
- T. Kanaya, et al., “Microscopic Basis of Free-Volume Concept as Studied by Quasielastic Neutron Scattering and Positron Annihilation Lifetime Spectroscopy,” Physical Review E, Vol. 60, No. 2, 1999, pp. 1906-1912. doi:10.1103/PhysRevE.60.1906
- S. Magazu, et al., “Mean-Square Displacement Relationship in Bioprotectant Systems by Elastic Neutron Scattering,” Biophysical Journal, Vol. 86, No. 5, 2004, pp. 3241-3249. doi:10.1016/S0006-3495(04)74372-6
- J. Hansen, T. Kanaya, K. Nishida, K. Kaji, K. Tanaka and A. Yamaguchi, “Role of Vibrational Softening in Fast Dynamics of an Amorphous Polyimide Far Below Tg,” Journal of Chemical Physics, Vol. 108, No. 15, 1998, pp. 6492-6497. doi:10.1063/1.476055
- G. P. Johari and E. Whalley, “Dielectric Properties of Glycerol in the Range 0.1 - 105 Hz, 218 - 357 K, 0 - 53 kb,” Faraday Symposia Chemical Society, Vol. 6, 1972, pp. 23-41.
- G. P. Johary, “Glass Transition and Secondary Relaxations in Molecular Liquids and Crystals,” Annals of the New York Academy of Sciences, Vol. 279, 1976, pp. 117- 140. doi:10.1111/j.1749-6632.1976.tb39701.x
- S. Kahle, et al., “Confirmation of a Calorimetric Peculiarity in the Crossover Region of Glass Transition in Poly(n-Hexyl Methacrylate) by Differential Scanning Calorimetry,” Journal of Molecular Structure, Vol. 479, No. 2-3, 1999, pp. 149-162. doi:10.1016/S0022-2860(98)00866-7
- S. Magazu, C. Mondelli and G. Romeo, “Landscape Excitation Profiles and Excess Thermodynamic Properties of Disaccharide Aqueous Solutions,” Journal of Biological Physics, Vol. 32, No. 2, 2006, pp. 145-151. doi:10.1007/s10867-006-9009-9
- W. Doster, S. Cusack and W. Petry, “Dynamical Transition of Myoglobin Revealed by Inelastic Neutron Scattering,” Nature, Vol. 337, 1989, pp. 754-756. doi:10.1038/337754a0
- W. Kauzmann, “The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures,” Chemical Reviews, Vol. 43, No. 2, 1948, pp. 219-256. doi:10.1021/cr60135a002
- U. Mohanty, et al., “Supercooled Liquids,” Advances in Chemical Physics, Vol. 89, 1995, p. 89. doi:10.1002/9780470141489.ch2
- U. Mohanty, “On the Nature of Supercooled and Glassy States of Matter,” Physica A: Statistical Mechanics and Its Applications, Vol. 177, No. 1-3, 1991, pp. 345-355. doi:10.1016/0378-4371(91)90172-9
- M. Goldstein, “Viscous Liquids and the Glass Transition: A Potential Energy Barrier Picture,” Journal of Chemical Physics, Vol. 51, No. 9, 1969, pp. 3728-3739. doi:10.1063/1.1672587
- C. Leon and K. L. Ngai, “Rapidity of the Change of the Kohlrausch Exponent of the α-Relaxation of Glass-Forming Liquids at TB or Tβ and Consequences,” Journal of Physical Chemistry B, Vol. 103, No. 20, 1999, pp. 4045- 4051. doi:10.1021/jp983756h
- C.-Y. Wang and M. D. Ediger, “Anomalous Translational Diffusion: A New Constraint for Models of Molecular Motion,” Journal of Physical Chemistry B, Vol. 104, 2000, p. 1724.
- M. Beiner, H. Huth and K. Schroter, “Crossover Region of Dynamic Glass Transition: General Trends and Individual Aspects,” Journal of Non-Crystalline Solids, Vol. 279, No. 2-3, 2001, pp. 126-135. doi:10.1016/S0022-3093(00)00409-9
- S. Kahle, J. Korus, E. Hempel, et al., “Glass-Transition Cooperativity Onset in a Series of Random Copolymers Poly(n-Butyl Methacrylate-Stat-Styrene),” Macromolecules, Vol. 30, No. 23, 1997, pp. 7214-7223. doi:10.1021/ma961933b
- C. A. Solunov, “Cooperative Molecular Dynamics and Strong/Fragile Behavior of Polymers,” European Polymer Journal, Vol. 35, No. 8, 1999, pp. 1543-1556. doi:10.1016/S0014-3057(98)00226-2
- L. Abate, I. Blanco, C. Branca, S. Magazù, G. Malsano, F. Migliardo and G. Romeo, “Homologous Disaccharide Properties at Low Temperatures,” Journal of Molecular Liquids, Vol. 103-104, 2003, pp. 177-180. doi:10.1016/S0167-7322(02)00137-X
- C. A. Solunov, “Cooperative Molecular Dynamics and Strong/Fragile Behavior of Polymers,” European Polymer Journal, Vol. 35, No. 8, 1999, pp. 1543-1556. doi:10.1016/S0014-3057(98)00226-2
- C. A. Solunov, “The Apparent Activation Energy and Relaxation Volume from the Point of View of Adam-Gibbs Theory,” Journal of Physics: Condensed Matter, Vol. 14, No. 31, 2000, p. 7297. doi:10.1088/0953-8984/14/31/302
- C. A. Solunov, In: S. J. Rzoska, V. P. Zhelezny, Eds., Nonlinear Dielectric Phenomena in Complex Liquids, Kluwer Academic Publications, Netherlands, 2004, p. 275.
- C. A. Angell, In: J. C. Dore and J. Teixeira Kluwer, Eds., Hydrogen-Bonded Liquids, Academic Publishers, Dordrecht, 1991, pp. 59-79.
- C. A. Angell, “Two-State Thermodynamics and Transport Properties for Water from ‘Bond Lattice’ Model,” Journal of Physical Chemistry, Vol. 75, No. 24, 1971, pp. 3698-3705. doi:10.1021/j100693a010
- [61] C. A. Angell, In: K. L. Ngai and G. B. Write, Eds., Relaxation in Complex Systems, National Technology Information Service, Washingtong DC, 1984, pp. 3-11.
- [62] V. Velikov, S. Borick and C. A. Angell, “The Glass Transition of Water, Based on Hyperquenching Experiments,” Science, Vol. 294, No. 5550, 2001, pp. 2335-2338. doi:10.1126/science.1061757
- [63] E. Donth, “The Size of Cooperatively Rearranging Regions at the Glass Transition,” Journal of Non-Crystalline Solids, Vol. 53, No. 3, 1982, pp. 325-330. doi:10.1016/0022-3093(82)90089-8
- [64] F. Fujara, B. Geil, H. Sillescu and G. Fleisher, “Translational and Rotational Diffusion in Supercooled Orthoterphenyl Close to the Glass Transition,” Zeitschrift für Physik B Condensed Matter, Vol. 8, No. 2, 1992, pp. 195-204.
- [65] M. T. Cicerone, F. R. Blackburn and M. D. Ediger, “How Do Molecules Move near Tg? Molecular Rotation of Six Probes in o-Terphenyl across 14 Decades in Time,” Journal of Chemical Physics, Vol. 102, No. 1, 1995, pp. 471- 479. doi:10.1063/1.469425
- [66] E. Donth, “Phenomenological Treatment of Dynamic Glass Transition Heterogeneity,” Acta Polymerica, Vol. 50, No. 7, 1999, pp. 240-251. doi:10.1002/(SICI)1521-4044(19990701)50:7<240::AID-APOL240>3.0.CO;2-H
- [67] M. H. Cohen and D. Turnbull, “Molecular Transport in Liquids and Glasses,” Journal of Chemical Physics, Vol. 31, No. 5, 1959, pp. 1164-1169. doi:10.1063/1.1730566
- [68] E. Donth, “The Size of Cooperatively Rearranging Regions at the Glass Transition,” Journal of Non-Crystalline Solids, Vol. 53, No. 3, 1982, pp. 325-330. doi:10.1016/0022-3093(82)90089-8
- [69] F. H. Stillinger and J. A. Hodgdon, “Translation-Rotation Paradox for Diffusion in Fragile Glass-Forming Liquids,” Physical Review E, Vol. 50, No. 3, 1994, pp. 2064-2068. doi:10.1103/PhysRevE.50.2064
- [70] A. Einstein, “Über Die von der Molekularkinetischen Theorie der Wärme Geforderte Bewegung von in Ruhenden Flüssigkeiten Suspendierten Teilchen,” Annalen der Physik, Vol. 322, No. 8, 1905, pp. 549-560. doi:10.1002/andp.19053220806
- [71] P. Debye, “Polar Molecules,” Dover, New York, 1929.
- [72] C. F. Behrens, T. G. Christiansen, T. Christensen, J. C. Dyre and N. B. Olsen, “Comment on ‘Dynamic Viscosity of a Simple Glass-Forming Liquid’,” Physical Review Letters, Vol. 76, No. 9, 1996, p.1553. doi:10.1103/PhysRevLett.76.1553
- [73] J. Dufour, L. Jorat, A. Bondeau, A. Sibilini and G. Noyel, “Shear Viscosity and Dielectric Relaxanon Time of Dibutyl Phthalate Down to Glass Transition Temperature,” Journal of Molecular Liquids, Vol. 62, No. 1-3, 1994, pp. 75-82. doi:10.1016/0167-7322(94)00764-0
- [74] E. Cornicchi, G. Onori and A. Paciaroni, “PicosecondTime-Scale Fluctuations of Proteins in Glassy Matrices: The Role of Viscosity,” Physical Review Letters, Vol. 95, No. 15, 2005, Article ID: 158104. doi:10.1103/PhysRevLett.95.158104
- [75] I. Chang and H. Sillescu, “Heterogeneity at the Glass Transition: Translational and Rotational Self-Diffusion,” Journal of Physical Chemistry B, Vol. 101, No. 43, 1997, pp. 8794-8801. doi:10.1021/jp9640989
- [76] E. W. Fisher, E. Donth and W. Steffen, “Temperature Dependence of Characteristic Length for Glass Transition,” Physical Review Letters, Vol. 68, No. 15, 1992, pp. 2344- 2346. doi:10.1103/PhysRevLett.68.2344
- [77] E. Rössler, “Indications for a Change of Diffusion Mechanism in Supercooled Liquids,” Physical Review Letters, Vol. 65, No. 13, 1990, pp. 1595-1598. doi:10.1103/PhysRevLett.65.1595
- [78] R. Bohmer, “Nanoscale Heterogeneity if Glass-Forming Liquids: Experimental Advances,” Current Opinion in Solid State and Materials Science, Vol. 3, No. 4, 1998, pp. 378-385. doi:10.1016/S1359-0286(98)80048-X
- [79] R. Bohmer, et. al., “Nature of the Non-Exponential Primary Relaxation in Structural Glass-Formers Probed by Dynamically Selective Experiments,” Journal of Non- Crystalline Solids, Vol. 235-237, 1998, pp. 1-9. doi:10.1016/S0022-3093(98)00581-X
- [80] H. Sillescu, “Heterogeneity at the Glass Transition: A Review,” Journal of Non-Crystalline Solids, Vol. 243, No. 2-3, 1999, pp. 81-108. doi:10.1016/S0022-3093(98)00831-X
- [81] S. C. Glotzer, “Spatially Heterogeneous Dynamics in Liquids: Insights from Simulation,” Journal of Non-Crystalline Solids, Vol. 274, No. 1-3, 2000, pp. 342-355. doi:10.1016/S0022-3093(00)00225-8
- [82] J. P. Garrahan and D. Chandler, “Geometrical Explanation and Scaling of Dynamical Heterogeneities in Glass Forming Systems,” Vol. 89, No. 3, 2002, Article ID: 035704. doi:10.1103/PhysRevLett.89.035704
- [83] J. P. Garrahan and D. Chandler, “Coarse-Grained Microscopic Models of Glass Formers,” Proceedings of the National Academy of Science USA 100, 3 August 2003, pp. 9710-9714.
- [84] E. W. Fisher, E. Donth and W. Steffen, “Temperature Dependence of Characteristic Length for Glass Transition,” Physical Review Letters, Vol. 68, No. 15, 1992, pp. 2344- 2346. doi:10.1103/PhysRevLett.68.2344
- [85] I. Chang and H. Sillescu, “Heterogeneity at the Glass Transition: Translational and Rotational Self-Diffusion,” Journal of Physical Chemistry B, Vol. 101, No. 43, 1997, pp. 8794-8801. doi:10.1021/jp9640989
- [86] J. D. Ferry, L. D. Grandine and E. R. Fitzgerald, “The Relaxation Distribution Function of Polyisobutylene in the Transition from Rubber-Like to Glass-Like Behavior,” Journal of Applied Physics, Vol. 24, No. 7, 1953, p. 911. doi:10.1063/1.1721401
- [87] S. Sastry, “The Relationship between Fragility, Configurational Entropy and the Potential Energy Landscape of Glass-Forming Liquids,” Nature, Vol. 409, 2001, pp. 164- 167. doi:10.1038/35051524
- [88] A. Q. Tool, “Relation between Inelastic Deformability and Thermal Expansion of Glass in Its Annealing Range,” Journal of American Ceramic Society, Vol. 29, No. 9, 1946, pp. 240-253. doi:10.1111/j.1151-2916.1946.tb11592.x
- [89] A. Q. Tool and C. G. Eichlin, “Variations Caused in the Heating Curves of Glass by Heat Treatment,” Journal of American Ceramic Society, Vol. 14, No. 4, 1931, pp. 276- 308. doi:10.1111/j.1151-2916.1931.tb16602.x

