Open Journal of Metal
Vol.2 No.1(2012), Article ID:18317,6 pages DOI:10.4236/ojmetal.2012.21005
Energy Parameter Correlation of Failure Life Data between Cyclic Ball Indentation and Low Cycle Fatigue
Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai, India
Email: raghuprakash@iitm.ac.in
Received December 25, 2011; revised January 26, 2012; accepted February 15, 2012
Keywords: Cyclic Indentation; Fatigue; Plastic Dissipation Energy Density; Pile-Up
ABSTRACT
Material properties provide important information about the fatigue life which makes life extension of critical components in various industries possible. The conventional methods of determining tensile strength and fatigue life through ASTM or equivalent standard specimen have their limitations due to size requirements of test specimen. Automated Ball Indentation (ABI) is a semi-invasive technique that is useful for determining the material properties. A tungsten carbide ball of diameter 1.57 mm is used to load the test specimen and the force vs. displacement response is used to estimate material properties. Methods have been formulated in the past to predict the fatigue life of the specimen by correlating Cyclic Indentation and Low Cycle fatigue data. In this work, investigation of the role of plastic dissipation energy in failure and its correlation for the two processes by Finite Element simulations in ABAQUS is attempted. Results such as force vs. displacement response, residual depth and plastic diameter with Haggag’s [1] formulation and experimental results are validated first. Then, the plastic dissipation energy density, which is a comparable parameter, is plotted for both Cyclic Indentation and Low Cycle Fatigue. A reasonably good correlation is obtained which also validates the failure life predicted from knee-point approach. Dependence of the pile-up profile of variables such as method of loading and the friction between the contacting bodies is also discussed.
1. Introduction
In applications such as power plants, chemical plants and aircraft industry, it is helpful to assess the residual life for predicting component failure because materials degrade over a period of time. Fatigue failure due to repeated loading and unloading is responsible for most of the mechanical failures. Most of the conventional methods of determining tensile strength and fatigue strength are destructive in nature and have limitations due to the size of specimen required.
Automated Ball Indentation (ABI) test technique is a semi-invasive and non-destructive technique [1] to determine the mechanical properties of metallic materials. In this method, a tungsten carbide spherical ball of nominal diameter of 1.57 mm is used to load the material under cyclic load-unload sequence and the force vs. displacement response is obtained. The indentation depth is progressively increased to the maximum defined penetration depth, which is about 25% of indenter’s diameter. The indenter material is so chosen that its hardness is much greater than that of the test material, and its deformation is negligible.
2. Prior Studies
Several researchers [1-4] have studied the force-displacement response during an indentation test using a spherical indenter to derive the material’s mechanical properties. Spherical indenter is preferred because of the simplicity of the indenter geometry and the absence of stress concentration.
While indentation tests are nondestructive and easy to use, the test results are difficult to analyze because of the complicated tri-axial stress state under the ball indenter. However, this kind of barrier has been greatly removed by finite element (FE) analyses. Byun et al. [2] measured through-the-thickness material properties in SA508 Gr.3 pressure vessel steels using ball indentation technique experimentally. Indentation energy to fracture (IEF) parameter was obtained using critical stress to strain concept, which allows the nondestructive determination of fracture energy from ABI-measured stress-strain curves by Haggag et al. [1].
Studies have attempted to relate plastic dissipation energy with fatigue failure of material. Klingbeil [5] proposed a theory for fatigue crack growth in ductile solids based on the total plastic dissipation per cycle. Fatigue crack growth rate is attempted to be formulated in terms of the total plastic dissipation energy and the monotonic plane strain or plane stress toughness of the material. Prakash et al. [6] predicted the fatigue life of Al 7175- T7315 using the knee point approach by correlating the experimental indentation and low cycle fatigue data.
3. FE Modeling of Ball Indentation and Low Cycle Fatigue
3.1. Input Parameters
Simulation of ball indentation process for the material Al 7175-T7315 was performed using ABAQUS finite element code. A 2D axi-symmetric formulation was used to reduce computation time and memory requirement. The whole model comprised of two parts, viz. indenter and material plate. Indenter was modeled both as a deformable and rigid sphere of diameter 1.57 mm, while the material plate as a deformable cylinder of radius 15 mm and height 10 mm.
The boundary conditions for indentation applied were as follows: 1) the bottom face of the test specimen was constrained in displacement in the vertical direction; 2) The left face of the test specimen was constrained to not move in the horizontal direction; 3) Displacement and force was applied to the reference point on the sphere, and it could move only in the vertical direction.
Table 1 shows the material properties provided for Al 7175-T7315. Figure 1 shows the engineering stressstrain curves and the true stress-strain curves obtained from tensile test.
Figure 2 presents the enlarged view of meshed ABI specimen and low cycle fatigue specimen. The plate was meshed with eight-node bi-quadratic quadrilateral elements with reduced integration elements (CAX8R), 11671 in number. Eight-node elements were preferred over 4-node elements for better convergence of results. Fine meshing was made near the contact region and coarser away from it to reduce computational time. The smallest element edge was less than 10 μm.
3.2. Method of Loading
As shown in Figure 3, the types displacement controlled loading (static indentation) were considered: 1) one cycle of displacement load of 0.05 mm; 2) five cycles of displacement load of 0.05 mm; 3) five cycles of varying load from 0.04 mm to 0.20 mm.
Force-Controlled loading (cyclic indentation) was given

Table 1. Input properties for Al 7175-T7315.
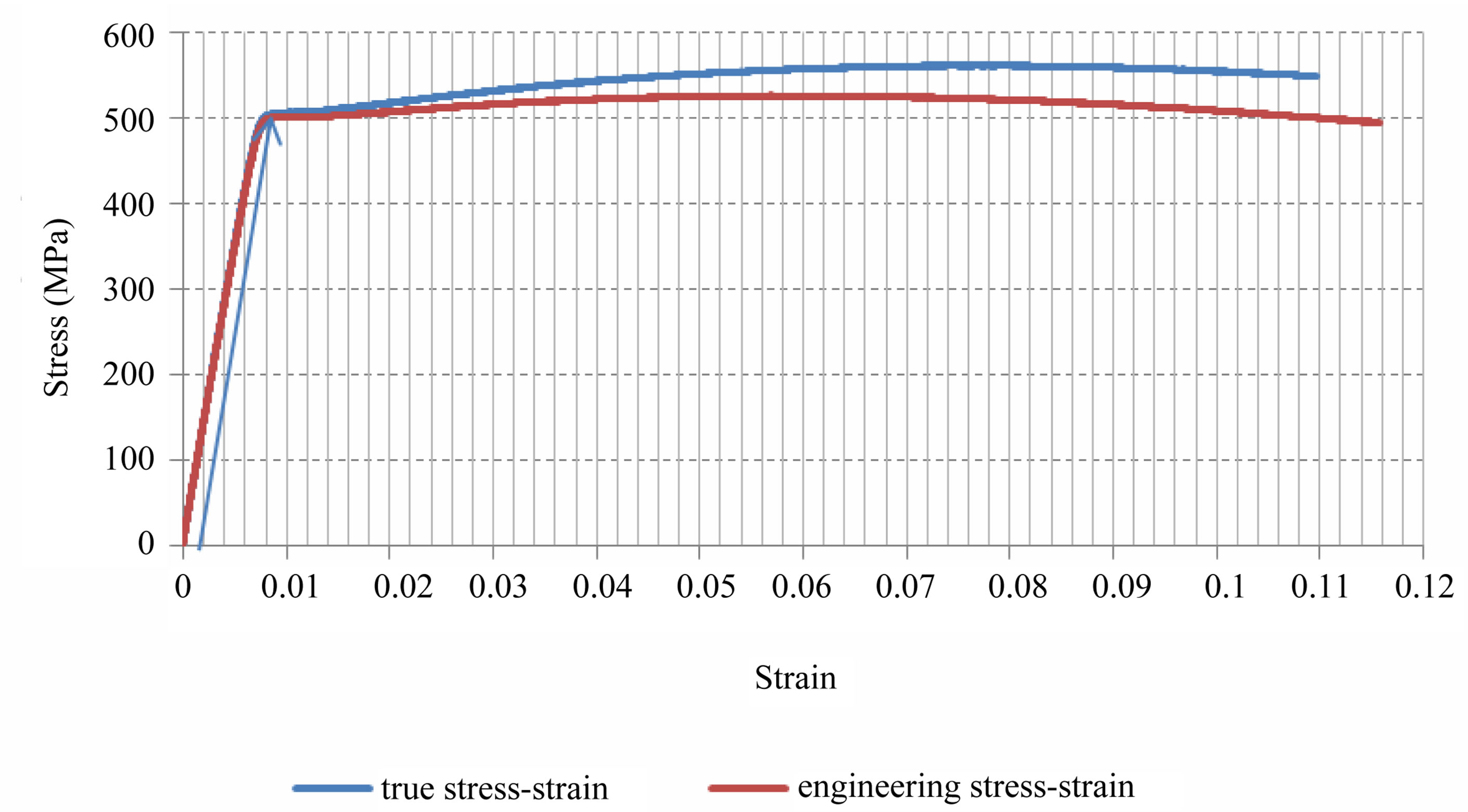
Figure 1. Engineering stress-strain curve and true stress-true strain curve of Al-alloy 7175-T351.

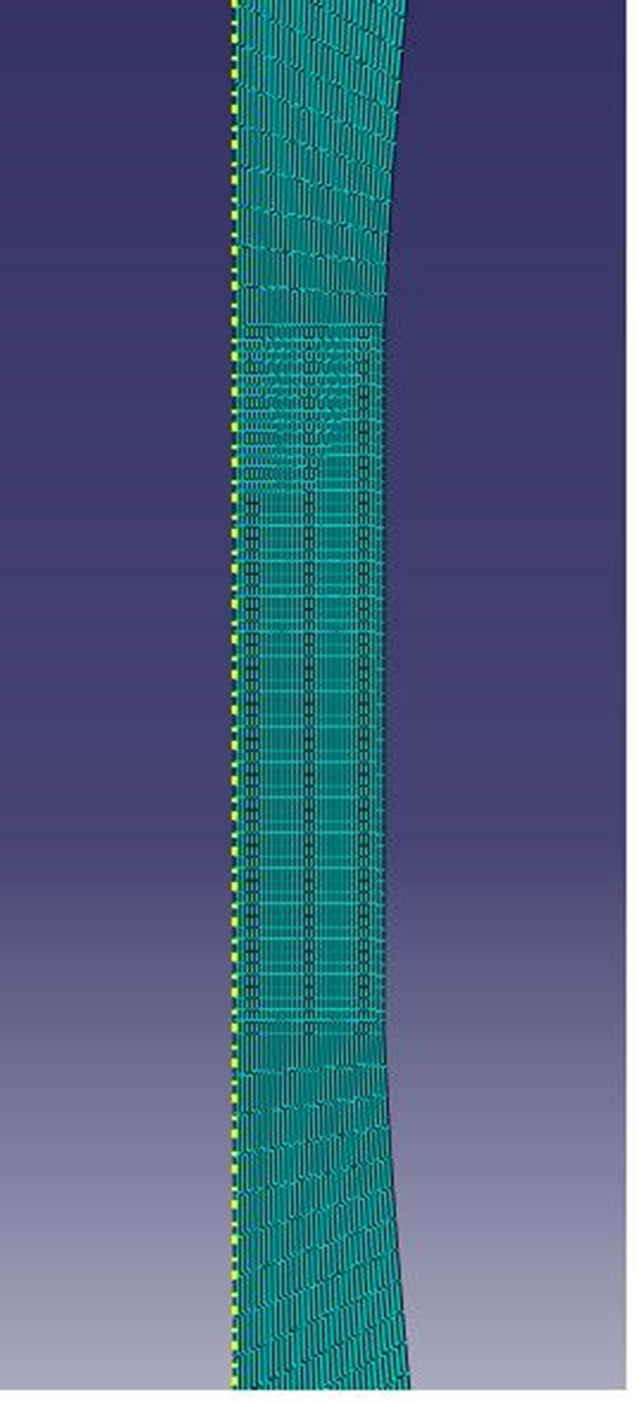
Figure 2. Meshing for the test specimen for the simulation of ball indentation and low cycle fatigue.
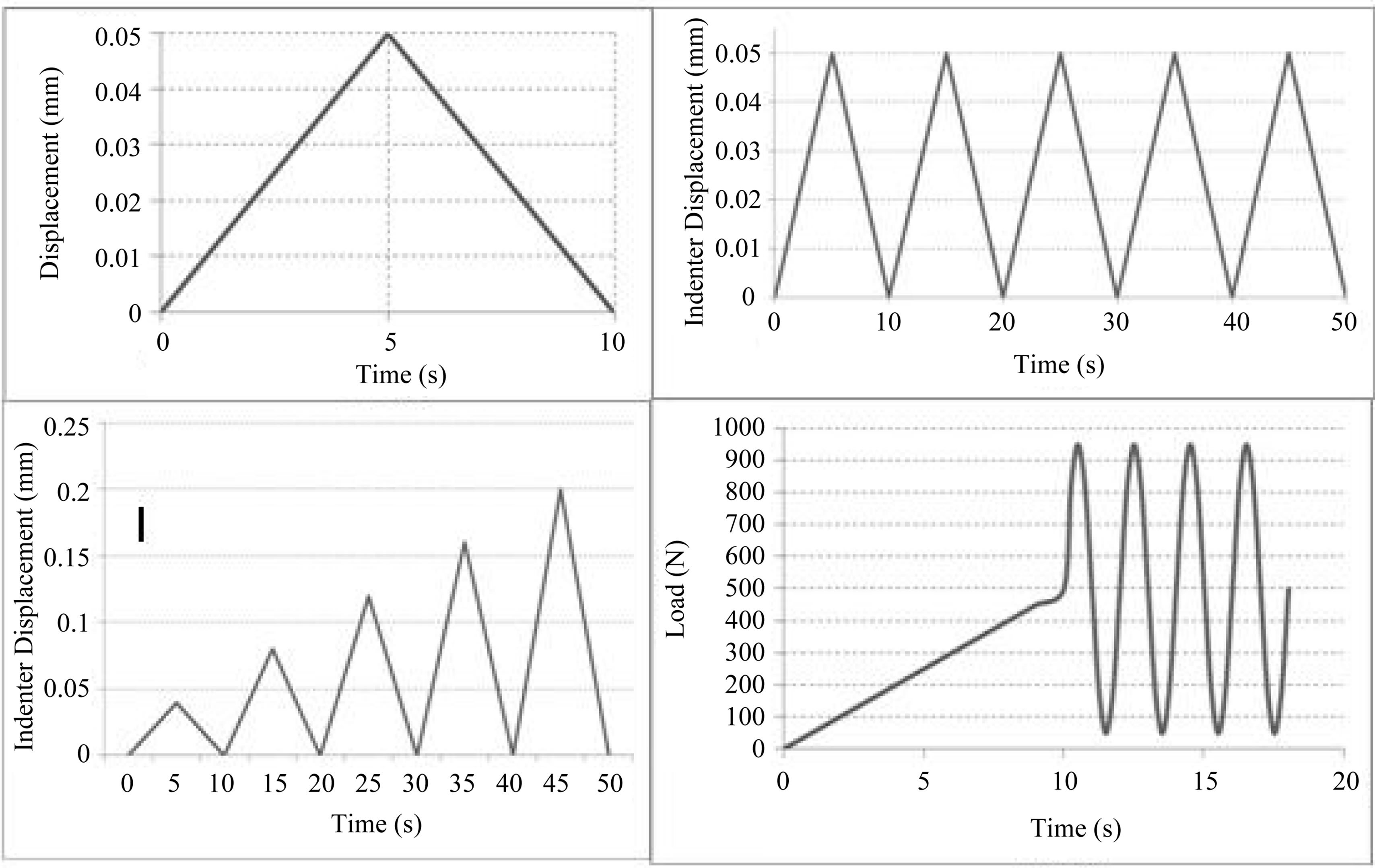
Figure 3. Various modes of loading.
by applying a compressive ramp load till 500 N and then a compressive periodic load varying between 50 N and 950 N. The spherical ball and plate contact was modeled by varying the coefficient of friction between 0.1 and 0.3, and by making it as a function of contact pressure. Both rigid and deformable indenter used, but ultimately the rigid indenter was preferred to simplify analysis.
Low cycle fatigue simulation was performed similar to experiments conducted earlier as per ASTM E 606 standards [7]. The geometry of Al alloy (7175-T351) LCF specimen was modeled and material properties as obtained from the tensile test were used for the model.
The material was loaded beyond the yield strength and various components of stress contours and elastic and plastic strain were studied. In the LCF specimen, CAX- 4R 4500 quadratic elements were used and fine meshing in the central region of the specimen, which is the probable failure region.
4. Results and Discussions
4.1. Validation of Results
Results were validated by the following methods:
The plastic strain and plastic diameter were validated using Haggag’s formulations, which showed the maximum deviation of 6.6 % and 5 % respectively (Figure 4). The force-displacement curve for static indentation curve obtained from simulation was compared with the expe-

Figure 4. Equivalent plastic strain for one cycle of loading.
rimental results (Figure 5), which showed a peak deviation of approx. 8%. The total depth of indentation vs number of cycles was compared with the experimental results and it showed an error of approx. 9.5% (Figure 6). The yield-strength, elastic modulus and the general nature of the curve as obtained from the stress-strain curve from FE simulation was found to match with the input material data (Figure 7).
4.2. Analysis of Results
Force-displacement curves obtained from FE simulation of indentation were studied along with those of stressstrain curves. Since, for one half-cycle the stress-strain curve was expected to replicate the input stress-strain data, parameters such as yield strength, elastic strain and elastic modulus were obtained. They were found to be in concurrence with the material properties provided as input. The validation of results with Haggag’s formulations and from experimental results was also satisfactory. The total depth of indentation vs. number of cycle obtained through cyclic indentation was compared with that obtained through experiments.
Figure 8 shows the force-displacement curves obtained for fives cycles of constant and varying loading and unloading. The area under the loading unloading forcedisplacement curve is the plastic dissipation energy. The nature of plots was same as found experimentally. It may be noted that the material has strain hardening response, and for the purpose of analysis, stable strainhardening response was considered.
Figure 9 shows the stress-strain hysteresis loops for 25 cycles. The curves stabilize after initial few cycles. The area under the hysteresis curves is the plastic dissipation energy density.
4.3. Energy Correlation
The plastic dissipation energy density contours were studied for cyclic indentation [8] and low cycle fatigue [9] to find the region where it had the greatest value, and hence was most likely to fail. At these nodes, the values after each cycle were plotted and found to be almost linear.
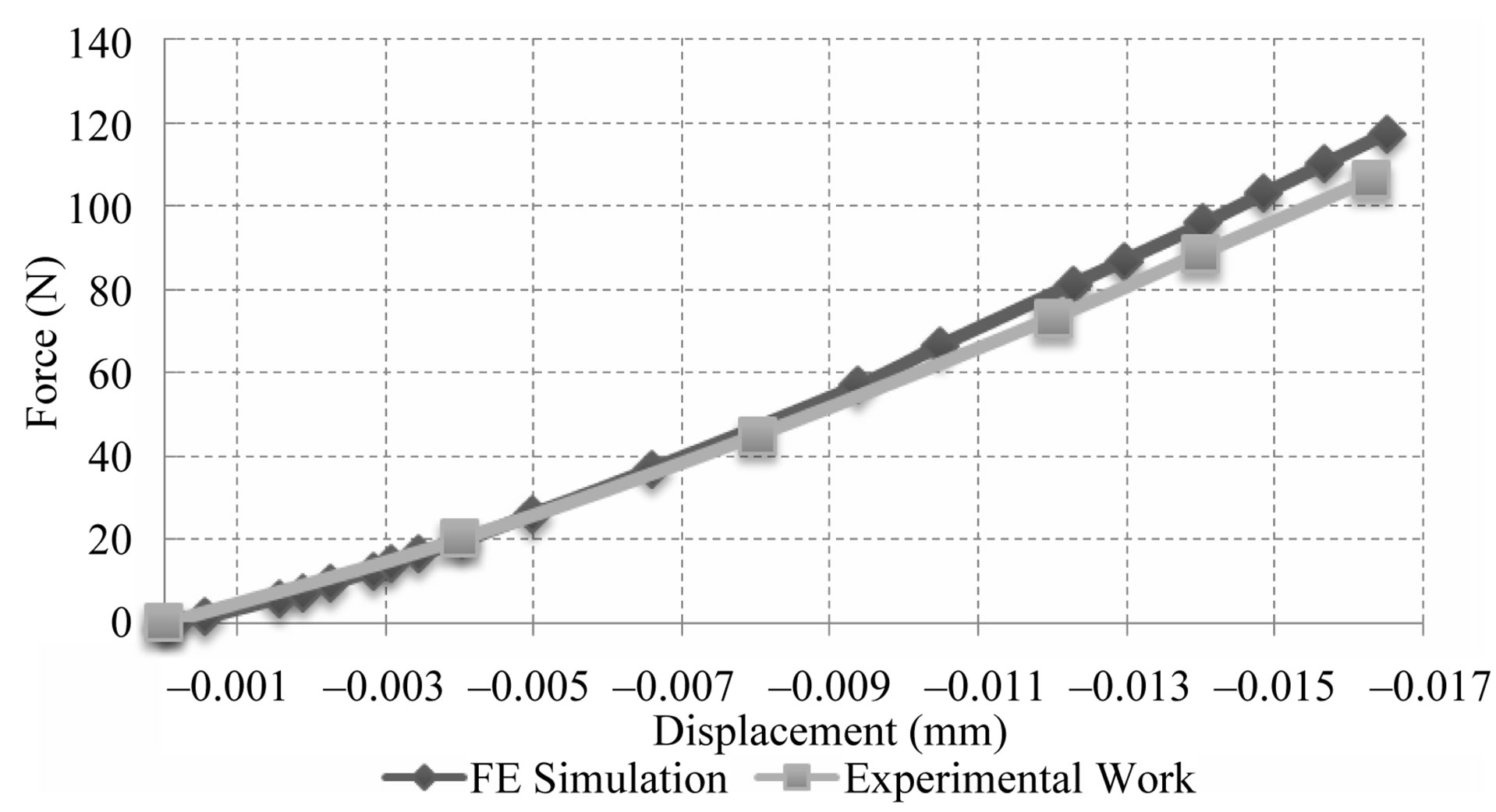
Figure 5. Comparison of force-displacement response for FE simulation with experimental data.

Figure 6. Comparison of total depth of penetration for FE simulation with experimental data.
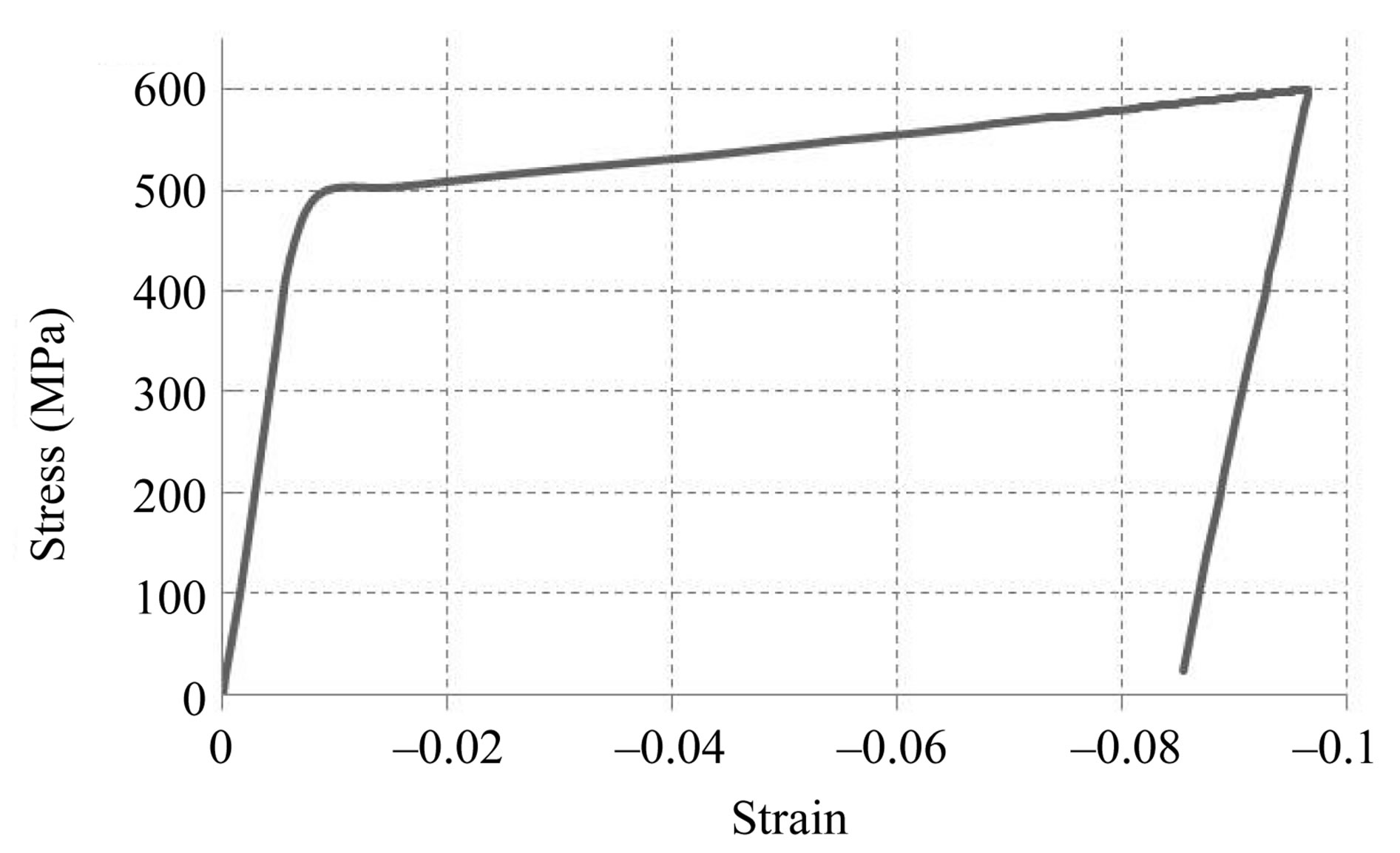
Figure 7. Stress-strain curve for one cycle of static indentation.
The objective of the work was to study the plastic dissipation energy density in the material and to check if a correlation existed between the two. Figure 10 shows the correlation for 210 cycles. The number of cycles as predicted before through the knee-point approach was also validated. Figure 10 presents the plastic dissipation energy (PDE) contours of indenter contact region. Also shown by the side is the plastic dissipation energy contour for a smooth LCF specimen. It can be seen that there is a peak PDE at a location below the indenter contact, which represents the location for first crack initiation in cyclic indentation.

Figure 8. Force-displacement response for five cycles of constant loading and varying loading.
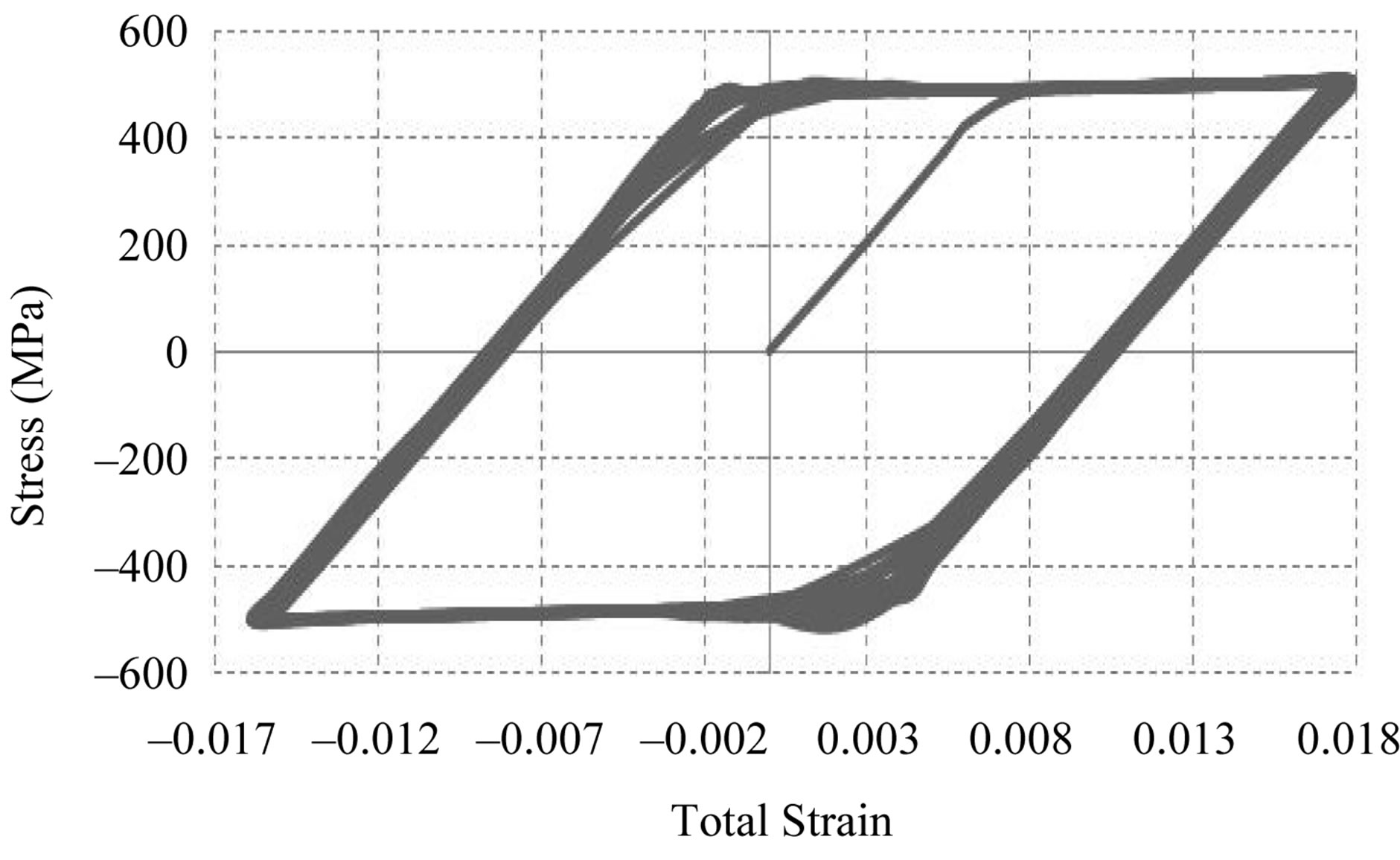
Figure 9. Stress-strain hysteresis response for 25 cycles of loading under low cycle fatigue.
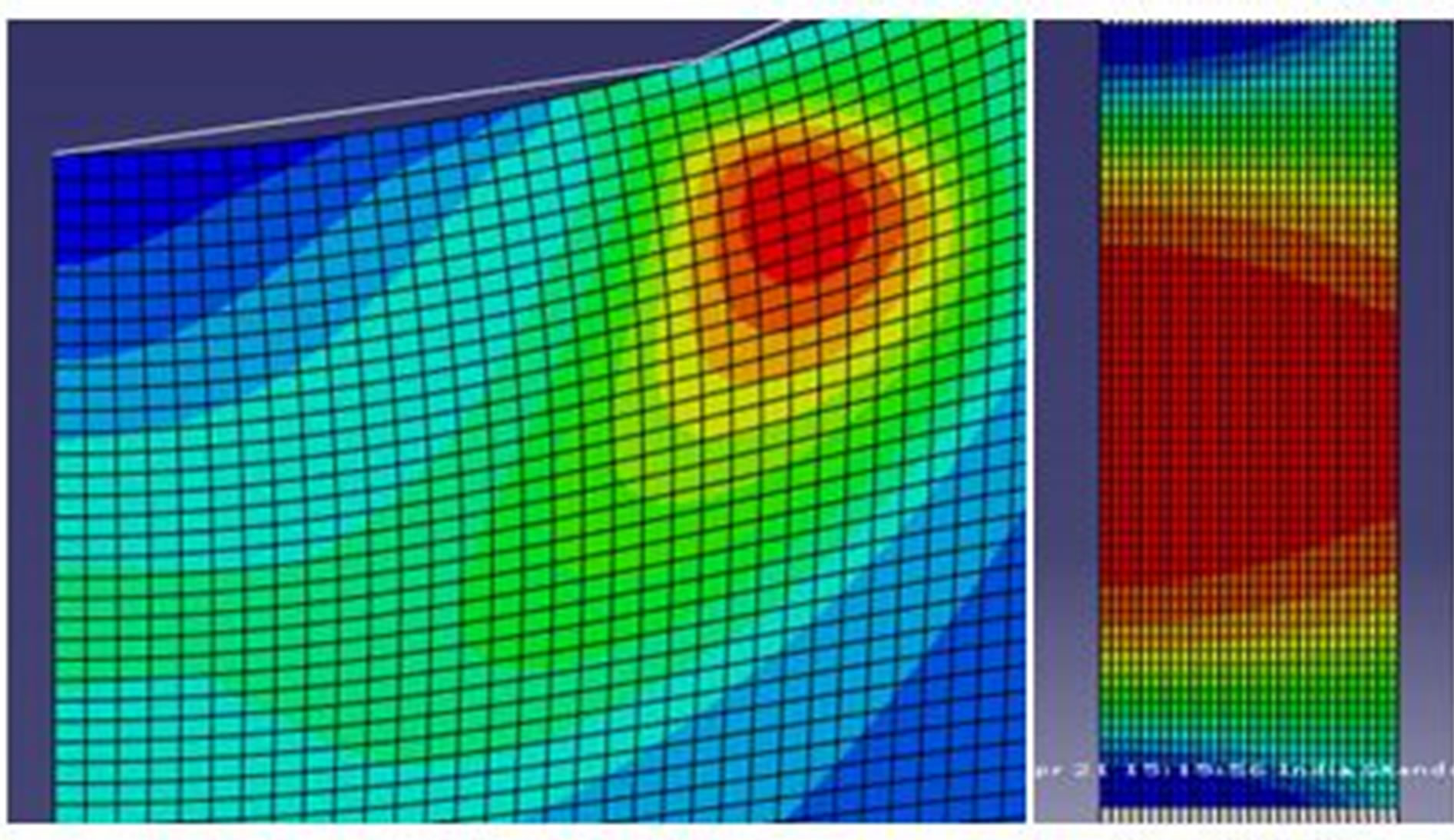
Figure 10. Plastic dissipation energy contours for cyclic indentation and low cycle fatigue.
Figure 11 presents the plot of plastic dissipation energy density as a function of cycles of loading for both smooth LCF specimen and for cyclic indentation specimen. It can be seen that both have different slopes as a function of cycles of loading, The point of intersection of these two graphs can be considered as point of failure for the indentation specimen.
From Figure 11(PDED)CI = (5.38 nCI + 147.6)
(PDED)LCF = (7.54 nLCF – 2.96)
where
(PDED)CI is the plastic dissipation energy density for cyclic indentation(PDED)LCF is the plastic dissipation energy density for low cycle fatiguenCI is the number of cycles for cyclic indentation, and nLCF is the number of cycles for low cycle fatigue.
Thus, energy parameter at failure was defined as follows:
(Energy parameter)CI = 321 X (PDED)CI
(Energy parameter)LCF = 254 X (PDED)LCF
The energy parameter was plotted with number cycles shown in Figure 12 and was found to be equal for CI and

Figure 11. Comparison of plastic dissipation energy Density for CI and LCF.

Figure 12. Comparison of energy parameter for CI and LCF.
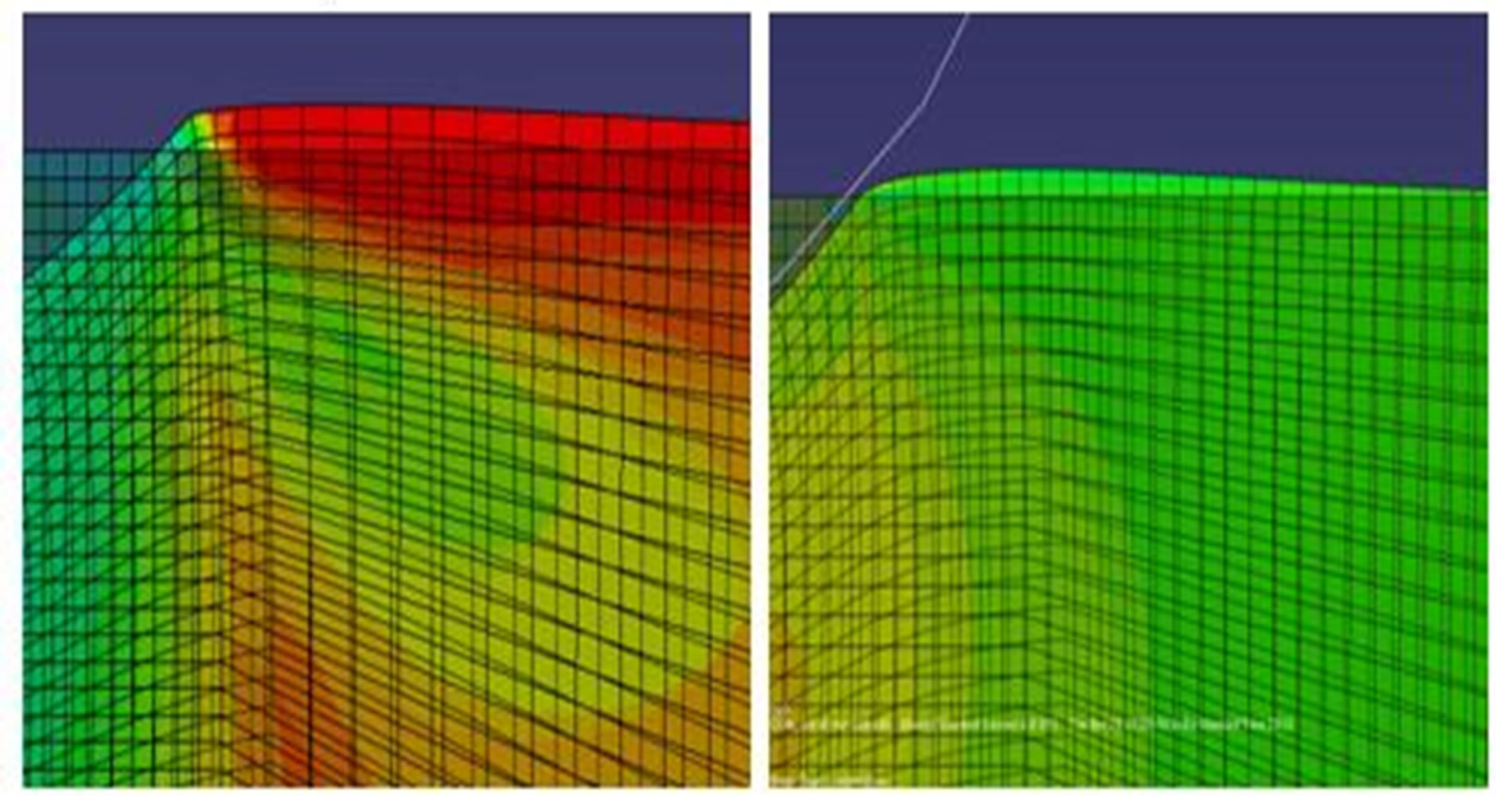
Figure 13. Pile-up profile for a loading of 0.25 mm and 0.15 mm.
LCF after 261 cycles. Since this value falls between the number of cycles equired for failure for CI and LCF as predicted by the knee-point approach, the correlation can be said to be acceptable.
Pile-up was found to occur at the indenter plate interface and the profile was studied by varying amplitude of displacement-loading as shown in Figure 13.
5. Conclusions
1) The success of the FE simulation of ball indentation and low cycle fatigue process could be gauged from the fairly acceptable validation of the results with the experimental data and analytical results.
2) The region where the material was likely to fail due to accumulation of plastic dissipation energy was located and was found to be consistent with previous studies.
3) The plastic dissipation energy density values for LCF and CI were correlated and the energy parameter was found. Upon plotting the energy parameter for LCF and CI, a satisfactory correlation was found.
4) The energy correlation technique could be used to predict the fatigue failure life of not only Al alloy but other materials through the same approach.
REFERENCES
- T. S. Byun, J. H. Hong, F. M. Haggag, K. Farell and E. H. Lee, “Measurement of through the Thickness Variations of Material Properties in SA508 Gr.3 Pressure Vessel Steels Using Ball Indentation Test Technique,” International Journal of Pressure Vessels & Piping, Vol. 74, No. 3, 1997, pp. 231-238. doi:10.1016/S0308-0161(97)00114-2
- F. M. Haggag, T. S. Byun, J. H. Hong, P. Q. Miraglia and K. L. Murty, “Indentation-Energy-to-Fracture (IEF) Parameter for Characterization of Carbon Steels Using NonDestructive Automated Ball Indentation (ABI) Technique,” Scriptia Materialia, Vol. 38, No. 4, 1998, pp. 645- 651. doi:10.1016/S1359-6462(98)00519-3
- J. M. Collin, T. Parenteau, G. Mauvoisin and P. Pilvin, “Material Parameters Identification Using Experimental Continuous Spherical Indentation for Cyclic Hardening,” Computational Materials Science, Vol. 46, No. 2, 2009, pp. 333-338. doi:10.1016/j.commatsci.2009.03.016
- S. Mesarovic and N. A. Fleck, “Spherical Indentation of Elastic-Plastic Solids,” The Royal Society, Vol. 455, No. 1987, 1999, pp. 2707-2728. doi:10.1098/rspa.1999.0423
- N. W. Klingbeil, “A Total Dissipated Energy Theory of Fatigue Crack Growth in Ductile Solids,” International Journal of Fatigue, Vol. 25, No. 2, 2003, pp. 117-128. doi:10.1016/S0142-1123(02)00073-7
- R. V. Prakash, P. Bhokardole and C. S. Shin, “Investigation of Material Fatigue Behaviour through Cyclic Ball Indentation Testing,” Journal of ASTM International, Vol. 5, No. 9, 2008, pp. 1-15. doi:10.1520/JAI101042
- “Standard Practice for Strain-Controlled Fatigue Testing,” ASTM International, Designation E 606, West Conshohocken, USA.
- F. Yang, L. Peng and O. Kenji, “Cyclic Indentation in Aluminium,” Journal of Material Science, Vol. 42, No. 12, 2007, pp. 4513-4520. doi:10.1007/s10853-006-0480-2
- V. T. Troschenko and P. A. Fomichev, “An Energy Criterion for Fatigue Failure,” Strength of Materials, Vol. 25, No. 1, 1993, pp. 1-7. doi:10.1007/BF00767729

