Open Journal of Composite Materials
Vol.05 No.01(2015), Article ID:52795,7 pages
10.4236/ojcm.2015.51005
Dynamic Mechanical Behavior of Luffa cylindrica Fiber-Resorcinol Composites
Chhatrapati Parida1*, Chinmay Pradhan2, Sarat Kumar Dash3, Sarat Chandra Das4
1Depatment of Physics, Orissa University of Agriculture and Technology, Bhubaneswar, India
2Post Graduate Department of Botany, Vani Vihar, Utkal University, Bhubaneswar, India
3Department of Education in Science and Mathematics, National Council of Educational Research and Training, Bhubaneswar, India
4Department of Chemistry, Salipur College, Salipur, India
Email: *sivaji_1976@yahoo.co.in, chinmay-pr@yahoo.com, skdash59@yahoo.com, ctkscd@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 October 2014; revised 18 November 2014; accepted 10 December 2014
ABSTRACT
Dynamic mechanical behaviour of resorcinol-formaldehyde matrix and its composites reinforced with natural fibers of Luffa cylindrica (LC) has been studied. The effects of fiber loading, alkali treatment on fiber, temperature and frequency on storage modulus and mechanical-loss factor of the composites were studied. The dynamic mechanical behaviour of the composites and pure matrix has been investigated in the frequency range from 0.1 Hz to 10 Hz and temperature range from 26˚C to 100˚C. The experimental results show that the values of storage modulus of the composites increase with increase in fiber loading. The storage modulus of treated LC fiber composites were found to be enhanced when compared with the untreated fiber composites. It was also found that mechanical-loss factor was more when untreated LC fibers were incorporated in the composites and decreased with the incorporation of treated LC fiber. The storage modulus of all the composites increased with frequency but decreased with rise of temperature. The glass transition temperature of the composites was evaluated from the peaks of tan delta variations.
Keywords:
LC, Storage Modulus, Mechanical Loss Factor, Tan Delta, Visco-Elastic Nature

1. Introduction
Most of the materials are subjected to cyclic loading or cyclic deformation during their service performance. For example automobile tires, springs, and dampers are always exposed to cyclic loading. Resorcinol and resorcinol- formaldehyde (RF) resins have been extensively used to promote the bonding between rubber compounds and various reinforcing material [1] . The tire industry is the biggest user of these products where rayon, nylon, fiberglass, polyester, steel and aramid have all been successfully bonded to natural/synthetic rubber compositions. Resorcinol and resorcinol-formaldehyde (RF) resins are also used in conveyor belts, v-belts, power transmission belts and pneumatic and hydraulic hoses. The polymer composites to be used in above mentioned applications require stiffness along with flexibility. The stiffness of the composites can be enhanced by reinforcing natural fibers like LC fibers. These polymer composites are in fact viscoelastic materials. They exhibit a combination of elastic behaviour as well as viscous behaviour. Thus a complete description of viscoelastic properties of these composites can be provided by dynamic mechanical experiments with variation in temperature, frequency and fiber loading. Therefore, dynamic mechanical analysis is an important tool in studying the viscoelastic nature of the composites.
Laly A. Pothan et al. in 2003 [2] studied the dynamic mechanical analysis of banana fiber reinforced polyester composites with special reference to the effect of fiber loading, frequency and temperature. The loss modulus and damping peaks were found to be lowered by the incorporation of the banana fiber into the matrix. Smita Mohanty et al. in 2004 [3] studied the dynamic mechanical behaviour of sisal fiber reinforced polypropylene composites. The damping properties of the composites were found to decrease with the addition of sisal fibers and the storage modulus of the composites was enhanced by giving chemical treatments to the sisal fibers. V. G Geethamma et al. in 2005 [4] studied the dynamic mechanical behavior of natural rubber and its composites reinforced with short coir fibers. They reported that the value of mechanical loss factor decreased with increase in frequency whereas the value of storage modulus increased with increase in frequency. Maya Jacob et al. in 2006 [5] studied dynamic mechanical behaviour of natural rubber reinforced with sisal and oil palm fibers. The storage modulus of the composites was found to increase with increase in wt fraction of fiber due to the increased stiffness imparted by the sisal and palm fiber. Loss modulus increased with loading of fiber in the composites while the damping property was found to decrease. Mehdi Tajvidi et al. in 2006 [6] studied the polypropylene composites reinforced by kenaf fibers and bamboo fibers. They reported that storage modulus and loss modulus increased for all composites compared to the pure matrix which indicated increase in stiffness and elasticity of composites. A decrease in loss factor was observed for all the composites with incorporation of fiber. Zhaogian Li et al. in 2011 [7] reported the dynamic mechanical properties of PLA composites reinforced with sisal fiber. The loss modulus of the composites was found to decrease with addition of sisal fiber. They also reported increase in storage modulus of composites when treated sisal fibers were incorporated. As such the present studies include the analysis of resorcinol-formaldehyde resin and LC fiber composites as a function of frequency, fiber treatment, fiber loading and temperature.
When a sinusoidal oscillating load is applied on a sample, the sample will also deform sinusoidally. This will be reproducible if the material is deformed within its linear viscoelastic region.
The sinusoidal stress applied to any material is given by
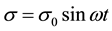 (1)
(1)
where σ is the stress at any time, σ0 is the maximum stress, and ω is the angular frequency of the applied stress. The resultant wave shape of the strain due to sinusoidal stress is dependent on viscoelastic nature of the material. The two extremes of the material’s behavior, elastic nature and viscous nature, provide the limiting extremes that will add to give the strain wave. The behavior can be understood by evaluating each of the two extremes. The material at the spring-like, or Hookean limit, will respond elastically with the oscillating stress. The strain at any time can be written as:
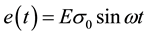 (2)
(2)
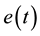 is the strain at any instant of time (t), E is the modulus.
is the strain at any instant of time (t), E is the modulus.
The above equation can be precisely expressed as
 (3)
(3)
e0 represents maximum strain.
The difference between the applied stress and the resultant strain is an angle δ; the elastic response at anytime can be written as:
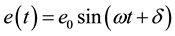 (4)
(4)
It can be separated into the in-phase and out-of-phase strains.
The in phase strain can be expressed as
 (5)
(5)
The corresponding in phase moduli or storage moduli is expressed as E'.
The out of phase strain can be expressed as
 (6)
(6)
The corresponding out of phase moduli or loss moduli is expressed as E''.
The vector sum of these two components gives the overall or complex strain on the sample:
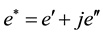 (7)
(7)
The ratio of the loss modulus to the storage modulus is also the tan of the phase angle and is called damping:
So the damping,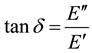 (8)
(8)
2. Experimental
The chemicals such as calcium chloride (CaCl2 2H2O, 97%), sodium carbonate (Na2CO3, 95%), di sodium hydrogen phosphate (Na2HPO4 2H2O, 99.5%), resorcinol (C6H4O2), formaldehyde (HCHO), maleic anhydride [C2H2(CO)2O], ethylenediamine [C2H4(NH2)], sodium hydroxide (NaOH), sodium hypochlorite (NaClO), di- vinyl benzene and methane sulphonic acid all of AR grade were procured from E. Merck, India.
The LC fibers were cut into small pieces of length around 2 cm, washed thoroughly with deionized water and then dried at 70˚C in vacuum oven for 20 minutes. The dried LC fibers were treated with alkali followed by bleaching and acid hydrolysis. For giving alkali treatment, the LC fibers were soaked in a 5% NaOH solution at 80˚C for 1h. The soaked LC fibers were then washed with fresh water for 30 minutes to remove any excess NaOH sticking to the surface of LC fiber. The fibers were then dried at room temperature for 48 h followed by drying in oven at 60˚C for 6h. During alkali treatment given to the LC fibers the hemicelluloses and lignin present in the fibers are extracted. In this way the number of −OH groups present in the fiber is reduced. The decrease in −OH groups increases hydrophobicity of fibers which strengthen the bonding between fiber and matrix. There is disruption of hydrogen bonds in the network structure of cellulose due to the alkali treatment. Thus it increases the surface roughness and the adhesion between fiber and matrix. This treatment depolymerizes cellulose and exposes the short length crystallites of cellulose. The alkali treated LC fibers were then bleached with 2% sodium hypochlorite solution. The mixture was continuously stirred for 2 h at 80˚C and was poured through a filter paper in a funnel. The solid fibers were trapped by the filter paper and were washed with distilled water till neutral pH was obtained. The pulp obtained after bleaching is termed usually as micro crystalline cellulose (MCC). The colour of the bleached LC fibers appear yellowish from black. The bleached LC fiber/water suspension was prepared and kept on an ice bath. H2SO4 was added slowly under continuous stirring to the suspension placed in an ice water bath, until the final concentration of 60% H2SO4 was reached. The obtained suspension was then heated at 45˚C under continuous stirring for 2 h. In order to remove excess acid the mixture was washed and centrifuged using an ultracentrifuge at 30˚C for 20 minutes with 7000 rpm.
Composites were synthesized by taking RF resin and both chemically treated and untreated LC fibers. The prepared grounded RF resin and LC were mixed in different wt proportion. In sample B1 and B2, the matrix and untreated LC fiber are in wt ratio 1:1 and 1:2 respectively. In sample B4 and B5, the matrix and treated LC fiber are in wt ratio 10:1 and 5:1 respectively. B3 sample contains only powdered RF matrix. Maleic anhydride (1 g) and ethylene di-amine (4.6 ml) were added as cross linkers to 1 g of RF resin. The mixture was heated at constant temperature of around 70˚C for 9 h to get composites. After cooling the composite was washed with distilled water, followed by washing in ethyl alcohol to remove monomers present in it. The grounded composite was then exposed to ultrasonic vibration at 30 kHz for 1 h at room temperature using a sonicator (1.5 L50 H/Deluxe, India). Sonication was responsible to enhance dissolution of particles by breaking intermolecular interactions. The particles of the samples are agitated when exposed to ultrasonic wave and hence particle size decreases. 10 g of powdered composites was then mixed with 10 g of commercial divinyl benzene and kept for 12 h at room temperature of 28˚C. The material was made acidic by addition of 0.25 ml of methane sulphonic acid. The sample was swollen as it absorbed sufficient divinyl benzene in to it. This facilitates the sample to be softened and a paste like material was obtained. This material can easily be shaped and moulded by using mould of different dimensions. The paste was kept in a small mould (10 cm × 2 cm). The mould was heated for 4 h at 60˚C and was cured to get cross linked composite. The dynamic mechanical thermal analysis was conducted using rectangular test specimens having a dimension of 35 mm × 5 mm × 2 mm under 3 point flexural mode using a TA Instruments, USA. The ends of the specimens are freely supported and a load is applied at the middle point. A motor was attached to apply an oscillatory deformation to the specimen. Maximum strain amplitude was set at 0.2%. The specimen was heated at the rate of 3˚C/min under nitrogen atmosphere. The experiment was conducted at three different frequencies 0.1 Hz, 1 Hz, 10 Hz in the temperature range of 30˚C to 100˚C. The variation of storage modulus and loss factor were recorded with variation in temperature and frequency.
3. Results and Discussion
3.1. Variation of Storage Modulus with Frequency, Fiber Loading and Fiber Treatment
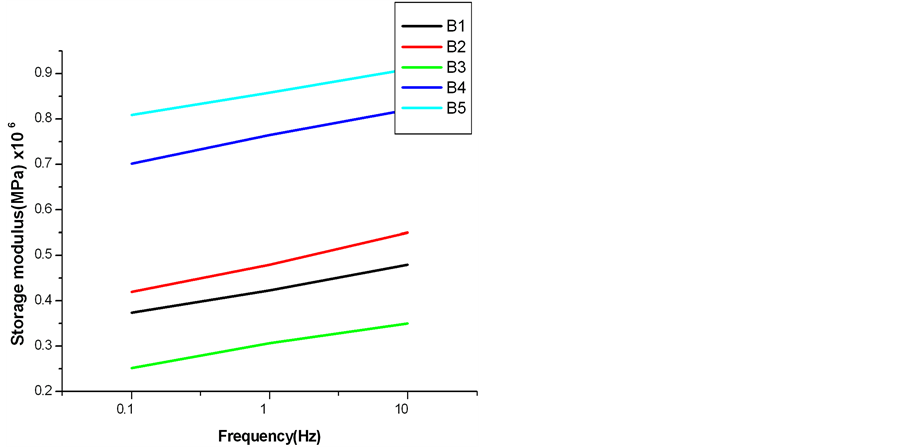
The values of storage modulus of all the composites and matrix at three measured frequency are given in Table 1. The storage modulus of RF matrix (sample B3) is found to be 0.252 MPa, 0.307 MPa and 0.35 MPa at 0.1 Hz, 1 Hz and 10 Hz respectively. It can be seen that with increase in frequency, the magnitude of storage modulus increases. This trend is observed for all the composites and also for the matrix. Under cyclic loading when the frequency of the applied stress is increased the time interval is very less and the molecules may not get time to undergo permanent deformation. Therefore the materials probably exhibit more elastic behaviour at higher frequency. The more the elastic nature the more will be the storage modulus of the materials. They behave more like a solid at high frequencies.
Figure 1 shows the variation of storage modulus of all the composites and matrix with frequency at different fiber loadings.
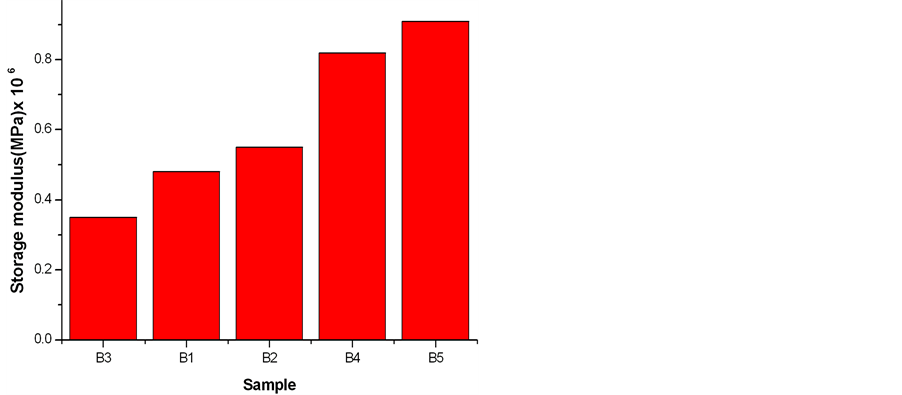
As observed from Table 1 and Figure 1 the values of storage modulus for RF matrix (sample B3) was found to be 0.307 MPa at 1 Hz. When the matrix was incorporated with untreated LC fiber in the wt ratio 1:1 the storage modulus increases to 0.423 MPa in sample B1. With further increase in wt of untreated LC fiber in the matrix storage modulus is increased to 0.48 MPa in sample B2. When the rigid LC fibers are incorporated with the matrix, it increases the stiffness of the composites. With fiber loading the stiffness increases leading to increase in modulus. The storage modulus of all the composites are enhanced compared to the pure matrix (sample B3). But the storage modulus of untreated LC fiber composites (sample B1 and sample B2) are less compared to the treated LC fiber composites (sample B4 and sample B5). The storage modulus is maximum for sample B5 at all frequencies where the composites are formed with treated fiber: matrix ratio 1:5. This suggests that when the treated LC fibers are incorporated in composites, the composites exhibit more elastic nature. The variation of storage modulus with fiber loading can be understood from Figure 2.
When the LC fibers are treated with alkali, globular protrusions present on the surface of fiber are removed which leads to the formation of large number of voids. These voids promote better mechanical anchorage between treated LC fiber and matrix. Due to improved interfacial adhesion between treated LC fiber and matrix
Table 1. Values of storage modulus at different frequencies at 26˚C.
Figure 1. Variation of storage modulus with frequency of all the samples.
Figure 2. Variation of storage modulus of all the samples with fiber loading and fiber treatment.
the storage modulus is enhanced for sample B4 and sample B5. However the interfacial adhesion is poor for sample B1 and sample B2 and thus the modulus is very low.
3.2. Variation of Storage Modulus with Temperature
The variation of storage modulus with temperature at different frequencies for the sample B2 is given in Figure 3.
As observed from Figure 3 the values of storage modulus at all the three frequencies decrease with increase in temperature. This trend is also observed for all other samples. With rise of temperature the mobility of molecule increases and the elastic behaviour tends to decrease and there is a transition from glassy to rubbery stage. This transition is known as glass transition. The variation of storage modulus with frequency is observed at low temperatures only. But beyond glass transition variation of modulus is not observed with frequency. At a temperature of around 45˚C storage modulus remains constant independent of temperature and frequency.
3.3. Variation of Loss Factor (tanδ) with Temperature, Frequency, Fiber Loading and Fiber Treatment
The tanδ curves of matrix and other composites are shown in Figure 4. As observed from Figure 4 the value of tanδ for all the samples increase initially with temperature, attains a maxima between 30˚C and 40˚C beyond which it decreases. The peak of the tan δ curve is known as glass transition temperature, where there is transition from glassy state to rubbery state. Beyond this transition temperature the composite loses its elastic nature and behaves more like a viscous material. The glass transition temperatures are found to vary with fiber treatment and fiber loading.
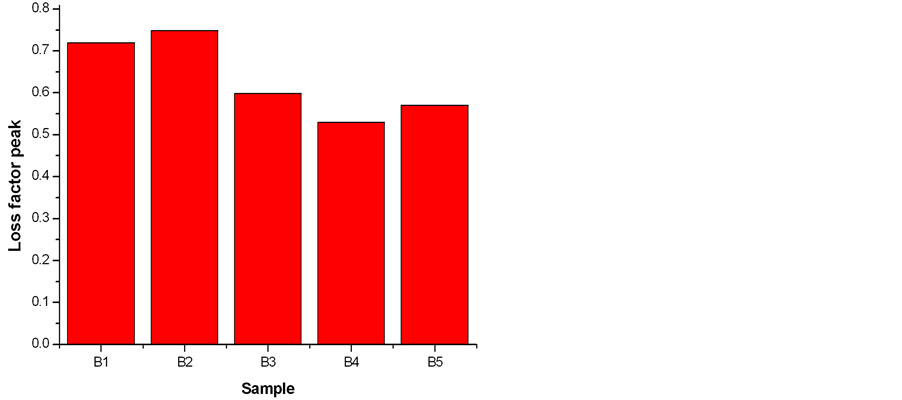
The variation of tanδ peak with fiber loading is given in Figure 5.
As observed from Figure 5 the peak of tanδ curve for untreated LC fiber composites (in sample B1 and B2) are more compared to the matrix (sample B3). Incorporation of untreated LC fibers in the matrix increases the

Figure 3. Variation of storage modulus of sample B2 with temperature at different frequencies.
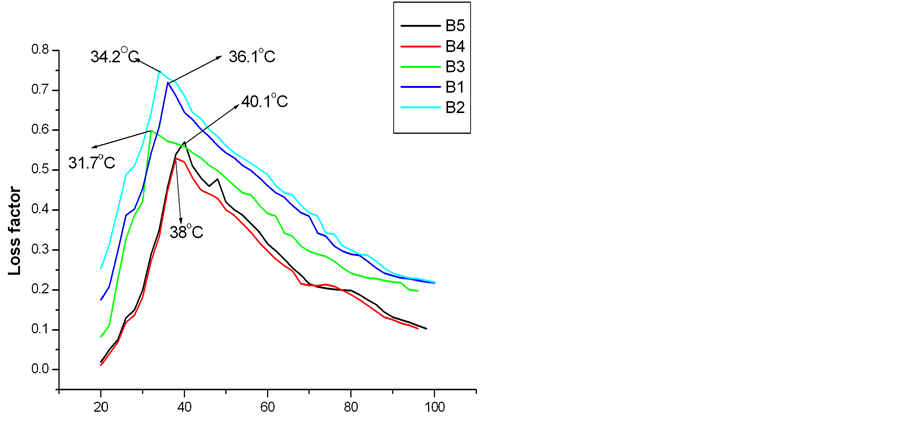
Figure 4. Variation of tanδ with temperature for at various fiber loading.
heat build up in the composites. That gives higher damping and more heat dissipation when untreated LC fiber is incorporated. However, the tanδ peak values are less for the treated LC fiber composites in sample B4 and sample B5 compared to the matrix. The results indicate that the poorer the interfacial bonding between the LC fiber and matrix the higher will be the damping at the interfaces. There is weak interfacial adhesion in untreated LC fiber composites (samples B1 and sample B2). But when the treated LC fibers are used in the composites there is considerable enhancement of bonding between fiber and matrix. Due to strong hydrogen bonding between LC fiber and matrix damping becomes less at the interface. Therefore, the fiber treatment is responsible for decreasing the damping at the interface as well as increasing the mechanical properties of the composites.
The values of glass transition temperatures of all the samples are given in Table 2.
The glass transition temperature is found to be minimum for matrix (sample B3) at 31.7˚C. With the addition of untreated LC fiber in the matrix, the glass transition temperature increases to 34.2˚C in sample B2 and 36.1˚C in sample B1. When the treated LC fibers are reinforced into the matrix, the transition temperature further increases to 38˚C in sample B4 and 40.1˚C in sample B5. The value of glass transition temperature is an indication of molecular interaction between LC fiber and matrix. When fiber is loaded into the matrix, molecules are immobilized at the interface due to the presence of fiber which decreases the mobility of polymer molecules and glass transition temperature shifts towards higher value. More will be the fiber-matrix interaction less will be the mobility of polymer molecules and more will be the glass transition temperature. The results show that glass transition temperature is maximum for treated LC fiber composites (sample B5) due to strong adhesion between treated LC fiber and matrix.
4. Conclusions
Storage modulus and mechanical loss factor of treated LC fiber composites, untreated LC fiber composites and
Figure 5. Variation of tanδ peak with fiber loading in all samples.
Table 2. Glass transition temperature of all the samples.
pure matrix are studied in all the samples. Storage modulus of all the samples increases with increase in frequency but loss factor of all the samples decreases with frequency. Storage modulus of the composites increases with increase in fiber loading. Storage modulus of treated LC fiber composites are more compared to untreated LC fiber composites.
The more the bonding between LC fiber and matrix, the less loss factor or damping at the interface of the composites will be. Composites having high mechanical properties are found to experience less damping at the interface. The sample B5 and sample B4 (treated LC fiber composites) show the highest mechanical strength as well as lowest damping.
The glass transition temperature indicates molecular interaction between fiber and matrix. It shifts towards high temperature with increase in fiber loading. The shifting of glass transition temperature is maximum for treated fiber composites (sample B5) due to high interfacial bonding between fiber and matrix. Similar investigations have been reported by Smita Mohanty et al. in 2004 [3] for sisal fiber reinforced polypropylene composites. The values of storage modulus of the composites increased with fiber loading and fiber treatment. The storage modulus of the sisal/polypropylene composites increased with temperature whereas the loss modulus decreased with temperature. These findings are in good agreement with our results. Further investigations are required for proper use of these composites in materials which are subjected to cyclic loading like tires, dampers and springs etc. [4] .
References
- Panico, R., Powell, W.H. and Richer, J.-C. (1994) A Guide to IUPAC Nomenclature of Organic Compounds. Blackwell Science, Oxford.
- Pothen, L.A. and Thomas, S. (2003) Polarity Parameters and Dynamic Mechanical Behavior of Chemically Modified Banana Fiber Reinforced Polymer Composites. Composites Science and Technology, 63, 1231-1240. http://dx.doi.org/10.1016/S0266-3538(03)00092-7
- Mohanty, S., Verma, S.K., Nayak, S.K. and Tripathy, S.S. (2004) Influence of Fiber Treatment on the Performance of Sisal Polypropylene Composites. Journal of Applied Polymer Science, 94, 1336-1345. http://dx.doi.org/10.1002/app.21161
- Geethamma, V.G., Kalaprasad, G., Gabriel, G. and Thomas, S. (2005) Dynamic Mechanical Behavior of Short Coir Fiber Reinforced Natural Rubber Composites. Composites Part A: Applied Science and Manufacturing, 36, 1499-1506.
- Jacob, M., Francis, B., Thomas, S. and Varughese, K.T. (2006) Dynamical Mechanical Analysis of Sisal/Oil Palm Hybrid Fiber-Reinforced Natural Rubber Composites. Polymer Composites, 27, 671-680. http://dx.doi.org/10.1002/pc.20250
- Tajvidi, M., Folk, R.H. and Hermanson, J. (2006) Effect of Natural Fibers on Thermal and Mechanical Properties of Natural Fiber Polypropylene Composites Studied by Dynamic Mechanical Analysis. Journal of Applied Polymer Science, 101, 4349-4371.
- Li, Z.G., Zhou, X.D. and Pei, C.H. (2011) Effect of Sisal Fiber Surface Treatment on Properties of Sisal Fiber Reinforced Polylactide Composites. International Journal of Polymer Science, 2011, Article ID: 803428.
NOTES
*Corresponding author.