Journal of Power and Energy Engineering
Vol.03 No.08(2015), Article ID:58695,18 pages
10.4236/jpee.2015.38005
PI and RST Control Design and Comparison for Matrix Converters Using Venturini Modulation Strategy
Bekhada Hamane1, Mamadou Lamine Doumbia1, Hicham Chaoui2, Mohamed Bouhamida3, Ahmed Chériti1, Mustapha Benghanem3
1Department of Electrical and Computer Engineering, UQTR, Trois-Rivières, Canada
2Center for Energy Systems Research, Department of Electrical and Computer Engineering, Tennessee Technological University, Cookeville, USA
3Department of Electrical Engineering, University Mohamed Boudiaf, Oran, Algeria
Email: bekhada.hamane@uqtr.ca, mamadou.doumbia@uqtr.ca, hchaoui@tntech.edu, m_bouhamida@yahoo.com, ahmed.cheriti@uqtr.ca, mbenghanem69@yahoo.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 July 2015; accepted 7 August 2015; published 10 August 2015
ABSTRACT
This paper presents a thorough design and comparative study of two popular control techniques, i.e., classical Proportional Integral (PI) and RST, for Matrix Converters (MCs) in terms of tracking the reference and robustness. The output signal of MCs is directly affected by unbalanced grid voltage. Some research works have attempted to overcome this problem with PI control. However, this technique is known to offer lower performance when it is used in complex and nonlinear systems. On the other hand, RST control offers better performance, even in case of highly nonlinear systems. Therefore, the RST can achieve better performance to overcome the limitation of PI control of nonlinear systems. In this paper, a RST control method is proposed as output current controller to improve the performance of the MC powered by unbalanced grid voltage. The overall operating principle, Venturini modulation strategy of MC, PI control and characteristics of RST are presented.
Keywords:
Matrix Converter, Unbalanced Grid, Venturini Modulation Strategy, PI Control, RST Control

1. Introduction
Recent advances in power electronics have enabled the emergence of Matrix Converter (MC) for direct AC/AC conversion [1] . Interest in this converter topology was rather academic with efforts provided in many research laboratories [1] . MC uses bidirectional current and voltage power switches that connect converter input and output phases [2] . The direct conversion is performed without intermediate DC link circuit for energy storage [2] [3] . MC was introduced firstly in 1976. To prevent the spread of current harmonics caused by the MC to the supply network, an input LC filter is used. It provides a very low impedance path and absorbs current harmonics [1] [2] . Venturini and Alesina proposed a generalized high-frequency switching strategy in 1980 [3] . The objective of this control strategy is to achieve an ideal electronic transformer capable of varying the voltage, current, frequency and power factor [4] . Another method, known as the direct transfer function approach, proposes the multiplication of the input voltages vectors by the modulation matrix M to obtain a vector of output voltages which correspond to a point of synthesis [4] . However, the simultaneous commutation of controlled bidirectional switches used in MC is very difficult to achieve without generating over current or overvoltage spikes which can destroy the power semiconductors [3] . Also, the load side of the MC is directly affected by the distorted and/or unbalanced input voltages due to the lack of DC intermediate circuit in the MC. The performance of the MC deteriorates, when it is exposed to the harmonic and non-sinusoidal currents and some papers have presented mitigation methods [3] [5] . Conventional PI controller works well only if the mathematical model of the system could be computed. However, it is difficult to implement the conventional PI controller for variable as well as complex systems [5] [6] . So, RST Controller is investigated. This regulator, whose synthesis is purely algebraic, is a sophisticated algorithm based on pole placement method which exploits many numerical resources [7] [8] . The method used to determine the gains of the PI controller is the compensation method of poles, we note here that the interest of the compensation of the poles occurs only if the system parameters are accurately identified as gains 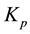 and
and 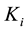 are based on these same parameters. If the actual parameters are different from those used in the synthesis, the compensation is ineffective. In the literature, control law design approaches can be divided into two categories. The first category consists of a nonlinear systems linearization around an operating point of the states. In this case, classical linear control laws are applied for the approximated system. These methods are popular in the industry and are mainly used for their simplicity. However, the control system’s performance and stability are not guaranteed for the overall system. The second category deals with nonlinear controllers design based on nonlinear systems dynamics. In this category, the characteristics of nonlinear systems are preserved. However, the design approach difficulties arise with the complexity of the nonlinear systems dynamics. Furthermore, these approaches assume a precise mathematical system model and are able to cope with nonlinearities to a certain degree. But, their performance also degrades in the presence of varying operating conditions, and higher uncertainties and disturbances. Therefore, this paper aims to compare the most popular techniques in the industry with similar design complexity. This work presents a modeling, theoretical analysis and an in-depth comparison of both the classical PI and RST Controller for MCs. Results show the superiority of the RST strategy with faster dynamic response and better robustness. To show the effectiveness of the control methods, the performance of the system is analyzed and compared in various operating conditions.
are based on these same parameters. If the actual parameters are different from those used in the synthesis, the compensation is ineffective. In the literature, control law design approaches can be divided into two categories. The first category consists of a nonlinear systems linearization around an operating point of the states. In this case, classical linear control laws are applied for the approximated system. These methods are popular in the industry and are mainly used for their simplicity. However, the control system’s performance and stability are not guaranteed for the overall system. The second category deals with nonlinear controllers design based on nonlinear systems dynamics. In this category, the characteristics of nonlinear systems are preserved. However, the design approach difficulties arise with the complexity of the nonlinear systems dynamics. Furthermore, these approaches assume a precise mathematical system model and are able to cope with nonlinearities to a certain degree. But, their performance also degrades in the presence of varying operating conditions, and higher uncertainties and disturbances. Therefore, this paper aims to compare the most popular techniques in the industry with similar design complexity. This work presents a modeling, theoretical analysis and an in-depth comparison of both the classical PI and RST Controller for MCs. Results show the superiority of the RST strategy with faster dynamic response and better robustness. To show the effectiveness of the control methods, the performance of the system is analyzed and compared in various operating conditions.
2. Mathematical Model of Matrix Converter
This part consists of a brief description and modeling of each element of the matrix converter. We start with modeling the MC, then the input filter and it ends with the load RL. Ideal bidirectional switches are represented by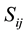 , where
, where 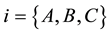 and
and 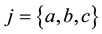 represent respectively the index of input and output voltage [1] [9] [11] :
represent respectively the index of input and output voltage [1] [9] [11] :
 (1)
(1)
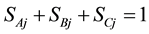 (2)
(2)
The basic diagram of a MC is represented in Figure 1, which the clipping circuit is used to protect the converter against surges that could come from a sudden disconnection of the load [1] .
With these restrictions, a 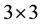 matrix converter has 27 possible switching states [1] . Let
matrix converter has 27 possible switching states [1] . Let  be the duty cycle of switch
be the duty cycle of switch , defined as [1] [10] [11] :
, defined as [1] [10] [11] :
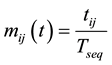 (3)
(3)
where, 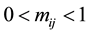 ,
,  and
and 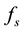 is the switching frequency.
is the switching frequency.
The transfer matrix of the converter is defined by [1] [3] [10] [11] :
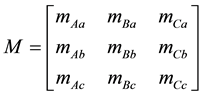 (4)
(4)
Figure 2 shows an example of the duration of conduction of the switches during a switching sequence 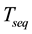 of the MC [1] [12] .
of the MC [1] [12] .
Figure 1. Basic circuit of a Matrix Converter.
Figure 2. Example of the operation timing of switches during a switching period.
2.1. Modeling of the Matrix Converter
The input voltage and current of the matrix converter are given by [1] [10] [11] [13] :


Assuming the relationship between the output and the input signal of the matrix converter [1] [10] [11] [14] :

The matrix converter will be designed and controlled to provide desired output voltage and output current [1] [10] [11] [13] :


The neutral to phase output voltages 


The input current 





2.2. Modeling of the Input Filter
The LC input filter [15] (represented as shown in Figure 3) is a series resonant circuit tuned to the frequency of harmonics and connected in shunt. It provides a very low impedance path and absorbs harmonic currents [1] [3] [14] . At the fundamental frequency, the filter acts as a reactive power compensator [1] [3] . The LC input filter may be modeled with the equivalent circuit [15] . From the Kirchhoff’s laws, node equations and Laplace transformation.
The filter output voltage and input current are obtained as Equation (12) and Equation (13) [1] [10] [12] .


2.3. Modeling of the Load RL
Generally, the neutral at the load (n) is isolated from that of the source (N) as shown in Figure 1. Therefore, the objective is calculating the load current, it is necessary to know the potential at the output of the MC corresponding to the neutral of the load. In this case, we have [1] [16] :

The potential difference between the two neutral is given by [1] [16] :

As the transfer function of the load current is given by [1] [16] :

3. Venturini Modulation Strategy of Matrix Converter
This method can produce the sinusoidal input current with unity power factor independently of load [4] [9] . The principle is to synthesize the desired three-phase output voltage from the input during each defined switching period. The initial equations of Venturini method are obtained as the product the ratio
Figure 3. Input filter scheme.

According to the optimal amplitude in expression of Venturini, the modulation function is [1] [11] [14] [17] :

The 

Therefore, only six duty cycles are sufficient to calculate the gate signals of the power switches [10] [11] [13] .

The carrier signal is expressed by [10] [11] [13] :

4. Control Design
This section deals with the design and synthesis of the PI and RST controllers. Both controllers are designed to achieve current reference tracking with constant and varying current reference signals. This also has to be achieved under both balanced and unbalanced grid voltage conditions.
4.1. PI Controller Design
Current measurements of the load RL using a PI controller is illustrated by Figure 5.
Figure 4. Obtaining logical instructions X and Y.
Figure 5. PI Controller for matrix converter.
The transfer function of the system is:

The values of A and B are:

The transfer function of the open-loop including the regulator is:

To cancel the pole, a zero was added at the same location as the pole [18] . Equation (24) gives a pole value:

The transfer function of the open-loop becomes:

The transfer function of the closed loop is expressed by:

Which:

For a response time



4.2. RST Controller Design
The closed-loop system of the RST controller for MC is given by the following block diagram in Figure 6.
The goal of this section to determinate the RST controller’s current. This type of controller is a structure with two freedom degrees and compared to a one degree of freedom structure, it has the main advantage that it allows the designer to specify performances independently with reference trajectory tracking (reference variation) and with regulation [7] [17] . It is based on the pole placement theory [8] , which consists in specifying an arbitrary stability polynomial 



With:

For our model, we obtain [17] :

The terms A and B are expressed by Equation (22). According to the robust pole placement strategy [8] , the polynomial D is written as [17] :

To accelerate the system, the following conditions were adopted:

With 


By identifying Equation (31) and Equation (34), coefficients of polynomial D were found and are linked to the coefficients of R and S by the Sylvester Matrix [7] [17] . Thus, the parameters of the RST controller can be determined as follows:
Figure 6. RST Controller for matrix converter.

The reference current is calculated as shown in Figure 7 [13] [18] .
The measured load’s current and the reference load’s current are given by Equation (36) [13] [18] :

5. Simulations Results
The PI and RST are used to control a matrix converter and a set of simulation runs is performed using SimPowerSystems toolbox of Matlab/Simulink software. The input filter parameters are calculated as given in [14] . Bidirectional switches MOSFET are considered ideal and ode23tb simulation solver was used. The MC system’s parameters are listed in Table 1.
Figure 7. Load reference current.
Table 1. System Parameters.
5.1. Balanced Grid Case with PI Controller
Figure 8 shows the balanced grid voltage.
・ Constant reference current
Figure 9 shows the output voltage and linear load current using PI controller for balanced grid voltage with constant current reference. Figure 10 presents load current and variation of the ratio
・ Time-varying reference current
Figure 12 shows the output voltage and linear load current using PI controller for balanced grid voltage with stepped changing reference current. Figure 13 presents load current and variation of the ratio
Figure 8. Balanced grid voltage.
Figure 9. Output voltage and load current (PI, balanced grid and with constant
Figure 10. Load current and variation of the q (PI, balanced grid and with constant
Figure 11. Harmonics spectrum of load current (PI, balanced grid and with constant
Figure 12. Output voltage and load current (PI, balanced grid and with stepped changing
Figure 13. Load current and variation of the q (PI, balanced grid and with stepped changing
Figure 14. Harmonics spectrum of load current (PI, balanced grid an with stepped changing
5.2. Balanced Grid Case with RST Controller
・ Constant reference current
Figure 15 shows the output voltage and linear load current using RST controller for balanced grid voltage with constant current reference. Figure 16 presents load current and variation of the ratio
・ Time-varying reference current
Figure 18 shows the output voltage and linear load current using RST controller for balanced grid voltage with stepped changing reference current. Figure 19 presents load current and variation of the ratio
Figure 15. Output voltage and load current (RST, balanced grid and with constant
Figure 16. Load current and variation of the q (RST, balanced grid and with constant
Figure 17. Harmonics spectrum of load current (RST, balanced grid and with constant
Figure 18. Output voltage and load current (RST, balanced grid and with stepped changing
Figure 19. Load current and variation of the q (RST, balanced grid and with stepped changing
Figure 20. Harmonics spectrum of load current (RST, balanced grid an with stepped changing
5.3. Unbalanced Grid Case with PI Controller
In this case, the amplitude of the input voltage of phase b is reduced to 20% relative to the phases a and c (Figure 21).
・ Constant reference current
Figure 22 shows the output voltage and linear load current using PI controller for unbalanced grid voltage with constant current reference. Figure 23 presents load current and variation of the ratio
・ Time-varying reference current
Figure 25 shows the output voltage and linear load current using PI controller for unbalanced grid voltage with stepped changing reference current. Figure 26 presents load current and variation of the ratio
Figure 21. Unbalanced grid voltage.
Figure 22. Output voltage and load current (PI, unbalanced grid and with constant
Figure 23. Load current and variation of the q (PI, unbalanced grid and with constant
Figure 24. Harmonics spectrum of load current (PI, unbalanced grid and with constant
Figure 25. Output voltage and load current (PI, unbalanced grid and with stepped changing
Figure 26. Load current and variation of the q (PI, unbalanced grid and with stepped changing
Figure 27. Harmonics spectrum of load current (PI, unbalanced grid an with stepped changing
5.4. Unbalanced Grid Case with RST Controller
・ Constant reference current
Figure 28 shows the output voltage and linear load current using RST controller for unbalanced grid voltage with constant current reference. Figure 29 presents load current and variation of the ratio
・ Time-varying reference current
Figure 31 shows the output voltage and linear load current using RST controller for unbalanced grid voltage with stepped changing reference current. Figure 32 presents load current and variation of the ratio
Figure 28. Output voltage and load current (RST, unbalanced grid and with constant
Figure 29. Load current and variation of the q (RST, unbalanced grid and with constant
Figure 30. Harmonics spectrum of load current (RST, unbalanced grid and with constant
5.5. Discussion the Results of Simulations
In Figure 9 and Figure 15, the voltage at the output of the matrix converter is formed by a succession of pulse widths conversely proportional to the frequency of the reference voltage

Figure 31. Output voltage and load current (RST, unbalanced grid and with stepped changing
Figure 32. Load current and variation of the q (RST, unbalanced grid and with stepped changing
Figure 33. Harmonics spectrum of load current (RST, unbalanced grid an with stepped changing
The THD increases for the unbalanced grid unlike in the balanced case (Figure 11 and Figure 17). However, the output currents are almost balanced, but are distorted. With the RST strategy, the signal quality of load current is much better than PI. Indeed, the THD is improved by 10.82% in the case of balanced grid, while this improvement is around 7.70% in the case of unbalanced grid Constant reference current

Table 2 and Table 3 show the values of THD for balanced and unbalanced cases presented above.
Table 2. THD of load current with balanced grid.
Table 3. THD of load current with unbalanced grid.
Table 4. SSE with balanced grid.
Table 5. SSE with unbalanced grid.
Table 4 and Table 5 show the Sum Squared Error (SSE).
In terms of the response of the system and the static error, the PI controller gives little better results than RST controller as it can be seen the Table 4 and Table 5.
6. Conclusion
In this paper, a thorough theoretical modeling, analysis and comparison are presented for PI and RST control of MCs. A comprehensive control compensation method is used to find the PI gains. Moreover, the use of the pole placement technique is also shown to determine the RST’s polynomial coefficients. Results for a balanced grid show lower load current THD as opposed to the unbalanced grid case, which is expected. However, RST control shows better performance. Nonlinear controllers tend to outperform these techniques at the expense of added complexity and computation. However, it is noteworthy that compared controllers are known for similar design complexity, which has been driving their use in the industry.
Cite this paper
BekhadaHamane,Mamadou LamineDoumbia,HichamChaoui,MohamedBouhamida,AhmedChériti,MustaphaBenghanem, (2015) PI and RST Control Design and Comparison for Matrix Converters Using Venturini Modulation Strategy. Journal of Power and Energy Engineering,03,36-54. doi: 10.4236/jpee.2015.38005
References
- 1. Dendouga, A. (2010) Contrôle des puissances active et réactive de la machine asynchrone à double alimentation (DFIM). PhD Thesis, University of Batna, Batna.
- 2. Luis, F.P.A. (2011) Maximum Power Point Tracker of Wind Energy Generation Systems using Matrix Converters. Master’s Thesis, Technical University of Lisbon, Lisbon.
- 3. Hulusi, K., Ramazan, A., Hüseyin, D., et al. (2008) A Novel Compensation Method Based on Fuzzy Logic Control for Matrix Converter under Distorted Input Voltage Conditions. Proceedings of the 2008 International Conference on Electrical Machines, Vilamoura, 6-9 September 2008, 1-5.
- 4. Venturini, M., Alesina, A., et al. (1980) The Generalised Transformer: A New Bidirectional Sinusoidal Waveform Frequency Converter with Continuously Adjustable Input Power Factor. Proceedings of the Power Electronics Specialists Conference (PESC’ 80), Atlanta, 16-20 June 1980, 242-252.
- 5. Filho, M.E.O., Filho, E.R., Quindere, K.E.B., Gazoli, J.R., et al. (2006) A Simple Current Control for Matrix Con-verter. Proceedings of the International Symposium on Industrial Electronics, Montreal, 9-13 July 2006, 2090-2094.
- 6. Ram, G., Lincoln, S.A., et al. (2012) Fuzzy Adaptive PI Controller for Single Input Single Output Non-Linear System. ARPN Journal of Engineering and Applied, Sciences, 7, 1273-1280.
- 7. Hachicha, F., Krichen, L., et al. (2011) Performance Analysis of a Wind Energy Conversion System Based on a Doubly-Fed Induction Generator. Proceedings of the 8th International Multi-Conference on Systems, Signals & Devices, Sousse, 22-25 March 2011, 1-6.
- 8. Bouhamida, M., Denai, M.A., et al. (2005) Robust Stabilizer of Electric Power Generator Using H∞ with Placement Constraints. Journal of Electrical Engineering, 56, 176-182.
- 9. Oubelli, A.L. (2011) Mise En æuvre d’un modèle générique du convertisseur matriciel dans les environnements EMTP-RV et MATLAB-SIMULINK. Master’s thesis, Ecole Polytechnique de Montréal, Montréal.
- 10. Hamane, B., Doumbia, M.L., Cheriti, A., Belmokhtar, K., et al. (2014) Comparative Analysis of PI and Fuzzy Logic Controllers for Matrix Converter. Proceedings of the 9th International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, 25-27 March 2014, 25-27.
- 11. Hamane, B., Doumbia, M.L., Cheriti, A., Belmokhtar, K., et al. (2013) Modeling and Control of a Matrix Converter Using Fuzzy Supervisory Controller. Proceedings of the 3rd International Conference on Systems and Control (ICSC), Algiers, 29-31 October 2013, 433-438.
- 12. Afonso, L.P. (2011) Maximum Power Point Tracker of Wind Energy Generation Systems Using Matrix Converters. Master’s Thesis, Higher Technical Institue of Technical University of Lisbon, Lisbon.
- 13. Boukadoum, A., Bahi, T., Oudina, S., Souf, Y., Lekhchine, A.S., et al. (2012) Fuzzy Control Adaptive of a Matrix Converter for Harmonic Compensation Caused by Nonlinear Loads. Energy Procedia, 18, 715-723.
- 14. Ghedamsi, K. (2008) Contribution à la modélisation et la commande d’un convertisseur direct de fréquence Application à la conduite de la machine asynchrone. PhD Thesis, National Polytechnic School of Process Control Laboratory, El-Harrach.
- 15. Dendouga, A., Abdessemed, R., Essounbouli, N., Megherbi, A.C., et al. (2013) Robustness Evaluation of Vector Control of Induction Motor fed by SVM Matrix Converter. 3rd International Conference on Systems and Control (ICSC), Algiers, 165-170.
- 16. Rodriguez, S.E., Blaabjerk, F., et al. (1985) Modelling, Analysis and Simulation of Matrix Converters. Applications, IA-21, 1337-1342.
- 17. Belabbes, A., Hamane, B., Bouhamida, M., Draou, A., Benghanem, M., et al. (2012) Power Control of a Wind Energy Conversion System based on a Doubly Fed Induction Generator using RST and Sliding Mode Controllers. Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’12), Santiago de Compostella, 28-30 March 2012.
http://www.icrepq.com/icrepq%2712/298-belabbes.pdf - 18. Mai, T.D., Mai, B.L., Pham, D.T., Nguyen, H.P., et al. (2007) Control of Doubly-Fed Induction Generators Using Dspace R&D Controller Board—An Application of Rapid Control Coordinated with Matlab/Simulink. Proceedings of the International Symposium on Electrical & Electronics Engineering, 3, 302-307.



































