Journal of Power and Energy Engineering
Vol.03 No.05(2015), Article ID:56235,14 pages
10.4236/jpee.2015.35005
Performance Analysis of Unbalance Radial Feeder with Time Varying Composite Load
Jagdish Prasad Sharma1, H. Ravishankar Kamath2
1Mewar University, Chittorgarh, India
2Malwa Institute of Technology, Indore, India
Email: jpsharma.cseb@gmail.com, Rskamath272@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 April 2015; accepted 7 May 2015; published 12 May 2015
ABSTRACT
The focus of this paper is to present performance indices for unbalance radial feeder having different characteristic and composition of time varying static ZIP load models. These provide a framework for benchmarking of distribution automation projects. 15 minutes characteristics time interval for load flow and load modeling are considered to meet smart grid implementation criterion. A forward-backward sweep method is employed for load flow solution. Developed performance indices were illustrated on modified IEEE 37 node test feeder. Performance indices are useful for analysis, operational, planning and integration of stochastic renewable sources.
Keywords:
Performance Indices, Radial Distribution Feeder, Voltage Sensitive Load, Modeling, Unbalance Load Flow, Stochastic Load Modeling

1. Introduction
In a deregulated environment for making the correct investment decisions, a power flow computation is very important for operational, design and planning point of view. For adequate analysis and maximum benefit from the emerging smart grid technologies, an efficient load flow solution and detailed modeling of distribution feeder required. An efficient power flow analysis power-flow solution must be able to model the special features of distribution systems in sufficient detail. The distribution system has following distinctive properties:
High resistance to reactance ratio,
Radial structure,
Extremely large number of branches/nodes, and
Unbalanced and multi-phase (usually three phases).
More recent methods are based on the concept of doing backward and/or forward sweep, and take into account the radial structure of distribution systems. G. W. Chang, S. Y. Chu, and H. L. Wang [1] have proposed a load flow solution for radial distribution network by using improved backward/ forward sweep algorithm. D. Shirmohammadi [2] stated that the ladder network method could be performed in two directions: a backward sweep for current summation and then a forward sweep for voltage calculation. Das, Nagi, Kothari [3] fully exploited radial characteristics of balanced feeder along with a unique numbering scheme for lateral, node and branch. The work mentioned in [3] is extended, with emphasis on the modelling of unbalanced loads in [4] . Backward and/or forward sweep methods usually result in faster convergence and have a reduced number of equations, in comparison with conventional methods [2] - [5] . Network topology is an important aspect in distribution network studies. In this paper, the numbering method reported in [6] [7] is utilized. Radial distribution feeder generally has three categories of consumers: residential, commercial and industrial respectively. Each category is comprised of statics ZIP load models in proportions. Field measurements based daily load curves for residential, commercial and industrial consumers are defined statistically in [8] . Impact of composite load modeling was investigated for state estimation of a distribution network [9] . Pei-Hwa Huang, Ta-Hsiu Tseng [10] investigated the effect of load characteristics of system voltage stability analysis with the static ZIP load models. Static ZIP load models have three different characteristics i.e. constant power, constant current and constant impedance. In a practical system, these different load models vary throughout the day. Thus load characteristics and composition varies with time throughout the day. So it became inevitable to have a more detailed customer load modeling with a daily time varying load profile at each node to analyze stochastic behaviors of feeder. The objective of this paper is to develop an efficient unbalance load flow algorithm based on backward and forward sweep method using two port parameters, which takes into account the detailed and extensive modeling necessary for a smart grid environment. The developed algorithm is tested on modified IEEE 37 node test feeder. This paper is incorporated following features:
Consideration of voltage-dependency characteristics and composition in load modeling provides the actual behavior of the loads in response to voltage variations.
15 minutes characteristics time interval load curve for the industrial, commercial and residential loads are developed to meet smart meter measurement criterion.
Unbalance charactertics are accounted in load and feeder component modeling.
This algorithm gives node voltages as well as their angle and can handle the effect of charging capacitances of the network. So this method can be used for reactive power compensation studies.
Developed performance indices computed for whole day. These performance indices are substation reserve capacity, voltage unbalance factor, feeder power loss to load ratio, branch loading, voltage deviation, and power factor.
2. Modeling of Composite Time Varying Load
If detailed load data are not available to a utility, at least a rough approximation is believed as a better option rather than none, since it brings attention to the critical characteristics of loads and their relative compositions, diversity, etc. Load modeling aims to characterize the form of daily use of electricity by various types of consumers connected to each load point. For this one has to specify type of consumer, correspondent load model and daily load curve. Aggregated load at each load point are a summation of consumption values of each type of consumer (residential, commercial, industrial, or other). This paper has considered that each load point has a mix of time varying load for industrial, residential and commercial consumers in a random proportion. Consumers are generally grouped into three major classes: residential, commercial and industrial. In this paper IEEE 37 node test feeder assumed to be supplying power to a delta connected load at each node having a mix of industrial, residential, and commercial type consumers.
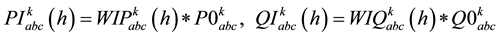 (1)
(1)
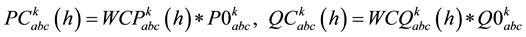 (2)
(2)
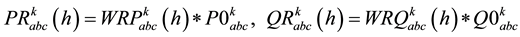 (3)
(3)
The spot load at each node k shared among industrial, residential and commercial consumers and participation of each category load is characterized by relevant factors. The specific value of aforesaid relevant factor is generated by normalization of normally distributed pseudorandom numbers at each 15 minutes characteristics time interval h such that following condition must be satisfied for all load buses.
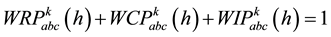 (4)
(4)
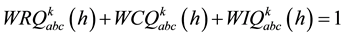 (5)
(5)
Critical load characteristics for each type of consumers may express by means of the sum of constant impedance (Z), constant current (I) and constant power (P) load models. In this paper voltage dependency of active and reactive power consumption are modelled by three components: constant impedance (Z), a constant current (I) and a constant power (P) injections. Each category consumers have consumer constant Impedance [Z], constant current [I], and constant power [P] components [12] . The participation of each category load is characterized following Equations.
 (6)
(6)
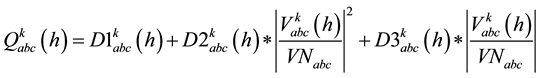 (7)
(7)
The calculation of load current is carried out as mentioned in W. H. Kersting [13] . The ZIP load composition for each load category is given in Table 1.
ZIP active and reactive load compositions for each node k at each 15 minutes characteristics time interval h are characterized by following relevant factors.
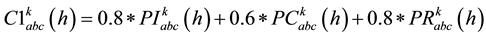 (8)
(8)
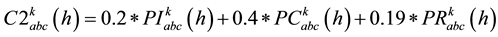 (9)
(9)
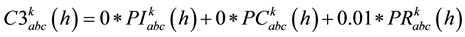 (10)
(10)
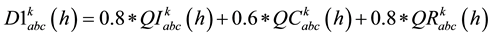 (11)
(11)
 (12)
(12)
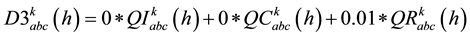 (13)
(13)
As measurements of individual consumers load are taken by electronic equipment that accumulates them in programmed intervals by the utilities (1, 5 or 15 min) and this accumulation is called average power (demand) for these intervals. In this paper, the load curves defined at intervals of 15 minutes were developed, resulting therefore in 96 intervals in daily curve. Modeling load patterns of residential, commercial and industrial customer are carried out by using daily load profiles reported in [11] . To incorporate the complexity of load, these load profiles are fitted in MATLAB 7th order polynomial Equation as shown on Figure 1.
Table 1. ZIP load composition for different load class.
3. Feeder Component Modeling
In this section all components of a power distribution system are modeled as two-port network elements. For accurate modeling, distribution system can be broken into “series” components and “shunt “components. Series component of feeder is shown in Figure 2.
Series components of a distribution system are line segments, switches, transformers and voltage regulators, while shunt components of comprise of spot loads, distributed loads and capacitor banks. Both series and shunt components are modeled using ABCD parameters [13] . The general Equations for each component connected between node-n (Input node) and node-m (output node) are given by
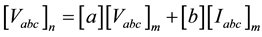 (14)
(14)
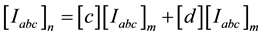 (15)
(15)



Figure 1. Typical daily load profile for consumers.
Figure 2. Feeder component connection.
Characterization of each component of feeder is fairly standardized for all components without having to actually check the type of the device.
3.1. Distribution Line
The feeder line modelling and the line parameters can be obtained by the method developed by Carson and Lewis [13] . In this paper 




3.2. Distribution Transformer
The impact of the numerous transformers in a distribution system is significant. Transformers affect system loss, zero sequence current, grounding method, and protection strategy. Distribution transformer model as shown in Figure 4 can be used for power flow, short circuit and contingency studies for large-scale unbalanced distribution system.
A three-phase transformer is presented by two blocks as shown in Figure 4. One block represents two port model and the other block models the core loss as a function of voltage on the secondary side of the transformer. Transformer core are assumed equivalent to Y connected constant power load. Single-phase transformer is represented by series leakage impedance and shunt core loss function [14] on the secondary terminal and core loss characteristic vary depending upon the quality of the transformer. Tests have indicated that real and reactive power core losses in per unit can be approximated as follows.
Figure 3. PI model of line.
Figure 4. Distribution transformer model.


where 
It must be noted that above coefficients are machine dependent constants. For this paper, core losses are represented by the functions and typical constants shown above. Per unit leakage admittance matrix are used for two port model [14] , but in this paper each two port model is represented in ABCD parameter as mentioned below.



where
Voltage regulator and shunt capacitor banks are commonly used in distribution systems to help in voltage regulation and to provide reactive power support. In this paper, the voltage regulator and capacitor are not modelled.
4. Proposed Load Flow Algorithm
4.1. Connectivity Matrix Developments
Connectivity matrix establishes a relationship between two buses connecting through a line segment. A simple distribution system as shown in Figure 5 is used to illustrate development of connectivity matrix as an example.

First Column of the connectivity matrix denotes number of an outgoing line segment from each sending bus. Second, fourth and sixth column of the connectivity matrix represent receiving end bus from each sending bus, while third, fifth and seventh column of the connectivity matrix represents line segment connect above to receive bus to each sending bus. If any connectivity failed to present, the corresponding element in above matrix will contain null-entries.
4.2. Three Phase Unbalance Load Flow
The forward/backward sweep (FBS) method is highly related to the physical models and includes following steps.
a) Initialization of Node Current: Firstly, all the buses are initialized to the voltage specified at the source bus of the network which is usually 1Ð00 p.u.
b) Backward sweep: This compute branch current from end nodes and update nodal currents and voltages from end node to the source node, passing through the series feeder components

c) Forward sweep: This compute node voltage from source nodes to end node and update nodal voltages from source node to end node, passing through the series feeder components.

Figure 5. Simple distribution system.
d) Compute Error: The difference between calculated and specified complex bus voltages for source node is referred as the error value in per unit.

e) Convergence Criterion: For load flow convergence, process adopted here is a distributed radial backward/forward sweep with convergence criterion as seen below.

If above the relationship does not satisfied them, change in apparent power at last nodes of main feeder, laterals and sub laterals are calculated using below Equations.

Update each last node k voltage using Equation (33) for the next iteration.

This Forward sweep (FS) and Backward sweeps (BS) process is continued till load flow convergence. The following constraints are considered in the formulation of the problem.
All service zones are connected and served by the feeder.
Radial network configuration must be maintained for distribution feeders.
4.3. Computational Steps for Proposed Algorithm
Propose algorithm is based on the forward-backward sweep method and implemented through the following steps.
Step 1: Read input data regarding the unbalanced radial distribution feeder and generate connectivity matrix
Step 2: Generate a daily load profile for various categories of consumers connected each node for each 15 mintues characteristics time interval.
Step 3: Normalization of randomly generated load relevant factor for various categories consumers at each node and decompose each load category connected to each node into three different load models for each 15 minutes characteristics time interval.
Step 4: Set characteristics time interval = 1 and tolerance.
Step 5: Initialize the variables and voltage at each node; correspondingly calculate total load current at each bus.
Step 6: Initialize iteration. Assign initial voltages = 1 PU for each bus.
Step 7: Compute backward sweep method and update/compute all bus currents from bus load from the last node to the first node), passing through the series feeder components
Step 8: Compute forward sweep method by assigning bus voltage = 1 pu for substation and update/compute all bus voltage from bus load from the first node to the last node.
Step 9: Compute error using Equation (31).
Step 10: Check convergence criterion for two consecutive iteration Equations (32). If criterion is not satisfied go to the next step, otherwise go to step 12.
Step 11: Update each last node voltage using Equations (33) and (34) and go to step 7.
Step 12: Compute all performance indices. Check whether the characteristics time interval is less than 96. If yes increase characteristics time interval by 1 and go to step 5, otherwise go to the next step.
Step 13: Store results.
5. Proposed Performance Indices
Development of indices is beneficial to evaluate feeder performance over an each 15 minute time interval. Formulation of performance indices is described below.
5.1. Apparent Power Unbalance Indice (APBI)
Apparent Power unbalance Indice [15] indicates the level of balance condition between three phases as follows.


5.2. Voltage Unbalance Factor (VUF)
Unbalanced three-phase loads or no uniformly spread single-phase loads, time-varying operations will lead to voltage variation and unbalance at three-phase equipment terminals. The effect of voltage unbalance is quite severe and voltage unbalance factor (VUF) [15] expressed as


5.3. Substation Reserve Capacity Indice (SRCI)
Measurement indice can be developed to assess the distribution feeder performance in terms of substation reserve capacity [16] . The apparent power flowing through the segment connecting from substation node (node 0) to the first node of the feeder (node 1) can be used for determining of loading level for the three-phase substation.

5.4. Feeder Loss-to-Load Ratio Indice (FLLRI)
Ratio of feeder losses to the total loads [16] being served by the feeder could be used as an indice to measure the performance of the feeder in terms of power losses.

5.5. Voltage Deviation Indice (VDI)
Voltage deviation Indice [17] is defined for the purpose of observing the effectiveness of the voltage correction in the system. Voltage deviation is the difference between the nominal voltage and the actual voltage. Minimizing the voltage deviation at every node of the system can make the voltage profile of the network better. A voltage deviation Indice (VDI) for each 15 minute interval is defined as normalized maximum voltage difference at node k.

5.6. Branch Current Loading Indice (BCLI)
This Indice [17] gives important information about level of current loading in branch regarding the maximum capacity of conductors. Phase branch current for each 15 minutes time interval are calculated proposed algorithm and in some branch of distribution calculated current may be greater than the current capacity. A closer value of theseIndice towards means reserve capacity for demand growth. The branch current loading Indice is calculated for the branch “m” as below.

5.7. Minimum Power Factor (MPF)
The power factor has been increasingly recognized as one of the principal measures of efficiency and improves the voltage profile. Residential, commercial loads have a low power factor and reactive power for these loads is delivered from the source. Industrial consumers are compelled to compensate the reactive power otherwise are penalized (power factor surcharge penalty).To minimize the negative effects of low power factor on feeder power distribution on the feeder lines, it is imperative to record what time of the day the node has lower power factor.

6. Simulation Results and Analysis
In order to illustrate the validity and effectiveness of the proposed method, modified IEEE 37 node test feeder [18] is used. For load flow base voltage and base MVA are chosen as 4.8 KV and 2.5 MVA respectively. Following modification has been applied to the original test network.
Twenty-four hourly random load scenarios at each node is a combination residential, commercial and industrial consumer having ZIP load models. Voltage regulator is also removed.
As mentioned in Figure 6 the maximum overloading of substation transformer is 7.884% at 48 characteristics time interval during midday. Substation transformer overloading raises between 35 to 71 characteristics time interval. This situation could be relived with solar PV penetration as during above period generation from PV resources is typically higher and may be greater than the load level.
Increased feeder loading also increases feeder loss as shown in Figure 7. It observed that maximum feeder loss to load ratio (FLLR) occurs at 51, 48 and 52 characteristics time interval for phase A, B and C respectively. It is also observed that phase C is heavily loaded as compared to both phases A and B. Peak load KVA for phase A, Phase B and Phase C appears at 48, 52 and 51 characteristics time interval respectively.
A general trend of deviation of voltage magnitude and voltage unbalance from their nominal values was observed along the feeders, especially with feeders supplying greater distances, loads, PV generation, and their unequal connection between phases. As mentioned in Figure 8 the voltage unbalance factor varies between 0.5485 and 0.8632.
From Figure 9, it is observed that apparent power unbalance varies between 189.8 and 293.5 KVA. Both maximum voltage unbalance factor and feeder unbalance apparent power occur at 51 characteristic time interval. This characteristics time interval has maximum FLLR for phase A also.
From Figure 10, it is observed that branch emanating from substation found a most critical branch for a whole day. Phase A is overloaded between 27 to 88 characteristics time interval, while phase C is overloaded between 30 to 82 characteristics time interval. Phase B has always had under load condition for a whole day.
From Figure 11, it is clear that power factor for phase B is very poor throughout a day and minimum power factor for phase A, phase-B and phase-C are 0.8943, 0.3856 and 0.7516 respectively. It is also observed that minimum power factor node for phase A and phase B are 738 and 724 for a whole day. Phase C of node 799 have weakest power factor and node 740 got second weakest node for same. Local reactive compensation devices can be installed for power factor improvement.
From Figure 12, it was observed that the voltages had been violated mostly in phases A. The voltages were rather low. Node 740 for phase A have a maximum voltage deviation Indice for a whole day. The losses on the phase A were also high as mentioned in Figure 9. Phase A voltage deviation indice exceed its value from unity during 34 to 71 characteristics time interval. During same period substation transformer overloaded. From Figure 6, Figure 7 and Figure 10, it is concluded that feeder performance can be improved by adding additional energy source.
Figure 6. Substation reserve capacity indice for feeder.
Figure 7. Feeder loss to load ratio for feeder.
Figure 8. Daily voltage unbalance factor of feeder.
Figure 9. Daily apparent powers unbalance indice of feeder.
Figure 10. Daily branch loading indice of feeder.
Figure 11. Daily minimum power factor of feeder.
Figure 12. Daily maximum voltage deviation of feeder.
7. Conclusion
An efficient load flow algorithm for the unbalance radial distribution feeder with voltage sensitive and time varying load is developed. Proposed algorithm is tested on highly unbalance IEEE 37 node test feeder and found good convergence property makes it’s suitability for large-scale distribution systems. Characteristics and composition of residential, industrial and commercial consumers are accounted through voltage dependent and time varying load models, which plays an important role in the planning and operation of distribution networks. Low
computational time, storage of all data in vector form and connectivity matrixes has great potential to be used in on-line operation. Performance indices and 15 minutes characteristics time interval load modeling finds suitability for benchmarking of distribution automation projects. The proposed algorithm can also be an efficient tool for evaluating the impact of integration of stochastic renewable energy resources and loads with large variance in the smart distribution networks.
References
- Chang, G.W., Chu, S.Y. and Wang, H.L. (2007) An Improved Backward/Forward Sweep Load Flow Algorithm for Radial Distribution Systems. IEEE Transactions on Power Systems, 22, 882-884. http://dx.doi.org/10.1109/TPWRS.2007.894848
- Shirmohammadi, D. (1988) A Compensation-Based Power Flow Method for Weakly Meshed Distribution and Transmission Networks. IEEE Transactions on Power Systems, 3, 753-762. http://dx.doi.org/10.1109/59.192932
- Das, D., Nagi, H.S. and Kothari, D.P. (1994) Novel Method for Serving Radial Distribution Networks. IEE Proceedings of Generation, Transmission and Distribution, 141, 291-299. http://dx.doi.org/10.1049/ip-gtd:19949966
- Cheng, C.S. and Shirmohammadi, D. (1995) A Three-Phase Power Flow Method for Real-Time Distribution System Analysis. IEEE Transactions on Power Systems, 10, 671-679. http://dx.doi.org/10.1109/59.387902
- Wang, Z., Chen, F. and Li, J. (2004) Implementing Transformer Nodal Admittance Matrices into Backward/Forward Sweep-Based Power Flow Analysis for Unbalanced Radial Distribution Systems. IEEE Transactions on Power Systems, 19, 1831-1836. http://dx.doi.org/10.1109/TPWRS.2004.835659
- Jamali, S. and Shateri, H. (2005) Optimal Siting of Recloser and Sectionalizers to Reduce Non-Distributed Energy. Proceedings of the IEEE/PES T&D Conference & Exhibition, Dalian, 14-18 August 2005.
- Kalantar, M., Jamali, S. and Shateri, H. (2009) Load Flow Method for Distribution Networks with Dispersed Generation Units. The 44th International Universities Power Engineering Conference, UPEC2009, Glasgow, 1-4 September 2009, 1-5.
- Jardini, J.A., Tahan, C.M.V., Gouvea, M.R., Ahn, S.U. and Figueiredo, F.M. (2000) Daily Load Profiles for Residential, Commercial and Industrial Low Voltage Consumers. IEEE Transactions on Power Delivery, 15, 375-380.
- Karimi, M., Mokhlis, H., Bakar, A.H.A., Shahriari, A., Faradonbeh, M.A. and Rosli, H.M. (2012) Impact of Load Modeling in Distribution State Estimation. IEEE International Power Engineering and Optimization Conference (PEOCO2012), Melaka, 6-7 June 2012. http://dx.doi.org/10.1109/PEOCO.2012.6230837
- Huang, P.-H. and Tseng, T.-H. (2012) Analysis for Effects of Load Characteristics on Power System Voltage Stability. AASRI Conference on Power and Energy Systems, Volume 2, 229-234.
- Integration of Storage in Electrical Distribution Systems and Its Impact on the Depth of Penetration of DG. http://canmetenergy-canmetenergie.nrcanrncan.gc.ca/fichier.php/codectec/En/2009-174/2009-174.pdf
- Lee Willis, H. (2004) Power Distribution Planning Reference Book. CRC Press, Boca Raton.
- Kersting, W.H. (2007) Distribution System Modeling and Analysis. CRC Press, Boca Raton. http://dx.doi.org/10.1201/9781420009255.ch21
- Chen, T.-H., Chen, M.-S., Inoue, T., Kotas, P. and Chebli, E.A. (1991) Three-Phase Cogeneraor and Transformer Models for Distribution System Analysis. IEEE Transactions on Power Delivery, 6, 1671-1681. http://dx.doi.org/10.1109/61.97706
- Moussa, A., El-Gammal, M., Abdallah, E.N. and Attia, A.I. (2004) A Genetic Based Algorithm for Loss Reduction in Distribution Systems. Alexandria Engineering Journal, 43, 729-735.
- Alam, M.J.E., Muttaqi, K.M., Sutanto, D., Elder, L. and Baitch, A. (2012) Performance Analysis of Distribution Networks under High Penetration of Solar PV. http://www.cigre.org
- Ochoa, L.F., Padilha-Feltrin, A. and Harrison, G.P. (2006) Evaluating Distributed Generation Impacts with a Multiobjective Indice. IEEE Transactions on Power Delivery, 21, 1452-1458.
- IEEE PES Distribution System Analysis Subcommittee. Distribution Test Feeders. http://ewh.ieee.org/soc/pes/dsacom/testfeeder
Appendix: Nomenclature
















